Unrelated helpers will not fully compensate for costs imposed on breeders when they pay to stay

Abstract

Unrelated subordinates may invest in costly help to avoid being evicted from groups (the ‘pay-to-stay’ hypothesis). However, the effectiveness of eviction to enforce help should depend on its being applied accurately and on the costs it imposes on both dominants and subordinates. The relative cost of being evicted is a function of the population frequency of eviction when population growth is limited by density-dependent factors. We describe a stage-structured pay-to-stay model incorporating density-dependent population growth, costly eviction and occasional errors. Breeders demand some amount of help and evict subordinates that do not provide it. Helpers decide on the amount of help they will provide. The threat of eviction alone is sufficient to enforce helping. However, helping will not be favoured if helpers do not impose costs on breeders. The amount of help provided is less than the cost that subordinates impose upon breeders, when any help is provided. Thus, the net fitness effect of a helper under pay-to-stay alone is negative, even if it is investing in cooperative behaviour. Constraints on dispersal have no effect on the amount of help, although they may influence the tolerance threshold of breeders and group stability, depending on the mechanism of density dependence.

1. Introduction

In cooperatively breeding societies, some individuals join or remain in a group and help raise the offspring of others (Brown 1978; Taborsky 1994; Solomon & French 1997; Cockburn 1998). For these individuals, helping and delaying reproduction entail costs (Taborsky 1984; Grantner & Taborsky 1998; Heinsohn & Legge 1999), while substantial benefits may accrue to other group members. This apparent altruism has long interested evolutionary biologists. In many cases, indirect (kin-selected) benefits can be invoked to explain cooperative breeding (Emlen 1995; Russell & Hatchwell 2001; Griffin & West 2003). However, some cooperatively breeding societies are composed of non-relatives (e.g. Stacey & Koenig 1990), and, even in kin associations, among-kin competition may reduce the indirect benefits of helping relatives (West et al. 2002). Thus, there has been increasing interest in understanding how direct benefits influence cooperative breeding.

The decision to become a ‘helper’ in a cooperatively breeding society actually involves several related decisions (Cahan et al. 2002), which include: (i) to stay in the group rather than attempt to disperse and breed independently; (ii) to help raise offspring of others; and, in some cases, (iii) to inhibit one’s own reproduction. Several general hypotheses have been proposed to explain the decision to delay dispersal, all of which emphasize the relative benefits of staying in the group versus dispersing (Emlen 1995).

If a subordinate chooses to stay in a group, it may help. Help, in this paper, is defined as a behaviour that is costly to the helper but that benefits breeders in some way. It is important to note that this definition applies to the behaviour, not the overall effect of the presence of the helper on the fitness of either the helper or breeder. Helpers may also be costly to breeders, because they compete with breeders for food or other resources (Gaston 1978), parasitize reproduction (Dierkes et al. 1999; Skubic et al. 2004), attract predators (Strickland & Waite 2001) or cause damage to eggs or offspring (von Siemens 1990; Legge 2000). Thus, the fitness of breeders could still be lower with helpers than without, despite the positive fitness effects of helping.

Subordinates that help may gain indirect benefits if they are helping to produce related young (Hamilton 1964; Griffin & West 2003) or direct benefits if some of the young in the group are their own. Another potential benefit of helping is that, by doing so, a helper may increase the likelihood of being accepted in a group (the ‘pay-to-stay’ hypothesis; Gaston 1978; Kokko et al. 2002). If subordinates are costly to breeders the latter may attempt to evict or otherwise inflict costs on them, particularly if they do not contribute to raising offspring (Clutton-Brock & Parker 1995). Help may therefore be ‘rent’ to avoid eviction (or other forms of punishment; Taborsky 1985; Bergmüller & Taborsky 2004. Similarly, refraining from reproduction could also be a form of payment to avoid expulsion or harassment (Johnstone & Cant 1999; Johnstone 2000; Hamilton 2004).

Although the pay-to-stay hypothesis is a compelling explanation for help in both kin and non-kin associations, and has been the focus of several empirical studies (Mulder & Langmore 1993; Balshine-Earn et al. 1998; Mitchell 2003; Bergmüller & Taborsky 2004), theoreticians have paid relatively little attention to this topic. A notable exception is Kokko et al. (2002), who recognized the parallels of pay-to-stay with reproductive skew theory (Vehrencamp 1983; Keller & Reeve 1994; Johnstone 2000), and modelled help as a transaction between dominants demanding help and subordinates offering help. Their model predicted that help as a form of payment (as opposed to either no help or help provided for other reasons, such as indirect benefits) is likely when: (i) subordinates are costly to dominants; (ii) survival of breeders and helpers is high; (iii) relatedness between breeders and helpers is low or, if relatedness is high, the costs of helping are also high; and (iv) there are tight to moderate ecological constraints (e.g. low survival from expulsion or dispersal through finding a new breeding territory or limited breeding vacancies).

The effectiveness of eviction as a form of punishment depends on the cost of eviction to both the dominant evictor and the subordinate evictee, and on the ability of dominants to accurately assess transgression. In the model of Kokko et al. (2002), eviction was cost free for dominants and, because dominants and subordinates had perfect information, was always applied correctly. However, eviction is unlikely to be cost free for either party. The energy expenditures associated with agonistic behaviour can be very high for dominant members of breeding groups (see, for example, Taborsky & Grantner 1998). Furthermore, subordinates may resist attempts to expel them from the group (see, for example, Clutton-Brock et al. 1998). Eviction is also unlikely to always be correctly applied, particularly when a dominant must decide whether a helper is meeting some threshold level of help.

The costs of eviction to subordinates depend on any direct costs imposed during eviction (e.g. injury), and on the likelihood of surviving from eviction through finding a breeding opportunity (ecological constraints). Although there is abundant empirical evidence that ecological constraints influence differences in dispersal tendency within populations (Stacey & Koenig 1990; Komdeur 1993; Komdeur et al. 1995; Hatchwell & Komdeur 2000), recent theoretical work suggests that these may not necessarily influence among-population differences in dispersal when population growth is limited by density-dependent factors (Pen & Weissing 2000; Kokko & Ekman 2002). This is because the incentives to disperse and competition for dispersal opportunities are functionally related. When constraints are low, the pay-off to dispersing is high. However, if most individuals disperse, there will be increasing competition for vacant positions, reducing the relative pay-off to dispersing. Because the pay-to-stay hypothesis emphasizes the benefits of being accepted in the group versus being expelled, the same logic should also be relevant. The cost of eviction to a subordinate should depend on the prevalence of eviction in the population.

In this paper, we present a model of the pay-to-stay hypothesis, which we use to predict the evolutionarily stable helping effort of unrelated helpers and whether any help at all is expected. We examine the influences of ecological constraints and benefits of philopatry (such as survival within groups and the likelihood of inheriting a territory) on these. Our model retains the basic structure of transactional models (Johnstone 2000). We assume that all subordinates initially live in groups, and do not leave on their own, that is, they remain in the group until either evicted or the breeder dies, in which case the subordinate either inherits the territory or is forced to disperse. Dominants demand some amount of help and will evict subordinates that do not provide this amount. Our model differs from previous transactional models of helping because eviction is costly to dominants, whereas the cost to a subordinate that is evicted depends upon the frequency of eviction. Our model also incorporates imperfect information about the expected amount of help demanded and provided, and errors in the imposition of punishment. Because of these, subordinates cannot be certain when they will be evicted.

2. The Model

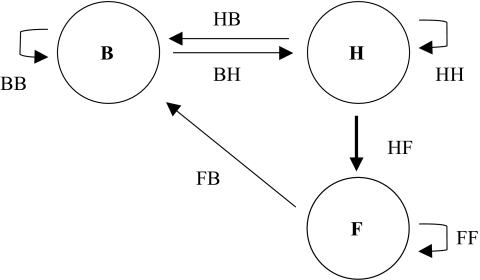
We use a transition matrix approach to find the fitness effects of a change in help or tolerance threshold (Taylor & Frank 1996). We divide the population into three states: breeders, helpers and floaters (figure 1). Breeders are mature individuals that produce offspring. Helpers remain on a breeder’s territory and do not reproduce. Despite our use of the term ‘helpers’, they may not necessarily offer any help. The third possible state is that of the floater. Floaters are former helpers that have been evicted. These search for opportunities to breed.

Figure 1.

Life cycle of a cooperative breeder. Breeders (B) produce young that disperse to another territory and become helpers (H). Helpers may be evicted from the group, and become floaters (F).

We assume helpers and breeders are unrelated and that helpers do not contribute offspring to the brood. A previous model of the pay-to-stay hypothesis (Kokko et al. 2002) has found that other voluntary reasons for helping (such as indirect benefits) restrict rent paying to a very limited range of conditions. In this model, we wished to explore whether the threat of eviction alone could explain helping behaviour, and set up the model so that voluntary helping would be unlikely. We acknowledge that in most groups the threat of eviction will interact with other direct and indirect benefits of helping. Elsewhere, we will consider these interactions.

Groups in which helpers gain no indirect benefit from helping may arise in at least three ways. First, subordinates may remain on their natal territory, but, by the time that juveniles are of the size or age that they could begin to help, breeders have died and been replaced by non-relatives. In the African cichlid Neolamprologus pulcher, breeders and helpers may be unrelated because of such an exchange of breeders (Taborsky & Limberger 1981). Second, juveniles may disperse from their natal territory but settle as subordinates on another breeder’s territory. This pattern of dispersal is known from several birds and fishes (birds: pied kingfisher (Reyer 1990); dunnock (Davies 1992); speckled warbler (Gardner et al. 2003); fishes: anemonefish (Fricke & Holzberg 1974); damselfish (Sweatman 1983); Symphodus ocellatus (Taborsky et al. 1987); Pelvicachromis pulcher (Martin & Taborsky 1997); N. pulcher (Bergmüller & Taborsky 2004; Stiver et al. 2004)), although, in some cases, these juveniles apparently do not help (see, for example, Gardner et al. 2003; Mitchell 2003). Finally, even if breeders are relatives of helpers, within-group competition may, in theory, counteract all or most relatedness benefits leading to groups with effectively unrelated breeders and helpers (West et al. 2002).

Breeders survive each time step with probability S_b. If they survive, they produce F(h,p) young, who initially begin as helpers and remain so unless they inherit the territory, leave after the death of the breeder or are evicted. We assume that the breeder produces all of the offspring in the group; that is, there is no reproductive parasitism by helpers. The presence of helpers influences the number of offspring produced by the breeder. Helpers are costly to breeders (see § 1), costing the equivalent of c offspring per helper (there are, on average, n_h helpers per breeder). However, that cost can be partly or completely overcome by helping, h, so that the net effect of the presence of a helper on offspring production is h–c. Also, helpers that must be evicted impose another cost, equivalent to s offspring per eviction. Whether helpers are evicted (D(h,p)) depends upon both the help offered by helpers and the tolerance threshold, p.

$$F(h,p)=F_{\text{o}}+n_{\mathrm{h}}(h-c-sD(h,p)).$$ (2.1)

We assume that the probability of being evicted (D(h,p)) is a step function in the absence of errors by the breeder, so that individuals that help, h, less than some threshold demanded by the breeder, p, are evicted. However, breeders are likely to make errors, occasionally punishing helpful subordinates or tolerating lazy ones. To incorporate such errors, we use the following function to model the probability of being evicted, given p and h:

$$D(h,p)=\begin{array}{cc}\frac{1}{1+e^{-(p-h)/\delta }}& \text{if}p>0\\ 0& \text{if}p=0\end{array}.$$ (2.2a,b)

If p exactly equals h, breeders evict with a probability of 0.5. The likelihood of making errors is influenced by both the difference between the breeders’ demand and the help offered, and by δ(δ≥0). Errors are more likely when the difference between p and h is small. For a given difference, errors are more likely when δ is large.

If they are not evicted, ‘helpers’ continue as such, surviving with probability S_n if they do not help. We assume that helping is costly to helpers in terms of reduced survival, so that the survival rate of a helper that invests in help is S_h(h). We model this using the following function:

$$S_{\mathrm{h}}(h)=S_{\mathrm{n}}{e}^{-gh},$$ (2.3)

where g is a parameter that describes the effect of help on survival. If g is large, an increase in help greatly reduces the survival of a helper.

If they survive, helpers may inherit the territory after the death of the breeder, and begin to reproduce as breeders. However, the probability that they inherit the territory on which they helped is modified by a factor, β. For example, they may compete with neighbours or floaters to inherit the territory, or territories may be abandoned after the death of a breeder. For simplicity, we assume that if an individual does not inherit the territory after the death of the breeder, it becomes a floater. However, results are similar if they persist as helpers (I. M. Hamilton, unpublished modelling results).

If helpers are evicted, they become floaters. Helpers survive eviction and become floaters with probability, K. This value may reflect density-independent factors, such as injuries obtained during eviction, or density-dependent factors such as the availability of a safe habitat in which to float (such as an aggregation or a non-breeding territory). Floaters remain as floaters until they die (which they do with probability 1−S_f), or encounter a vacant breeding position (with probability, α).

The transitions between states are shown on figure 1. These can be arranged in a matrix, A (for an explanation of how A is derived from figure 1, see the appendix in Pen & Weissing (2000)):

$$\mathbf{A}=\left[\begin{array}{ccc}\mathrm{BB}& \mathrm{HB}& \mathrm{FB}\\ \mathrm{BH}& \mathrm{HH}& \mathrm{FH}\\ \mathrm{BF}& \mathrm{HF}& \mathrm{FF}\end{array}\right].$$ (2.4)

The transition matrices for helpers (A_h) and breeders (A_b) depend on the tactic used by helpers and breeders, respectively, and the expected levels of help and tolerance they may receive from others ($\overline{h}$, $\overline{p}$). When groups are composed of non-relatives, $\overline{h}$ and $\overline{p}$ equal the evolutionarily stable population levels of help, h*, and tolerance, p*, respectively. These matrices are as follows:

$$\begin{array}{cc}{\mathbf{A}}_{\mathrm{h}}=\hfill & \left[\begin{array}{ccc}{S}_{\mathrm{b}}\hfill & (1-S_{\mathrm{b}})S_{\mathrm{n}}\beta \hfill & \alpha S_{\mathrm{f}}\hfill \\ S_{\mathrm{b}}F(\overline{h},\overline{p})\hfill & S_{\mathrm{b}}{S}_{\mathrm{h}}(h)(1-D(h,\overline{p}))\hfill & 0\hfill \\ 0\hfill & S_{\mathrm{b}}{S}_{\mathrm{h}}(h)D(h,\overline{p})K\hfill & (1-\alpha )S_{\mathrm{f}}\hfill \\ \hfill & +(1-S_{\mathrm{b}})S_{\mathrm{n}}(1-\beta )K\hfill & \hfill \end{array}\right],\hfill \\ {\mathbf{A}}_{\mathrm{b}}=\hfill & \left[\begin{array}{ccc}{S}_{\mathrm{b}}\hfill & (1-S_{\mathrm{b}})S_{\mathrm{n}}\beta \hfill & \alpha S_{\mathrm{f}}\hfill \\ S_{\mathrm{b}}F(\overline{h},p)\hfill & S_{\mathrm{b}}{S}_{\mathrm{h}}(\overline{h})(1-D(\overline{h},\overline{p}))\hfill & 0\hfill \\ 0\hfill & S_{\mathrm{b}}{S}_{\mathrm{h}}(\overline{h})D(\overline{h},\overline{p})K\hfill & (1-\alpha )S_{\mathrm{f}}\hfill \\ \hfill & +(1-S_{\mathrm{b}})S_{\mathrm{n}}(1-\beta )K\hfill & \hfill \end{array}\right].\hfill \end{array}$$ (2.5a,b)

Assuming zero population growth, the average fitness of the population is simply:

$$\mathit{w}=\mathbf{v}\mathbf{A}\mathbf{u},$$ (2.6)

where v is the dominant left eigenvector of A, when the dominant eigenvalue, λ, which is the population growth rate, is 1. The vector v contains the relative reproductive values (v_i) of breeders, helpers and floaters. The vector u is the dominant right eigenvector of A and includes the relative frequencies (u_j) of breeders, helpers and floaters.

$$\mathbf{v}=\left[\begin{array}{ccc}{\mathit{v}}_b& {\mathit{v}}_h& {\mathit{v}}_f\end{array}\right],\mathbf{u}=\left[\begin{array}{c}{\mathit{u}}_{\mathit{b}}\\ {\mathit{u}}_{\mathrm{h}}\\ {\mathit{u}}_{\mathrm{f}}\end{array}\right]$$ (2.7)

We obtained reproductive values and class frequencies as described in the electronic Appendix.

By assuming that the population is stable, we must make an assumption about how density dependence works in this system. To do this, we assume that one parameter can be expressed as a combination of other parameters in the model. We assumed that either β, the probability of inheriting a territory, or K, the probability of surviving dispersal, was density dependent. This may be because of increased competition for inherited territories or for positions as floaters with other floaters or members of neighbouring groups when densities are high. Model results are similar if we assume density dependence acts through the probability of finding a new territory, α. To satisfy the assumption that the reproductive value of floaters is 1 when the population growth rate, λ, is 1, β must be equal to β* or K must be equal to K* (see Appendix A).

Assuming either β=β* or K=K*, the relative reproductive values of breeders, helpers and floaters reduce to:

$${\mathbf{v}}^{*}=\left[\begin{array}{ccc}{\mathit{v}}_{\mathrm{b}}& =& \frac{1-S_{\mathrm{f}}(1-\alpha )}{\alpha S_{\mathrm{f}}}\\ {\mathit{v}}_{\mathrm{h}}& =& \frac{(1-S_{\mathrm{b}})(1-S_{\mathrm{f}}(1-\alpha ))}{\alpha S_{\mathrm{f}}{S}_{\mathrm{b}}F(\overline{h},\overline{p})}\\ {\mathit{v}}_{\mathrm{f}}& =& 1\end{array}\right].$$ (2.8)

The equilibrium relative class frequencies, u_j, are found by substituting β=β* or K=K* into:

$$u^{*}=\left[\begin{array}{cc}{u}_{\text{b}}=& 1\\ u_{\text{h}}=& \frac{S_{\text{b}}{F}_{\text{o}}}{1-S_{\text{b}}\{S_{\text{h}}(\overline{h})[1-D(\overline{h},\overline{p})]-[h-c-sD(\overline{h},\overline{p})]\}}\\ u_f=& \frac{u_{\text{h}}{S}_{\text{h}}(\overline{h})K[S_{\text{b}}D(\overline{h},\overline{p})+(1-\beta )(1-S_{\text{b}})]}{(1-S_{\text{f}}[1-\alpha ])}\end{array}\right].$$ (2.9)

We use these vectors and the transition matrices A_h and A_b to examine the effects of a slight change in helping tendency on the fitness of a helper and a slight change in the tolerance threshold on the fitness of a breeder (Taylor & Frank 1996; Frank 1998). Because we assume that relatedness is 0, the effects of these changes are as follows:

$$\begin{array}{cc}\frac{\partial w(h,\overline{h},p,\overline{p})}{\partial h}=& {\mathbf{v}}^{*}\frac{\partial {\mathbf{A}}_{\mathbf{h}}}{\partial h}{\mathbf{u}}^{*}={\mathbf{v}}^{*}\underset{ij}{\overset{}{\Sigma }}\frac{\partial a_{ij}}{\partial h}{\mathbf{u}}^{*},\\ \frac{\partial w(h,\overline{h},p,\overline{p})}{\partial p}=& {\mathbf{v}}^{*}\frac{\partial {\mathbf{A}}_{\mathbf{b}}}{\partial p}{\mathbf{u}}^{*}={\mathbf{v}}^{*}\underset{ij}{\overset{}{\Sigma }}\frac{\partial a_{ij}}{\partial p}{\mathbf{u}}^{*},\end{array}$$ (2.10a,b)

where v* and u* are the vectors v and u at the population average values of h and p, and a_ij is the content of the ith row and jth column of A.

We solve for the values, p∘ and h∘, which are those values of p and h that satisfy the following conditions:

$$\frac{\partial \mathit{w}(h^{\circ },\overline{h^{\circ }},p^{\circ },\overline{p^{\circ }})}{\partial h}=0\text{condition}(1),$$

$$\frac{\partial \mathit{w}(h^{\circ },\overline{h^{\circ }},p^{\circ },\overline{p^{\circ }})}{\partial p}=0\text{condition}(2).$$

The evolutionarily stable strategy (ESS) is {p∘, h∘} when these are satisfied and the pay-off to an individual that uses p∘ and h∘ exceeds that of one that either does not help (h=0) or does not demand help (p=0). This leads to the following further conditions for {p∘, h∘} to be an ESS:

$$\mathit{w}(h^{\circ },\overline{h^{\circ }},p^{\circ },\overline{p^{\circ }})>\mathit{w}(0,\overline{h^{\circ }},p^{\circ },\overline{p^{\circ }})\text{condition}(3),$$

$$\mathit{w}(h^{\circ },\overline{h^{\circ }},p^{\circ },\overline{p^{\circ }})>\mathit{w}(h^{\circ },\overline{h^{\circ }},0,\overline{p^{\circ }})\text{condition}(4).$$

All values were confirmed by simulation, as described in Appendix A.

3. Results

3.1 No help without punishment

If p and $\overline{p}$ are set to 0, so that $\overline{p}$, then equation (2.10a) is as follows:

$$\frac{\partial \mathit{w}(h^{\circ },\overline{h^{\circ }},0,0)}{\partial h}=-\frac{(1-S_{\mathrm{b}})(1-(1-\alpha )S_{\mathrm{f}})S_{\mathrm{b}}{S}_{\mathrm{n}}g{\mathrm{e}}^{-gh}}{\alpha S_{\mathrm{f}}\left(1-S_{\mathrm{b}}{S}_{\mathrm{n}}{\mathrm{e}}^{-g\overline{h}}\right)}.$$ (3.1)

This is negative for all values of help, unless g, the survival cost of helping, is less than 0. In other words, if there is no threat of expulsion, subordinates will not help unless they gain a direct (survival) benefit from helping.

3.2 Help exceeds zero

The value of h∘, the equilibrium value of help (if there is to be any help at all in the system) that satisfies conditions 1 and 2, does not depend on the mechanism of density dependence. This value is:

$$h^{\circ }=\frac{g(c+s)-W(x)}{g},$$ (3.2a)

where W(x) is the Lambert W function (Corless et al. 1996):

$$W(x){\mathrm{e}}^{W(x)}=x,$$ (3.2b)

and

$$x=\frac{gs{\mathrm{e}}^{g(c+s)}}{S_{\mathrm{b}}{S}_{\mathrm{n}}}.$$ (3.2c)

The solution to equations (3.2) was evaluated by numerical approximation in MAPLE, v. 9.0 (Waterloo Maple Inc.) and confirmed by simulation (see Appendix A).

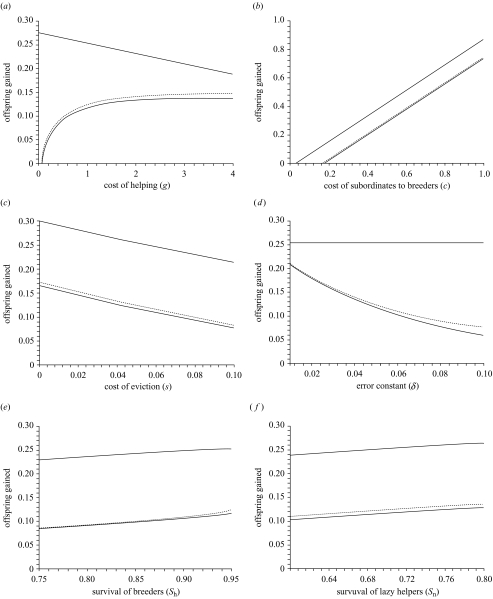
As shown in figures 2–4, of the parameters appearing in matrices A_h and A_b (equation (2.4)), h∘ is influenced only by the costs of helping, g, of eviction, s, the cost that helpers impose on breeders, c, and on the intrinsic survival of breeders and helpers (S_b and S_n, respectively). The expected level of help increases with increasing cost of helpers to breeders and increasing survival of either breeders or helpers. It decreases with increasing costs of expulsion or of help. Notably, this value is influenced neither by the likelihood of errors in eviction (a function of δ; figure 2d), nor by the level of ‘ecological constraints’ (i.e. S_f, K and α do not appear in equations (3.2); figures 3 and 4).

Figure 2.

Influences of model parameters on the evolutionarily stable amount of help offered by helpers (h*, thick solid line) and the tolerance threshold of breeders, below which they will evict helpers (p*, thin lines). Tolerance thresholds are shown for two values of brood sizes in the absence of help (solid line: F₀=1.0; dotted line: F₀=1.5). Help offered does not change with F₀. Density dependence acts through the probability of inheriting a territory. Parameters shown are: (a) g, the cost of helping on helper survival; (b) c, the reduction in brood size resulting from the presence of a subordinate; (c) s, the cost of eviction for breeders; (d) δ, a parameter that influences the likelihood of mistakenly evicting or tolerating a helper; (e) S_b, the survival rate of breeders; and (f) S_n, the survival rate of subordinates if they do not help. For all panels, parameters that are not varied are g=1, c=0.3, s=0.05, δ=0.05, S_b=0.95, S_n=0.7, S_f=0.1, α=0.3, K=0.4.

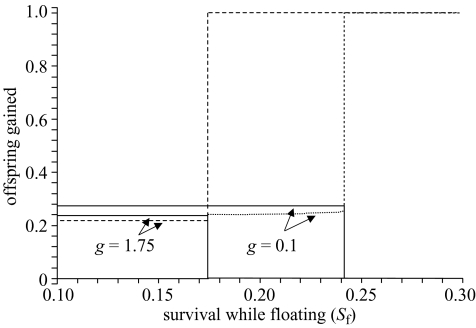
Figure 4.

Ecological constraints (in this example, S_f, the survival rate after eviction, but before finding a new territory) influence whether any help is offered, when density dependence acts through the probability of inheriting a territory. When survival rate is low (and ecological constraints are high), help is offered. When survival rate is high (and ecological constraints are low) no help is offered, and breeders’ demand for help (tolerance threshold) is very high. The lines represent two values of the survival cost of help, g, as noted on the figure. Solid lines represent the amount of help offered (h*), dotted lines are the tolerance threshold of breeders (p*). For the purposes of illustration, the maximum tolerance threshold is set to p=1.0. Parameters are c=0.3, s=0.05, δ=0.005, S_b=0.95, S_n=0.7, F₀=1, α=0.5, K=0.4.

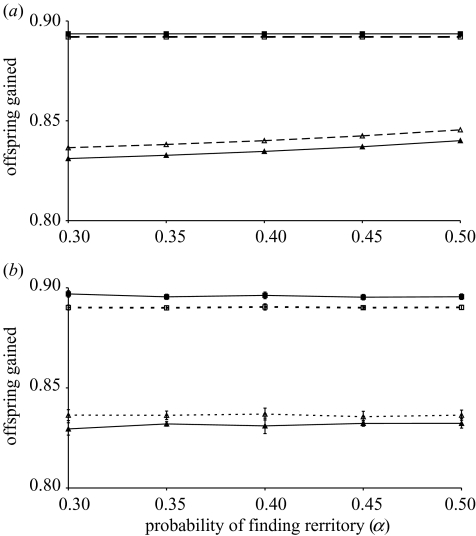
Figure 3.

Influences of ecological constraints on the evolutionarily stable amount of help offered by helpers (h*, squares) and the tolerance threshold of breeders, below which they will evict helpers (p*, triangles) when density dependence acts through: (a) the probability of inheriting a territory; or (b) the probability of surviving dispersal (eviction). Solid lines and symbols represent low helping costs, g=0.1. Dashed lines and open symbols represent higher helping costs, g=0.2. When the probability of finding a territory after eviction is low, ecological constraints can be considered to be high. Because values for (b) could not be found analytically, values presented are the ±s.d. for 15 simulations (see Appendix A). Ecological constraints do not influence the amount of help offered, and only slightly influence the tolerance threshold in (a) (and not at all in (b)). Fixed parameters differ from those used in figures 2 and 4 to illustrate that stable groups will form at high c, and they differ between (a) and (b) because differences in the mechanism of density dependence lead to different parameter values under which grouping is stable. In (a), c=0.9, s=0.01, δ=0.01, S_b=0.95, S_n=0.7, F₀=2, S_f=0.1, K=0.4. In (b), c=0.9, s=0.001, δ=0.01, S_b=0.99, S_n=0.9, F₀=1, S_f=0.1, β=0.7.

The equilibrium level of help will exceed the cost that helpers impose on breeders only when the following inequality is satisfied:

$$g<\frac{\ln (S_{\mathrm{b}}{S}_{\mathrm{n}})}{c}.$$ (3.3)

However, because S_b and S_n are proportions, ln(S_bS_n) is always negative. In other words, the amount of help received by a breeder cannot exceed the costs imposed upon it by subordinates that remain in the group unless g, the cost of helping to the helper, is negative. Thus, when punishment is only in the form of expulsion, and helping imposes a net reduction in helper survival, we predict that helping by non-relatives will not fully cover the costs imposed upon breeders by helpers (i.e. the net fitness effect of helpers on breeders will be negative). If g<0, helping in excess of c may be favoured. Survival of helpers must increase with helping effort for there to be a positive net fitness effect of helping for breeders at the ESS.

Although helping will only exceed c if inequality (3.3) is satisfied, helping will exactly equal these costs if there is no cost of expulsion to the breeder, i.e. if s=0. Although it seems unlikely that expulsion would be cost free for either party, it may be of very low cost to breeders, in which case h∘ would approach c.

The equilibrium tolerance threshold, p∘, depends on the form of density dependence. Because of the complexity of the analytical solution when density dependence acts through the probability of inheriting a territory, we do not present it here. Rather, we show the values of p∘ for various combinations of parameters in the model on figures 2 and 3.

The value of p∘ is always less than h∘ when {p∘,h∘} is the ESS (see below; figures 2 and 3). Thus, we expect that conflict within the group will be rare, and eviction will occur only when breeders make errors. The tolerance threshold is influenced by ecological constraints when density dependence acts through β (figures 3a and 4). When S_f, K or α increase (and, therefore, density-independent constraints on dispersal decrease), the value of p∘ increases slightly. Because h∘ does not change when constraints decrease, we expect more conflict within groups when this is so.

The likelihood of errors also influences the tolerance threshold. An increase in δ, and therefore in the likelihood of errors, leads to a decrease in the tolerance threshold (i.e. less help is required to be accepted). The tolerance threshold increases with increases in the cost of helpers to breeders, c, and the survival of breeders, S_b, or helpers, S_n, while it decreases with increasing cost of expulsion, s. The tolerance threshold generally increases with the cost of helping, g, although it may decline very slightly with increasing g when g is very high (e.g. when g approaches 4.0 in figure 2a).

When density dependence acts through the probability of surviving dispersal, there is no analytical solution for p∘. However, the solution could be found through simulation as described in Appendix A. Again, p∘ is less than h∘ when {p∘,h∘} is the ESS. The effects of model parameters on p∘ are identical to those in the previous case, except that ecological constraints (S_f and α) no longer influence the tolerance threshold, p∘ (figure 3b).

3.3 No help can invade help

There are two ways that the ESS value of help could be zero. The first of these is when the solution to equations (3.2), h∘=0 This is so, if helping is costly (g>0), when

$$S_{\mathrm{b}}{S}_{\mathrm{n}}⩽\frac{s}{c+s}.$$ (3.4)

This implies that if helpers are not costly to breeders (i.e. c=0), then help is never favoured. If c=0, the right-hand side of equation (3.4) is 1, and, because survival of helpers and breeders must be less than this, the pay-off to helping can never exceed that of not helping. Helping is also unlikely when the survival of either breeders or helpers, or both, is very low, or when the costs of expulsion are high in relation to the costs imposed upon breeders by the helper’s presence.

Alternatively, lack of helping could be favoured, even when h∘>0, if condition 3 is not satisfied, that is, $w(h^{\circ },{\overline{h}}^{\circ },p^{\circ },{\overline{p}}^{\circ })<w(0,{\overline{h}}^{\circ },p^{\circ },{\overline{p}}^{\circ })$). If density dependence acts through territory inheritance, this is so when

$$F_0>\left[-(g+S_{\mathrm{b}}W(x))(1-S_{\mathrm{f}}(1-\alpha ))\left[gs\left(\phi (1+{\mathrm{e}}^{-p^{\circ }/\delta })\right)-S_{\mathrm{n}}{S}_{\mathrm{b}}W(x)\left({\mathrm{e}}^{-p^{\circ }/\delta }(\phi +1)\right)\right]\right]\times {\left[K{S}_{\mathrm{f}}{S}_{\mathrm{b}}g\alpha \left[gs(1+{\mathrm{e}}^{-p^{\circ }/\delta })-S_{\mathrm{n}}{S}_{\mathrm{b}}W(x)(\phi +1)\right]\right]}^{-1},$$ (3.5a)

and

$$\phi ={\mathrm{e}}^{(g(c+s)-p^{\circ }g-W(x))/(g\delta )}.$$ (3.5b)

If equations (3.5) are not satisfied, some amount of help, described by h∘, is expected. Inequality (3.5) is less likely to be satisfied, when S_f, S_b, δ, α, c, g and K are low. Thus, whether there is any help at all in the system (i.e. inequality (3.5) is not satisfied) is more likely when ecological constraints are high, the costs of help (to helpers) are low, probability of inheriting the territory is high, errors are unlikely to occur or the costs imposed on breeders are low. When this is so, the ESS level of help is again described by equations (3.2).

When density dependence acts through dispersal, the solution to condition (3) can be found analytically, but is too complex to be informative. However, whether helping is an ESS is influenced only by the intrinsic survival rate of helpers, S_n, the cost of helping, g, and the probability of inheriting a territory. Under this condition, helping is more likely to be an ESS when the cost of helping is low, the intrinsic survival of helpers is low and the probability of inheriting a territory is high. It is not influenced, however, by ecological constraints or by the likelihood of erroneous eviction.

Whenever lack of helping is the ESS, inequality (3.4) also describes whether punishment will be favoured. In other words, if inequality (3.4) is not satisfied, and helpers do not help, then the eviction threshold should be the maximum possible in the system (i.e. helpers should be evicted). If inequality (3.4) is satisfied, these ‘lazy’ helpers will be tolerated (i.e. p∘=0).

4. Discussion

Our model demonstrates that the pay-to-stay framework is a plausible explanation for helping in non-kin associations. When there is no threat of expulsion, subordinates should never help unless they gain a direct benefit from doing so (equation (3.1)). However, when dominants may expel subordinates, the model predicts that some help may be provided (equation (3.2)). The amount of help predicted in our model is low compared with the costs that helpers impose on breeders; therefore, we conclude that pay-to-stay, while potentially an important mechanism to enforce help, is, by itself, unlikely to explain observed levels of help in many systems.

Our model predicts that the stable level of help provided by unrelated subordinates should be lower than the costs they impose when help is payment to avoid eviction. This is in contrast to the predictions of the model of Kokko et al. (2002), in which the only helpers that would be tolerated despite imposing a net fitness cost on breeders were relatives. In our model, help will only compensate for costs imposed if (i) eviction is not costly to dominants or (ii) subordinates gain a direct survival benefit from helping.

Why are the net fitness effects of helpers always negative? In our model, helpers cannot be sure if they will be evicted. Because of this uncertainty, helpers and breeders must base their decisions to help and evict on the population-average helping and tolerance levels (Kokko 2003). In a hypothetical population in which helpers helped in excess of c, eviction would be costly to breeders (because of direct costs and the loss of help). Each breeder could do better by lowering its tolerance threshold to slightly less than that of the population average, so that it would expel helpers less often but receive just as much help. Similarly, if helpers were costly, then there would be a benefit to raising the tolerance threshold. Thus, the level of help demanded converges on c, modified by the likelihood of erroneously evicting helpers. The direct costs of eviction further lower the demand for help and, hence, the ESS level of help, as tolerating mildly costly helpers may yield a higher pay-off than evicting them.

In our model, offspring production should decline with increasing group size despite active help. However, unless the cost of expelling subordinates is large, the expected decline in breeder fitness should be slight. Several correlational and experimental studies of helping have found that the presence of helpers has little effect on the reproductive success of breeders (see, for example, Magrath & Yezerinac 1997; Legge 2000; Eguchi et al. 2002) or even a negative effect (Legge 2000). In these systems, auxiliaries at the nest were observed to invest substantially in helping. This is consistent with our prediction, although it is not known whether the pay-to-stay framework applies in these cases.

In many other studies, positive effects of helping have been found (Taborsky 1984; Stacey & Koenig 1990; Mumme 1992; Boland et al. 1997; Griffin & West 2003). This implies that other mechanisms, instead of or in addition to the threat of eviction, probably enforce helping in many natural groups. Most cooperative breeding groups are composed of relatives (Solomon & French 1997; Cockburn 1998), so indirect benefits may explain elevated levels of help in these cases. However, if the threat of eviction remains pertinent, higher levels of relatedness may not necessarily lead to greater help. Breeders may be less willing to evict relatives, allowing helpers to reduce their investment in help (Kokko et al. 2002). We expect that direct benefits of helping, such as opportunities for subordinates to help raise their own young in parasitized or shared broods or group augmentation could also lead to greater help than that predicted in this model. If subordinates are in competition with one another for a limited number of vacant helping positions, help may escalate as subordinates attempt to outbid one another for these (Ragsdale 1999). Also, we expect that help would increase if subordinates could assess the tolerance thresholds of individual breeders, rather than playing against the population average tolerance threshold (Kokko et al. 2002; Kokko 2003).

Our model predicts that helping in excess of the costs imposed upon breeders can be favoured when subordinates gain a survival benefit from helping (g is negative; inequality (3.3)). How could such a relationship arise, given that helping is presumably costly to helpers? We suggest that non-evictive harassment of helpers may generate just such a relationship if dominants impose costly harassment on ‘lazy’ helpers without expelling them, but relax this harassment as help increases (as suggested in naked mole-rats; Reeve 1992). Although helping would still be costly, the net effects of increasing help on survival within the group could be positive because of reduced harassment. This suggests that breeders may better enforce cooperation by threatening harassment within the group in addition to expulsion. It would be fruitful to approach this question in the future using a negotiation framework (McNamara et al. 1999).

Our model supports several of the general predictions made by Kokko et al. (2002), indicating that many of the basic predictions of the pay-to-stay framework are robust. As in their model, helping by non-relatives cannot be stable if subordinates are not costly to dominants. Also, intrinsic survival of group members in general (S_bS_n) must be relatively high for there to be any help at all. When S_bS_n is low, ‘helpers’ may be tolerated even if they do not help (inequality (3.4)), whereas at very high levels of breeder survival, subordinates should accept expulsion rather than help (inequality (3.5)).

Kokko et al. also predicted that helping should be favoured when ecological constraints are tight to moderate. By contrast, we found that ecological constraints did not influence the stable level of help under any conditions, but could influence the tolerance threshold and whether there would be any help at all. Ecological constraints were only important when density dependence acted through the probability of inheriting a territory. When density dependence acted through the probability of surviving from eviction to finding a new territory (i.e. by influencing K and, in unpublished results (I. M. Hamilton), α), we found no effect of ecological constraints on the amount of help, the tolerance threshold or whether any help at all was favoured.

Several other models have predicted that, at equilibrium, ecological constraints should have no or little influence on the decision to delay dispersal when density dependence acts upon the probability of a floater finding a new territory (Pen & Weissing 2000; Kokko & Ekman 2002). In all of these models, ecological constraints are functions of the decision to stay (or in our model, to help enough to be allowed to stay). When constraints are high, the few individuals that successfully disperse gain a high pay-off. In our model, the value of K*, the density-dependent probability of surviving dispersal, increases as the other two variables influencing ecological constraints (probability of finding a territory or of surviving as a floater) decrease. Thus, these three measures of ecological constraints effectively cancel one another out.

We also examined the influence of density dependence acting through a different mechanism, which is the probability of inheriting a territory, and found that, in this case, ecological constraints did influence the decision to help. The value of β*, the density-dependent probability of inheriting a territory, decreases slightly as ecological constraints decrease (i.e. K, S_f or α increase). Intuitively, this makes sense if, for example, helpers queuing to inherit a territory face increased competition from floaters or neighbours as the number of floaters surviving and/or establishing new territories increases. Thus, as constraints relax, the probability of inheriting a territory decreases, whereas that of finding a territory after expulsion increases, and subordinates have less incentive to stay in the group. To maintain the level of help at h∘, breeders must demand more help. When ecological constraints are very low, this is unstable and all helpers accept expulsion rather than helping.

Both mechanisms of density dependence that we model here are probably relevant to cooperative breeders. Many cooperative and non-cooperative species alike live in saturated habitats (Kokko & Lundberg 2001), where there may be intense competition among floaters for breeding vacancies (e.g. Komdeur et al. 1995). Thus, density-dependent population regulation through competition among floaters (i.e. K or α in our model) is probably common in territorial species in general. However, subordinates that queue to inherit a territory may face competition with floaters or neighbours (Kokko & Ekman 2002); in N. pulcher, territories are often taken over by fish that were not group members, and former helpers may be expelled afterwards (Balshine-Earn et al. 1998). This could lead to density-dependent regulation through territory inheritance.

Finally, this model predicts that associations between unhelpful subordinates and breeders can be stable. Unhelpful subordinates are observed in many breeding groups containing unrelated subordinates (e.g. anemonefish (Mitchell 2003) and speckled warblers (Gardner et al. 2003)). Our model predicts that such groups are more likely when the cost of eviction is high, the cost of subordinate presence is low or survival on the breeding territory is low (inequality (3.4)). High costs of fighting also probably favour tolerance of costly group members in other social situations (see, for example, Maynard Smith & Ridpath 1972; Krause & Ruxton 2002). Importantly, helpers may have some control over the costs of eviction for breeders. If breeders are confined to a territory, they cannot easily move away from costly subordinate. Therefore, whether a subordinate leaves is, at least in part, its own decision. An obstinate subordinate may impose higher eviction costs, and thus, such an individual may be more likely to be tolerated. Although this is beyond the scope of the present model, incorporating the process of eviction itself as the outcome of a game between breeders and helpers would provide an interesting extension to the framework described here.