Coordinated effects of distal mutations on environmentally coupled tunneling in dihydrofolate reductase

Abstract

One of the most intriguing questions in modern enzymology is whether enzyme dynamics evolved to enhance the catalyzed chemical transformation. In this study, dihydrofolate reductase, a small monomeric protein that catalyzes a single C-H–C transfer, is used as a model system to address this question. Experimental and computational studies have proposed a dynamic network that includes two residues remote from the active site (G121 and M42). The current study compares the nature of the H-transfer step of the WT enzyme, two single mutants, and their double mutant. The contribution of quantum mechanical tunneling and enzyme dynamics to the H-transfer step was examined by determining intrinsic kinetic isotope effects, their temperature dependence, and activation parameters. Different patterns of environmentally coupled tunneling were found for these four enzymes. The findings indicate that the naturally evolved WT dihydrofolate reductase requires no donor–acceptor distance fluctuations (no gating). Both single mutations affect the rearrangement of the system before tunneling, so some gating is required, but the overall nature of the environmentally coupled tunneling appears similar to that of the WT enzyme. The double mutation, on the other hand, seems to cause a major change in the nature of H transfer, leading to poor reorganization and substantial gating. These findings support the suggestion that these distal residues synergistically affect the H transfer at the active site of the enzyme. This observation is in accordance with the notion that these remote residues are part of a dynamic network that is coupled to the catalyzed chemistry.

The mechanisms by which enzymes catalyze chemical reactions have been studied extensively. Yet, the question of whether enzyme dynamics evolved to enhance enzymatically catalyzed chemical reactions remains open. To avoid terminology confusion, the term dynamics, as used in this work, needs to be defined. Several researchers construe dynamics only as nonequilibrium motions along the reaction coordinate (1), whereas most enzymologists interpret dynamics as any motion in the reaction's environment (2, 3). In this article, we use the latter definition and address the possibility that dynamics of the whole protein (not only of its active site) play a role in catalysis. Dihydrofolate reductase (DHFR) was chosen as a model system because it is a small enzyme and its dynamics have been studied experimentally and theoretically. DHFR catalyzes a simple chemical transformation (C-H-C transfer) that can be examined experimentally in great detail. Hence, changes in protein dynamics and their effects on the chemical step can be examined and related to the catalytic activation of the C-H bond.

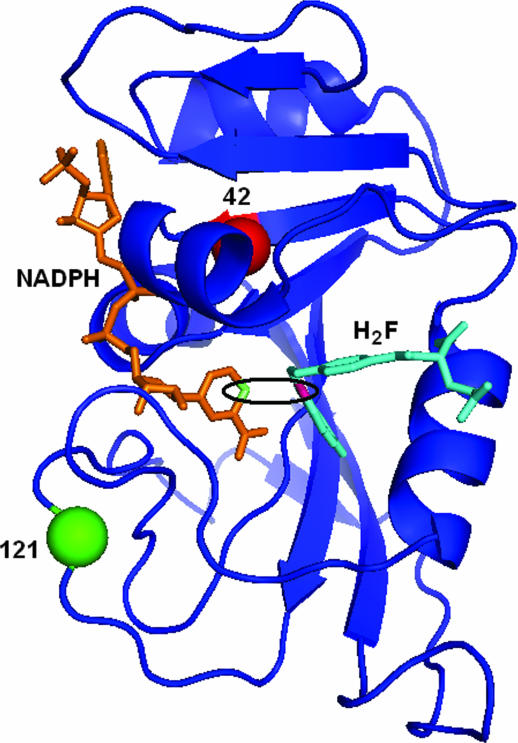
DHFR is a flexible, monomeric protein. Fig. 1 presents the structure of Escherichia coli DHFR (ecDHFR) and highlights the active site and the two residues under investigation (G121 and M42). The enzyme catalyzes the reduction of 7,8-dihydrofolate (H₂F) to 5,6,7,8-tetrahydrofolate (H₄F) with the stereospecific transfer of a hydride from the pro-R C4 position of the nicotinamide ring to the si face of the C6 of the pterin ring (2). DHFR has served as a platform for many theoretical and experimental studies, a few of which are discussed below.

Fig. 1.

A 3D structure of WT ecDHFR with the cofactor, NADPH, shown in orange and the substrate, H₂F, shown in cyan. The C₄ position of NADPH and the C₆ position of H₂F are highlighted in lime and pink, respectively. The active site is emphasized by the black ellipse. Residues 121 and 42 are labeled with green and red spheres, respectively.

The kinetic mechanism of ecDHFR was derived from equilibrium-binding, steady-state, and presteady-state kinetic studies (2, 4). These studies revealed a rather complex kinetic cascade within which the step that includes hydride transfer is mostly rate-limiting at high pH. Similar kinetic schemes have been drawn for various mutants of ecDHFR (5–14), setting the framework for studies of the relationship between kinetics and dynamics.

Changes in protein dynamics in response to ligand binding, substrate turnover, and mutagenesis have been probed by using numerous experimental and theoretical approaches. Structures of ecDHFR obtained by x-ray diffraction studies in unbound form and in binary and ternary complexes with various ligands suggest that the enzyme assumes open, closed, and occluded conformations along the reaction pathway (15). NMR relaxation experiments confirmed the conformational changes involving these loops and indicated that binding of the substrate and cofactor induces such changes both in and distal to the active site during the catalytic cycle (16–18). These studies probed the distribution of conformational ensembles that ecDHFR assumes and addressed the role of the different ensembles in catalysis. NMR studies with G121V (one of the mutants studied here) suggested that G121 affects catalysis by altering the distribution of conformational ensembles (14, 16–19).

Theoretical studies have further enhanced our understanding of the role of enzyme structure and dynamics and the impact of mutations on enzyme catalysis. Classical molecular dynamics simulations (20–22) have been used to identify correlated and anticorrelated motions within many of the same regions implicated by the NMR relaxation experiments (16–18). These correlations exist in the reactant complex, but are diminished in the product complex, which implies a possible role of dynamics in catalysis. Distal ecDHFR mutants with reduced activities exhibit reduced correlated motions compared with the WT enzyme. More recently, hybrid quantum/classical molecular dynamics simulations have implicated a network of coupled motions extending throughout the entire protein and its ligands (23–28). These coupled motions, representative of equilibrium, thermally averaged conformational changes along the reaction coordinate, lead to active site configurations that enhance the hydride transfer. These hybrid simulations have been expanded to constrained systems in which a constraint was placed on the distances between α-carbons of distal residues (29). The results suggest that freezing the motion between two distal residues can deteriorate the network of coupled motions and alter the conformational sampling of the entire protein. Simulations on ecDHFR using different methodologies, such as classical molecular dynamics or quantum mechanical/molecular mechanical and variational transition-state theory, were also consistent with that finding supporting a network of coupled motions susceptible to perturbation by nonlocal structural effects (3, 21, 30–32).

Particularly germane to this article are hybrid simulations for single, double, and triple mutants involving distal residues of ecDHFR (including G121 and M42) that indicated each mutant entertains a unique distribution of enzyme motions (25). These simulations indicate that distal mutations alter the sampling of configurations conducive to hydride transfer, and therefore interrupt the coupling between motions of the distal residues involved in the proposed network.

The amino acids M42 and G121 of ecDHFR are of particular interest because they are remote from the active site and yet highly conserved. Both theoretical calculations (25) and experimental measurements (5, 33) indicated possible functional coupling of these residues in the turnover cycle. Additionally, some theoretical studies of DHFR and related systems suggest that the C-H-C transfer event per se is expected to be at the ns-fs time scale and that most of the ms events, relevant to the presteady-state measurements, are likely to be associated with the prearrangement of the potential surface before the activation of the C-H bond (28).

Probing the C-H-C transfer step and effects of mutations on that specific step has the potential to directly address coupling between the altered residues and the catalyzed chemistry. Such a direct probe could provide information more relevant to theoretical calculations because they commonly focus on the “chemical step” rather than the full cascade of mechanistic-kinetic events that might be addressed, such as preorganization (34). Methods that focus on intrinsic kinetic isotope effects (KIEs) and their temperature dependency have been developed for this purpose (35–39). These methods selectively extract information regarding the physical nature of the chemistry (covalent bond making and breaking, e.g., C-H-C transfer). Features such as H tunneling and coupling of the reaction coordinate to its environment can then be explored (as discussed in more detail below). In contrast to rate measurements, the competitive KIE measurements are only probing effects of reactive enzymatic forms and conformations (only the isotopic distribution in the reaction's products is analyzed).

The current work compares the effects of two distal mutations (G121V and M42W) and their double mutant (G121V–M42W) on the nature of the catalyzed H transfer. The aim is to examine and evaluate previous suggestions that these remote residues affect the enzyme dynamics and are part of a dynamic network that is coupled to the reaction coordinate (23–26, 33). The data presented here indicate that, despite a large effect of the single mutations on the H-transfer rate (33), their effect on the nature of the transfer (rearrangement, tunneling, and coupling to environmental vibrations) is small. The double mutant, on the other hand, substantially alters the H-transfer mechanism consistent with the participation of both G121 and M42 in the network of coupled motions tied to the chemical transformation at the active site of the enzyme.

Results and Discussion

Competitive KIEs and Their Temperature Dependence.

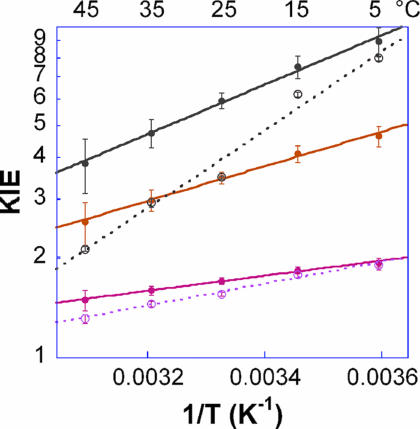
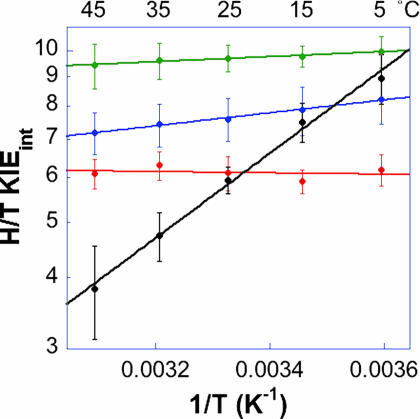
Competitive KIE experiments were conducted with G121V–M42W by using a method as described (37, 40). The findings were compared with those for the WT enzyme (35) and the two single mutants, G121V (40) and M42W (41). Fig. 2 presents the observed and intrinsic KIEs in the form of an Arrhenius plot. The intrinsic KIEs were used to calculate the isotope effect on the activation parameters A₁/A_h and ΔE_ah−1, where A₁/A_h and ΔE_ah−1 are the isotope effect on the preexponential Arrhenius factors and the difference in activation energy between light and heavy isotopes, respectively. To compare the results for this double mutant to those for the WT enzyme (35) and the two single mutants (40, 41), Fig. 3 presents the intrinsic H/T KIEs for all of the isozymes on an Arrhenius plot (the same trend was observed for the H/D and D/T KIEs; data not shown), and Table 1 summarizes their H-transfer rates and activation parameters.

Fig. 2.

Arrhenius plots of observed (○) and intrinsic (●) KIEs for the G121V–M42W-ecDHFR. H/T KIEs are in gray, H/D KIEs are in orange, and D/T KIEs are in pink. The lines represent the nonlinear regression to Eq. 5.

Fig. 3.

Comparison of the Arrhenius plots of intrinsic H/T KIEs of WT (red; ref. 37), G121V (green; ref. 40), M42W (blue; ref. 41), and G121V–M42W (black) ecDHFRs.

Table 1.

Comparative KIEs on Arrhenius preexponential factors

Parameters	DHFR				S.C. range (46,49,51)
	WT (35)	G121V (41)	M42W (44)	G121V–M42W (This work)
kH*	228 ± 8 s−1	1.4 ± 0.2 s−1	5.6 ± 0.4 s−1	0.03 ± 0.005 s−1
AH/AT	7.0 ± 1.5	7.4 ± 1.6	2.8 ± 0.2	0.1 ± 0.1	0.5–1.6
AH/AD	3.5 ± 0.5	4.7 ± 1.5	2.1 ± 0.2	0.04 ± 0.03	0.6–1.4
AD/AT	1.70 ± 0.14	1.7 ± 0.07	1.35 ± 0.05	0.25 ± 0.09	0.9–1.2
ΔEaT-H†, kcal/mol	−0.1 ± 0.2	0.23 ± 0.03	0.58 ± 0.04	3.6 ± 0.3

*Presteady state rates of H transfer at 25 °C and pH 7 (33)

^†Similar trends were observed for H/D and D/T (data not shown).

The preexponential Arrhenius factors (A_H/A_T, A_H/A_D, and A_D/A_T) for the WT enzyme and two single mutants are larger than unity [and above their upper semiclassical limits (42)], whereas the double mutant has values smaller than unity. Traditionally, semiclassical analysis (43–45) with Bell correction (46) would suggest that the H transfer in the first three systems involves “extensive tunneling” (of both isotopes), whereas the double mutant transfer involves “moderate tunneling” (only the lighter isotope tunnels) (47–50).

The slopes seen in Fig. 3 and the ΔE_aH-T values in Table 1 indicate that the WT enzyme's intrinsic KIE has no temperature dependence (within experimental error) and the G121V and M42W mutants' intrinsic KIEs have weak, but nonzero, temperature dependencies (within experimental error). The intrinsic KIEs for G121V–M42W are far more temperature-dependent than any of those measured for the WT, G121V, or M42W DHFRs. Actually, the ΔE_aT-H of 3.6 ± 0.3 kcal/mol is larger than the semiclassical value predicted from the Bigeleisen equation (43–45). Traditionally, the inflated ΔE_a and the A_H/A_T < 1 would be interpreted as an indication of more H tunneling than T tunneling (46), also denoted as moderate tunneling (47–50). In this article, because we want to compare the four systems (WT, G121V, M42W, and G121V–M42W ecDHFR) to each other by using one comprehensive approach, we will use the interpretation of Marcus-like models as discussed later.

Table 1 also presents the single turnover rates (33) to illustrate the mutations' effects on the overall rates. It is apparent that despite the 42- and 163-fold slower reaction rates for the single mutants, their A₁/A_h and ΔE_a values are not dramatically different compared with that of the WT enzyme. The double mutant, on the other hand, is not only 7,600-fold slower, but also has A₁/A_h values below the semiclassical limits and larger ΔE_a values. These data are in accordance with a similar H-tunneling mechanism for the first three enzymes and a substantially different nature of H tunneling for the double mutant. These differences are discussed in detail later by the framework of Marcus-like models. Such a framework is also vital because of the relatively small size of the KIEs. Traditional semiclassical models predict that temperature-independent KIEs would be much larger than reported here (50), thus raising the question of the validity of the traditional, Bell correction interpretation.

Activation Parameters of Reaction Rate.

The traditional models would also predict that temperature-independent KIEs would only result from temperature-independent rates (E_a close to 0). Thus, the activation parameters of the first-order rate constant (k_cat) were determined by initial velocity measurements measured at saturating concentrations of substrates at high pH (pH 9, adjusted at each experimental temperature) over the temperature range of 5–45°C (Table 2). At high pH, the first-order rate constant, k_cat, mostly represents the hydride transfer step, that becomes primarily rate-limiting on k_cat because of the requisite protonation of N5 of H₂F before the hydride transfer (33). The observed nonzero energy of activation (E_a) cannot be justified solely by a tunneling correction or other “traditional models.” Thus, again, Marcus-like models are invoked when discussing the findings. These models have been used to rationalize both temperature-dependent or -independent KIEs with various KIEs and activation energies (34, 50–56).

Table 2.

Comparative activation parameters of initial velocity measurements at pH 9

Parameters	DHFR, kcal/mol
	WT	G121V	M42W	G121V–M42W
Ea	5.56 ± 0.58	5.30 ± 0.12	5.09 ± 0.83	3.91 ± 0.18
ΔH‡	4.95 ± 0.58	4.69 ± 0.12	4.48 ± 0.83	3.30 ± 0.18
T·ΔS‡ (25°C)	−11.79 ± 0.56	−12.20 ± 0.41	−12.23 ± 0.80	−15.72 ± 0.38
ΔG‡ (25°C)	16.74 ± 0.81	16.89 ± 0.43	16.71 ± 1.15	19.02 ± 0.42

The activation parameters (ΔH^‡, TΔS^‡, and ΔG^‡) of k_cat at high pH (shown in Table 2) can be considered representative of these parameters on the H-transfer step (33). Apparently, all of the parameters for the WT enzyme and the two single mutants are the same (within experimental error). The double mutant, on the other hand, has a slightly lower enthalpy of activation (≈1 kcal/mol), and a lower entropy of activation (≈3 kcal/mol at 25°C), which leads to a free energy of activation that is larger than the other systems by ≈2.5 kcal/mol (at 25°C). Assuming that the k_cat at high pH is indeed mostly dictated by the chemical step, this trend further indicates that the preorganization (or reorganization) of the system, as expressed by ΔS^‡, is larger for the double mutant, resulting in a less efficient H transfer relative to the single mutants and the WT enzyme. Interestingly, a previous study of single mutants of soybean lipoxygenase-1 (SLO-1) (57) also indicated high sensitivity of the temperature dependence of KIEs to changes induced by mutations. The results with three mutants (L546A, L754A, and I553A) indicated similar KIEs at 30°C but substantial changes in A₁/A_h and inflated ΔE_a relative to the WT enzyme. Marcus-like analysis of these data could distinguish between effects on rearrangement and gating. The analogy to the current findings is also interesting because the two systems are quite different: the SLO-1 reaction is a nonadiabatic hydrogen-electron coupled transfer, whereas that of DHFR is an adiabatic hydride transfer (27).

Kinetic Complexity.

For all enzymes compared here, the observed KIEs are smaller than their corresponding intrinsic KIEs. This is a common feature in enzymology that can be rationalized by kinetic complexity, namely, isotopically insensitive kinetic steps masking the intrinsic KIEs (58–60). Because the observed KIEs were measured under irreversible reaction conditions (40) the kinetic complexity can be formulated as follows (58–60):

where ^h(k_cat/K_M)_{l_obs} is the observed l/h KIE on k_cat/K_M, and k_l/k_h is the intrinsic l/h KIE on the H-transfer step. C_f represents the forward commitment to catalysis, which is the sum of the ratios between the rate of the forward, isotopically sensitive, hydride transfer step and each of the rates of the preceding, backward, isotopically insensitive steps.

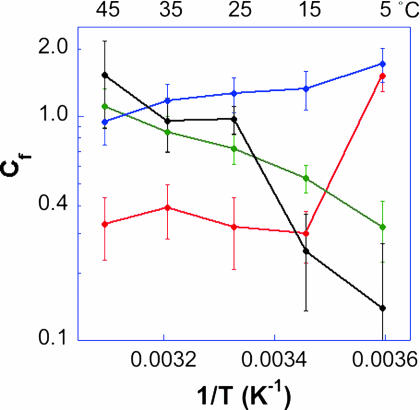
Fig. 4 presents the forward commitment (C_f) values of the WT, G121V, M42W, and G121V–M42W DHFRs as Arrhenius plots (logarithmic scale of C_f vs. the reciprocal of the absolute temperature). The temperature dependencies of the observed KIEs and forward commitments (C_f) of the compared isozymes are quite diverse. The comparison of Figs. 3–5 illustrates that the intrinsic KIEs and their corresponding observed KIEs are not related to each other by any simple function. Apparently, the factors affecting the isotopically sensitive step and the other kinetic steps are affected differently by the mutation (as are all microscopic rate constants). This observation emphasizes that great caution is needed when analyzing measured KIEs and their temperature dependence and further underlines the importance of exposing intrinsic effects.

Fig. 4.

Comparison of the Arrhenius plots of the commitment to catalysis (C_f) on k_cat/K_M for the WT (red; ref. 37), G121V (green; ref. 40), M42W (blue; ref. 41), and G121V–M42W (black) ecDHFRs.

Fig. 5.

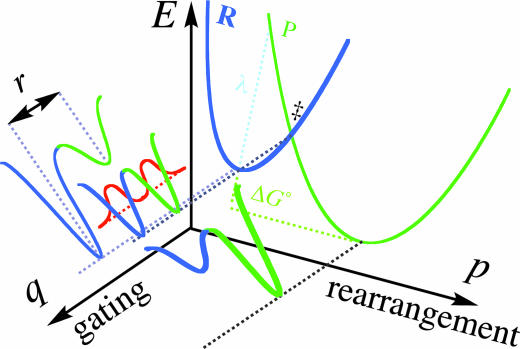
Illustration of Marcus-like models showing energy surface of environmentally coupled hydrogen tunneling. Two orthogonal coordinates are presented: p, the environmental energy parabolas for the reactant state (R) and the product state (P) along which the rearrangement process take place; and q, the H-transfer potential surface at each p configuration. The donor–acceptor distance (r in Eq. 5) fluctuates along the q coordinate. In Marcus-like models this distance fluctuates harmonically around r₀, thereby changing the tunneling probability [a phenomenon denoted gating by Klinman and coworkers (34, 69)]. In cases where r₀ is ideal for tunneling, the KIEs will be temperature independent. Otherwise, these thermal fluctuations will lead to the temperature dependency of the KIEs.

Marcus-Like Models and Environmentally Coupled Tunneling.

The interpretation of the data from the methods used here depends on the availability of a theoretical model that can address rates, KIEs, and their temperature dependency. In many cases, models based on transition-state theory, assuming a 1D rigid potential surface, successfully reproduced temperature-dependent KIEs either with or without a tunneling correction (46). Those models can rationalize temperature-independent large KIEs providing there is no activation energy for the isotopically sensitive step (34, 47, 61). However, such models cannot explain temperature-independent small KIEs with a significant activation energy. In an attempt to explain experimental results with such KIEs, several phenomenological models were proposed in recent years that fall under the title Marcus-like models (e.g., refs. 34, 36, 51, 53, 54, and 62–64). These models were constructed based on a single kinetic step (the chemical step), and thus pertain to the experimental measurements described here. Although these different models originate from different basic principles, they all share several mathematical and physical features. In short, these models suggest that (i) the hydrogen should be treated quantum mechanically throughout the reaction coordinate (including tunneling); (ii) fluctuations of the reaction's potential surface occur on a time scale similar to or slower than the hydrogen-transfer rate, and thus determine the overall rate of hydrogen transfer (the solvent coordinate is the reaction coordinate as described in refs. 50, 65, and 66); and (iii) these fluctuations can be treated as two orthogonal vibrations, one that represents fluctuations in the donor–acceptor distance (the q coordinate) and the second that represents changes in the system's symmetry (the p coordinate) as illustrated in Fig. 5. For more extensive discussion of such Marcus-like models see refs. 34 and 50.

A general description of such model can be demonstrated in the following rate equation:

where C is a constant with insignificant temperature dependence, MT is a Marcus term that is mostly isotopically insensitive with the general form of:

where λ is the reorganization (or preorganization) energy and ΔG° is the reaction's thermophilicity (the driving force for the reaction) (67, 68), R is the gas constant, and T is the absolute temperature. HTT is the tunneling term, which is sensitive to the mass of the isotopic atom and the distance between donor and acceptor energy wells in any conformation that enables significant tunneling. This term represents the H-tunneling probability and includes the Franck-Condon nuclear overlap integral between the donor and acceptor wave functions. It depends on the tunneling mass and the vibration state of the tunneling conformation (34, 52). HTT is an exponential function consisting of two terms. The first term is the integrated tunneling probability of all of the relevant donor–acceptor distances as a function of the isotopic mass (m_i) and frequency (ω_i). The second term is an exponential function of the energy involved in reaching each donor–acceptor distance (E_X) and is often defined as “gating.” An example of HTT would be (52):

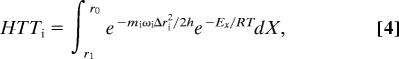where Δr_i is the distance between the donor and acceptor wells at each conformation, ranging from the equilibrium distance (r₀) to r₁, and X is the gating coordinate. The HTT is obviously isotopically sensitive and has an Arrhenius temperature dependency.

Mathematically speaking, all of these models separate the temperature dependence of the reaction rate (affected by both MT and HTT) from that of the KIEs (affected mostly by HTT). This feature enables Marcus-like models to accommodate systems with both temperature-dependent and temperature-independent KIEs, whether the activation barrier for the reaction is significant or not.

Various terms have been coined in these models to characterize hydride transfer in an enzymatic system, including “vibrationally enhanced tunneling” (53), “rate-promoting vibrations” (54), and “environmentally coupled tunneling” (69). In this article we use the terminology that was coined by Nagel and Klinman (34) and Franciso et al. (69), although other terms used by others, or newer terms by Klinman (70), are just as valid. Using this terminology, the thermally activated fluctuations of the system that alter the symmetry of the potential surface are referred to as “rearrangements” (the Marcus term, see Eq. 4) and the fluctuations of the donor–acceptor distance that actively modulate the tunneling barrier as gating (the Frank-Condon term, e.g., Eq. 5).

Rationalization of Current Findings.

The temperature independence of the KIEs, with large A₁/A_h values, and nonzero E_a values for the WT ecDHFR (Fig. 3 and Table 1) has been rationalized in the context of a full tunneling Marcus-like model with ideal rearrangement of the potential surface (along the p coordinate in Fig. 5) (35). The average donor–acceptor distance in this system appears to be ideal for tunneling. That is to say, the environmental reorganization that must occur before tunneling can proceed has evolved to optimize reactive conformation for ground-state tunneling. Consequently, no thermally activated fluctuations along the q coordinate contribute to the tunneling rate and the KIEs are temperature independent (35). In this case, the observed E_a arises from the Marcus term (see Eqs. 2 and 3). For more details, see refs. 34 and 50, which discuss the Marcus-like models in great detail and describe how the temperature dependency of KIEs can be used as a probe for determining the coupling between the enzyme environment and the catalyzed reaction coordinate.

For both single mutants, the slightly inflated KIEs and their weak temperature dependence indicate that the rearrangement is not as perfect as for their WT counterpart, and that the average donor–acceptor distances are longer than that for the WT enzyme. Consequently, some thermally activated fluctuations along the q coordinate are required, leading to the slight temperature dependences of these KIEs (40, 41). Compared with that for G121V and M42W mutants, the steep temperature dependence of the KIEs for G121V–M42W DHFR suggests poor rearrangement and an average donor–acceptor distance that is too long to enable tunneling. Essential thermally activated gating fluctuations in this double mutant lead to the large temperature dependence of the KIEs.

The above comparison suggests that the average distance between the donor and the acceptor for hydride transfer is perfect for the WT, less perfect for the G121V and M42W mutants, and significantly altered for the G121V–M42W mutant. Consequently, the hydride transfer with the G121V and M42W mutants seems to occur in a conformation closer to that of WT DHFR relative to the G121V–M42W mutant. These findings indicate that distal residues G121 and M42, both >15 Å away from the active site and 21 Å from each other, affect the hydride transfer at the active site in a synergistic fashion and constitute experimental support for the theoretical simulations suggesting that these residues are part of a dynamic network coupled to the catalyzed chemistry (24–26, 71).

Finally, a sequence-based statistical analysis (72) also indicated that these residues evolved in a coupled manner (28). Because functional coupling, as examined in the present work, may lead to an evolutionary bias, the relationships identified by the present study offer insight into the genetic coupling between G121 and M42.

Conclusions

The current work examines the effects of remote DHFR mutations (G121V and M42W) on the enzyme-catalyzed hydride transfer step by measuring KIEs and their temperature dependence. The results are interpreted in the framework of Marcus-like models. The findings for the G121V–M42W ecDHFR are compared with those for the G121V, M42W, and WT enzymes. The comparison indicates that the nature of the hydride transfer is slightly changed for the G121V and M42W mutants, but is significantly altered for the G121V–M42W double mutant. The WT DHFR reaction involves environmentally coupled H tunneling, which does not require thermally activated fluctuations of the donor–acceptor distance. Both single mutations mostly affect the prearrangement of the system before tunneling, leading to the observed slower reaction. The tunneling conformations of G121V and M42W were slightly altered to less ideal average tunneling conformations (r₀) relative to the WT, so some thermally activated gating fluctuations were required. The double mutant, on the other hand, demonstrated substantial changes in the nature of H transfer in accordance with the idea that these remote residues are part of a dynamic network that extends throughout the enzyme and are coupled to the catalyzed chemistry (24–26). The observation that most of the reduction in the double mutant's H-transfer rate is entropic (Table 2) and the fact that only the double mutant has substantially temperature-dependent KIEs suggest that the simultaneous distortion of G121 and M42 affects the reorganization of the system (as expressed by ΔS^‡) in a way that prohibits efficient ground-state tunneling. Because similar effects on each single mutant were much smaller (or negligible within experimental error), the current findings support a synergistic effect of G121 and M42 (both remote from the active site) on the catalyzed C-H transfer, in accordance with the proposed network of coupled motions that may have evolved to be coupled to the catalyzed reaction (25–28).

The importance of protein dynamics in enzymatic reactions has implications for protein engineering and rational drug design. Apparently, not only the catalytic active site should be mimicked, but the flow of vibrational energy through the protein and its coupling to the catalyzed bond activation need to be addressed. It is likely that only high-level theoretical studies like those conducted with WT and G121V DHFRs (3, 20–25, 30, 32, 71, 73) can fully interpret the role of tunneling and overall protein dynamics in catalysis at the molecular level.

The correlation between the genomic coupling (28) and the functional coupling arises despite the hydride transfer step for the WT DHFR is not rate-limiting under physiological conditions. However, mutations of conserved residues would turn that step into the rate-limiting step, as has been found in several mutants of DHFR (6, 33, 74) and offer an explanation as to how a hidden kinetic step may still impose evolutionary constraints.

Materials and Methods

All materials were purchased from Sigma (St. Louis, MO) unless otherwise indicated. 7,8-Dihydrofolate (H₂F) was prepared by dithionite reduction of folic acid as described by Blakely (75). All of the mixed-labeled cofactors (R[4-²H]-NADPH, R[4-³H]-NADPH, [Ad-¹⁴C]-NADPH, R[4,4-²H,³H]-NADPH, and [Ad-¹⁴C, 4-²H₂]-NADPH) were synthesized as described (36, 37, 39, 40, 76).

WT ecDHFR and its mutants G121V, M42W, and G121V–M42W were expressed, purified, and stored as described (5, 33, 77).

The kinetic experiments and data processing procedures have been described in great detail (40, 41,). In short, to measure the H/T KIE, NADPHs labeled with H or T at the 4R position were mixed and reacted with H₂F in the presence of the mutated DHFR under the conditions specified for each experiment. NADPH that was labeled with H was also labeled by ¹⁴C in its adenosine ring to serve as a tracer for the conversion of these molecules. The reaction was quenched at different time points and at completion, and the depletion of the T in the product was analyzed as a function of fractional conversion to yield the KIE on the second-order rate constant k_cat/K_M. D/T KIEs were measured by using the same procedure but with D, instead of H, labeled NADPH. The observed H/T and D/T KIEs were used to calculate the intrinsic KIEs k_l/k_h, where k_i is the rate of the C-H-C transfer with isotope i, and l or h represent the light or heavy isotope, respectively).

The isotope effects on the activation parameters for the intrinsic KIEs were calculated by nonlinear fit to the Arrhenius equation for KIEs:

Initial velocity measurements were performed at saturating substrate and cofactor concentrations over a temperature range of 5–40°C (40, 74). All experiments were conducted at high pH (adjusted at each experimental temperature) to ensure that the H transfer was mostly rate-limiting (2, 4, 33). The calculated steady-state rates (k_cat) for each temperature were fit to the Arrhenius equation through a nonlinear least-squares regression to obtain the activation parameters.

Abbreviations

DHFR

dihydrofolate reductase

ecDHFR

Escherichia coli DHFR

KIE

kinetic isotope effect.