Effect of force on mononucleosomal dynamics

Abstract

Using single-molecule optical-trapping techniques, we examined the force-induced dynamic behavior of a single nucleosome core particle. Our experiments using the DNA construct containing the 601 nucleosome-positioning sequence revealed that the nucleosome unravels in at least two major stages. The first stage, which we attributed to the unraveling of the first DNA wrap around the histone octamer, could be mechanically induced in a reversible manner, and when kept at constant force within a critical force range, exhibited two-state hopping behavior. From the hopping data, we determined the force-dependent equilibrium constant and rates for opening/closing of the outer wrap. Our investigation of the second unraveling event at various loading rates, which we attributed to the inner DNA wrap, revealed that this unraveling event cannot be described as a simple two-state process. We also looked at the behavior of the mononucleosome in a high-salt buffer, which revealed that the outer DNA wrap is more sensitive to changes in the ionic environment than the inner DNA wrap. These findings are needed to understand the energetics of nucleosome remodeling.

Eukaryotic genomic DNA is organized into chromatin, a highly condensed yet dynamic structure. The fundamental unit of chromatin is the nucleosome core particle, which consists of 146 bp of DNA wrapped ≈1.7 turns around a histone octamer complex. However, this nucleosomal organization of the DNA imposes a significant barrier to binding for many proteins involved in various cellular processes such as transcription and the regulation of gene expression. How these proteins gain access to the occluded DNA sites is still a subject of continued research.

One type of study has concentrated on proteins whose function is to modify or remodel the structure of chromatin to facilitate the access of protein regulators to the DNA (1–3). Other studies using restriction enzyme accessibility assay (4) and fluorescence experiments (5) showed that, in vitro, nucleosomal DNA also undergoes spontaneous structural fluctuations. Conceivably, proteins may access occluded DNA binding sites via such fluctuations. One aspect that has become increasingly important to understand this dynamic behavior is the recognition that many DNA translocases, such as RNA polymerase (6–8), can exert significant amounts of force and torque on nucleosomes. The question then arises: how does the addition of force affect the dynamics of nucleosomes?

Previous optical trap experiments on chromatin fibers (9–11) indicated that the nucleosome opens in at least two major stages. Studies on nucleosomal arrays done by Brower-Toland et al. (9) using the sea urchin 5S nucleosome positioning sequence showed what appears to be a plateau-like unraveling event occurring at low forces (≈5 pN) and another unraveling event characterized by abrupt and sudden force-extension transitions, referred to here as “rips,” at higher forces (>15 pN). According to Brower-Toland et al., the high-force rips represent the unraveling of the inner DNA wrap from the histone octamer, whereas the low-force transition represents the gradual unpeeling of the outer DNA wrap from the histone octamer. Moreover, because they continued to observe high-force rips after successive pulling–relaxation cycles, Brower-Toland et al. suggested that the DNA was able to rewrap around the histone octamer, an event later confirmed by Gemmen et al. (11). However, these experiments are limited by their use of nucleosomal arrays, which makes it difficult to assign the observed transitions to individual nucleosomes. Furthermore, nucleosome–nucleosome interactions may modify the thermodynamics and the kinetics of the process. Here we present experiments designed to follow in real time the dynamics of individual nucleosomes subjected to different degrees of tension, thereby eliminating these ambiguities.

Results and Discussion

Reconstitution Onto Long DNA Templates.

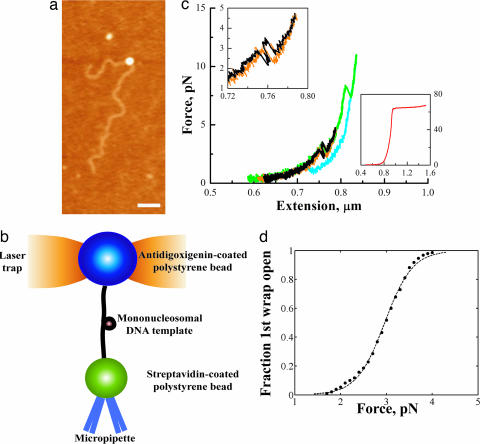
Because the mononucleosomes were reconstituted directly onto a long DNA fragment, a main concern was whether the reconstituted core particle was positioned correctly on the template. The 601 nucleosome-positioning sequence has been shown to compete very well against random genomic DNA (12). However, those studies never involved the random DNA directly attached to the 601 sequence, as it was in our case. To verify that we were able to reconstitute a nucleosome onto the 601 sequence embedded within a long piece of DNA (3,547 bp), we obtained atomic force microscopy (AFM) images of the reconstituted nucleosomes in air (Fig. 1b). The 601 sequence was positioned 374 nm from one end and 782 nm from the other end. Analysis of the AFM images showed the nucleosome positioned around 375 (±12) nm from one end and around 735 (±14) nm from the other end, close to the predicted values, thus confirming the correct positioning of the reconstituted particles.

Fig. 1.

Pulling the mononucleosome revealed two distinct rips. (a) Experimental setup. The antidigoxigenin-coated polystyrene bead was held in the optical trap, whereas the streptavidin-coated polystyrene bead was held onto a micropipette via suction. The mononucleosome is tethered between the beads. (b) AFM image of a mononucleosome reconstituted on a 3,547-bp piece of DNA. (Scale bar, 200 nm.) (c) Representative force-extension curves of the mononucleosome. Black and green indicate when the fiber was being pulled; orange and blue indicate when the fiber was being relaxed. (Upper Left Inset) Close-up of the low-force transition. (Lower Right Inset) A typical curve for naked B-form DNA. (d) Probability of the first wrap unraveling as a function of force was obtained by summing a normalized histogram of the first wrap opened vs. force. The solid line is the probability p(E) of a two-state system of the general form: p(E) = 1/(1 + e^E/kB^T). Best fit of the data yielded a ΔG(unwrap) of ≈24.7 kJ/mol.

Dynamic Behavior of Nucleosomes: The Low-Force Transition.

When a DNA fiber with no nucleosome was pulled, the force increased monotonically with extension, giving a force extension curve characteristic of naked B-form DNA (13) (Fig. 1c Lower Right Inset). However, when a nucleosome particle was present, two abrupt transitions were seen. Fig. 1c shows representative force-extension curves observed for the mononucleosomal fiber, when pulled just past the first transition (black) and when pulled past the second transition (green). The force for the first transition was distributed around 3 pN, whereas the second transition occurred at higher forces with a broader force distribution, centered at ≈8–9 pN. The size of the low-force rip was 21 (±0.22) nm and that of the high-force rip was 22 (±0.18) nm. Thus, each rip corresponds roughly to one DNA wrap around the histone octamer. We also observed rewrapping events around 21 (±0.20) nm in size at <5 pN, indicating that the histone octamers do not immediately dissociate completely from the DNA fiber when subjected to force and that the nucleosome core particles can reform one DNA wrap at a time. In addition, the pulling and relaxation curves of the low-force transition, which we attributed to the unraveling of the outer DNA wrap around the histone octamer, essentially coincided when the fiber was not pulled beyond the high-force transition (black and orange), indicating that the wrapping and unwrapping of this outer turn occurred reversibly at the pulling and relaxation rates used in these experiments. However, when the fiber was pulled beyond the high-force transition, the low-force process no longer occurred reversibly (green and blue).

Because the low-force transition could be mechanically induced in a reversible fashion, it was possible to determine a ΔG of unwrapping for the first outermost turn of the DNA from the reversible work done in the process. An analysis of the areas under the force extension curves through the transition yielded a ΔG(unwrap) of 22.4 (±0.324) kJ/mol. Another independent method for determining ΔG(unwrap) takes into account the stochastic nature of the unraveling event for the low-force transition. By plotting the fraction of the low-force wrap transitions observed as a function of the applied force (14, 15), and assuming a two-state process, we obtained a ΔG(unwrap) of 24.7 (±0.499) kJ/mol after correcting for the free energy due to tethering and stretching of the molecule (0.51 kJ/mol) (14–16), in good agreement with the previously determined value. (Fig. 1d)

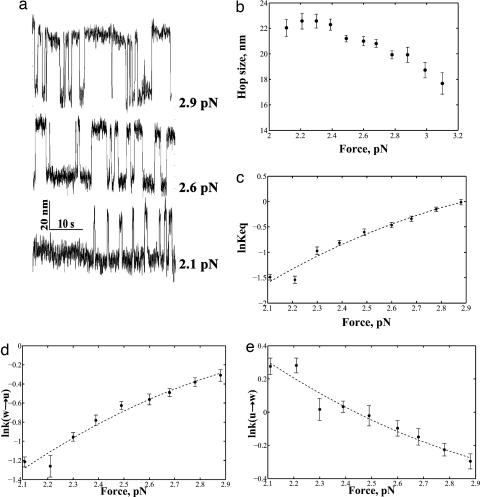
Several force-extension curves displayed an interesting dynamic behavior within the first transition during pulling and relaxation, especially at forces close to the low-force transition rip, suggesting bistable behavior (Fig. 1c Upper Left Inset). To better characterize this processes, a different type of experiment was used in which a constant force, ranging between 2 and 3 pN, was imposed on the nucleosome core particle using a force-feedback algorithm. Under these conditions, the nucleosomal core particle is seen to make transitions (hop) between an opened and a closed state, whose extensions coincide with those observed for the wrapped and unwrapped states (Fig. 2a). Interestingly, we found that the change in the end-to-end distance between the wrapped and unwrapped states of the hopping molecule was sensitive to force, decreasing approximately linearly with increasing force (Fig. 2b).

Fig. 2.

Two-state hopping of the low-force transition. (a) Length vs. time traces of the low-force transition at various forces. (b) Plots of the size of the hopping transition as a function of force. (c) Logarithm of the K_eq plotted as a function of force. (d) Logarithm of the rate of going from the wrapped to the unwrapped state plotted as a function of force. (e) Logarithm of the rate of going from the unwrapped to the wrapped state as a function of force (error bar shows standard error).

Imposing a constant force on the molecule makes it possible to control the thermodynamics and kinetics of the unraveling of the first wrap in real time. Additional tension then tilts the equilibrium toward the unwrapped state. By plotting histograms of the dwell times in the wrapped and unwrapped states for the low-force transition and fitting them to single exponentials, we obtained the average rate constants (and lifetimes) for the wrapped and unwrapped states at a given force (14). A ratio of the average lifetimes of the molecule between the two states yielded the equilibrium constant K_eq(F) for the opening and closing of the first wrap at a given force. The relationship between the equilibrium constant and force is described by the following formula (17)

where ΔG^o is the standard free energy for unwrapping at zero force, Δx(F) is the change in end-to-end distance between the wrapped and unwrapped state at a given force, and ΔG_stretch^w-u is the correction for the free energy reduction of the unwrapped state due to stretching of the DNA. Extrapolating to zero force gives us ΔG^o equal to 29.7 (±2.42) kJ/mol, which agrees well with the values obtained by the two independent methods described above (Fig. 2c). It should be noted that the K_eq so determined, ≈6.6 × 10⁻⁶, is comparable to what was obtained from bulk restriction enzyme accessibility assays (4) (i.e., between 10⁻⁵ and 10⁻⁶).

As described above, the distributions of dwell times in each state give the kinetic rate constants at a given force. The effect of force on the kinetic rate constant can be fitted by an Arrhenius-like expression of the form (14)

where k_m represents the contribution of the nonnucleosomal DNA and the bead fluctuations to the absolute rates, k^o_w→u is the unwrapping rate at zero force, Δx_w^‡→u is the distance from the wrapped to the transition state at a given force, and ΔG^w→‡_stretch is the free energy correction due to stretching of the DNA. A similar expression can be used for the reverse reaction. By plotting lnk vs. force and extrapolating to zero force, values of k^o_w→u = 0.00038 s⁻¹ and k^o_u→w = 58.2 s⁻¹ are obtained. Thus, rewrapping of the DNA around the histone octamer is fast, with the nucleosome spending most of the time in the fully wrapped state. Our measured rate of unwrapping is slower than those reported from FRET measurements (5); this is most likely because we were observing a cooperative macroscopic unwrapping induced by a kinetic coordinate imposed by tension, whereas the FRET studies involve more microscopic, smaller, and local dynamics.

The High-Force Transition as a Function of Loading Rate.

When the fiber was pulled up to the high-force transition, attributed here to the unwrapping of the internal DNA turn around the histone octamer, the force-extension curves were no longer reversible, i.e., the rate of pulling was faster than the slowest relaxation time for the system. Successive force extension curves result in a distribution of forces for the high-force transition. The fraction, N(F, r), of molecules with the inner wrap still closed at a given force F can be described by (14, 17, 18)

At forces >3 pN, the above equation may be simplified to the following form:

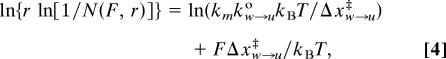where r is the loading rate (in pN/s) and k^o_w→u is the zero-force opening rate. The expressions above show that it is possible to determine the position of the transition state if the molecule is pulled at different loading rates r.

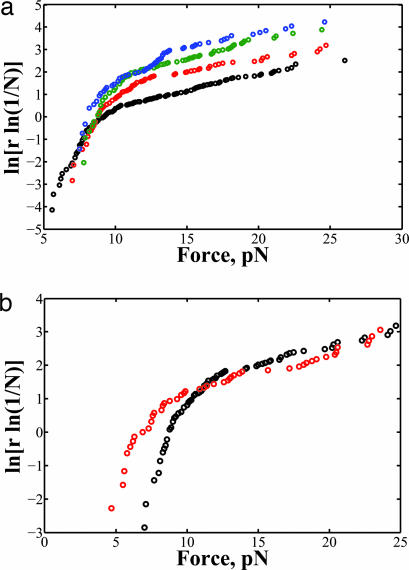
Plots of ln[r ln(1/N)] vs. force at loading rates of 2.4, 5.3, 7.8, and 11 pN/s are shown in Fig. 3. Unlike what is predicted by the general two-state model by Evans et al. and reported in previous single-molecule experiments (14, 15, 18), these plots were not linear. Therefore, the unraveling of the inner DNA wrap does not follow a simple two-state process, but rather involves multiple transition states and intermediates.

Fig. 3.

Behavior of the high-force transition. (a) The force distribution of the inner DNA wrap unraveling at loading rates, r, 2.4 (black), 5.3 (red), 7.8 (green), and 11 pN/s (blue). (b) Comparison of the force distribution at different ionic strengths at r = 5.3 pN/s. The high ionic strength buffer is indicated in red.

Effect of High-Salt Concentration on Mononucleosome Dynamics.

Interactions between the histone octamer and DNA have been shown to be mainly electrostatic (19). Thus, by increasing the buffer's ionic strength, it should be possible to weaken the electrostatic interactions between DNA and octamer and alter, consequently, the dynamic behavior of the mononucleosome. Here, we looked at the behavior of the mononucleosome in a buffer of twice the ionic strength than that used in the previous experiments.

Under the new buffer conditions, we still observed a high- and a low-force transition (Fig. 4a). However, the low-force transition (between 2 and 3 pN) resembles more a plateau than a well defined rip. Nevertheless, this low-force transition retains its reversible characteristics as long as the fiber was not pulled beyond the high-force transition. The area under the low-force transition yielded a ΔG(unwrap) of 23.2 (±1.17) kJ/mol, which is comparable to the values obtained in the lower ionic strength buffer. Although the low-force transition still displayed “hopping” under constant force, these data revealed that this behavior could longer be described by a simple two-state process (Fig. 4b), making it difficult to determine kinetic rate coefficients. These results indicate that the first wrap is very sensitive to changes in the ionic environment. The observed intermediates in hopping behavior also indicate that wrapping of the DNA around the histone octamer under increased shielded electrostatic interactions had become a less cooperative process.

Fig. 4.

Effect of high salt on the mononucleosome. (a) Typical force-extension curves of the mononucleosome in high ionic strength buffer. (b) Length vs. time trace of the low-force transition at 2.7 pN shows intermediates (indicated by arrow).

A distinct rip was still seen for the high-force transition. Plots of ln[r ln(1/N)] vs. force at different loading rates exhibited similar behavior to that observed at lower salt ionic strength, but the transitions were shifted to lower force values. This observation is again consistent with the idea that shielding the electrostatic interactions leads to reduced DNA–histone octamer affinity, lowering the force at which the inner wrap unraveled (Fig. 4b).

The behavior observed in the high ionic strength buffer points to a link between the strength of the electrostatic interactions and nucleosomal dynamic behavior. In the experiments presented here, increased ionic strength shields the histone octamer's positive charges, thus weakening its interaction with the DNA. Therefore, it is possible that histone modification might induce behavior similar to what is observed here in the high-salt experiments. During transcriptional activation, nucleosomes associated to certain genes are subjected to histone acetylation, which reduce the effective positive charge of the histone octamer (1, 20). In fact, Brower-Toland et al. studies (21) conducted on chromatin reconstituted with acetylated histones showed that the high-force rips occurred at lower forces compared with fibers reconstituted with nonacetylated histone octamers.

Theoretical Model.

To establish a connection between the experimental observations and the mechanical peeling of DNA off a nucleosome, we have constructed a model (see Supporting Text and, which are published as supporting information on the PNAS web site) of the nucleosomal core particle containing sufficient level of detail to rationalize the experiments. This model extends previous theoretical treatments of the nucleosome as a semiflexible polymer wrapped around a helical spool (22) by incorporating conformation fluctuations of the unbound DNA ends (23), thermal spool reorientation, and detailed interactions between DNA and core-particle proteins. Here, we extract several results from this model to infer the physical processes that underlie the experimentally observed force-extension behavior and hopping transitions.

The goal in this theoretical treatment is to achieve an entirely independent model of the nucleosomal core particle, i.e., avoiding a direct fit to the experimental data. We have fixed the spool geometry to that of the crystal structure (24), the ΔG(F = 0) of nucleosome formation used is −30 k_BT (4, 25, 26), and the DNA persistence length 40 nm, as determined for the current experimental conditions. Here, we adopted a simple binding model where we assumed a homogeneous profile for the binding energy of the DNA to the histone octamer, where the binding free energy per base pair, g_bind(F = 0), is −2.41 pN·nm.

Tension causes the nucleosome core particle to partly unwrap the DNA ends that emanate from the spool in the direction of the tension. The length of wrapped chain and the spool orientation dictate the orientation of the chain ends that emerge from the spool surface. The chain ends must bend substantially for bound chain lengths that do not end with orientations that conveniently align with the tension. The corresponding bending energy results in a free energy that oscillates with the amount of bound chain; these oscillations represent distinct thermodynamic states with various amounts of wrapped chain. Thus, a spool under tension exists in variously wrapped states that are separated by a half-integer number of wraps and characterized by different spool reorientation. These distinct states are a manifestation of the spool geometry rather than an assumption artificially inserted into the theory. We identify the experimentally observed rips with the nucleosome core particle transitioning through these stable wrap states determined by our theoretical model.

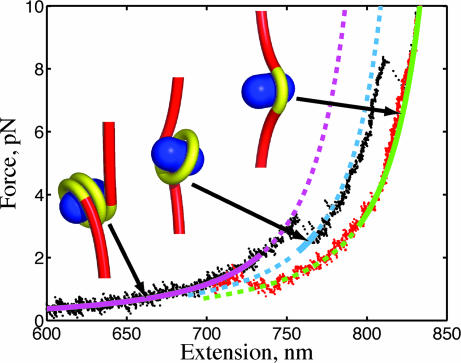
We proceeded to directly compare our theoretical model with the experimental force-extension behavior to verify that the experimental transitions agree with the predicted lengths released in the theoretical model. In Fig. 5, we plot a typical force-extension curve with the theoretical curves for the three distinct wrap states, identified by the minimum-energy spool conformations next to each curve. In this model, the thermodynamically preferred number of wraps corresponds to ≈1.5 (purple) at low tension to ≈1 wrap at intermediate tension (blue) and <0.5 wrap at high tension (green). The theoretical force-extension curve displays a solid segment to indicate the force range where each wrapped state has the lowest free energy. The dashed segment in these curves identifies, for each wrapped state, conditions where that state is thermodynamically stable but not preferred (i.e., such state doesn't have the lowest free energy). As a further test of our model, we note that the low-force equilibrium occurs at 2.25 pN in the theory, which compares reasonably well with the experimental value of 2.90 pN.

Fig. 5.

Force-extension curve of a spool model for the nucleosome. Theoretical curves for 1.5 wrap (purple), 1 wrap (blue), and 0.5 wrap (green) are plotted with experimental data for increasing (black) and decreasing (red) tension. The solid curve segment identifies that the state is thermodynamically preferred (minimum free energy), and the dashed segment indicates the state is stable but not preferred.

However, the homogeneous binding affinity model does not capture other experimental details. First, the two free-energy barriers from the homogeneous binding model are predicted to be equal in magnitude, contradicting the experimental observation that the low-force rip is reversible with a free energy barrier that is comparable to the thermal energy and the high-force rip is irreversible with a substantially larger free energy barrier. Second, we show in Fig. 2 that the hop size at the low-force transition is a decreasing function of the applied force. The homogeneous binding model predicts the opposite trend. Adding an energetic term to account for unfavorable DNA–DNA interactions (22) does not capture the experimentally observed decrease in the hop size with applied force. However, this trend is seen when we adopt a site-specific binding affinity into the model (see supporting information).

Conclusions

One limitation to studying nucleosomal arrays is the difficulty to distinguish between the behavior of individual nucleosomes, as well as the energetic contributions from DNA–protein interactions vs. nucleosome–nucleosome interactions. Here, we avoid these complications and ambiguities by manipulating a single nucleosome core particle. These studies clearly reveal two distinct transitions during the pulling and relaxation of individual nucleosomes. We found that the outer nucleosomal DNA wrap unravels at low forces (2–3 pN) and exhibits dynamic (hopping) behavior, whereas the inner wrap unravels at higher forces (up to 20–30 pN) and does not exhibit dynamic behavior. It should be noted that we also pulled DNA moieties containing repeating arrays of the 5S nucleosome positioning sequence as used by Brower-Toland et al., and the observed behavior for that construct reflected those we presented here (data not shown). Therefore, although the energetics for nucleosome formation may vary for different DNA sequences, the general mechanism for unraveling remains the same. We also were able to directly observe rewrapping events, confirming what was seen in the Gemmen et al. studies (11). Furthermore, our studies with the mononucleosome showed a decrease in hop size with increasing tension, a behavior that would have been difficult to observe with nucleosomal arrays. One possible culprit for this observed behavior is site-specific binding affinity of the DNA to the histone proteins (see supporting information); such effects would impact the force-dependent accessibility of the bound DNA.

The differences in energy between the inner and outer wraps, as well as the greater sensitivity of the outer wrap to ionic strength, suggest a significant difference in the types and extent of the interactions between the first and second wraps with the surface of the histone octamer. These results can be rationalized in terms of the nucleosome structure (24), which shows the inner wrap interacting more extensively with the histone octamer relative to the outer wrap. Also, the dramatic change in the unraveling behavior of the outer DNA wrap in the higher salt buffer confirms that the interactions of the outer DNA wrap with the histone octamer are dominated by electrostatic interactions, whereas the interactions between the inner DNA wrap and the histone octamer involve both electrostatic interactions, as evidenced by the lowering of the force at which the transition occurs with salt, and other stabilizing, nonelectrostatic interactions that help to counteract some of the destabilizing effects of high ionic strength. Unfavorable DNA–DNA interactions may also act to destabilize the outer wrap relative to the inner wrap (22).

The near-quantitative agreement between theory and experiment lends credence to the interpretation presented here that the hopping transitions corresponds to the peeling/unpeeling of DNA from the histone octamer. The thermodynamic preference and stability determined from the model reflect the experimentally observed hysteresis in the force-extension curve. Furthermore, by considering the differences in the binding affinities of different regions of the histone octamer to the DNA, as well as DNA–DNA repulsive effects (22), we were able to capture the observed experimental behavior, such as the relation between the hop size and tension.

Our results provide more insight to the energetic barriers an elongating RNA polymerase (and other DNA translocases) must overcome to move through a single nucleosomal core particle. Accordingly, an RNA polymerase molecule should be able to generate enough mechanical force to induce the opening of the first DNA wrap around the histone octamer (unpublished results) and should be able to generate forces of ≈20 pN or more to undo the second DNA wrap or, alternatively, rely on such chromatin modifying factors as histone acetyltransferases, ATP-dependent remodeling factors, and other transcription elongation factors.

Materials and Methods

DNA Template.

A 282-bp piece of DNA containing the 601 nucleosome positioning sequence (12), kindly provided to us by Jonathan Widom (Northwestern University, Evanston, IL), was inserted into plasmid pP1A2–6 (7) between ClaI and SbfI. For the optical trapping experiments, a 2,582-bp piece of DNA was constructed by using PCR. The DNA was labeled on one end with digoxigenin (Roche, Mannheim, Germany) and on the other with biotin-dNTPs (Invitrogen, Carlsbad, CA) using Klenow exo- (New England Biolabs, Ipswich, MA). The 601 insert was located around the center of the PCRed DNA. For the AFM studies, the insert was flanked by 1,099 bp of DNA on one end and by 2,301 bp of DNA on the other.

Reconstitution of Nucleosomes.

Chicken erythrocyte histone octamers, kindly provided by Jonathan Widom, was used to reconstitute the mononucleosome. Ten micrograms of DNA was mixed with the histone octamers at a DNA/histone octamer molar ratio of 1:1 in 10 mM Tris·HCl/1 mM EDTA/2 M NaCl/0.5 mM phenylmethylsulfonyl fluoride/1 mM benzamidine hydrochloride and loaded onto microdialysis buttons, made from thin-walled PCR tubes. Reconstitution reactions were carried out as described by Thåstrom et al. (27). The recovered reconstituted samples were stored on ice at 4°C until further use.

AFM Studies.

The mononucleosomes were fixed via dialysis at 4°C in 0.1% glutaraldehyde in 1 mM EDTA (pH 8.0) for 24 h. Excess glutaraldehyde was removed by further dialyzing at 4°C for 24 h against 1 mM EDTA (pH 8.0) (28). For AFM imaging, 1:50 dilutions with 10 mM Tris-HCl/1 mM EDTA of the samples were deposited onto mica surfaces that were treated with 1 mM spermidine for 5 min, washed with distilled water, and dried with N₂ gas. AFM images were obtained by using the Nanoscope IIIA Scanning Probe Microscope (Digital Instruments, Santa Barbara, CA). Analysis of the AFM images was done by using WSxM and SigmaPlot.

Optical Trap Experiments (29).

The mononucleosome was tethered between a streptavidin-coated polystyrene bead (Spherotech, Libertyville, IL), held by a micropipette via suction, and an antidigoxigenin-coated polystyrene bead, held in the optical trap (Fig. 1a). Experiments were done in 10 mM Tris-acetate/50 mM potassium acetate (KOAc)/10 mM magnesium acetate/1 mM DTT/0.1 mg/ml BSA. For the high ionic strength experiments, the KOAc concentration was increased to 200 mM. The mononucleosomal fibers were stretched at a constant velocity relative to the trapped bead.

Abbreviation

AFM

atomic force microscopy.