Population Pharmacokinetics of Atazanavir in Patients with Human Immunodeficiency Virus Infection

Abstract

Atazanavir (ATV) is a new azapeptide protease inhibitor recently approved and currently used at a fixed dose of either 300 mg once per day (q.d.) in combination with 100 mg ritonavir (RTV) or 400 mg q.d. without boosting. ATV is highly bound to plasma proteins and extensively metabolized by CYP3A4. Since ATV plasma levels are highly variable and seem to be correlated with both viral response and toxicity, dosage individualization based on plasma concentration monitoring might be indicated. This study aimed to assess the ATV pharmacokinetic profile in a target population of HIV patients, to characterize interpatient and intrapatient variability, and to identify covariates that might influence ATV disposition. A population analysis was performed with NONMEM with 574 plasma samples from a cohort of 214 randomly selected patients receiving ATV. A total of 346 randomly collected ATV plasma levels and 19 full concentration-time profiles at steady state were available. The pharmacokinetic parameter estimates were an oral clearance (CL) of 12.9 liters/h (coefficient of variation [CV], 26%), a volume of distribution of 88.3 liters (CV, 29%), an absorption rate constant of 0.405 h⁻¹ (CV, 122%), and a lag time of 0.88 h. A relative bioavailability value was introduced to account for undercompliance due to infrequent follow-ups (0.81; CV, 45%). Among the covariates tested, only RTV significantly reduced CL by 46%, thereby increasing the ATV elimination half-life from 4.6 h to 8.8 h. The pharmacokinetic parameters of ATV were adequately described by a one-compartment population model. The concomitant use of RTV improved the pharmacokinetic profile. However, the remaining high interpatient variability suggests the possibility of an impact of unmeasured covariates, such as genetic traits or environmental influences. This population pharmacokinetic model, together with therapeutic drug monitoring and Bayesian dosage adaptation, can be helpful in the selection and adaptation of ATV doses.

Atazanavir (ATV) is a novel and recently marketed azapeptide with a potent inhibitory effect on human immunodeficiency virus (HIV) protease (19). Unlike other HIV protease inhibitors (PIs), ATV does not seem to cause insulin resistance or dyslipidemia when used as a single PI in triple-therapy regimens (9, 22). Its pharmacokinetic profile is considered to allow once-daily dosing with a low pill burden (13). ATV is currently used at a fixed dose of either 300 mg once per day (q.d.) in combination with 100 mg of ritonavir (RTV) or, less frequently, at 400 mg q.d. without boosting (4).

Atazanavir is bound to both α₁-acid glycoprotein and albumin to similar extents (89% and 86%, respectively) (13) and independently of its concentration in plasma. The drug is metabolized mainly by hepatic cytochrome P450, primarily the CYP3A4/CYP3A5 isoenzymes (6). ATV inhibits UDP glucuronyltransferase UGT1A1 (12, 28), CYP3A, and P-glycoprotein transport in vitro (18). Therefore, as with other PIs (10), the potential for drug-drug interactions is high, and care should be taken when selecting ATV for coadministration (15). Some unexpected drug interactions, including those with tenofovir (25) and proton pump inhibitors (11), have been identified. Large interpatient and intrapatient variabilities in ATV disposition have been previously reported (J.-B. Guiard-Schmid et al., Abstr. 3rd IAS Conf. HIV Pathog. Treat., abstr. 3.2C13, 2005), and poor adherence to recommendations regarding food intake or drug interactions may further weaken antiviral coverage. Quantifying and explaining the variability in exposure are crucial for better pharmacotherapy management, as insufficient concentrations in plasma are clearly associated with a rebound in viral load and an increased risk for the emergence of viral resistance. Recent studies have shown that exposure, measured by the area under the concentration-time curve (AUC), predicted both viral suppression and increased serum bilirubin concentration (2; D. Gonzalez de Requena et al., Abstr. 6th Int. Workshop Clin. Pharmacol. HIV Ther., abstr. 60, 2005; E. O'Mara et al., 41st Intersci. Conf. Antimicrob. Agents Chemother., abstr. A-507, 2001). Gonzalez de Requena et al. recommended that the trough plasma concentration (C_trough) of atazanavir should range between 150 and 850 ng/ml, which was suggested as the optimal drug concentration interval associated with the highest probability of virological response and with the lowest probability of unconjugated-bilirubin increase. Therefore, new strategies based on target concentration dosage adaptation have gained increasing importance for better management of HIV-infected patients (20), and therapeutic drug monitoring (TDM) with Bayesian dosage adaptation has been proposed as a way to individualize therapy according to plasma ATV concentration. This approach must be based on accurate knowledge of the drug's average pharmacokinetic profile and variability.

The objectives of this study were to determine the population pharmacokinetic parameters of ATV and its variability in patients receiving ATV, either alone or with the RTV booster, and to define factors which might explain its pharmacokinetic variations. The population analysis was used to build up a Bayesian strategy for dosage regimen individualization based on TDM.

MATERIALS AND METHODS

Study population.

HIV-1 infected patients participating in the Swiss HIV Cohort Study (www.shcs.ch) were studied. All patients were taking ATV as part of their antiretroviral regimens and had at least one plasma ATV concentration sample available for the analysis. Patients received ATV either alone or in combination with RTV. Most data were collected at random time points (sparse data) from June 2003 to January 2005, within the scope of a routine TDM program, in accordance with local treatment guidelines. Intensive pharmacokinetic data (rich data) from a previous drug-drug interaction study of 13 HIV-infected patients (7) were also included in the model-building database.

All samples were obtained under steady-state conditions (i.e., the drug regimen was unchanged for at least 1 month). In addition to dosing- and sampling-time information, the following data were recorded for each patient: sex, body weight, height, age, race, CD4⁺ T-cell count, viral load, serum creatinine level, and concomitant medication. Total bilirubin concentrations were available for a subset of patients (109 bilirubin levels for 78 patients).

Analytical method.

Blood samples (5 ml) were collected into lithium heparin or potassium-EDTA Monovette syringes (Sarstedt, Nümbrecht, Germany). Plasma was isolated by centrifugation, virus inactivated in a water bath at 60°C for 60 min, and stored at −20°C until analysis. Plasma ATV levels were determined by reverse-phase high-performance liquid chromatography according to a validated method (8). The calibration curves are linear up to 10 μg/ml, with a lower limit of quantification of 0.2 μg/ml. The method is precise, with mean interday coefficients of variation (CVs) within 1.1 to 6.1%, and accurate (range of interday deviations, +0.3 to +2.3%). Our laboratory is included in an external quality assurance program (Association for Quality Assessment in TDM and Clinical Toxicology, The Hague, The Netherlands).

All concentrations were initially included in the pharmacokinetic analysis.

Model-based pharmacokinetic analysis.

The model-based pharmacokinetic analysis was performed using the NONMEM computer program (version V running with NM-TRAN, version II) (17). This program uses mixed (fixed and random)-effects regression to estimate population means and variances of the pharmacokinetic parameters and to identify factors which influence them.

Structural model.

A stepwise procedure was used to find the model that fitted the data best. First, one- and two-compartment models with first-order absorption from the gastrointestinal tract were compared based on the data from the 13 patients who underwent intensive kinetic investigation (rich data). The analysis of the entire population (sparse data) was then conducted on the basis of these initial estimates. The final pharmacokinetic model was a one-compartment model with first-order absorption and elimination. The estimated parameters are the apparent clearance (CL), the apparent volume of distribution of the central compartment (V), and the absorption rate constant (k_a). Since ATV was only administered orally, CL and V represent apparent values (CL/F and V/F, respectively, where F is the oral bioavailability). A relative bioavailability for the sparse data set (F_sparse) was allowed in the model to determine a potential scale shift associated with possible undercompliance for some patients, while F_rich was fixed to a value of 1.

Statistical model.

Exponential errors following a log-normal distribution were assumed for the description of the interpatient variability of the pharmacokinetic parameters and were shown by the equation , where θ_j is the individual pharmacokinetic parameter of the jth individual, θ is the geometric average population value, e is the Euler's number, and ηj, is the random effect value, which is an independent, normally distributed effect with a mean of 0 and a variance of Ω.

A combined proportional-and-additive error model was assigned to the intrapatient (residual) variability. Separate residual-error models were used for the rich- and sparse-data sampling cohorts.

Covariate model.

The covariate analysis was performed using a stepwise approach. Individual Bayesian parameter estimates were obtained based on the final model without any covariates, and the relationship between those individual estimates and the covariates (demographic characteristics and comedications) was analyzed using a generalized additive model (GAM) (14, 16). This approach enables a straightforward display of the role of the various covariates. It uses a stepwise addition/deletion method, where each covariate is introduced in the model through any prespecified functional linear or nonlinear representation. At each step, the model is improved by the addition or deletion of the single term that results in the largest decrease in the Akaike information criterion (1). The search stops when the Akaike information criterion reaches a minimum value. Calculations were used with the statistical program S-plus (version 3; Statistical Sciences, Inc., Seattle, WA). The population model was built up using NONMEM on the basis of the results of the GAM analysis. Potentially influential covariates were incorporated sequentially into the pharmacokinetic model. The typical value of a given parameter θ (e.g., CL) was modeled to depend linearly on the covariate X (such as body weight; categorical covariates being coded as indicator variable 0 or 1) and was shown by the equation θ = θ_a (1 + θ_b X), where θ_a is the mean estimate and θ_b is the relative deviation of the mean due to the X covariate.

The baseline covariates (X) evaluated for inclusion during model building were sex, race, age, body weight, creatinine clearance, and comedications (Table 1). At the end of the analysis, all patient characteristics that showed an influence on the parameters were evaluated again by comparing the full model (with all factors included) with a model from which each of the factors was deleted sequentially.

TABLE 1.

Characteristics of 214 model-building patients and 78 model validation patients evaluated in the population pharmacokinetics analysis of atazanavir

Baseline characteristic	Model-building patients		Model validation patients
	Value	% or range	Value	% or range
Sex (men/women) (no.)	154/60	72/28	52/26	67/33
Median age (yr)	42	19-78	42	20-71
Median body wt (kg)	69	43-117	70	44-97
Median ht (cm)	173	148-194	172	148-192
Median creatinine level (mmol/liter)	83	22-165	88	51-193
Ethnicity (no. of patients)
Caucasian	183	86	64	82
African	20	9	11	14
Asian	7	3	3	4
Hispanic	4	2
Concomitant medications
Protease inhibitors
Ritonavir	167	78	49	63
Lopinavir-ritonavir	11	5	13	17
Amprenavir	3	1	4	5
Saquinavir	9	4	15	19
Nelfinavir	1	0.5	2	3
Reverse transcriptase inhibitors
Efavirenz	30	14	17	22
Nevirapine	8	4	8	10
Lamivudine	116	54	45	58
Zidovudine	44	21	21	27
Stavudine	12	6	7	9
Didanosine	68	32	10	13
Abacavir	24	11
Tenofovir	124	58	36	46
Fusion inhibitor T20	7	3	1	1
CYP450 inducers
CYP450 inhibitor fluconazole	1	0.4
Pump inhibitors omeprazole and esomeprazole	3	1

Parameter estimation and model selection.

The data were fitted by use of the first-order conditional method (FOCE in NONMEM). Goodness-of-fit statistics and graphical displays were used to compare models. The goodness-of-fit criterion was the change in the objective function (ΔOF) resulting from the addition of a covariate, which approximates a χ² distribution and can be regarded as statistically significant (P < 0.05) if it exceeds 3.8 for one additional parameter. A simulation based on the final pharmacokinetic estimates was performed with NONMEM using 1,000 individuals to calculate the 95% prediction intervals. The concentrations encompassing the 2.5th and 97.5th percentile at each time point were retrieved to construct the prediction interval. The figures were generated with S-PLUS (Statistical Sciences; version 3, 2000).

Model validation.

Model validation was based on both qualitative and quantitative evaluations of the predictive performance of the model using an external data set of sparse observations collected from February 2005 to July 2005.

The final population parameter and variance estimates were used to calculate concentration predictions for the validation data set. The predictions were then compared with actual concentration values (3). The mean prediction error and root mean squared prediction error were calculated to derive bias and precision at both population and individual levels, using population predictions and individual predictions, respectively, versus actually observed concentrations (24). Diagnostic plots (observations versus population and individual predictions; residuals versus predictions and covariates) were also used to visualize how well the model was able to predict the external data set.

Dosage regimen individualization.

The results of the population pharmacokinetic analysis can be used to build up a Bayesian approach for exploiting drug concentration measurements (23). Considering the average population value of the kinetic parameters, θ_pop (at a given level of influential covariates), their respective variances, ω², the residual variability that includes the proportional component (σ_prop²) and the additive component (σ_add²), and the observed single plasma concentration, C_obs, at time postdose, t_obs, the a priori values of CL_pop, V_pop, k_a,pop, and F_sparse,pop can be altered according to the Bayesian strategy to meet a posteriori maximum likelihood estimates for an individual patient of CL_ind, V_ind, F_ind, and k_a,ind, which minimize the following function:

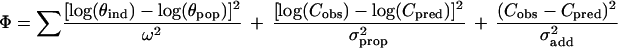in which the concentration predictions, C_pred, are calculated from the individualized parameters, θ_ind. Because exponential (constant CV) error models were assumed during the population analysis, the θ and C values should be entered as logarithms in the above equation.

A simulation based on the final pharmacokinetic estimates and their variabilities was also performed with NONMEM using 1,000 individuals to derive an ATV dosage regimen with a consensual therapeutic target of 150 ng/ml that would be reached by at least 80% of the patients.

Pharmacodynamic analysis.

Individual Bayesian estimates of peak and trough plasma atazanavir concentrations and the AUC from 0 to 24 h (AUC_0-24) were used to explore their relationships with treatment outcomes (viral load and CD4⁺ T-cell count) and tolerability (bilirubinemia). These relationships among plasma ATV concentrations and viral load, CD4⁺ T-cell count, and bilirubin concentration were explored by using the Pearson correlation.

Logistic regression was used to assess the effects of ATV exposure on viral suppression, CD4⁺ T-cell count, and hyperbilirubinemia, defined according to the preset cutoff values of 400 RNA copies/mm³, 350 cells/mm³, and 21 μmol/liter, respectively. The associations among different plasma ATV C_trough levels (150, 500, 700, and 850 ng/ml), elevated bilirubin (>21 μmol/liter), and failure (viral load above 400 copies/mm³) were assessed with a chi-square test approach. Statistical significance was assigned at a P value of <0.05.

RESULTS

Data.

A total of 574 samples from 214 patients were included in the population analysis. Most blood samples (n = 346) were drawn periodically at 1- to 3-month intervals during follow-up visits (sparse data set). In addition to random samples, 19 full concentration-time profiles at steady state were available from 13 patients receiving ATV at 300 mg q.d. with RTV boosting (n = 228; 12 time points per pharmacokinetic profile before the dose and from 0.5 to 24 h after drug intake; rich data set) (7). Median numbers of 1 (range, 1 to 6) and 12 (range, 12 to 24) samples per subject were available in the sparse and the rich data sets, respectively. Of the 346 sparse samples used for model building, 43 (12%) were collected up to 2 h after dosing, 88 (23%) were obtained between 2 and 8 h after dosing, and the remaining 215 (65%) were taken later than 8 h after drug intake. Patients received once-daily RTV-boosted ATV (n = 167; most at 300 mg q.d.) or once-daily unboosted ATV (n = 47; mostly at 400 mg q.d.), always associated with other antiretroviral agents.

Table 1 lists the baseline demographic characteristics of these patients and their concomitant medications. The baseline demographics for the validation and model-building data sets were similar.

Population pharmacokinetic analysis.

The measured concentrations ranged between 50 and 6,680 ng/ml. A one-compartment model with first-order absorption from the gastrointestinal tract was found to describe the rich data set appropriately, and no further reduction in the objective function (ΔOF = −0.0) was observed with the use of a two-compartment model. The introduction of a lag time improved significantly the fit (ΔOF = −14.2). The assignment of interpatient variability values to the CL (ΔOF = −134.5), the V (ΔOF = −9.9), and the k_a (ΔOF = −17.2) significantly improved the description of the data. The final population parameters of the rich data with their intersubject variability were a CL of 6.21 liters/h (CV, 33%), a V of 124 liters (CV, 34%), a k_a of 0.405 h⁻¹ (CV, 122%), and a lag time of 0.876 h.

These parameter estimates were used as the initial estimates for the model, including both the sparse and rich data sets. Since the absorption rate constant, k_a, and the lag time could not be estimated appropriately due to the few measurements during the absorption phase, the population mean estimate and variance of k_a and the mean estimate of the lag time were fixed to the final values obtained from the rich data set. The introduction of a relative bioavailability value, F_sparse, according to the data set (keeping the value for the rich study fixed at unity) as a means of determining the scale shift (if any) associated with undercompliance in the sparse study revealed a significant improvement in the fit (ΔOF = −25.5). The use of two distinct components of residual error according to the data set (rich and sparse studies) improved the fit as well (ΔOF = −12.2). The assignment of a proportional-and-additive error model to the residual intrapatient variability improved the pharmacokinetic model significantly compared to the assignment of the proportional-error model alone (ΔOF = −29.5). The error variances of the concentrations obtained in the rich data study (CV, 19%; standard deviation [SD], ±375 ng/ml) were expectedly smaller than in the population study (CV, 38%; SD, ±486 ng/ml). Interpatient variabilities were assigned to CL, V, and k_a, as suggested by the rich data study model. The variance in k_a was not different from that estimated in the rich data study (η = 1.49; CV, 122%; ΔOF = +0.4). The addition of an interpatient variability to F_sparse (CV, 50%) resulted in a better description of the data (ΔOF = −19.3) and captured some variability of CL, which decreased from 49% to 29% (CV). The variabilities in both F_sparse and CL were necessary, however, to fit the data appropriately (ΔOF = +141 when the variability of CL is fixed at 0).

The pharmacokinetic estimates and the variabilities (CVs) of the population model without covariates were a CL of 7.12 liters/h (27%), a V of 85 liters, a k_a of 0.405 h⁻¹ (122%), a lag time of 0.88 h, and an F_sparse of 0.732 (52%).

A GAM analysis was conducted to select the covariates which could potentially influence ATV disposition. Among the demographic covariates and the comedications included, only body weight and ritonavir and nevirapine coadministration appeared to be highly linearly correlated with CL. Small influences on CL of age, sex, race, creatinine clearance, and coadministration of a nonnucleoside reverse transcriptase inhibitor (efavirenz plus nevirapine), tenofovir, abacavir, lamivudine, and antiacids could be detected as well.

The model-building steps for the covariate analysis in NONMEM were based on the results of the GAM analyses and are summarized in Table 2. The inclusion of demographic covariates (age, race, sex, and body weight) with CL did not significantly improve the pharmacokinetic model. Among the comedications presenting a potential influence on CL, only ritonavir (ΔOF = −27.3) significantly improved the fit, showing a reduction in atazanavir CL of 46% after the administration of ritonavir. Assigning ritonavir as a covariate of F resulted in a similar fit (ΔOF = −23.3). However, since ATV is a low-extraction drug and highly bound to proteins, the effect of ritonavir on CL was preferred.

TABLE 2.

Summary of the models used to examine the influence of patient covariates on atazanavir oral CL and oral V

Hypothesisa	Modelb	θa	θb	ΔOFc
Demographic/physiologic characteristics
Does BW influence CL?	θa (1 + θb · BW)	7.32	0.2	−2.2
Does age influence CL	θa (1 + θb · age)	7.35	−0.3	−2.6
Does sex influence CL? (male: sex = 1)	θa (1 + θb · sex)	7.24	0.038	−0.1
Does ethnicity influence CL?
Caucasian (q = 0) vs non-Caucasian (q = 1)		8.20	6.78	−3.0
African (q = 0) vs non-African (q = 1)	θa · (1 − q) + θb · q	6.80	8.4	−3.1
Asian (q = 0) vs non-Asian (q = 1)		7.28	4.8	−1.5
Hispanic (q = 0) vs non-Hispanic (q = 1)	θa (1 − θb · CLCR)	7.12	12.9	−1.9
Does CLCR influence CL?		7.14	−0.2	−1.7
Concomitant HIV medications
RTV	CL = θa · (1 + θb · RTV)	12.9	−0.46	−29.5
	F = θa · (1 + θb · RTV)	0.81	0.85	−23.3
NVP	CL = θa · (1 + θb · NVP)	7.12	0.41	−1.5
NNRTI	CL = θa · (1 + θb · NNRTI)	7.08	0.08	−0.6
TNV	CL = θa · (1 + θb · TNV)	6.8	−0.16	−3.6
ABC	CL = θa · (1 + θb · ABC)	7.00	0.14	−1.2
3TC	CL = θa · (1 + θb · 3TC)	7.47	−0.06	−0.5
Other medications
AA	CL = θa · (1 + θb · AA)	7.09	0.62	−2.3

^aCL_CR, creatinine clearance; q, an indicator variable; NVP, nevirapine; NNRTI, nonnucleoside reverse transcriptase inhibitor (efavirenz plus nevirapine); TNV, tenofovir; ABC, abacavir; 3TC, lamivudine; AA, antacids.

^bBody weight, age, and CL_CR are expressed as the relative deviations of the individual body weight, age, and CL_CR from the population mean.

^cDifferences in the NONMEM objective function (ΔOF) compared to the basic structural model, including no covariates and parameter estimates of a CL of 7.12 liters, a V of 83.5 liters, a k_a of 0.405 h⁻¹, an F_rich of 1, and an F_sparse of 0.732.

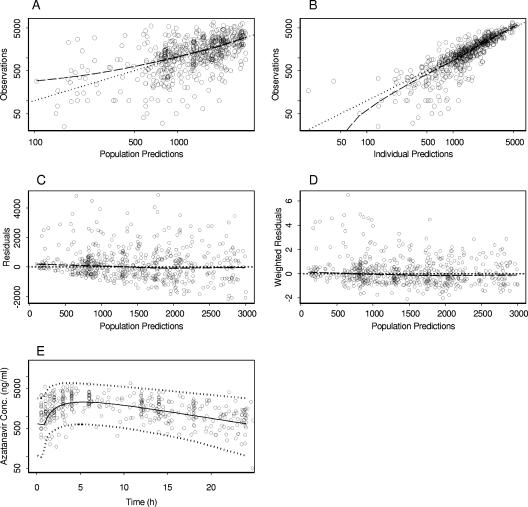
The parameter estimates for the final model are given in Table 3. Figure 1 shows the overall goodness of fit of this model to the data, along with the average population prediction and the 95% prediction interval.

TABLE 3.

Population pharmacokinetic parameter estimates of atazanavir

Parametera	Population mean		Interpatient variabilityb
	Estimate	SEc (%)	Estimate (%)	SEd (%)
CL/F (liters/h)	12.9	17	26	56
θritonavir	−0.46	18.0
V/F (liters)	88.3	9.5	29	80
ka (h−1)	0.405e		122e
Lag time (h)	0.88e
Frich study	1.0f
Fsparse study	0.81g	10.3	45	49
σprop,rich study (CV, %)h	19	75d
σadd,rich study (SD, ng/ml)i	±370	55
σprop,sparse study (CV, %)h	30	69d
σadd,sparse study (SD, ng/ml)i	±542	35

^aCL/F, mean apparent clearance; V/F, mean apparent volume of distribution; k_a, mean absorption rate constant; F, bioavailability.

^bEstimates of variability are expressed as CVs (%).

^cStandard errors of the estimates (SE) are defined as SE/estimate and are expressed as percentages.

^dStandard errors of the coefficient of variations, taken as [rad]SE_estimate/estimate[/rad], are expressed as percentages.

^eFixed to the estimate obtained in the rich data study.

^fSet at 1 because intravenous drug administration was not available.

^gRelative bioavailability to account for undercompliance in the sparse data study (see text).

^hResidual variabilities in the ATV plasma concentrations were associated with the proportional error term for the rich and the sparse data sets and expressed as CVs (%).

ⁱResidual variabilities in the ATV plasma concentrations were associated with the additive error term for the rich and the sparse data sets and are expressed as SDs.

FIG. 1.

Goodness-of-fit plots of the final model for atazanavir. The heavy broken lines are smoothed plots of the ordinate values. (A) A log-log plot of observed concentrations versus population predictions; the dotted line is the line of identity. (B) A log-log plot of observations versus individual predictions; the dotted line is the line of identity. (C) Population residuals versus population predictions; the dotted line is at the ordinate value of 0. (D) Population weighted residuals versus population predictions; the dotted line is at the ordinate value of 0. (E) Plasma concentrations in 136 HIV patients (circles) receiving atazanavir at 300 mg once daily, boosted with ritonavir, with the average population prediction (solid line) and a 95% prediction interval (dashed lines) shown.

Model validation.

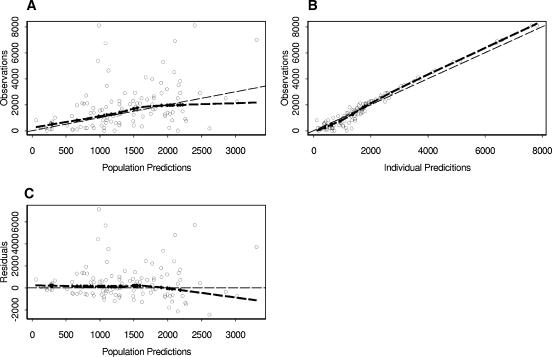
A total of 112 sparse data observations from 78 patients were included in the validation set database. The performances of both the population and individual predictors are satisfying, with biases of 4% and 15%, respectively. The higher bias observed for individual predictors suggests a slight model misfit, mainly at the high concentration values. We think that a selection bias in the validation data set, which included patients with different combinations of drugs that were not included in the model, might have had some unmeasured impact on the disposition of atazanavir. There remained a high variability, with root mean square prediction errors of 151% and 73% for the population and the individual predictions, respectively. These results, together with the plots of the population and individual predictions versus the observations (Fig. 2), confirm the absence of bias and the large unexplained interpatient variability.

FIG. 2.

Goodness-of-fit plots of the validation model for atazanavir. The heavy broken lines are smoothed plots of the ordinate values. (A) Observed concentrations versus population predictions; the dotted line is the line of identity. (B) Observations versus individual predictions; the dotted line is the line of identity. (C) Population residuals versus population predictions; the dotted line is at the ordinate value of 0.

Treatment efficacy and tolerability.

Viral load values ranged from 4 to 3,965,000 copies/mm³. Viral suppression (according to the reference cutoff of ≤400 copies/mm³) was observed in 69% of patients. CD4⁺ T-cell counts ranged from 9 to 1,498 cells/mm³. No correlation between individual Bayesian estimates of ATV exposure or concentrations (AUC_0-24, C_max, and C_trough) and viremia or CD4⁺ T-cell count was observed in this randomly selected patient population, using the continuous variables (linear regression, P ≥ 0.6 and P > 0.7, respectively) or the reference cutoffs of ≤400 copies/mm³ for viral load and ≥350 cell/mm³ for CD4⁺ T cells (logistic regression, P > 0.3 for both outcomes). The chi-square test between dichotomized ATV C_trough values (150, 500, 700, 850 ng/ml) and virological failure shows no statistically significant association as well (P > 0.3).

The total bilirubin concentration was elevated in 29% (32/109) of patients. Atazanavir exposure and concentrations were weakly, directly correlated with the total bilirubin level (r² = 13%, P = 0.0001; r² = 10%, P = 0.001; and r² = 7%, P = 0.006 for C_trough, AUC_0-24, and C_max, respectively). The chi-square test between dichotomized ATV C_trough values and bilirubin levels shows a statistically significant association between the following ATV cutoffs: 500 (P = 0.05), 700 (P = 0.01), and 850 (P = 0.02) ng/ml. The logistic regression between the ATV C_trough threshold of 850 ng/ml and a bilirubin elevation give an odds ratio of 3.14 (P = 0.02).

Dosage regimen adaptation.

A dosage adaptation is proposed based on the results of the population analysis, which assigned interpatient variabilities to oral CL, V, F_sparse, and k_a. The average CL_pop values without and with ritonavir were 12.9 liters/h and 7.0 liters/h, respectively; the V was 88.3 liters; the k_a was 0.405 h⁻¹; and the F_sparse was 0.81. After having measured a C_obs at t_obs, the a priori CL_pop, F_sparse,pop, V_pop, and k_a,pop values can be altered according to the Bayesian strategy to meet a posteriori maximum likelihood estimates of CL_ind, F_sparse,ind, V_ind, and k_a,ind corresponding to the individual patient. The minimization of the function Φ has no analytical solution but can be solved numerically after integrating the CL_pop, F_sparse,pop, V_pop, and k_a,pop population estimates with their respective ωCL², ωF_sparse², ωV², and ωka² variances; integrating the C_obs value with its additive and multiplicative residual errors σ_add² and σ_prop²; and integrating the corresponding prediction, C_pred, given by the Bateman equation at steady state. Such individual estimates of CL_ind, F_ind, V_ind, and k_a,ind enable the adaptation of an ATV dosing regimen to bring the concentrations to the effective target level to optimize viral suppression. For a patient, the predicted population coverage and C_trough levels are 1,046 ng/ml and 177 ng/ml, respectively, at the standard regimen of 400 mg ATV q.d. or 1,446 ng/ml and 600 ng/ml, respectively, at 300 mg ATV q.d. with ritonavir. However, taking into account the variability, we observe that a dosage of 800 mg q.d. or 100 mg twice daily of a nonboosted regimen would be necessary to ensure the maintenance of ATV levels above the threshold of 150 ng/ml in 80% of patients.

DISCUSSION

Pharmacological issues such as poor adherence to treatment, intolerance, and large interpatient differences in blood concentration following standard dosing regimens represent important determinants of HIV treatment failure. Despite a pharmacokinetic profile characterized by large interpatient and intrapatient variability, the same dose of ATV is currently administered to all patients without regard to differences in systemic blood and tissue disposition. Dosage individualization based on the ATV pharmacokinetic profile and variability in the target population of patients receiving ATV either alone or in combination with low-dose RTV would represent a suitable strategy for HIV treatment optimization.

The pharmacokinetic estimates of our population analysis are in agreement with previously reported data (CL = 7.09 liters/h, V = 83 liters [C. Solas et al., Abstr. 6th Int. Workshop Clin. Pharmacol. HIV Ther., abstr. 52, 2005]; and CL = 7.38 liters/h [25] in the presence of RTV). Food has been shown to greatly influence the absorption rate and bioavailability of ATV and may thus represent a relevant determinant of ATV variability in this analysis, as the relationship between food and drug intake was neither controlled nor recorded for the sparse data set (6). As expected, the coadministration of low-dose RTV reduced oral clearance by 46%, increasing the ATV elimination half-life from 4.6 h to 8.8 h and explaining a part of the interpatient variability of oral clearance. The elimination half-life observed was in accordance with those of previously reported studies (8.6 h [5], 8.1 h [Solas et al., Abstr. 6th Int. Workshop Clin. Pharmacol. HIV Ther., 2005], and 8.6 h [25] in the presence of RTV and 6.5 h without RTV [5]). Among the demographic covariates tested, no clear influence on ATV kinetics could be detected beyond the RTV effect. The absence of the effects of sex and age confirm previous data obtained after single-dose administration in healthy volunteers (E. O'Mara et al., Abstr. 1st IAS Conf. HIV Pathog. Treat., abstr. 180, 2001). Body weight did not affect ATV pharmacokinetics, and we could not find any study that explored the possible effect of this variable. For ethnicity, the presence of a majority of Caucasians in the present study (86%) may have limited the power to identify an association.

Since ATV is metabolized mainly by CYP3A4 enzymes, interactions with drugs acting on those isoforms were expected. A limited number of patients received comedications (other than antiretroviral therapy) expected to interfere with ATV disposition, e.g., CYP3A4 inducers or inhibitors and antiacid drugs. Thus, the study had limited power to detect an association between these comedications and ATV kinetics. In addition, the presence of RTV, a potent CYP3A4 and P-glycoprotein inhibitor coadministered in 78% of the study population, may have either compensated for decreases in drug exposure induced by efavirenz or other CYP3A4 inducers or masked an effect of the less-potent inhibitors. Since the activity of the cytochrome P450 varies greatly in the population, it is difficult to estimate the magnitude and relevance of such a mutual interaction in a randomly selected cohort of patients.

A correlation between plasma ATV trough concentrations and antiviral efficacy has been reported in some studies (6; Gonzalez de Requena et al., Abstr. 6th Int. Workshop Clin. Pharmacol. HIV Ther.) but not all (27). The combination of ATV trough levels and the baseline resistance mutation of viral protease (genotypic inhibitory quotient) seems to be a more robust virological response marker (2, 26) (I. Pellegrin et al., Abstr. 14th Int. HIV Drug Resist. Workshop, abstr. 8, 2005; Solas et al., Abstr. 6th Int. Workshop Clin. Pharmacol. HIV Ther.). In our study, we did not observe a relationship between ATV exposure and antiviral effectiveness. However, no viral genotyping was available for analysis, and our transversal study design could not correctly address this question.

The weak direct correlation between C_trough and bilirubin concentration is in agreement with previous observations (Gonzalez de Requena et al., Abstr. 6th Int. Workshop Clin. Pharmacol. HIV Ther.) and suggests the influence of additional factors such as the impact of UGT1A1 gene polymorphism on bilirubin elevation recently reported by Rotger et al. (21).

The recommended C_trough interval for atazanavir is 150 to 850 ng/ml (Gonzalez de Requena et al., Abstr. 6th Int. Workshop Clin. Pharmacol. HIV Ther.). Our study showed that patients with an atazanavir C_trough higher than 850 ng/ml presented a threefold-higher risk of bilirubin elevation than patients with a C_trough lower than that level. Our results strengthen the predictive value of the atazanavir C_trough threshold of 850 ng/ml on the bilirubin elevation. We noticed that 24% and 50% of patients presented with a bilirubin elevation when their C_trough values were lower and higher than 850 ng/ml, respectively, which is in accordance with the results reported by Gonzalez de Requena et al. (Abstr. 6th Int. Workshop Clin. Pharmacol. HIV Ther.). Looking at the lower limit of the suggested therapeutic range, 41% of patients without and 0% of patients with RTV had a C_trough below 150 ng/ml. Because of the short half-life and the high variability of ATV kinetics, the adjustment of the C_trough to the consensual target of 150 ng/ml under the 400-mg q.d. regimen without ritonavir would lead to subtherapeutic levels in about half of the patients. Our results strongly support the preferable use of ATV with RTV boosting, but, in the absence of RTV, a twice-daily schedule would be recommended for ATV.

In conclusion, the pharmacokinetic parameters of ATV in a population of HIV patients were adequately described by our population model. Cotreatment with RTV significantly improved ATV pharmacokinetics. A large interpatient variability still remains unexplained and suggests the possibility of effects of additional unavailable covariates, such as host genetic traits and environmental factors. The relatively high residual variability could be circumvented by optimization of compliance, by better adherence to the recommendations regarding food intake, and possibly by drug plasma level monitoring. The Bayesian strategy based on this population analysis for target concentration dosage adaptation should help in the individualization of ATV therapy.