Stochastic re-calibration: contextual effects on perceived tilt

Abstract

The human visual system exaggerates the difference between the tilts of adjacent lines or grating patches. In addition to this tilt illusion, we found that oblique flanks reduced acuity for small changes of tilt in the centre of the visual field. However, no flanks—regardless of their tilts—decreased sensitivity to contrast. Thus, the foveal tilt illusion should not be attributed to orientation-selective lateral inhibition. Nor is it similar to conventional crowding, which typically does not impair letter recognition in the fovea. Our observers behaved as though the reference orientation (horizontal) had a small tilt in the direction of the flanks. We suggest that the extent of this re-calibration varies randomly over trials, and we demonstrate that this stochastic re-calibration can explain flank-induced acuity loss in the fovea.

1. Introduction

In figure 1, the central target is horizontal, yet it appears to be tilted away from the flanks. This ‘tilt illusion’ (Gibson 1937; Over et al. 1972) has been explained by lateral interactions between orientation-selective neurons (see Howard (1982) for a review). Lateral interactions have also been invoked to explain the effects of flanks on contrast discrimination (Polat & Sagi 1993, 1994; Zenger & Sagi 1996; Adini et al. 1997; Solomon et al. 1999; Solomon & Morgan 2000), i.e. decisions regarding which of two grating patches has the higher contrast. Finally, flanks can also produce ‘crowding’. That is, they can make it hard to identify a nearby shape. In particular, flanks can impair the identification of orientation (Andriessen & Bouma 1976; Parkes et al. 2001). Note that this acuity loss is an effect on sensitivity, whereas the tilt illusion is an effect on bias (Morgan et al. 1990). The question is whether the contextual effects on apparent tilt, contrast discrimination and acuity can all be explained by a common mechanism.

Figure 1.

Typical stimulus. Note the tilt illusion: the central target is horizontal, yet it appears to be tilted away from the flanks.

Previously (Solomon et al. 2004), we fit a model of lateral interactions to data on crowding and the tilt illusion, which were gathered using parafoveal stimuli. There are reasons for thinking that different mechanisms may be involved when observers do look directly at the stimuli, that is, when they are in fovea. Contextual effects on foveal contrast discrimination are well established (Polat & Sagi 1993; 1994; Zenger & Sagi 1996; Adini et al. 1997; Solomon et al. 1999; Solomon & Morgan 2000), but those on parafoveal contrast discrimination are considerably more fragile (Solomon & Morgan 2003; Giorgi et al. 2004; Shani-Hershkovich 2005). The tilt illusion is strong both in the fovea (Gibson 1937) and in the parafovea (Solomon et al. 2004), but crowding is relatively weak in the fovea (Jacobs 1979; Levi et al. 1985). Our current study was motivated by a desire to see whether our earlier modelling effort would generalize to new data collected with foveal targets. As discussed below, the answer is a clear ‘no’. If we are to believe that contrast discrimination and acuity are both limited by the same source of additive noise, then our data force us to reject the notion that the tilt illusion is caused by lateral inhibition.

2. Material and methods

There were two observers, the first author (JAS) and another experienced psychophysical observer (CG). The 10.8 cd m⁻² display was viewed in a dark room from a distance of 115 cm. Luminances of vertically adjacent pixels were effectively independent, and could obtain any value between 0.15 and 20 cd m⁻². Target and flanks were Gabor patterns whose wavelength and spread were $\lambda =0.25°$ and $\sigma =0.18°$, respectively. The centre-to-centre separation between the target and each flank was 1.06°.

Since contextual effects on contrast discrimination are sensitive to relative spatial phase (Solomon et al. 1999), we initially decided to present all targets and flanks in cosine phase, i.e. (as in figure 1) all Gabor patterns had a central bright stripe. The black fixation square (3.31° per side) shown in figure 1 remained visible, except during each 100 ms target presentation. We did not use any sort of mask.

To measure the contextual effects on contrast discrimination, targets and flanks were presented twice on each trial. The 100 ms presentations were separated by 500 ms. Only horizontal targets were used. In one presentation, the target appeared with a pedestal contrast, which varied between blocks. In the other presentation, the target contrast was somewhat greater. The QUEST procedure (Watson & Pelli 1983) converged on the increment required for observers to select this latter presentation with 81% accuracy.

Psychometric data were maximum-likelihood fit with a Weibull distribution $P_{\text{C}}(\mathrm{\Delta }c)=0.5+0.49(1-\text{exp}[-{(\mathrm{\Delta }c/c_t)}^{\beta }])$, modified to accommodate observer's inability to respond perfectly to perfectly obvious stimuli (Wichmann & Hill 2001). In the preceding expression, Δc is the contrast difference between the two presentations in each trial and P_C is the probability of a correct response. The best-fitting value for c_t is taken to be the observer's threshold for contrast discrimination. Since the (unmodified) QUEST procedure cannot simultaneously constrain threshold and psychometric slope, the latter was constrained to the moderate value conventionally employed in just these circumstances (Itti et al. 2000): $\beta =2$.

The method of single stimuli (MoSS) was used to measure sensitivities and biases for orientation identification. On each trial, the observer saw a single presentation of the target with (or without) flanks, and had to indicate whether the target was tilted clockwise or anticlockwise of an implicit horizontal standard. Although no explicit horizontal standard was defined for the observer, there were abundant environmental cues, such as the edges of the display and gravity. There were eight different target tilts and eight different flank tilts. All conditions were interleaved within each block of trials

All targets and flanks were presented at 50% of the display's maximum contrast. Psychometric data were maximum-likelihood fit with a (modified) standard normal distribution $P_{\text{ACW}}(t)=0.01+0.98\Phi [(t-\mu /\sigma )]$, where $P_{\text{ACW}}$ is the probability of an ‘anticlockwise’ response, $\Phi []$ is the standard normal cumulative distribution function, t is the target tilt and the parameters reflect two different aspects of performance: bias −μ and acuity 1/σ.

3. Results

(a) Contrast sensitivity

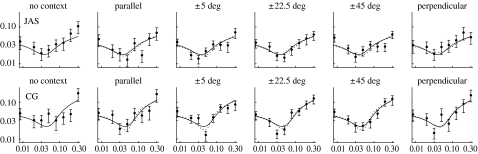
Contrast-discrimination thresholds appear as a function of pedestal intensity in figure 2. The leftmost point in each panel reflects the detection threshold (i.e. for zero-contrast pedestals). The thresholds form ‘dipper functions’, in which maximum sensitivity was achieved with non-zero pedestal contrasts. The shape of this function is consistent with nonlinear transduction of stimulus contrast (Stromeyer & Klein 1974). Foley's (1994) four-parameter transducer model was fit to each observer's data, using the same parameter values for all flank tilts (see figure 2).

Figure 2.

Context has little effect on contrast discrimination. Each panel shows threshold contrast increment c_t, versus pedestal contrast c, in a different context. Error bars contain 95% confidence intervals. All curves adhere to a transducer model of contrast discrimination (Foley 1994), in which $(a{(c+c_t)}^p/(b^{p-q}+{(c+c_t)}^{p-q}))-(a{c}^p/(b^{p-q}+c^{p-q}))=1$. Baseline values (solid curves) for JAS are: a=19, b=0.044, p=3.6 and q=0.7; for CG: a=11, b=0.056, p=3.6 and q=0.5. When p was allowed to vary with the surround orientation, a slightly but significantly better fit (dotted curves) was obtained for each observer.

To see if there were any systematic deviations from this baseline fit, four new fits were obtained to each observer's results. In each of these new fits, one of the four parameters in Foley's (1994) model was allowed to vary linearly with the surround orientation. No-context conditions were excluded. The likelihood of each new fit was then compared to that for a nested model, in which the parameter value did not vary with surround orientation. The ratio of these likelihoods could then be used to assess the significance of any systematic effect of surround orientation (Mood et al. 1974). Results of this analysis are summarized in table 1. Table entries show how each parameter changes as the surround rotates away from horizontal (i.e. parallel to the target) to vertical (i.e. perpendicular to the target). Asterisks indicate a significant (p<2×10⁻⁶) linear trend. We can be pretty confident (p>0.8) of no linear trend for the b parameter when fitting CG's data. For all other non-significant trends, p>0.2.

Table 1.

How transduction parameters change as context rotates away from horizontal. (Asterisks indicate a significant improvement over the baseline fit.)

	a (gain)	b (semi-saturation)	p (numerator exponent)	q (exponent difference)
JAS	21→16*	0.044→0.041	3.4→1.8*	0.63→0.75*
CG	11→10	0.056→0.055	5.0→3.1*	0.50→0.47

Table 1 indicates that only the numerator exponent (parameter p) decreased significantly for both observers as the context rotated away from the target's orientation. The consequences of this decrease are illustrated by the dotted curves in figure 2. Essentially, this decrease causes the dipper functions to have shallower ‘dips’.

Although the no-context condition was excluded from the analysis described in table 1, we did separately fit the results from that condition with Foley's (1994) model. The values for transducer gain (parameter a) that best fit the results of the no-context condition (12 for JAS, 9.0 for CG) were less than those that best fit the results from every other condition. Similarly, the values for semi-saturation1 (parameter b) that best fit the results of the no-context condition (0.068 for JAS, 0.18 for CG) were greater than those that best fit the results from every other condition. Thus, we can be confident that no flanks—regardless of their tilts—decreased sensitivity to contrast.

This finding is consistent with earlier reports (Snowden & Hammet 1998; Petrov et al. 2005) that surrounding gratings have little effect on contrast sensitivity. However, our results are not consistent with some earlier findings (Yu et al. 2001, 2003), in that ours do not exhibit parallel-surround-induced threshold elevation. We believe this is due to a difference in stimulus geometry: Yu et al. used abutting surrounds, we did not.

(b) Tilt acuity and bias

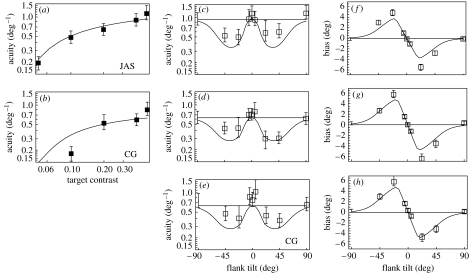
Acuity was assessed by having observers decide whether the central target was clockwise or anticlockwise of horizontal. Measurements of acuity and bias appear as functions of flank tilt in figure 3. Negative values indicate clockwise tilts.

Figure 3.

Orientation identification: measurements and model fits. Panels (a, b) show that acuity increases with contrast in the absence of context. Panels (c–e) show acuity versus flank tilt (with respect to the reference orientation). Panels (f–h) show bias versus flank tilt. Error bars contain 95% confidence intervals. Curves adhere to a stochastic re-calibration model of orientation identification (see text). Parameter values for JAS (a, c and f) are: s=0.24, ${\theta }_{\text{M}}=5.0$, μ=40° and σ=28°; for CG (b, d, e, g and h): s=0.34, ${\theta }_{\text{M}}=5.6$, μ=44° and σ=28°. Points appearing with error bars on the left of panels (c–h) correspond to measurements made sans context. Horizontal lines correspond to model predictions for this condition.

Figure 3a,b shows that when flanks were absent, acuity increased with target contrast, at least up to 0.5. Acuity for 12 cycle deg⁻¹ targets had been reported to hit a ceiling at about 20% contrast (Regan & Beverley 1985). Bowne (1990) reviewed and re-measured this relationship and found a more gradual saturation of acuity, particularly for targets of lower spatial frequency. Both of these studies employed 2AFC procedures unlike our MoSS paradigm. Our procedure and results more closely match those of Itti et al. (2000), the major differences being (i) our targets were foveal and (ii) our acuities were uniformly higher.

Figure 3f,g shows that tilted flanks produce angular biases of opposite sign. That is, truly horizontal targets appear to be tilted away from tilted flanks. The largest biases were obtained with the ±22.5° flanks. Like Wenderoth et al. (1979), who measured the tilt illusion using various techniques, we found the biases induced by ±45° flanks to be somewhat smaller than those induced by less oblique flanks. In general, however, our estimates of bias are larger. The most salient difference between our current measurements of bias and those similarly obtained in the parafovea by Solomon et al. (2004) is that these show absolutely no sign of small-angle assimilation (i.e. biases of the same sign as flank tilt).

In Figure 3c (and d), the error bars without a box on the left indicate acuity in the absence of flanks. Note that since this condition is identical to that illustrated by the rightmost box in figure 3a (and b), any difference between these two data points must be ascribed to either measurement error or cognitive set. Figure 3c,d shows that grossly oblique flanks (i.e. ±22.5 and ±45°) reduced acuity, while if anything, the horizontal, near-horizontal and vertical flanks increased it. Note that horizontal flanks may repel tilted targets, so that target tilts appear larger than they really are. Thus, a small increase in acuity with horizontal flanks should not be wholly unexpected.

To ensure that any deviation from our earlier findings (Solomon et al. 2004) was not due to our decision to phase-lock our current target and flanks, CG re-ran part of the experiment with one difference. This time the spatial phases of the target and every flank were randomly re-determined on every trial. The results of this experiment (figure 3e,h) were virtually identical to those of experiment 1. Thus, as argued by Howard (1982), purely spatial interactions (as opposed to those with some selectivity for orientation) are unlikely to form the basis of these contextual effects.

4. Discussion

Our main novel finding is that tilted flanks decrease tilt acuity for a foveal target, while parallel flanks have no effect on acuity. Our previous investigations of the parafovea revealed that parallel flanks have a large effect on acuity (Parkes et al. 2001; Solomon et al. 2004). Thus, foveal and parafoveal processing seem to be qualitatively different.

Prima facie, our results are also inconsistent with the findings of Mareschal et al. (2001, 2002), who found that tilt thresholds for foveal orientation discrimination decreased as the difference between the tilts of a target and surrounding grating increased. However, it is important to note that both presentations in each trial of their two-temporal-interval-forced-choice experiments (observers selected the target with the most clockwise or anticlockwise tilt) featured the same target/surround tilt difference, i.e. the surrounding grating moved during each trial. This procedure prevents independent assessment of perceptual bias and acuity.

Previously (Solomon et al. 2004), we noted that the pooling models traditionally invoked to explain the tilt illusion (Blakemore et al. 1970) were inconsistent with weak assimilation. Instead, we attributed the large angular expansion (i.e. repulsion) characteristic of the tilt illusion to lateral (divisive) inhibition between neurons with similar orientation preference and weak assimilation to a relatively weak lateral amplification, more tightly tuned for orientation.

Seemingly inconsistent with the notion of lateral inhibition, we now find that parallel flanks do not decrease acuity. Lateral amplification (Chen & Tyler 2002; Solomon et al. 2004) could elevate acuities decreased by horizontal and near-horizontal flanks, but not without producing unwanted assimilation. An even more inescapable reason for rejecting the notion of lateral inhibition is that none of our flanks—regardless of their tilts—actually decreased sensitivity to contrast.

Though often implicit, all of the models cited thus far have assumed acuity and/or contrast discrimination to be limited by an additive noise. For example, in Foley's (1994) model of contrast discrimination, threshold accuracy is obtained whenever the detector's response to the target+pedestal exceeds its response to the pedestal alone by a value that does not depend on the responses themselves. However, the variance of neural responses typically does increase with response strength (Vogels et al. 1989). Accordingly, it is conceivable that lateral inhibition could reduce both signal and noise in the neurons responsible for contrast discrimination, leaving their ratio and thus threshold unchanged.

Therefore, it would be premature to conclude that lateral inhibition cannot be responsible for the contextual effects reported here. However, for reasons outlined in appendix A, it also seems premature to propose a model in which both orientation identification and contrast discrimination are limited by the same source of multiplicative noise. Instead, we sought an explanation for the tilt illusion that was compatible with the notion of additive noise.

Other than lateral inhibition, what might produce the foveal tilt illusion? Gibson (1937) suggested that the labels ‘horizontal’ and ‘vertical’ shift from mechanisms preferring these orientations to those aligned with the visual context. More recent work, however, suggests that there is nothing special about these norms when it comes to the tilt after-effect (Mitchell & Muir 1976) or the tilt illusion (O'Toole & Wenderoth 1977; Wenderoth et al. 1979); similar repulsion can be obtained with oblique reference orientations.

An alternative, yet formally equivalent, notion of re-calibration is one in which the labels stay put while the orientation preferences shift toward the flank orientation (Gilbert & Wiesel 1990). Although experiments in area V1 of cats suggest a predominance of shifts away from the flank (or adapting) orientation (Gilbert & Wiesel 1990; Dragoi et al. 2000), experiments in the medial temporal cortex (area MT, also known as V5) of macaque suggest shifts toward adapting orientations (Kohn & Movshon 2004).

Re-calibration explains shifts in bias, but it does not immediately explain loss of acuity. Note that bias is not the perceived tilt, it is merely the average perceived tilt. From trial to trial, the perceived tilt is perturbed by sensory noise. Acuity reflects the variance of this noise. We suggest that acuity losses can be explained if the extent of re-calibration were to fluctuate from trial to trial, leading in effect to a fluctuating bias, which would be indistinguishable from an increase in sensory noise (Wickelgren 1968). We call this process ‘stochastic re-calibration’. The solid curves in figure 3 show how well a neural model of stochastic re-calibration can fit the data.

The model is described in detail in appendix B. One of its key features is an opponent process (Regan & Beverly 1985; Solomon et al. 2004), in which each neuron is paired with another having the opposite orientation preference with respect to the reference. The pair whose outputs are most different determines identification. (NB, the pair with the greatest difference in response is not necessarily the pair with the greatest overall response.) The orientation bandwidth of the model neurons was derived from the observer's acuity without flanks. Their contrast response was derived from the contrast-discrimination results (see figure 2).

For oblique flanks to reduce acuity, re-calibration must be stochastic. We suppose that there is a proportion of trials in which the horizontal reference orientation is used. On the remaining trials, the effective reference is drawn toward the flank orientation. We also assume that the frequency of re-calibration decreases with the difference between the true reference and flank orientations. This prevents recalibration when the flanks are orthogonal to the reference.

To date, the most versatile model of tilt and contrast discriminations is that of Itti et al. (2000). Its versatility is evident from its successful simulation of human performance with a variety of masking stimuli. However, without modification, it cannot simulate performance in one-interval tasks, such as ours, and contains no provision for observer bias. Even their simplified (i.e. additive noise) model contains more free parameters than ours. Thus, we prefer to use our lower-dimensional model for present purposes.

Stochastic re-calibration can explain our foveal data, but it cannot explain why flanks aligned with the reference orientation reduce acuity for parafoveal targets. We cannot rule out the possibility that stochastic re-calibration contributes to parafoveal ‘crowding’, but another mechanism—such as compulsory pooling (Parkes et al. 2001)—must also be involved.

The major implication of our work is that visual context can affect orientation judgments differently from the way context affects letter identification. Context can reduce acuity without crowding the target and lateral inhibition is not required. Instead, we have shown that acuity loss can result from a stochastic fluctuation of the re-calibration putatively responsible for the tilt illusion.

Appendix A

Appendix A. Contrast discrimination and multiplicative noise

Multiplicative-noise models of contrast discrimination have been considered before, but such considerations typically focus either on contrast detection (e.g. Swets et al. 1961) or contrast masking (Kontsevich et al. 2002). The only successful attempt at explaining the entire dipper function—from detection all the way to masking—was reported by Itti et al. (2000). Neurons in their model undergo the same nonlinear transformation as those in Foley's (1994) model, which can be specified with four free parameters, but another two free parameters (the intensity of the ‘dark current’ η and the exponent relating response strength to response variance α) were required to obtain decent fits. This surfeit of free parameters is evident from their finding that dipper functions could not adequately constrain an additive-noise model, in which α was effectively set to 0 and the other five parameters were allowed to vary freely.

Solomon (in press) compared four-parameter additive-noise models with four-parameter multiplicative-noise models. Fits of the former to full dipper functions were more satisfying than those of the latter. Because the benefits and limitations of multiplicative-noise-based accounts have yet to be fully examined, we have decided to stick with the more conventional additive-noise-based account of contrast discrimination in this paper.

Appendix B

Appendix B. The stochastic re-calibration model

We instantiate the idea of re-calibration using an opponent process for orientation identification (Solomon et al. 2004). Consider a population of orientation-selective neurons in the centre of the visual field. Let $r({\theta }_{\text{t}};c,\theta )$ represent the response of the neuron with preferred orientation θ to a target having contrast c and orientation θ_t. By definition, an ‘opponent pair’ of these neurons will have the net response $d(\theta ;c,{\theta }_{\text{t}},{\theta }_0)=r({\theta }_{\text{t}};c,{\theta }_0+\theta )-r({\theta }_{\text{t}};c,{\theta }_0-\theta )$, where θ₀ is the effective reference orientation. The probability of an ‘anticlockwise’ response is determined as a Gaussian function of the greatest difference between opponent pairs, i.e. $\Phi [d({\theta }^{\prime };c,{\theta }_{\text{t}},{\theta }_0)]$, where θ′ is the mode of $|d(\theta ;c,{\theta }_{\text{t}},{\theta }_0)|$.

The contrast response of our model neurons was derived from the aforementioned four-parameter fits to our contrast-discrimination results: $r({\theta }_{\text{t}};c,\theta )=ag{({\theta }_{\text{t}};\theta )}^p/[b^{p-q}+g{({\theta }_{\text{t}};\theta )}^{p-q}]$. Best-fitting values for the parameters a, b, p and q can be found in the legend of figure 2. Using a circular Gaussian to describe the orientation tuning of our model neurons $g({\theta }_{\text{t}};\theta )=\text{exp}[-{\text{sin}}^2({\theta }_{\text{t}}-\theta )/\gamma ]$, we found the bandwidth γ, which best fit experiment 1's orientation-identification results without flanks. These values, 0.1 for JAS and 0.15 for CG, correspond to full bandwidths of 31 and 37° at half-height.

We suppose that there is a proportion of trials 1−α, in which the actual reference orientation is used (i.e. θ₀=0). On the remaining trials, the effective reference is drawn toward the flank orientation θ_f, such that ${\theta }_0=\text{min}\{s{\theta }_{\text{f}},{\theta }_{\text{M}}\}$, where s and θ_M are free parameters. We also assume that re-calibration is less frequent when the true reference and flank orientations are very different, specifically $\alpha =1-\Phi [({\theta }_{\text{f}}-\mu )/\sigma ]$, where μ and σ are free parameters. Model fits appear as solid curves in figure 3. They qualitatively capture all aspects of the data; however, the model's prediction for the ratio of sensitivity loss to maximum bias is slightly high.