Pathogen responses to host immunity: the impact of time delays and memory on the evolution of virulence

Abstract

Current analytical models of the mammalian immune system typically assume a specialist predator–prey relationship between invading pathogens and the active components of the immune response. However, in reality, the specific immune system is not immediately effective following invasion by a novel pathogen. First, there may be an explicit time delay between infection and immune initiation and, second, there may be a gradual build-up in immune efficacy (for instance, during the period of B-cell affinity maturation) during which the immune response develops, before reaching maximal specificity to the pathogen. Here, we use a novel theoretical approach to show that these processes, together with the presence of long-lived immune memory, decouple the immune response from current pathogen levels, greatly changing the dynamics of the pathogen–immune system interaction and the ability of the immune response to eliminate the pathogen. Furthermore, we use this model to show how distributed primary immune responses combine with immune memory to greatly affect the optimal virulence of the pathogen, potentially resulting in the evolution of highly virulent pathogens.

1. Introduction

The mammalian immune system is a highly complex, dynamical system comprising many interacting processes. Therefore, although there is considerable understanding about many of the individual processes, the inherent nonlinearities make it difficult to predict how the immune system as a whole will behave when challenged by an invading pathogen, and how the pathogen may evolve in the face of this immune response. To help understand the nature of these interactions, attempts have been made to describe immune function using mathematical models. While some large-scale, biologically realistic simulation models have been developed (Bezzi et al. 1997; Kleinstein & Seiden 2000; Kohler et al. 2000), arguably most progress has been made through the use of generic, mathematically tractable analytical models that are easy to interpret and provide general insights into the overall behaviour of the system; in particular, the work of Nowak and May (Nowak & May 2000) and Antia and colleagues (Antia & Koella 1994; Antia et al. 1994; Antia & Lipsitch 1997; Ganusov et al. 2002) have been instrumental in developing this burgeoning field. However, in the desire for simplicity, these models often make limiting assumptions about the nature of the various processes. In particular, details concerning the build-up of the immune response and the inherent time delays between pathogen challenge and immune activation are often omitted.

Time delays in the specific immune response may arise through a number of different processes. For instance, within the humoral response, the time taken for B cells to bind to the novel antigens of an invading pathogen and initiate the various pathways that lead to a fully effective and highly specific immune response can be substantial. One example of such a delay is the period of clonal expansion where the binding B cells are stimulated to divide by T cells that recognize the antigen–MHC complex on their surface, resulting in a population of clones producing massive quantities of antibodies that target the invading antigen (Kelsoe 1996; Roitt & Delves 2001). During this division phase somatic hypermutation produces sub-populations of B cells with differing affinities for the antigen, which then undergo selective expansion, in a process known as affinity maturation, resulting in a highly efficient immune response against the specific antigen (Eisen & Siskind 1964; MacLennan et al. 2000; Tarlinton & Smith 2000; Roitt & Delves 2001). Similar delays following infection occur during the development of T-cell affinity, and substantial delays can even occur during cell proliferation of the innate immune response (Ahmed & Gray 1996; Roitt & Delves 2001). While the precise duration of these delays depend on the nature of the invading pathogen, detectable levels of T and B cells may typically be observed within 3–4 days following infection, with proliferation and maturation continuing for up to six or seven weeks (Ahmed & Gray 1996; Tarlinton & Smith 2000; Iber & Maini 2002). Clearly, these delays may be considerable compared to the reproductive potential of an invading virus or bacterium, and the more prolonged the period of cell proliferation or affinity maturation, the larger the window of opportunity for the pathogen to exploit the host before it is suppressed by the immune system. However, a key feature of the adaptive immune response is the ability to maintain long-lived immune memory towards specific pathogens. This memory enables a rapid and prolific secondary response that may either prevent re-invasion of an eradicated pathogen, or maintain suppression of a circulating pathogen that was not eradicated by the primary response. Hence, immune memory closes the window of opportunity for the pathogen, further modifying the endpoint of virulence evolution. Therefore, the length of the time delay between infection and immune initiation, the subsequent rate of effective immune build-up and the presence of specific immune memory may all have profound implications for the pathogen's host exploitation strategy and the evolution of virulence.

So, how should a pathogen exploit the time window before initiation of host immunity? How should it respond to the rate of immune build-up? How does the presence of immune memory affect pathogen evolution? Our aim is to address these issues using a novel modelling framework that incorporates both an explicit time delay between pathogen invasion and initiation of the specific immune response and also a gradual build-up of immune competence following initiation, mirroring the various pathways of the immune system. We show that these time delays can have a profound impact on the dynamics of the pathogen within the host and on whether the immune system is able to eliminate the invading pathogen. We then incorporate immune memory and explore how this long-lived component to the host's immune system affects the pathogen's population dynamics. Finally, we use both models to explore how the within-host selection pressures generated by the immune system influence the evolution of pathogen virulence. Whereas many models of the evolution of virulence assume that increased host mortality acts as a cost to high pathogen virulence, we show that over-stimulation of the host's immune system can be sufficient to impose an upper limitation on virulence, potentially maintaining virulence levels below those likely to cause harm to the host.

2. Baseline pathogen–immune system model

We develop a series of structured population models to explore how delayed specific immune responses and the presence of immune memory affect the dynamics of the pathogen–immune system interaction. First, we consider a baseline model of the system with no long-lived memory (further details are given in the electronic supplementary material), describing the pathogen–immune interaction with a series of delay differential equations which incorporate an explicit time delay between pathogen challenge and immune initiation (Buric et al. 2001; Buric & Vasovic 2002). We do not attempt to explicitly model each individual component of the immune response, but rather we adopt a phenomenological approach to qualitatively describe the gradual build-up of an effective immune response. To achieve this we make use of a linear chain of ordinary differential equations (MacDonald 1978, 1989; Mangel & Bonsall 2004) to construct a distributed immune response mimicking, for instance, the process of selective expansion that leads to the build-up of specific immunity. The full baseline model is:

$$\begin{array}{c}\frac{{\text{dP}}_{(t)}}{\text{d}t}={\text{P}}_{(t)}[r-d-f(I_n)],\\ \frac{\text{d}{I}_i}{\text{d}t}=c(I_{i-1}-I_i),i=1\dots n,\\ \frac{\text{d}{I}_0}{\text{d}t}=c({\lambda }_0{\text{P}}_{(t-\tau )}-I_0).\end{array}$$

Here, the first equation describes the within-host dynamics of a pathogen (P) such as a virus, bacterium or protozoan, which replicates within the host at rate r and dies at a background rate d; this loss rate incorporates both natural pathogen decay and also loss through the action of the non-specific immune system. Hence, in the absence of a specific immune response, the pathogen load increases at net rate (r−d). However, assuming the host mounts a specific immune response (I_n), pathogen density declines as some function of the magnitude of this response, f(I_n). Note that this is a general function that may take a range of forms describing the impact of the immune system on the pathogen, however, for simplicity, we assume a simple linear response such that f(I_n)=αI_n where α measures the per capita impact of immunity on the pathogen. The immune response is distributed with shape parameter c, which represents the rate of the cellular and biochemical reactions involved in the immune pathway, and comprises a chain of length n+1 (described by the equations $\text{d}{I}_0/\text{d}t\cdots \text{d}{I}_n/\text{d}t$), where n represents the physiological complexity of the immune response. This distributed response is a mixture of exponentials (see electronic supplementary material), and may be thought of as representing the period of affinity maturation leading to the build-up of effective immunity following an initial pathogen challenge. Similar approaches have been adopted to model the intracellular development of viruses such as HIV, showing that the predictions of these models differed greatly from corresponding models without a distributed delay in terms of both the transient dynamics and long-term stability (Grossman et al. 1999; Lloyd 2001; Culshaw et al. 2003). Finally, we allow for a possible discrete time delay (τ) between infection and initiation of the immune response such that the level of immunity is λ₀ times the infection load (P) τ steps ago.

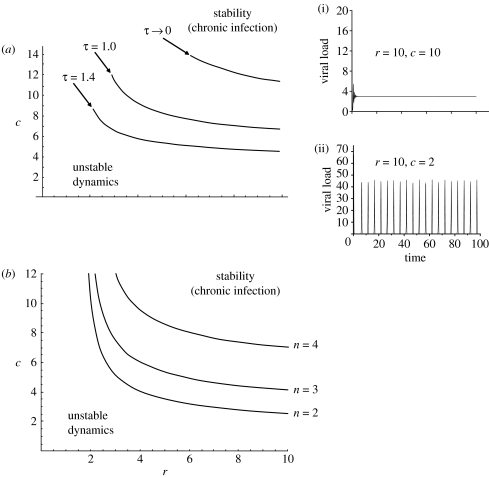
Analysis of the model follows standard methods for analysing delay-differential equations (see electronic supplementary material) showing there are two outcomes of the interaction (figure 1). Combinations of high pathogen replication rates (r) and high values of the shape parameter (c) result in stable dynamics, where the pathogen persists as a chronic infection within the host. However, low r and c values lead to unstable dynamics, in the form of potentially high-amplitude pathogen cycling within the host. By taking the expectation of the solution of the chain with respect to time to give the average delay ($\overline{t}$) shows that as shape parameter (c) increases, the mean delay ($\overline{t}$) declines: short-time delays are more likely to lead to stable dynamics (see electronic supplementary material). The presence of a time delay before the initiation of the immune response is crucial in determining whether the pathogen is able to persist; the region of stability (chronic infection) becomes very small as τ tends towards 0, whereas chronic infection is more likely if there is a large time delay (high τ) between pathogen challenge and immune initiation (figure 1a).

Figure 1.

Predictions of the baseline model showing the dynamic outcomes of the pathogen–immune system interaction as functions of r, the pathogen replication rate and c, the immune pathway shape parameter. (a) Showing the boundary between stable and unstable regions of parameter space as a function of the time delay between pathogen challenge and immune initiation (τ). Also shown (inset) are two time-series of the model run from different locations of r−c parameter space (i) r=10, c=10; (ii) r=10, c=2. (b) Showing the boundary between stable and unstable regions of parameter space as a function of the chain length (n) used to model the build-up of immunity.

Stable pathogen persistence is also favoured if the immune response is not highly distributed (i.e. there is a short chain in the build-up of immunity; figure 1b). While the impact of single time delays on dynamical systems is well recognized, the interaction between fixed (τ) and distributed delays can lead to stability switches, resulting in unintuitive dynamical consequences: explicit time delays may disrupt the stability of equilibria but, less frequently observed is the phenomenon observed here where delays can lead to restabilization of unstable equilibria (Cooke & Grossman 1982).

3. Incorporating immune memory

The precise relationship between memory cells and those of the primary immune response is the subject of some debate, but it is generally believed that memory B cells develop in parallel with the primary immune response, derived from the same naive precursor cells (Ahmed & Gray 1996; Tarlinton & Smith 2000; Gourley et al. 2004). We, therefore, modify the baseline model to include a long-lived specific memory component (M) which is generated during production of the primary immune response, at rate γ, and decays at a (low) density-independent rate, δ. It is unclear exactly at what point following infection that memory cells begin to form, although there is some evidence that memory cell formation may begin three to four days after stimulation of the immune response, but it may be as much as 14 days post-infection (Liu et al. 1987; Tarlinton & Smith 2000; Iber & Maini 2002; Inamine et al. 2005). We, therefore, allow for such a lag by the inclusion of an explicit delay term (τ_M) before initiation of the immune memory. In the presence of the pathogen, this memory component is activated to re-stimulate the immune response at rate λ_M, which then combats the infection as before. The full model incorporating immune memory is:

$$\begin{array}{c}\frac{{\text{dP}}_{(t)}}{\text{d}t}={\text{P}}_{(t)}[r-d-f(I_n)],\\ \frac{\text{d}{I}_i}{\text{d}t}=c(I_{i-1}-I_i),i=1\dots n,\\ \frac{\text{d}{I}_0}{\text{d}t}=c({\lambda }_0{\text{P}}_{(t-\tau )}+{\lambda }_M{M}_{(t)}{\text{P}}_{(t)}-I_0),\\ \frac{\text{d}M}{\text{d}t}=\gamma I_{0(t-\tau m)}-\delta M_{(t)}.\end{array}$$

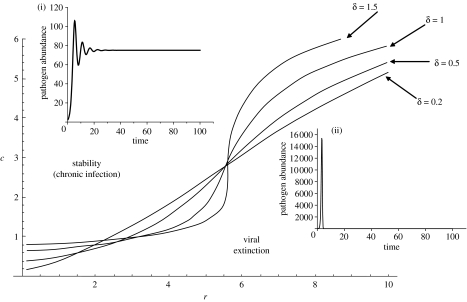
Stability analysis (see electronic supplementary material) shows that there are two outcomes of the interaction: stable, chronic infection and unstable dynamics characterized by either sustained oscillations or pathogen exclusion, defined as when pathogen load falls below an arbitrarily low threshold value. Unlike the baseline model, the presence of immune memory results in fast-replicating pathogens being more prone to exclusion (figure 2). Furthermore, if the pathogen can persist to produce a chronic infection, the equilibrium level of the pathogen in the presence of immune memory is the level attained in the absence of memory multiplied by the factor,

$$\frac{\delta \alpha {\lambda }_0}{\delta \alpha {\lambda }_0+\gamma {\lambda }_m(r-d)}.$$

Hence, immune memory always reduces the equilibrium level of the pathogen and the degree of reduction increases as either γ or λ_m is increased and, paradoxically, as the pathogen's net replication rate (r−d) increases; chronic infections with fast-replicating pathogens are likely to be suppressed to a greater extent than those of slow-replicating pathogens. Finally, the boundary separating the regions of chronic infection and pathogen exclusion is highly nonlinear, and this nonlinearity is exaggerated if the memory is short lived (high δ; figure 2).

Figure 2.

Predictions of the model incorporating immune memory, showing the dynamic outcomes of the pathogen–immune system interaction as functions of r, the pathogen replication rate, c, the immune pathway shape parameter and δ, the rate of memory decay. Eradication of the pathogen (defined as when P (t) falls below 0.007 and is then bounded at 0, else the dynamic is defined as unstable) is ensured through numerical simulations (using a fourth order Runge–Kutta algorithm with step size (dt) of 10⁻³). The insets show: (i) stable chronic infection (r=2, c=6) above the stability boundaries and (ii) pathogen exclusion (r=4, c=1) below the stability boundaries.

4. The evolution of pathogen virulence

Typically, models of the evolution of virulence assume the cost (to the pathogen) of high virulence is host death (Antia et al. 1994; Ganusov et al. 2002; Ganusov & Antia 2003); the more virulent the pathogen, the faster it kills the host, and so the lower the pathogen's fitness. These models suggest that the optimal level of virulence is just below that sufficient to kill the host. However, many pathogens appear to be maintained at levels far below those necessary to induce host mortality (Levin & Antia 2001; Meyers et al. 2003), with death only occurring in immuno-compromised hosts. Hence, there may be some other limitation to high virulence that is reached before host mortality occurs and it may be that over-stimulation of the host's immune response can act as a sufficient constraint to restrict the evolution of high levels of pathogen virulence. It has previously been proposed that levels of immunity and, in particular, the strength of cell-directed immune responses are correlated with viral replication rate such that fast-replicating viruses are more ‘visible’ to the immune system (Almogy et al. 2002). Here, we use our model to explore how time delays and distributed immune responses affect the evolution of pathogen virulence, given a trade-off between pathogen replication rate and immune stimulation.

Previous workers have highlighted the difficulty of rigorously defining the term ‘virulence’ in such within-host models (Antia et al. 1994; Ganusov et al. 2002; Ganusov & Antia 2003). While there will be important dose-effects determining the overall damage caused to a host and the likelihood of pathogen-induced host mortality, in an evolutionary context virulence should be defined as a life-history trait of the pathogen that may be subjected to natural selection. Hence, virulence acts at a per capita rate such that for a given pathogen load and over a given time period a more virulent virus, for instance, will lyse more host cells than a more benign virus, increasing damage to the host. In this respect, Antia and colleagues (Antia et al. 1994; Antia & Lipsitch 1997; Ganusov et al. 2002) showed that in a homogenous host population the virulence of a pathogen, as measured by the dose required to kill 50% of infected hosts (its LD50), increases with its per capita growth rate, r. While it has been shown that pathogen virulence (defined as the case fatality rate) in heterogeneous populations may not be proportional to r (Ganusov & Antia 2003), for simplicity given our model structure and for ease of comparison with the majority of previous models we assume that virulence, defined here as the amount of cellular damage caused by a pathogen within its host, is directly proportional to the pathogen's per capita reproductive rate, r.

Given a definition of virulence (the pathogen trait under selection) it is also important to rigorously define the measure of fitness of the pathogen that is maximized by natural selection. In an epidemiological context the fitness of the pathogen may be defined by its basic reproductive ratio, R₀, which is measured as the number of number of secondary cases infected by a single infected host in a completely susceptible population (Anderson & May 1992). Therefore, the overall infectiousness of a given host will depend on the total number of infectious particles produced by that host over the lifetime of the infection, and the transmissibility of the pathogen at any moment in time will be directly proportional to its abundance within the host (Antia et al. 1994; Antia & Lipsitch 1997; Ganusov et al. 2002; Gilchrist et al. 2004). Therefore, since infection may be chronic, the appropriate measure of the pathogen's fitness is its ‘lifetime’ reproductive success, i.e. the cumulative pathogen load throughout the duration of infection.

Given the above considerations, we model the evolution of virulence by determining the fitness of the pathogen with respect to varying replication rate (r), given that high r may increase stimulation of the host's immune response. That is

$$F(r)={\int }_0^T\text{P}(t)\text{d}t,$$ 4.1

where F(r) is the function to maximized with respect to the pathogen's replication rate (r), and T is the lifetime of the infection. To calculate the pathogen's fitness, equation (4.1) is placed within the dynamic models presented previously, allowing full consideration of the relationship between pathogen reproductive rate, immune stimulation and pathogen lifetime reproductive success. The optimal virulence (r^*) is the value of r that maximizes equation (4.1) within the setting of the previous models either with or without the presence of immune memory.

At present we have no a priori information about the shape of the trade-off between replication rate (r) and stimulation of the primary immune response (λ₀). Therefore, we assume there is a monotonic increasing relationship between pathogen replication and immune stimulation, such as may occur through cells infected with high reproducing pathogens presenting more targets for the cell-directed immune response (Almogy et al. 2002; Gilchrist et al. 2004). In the simplest scenario, there might be a linear relationship between r and λ₀ although other functional forms may be possible, such as an accelerating relationship due to increased rates of stimulation, or a decelerating relationship due to immune exhaustion. Therefore, to account for different possible mechanisms of immune stimulation we explore the evolution of pathogen virulence under two different functional forms:

1. decelerating at the origin (concave), of the form ${\lambda }_0=\frac{xr}{1+yr}$ and

2. accelerating at the origin (convex), of the form ${\lambda }_0=a\text{exp}(rb)$,

where the parameters a, b, x and y determine the strength of the trade-off. Once again, these functional relationships are placed within the full dynamic models described previously and the cumulative pathogen load over the duration of the infection is calculated as the measurement of pathogen fitness.

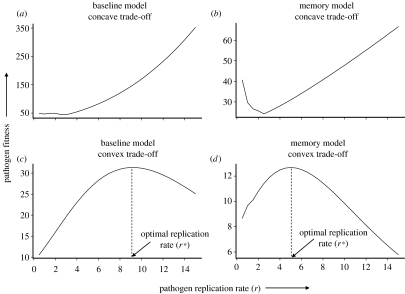
Regardless of whether there is immune memory or not, a concave relationship between pathogen virulence and immune stimulation tends to result in pathogen fitness being maximized at the highest values of r (figure 3a,b), suggesting that a pathogen should evolve maximal virulence (r^*→∞), irrespective of the strength of the immune response (Gilchrist et al. 2004). Such a concave trade-off implies that the pathogen experiences diminishing costs, in terms of increased stimulation of the immune system, and so it will always benefit from a further increase in replication rate. Indeed, similar results are found assuming a linear relationship between r and λ₀; it will always pay the pathogen to increase its reproductive rate to ‘keep ahead’ of the immune response. Note, however, that in the presence of immune memory, the distribution of virulence may be bimodal, with a small, local optimum approaching zero (figure 3b). Hence, even though there is a greater benefit to being highly virulent, pathogens may get caught in this locally fit, avirulent state. However, pathogens with high mutation rates, such as RNA viruses (Drake et al. 1998) may be able to jump across this fitness trough and rapidly evolve to be highly virulent.

Figure 3.

Expected fitness (lifetime reproductive success) of a pathogen as a function of its replication rate (r) under different model assumptions. (a) Baseline model, assuming a concave trade-off between pathogen replication rate (r) and immune stimulation (λ₀), (b) Model incorporating immune memory, assuming a concave trade-off between pathogen replication rate and immune stimulation, (c) Baseline model, assuming a convex trade-off between pathogen replication rate and immune stimulation and (d) Model incorporating immune memory, assuming a convex trade-off between pathogen replication rate and immune stimulation.

When the trade-off between pathogen virulence and immune stimulation is convex, intermediate virulences tend to be optimal (0<r^*<∞; figure 3c,d; Gilchrist et al. 2004). Clearly, very low replication rates are sub-optimal, as they do not allow the pathogen to achieve its full reproductive potential; of course if r<d, the pathogen is unable to sustain itself even in the absence of host immunity. Furthermore, high replication rates over-stimulate the immune response, resulting in very short-lived infections, with little opportunity for pathogen transmission (Almogy et al. 2002; Coombs et al. 2003; Gilchrist et al. 2004). Hence, intermediate replication rates are optimal. Therefore, host immunity can impose sufficient selective pressure on the pathogen to maintain its virulence at sub-maximal levels, without the need to invoke host mortality as a constraint.

It is interesting to consider the impact of innate immunity on the evolution of pathogen virulence. In the model, we account for innate immunity within the density-independent mortality of the pathogen, d. The fitness profiles plotted in figure 3 all assumed a constant, arbitrary value of d. Increasing d would act to shift these profiles to the right such that for a given per capita reproductive rate, r, the net reproductive rate would be reduced. Therefore, in the case of a convex trade-off (figure 3c,d), the optimal replication rate (r^*) would be correspondingly larger to compensate for the greater mortality rate. Hence, strong innate immune responses may further drive the evolution of high pathogen virulence.

For the remainder of this analysis, we only consider pathogen evolution assuming a convex relationship between replication rate and immune production, where intermediate levels of pathogen virulence tend to be optimal. For both the baseline model and the model incorporating immune memory, the optimal virulence is highly dependent on the physiological complexity of the immune system and the rate of immune build-up (i.e. the length of the chain in the model), although the trend is opposite for the two models (figure 4). For the baseline model, increasing immune complexity (i.e. increasing n) leads to a decrease in the optimal virulence (figure 4a). Long chain lengths (with a constant value of c) mean that the active component of the immune response is increasingly decoupled from the current pathogen load within the host. Therefore, with such a distributed response, the over-stimulation of immunity caused by high pathogen replication rates mean the pathogen is highly likely to be eradicated. The best evolutionary strategy is for the pathogen to replicate at lower rates, effectively hiding from the immune response and maximizing its long-term persistence in the host, albeit at a very low level. Conversely, when there is a long-lived immune memory (figure 4b), long chain lengths mean the pathogen is always ultimately excluded and so its best strategy is to replicate at increasing rates, maximizing transmissibility in the short-time window available before it is eradicated.

Figure 4.

Predicted optimal pathogen replication rates (r^*) for (a) the baseline model and (b) the model incorporating immune memory, as a function of the chain length (n) used to model the build-up of immunity.

5. Discussion

We have developed a novel modelling framework of the within-host pathogen–immune system dynamics that mimic the delayed, distributed build-up of an effective immune response following pathogen challenge. The presence, and duration, of these time delays has fundamental implications for whether the immune system is able to eliminate the pathogen and, ultimately, for the optimal virulence of the pathogen.

Typically, most models describe the immunity–pathogen interaction as a specialist predator–prey relationship, whereby the immune response is instantaneously stimulated by the presence of the pathogen and depletes the pathogen population at a fixed rate determined by their relative densities at any moment in time (Nowak & May 2000). Therefore, when pathogen densities are suppressed to very low levels, immunity is similarly reduced, releasing the pathogen from its impact. In contrast, however, we have shown here that time delays and distributed responses within the immune system decouple it from the pathogen, so that immunity acts much more like a generalist predator with its abundance at any point in time remaining largely unchanged by current levels of infection. This is particularly apparent when there is a long-lived, highly distributed memory component, which buffers the overall immune system against fluctuations in pathogen levels. One expectation is that the total immune pressure can remain at high levels even when the pathogen is at very low levels, potentially resulting in its eradication and imposing a strong selection pressure on the evolution of virulence.

Related effects on the evolution of virulence due to changes in the administering of vaccines and their efficacy are also known to affect pathogen epidemiology and evolution (McLean 1995; Gandon et al. 2001). Imperfect vaccines, particularly those aimed at reducing pathogen replication rates are predicted to lead to the evolution of higher pathogen virulence (Gandon et al. 2001). In comparison, we have shown here that host immunity can impose selection to influence the evolution of pathogen virulence; immune responses that effect a change in the death rate of the pathogen are predicted to drive the evolution of higher pathogen virulences. Hence, understanding the impact of different immune responses, similar to elucidating the effects of imperfect vaccines, leads to counter-intuitive predictions of the evolution of pathogen virulence.

Owing to the decoupling between pathogen levels and immune pressure that occurs with long developmental chains we suggest that the model is able to approximate the ‘program’-type dynamics that are known to occur for particular immune responses such as the CD8 T cell responses where the immune system tracks the pathogen load for only a brief period following infection, before committing to a response independent of subsequent pathogen levels (Antia et al. 2003). Our model framework, therefore, is sufficiently flexible to account for much of the continuum of pathogen–immune system interactions ranging from ‘predator–prey’-type immune stimulation at one end and decoupled, ‘program’-type stimulation at the other, with simple adjustments to relatively few parameters. We believe this flexibility in the model makes it an ideal framework with which to examine a wide variety of possible scenarios of immune system modelling.

Whereas the majority of models consider the cost to a pathogen of high virulence is host death (Antia et al. 1994; Ganusov et al. 2002; Ganusov & Antia 2003), our model suggests that virulence may be constrained by the host's immune response. Such a suggestion has previously been made for viruses replicating within host cells (Almogy et al. 2002; Coombs et al. 2003; Gilchrist et al. 2004). Infected host cells are probed by active T cells with non-specific T-cell receptors (TCRs) and the number of antigens on the surface of the cell that are recognized by these TCRs is directly proportional to the replication rate of the virus within that cell. Hence, the more vigorous the virus's replication rate, the more antigens are presented and the quicker the cell, and the associated virus, is destroyed. Conversely, a slow replicating virus, although not producing many new virions, will remain ‘hidden’ from the T cells (Almogy et al. 2002). Since pathogen fitness depends on its total progeny output throughout the duration of an infected cell's life (Coombs et al. 2003), there is a trade-off between pathogen replication and cell lifespan, mediated by the host's immune response.

This immunity-imposed limitation on virulence becomes particularly important when we consider how it interacts with the inherent time delays in the immune response. Since, in the presence of immune memory, highly distributed responses inevitably lead to eradication of the pathogen, host immunity may select for increased virulence, as the pathogen makes the most of the short-time window available before it is removed. Hence, there may be a trade-off as far as the host is concerned between tolerating a chronic, relatively benign infection, or inducing an acute, but highly pathogenic infection (such as in respiratory diseases like SARS or influenza). Such predictions and expectations necessitate the development of more appropriate theoretical frameworks that capture the details of the biology of the immune system, the dynamics of the infection and the evolution of virulence for explaining the diversity and complexity of host immunity–pathogen interactions.