Short- and long-term population dynamical consequences of asymmetric climate change in black grouse

Abstract

Temporal asymmetry in patterns of regional climate change may jeopardize the match between the proximate and ultimate cues of the timing of breeding. The consequences on short- and long-term population dynamics and trends as well as the underlying mechanisms are, however, often unknown. Using long-term data from Finland, we demonstrate that black grouse (Tetrao tetrix) have responded to spring warming by advancing both egg-laying and hatching. However, early summer (the time of hatching) has not advanced, and chicks have to face colder post-hatching conditions. Demonstrating that these conditions are critical to post-hatching survival, we show that chicks are increasingly suffering higher mortality because they hatch too early. Consequently, breeding success and population size has severely declined over the past four decades. Finally, we modelled the impact of this particular climate change scenario on population dynamics and show that the mismatch can further explain the observed collapse of cyclic fluctuations. Because the evolutionary response of grouse is lagging behind the novel selective pressures, seasonally asymmetric climate change is likely to constitute an important determinant of future short- and long-term changes in the dynamics of black grouse populations.

1. Introduction

Climatic conditions influence biological processes (Sæther 1997) and changes in long-term climatic trends are demonstrably affecting living systems (Parmesan & Yohe 2003). Consequently, evaluating possible response scenarios in natural populations has become an urgent endeavour for ecologists. A large variety of response types have been proposed, some of which are very complex (Stenseth et al. 2002). In birds, climate change may influence demographic rates directly (Sæther et al. 2000; Sillett et al. 2000), but more commonly it is linked to range shifts (Parmesan & Yohe 2003) or changes in breeding phenology. For instance, variation in climate change between wintering and nesting grounds may adversely affect arrival times in migratory birds (Forchhammer et al. 1998; Brown et al. 1999; Crick & Sparks 1999; Dunn & Winkler 1999), or the response of a non-migratory bird population may not match that of its prey (Visser et al. 1998). A mismatch may also occur when patterns of regional climatic change differ between the egg-laying and hatching season, i.e. when climate change is seasonally asymmetric. Consequently, the synchrony between offspring requirements and maximum food availability may become disrupted. However, the overall population dynamical consequences of a temporally increasing mismatch, such as changes in both short-term fluctuations and long-term trends in population size, as well as the underlying mechanism by which the effect is brought about, remain commonly unidentified.

The black grouse is a ground nesting, forest dwelling gallinaceous bird still common throughout the taiga zone of Finland, but populations have declined strongly nationwide at least since the beginning of the 1960s (Helle et al. 2002; figure 1a). Females generally mate at the beginning of May and initiate egg-laying within 3 days after mating. Eggs are laid at an interval of 18–20 h. Incubation starts after the last egg has been laid and normally lasts 23–26 days. The total time from mating to hatching is therefore about 40 days and the hatching peak is generally around mid-June. Chicks are precocial and readily start to forage on their own after they have hatched synchronously. The ability to fly has already developed by the age of 4–5 days and the chicks rely entirely on an insect diet. Food choice gradually shifts towards a pure plant diet, the first moult of primaries begin and thermoregulation capacity develops fully at the age of three weeks (Höglund 1955; Hissa et al. 1983). Thus, the effect of weather conditions on brood survival is likely to be strongest during the critical post hatch period (Slagsvold 1975; Sæther et al. 2004).

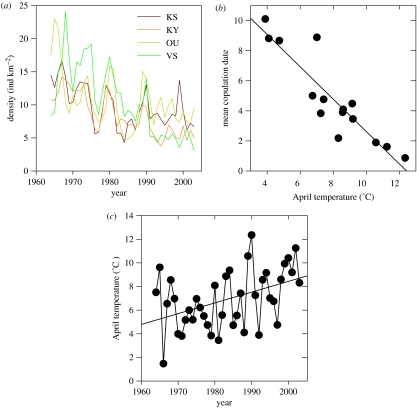
Figure 1.

(a) Density of black grouse in four Finnish game districts 1964–2003. KS; Keski-Suomi, KY; Kymi, OU; Oulu, VS; Varsinais-Suomi. The population under study is KS. (b) Relationship between mean maximum daily temperature during the last three weeks in April and mean copulation date. (c) Mean maximum daily temperature of the last three April weeks from 1964 to 2003.

Another particular feature of grouse populations, including also other grouse species such as capercaillie (Tetrao urogallus) and hazel grouse (Bonasa bonasia), is that they used to fluctuate in a cyclic manner, at a period of 6–7 years until the Mid-1980s. Ever since, the cyclic nature seems to have disappeared (Ranta et al. 2004). Up to date, this phenomenon still lacks a plausible explanation.

The scope of this study is the following. Combining both field and population census data, we evaluate changes in climatic patterns during both mating and hatching season as well as its consequences on the breeding phenology. In a second step, we demonstrate a strong link between the conditions experienced during a critical post hatch period and reproductive success. Thus, we show that seasonally asymmetric changes in climatic patterns increasingly cause black grouse chicks to hatch too early, i.e. under increasingly unfavourable conditions, having straightforward consequences on long-term breeding success and population size. The question on whether or not grouse are responding to these altered selective pressures is addressed. On the basis of these results, we finally present a model to show how such a scenario is capable of altering the cyclic nature of grouse population dynamics.

2. Material and methods

(a) Timing of breeding

Mean annual copulation dates were computed from a total of 691observations (annual mean 46.1 copulations, s.e.=8.8) of individual copulations from a total of seven different leks in the district of Keski-Suomi (Central Finland) during 1987–1998 and 2001–2003. The number of leks varied annually, but in any year, mating peaks in different sites were highly synchronous. The vast majority of copulations in the data represent different females since they only rarely mate more than once (Alatalo et al. 1996). Throughout the study period the investigated leks were of considerable size (more than 15 males). Furthermore, it has been shown previously that the timing of mating is independent of lek size (Alatalo et al. 1992). From this data, we further observed the exact hatching date for a subset of 47 radio-tagged females, during 1987–1991 and 2001–2003. None of these hens had mated multiply. Climatic data (mean, minimum and maximum daily temperatures) from Tikkakoski Weather Station in Central Finland was provided by the Finnish Meteorological Institute (contract no. dno 1/410/03). We produced cross-correlations between annual mean copulation/hatching dates and sliding windows of spring temperature using minimum, mean and maximum daily temperatures. We let the length of the sliding window vary from 1 to 6 weeks and let the start of the window vary between February 1 and May 1. For either minimum, mean or maximum daily temperature it was the last three April weeks that produced the strongest relationship, but results were strongest for maximum temperature. The resulting model, using mean maximum daily temperature, was then used to calculate mean copulation and hatching dates from 1964 to 2003. Long-term trends in temperature of the above mentioned April period (pre-mating season) as well as of the month of June (the hatching season) are evaluated.

(b) Linking changes in reproductive success to early life conditions and evolutionary response

Grouse census data for the district of Keski-Suomi were obtained from annual census counts performed in mid-August by volunteer hunters. The censuses were performed on transect lines from 1964 to 1988 and on wildlife triangles from 1989 onwards (Lindén et al. 1996). Otherwise, the sampling method (three persons covering a 60 m band) and the sampling unit (individuals per km²) were the same for both census methods. Annual means of monitored distance are 2030 km for the former and 630 km for the latter method. According to Lindén et al. (1989), results of both methods were very much in accordance when done simultaneously in 1989. Also, the prominent negative trend in population size is consistent throughout both census periods. On the basis of these findings we justify the combination of both monitoring systems. Juveniles and adults were counted separately. We used the residuals of young bird density regressed on adult density as a measure of reproductive output (Lindström et al. 1997). All data was log transformed. We produced cross-correlations between time-series of reproductive output and conditions (minimum, mean, maximum daily temperatures) of post-hatching periods of different lengths (1–25 days), using the calculated annual mean hatching date as the starting day. To minimize confusion hereafter, it is important to understand that the reproductive output is actually observed, while the annual hatching peaks and hence also the post-hatching periods, have been calculated (see §2). Analyses were performed using both detrended and non-detrended data, but we present results for non-detrended data only. The reason for doing so is because the negative trend is a biological fact and is therefore of particular interest. Results using detrended data, however, lead to the very same conclusions, with correlations on average being slightly lower. To assess whether or not an evolutionary response is occurring, we used a stepwise regression analysis of observed hatching dates on both April temperature and year. With an evolutionary response, the variable ‘year’ should be included in the model and its regression coefficient estimate should be positive.

(c) Asymmetric climate change and the loss of cyclicity

It has previously been shown that the cyclic nature of grouse fluctuations had ceased by the middle of the 1980s (Ranta et al. 2004). Although census data date back only to 1964, we can say, based upon data on hunting statistics that the cyclic nature was consistent for most of the twentieth century (Lindström et al. 1995).

To demonstrate how the suggested, climate-based mechanism (see §3) could affect the cyclic nature observed in Finnish grouse population dynamics, we utilized a population model (Royama 1992; Kaitala et al. 1996a), which has previously been shown to produce population fluctuations closely resembling those observed (Kaitala et al. 1996a,b; Lindström et al. 1999),

$$x(t+1)=x(t)\text{exp}\left(1-\frac{1}{x^{a_1}(t)x^{a_2}(t-1)}\right).$$ 2.1

Here, x(t) is the population size at time t and a₁ and a₂ are parameters determining direct and delayed density dependent feedback, respectively. Parameter values a₁=−0.0732 and a₂=−0.8819, for example, produce damped cycles with 6–7 year periodicity before an equilibrium is reached. However, if this process is subjected to environmental perturbations, μ, reducing the population productivity at random intervals

$$x(t+1)=\mu (t)x(t)\text{exp}\left(1-\frac{1}{x^{a_1}(t)x^{a_2}(t-1)}\right),$$ 2.2

the population size fluctuations display sustained oscillations. It has previously been shown (Kaitala et al. 1996a,b) that a frequency of about once in 10 years (p=0.1) and perturbation drawn from a uniform random distribution μ∼U[0.4,0.6], produce the kind of dynamics observed in Finnish grouse populations.

By interpreting μ as the match between timing of copulation and the subsequent hatching conditions, we can model the effects of climate change: increasingly poor match may result in more severe perturbations (smaller μ values). In addition, climate change may affect the frequency, p, of such perturbations. To look at how perturbation frequency, p and severity, μ, change the population dynamics of the model given in equation (2.2), we covered the parameter space for p=0.05–0.95 and average μ, $\overline{\mu }$=0.2–0.75, so that μ(t)∼N($\overline{\mu }$,0.03), truncated to: $\overline{\mu }$−0.15≤μ(t)≤$\overline{\mu }$+0.15. Note that unlike in previous papers (Kaitala et al. 1996a,b; Lindström et al. 1999), we draw μ(t) from a truncated normal distribution as this represents the distribution of environmental disturbances better than uniform random distribution. Our analyses showed, however, that our conclusions are robust to this as uniform disturbance distribution produces very similar results. We set a₁=−0.0732, a₂=−0.8819 and each parameter combination was run 100 times. Within each run, the model was set to run for 200 generations and the last 100 time-steps were analysed by using autocorrelation function to see if the dynamics are cyclic and, if so, what is the characteristic cycle length.

3. Results

The lek observation data from central Finland show that the onset of breeding and subsequent hatching is temperature dependent; correlations of observed annual mean copulation/hatching dates were strongest when using mean maximum temperature of the last three weeks in April (r=−0.91 and −0.84, P<0.001 and <0.01, respectively; figure 1b). Using minimum and mean daily temperatures produces the same April period, but correlations are somewhat weaker. Based on these two relationships, we modelled the timing of both breeding and subsequent hatching from 1964 to 2003. The results suggest that mean copulation date has advanced significantly due to a temporal increase in temperature of the three week April period (r=−0.43, P<0.01; figure 1c). Consequently, the calculated mean hatching date has advanced at a pace of about one day per decade. For the period from 1964 to 2003, the calculated hatching peaks ranged between June 9th and June 19th. For the subset of individual radio-tagged hens, observed hatching date was also significantly related to observed copulation date (r=0.51, P<0.001, N=47). This supports the result that advanced mating also leads to advanced hatching.

The trend in spring warming is not present in early summer, when chicks are hatching: June temperature has not increased during the past four decades (r=−0.09, P=0.59, N=40) and is uncorrelated with spring temperature (r=−0.20, P=0.23, N=40).

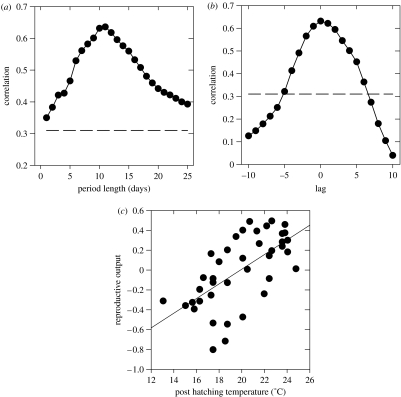
Chick survival, measured here as an annual reproductive output (Lindström et al. 1997), was strongly influenced by the conditions experienced during early life. Our results suggest that the effect of temperature on chick survival is strongest during the first ten days after the calculated hatching peak (figure 2a). The effect was strongest when using maximum daily temperatures. However, correlations using minimum and mean daily temperatures, although somewhat lower, were still significant and produced the same critical period of about 10 days. The correlations remain significant for longer periods, as subsequent windows are serially correlated. However, partial correlations (controlling for the previous period) are significant for post-hatching periods of 6 and10 days only. Setting the critical period to 10 days (r=0.63, P<0.001, N=40), we checked the reliability of the correlation by producing time-series of mean maximum daily temperatures for subsequent 10 day windows with different lags in respect to calculated mean hatching date. Our rationale is that if the first ten days in the life of chicks are the most critical, weather conditions of 10 day periods starting well before or after the calculated hatching date should have less impact on reproductive success, if at all. Figure 2b shows that this is the case; the correlations indeed peak when the period starts at the estimated mean hatching date. Figure 2c presents the relationship between reproductive output and temperature conditions experienced during this critical 10 day period.

Figure 2.

(a) Cross-correlations of mean maximum temperature with reproductive output for post-hatching periods of different lengths (N=40). The dashed line marks the level of significance. (b) Cross-correlations of mean maximum temperature with reproductive output for subsequent10 day periods. The lag indicates the starting day of the period in respect to the annual mean hatching date (which is set at 0). (c) Relationship between mean maximum temperature of 10 day post-hatching period and reproductive output (residuals of young bird density regressed on adult density), r=0.63, P<0.001, N=40.

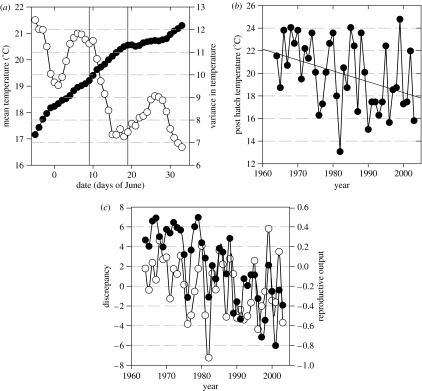
Looking at the temporal development of early summer conditions (figure 3a), we find that long-term mean temperatures experienced by the chicks during their first ten days rise steadily whereas the variances decrease markedly, especially within the range of expected mean hatching dates. Due to the advance in hatching, the temperatures experienced during this critical post-hatching period have decreased over time (r=−0.36, P=0.02; figure 3b). The cause for this decreasing trend can be explained by the temporal change in the distribution of good and bad years; bad years got worse and more frequent, but good years have not got any better, but scarcer. Comparing the periods 1964–1983 and 1984–2003 we find that the frequency of warm years (mean maximum daily temperature above an arbitrary temperature of 20 degrees) has dropped roughly by half from 0.70 to 0.35. The timing of hatching (calculated mean hatching date) was positively related to the observed reproductive output (r=0.5, P=0.001). However, early (i.e. bad) years have increased in frequency, which may at least partially account for the severe decline in observed reproductive output in time (r=−0.77, P<0.001).

Figure 3.

(a) Mean maximum daily temperature (filled circles) and its variance (open circles) of subsequent 10 day windows in early summer for the period 1964–2003. The date indicates the start of the 10 day period. The range of expected mean hatching date is demarcated with vertical lines. (b) Experienced conditions (mean maximum daily temperatures) during the first 10 days as a function of time. (c) Time-series of reproductive output (filled circles) and the deviation of expected and observed post-hatching conditions (discrepancy, open circles) plotted against time.

The association between temperatures of critical post-hatching periods and spring temperature is not consistent (r=−0.24, P=0.13, N=40): that is because some early years are warmer, and some late years colder, than expected from long-term means. The residuals of this linear relationship represent a measure of the discrepancy between expected and observed conditions. According to our hypothesis, this discrepancy should be positively related to breeding success, and it is (r=0.53, P<0.001). Figure 3c shows parallel plots of both the breeding success and discrepancy against time.

We did not find any evidence of an evolutionary response; stepwise regression of observed hatching dates on both April temperature and year showed no significant effect of year (P=0.43, d.f.=46), and its regression coefficient was even slightly negative (β=−0.11).

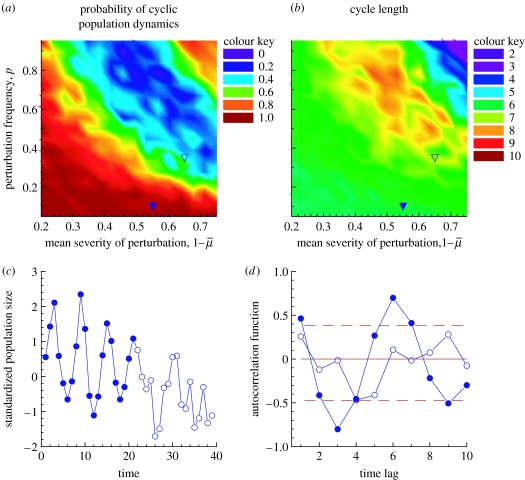
Our simulation results using model (2.2) were straightforward. The probability of observing cyclic dynamics was strongly affected by both the frequency and the severity of the climate induced disturbance (figure 4a). As suggested by figure 4b, the cycles seem to collapse by period lengthening rather than by period shortening. A typical realization of the resulting population fluctuation for a period identical to the studied period is shown in figure 4c. The autocorrelation functions for the first and second halves of the series (figure 4d) show that the first half is cyclic, but the second is not.

Figure 4.

Contour plots for the probability of (a) cyclic population fluctuations and (b) cycle length as a function of the mean severity of perturbation, 1−$\overline{\mu }$ and frequency, p, of an environmental perturbation. In (a) and (b) we have marked two points in the parameter space where the Finnish grouse dynamics could have been originally (filled triangle) and where they could be now (empty triangle). (c) shows a typical example of the resulting population fluctuations if the original parameters shift in time ($\overline{\mu }$ (t)=0.45−0.0025t; p(t)=0.1+0.009t). The first and second part of the time-series is depicted with different colours to demonstrate how the population dynamics change. The autocorrelation functions for these two parts of the time-series are shown in (d) with corresponding symbols.

4. Discussion

Our results demonstrate not only short- (decrease in breeding success, loss of cyclicity) but also potential long-term consequences (declining population size) of asymmetric climate change for a given population. Our first finding is that black grouse have advanced their breeding schedule as a result of advanced onset of spring. The onset of ideal hatching conditions in early summer, however, has not advanced, since the change in climatic patterns is temporally asymmetric. In order to remain synchronized with optimal post-hatching conditions, grouse should either delay mating or hatching (e.g. by prolonging incubation time), both of which was not the case. It has also been shown that heritability in the timing of breeding is very low in other bird species (Sheldon et al. 2003). Indeed, considering our results as well as the speed of current climate change, an evolutionary response is unlikely in the near future. The scenario of asymmetric climate change may therefore jeopardize the persistence of species that use climate-derived cues for the timing of breeding (Walther et al. 2002). In the absence of adaptive response, the dissonance between proximate cues (April temperature) and ultimate selection factors (post-hatching conditions) may increase in future.

In precocial birds like Galliformes, weather is most likely to affect early life stages (Sæther et al. 2004), such as the flightless post-hatching period; hence the overall effect should fade for periods longer than the critical period. Recognizing a critical time period during the life cycle sets an important biological context against which the effect of weather can be analysed. The importance of early life conditions on chick survival and hence reproductive output is demonstrated in figure 2a,b. Interestingly, the strongest results were obtained by using maximum daily temperatures, rather than e.g. minimum temperatures. The length of the critical period (10 days) approximately matches the flightless period, during which chicks rely on an insect diet and easily suffer from heat loss (Hissa et al. 1983). However, it is worth noticing that even periods shorter than 10 days are very significant. In the southern alps of Switzerland, Zbinden & Salvioni (2004) suggested a critical post hatch period of 5 days, for which they reported a positive relationship between reproductive success and temperature.

A plausible biological mechanism through which temperature may affect reproductive output includes interactions of hypothermia, starvation and predation; during colder weather, chick energy requirements increase but insect food is scarce and inactive (not easily observed by a chick). Chicks may also need to move more which increases the risks of both hypothermia and predation (Erikstad & Spidsø 1982).

The most critical consequence of asymmetric climate change now becomes more evident. Contrary to spring, early summer has not advanced. Figure 3a demonstrates nicely how much an advance in hatching of even a couple of days affect both the expected mean and variability in the conditions experienced during early life. This explains why late years have better breeding success than early years. Because both the severity and frequency of bad years (i.e. early years) have increased over time (figure 3b), the conditions experienced during the critical post-hatching season have become increasingly worse; hence breeding success has dropped significantly over time. Asymmetric climate change has therefore decreased the probability of encountering optimal rearing conditions. The plot of discrepancy (see §3) and reproductive output against time (figure 3c) suggests that in the long term, good years (high-positive residuals) are not enough to make up for the pronounced drops in breeding success produced by bad years (high-negative residuals).

In black grouse, annual variation in breeding success is commonly associated with annual fluctuations in population size (Lindström et al. 1997). Such variation can arise from a number of mechanisms. Age-related differences in reproductive output combined with annual variation in the strength of different age-classes (Lindström et al. 1997), or fluctuating predation pressure (Kurki et al. 1997) are just two examples. These mechanisms, however, explain short-term variation around a mean, but not necessarily a decrease of the long-term mean. Such a decrease is more likely to be driven by external processes, such as habitat loss and/or fragmentation, consistent increase in predation pressure (Kurki et al. 2000), long-term changes in environmental conditions (e.g. habitat degradation, climate change), or any combination of these (Storch 2000). The observed pattern of climatic change demonstrably represents such a process, with a strong potential in depressing long-term breeding success and subsequently long-term population size.

The population dynamics of black grouse in Finland have been extensively studied. The prominent and regular, 6–7 year fluctuations were identifiable until the Mid-1980s (Lindström et al. 1997; Ranta et al. 2004a). Since then, the cyclicity of the fluctuations has essentially vanished nationwide (Ranta et al. 2004). It has previously been shown (Ranta et al. 1997b), that stochastic density-independent but correlated environmental processes, commonly called the Moran effect (Moran 1953), when frequent or strong enough may qualitatively alter the characteristic dynamics. The current results provide us more insight into this.

First, as the frequency and severity of the density-independent perturbations have changed, they now occur too frequently and/or are too strong to sustain periodic oscillations (Lindström et al. 1995; Ranta et al. 1997a; Cattadori et al. 2005). Ranta et al. (1997b) showed for different types of dynamics that increasing frequency and strength of the Moran effect may lead to loss of cyclic components. Our simulation using a nonlinear second order autoregressive model shows that this could be happening; the probability of getting cyclic dynamics was strongly influenced by both frequency and severity of the climate-induced disturbance. It has been demonstrated that, in theory, cycles may collapse by either period shortening or lengthening (Royama 1992), but the general consensus is that cycles collapse by period shortening. In Europe, for instance, grouse and vole cycles grow shorter with decreasing latitude and eventually collapse in the south (Björnstad et al. 1995; Cattadori & Hudson 1999). Williams et al. (2004), however, provide empirical evidence that cycles of three North American grouse species collapse by period lengthening. This could be the case with Finnish black grouse; before disappearing, the cycle periods get longer. Alternatively, cycles have grown longer and are now too long to be detected from the data.

Second, the real world agent of density-independent perturbations has not been identified before but we now have a strong candidate. The potential mismatch caused by asymmetric climate change (i.e. long-term changes in post hatch conditions) acts as a Moran effect, of which both probability of occurrence (p) and strength (μ) have demonstrably increased in time. Finally, the relationship between reproductive output and post-hatching conditions is very prominent and the effect is localized for a critical period of the life cycle, both of which are important prerequisites when identifying external perturbations from population time-series (Royama 1992).

Temporally asymmetric changes in climatic patterns, as observed in our study, are possibly a common phenomenon, especially in the Northern Hemisphere. The potential consequences of such a particular scenario on natural populations, however, have barely been studied. Furthermore, our study is relevant in that we have identified a concrete mechanism which links the observed pattern of climate change to the weather conditions experienced in early life and ultimately to the population dynamics. It also adds to the multitude of possible scenarios and emphasizes that ultimately the effects of climate change need to be tracked down to biologically sound mechanisms. Despite of general trends, this can only be done on a case by case basis.

According to predictions, recent climate trends will continue in future (Climate change 2001), and the mismatch between the timing of breeding and optimal rearing conditions may become more severe. This may jeopardize any possible recovery of black grouse populations, and is likely to have widespread effects on other natural populations too.