Modelling dispersal of a temperate insect in a changing climate

Abstract

We construct a novel individual-based random-walk model to assess how predicted global climate change might affect the dispersal rates of a temperate insect. Using a novel approach we obtained accurate field measurements of daily movements for individuals over time to parameterize our model. Males were found to move significantly further on average than females. Significant variation in movement was evident among individuals; the most dispersive individuals moved up to five (females) and seven (males) times as far on average as the least dispersive individuals. Mean relative daily movement of both males and females were exponentially related to maximum daily temperature recorded within the grass sward. Variability, both within and among individuals, in relative daily movement was incorporated into the model using gamma probability distributions. Resultant dispersal functions for seasonal movement are predicted to be highly leptokurtic, which agrees well with observations from the field. Predictions of the model suggest that for populations at the polewards edge of the current range an increase of 3–5 °C in daily maximum temperature may increase the proportion of long-distance dispersers (those characterized as comprising the top 0.1% of furthest dispersing individuals under local conditions experienced during the 1963–1990 period) by up to 70%.

1. Introduction

In a changing environment a species must either move or adapt if it is to remain extant (Thomas et al. 2004; Hewitt & Nichols 2005), dispersal is therefore a critical trait involved in both the persistence and evolution of species (Clobert et al. 2001). The causes and mechanisms of movement are integral to the study of population dynamics and population genetics, yet despite much work they are still poorly understood (Clobert et al. 2001) and there remains a gap between theoretical models and our empirical observations of this important ecological process (Macdonald & Johnson 2001; Williamson 2002).

Dispersal functions are commonly leptokurtic, that is they have a higher peak and a longer, thicker tail relative to a normal distribution of equal mean and variance (Nichols & Hewitt 1994; Kot et al. 1996). The thickness of the dispersal tail is a measure of the probability of long-distance movements which are critical in determining rates of colonization and the potential range expansion of an invading species (Nichols & Hewitt 1994; Kot et al. 1996; Clobert et al. 2001; Williamson 2002). Models which incorporate a leptokurtic function can more accurately describe the probability of long-distance events and have successfully been used to explain spatial patterns of genetic variation occurring as a result of postglacial range expansion (Nichols & Hewitt 1994; Ibrahim et al. 1996). Such models have also reconciled apparent inconsistencies between traditional diffusion models of seed dispersal and evidence from the paleorecord (Clark 1998). Typically leptokurtic dispersal functions are based on hypothetical dispersal curves constructed using two kernels, one to describe relatively short local movement and the other to account for long-distance movement (Williamson 2002). While predictions of two-kernel models are consistent with indirect evidence of past range expansion, they provide less mechanistic insight into the underlying biology of movement than individual-based models. Individual-based models provide a better understanding of the processes of dispersal and can be used to justify forward projections (Yamamura et al. 2003).

Theoretical studies suggest that leptokurtic distributions can result from within- and between-individual variation in movement (Skalski & Gilliam 2000; Yamamura et al. 2003), population heterogeneity in movement (Yamamura 2002), individual behaviour at boundaries (Morales 2002) and variation in movement across heterogeneous landscapes (Morales & Ellner 2002) but quantifying such variation in behaviour is notoriously difficult to do (Doerr & Doerr 2005). In practice, this variability in movement may be the result of both intrinsic factors (or internal conditions) such as sex, age, social status, body size or energy reserves and environmental conditions such as season, habitat quality, competition, food quality, predators and parasites (Ims & Hjermann 2001; Tuda & Shima 2002) all of which may potentially contribute to the leptokurtosis of the dispersal curve.

In this paper, we test the hypothesis that the dispersal potential of a temperate grasshopper is dependent upon changes in regional climate by constructing an individual-based model which we then parameterize with data on weather-dependent daily movements observed in the field. We use a novel approach to quantify within- and between-individual variation in movement so overcoming the difficulty, so often encountered in modelling the tail of a dispersal curve, namely the lack of data on long-distance dispersal events (Doerr & Doerr 2005). It was found that both the mean and variance of daily movements were condition-dependent upon temperature. These data were used to parameterize gamma probability distributions for daily movement from which steps of a random walk could be derived. By taking into account, the variability in temperature between days, it was possible to project lifetime dispersal rates over the season. We use the model to predict how global climate change might affect the tail of the dispersal curve and hence the potential for long-distance movement and colonization.

2. Material and methods

(a) Study species

The lesser marsh grasshopper, Chorthippus albomarginatus De Geer (Acrididae: Orthoptera), is a medium-sized species which in Britain is largely restricted to the south and east (Marshall & Haes 1988). It is one of several species of Orthoptera that has undergone rapid range expansions during the last 10–15 years (P. Sutton 2003, personal communication). In Britain, it is considered a locally abundant species, while in temperate Asia, it is considered a notable economic pest (Uvarov 1977). It is found in a wide variety of grassland habitats over both wet and dry soil, from coastal sand dunes, to alongside rivers and roadside verges. C. albomarginatus is typical of temperate grasshopper species in that it has a univoltine life cycle with an obligate egg diapause stage. Nymphs emerge during May and June and develop through four nymphal instars. The first mature adults appear in July. Adult abundance declines in late August (Marshall & Haes 1988).

(b) Field site

Adult C. albomarginatus were tracked at a grassland field site in Cambridgeshire, England, at the Centre for Ecology and Hydrology, Monks Wood (Latitude: 52.402° N, Longitude: 0.235° W) during August 2001. The site is situated within 450 m of a meteorological station. The field, 250×42 m in size, was bordered by hawthorn hedgerows and woodland margins. 10 m wide areas of continuous grassland at the woodland margin ends of the field allowed free access to adjacent fields. The vegetation characterized as typically species-poor secondary grassland dominated by Agrostis stolonifera is most closely related to the national vegetation classification (NVC) plant community MG11. The site is subject to minimal management; it is unimproved, ungrazed, and is mown annually in late summer. The field was reasonably homogeneous in vegetation structure and composition, topography and soil composition. C. albomarginatus was the dominant grasshopper species at this field site.

(c) Mark–release–resighting

Adult grasshoppers were caught, marked in situ and released at the point of capture. A small piece (5×2 mm) of Scotchlite reflective tape (7610 high grain, available from 3M) was wrapped around the tibia of each of the two hind legs following Heller & von Helversen (1990) and Hein et al. (2003), who found that it did not significantly impede movement, and a uniquely numbered bee tag (Thorne (Beehives) Ltd) was glued to its pronotum with acylic ‘superglue’. In total, 309 and 407 daily movements were recorded from 114 males and 154 females, respectively.

The mark and release of individuals were carried out randomly throughout the field site to avoid any density-dependent effects associated with release from a single point source. Resighting of individuals was conducted at night when individuals were least active, using a head-torch. The field was staked at 10×10 m intervals with canes marked with reflective tape to provide a grid reference for recording positions. The entire field was searched with equal search effort (standardized as time per unit area) over 21 consecutive nights. On average, 69% of individuals sighted on a given night were resighted the following night (range 45–90%). The reflective tape allowed marked individuals to be seen up to 50 m away, allowing the site to be repeatedly searched with minimal disturbance and damage to the vegetation.

(d) Analysis

The straight distance between two consecutive night locations of an individual is referred to as a daily movement. A Mann–Whitney test was conducted to test differences between the sexes. Differences among individuals (for which at least eight daily movements were available, and the mean daily temperature for which did not significantly to that of other individuals) was tested using ANOVA on log (n+1) transformed data. To remove the effect of differences among individuals, daily movements were standardized by recalculating them as a percentage of an individual's mean of daily movements (male: n=129, females: n=119). This is hereon referred to as a ‘relative daily movement’. Mean relative daily movements were regressed against various meteorological variables available from the on-site meteorological station and from measurements of the microclimatic taken within the grass sward of the field-site using Tinytag Plus loggers (Gemini ISBN 162712). Since sample size varied between days, regression analyses were weighted by sample size. Statistical analyses were conducted using SPSS v. 11.5.

3. Results

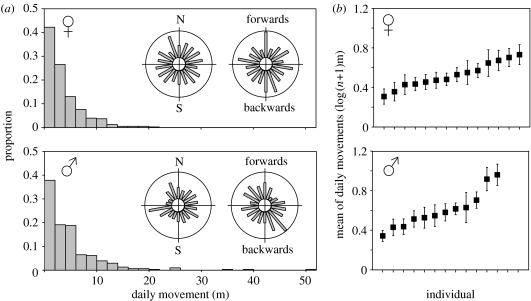
The frequency distributions of daily movements for both sexes were highly right-skewed towards movements of less than 2 m d⁻¹ (figure 1a). Males moved further on average than females (4.76 m versus 3.57 m: Z=1.975, p=0.048). This in part reflects differences between the sexes in regard to significant variability among individuals in mean daily movement (figure 1b: females: F_13,117=1.993, p=0.027; males: F_11,107=2.924, p=0.002). For example, the most active female was found to move five times further on average than the least active female, while there was up to a sevenfold difference between individual males. To test the statistical significance of the observed range and variance among individuals in mean daily movement, the probability distributions for daily movements in figure 1a were repeatedly sampled at random (figure 1a). Mean daily movements were calculated over 8 days (the minimum number of days for observed individuals in figure 1b) for 12 males and 14 females individuals. The proportions of times that the observed range and variance in mean daily movement among individuals arose purely by random after 100 000 simulations were 0.00442 and 0.00138, respectively for males, and 0.00586 and 0.03564, respectively for females.

Figure 1.

Daily movements of C. albomarginatus recorded in the field. (a) Probability distributions of daily movements for females (n=407, median=2.47 m, max.=21.9 m) and males (n=309, median=2.81 m, max.=50.9 m). Inset circular histograms show directional analyses of movements in respect to northing (left) and the previous day's movement (right). (b) Variation in mean daily movement among individuals (mean±1 s.e.).

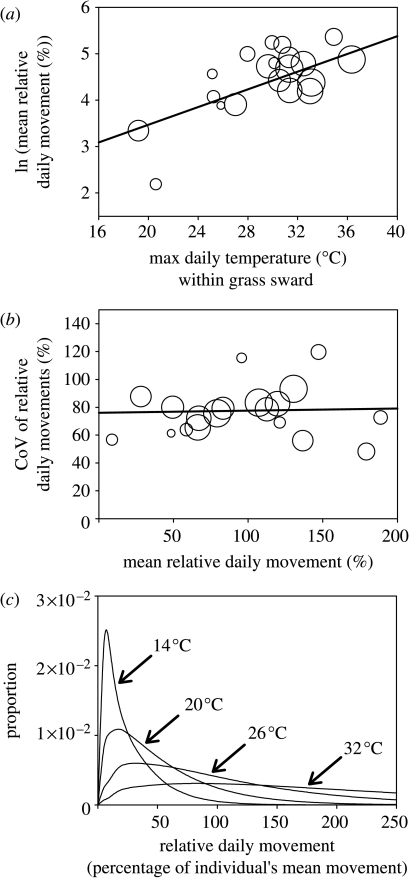
Both sexes showed significant exponential responses in mean relative daily movement to a variety of thermal conditions over the range of temperatures recorded on site, including mean daily ambient temperature (males: R²=0.21, F₁₈=4.82, p=0.042), daily maximum temperature (females: R²=0.24, F₁₇=5.32, p=0.034; males: R²=0.44, F₁₈=14.17, p=0.001) and total daily solar radiation (kJ; females: R²=0.28, F₁₇=6.55, p=0.02; males: R²=0.33, F₁₈=8.95, p=0.008) recorded at the meteorological station. However, the most reliable predictor of movement for both the sexes was maximum daily temperature recorded within the grass sward (females: R²=0.43, F₁₇=12.62, p=0.002; males: R²=0.37, F₁₈=10.68, p=0.004). Since the slopes (females: 0.101±0.031; males: 0.095±0.027) and intercepts (females: 1.35±0.95; males: 1.56±0.83) of this response did not differ between the sexes, data on relative daily movement from both sexes were pooled (figure 2a: R²=0.48, F₁₈=16.434, p=0.001). The coefficient of variation (CoV) of relative movement on a given day was found to be neither related to the mean relative movement of that day (figure 2c: R²=0.109, F₁₉=0.422, p=0.524; if a single outlying point excluded F₁₈=0.034) nor to the maximum daily temperature within the grass sward (R²=0.109, F₁₈=2.20, p=0.155; when the same single outlying point excluded F₁₈=0.014). The mean CoV value of 76.8% was used together with the response of mean relative daily movement to maximum daily temperature (figure 2a) to calculate changes the scale parameter β of the gamma probability distribution in order to model changes in potential relative daily movement throughout the season (figure 2c: see electronic supplementary material I for methods).

Figure 2.

(a) Mean relative daily movement (movements recalculated as a percentage of an individual's mean of daily movements) as a function of maximum daily temperature within the grass sward (sexes pooled). (b) Coefficient of variation of relative daily movements regressed against the mean of relative daily movement on a given day. Regressions above were weighted by sample size on a given day (n=2–23: represented by area of circle). (c) Examples of gamma probability distributions of relative daily movement generated for days with different maximum daily temperatures (°C) using the above relationships.

(a) Dispersal model

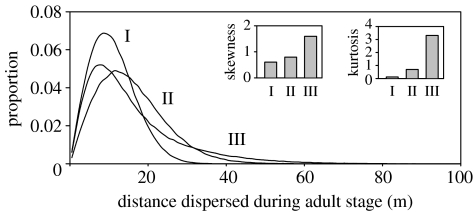
Three types of random walk model were compared: (i) a fixed-step model, (ii) a within-individual variation model and (iii) a within- and among individual variation model (figure 3). In the latter two models, the step movement is determined from a probability distribution. The introduction of within-individual variance into the model increased the mode, the skewness and the kurtosis of the dispersal function. When among individual variation was also introduced into the model, the skewness and the kurtosis of the dispersal function increased substantially but the mode was lower.

Figure 3.

Comparison of dispersal curves generated using three different random walk models (data for females; 1963–1990 period): I, a fixed-step model (mean=11.0 m; mode=8.5); II, a model assuming within-individual variation in step distance (mean=15.7 m; mode=11.5) and III, a model assuming both within- and between-individual variation in step distance (mean=15.7 m; mode=7.6). Mean daily movement in all models=2.04 m. Inset figures show relative skewness and kurtosis for each model.

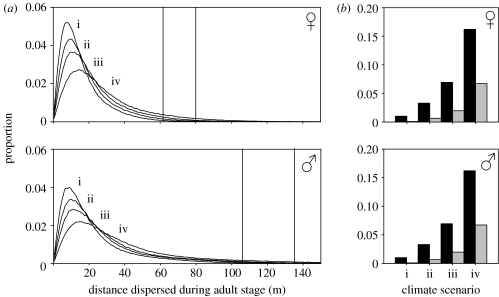
The effect of a change in seasonal temperature was modelled using the third model containing both within- and among individual variation. The model was run using four different seasonal frequency distributions of daily maximum temperatures: (i) that which was recorded on-site for the 1963–1990 period, (ii) that which was recorded on-site for the 1991–2000 period, (iii) a projected 3 °C increase relative to the 1963–1990 period and (iv) a projected 5 °C increase relative to the 1963–1990 period. An increase in seasonal temperature is expected to have a significant effect on the mean and potential movement of this grasshopper species (figure 4a). Predictions of the model suggest that the tail of the dispersal curve will substantially increase as the climate warms. The proportion of the population expected to move further than the distance dispersed by the furthest 1.0 and 0.1% of individuals (following suggested methods by Nathan 2005) under the 1963–1990 climatic scenario is projected to have increased under temperature conditions experienced during the 1990s by 3.3 and 7.0 times, respectively for females, and by 3.0 and 6.0 times, respectively for males (figure 4b). Under predicted climate change scenarios for the period 2070–2099 when temperatures in this region are expected to increase by up to 5 °C relative to the 1960–1990 period, the proportion of the population surpassing these distances is projected to increase by 16.2 and 67.0 times, respectively for females, and by 13.7 and 59.0 times, respectively for males (figure 4b).

Figure 4.

(a) Seasonal dispersal curves for adult grasshoppers predicted under four temperature scenarios: (i) maximum mean daily temperatures recorded on-site during the period 1963–1990; (ii) maximum mean daily temperatures recorded on-site during the period 1991–2000; (iii) a predicted increase of 3 °C in maximum daily temperatures relative to the 1963–1990 period and (iv) a predicted increase of 5 °C in maximum daily temperatures relative to the 1963–1990 period. (b) Projected impacts of potential climate change on the tail thickness of the dispersal curve for C. albomarginatus. Bars represent the proportion of the population which are predicted to move further than the distances (indicated by vertical lines in a) at which the furthest 1.0% (black bar) and 0.1% (grey bar) of the population dispersed under a 1963–1990 climate scenario.

Sensitivity of the model owing to potential errors in estimating both the mean and standard variation of relative daily movement and to changes in variability among individuals are given in the electronic supplementary material II. A change in the ‘level’ of movement had a substantial effect on predicted mean and standard deviation of movement although relatively little impact on skewness and kurtosis (electronic supplementary material II).

4. Discussion

Dispersal curves of organisms vary from species to species but one trait characteristic of many organisms is a highly leptokurtic distribution (Nathan 2005). Appropriate kernels can be fitted to such dispersal curves in order to more accurately describe long-distance movement (Nichols & Hewitt 1994; Ibrahim et al. 1996; Kot et al. 1996; Clark 1998) but they cannot help explain how leptokurtosis arises (Williamson 2002). Theoretical studies suggest that both within- and among-individual variability in movement influence the kurtosis of dispersal distributions (Skalski & Gilliam 2000; Yamamura et al. 2003) but quality data on such behaviour in the field tends to be extremely difficult to obtain (Doerr & Doerr 2005). In this study we were able to follow individuals through time to assess both within- and among-individual variability in daily movement.

If individuals are assumed to take random walks across a homogeneous landscape then one would predict that within-individual variation in daily movements to approximate a normal distribution. Instead, however, we found that daily movements were right-skewed and were best described using a gamma probability distribution. The propensity for the net movement of an organism to be lower than that predicted by diffusive processes or a simple extrapolation of daily movements is termed philopatry and has previously been shown in grasshoppers (Mason et al. 1995). One possible explanation for a lower than expected mean dispersal rate relates to habitat-heterogeneity (Morales & Ellner 2002). While vegetation across the field site appeared to be relatively homogenous, variability at the micro-habitat level in respect to grass sward length, a critical determinant of microclimatic conditions, is likely to be an important factor influencing grasshopper behaviour (Langmaack & Schrader 1997; Willott 1997; Schädler 1998).

Whatever the reasons determining variability in relative daily movement on a given day, there is no evidence to suggest that the mechanism(s) significantly interact with temperature. Since the CoV was consistent between days, only the ‘scale’ parameter β of the gamma distribution responded to temperature; the ‘shape’ parameter γ remained unchanged. This may suggest that an increase in temperature might simply lead to increased general activity and thus a greater tendency to move. While both sexes showed a similar exponential response of relative daily movement to temperature, this function may plateau at higher temperatures as the capacity to maintain optimal internal body temperatures increases.

Significant differences were also found between individuals. Males, despite their smaller size (approx. 80 mg), were found to move a third further on average than the much larger females (approx. 200 mg). The maximum distance dispersed by a male was more than double that of the furthest female. Much of this difference may relate to greater variability among male individuals in mean daily movement. The reasons why there is up to a sevenfold difference among individuals remains unclear. The tendency to disperse may relate to physiological internal conditions or it could simply reflect a behavioural trait such as an inherent ‘tendency to explore’ (Fraser et al. 2001; Hanski et al. 2002). What is clear is that unless variability among individuals is explicitly quantified, it will not be possible to fully understand nor model dispersal rates (Yamamura et al. 2003).

The dispersal curves generated by the random-walk model have the characteristic low-mode and long-tail consistent with estimates of lifetime dispersal distances for this species in the field (Ingrisch & Köhler 1998; modal distance: females<15 m, males<30 m; maximum distance: females=90 m, males=105 m) and for grasshoppers in general (Clark 1962; Aikman & Hewitt 1972; Mason et al. 1995; Narisu et al. 1999; Bailey et al. 2003). Predicted long-distance movements, however, are likely to be conservative given current assumptions of the model. For example, in reality individuals disperse across a heterogeneous habitat containing a mosaic of different habitat patches. These patches are likely to differ in their relative favourability which may influence both the extent and direction of their movements (Kindvall 1999; Conradt et al. 2001; Berggren et al. 2002; Hein et al. 2003). This, together with changes in behaviour in response to potential boundaries and barriers, will likely contribute to the leptokurtosis of the dispersal curve (Morales 2002; Morales & Ellner 2002). We might therefore expect long-distance movement to be greater across a spatially complex landscape, though such assumptions do not affect the relative importance of temperature on the tail of the dispersal curve. There remains, however, interestingly the possibility that temperature might affect the permeability of such barriers and unfavourable habitat to dispersal (Thomas & Jones 1993; Kindvall 1995).

Temperate grasshoppers are generally thought to have relatively limited dispersal capabilities (Richards & Waloff 1954; Uvarov 1977), but in a recent study of high-altitude arthropod migration over England a single male C. albomarginatus was caught during an aerial sample at 200 m (Chapman et al. 2004). This single orthopteran specimen represents just one of 6427 arthropods caught during three years of sampling. The frequency of high-altitude flights made by temperate orthopterans is expected to be very low. One might predict such long-distance dispersal events to be, at least in part, weather dependent (Uvarov 1977); however, the current model does not take into account the possibility of high-altitude flights or potential vectors such as cars (Tröger 1986) or livestock (Fischer et al. 1996). To account such factors, it would be necessary to incorporate an additional kernel into the model in order to simulate the probability of such events (Shigesada et al. 1995; Yamamura 2002). Despite such simplifying assumptions the model successfully demonstrates how leptokurtosis of dispersal curves can arise purely as a result of limited dispersal mechanisms such as walking, jumping and short flights. Furthermore, the model also demonstrates how rates of colonization and range expansion can be influenced by changes in seasonal temperature.

The consequences of temperature-dependent long-distance dispersal are that potential rates of colonization, range expansion and gene flow must be dynamic, both spatially across the species' geographical range and temporally between years. This could differentially affect levels of reproductive isolation between populations and the potential for local adaptation. Moreover, asynchronous responses of organisms to global climate change could lead to disequilibrium of current ecological interactions that will have direct implications for conservation and pest management. Using the model, it is possible to project how dispersal rates of C. albomarginatus are likely to respond to changes in regional climate. It can be predicted that a population living close to the polewards edge of its range is likely to have increased its dispersal ability during the relatively warm 1990s relative to the cooler period 1960–1990. During the 1990s, this species significantly expanded its range (P. Sutton, personal communication) although it is not known to what extent changes in dispersal rates contributed to this species' expansion of range. It is clear from the model predictions, however, that poikilotherms in general, and winged-insects in particular, could respond to higher temperatures at the polewards edge of their range in a way that may potentially increase their ability to track predicted future changes in global climate. For example, projected increases of 3–5 °C are predicted to substantially increase the proportion of females dispersing greater than 80 m by 20–67 times and the proportion of males dispersing greater than 137 m by 15–67 times (distances are those at which 0.1% of individuals are predicted to surpass under the 1963–1990 climate scenario).

Supplementary Material

Model construction

How the dispersal model was constructed and the assumptions made in regard to choosing an appropriate probability distribution to model the relative daily movement of individuals. Sensitivity and elasticity analyses are also provided.