Evolutionary games on cycles

Abstract

Traditional evolutionary game theory explores frequency-dependent selection in well-mixed populations without spatial or stochastic effects. But recently there has been much interest in studying the evolutionary game dynamics in spatial settings, on lattices and other graphs. Here, we present an analytic approach for the stochastic evolutionary game dynamics on the simplest possible graph, the cycle. For three different update rules, called ‘birth–death’ (BD), ‘death–birth’ (DB) and ‘imitation’ (IM), we derive exact conditions for natural selection to favour one strategy over another. As specific examples, we consider a coordination game and Prisoner's Dilemma. In the latter case, selection can favour cooperators over defectors for DB and IM updating. We also study the case where the replacement graph of evolutionary updating remains a cycle, but the interaction graph for playing the game is a complete graph. In this setting, all three update rules lead to identical conditions in the limit of weak selection, where we find the ‘1/3-law’ of well-mixed populations.

1. Introduction

Game theory was invented by von Neumann & Morgenstern (1944) as a mathematical approach to understand the strategic and economic decisions of humans. Hamilton (1967), Trivers (1971) and Maynard Smith & Price (1973) brought game theory to biology. Instead of analysing the interaction between two rational players, evolutionary game theory explores the dynamics of a population of players under the influence of natural selection (Maynard Smith 1982). In the classical setting of the replicator equation, the population size is infinite and interactions are equally likely between any two individuals (Taylor & Jonker 1978; Hofbauer et al. 1979; Zeeman 1980). Each individual obtains an average payoff which is interpreted as biological fitness; strategies reproduce according to their payoff. Successful strategies spread and eliminate less successful ones. The payoff depends on the frequency of strategies in the population. Hence, natural selection is frequency dependent. The replicator equation is deeply connected to the concept of an evolutionarily stable strategy (ESS) or Nash equilibrium. In the framework of the replicator equation, an ESS cannot be invaded by any mutant strategy (Hofbauer & Sigmund 1998). For recent books on game theory and evolutionary game theory, we refer to Fudenberg & Tirole (1991), Binmore (1994), Weibull (1995), Samuelson (1997), Fudenberg & Levine (1998), Hofbauer & Sigmund (1998), Gintis (2000) and Cressman (2003). Recent reviews of evolutionary game dynamics are Hofbauer & Sigmund (2003) and Nowak & Sigmund (2004).

While the traditional approach studies well-mixed, infinitely large populations, there have also been considerable efforts to characterize the game dynamics in spatial systems and other networks (Nowak & May 1992, 1993; Ellison 1993; Herz 1994; Lindgren & Nordahl 1994; Nowak et al. 1994; Killingback & Doebeli 1996; Nakamaru et al. 1997, 1998; Epstein 1998; van Baalen & Rand 1998; Eshel et al. 1999; Page et al. 2000; Skyrms & Pemantle 2000; Abramson & Kuperman 2001; Irwin & Taylor 2001; Ebel & Bornholdt 2002; Hauert et al. 2002; Brandt et al. 2003; Hauert & Szabó 2003, 2005; Le Galliard et al. 2003; Hauert & Doebeli 2004; Ifti et al. 2004; Szabó & Vukov 2004; Traulsen & Claussen 2004; Nakamaru & Iwasa 2005; Santos et al. 2006a,b). One observation was that cooperators and defectors can coexist indefinitely in the spatial settings of Prisoner's Dilemma (Nowak & May 1992). This ‘spatial reciprocity’ is a consequence of cooperators forming clusters, which can lead to a higher payoff for cooperators in the interior of the clusters than for defectors at the boundary.

Ellison (1993) has studied the coordination games in spatial settings and found that localized interactions facilitate faster convergence than global interactions. Nakamaru et al. (1997, 1998) have studied the interaction between tit-for-tat and always-defect in the repeated Prisoner's Dilemma on lattices. They have observed that ‘fertility’ selection is less favourable for cooperation than ‘mortality’ selection. Nakamaru & Iwasa (2005) analysed the evolution of altruism in a spatially structured population with punishment (Fehr & Gächter 2000; Sigmund et al. 2001).

There have also been extensions of the replicator equation into continuous space. This approach uses partial differential equations to describe evolutionary game dynamics (Vickers 1989; Hutson & Vickers 1992; Cressman & Vickers 1997). There is a long-standing tradition for studying spatial effects in ecology (Levin & Paine 1974; Durrett & Levin 1994; Hassell et al. 1994). For a recent review of population biology and network structure see May (in press).

In evolutionary games in finite populations, stochasticity plays an important role (Nowak et al. 2004; Taylor et al. 2004; Traulsen et al. 2005; Imhof & Nowak 2006). The most crucial quantities are the fixation probabilities. If a single individual playing a strategy A is added to a population playing strategy B, then there is a certain probability that A will generate an offspring lineage which will eventually take over the entire population. For a neutral mutant, this fixation probability is given by the inverse of the population size, $1/N$. If the fixation probability of A is greater than $1/N$, then selection favours the fixation of this strategy. The analysis of evolutionary game dynamics in finite populations requires a comparison of the fixation probabilities of the two strategies with each other and with $1/N$.

Lieberman et al. (2005) show how to calculate the fixation probability of a randomly placed mutant on various graphs. The traditional well-mixed population is the special case of a complete graph (all individuals are connected) with identical weights. For constant (instead of frequency-dependent) selection, any graphs that are circulations lead to the same fixation probabilities as the complete graph. A graph is a circulation if for each vertex the sum over all incoming weights equals the sum over all outgoing weights. Lieberman et al. (2005) also discussed the frequency-dependent selection (evolutionary games) on directed cycles.

Ohtsuki et al. (in press) studied the evolution of cooperation on a large variety of graphs. Using pair approximation (Matsuda et al. 1987, 1992; Harada et al. 1995), they found that selection favours the evolution of cooperation if $b/c>k$. The benefit-to-cost ratio of the altruistic act has to exceed the (average) number of neighbours per individual. Computer simulations suggest that this very simple rule works well for many different graphs including lattices, regular graphs, random regular graphs and scale-free networks. Of course, pair approximation makes certain assumptions that may or may not hold in a particular setting. Therefore, the attempt of this paper is to derive exact results for the fixation probabilities of evolutionary games on a simple family of graphs, the cycle. In these cases, direct calculations succeed, because a single invader always leads to one cluster that does not fragment into pieces. A cycle is a regular graph with k=2; each individual has exactly two neighbours. Therefore, we expect that $b/c>2$ will be a decisive rule for the evolution of cooperation on cycles.

In §2, we introduce the basic rules of the game, consider three different update mechanisms for the evolutionary dynamics and present results for general two person games. In §3, we study about the coordination games on cycles. In §4, we study the evolution of cooperation. Section 5 assumes that the updating (or the evolutionary competition) still occurs between nearest neighbour on a cycle, but the payoff of each individual is derived from random interactions among the whole population. In this case, we find that all three update mechanisms lead to the same criterion. Throughout the paper, we state the crucial results in the main text and show their derivations in appendix A.

2. Games on cycles

Consider a game between two strategies A and B. Denote by $a,b,c$ and d the payoff for A versus A, A versus B, B versus A and B versus B, respectively. The payoff matrix is given by

$$\begin{array}{l}\begin{array}{ccc}& A& B\end{array}\\ \begin{array}{c}A\\ B\end{array}\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\end{array}.$$ 2.1

Strategy A is a strict Nash equilibrium if a>c. In this case, strategy A is also evolutionarily stable, which means that B cannot invade A in an infinitely large, well-mixed population. Similarly, strategy B is a strict Nash equilibrium and evolutionarily stable if b<d. If a>c and b<d, then both strategies are strict Nash equilibria. In this case, a well-mixed population will either converge to one strategy or the other depending on the initial frequencies of the strategies. The strategy with the bigger basin of attraction is called ‘risk dominant’. A simple calculation shows that A is risk dominant if $a+b>c+d$.

If a>c and b>d, then A dominates B, which means that any mixed population will converge to a homogenous state using only strategy A. All these results are based on deterministic evolutionary game dynamics in infinitely large, well-mixed populations without spatial effects.

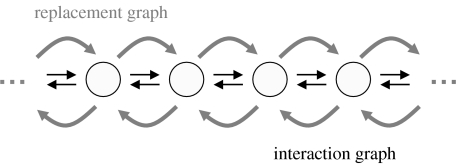
Real biological populations are neither well mixed nor infinite. Let us therefore consider a structured, finite population with individuals $i=1,\dots ,N$. The rate at which individual i plays the game with j is given by $h_{ij}$. The rate at which an offspring of individual i replaces j is given by $g_{ij}$. The matrix $G=[g_{ij}]$ specifies the ‘replacement graph’, while the matrix $H=[h_{ij}]$ specifies the ‘interaction graph’ (figure 1). In a series of other papers (Ohtsuki & Nowak in preparation; Ohtsuki et al. in press), we have used pair approximation and computer simulation to study the evolutionary games on a large variety of graphs. Here, instead, we derive exact results for the simple case that G and H are identical and given by cycles with equal weights.

Figure 1.

Evolutionary games on graphs (or social networks) are characterized by an interaction graph and a replacement graph. The interaction graph specifies who is interacting with whom in terms of the evolutionary game that is under consideration. The replacement graph specifies the local neighbourhood for updating the strategies (i.e. who competes with whom in the selection process). The simplest geometry is that both the replacement graph and the interaction graph are given by the same cycle, where each individual has exactly two neighbours and there is no boundary. This one-dimensional geometry allows an exact calculation which can be compared with approximative methods for other geometries.

Each player is interacting with its two immediate neighbours. The payoffs from these two interactions are added up. A parameter w measures the intensity of selection. The fitness of an individual is given by $1-w+wP$, where P is the individual's payoff. The case w=1 denotes strong selection: fitness equals payoff. The case $w\ll 1$ denotes weak selection: the payoff from the game represents only a small contribution to fitness. For w=0, we obtain neutral drift: all strategies have the same fitness. It is interesting to note that for the traditional replicator equation, the intensity of selection cancels out, but for stochastic game dynamics the intensity of selection plays an important role (Nowak et al. 2004). Often simple and illuminating results arise in the limit of weak selection, $w\to 0$.

We consider three different update rules: (i) ‘birth–death’ (BD) means that an individual is selected for reproduction proportional to fitness and the offspring replaces a randomly chosen neighbour; (ii) ‘death–birth’ (DB) means that a random individual is eliminated, and the neighbours compete for the empty site proportional to their fitness; and (iii) ‘imitation’ (IM) means that a random individual is chosen to update its strategy; it will either stay with its own strategy or imitate one of the neighbours' strategy proportional to fitness.

Imagine now that a single A individual is added to a population of $N-1$ B individuals. The A individual could die before reproducing or produce a lineage of A, which becomes extinct after sometime. In both cases, the population returns to a state of ‘all-B’. The other possibility is that A produces a lineage which will eventually take over the entire population, which means that B becomes extinct. In this case, the population will end up in the state ‘all-A’. Denote by ${\rho }_A$ the probability that a single A individual will take over a population of B. Denote by ${\rho }_B$ the probability that a single B individual will take over a population of A. The quantities ${\rho }_A$ and ${\rho }_B$ are called the fixation probabilities of A and B, respectively.

A neutral mutant has fixation probability $1/N$. Therefore, if ${\rho }_A>1/N$, then selection favours the fixation of A. If ${\rho }_A<1/N$, then selection opposes the fixation of A. If ${\rho }_A>{\rho }_B$ ,then selection favours A over B.

For strong selection $(w=1)$ and large population size $(N\to \infty )$, we find that selection favours the fixation of A and opposes the fixation of B, ${\rho }_A>1/N>{\rho }_B$, if

$$\begin{array}{ll}\text{BD}:\hfill & a+b>c+d,\hfill \\ \text{DB}:\hfill & a(a+b)>(c+d)d,\hfill \\ \text{IM}:\hfill & (3a+b)(a+b)>(c+d)(c+3d).\hfill \end{array}\}$$ 2.2

For the limit of weak selection $(w\to 0)$ and large population size $(N\to \infty )$, we find that ${\rho }_A>1/N>{\rho }_B$, if

$$\begin{array}{ll}\text{BD}:\hfill & a+b>c+d,\hfill \\ \text{DB}:\hfill & 3a+b>c+3d,\hfill \\ \text{IM}:\hfill & 5a+3b>3c+5d.\hfill \end{array}\}$$ 2.3

Interestingly, for BD updating, we find the same condition for weak and strong selection, and this condition is equivalent to risk dominance. For DB and IM updating, however, there are different conditions for weak and strong selection, and neither of those conditions are equivalent to risk dominance.

In the limit of weak selection, we can also derive simple conditions for any given population size, N. We find that ${\rho }_A>{\rho }_B$ if

$$\begin{array}{ll}\text{BD}:\hfill & (N-2)a+Nb>Nc+(N-2)d,\hfill \\ \text{DB}:\hfill & (3N-8)a+Nb>Nc+(3N-8)d,\hfill \\ \text{IM}:\hfill & (5N-12)a+3Nb>3Nc+(5N-12)d.\hfill \end{array}\}$$ 2.4

For large N, we recover the conditions given by (2.3). In contrast to (2.2) and (2.3), however, inequalities (2.4) do not specify whether ${\rho }_A$ or ${\rho }_B$ are greater or smaller than $1/N$. These conditions are derived in appendix A.

3. Pareto efficiency and risk dominance

Consider a coordination game. Strategies A and B are strict Nash equilibria. We have a>c and b<d. Suppose B is risk dominant, which means that $a+b<c+d$. But A is Pareto efficient, which means that a>d. Hence, strategy B has the bigger basin of attraction, but a homogeneous population of A has a higher payoff than a homogeneous population of B.

For BD updating, we always have ${\rho }_A<{\rho }_B$, which means that the fixation probability of A is smaller than that of B. BD updating on the cycle favours risk dominance over Pareto efficiency. For DB and IM updating, however, it is possible that the Pareto efficient strategy is favoured by selection. A particular example is given by the payoff matrix

$$\begin{array}{l}\begin{array}{ccc}& A& B\end{array}\\ \begin{array}{c}A\\ B\end{array}\left(\begin{array}{cc}10& 1\\ 9& 3\end{array}\right)\end{array}.$$ 3.1

Here, A is Pareto efficient, while B is risk dominant. Nevertheless, the conditions (2.2) and (2.3) hold for DB and IM updating, which implies that ${\rho }_A>1/N>{\rho }_B$ for large N. Therefore, these two update rules can lead to efficient outcomes of coordination games on cycles.

4. Prisoner's Dilemma on a cycle

As a specific example, consider Prisoner's Dilemma, which is given by the payoff matrix

$$\begin{array}{l}\begin{array}{ccc}& C& D\end{array}\\ \begin{array}{c}C\\ D\end{array}\left(\begin{array}{cc}R& S\\ T& P\end{array}\right)\end{array}.$$ 4.1

The ranking of the payoff values is $T>R>P>S$. The ‘temptation’ to defect, T, is greater then the ‘reward’ for mutual cooperation, R, which is greater than the ‘punishment’, P, for mutual defection, which is greater than the ‘sucker's payoff’, S. Since T>R and P>S, cooperators, C, are dominated by defectors, D. Both the traditional replicator dynamics and the stochastic dynamics in a well-mixed population of finite size (Nowak et al. 2004) lead to defection. Moreover, we have $R+S<T+P$, which means that BD updating on the cycle also favours defectors over cooperators.

But for DB or IM updating, it is possible that cooperators are favoured over defectors. A numerical example is given by

$$\begin{array}{l}\begin{array}{ccc}& C& D\end{array}\\ \begin{array}{c}C\\ D\end{array}\left(\begin{array}{cc}10& 1\\ 11& 2\end{array}\right)\end{array}.$$ 4.2

For this payoff matrix, the fixation probability of a single cooperator, ${\rho }_C$, is greater than $1/N$, while the fixation probability of a single defector, ${\rho }_D$, is less than $1/N$, for strong and weak selection, for DB and IM updating. Therefore, evolutionary game dynamics on cycles can favour cooperation over defection in Prisoner's Dilemma.

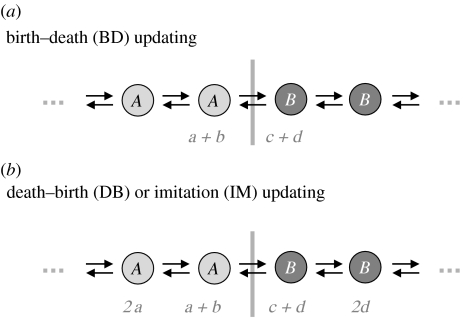
The intuitive reason for this finding is the following. On a cycle, an invasion attempt by a single cooperator leads to a single cluster of cooperators. The question is whether the boundary between cooperators and defectors moves in favour of cooperators or not. For BD updating, only the payoff of the two individuals (one cooperator and one defector) right at the boundary affects the stochastic dynamics. The cooperator always has a lower payoff than the defector. For DB and IM updating, the payoffs of the two individuals that are one place removed from the boundary also affect the dynamics. The ‘cooperator once removed’ always has a higher payoff than the ‘defector once removed’. Therefore, it is possible that the boundary moves in favour of cooperators (figure 2).

Figure 2.

(a) For BD updating, only the payoff of the two individuals right at the boundary between two clusters matters. The cluster of A players expands if $a+b>c+d$. (b) For DB and IM updating, the payoff of the four individuals closest to the boundary between two clusters matters. The cluster of A players increases if $2a+(a+b)>(c+d)+2d$ for DB updating and if $2a+3(a+b)>3(c+d)+2d$ for IM updating. All these results hold for weak selection. This figure gives the intuitive explanation of why cooperation can be favoured over defection for DB and IM updating, but not for BD updating.

For a simplified Prisoner's Dilemma given by two parameters denoting the cost, c, and benefit, b, of an altruistic act, we obtain the payoff matrix

$$\begin{array}{l}\begin{array}{ccc}& C& D\end{array}\\ \begin{array}{c}C\\ D\end{array}\left(\begin{array}{cc}b-c& -c\\ b& 0\end{array}\right).\end{array}$$ 4.3

The conditions for strong selection (equation (2.2)) cannot be used for this payoff matrix, because our analysis requires strictly positive fitness values. The conditions for weak selection (equation (2.3)) can be used, and here we obtain particularly elegant results. For BD updating, we find that ${\rho }_D>1/N>{\rho }_C$ for any choice of b, c and N. Hence, for BD updating, cooperation cannot evolve. For the other update mechanisms, however, we find that ${\rho }_C>1/N>{\rho }_D$ if

$$\begin{array}{ll}\text{DB}:\hfill & \frac{b}{c}>2+\frac{4}{N-4},\hfill \\ \text{IM}:\hfill & \frac{b}{c}>4+\frac{18}{N-6}.\hfill \end{array}\}$$ 4.4

Note that the DB condition requires N>4, while IM requires N>6. For large N, we obtain

$$\begin{array}{ll}\text{DB}:\hfill & \frac{b}{c}>2,\hfill \\ \text{IM}:\hfill & \frac{b}{c}>4.\hfill \end{array}\}$$ 4.5

These findings concur with the results obtained by pair approximation for regular graphs of degree k (Ohtsuki et al. in press). There we find that DB updating favours cooperators if $b/c>k$, while IM updating favours cooperators if $b/c>k+2$. Both results hold for large N and weak selection. In this framework, we also find that BD updating never favours cooperators. Since the cycle has degree k=2, the findings are in agreement.

5. Local updating but global interaction

Let us return to the general game between two strategies given by payoff matrix (2.1). Let us keep the cycle as the replacement graph, but use a complete interaction graph. This means that updating occurs locally among nearest neighbours, but interactions occur globally. Remarkably, the following results hold for all three update mechanisms.

In the limit of weak selection, we find that ${\rho }_A>{\rho }_B$ if

$$(N-2)a+Nb>Nc+(N-2)d.$$ 5.1

This inequality leads to $a+b>c+d$ for large N. Furthermore, for large N, we find that ${\rho }_A>1/N$ if

$$a+2b>c+2d.$$ 5.2

This condition is the ‘1/3-rule’ which has been observed previously for well-mixed populations. If strategies A and B are best replies to themselves, then the standard replicator equation has an unstable equilibrium at a frequency of A given by $x_A^{*}=(d-b)/(a-b-c+d)$. For stochastic game dynamics in a well-mixed population using the Moran process, the fixation probability ${\rho }_A$ exceeds $1/N$ for weak selection and large population size if $x_A^{*}<1/3$ (Nowak et al. 2004). This 1/3-rule has also been obtained for frequency-dependent selection in the Wright–Fisher process (Imhof & Nowak 2006).

6. Conclusion

We have studied the stochastic evolutionary game dynamics on cycles, which represent the simplest possible family of graphs. Each individual has two neighbours. A single invader leads to a single cluster, which does not fragment into pieces. Therefore, the transition matrix of the stochastic process is tri-diagonal, and the fixation probability of an invading strategy can be calculated explicitly. We consider three different update mechanisms for evolutionary dynamics, which we call ‘birth–death’ (BD), ‘death–birth’ (DB) and ‘imitation’ (IM). We explore the interaction between two strategies A and B and present conditions for the fixation probability ${\rho }_A$ to be greater than ${\rho }_B$. We also compare the two fixation probabilities with $1/N$, which is the fixation probability of a neutral mutant. For strong and weak selections, we find simple conditions (equations (2.2) and (2.3)) for large population size, N. For weak selection, we also find simple conditions for any population size (equation (2.4)).

Note that none of these conditions reduce to the simple criteria of a strict Nash equilibrium or an ESS. Therefore, if A is a strict Nash equilibrium or an ESS, then it can still be the case that ${\rho }_A$ is less than ${\rho }_B$ and/or less than $1/N$.

In coordination games, BD updating always favours the risk-dominant strategy, while DB and IM updating can favour Pareto efficiency over risk dominance. In Prisoner's Dilemma, BD updating always favours defectors, while DB and IM updating can favour cooperators over defectors. In the latter case, a cooperator lineage starting from a single cooperator invades a population of defectors with a probability of an advantageous mutant. If cooperators pay a cost c for neighbours to receive a benefit b, then DB updating favours the evolution of cooperation if $b/c>2$. For IM updating, we find $b/c>4$. These findings are in agreement with the results obtained by pair approximation for regular graphs (Ohtsuki et al. in press).

Note that these conditions are needed for the evolution of cooperation by spatial reciprocity alone (Nowak & May 1992) without any strategic complexity (Axelrod & Hamilton 1981; Axelrod 1984) or reputation effects (Nowak & Sigmund 2005). One can also study the synergistic interaction between spatial reciprocity and direct or indirect reciprocity, which will lead to less stringent conditions for the emergence and stability of cooperation.

The intuitive reason for the different behaviour of the update mechanisms is illustrated in figure 2. For BD updating, only the payoff of the two individuals right at the edge of a cluster plays a role, because two adjacent players directly compete for reproduction. The scale of interaction and competition is the same there. In contrast, for DB and IM updating, two individuals that are two-steps away from the edge of the cluster are also involved in the competition; therefore, the scale of competition is larger than that of interaction. For the struggle between cooperators and defectors, this is a crucial difference, because right on the edge, the defector always has a higher payoff than the cooperator, but the cooperator that is once removed from the edge can have a higher payoff still. There is an interesting parallelism between this observation and previous studies on viscous populations by Taylor (1992) and West et al. (2002), who show that cooperation is favoured when the scale of competition is larger than the scale of interaction.

Studying games on graphs leads to an understanding of how population structure affects the outcome of evolutionary dynamics. Compared to most other evolutionary graphs, the cycle has the particular advantage that the fixation probabilities in frequency-dependent selection can be calculated exactly. Moreover, the cycle represents the extreme case where the effect of spatial structure on evolutionary dynamics is strongest. On the other end of the spectrum is the well-mixed population, which is given by a complete graph (where all individuals are connected to each other). For Prisoner's Dilemma, this means that the condition $b/c>2$ is a minimum requirement. All other structures will demand a larger benefit-to-cost ratio for the evolution of cooperation.

Appendix A

Appendix A. Derivation of the results in the main text

Let us calculate ${\rho }_A$.

If the replacement graph is a cycle, then a single invader always leads a single connected cluster. Therefore, in order to describe the stochastic process, it is sufficient to count the number of players. Let i denote the number of A players. The state space of the stochastic process is given by $i=0,\dots ,N$, where N is the total population size, which is constant. At each time-step, the variable i can at most change by one unit. Denote the associated transition probabilities by ${\lambda }_i=\text{Pr}(i\to i+1)$ and ${\mu }_i=\text{Pr}(i\to i-1)$. We have $1-{\lambda }_i-{\mu }_i=\text{Pr}(i\to i)$.

There are two absorbing states i=N and i=0. The former corresponds to all-A and the latter to all-B. If the system has reached such a state it will stay there forever. All other states are transient. Denote by ${\rho }_A$ the probability to reach state i=N when starting from i=1. This quantity is the fixation probability of A. Similarly, the fixation probability of B, ${\rho }_B$, denotes the probability to reach state i=0 when starting from state $i=N-1$. A direct calculation (Karlin & Taylor 1975; Ewens 2004) shows that

$${\rho }_A=1/\left(1+\sum _{j=1}^{N-1}\prod _{i=1}^j\frac{{\mu }_i}{{\lambda }_i}\right).$$ A1

For the ratio of the two fixation probabilities, we find

$$\frac{{\rho }_A}{{\rho }_B}=\prod _{i=1}^{N-1}\frac{{\lambda }_i}{{\mu }_i}.$$ A2

Thus, we need to calculate ${\mu }_i/{\lambda }_i$ for each i.

For convenience, define $\alpha ,\beta ,\gamma$ and δ as $\alpha =1-w+2wa,\beta =1-w+2wb,\gamma =1-w+2wc$ and $\delta =1-w+2wd$. Here, $a,b,c\text{and}d$ are the entries of the payoff matrix and w denotes the intensity of selection.

(i) For BD updating, we find

$${\mu }_i/{\lambda }_i=\{\begin{array}{ll}(\gamma +\delta )/2\beta \hfill & (i=1),\hfill \\ (\gamma +\delta )/(\alpha +\beta )\hfill & (2\le i\le N-2),\hfill \\ 2\gamma /(\alpha +\beta )\hfill & (i=N-1).\hfill \end{array}$$

For strong selection (w=1), the relative size of $(\gamma +\delta )/(\alpha +\beta )$ compared to one is important. If it is less than one, which is the case when $a+b>c+d$, then ${\rho }_A$ is positive, otherwise ${\rho }_A=0$. For weak selection, we have

$${\rho }_A=\frac{1}{N}+\frac{w}{2N^2}\{(N^2-3N+2)a+(N^2+N-2)b-(N^2-N+2)c-(N^2-N-2)d\}$$

and

$$\frac{{\rho }_A}{{\rho }_B}=1+w\{(N-2)a+Nb-Nc-(N-2)d\}.$$

(ii) For DB updating, we obtain

$${\mu }_i/{\lambda }_i=\{\begin{array}{ll}(\beta +\delta )/2\beta \hfill & (i=1),\\ [(\gamma +\delta )/(\alpha +\beta )]& \\ [(\alpha +\beta +2\delta )/(\alpha +\beta +\gamma +\delta )]& (i=2),\\ [(\gamma +\delta )/(\alpha +\beta )]& \\ [(\alpha +\beta +2\delta )/(2\alpha +\gamma +\delta )]& (3\le i\le N-3),\\ [(\gamma +\delta )/(\alpha +\beta )]& \\ [(\alpha +\beta +\gamma +\delta )/(2\alpha +\gamma +\delta )]& (i=N-2),\\ 2\gamma /(\alpha +\gamma )& (i=N-1).\end{array}$$

For strong selection, ${\rho }_A>0$ if and only if $[(\gamma +\delta )/(\alpha +\beta )][(\alpha +\beta +2\delta )/(2\alpha +\gamma +\delta )]<1$, which is equivalent to $a(a+b)>(c+d)d$. For weak selection, we have

$${\rho }_A=\frac{1}{N}+\frac{w}{4N^2}\{(3N^2-11N+8)a+(N^2+3N-8)b-(N^2-3N+8)c-(3N^2-5N-8)d\}$$

and

$$\frac{{\rho }_A}{{\rho }_B}=1+\frac{w}{2}\{(3N-8)a+Nb-Nc-(3N-8)d\}.$$

(iii) Finally, for IM updating, we have

$${\mu }_i/{\lambda }_i=\{\begin{array}{ll}[(\gamma +\delta )/2\beta ]\hfill & \hfill \\ [(2\beta +\gamma +3\delta )/(2\beta +2\gamma +2\delta )]\hfill & (i=1),\hfill \\ [(\gamma +\delta )/(\alpha +\beta )]\hfill & \hfill \\ [(\alpha +\beta +\gamma +3\delta )/(2\alpha +2\beta +\gamma +\delta )]\hfill & (i=2),\hfill \\ [(\gamma +\delta )/(\alpha +\beta )]\hfill & \hfill \\ [(\alpha +\beta +\gamma +3\delta )/(3\alpha +\beta +\gamma +\delta )]\hfill & (3\le i\le N-3),\hfill \\ [(\gamma +\delta )/(\alpha +\beta )]\hfill & \hfill \\ [(\alpha +\beta +2\gamma +2\delta )/(3\alpha +\beta +\gamma +\delta )]\hfill & (i=N-2),\hfill \\ [2\gamma /(\alpha +\beta )]\hfill & \hfill \\ [(2\alpha +2\beta +2\gamma )/(3\alpha +\beta +2\gamma )]\hfill & (i=N-1).\hfill \end{array}$$

For strong selection, ${\rho }_A>0$ holds if and only if $[(\gamma +\delta )/(\alpha +\beta )][(\alpha +\beta +\gamma +3\delta )/(3\alpha +\beta +\gamma +\delta )]<1$, which is equivalent to $(3a+b)(a+b)>(c+d)(c+3d)$. For weak selection, we have

$${\rho }_A=\frac{1}{N}+\frac{w}{6N^2}\{(5N^2-17N+12)a+(3N^2+5N-12)b-(3N^2-5N+12)c-(5N^2-7N-12)d\}$$

and

$$\frac{{\rho }_A}{{\rho }_B}=1+\frac{w}{3}\{(5N-12)a+3Nb-3Nc-(5N-12)d\}.$$

If the interaction graph is complete, the total payoffs of A and B players are

$$e_A(i)=(i-1)a+(N-i)b,$$

$$e_B(i)=ic+(N-i-1)d.$$

Substituting $e_A(i)$ for a, b and $e_B(i)$ for c, d leads to the results shown in the main text.