Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2006 Sep 15;91(11):4317–4327. doi: 10.1529/biophysj.106.087817

The Fundamental Organization of Cardiac Mitochondria as a Network of Coupled Oscillators

Miguel Antonio Aon 1, Sonia Cortassa 1, Brian O'Rourke 1
PMCID: PMC1635654  PMID: 16980364

Abstract

Mitochondria can behave as individual oscillators whose dynamics may obey collective, network properties. We have shown that cardiomyocytes exhibit high-amplitude, self-sustained, and synchronous oscillations of bioenergetic parameters when the mitochondrial network is stressed to a critical state. Computational studies suggested that additional low-amplitude, high-frequency oscillations were also possible. Herein, employing power spectral analysis, we show that the temporal behavior of mitochondrial membrane potential (ΔΨm) in cardiomyocytes under physiological conditions is oscillatory and characterized by a broad frequency distribution that obeys a homogeneous power law (1/fβ) with a spectral exponent, β = 1.74. Additionally, relative dispersional analysis shows that mitochondrial oscillatory dynamics exhibits long-term memory, characterized by an inverse power law that scales with a fractal dimension (Df) of 1.008, distinct from random behavior (Df = 1.5), over at least three orders of magnitude. Analysis of a computational model of the mitochondrial oscillator suggests that the mechanistic origin of the power law behavior is based on the inverse dependence of amplitude versus frequency of oscillation related to the balance between reactive oxygen species production and scavenging. The results demonstrate that cardiac mitochondria behave as a network of coupled oscillators under both physiological and pathophysiological conditions.

INTRODUCTION

The heart is a collection of dynamically coupled nonlinear oscillators, and it has proven to be a rich source of data for those interested in complex phenomena. One of the earliest models of weakly coupled oscillators was described by Van der Pol, who reproduced some of the functional aspects of the heart by viewing it as a system of electrically coupled relaxation oscillators (1). Since then, numerous investigators have applied various analytical techniques to uncover “scale invariant” (fractal) processes in cardiac function. A well-studied example is the fluctuation of the beat-to-beat interval of the electrocardiogram. Time series plots of this parameter show variations that appear to have a similar morphology when viewed at temporal resolutions spanning several orders of magnitude. This is the temporal analogy to spatial fractal scaling observed in, for example, the branching patterns of a tree, the pulmonary bronchioles, or the arterial system (2).

Several methods have been developed to quantify such long-range correlations in time series, indicating that the events being correlated are not independent of each other. The methods include spectral analysis, which reveals the scale-free memory effect as a power law dependence of the frequency distribution (often displaying a “1/f” distribution (3)), and methods that plot fluctuations of a signal around a trendline when the data are aggregated over different time windows (e.g., fluctuation analysis (4), detrended fluctuation analysis (5), or relative dispersion analysis (6)). The potential importance of identifying these nontrivial correlations in complex physiological functions is that in disease conditions, it has been shown that the fractal character of the system can break down. Degeneration of the characteristic long-range correlation can be manifested either as i), an increase in the randomness of the fluctuations (i.e., toward uncorrelated white noise), ii), the appearance of correlations of the random walk type (i.e., Brownian noise), or iii), a narrowing of the frequency spectrum and/or the appearance of highly periodic behavior (e.g., the appearance of the Cheyne-Stokes frequency in the interbeat time series in patients with heart failure) (4,5,7).

Scale invariance has been observed in many biological systems that require a high degree of adaptability and a flexible response to changing environmental conditions. Hence, it has been argued that this organizational motif may permit complex control processes to respond without becoming “mode-locked” into a narrow range of function (4,5,7).

Mitochondrial oxidative phosphorylation is a prime example of a biological system regulated by a series of mechanisms that interact to provide a rapid and robust change in energy production to meet cellular demand. Therefore, in this study, we test the hypothesis that the mitochondrial network of the heart cell may be organized as a lattice of coupled relaxation-type oscillators (i.e., those exhibiting slow and fast phase components) that exhibit scale-free temporal organization. We have previously demonstrated that this network displays complex dynamic behavior when subjected to metabolic stress (8), including scale invariant spatiotemporal synchronization (9). Self-sustained and highly coordinated oscillations in mitochondrial membrane potential (ΔΨm) and reactive oxygen species (ROS) can be triggered under conditions of oxidative stress (8), which could be reproduced in a computational model of ROS-induced ROS release (10).

In addition to reproducing the dominant low-frequency (∼0.01 Hz) oscillations in energetic parameters observed under stress, the mathematical model also displayed a variety of stable high-frequency, low-amplitude oscillations when a single parameter was varied (10). This motivated us to employ the aforementioned analytical techniques to determine if long-range correlations exist in experimental time series of mitochondrial energetic parameters under physiological conditions. We demonstrate that the mitochondrial network behaves as a collection of weakly coupled oscillators with a broad frequency distribution under normal conditions that can transition to an oscillatory state with a single dominant frequency under conditions of metabolic stress. We suggest that this phase transition in time and space is due to an increase in the levels of the primary coupling factor, ROS. The findings reveal the fundamental spatial and temporal organization of mitochondria as a complex system of oscillators.

MATERIALS AND METHODS

Cardiomyocyte isolation

All experiments were carried out at 37°C on freshly isolated adult guinea pig ventricular myocytes prepared by enzymatic dispersion as previously described (11). See Supplementary Material for further details.

Fluorescent probes for two photon laser scanning microscopy and image acquisition and analysis

The cationic potentiometric fluorescent dye tetramethylrhodamine methyl ester (TMRM) (100 nM) was used to monitor changes in ΔΨm as previously described (8). Images were recorded using a two photon laser scanning microscope (Bio-Rad (Hercules, CA) MRC-1024MP) with excitation at 740 nm, and the red emission of TMRM was collected at 605 ± 25 nm (Tsunami Ti:Sa laser, Spectra-Physics, Mountain View, CA).

Analysis of TMRM time series

Extended time series of TMRM fluorescence (1500–4000 images) recorded at a maximal temporal resolution of 110 ms were subjected to relative dispersional analysis (RDA) and power spectral analysis (PSA).

RDA

RDA allows a quantitative determination of how the state of a process at a given point in time is influenced by the state of the system at previous time points (2,12,13). The relative dispersion or coefficient of variation (CV = standard deviation/mean) is repeatedly calculated while binning (coarse-graining) the data set at successively larger timescales. More specifically, we aggregated adjacent points in the time series of ΔΨm at 2, 4, 8, 16, and 32 successive values of the data set to calculate the CV for each grouping (12) and plotted it versus the aggregation number, m. The slope of this relation provides information as to the extent of long-term correlation (or memory) in the data set.

PSA

The power spectrum of the TMRM time series was analyzed after fast Fourier transform (FFT) of the fluorescence signal. Double log plots of amplitude versus frequency indicated a decrease in power proportional to 1/fβ, where f is frequency and β is the spectral exponent (2,12,13) (and see Supplementary Material). The Fourier transform of the TMRM signal was performed with the FFT routine of Microcal Origin (Version 6.0, Northampton, MA). Since this routine may use five different data windowing methods (rectangular, Welch, Hanning, Hamming, Blackman), we performed controls to examine how different windowing methods influenced the determination of β. Simulated pink noise (35,281 time points) was used as a control whose power spectrum should yield β = 1.0. The best fit of the simulated data was obtained with rectangular windowing (β = 1.0; r = 0.61) (see Supplementary Material); thus, we used this method to calculate FFT from the TMRM time series. The results did not differ significantly when different windowing methods were used.

Because the sampling rate was limited to ∼100 Hz and the data were not low-pass filtered, data points shown at frequencies >1.3 (i.e., five times the sampling rate) in the power spectrum may contain some minor frequency contamination due to aliasing. This effect should not significantly alter the conclusions of the study since the slopes were determined from the data points that satisfied the Nyquist criterion of at least two times the sample frequency.

To differentiate between the TMRM signal obtained from cells and pure brown noise, we applied RDA and PSA to either simulated brown noise or brown noise obtained from the integration of white noise (see legends for Figs. 3 and 4, and the text; see also Supplementary Material for additional controls).

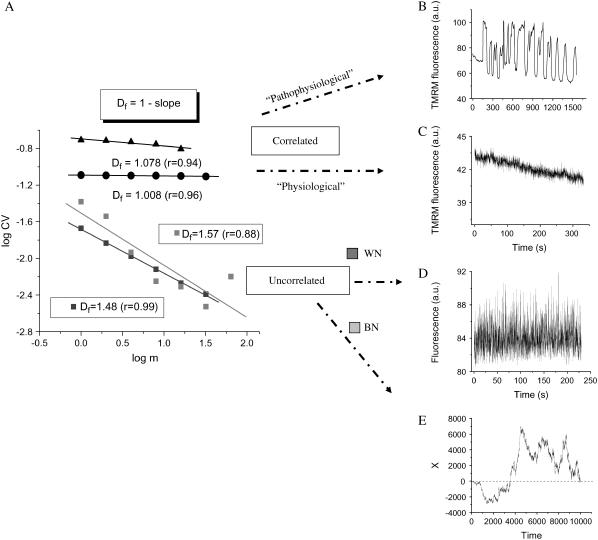
FIGURE 3.

FIGURE 3

Open in a new tab

RDA of the TMRM fluorescence time series from the mitochondrial network of cardiomyocytes. Freshly isolated ventricular cardiomyocytes were loaded with 100 nM TMRM and imaged by two photon microscopy, as described in Materials and Methods. The statistical analysis of the TMRM signal showed that the mitochondrial network of the heart cell functions as a highly correlated network of oscillators. (A) RDA: A log-log plot of the CV (= SD/mean) of the fluorescence distribution obtained at increasing values of the aggregation parameter, m (see also text), gives a fractal dimension, Df, close to 1.0, either for myocytes showing large (“pathophysiological”) oscillations in ΔΨm (panel A, solid triangles, and panel B) or those under “physiological” conditions (panel A, solid circles, and panel C). A completely random process obtained from the noise in the image background (panel D) (in fact, corresponding to the images shown in panel C) gives Df = 1.48 (∼1.5; panel A: WN, white noise, dark gray squares). The position of a Brownian particle as a random function of time simulates brown noise (panel E), Df = 1.57 (∼1.5; panel A: BN, brown noise, light gray squares) (see also Supplementary Material). The data obtained from RDA were subjected to linear regression and the slope calculated. Df was obtained as described in panel A.

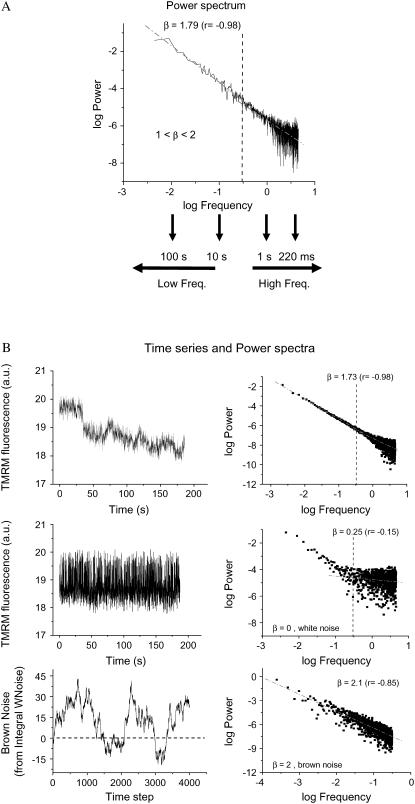
FIGURE 4.

FIGURE 4

Open in a new tab

PSA of TMRM fluorescence time series from the mitochondrial network of cardiomyocytes. Experiments were carried out as described in the legend of Fig. 1 and Materials and Methods. The time series of TMRM fluorescence was subjected to FFT as described in Materials and Methods. (A) PSA: The power spectrum was obtained from the FFT of the TMRM signal as the double log plot of the amplitude (power) versus the frequency. This relationship obeys a homogeneous power law (1/fβ; with f, frequency, and β, the spectral exponent) and is statistically self-similar, which means that there is no dominant frequency. The PSA reveals a broad spectrum of oscillation in normally polarized mitochondria with a spectral exponent of β = 1.79, whereas a random process (white noise) gives a β ∼ 0, meaning that there is no relationship between the amplitude and the frequency in a random signal. A β = 1.0 (Supplementary Material, Fig. S3) or 2.0 (Fig. 4 B, bottom panels) corresponds to pink or brown noise, respectively. The inverse power law spectrum arises from the coupling of frequency and amplitude in an orderly statistical sequence. The periods, in seconds or milliseconds, at the bottom of panel A are intended to facilitate the interpretation of the high- and low-frequency domains of the spectrum. (B) When the time series of the TMRM fluorescent signal is randomized (mid, left), we obtain a value of β close to zero (mid, right) as opposed to a β = 1.79 in the nonrandomized signal (right, top). The spectral exponent β = 1.79 (right, top) is consistent with long-range correlations that after signal randomization becomes white noise, with loss of correlation properties β = 0.25 (≅ 0) (mid, right) (12).

Additional controls

We investigated whether the excitation wavelength, λexc, and laser intensity affected the results obtained with RDA or PSA (see Supplementary Material for details).

Computational model of the mitochondrial oscillator

An integrated model of mitochondrial energetics (14), which was extended to include a shunt of electrons of the respiratory chain toward the generation of 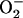Inline graphic, a ROS scavenging system, and a ROS-activated anion efflux pathway across the inner membrane (10), was used for the simulations shown in Fig. 2, using the parametric conditions described in Cortassa et al. (10).

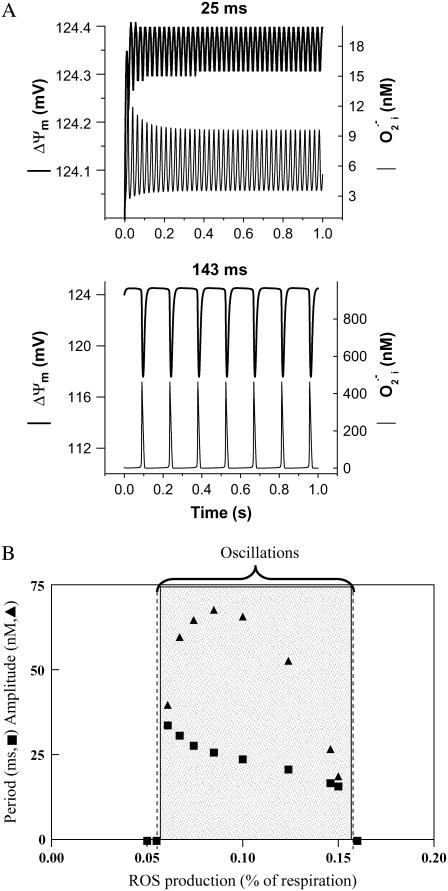
FIGURE 2.

FIGURE 2

Open in a new tab

Frequency and amplitude modulation of the mitochondrial oscillator model through changes in the balance between ROS production and ROS scavenging. (A) Oscillation periods of 25 ms and 143 ms are shown for SOD concentrations of 0.75 μM and 1.07μM, respectively. The model parameters used to run the simulations for shunt = 0.0744 (defined as the fraction of the electron flow in the respiratory chain diverted to the generation of superoxide anion, 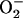Inline graphic) were concentration of respiratory chain carriers, ρREN = 2.5 × 10−6 mM; concentration of F1F0 ATPase, ρF1 = 2.03 × 10−3 mM; [Ca2+]i = 0.1 μM; Kcc = 0.01 mM; 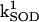Inline graphic = 2.4 × 106 mM−1s−1; 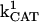Inline graphic = 1.7 × 104 mM−1s−1; GT = 0.5 mM; maximal rate of the adenine nucleotide translocase, VmaxANT = 5 mM s−1; maximal rate of the mitochondrial Na-Ca exchanger, 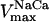Inline graphic= 0.015 mM s−1. The 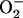Inline graphicconcentrations correspond to the mitochondrial matrix space and were calculated as described in Cortassa et al. (14). Remaining parameters were set as described in Cortassa et al. (10) and Cortassa et al. (14). (B) Under similar parametric conditions, the frequency and amplitude of the oscillations in 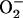Inline graphic delivered to the cytoplasm as a function of the fractional 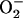Inline graphic production in the high-frequency domain (ms). Within the oscillatory region (shaded), the oscillatory period constantly decreased, whereas the amplitude reached a peak and then decreased as a function of the increase in ROS production. A similar analysis was performed in the low-frequency domain (seconds to minutes) for SOD concentrations of 1.87 μM (not shown). In the latter case, the amplitude of 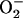Inline graphic (0.86 mM) did not change as a function of the shunt (from 0.05 to 0.25), whereas the period decreased from 276 s to 62 s, respectively.

Statistical analysis

Estimation of the statistical significance of differences in Df or β between controls and treatments and the calculation of correlation coefficients was performed with GraphPad Prism (version 2; San Diego, CA). The results are presented as mean ± SE (95% confidence interval) after a t-test (small samples, unpaired t-test with two tail p-values). The adequacy of the sample size (n values) was assessed with retrospective power calculations (8).

RESULTS

Frequency and amplitude modulation of the mitochondrial oscillator

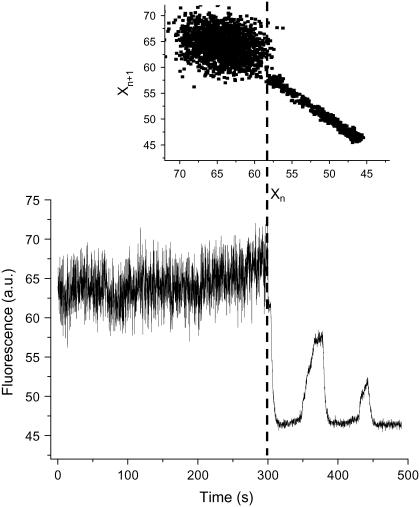
Under “physiological” conditions mitochondrial ΔΨm fluctuates at high frequency within a restricted amplitude range, implying depolarizations of only microvolts to a few millivolts. As we have shown previously, oxidative stress may elicit low-frequency, high-amplitude oscillations that characterize the “pathophysiological” response (Fig. 1; see video in Supplementary Material). A return plot illustrates how the distribution of frequencies and amplitudes of oscillation can change at the junction between physiology and pathophysiology (Fig. 1, inset). Although the physiological domain shows an apparently “noisy” appearance, the transition to pathophysiology is characterized by a highly correlated limit cycle type oscillation.

FIGURE 1.

FIGURE 1

Open in a new tab

Physiological and pathophysiological behaviors of the mitochondrial network in heart cells. Freshly isolated ventricular cardiomyocytes were loaded with 100 nM TMRM and imaged by two photon microscopy (150-ms time resolution) as described in Materials and Methods. The results obtained from a stack of 3720 images are shown (see the video of this experiment in Supplementary Material). Before the mitochondrial network reaches criticality (9,15,30), the ΔΨm (as measured by TMRM) oscillates at high frequencies and small amplitudes. After criticality, the network behavior evolves into “pathophysiological” behavior characterized by low-frequency, high-amplitude oscillations (8,10). The return plot of the time series shown in the inset was calculated by representing the fluorescent signal, Xn, with a lag of 150 ms with respect to itself, Xn+1. This graph allows a quick visualization of the richness of high-frequency, low-amplitude oscillations present in the physiological as opposed to the low-frequency, high-amplitude oscillations present in the pathophysiological regime.

We became interested in determining if the physiological domain also shows temporal correlations after model simulations revealed the potential for high-frequency, low-amplitude domains of the mitochondrial oscillator (Fig. 2 A). A systematic simulation study of the oscillatory behavior of ΔΨm and ROS, as a function of a fraction of the respiratory flux diverted to ROS production (i.e., superoxide anion 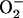Inline graphic), revealed that in the high-frequency domain both the period and amplitude of the oscillator could be modulated. The period decreased from 34 ms to 16 ms as the ROS leak was increased from 6% to 15% of the respiratory flux, whereas the amplitude of ROS pulses reached a maximum (66 nM 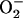Inline graphic) at ∼8% of respiration diverted to ROS and then decreased at higher frequencies (Fig. 2 B). The period (from 70 ms to 250 ms) and the amplitude of the ΔΨm (2–24 mV) and ROS oscillations (150 nM to 1 μM) could also be modulated by varying the superoxide dismutase (SOD) concentration (from 1.0 to 1.2 μM) within the high-frequency range when the fraction of respiration diverted to ROS was fixed at 7.4% (not shown, but see Cortassa et al. (10)).

These results suggest that the mitochondrial oscillator may, potentially, function as both a frequency- and amplitude-encoding ROS signaling mechanism in the physiological (high-frequency) domain. This hypothesis was explored using the statistical analysis of ΔΨm time series from isolated heart cells described below.

Temporal correlation of the mitochondrial network in the physiological domain

Heart cells loaded with TMRM, reporting ΔΨm, were imaged at a frame interval of 110 ms with two photon laser scanning microscopy. RDA and PSA were applied to time series composed of 1500–4000 time points.

The rationale underlying RDA is that for a system exhibiting completely random fluctuations, the CV, drops off more rapidly as the data are aggregated over longer timescales as compared with a system that shows long-term memory (see Materials and Methods). The double-log plot of CV versus the aggregation number, m, of adjacent time points shows an inverse power law correlation with a slope corresponding to a fractal dimension, Df = 1.008 ± 0.002 (Fig. 3 A; n = 10 time series; five independent experiments). An inverse power law with a slope corresponding to a fractal dimension close to 1.0 suggests that there is long-term memory in the system (Fig. 3, A and C). In this context, long-term memory means that the ΔΨm fluctuations are influenced by changes of ΔΨm in the past.

Unlike the high correlation exhibited by the mitochondrial network, processes without memory show completely random behavior (white or brown noise) characterized by an exponential (Poisson) law with slopes corresponding to Df = 1.5 (Fig. 3, A, D, and E) (12). Unlike white and brown noises, pink noise exhibited a Df close to 1.0 (see Supplementary Material). The long-term memory of the mitochondrial network was not only evident in the “physiological domain” but also in the “pathophysiological domain” (Fig. 3, A–C) (see also Supplementary Material and Aon et al. (8)). These results were substantiated with controls performed on the instrument noise of the background from the same image sequence (Fig. 3 D) or after random shuffling of ΔΨm time points to eliminate any deterministic component. Under either of these conditions, Df shifted from 1.0 to 1.5 (Fig. 3 A), indicating that the fluctuations in the signal were due to physiologically relevant, dynamic control mechanisms in mitochondrial metabolism rather than random variation. This was also confirmed later when inhibitors known to affect the mitochondrial oscillatory mechanism were applied (see below).

Power spectral analysis of ΔΨm

Correlations in time series are also revealed using PSA and are often characterized by an inverse power law relationship. As also shown using the RDA above, self-similar scaling suggests that events in different timescales (milliseconds, seconds, minutes) are tied together in an orderly statistical sequence. Thus, the power spectrum of such data usually follows an inverse power law proportional to 1/fβ (see Materials and Methods: PSA and FFT calculation).

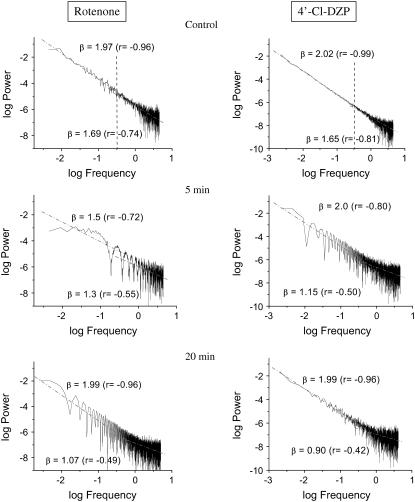
Applying PSA, we calculated the power spectra (displayed as a double log plot of amplitude versus frequency) after FFT of the ΔΨm time series from mitochondria under physiological conditions. The power spectrum of the mitochondrial network exhibited a bandwidth pattern with low-frequency components (<0.3 Hz, dashed line in Fig. 4 A) and a predominant (>90% of the data points) low-amplitude tail of higher frequencies (>0.3 Hz). The power spectrum could be described by a homogeneous inverse power law of the form 1/fβ with β = 1.737 ± 0.015 (n = 10 time series; five independent experiments) (Fig. 4 A). However, a value of β close to 2.0 (1.99 ± 0.03, n = 10) could be attributed to the low-frequency components, and 1.54 ± 0.03 (n = 10) for the high-frequency, low-amplitude region of the spectrum (see below). The frequencies >0.3 Hz thus behaved in the mid-range between pink (β = 1.0) and brown (β = 2.0) noise.

The observed power spectrum is indicative of highly persistent, correlated, long-term memory processes that scale for at least three orders of magnitude. Correspondingly, we obtained β ≈ 0 or β ≈ 2.0 for controls exhibiting random behavior (white noise) (Fig. 4 B, mid panels) or ordinary brown noise (Fig. 4 B, bottom panels), respectively. Moreover, β = 1.0 was obtained from time series that simulate pink noise (see Supplementary Material, Fig. S3).

Taken together, the results show that the collective behavior of the mitochondrial network (i.e., through ΔΨm) belongs to a statistically fractal, self-similar process characterized by a large number of frequencies in multiple timescales, rather than an inherent “characteristic” frequency.

Are reactive oxygen species intracellular messengers under physiological conditions as they are in pathophysiology?

The scale-free behavior of the mitochondrial network suggests that the mechanism described for the mitochondrial oscillator under pathophysiological conditions could share similar features in the physiological domain of behavior. We tested this by exposing heart cells to a respiratory inhibitor (rotenone), a ROS scavenger (TMPyP), and a mitochondrial benzodiazepine receptor (mBzR) inhibitor (4′-Cl-DZP). These pharmacological treatments decrease ROS production either by blocking respiration, by direct scavenging, or by inhibiting ROS-induced ROS release from mitochondria. Mechanistically, all of these agents inhibit oscillations in the pathophysiological domain (9,10).

Under physiological conditions, the presence of 15 μM rotenone or 64 μM 4′-Cl-DZP, but not TMPyP, rapidly (within 5 min) affected the high-frequency region of the spectrum but not the low-frequency one, with the exception of rotenone at 5 min. This effect on the high-frequency, low-amplitude domain of the spectrum (frequencies >0.3 Hz) (Fig. 5) was manifested as a strong decrease in the value of β, predominantly as a result of a significant loss of correlation (Fig. 5). The loss of correlation in the high-frequency domain of the spectrum is consistent with a weaker coupling between mitochondrial oscillators in the network, in agreement with a decrease in ROS, the proposed coupling factor (8).

FIGURE 5.

FIGURE 5

Open in a new tab

Effects of respiratory and IMAC inhibitors on the mitochondrial power spectrum under physiological conditions. Freshly isolated ventricular cardiomyocytes were incubated for at least 2 h in Dulbecco's modified Eagle's medium as described in Materials and Methods. After loading with 100 nM TMRM, the cells were imaged at 110-ms time resolution in the absence or the presence of 64 μM 4′-Cl-DZP or 15 μM rotenone at different times. The TMRM time series obtained (2000–3000 images) were analyzed by PSA and fitted with a straight line (Microcal Origin) separately for frequencies higher or lower than 0.3 Hz as described in the text and Materials and Methods.

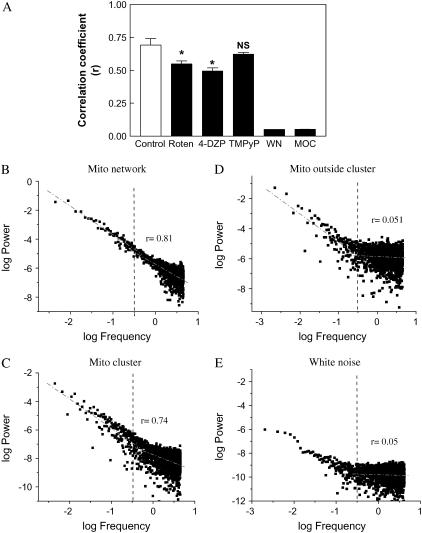
The major effects of rotenone and 4′-Cl-DZP on the high-frequency domain (i.e., frequencies >0.3 Hz) of the spectrum were compared with pure white noise, which exhibits a Pearson correlation coefficient of r ≈ 0, whereas mitochondria in the correlated network gave r = 0.70 ± 0.05 (n = 4 time series; two independent experiments; Fig. 6 A). A similar comparison was made for myocytes undergoing “pathophysiological” mitochondrial oscillations by separately analyzing mitochondria included within and outside of the synchronized oscillating cluster (9). Mitochondria that were not oscillating in synchrony with the cluster exhibited a power spectrum similar to white noise (r = 0.05; compare panels D and E of Fig. 6), whereas mitochondria within the cluster showed a high r over a wide frequency range (r = 0.74; Fig. 6 C), similar to the high r exhibited by mitochondria under physiological conditions (r = 0.81; Fig. 6 B; see Supplementary Material for discussion of the spatial implications of these results).

FIGURE 6.

FIGURE 6

Open in a new tab

Loss of correlation exhibited by mitochondrial oscillators in the high-frequency, low-amplitude domain of the power spectrum after treatment affecting ROS production, scavenging, or spreading. Isolated cardiomyocytes loaded with TMRM as described for the other experiments were treated for 30 min with 64 μM 4′Cl-DZP (n = 4, two experiments) or 15 μM rotenone (n = 4, two experiments) or for 2 h with 135 μM TMPyP (n = 4, two experiments). Treated cells were imaged at 110-ms time resolution and the TMRM fluorescence time series analyzed by PSA. (A) We determined the Pearson correlation coefficient, r, of the high-frequency, low-amplitude region of the spectrum as that represented by frequencies >0.3 Hz. Represented are the absolute values of r. We determined 0.3 Hz as delimiting the high-frequency region on the basis of analysis of white noise spectra since it contains 93% of the data points (panel E; the dashed line points out the 0.3 Hz frequency, which to the right corresponds to the high-frequency, low-amplitude domain of the spectrum, as in panels B–E). This analysis was also applied to randomized time series (see Fig. 4 B) or mitochondria oscillating outside the mitochondrial cluster (panel D). The region of the spectrum >0.3 Hz corresponds to random behavior characterized by r = 0.051 ± 0.001 (n = 4) as opposed to r = 0.70 ± 0.05 (n = 4) exhibited by the mitochondrial network under control conditions (panel B) or an oscillating mitochondrial cluster (panel C). In panels B–E, the dashed lines represent the linear fitting for the two separate regions of the spectrum to emphasize that the change in slope mainly happens in the high frequency domain (see also Fig. 5). In panel A, WN is white noise and MOC stands for mitochondria outside the cluster.

Origins of the inverse power law behavior

In an attempt to better understand the origin of the power law relationships observed experimentally, we examined the amplitude versus frequency dependence of our previously published computational model of the mitochondrial oscillator (10). The double log plot of amplitude versus frequency exhibits an inverse relationship (Fig. 7 and Supplementary Material). Two key factors contribute to this dependence—the SOD activity and the balance between the rate of ROS production and scavenging. Within the oscillatory domain, after a Hopf bifurcation (Fig. S4A in Supplementary Material and (10)), an increase in the SOD rate results in longer periods and higher amplitude oscillations (Fig. S4B in Supplementary Material). An extensive parametric analysis of the model revealed that this balance defines whether or not the system oscillates (10,15). Furthermore, the results suggest that the ROS balance also determines the frequency and amplitude of the mitochondrial oscillator. The rationale for interpreting this behavior is that given a constant background conductance of the inner membrane anion channel (IMAC) channel, having a lower SOD rate combined with a relatively high rate of ROS production leads to faster ROS accumulation in the mitochondrial matrix and triggers channel opening more readily. In contrast, with a faster rate of ROS scavenging (i.e., a higher SOD rate), it will take longer for ROS to accumulate in the matrix, resulting in a longer period.

FIGURE 7.

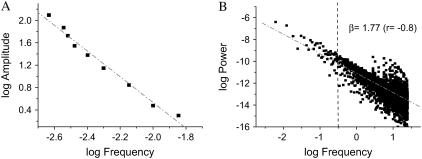
FIGURE 7

Open in a new tab

Inverse power law behavior and the amplitude versus frequency relationship exhibited by the mitochondrial oscillator. (A) Oscillations were simulated with our computational model of the mitochondrial oscillator ((10); see also Fig. S4 in Supplementary Material). The double log graph of the amplitude versus frequency (1/period) was plotted from ΔΨm oscillations with amplitudes in the range of 2–124 mV and periods ranging from 70 to 430 ms, respectively. The simulations for shunt = 0.1 and SOD concentrations from 0.9 × 10−4 to 1.3 × 10−3 were performed with the set of parameters described in the legend of Fig. 2 (see Cortassa et al. (10) and Cortassa et al. (14)) for detailed parameter descriptions). B) From the simulations, we selected five oscillatory periods in the high frequency domain (between 70 and 300 ms) and one from the low-frequency (1-min period) domain and attributed each one of them proportionally to a network composed by 500 mitochondria as described in Supplementary Material (see also Fig. S5). A matrix containing a total of 500 columns (mitochondria) and 6,000 rows was constructed. The time steps represented by the rows correspond to a fixed integration step of 20 ms for the numerical integration of the system of ordinary differential equations (see Supplementary Material). We applied RDA and PSA to the average value of each row of the matrix at, e.g., time 1, T1, that represents the experimental average value of fluorescent intensity of the ΔΨm probe (corresponding to mV) obtained every 110 ms from 500 mitochondria (on average) from each image of our stack.

We hypothesized that if the mitochondrial network was exhibiting a mixture of frequencies, then we should be able to simulate the inverse power law behavior obtained by either PSA or RDA. We simulated five different oscillatory periods ranging from 70 ms to 300 ms and one long period (1 min) oscillation (Fig. S4, Supplementary Material). A combination of 80% short period and 20% long period oscillations allowed us to simulate the inverse power law behavior observed experimentally by either PSA or RDA (Fig. 7 B and compare with Fig. 4 A; see also Supplementary Material). This result demonstrates that the mixture of a relatively modest number (six) of different periods of limit-cycle type of oscillation is enough to explain our experimental data. Using a similar approach, we were also able to simulate the transition from physiological to pathophysiological behavior (Fig. 1). This transition is effected when at least 60% of the mitochondrial network dynamics is dominated by the long period, high-amplitude ΔΨm oscillations (Fig. S6 in Supplementary Material), in agreement with experimental data (9).

The decrease in the spectral exponent, β, observed in the presence of inhibitors (Fig. 5) and the loss of correlation in the high-frequency domain of the spectrum (Fig. 6 A) could also be simulated by hypothesizing that a decrease in the levels of ROS in the network would introduce more random behavior (Fig. S6 in Supplementary Material). Thus, the behavior observed experimentally is consistent with an increase in the random behavior exhibited by the oscillators as a consequence of decreased ROS, the proposed coupling factor.

DISCUSSION

In this work, we demonstrate for the first time that both in the physiological and pathophysiological domains (Fig. 1), the mitochondrial network of cardiomyocytes functions as a highly correlated, coordinated network of oscillators. This indicates that each mitochondrion affects the temporal behavior of its neighbors such that the collective ensemble of mitochondria in a cardiac cell acts as a network. Under physiological conditions, the mitochondrial network exhibits a high temporal correlation for ΔΨm that is distinctly different from random behavior (Fig. 3). This is indicative of a self-similar fractal process. The power spectrum of such a distribution scales according to an inverse power law spanning at least three orders of magnitude (from milliseconds to a few minutes) and obeys a homogeneous power law (1/fβ) with β = 1.74 (Fig. 4), in the mid-range between pink (β = 1.0) and brown (β = 2.0) noise. Despite the value of β being close to that of brown noise, and even having a β ≈ 2.0 for frequencies below 0.3 Hz (Fig. 5, control panels), the correlative properties of the mitochondrial network were distinct from ordinary brown noise as demonstrated by RDA (Fig. 3 A). Moreover, the results indicate that decreasing mitochondrial ROS production at the level of the respiratory chain or blocking the ROS-induced ROS release mechanism by inhibiting the mitochondrial benzodiazepine receptor in the physiological domain consistently diminishes the extent of correlated behavior of the mitochondrial network in the high-frequency domain (Figs. 5 and 6, and Supplementary Material).

Importantly, with the help of our computational model of the mitochondrial oscillator (10), we are able to explain the mechanistic origin of the inverse power law behavior. The double log plot of amplitude versus frequency in Fig. 7 A demonstrates two essential features of the oscillatory dynamics displayed by mitochondria: i), the relationship between period and amplitude (i.e., the lower the period, the higher the amplitude), and ii), at periods >300 ms, the transition to a single dominant frequency with large ΔΨm depolarizations that define the limit of the physiological domain (Fig. S4 in Supplementary Material). Within the high-frequency, low-amplitude range of behavior that we attribute to the physiological domain, ΔΨm deflections of a few microvolts up to 30 mV can be seen.

Overall, the value of β obtained suggests the existence of processes exhibiting temporal responses to stimuli with a combination of persistency (closer to brown noise, i.e., spectra with mainly low-frequency components) and flexibility (closer to pink noise, i.e., spectra enriched in high- and low-frequency components). This interpretation is consistent with the mitochondrial network of the heart cell having both properties of constancy and flexibility, i.e., providing a steady supply of ATP to fuel contraction and adapting the rate of energy production to meet the changing metabolic demand as workload varies, respectively (14,16).

Mitochondria viewed as a network of coupled oscillators

Winfree (22) pioneered the analysis of synchronization among coupled oscillators in a network, later refined by Kuramoto (37) (reviewed in Strogatz (17) and Strogatz (18)). The relevance of this subject cannot be overstated, for autonomous periodicity plays a pervasive role in the timekeeping and coordination of biological rhythms (19–21). Winfree considered idealized systems of nearly identical weakly coupled sinusoidal oscillators modeled as such for mathematical simplicity (22). He found that below a certain threshold of coupling, each oscillator runs at its own frequency, thus behaving incoherently until a further increase in coupling overcomes the threshold for synchronization (18,22). This synchronization event was characterized as the analog of a phase transition, revealing an insightful connection between nonlinear dynamics and statistical physics (17,18). This type of transition is strikingly similar to our own observations of the mitochondrial network (9) at the turning point between the physiological and pathophysiological regimes (Fig. 1). This global phase transition (visualized as a cell-wide mitochondrial depolarization) occurs when a critical density (∼60%) of mitochondria accumulate ROS above a threshold to form an extended spanning cluster (9). Our results agree very well with the quantitative predictions derived from percolation theory, especially concerning the percolation threshold, the fractal organization exhibited by percolation processes at the threshold (23), and the critical exponents (9).

A main difference between our results and that of previous coupled oscillator models is that we find an inverse power law (by RDA and PSA) in the physiological regime. This suggests that, despite their weak coupling, the oscillators do not behave incoherently or randomly. If the coupling were random, we should have found white noise in the physiological regime (Fig. 6 and Supplementary Material). Instead, we found a broad band of frequencies proceeding simultaneously at different timescales, described by an inverse power law (Figs. 3 and 4 and Supplementary Material).

The mitochondrial oscillator as a putative signaling system

The possibility for high-frequency, low-amplitude oscillations in mitochondrial ROS and ΔΨm were predicted from simulations using our computational model of the mitochondrial oscillator (Fig. 2). Our experimental findings provide support for the hypothesis that mitochondrial oscillation may function as a frequency- and/or amplitude-encoded signaling mechanism under physiological conditions. The simulations indicate that the mitochondrial oscillator's period can be modulated over a wide range of timescales (10), suggesting that it may play a role as an intracellular timekeeper. Although the frequency distribution is broad under normal conditions, the long-term temporal correlations of the mitochondrial network could theoretically allow a change in one timescale to be felt across the frequency range.

We hypothesize that mitochondrial oscillations in the physiological domain are associated with ROS-dependent signaling since they do not represent a substantial energetic burden for the cell. Our hypothesis is based on i), the associated pulses of ROS in the nM range that are concomitant with the low-amplitude ΔΨm oscillations (Fig. 2 A); and ii), their possible modulation in amplitude and frequency as a function of two feasible physiological variables, i.e., the degree of ROS production by the respiratory chain (Fig. 2 B) or the rate of superoxide scavenging by SOD (see Supplementary Material Fig. S4A).

The dual role of ROS as either toxic or signaling molecules with important effects on signaling cascades has been extensively recognized (24–26). One major molecular mechanism of ROS signaling is associated with intracellular redox sensing by sensitive thiols of cysteine residues present in kinases and phosphatases. For example, cytoplasmic signaling kinases such as mitogen-activated MAP kinases (e.g., p38, JNK, ERK), apoptosis regulating kinase (ASK1), and several isoforms of protein kinase C (e.g., PKC-α) can be activated by ROS or a prooxidative shift in the antioxidant capacity (24–26). Nuclear transcription factors can be activated either indirectly, via the above-mentioned signal cascades, or directly by ROS, and recent evidence also suggests that mitochondrial ROS production may be important for the activation of hypoxia-inducible factor (HIF; (27)).

The significance of inverse power laws for heart (patho)physiology

A main contribution of this work is to show that inverse power laws also characterize the normal, physiological behavior of the mitochondrial network. Inverse power laws express the inherent relatedness and nonrandom interactions of cellular processes proceeding, simultaneously, at different timescales. A profound implication of the power law behavior exhibited by the mitochondrial network is that beyond a critical level, the loss of a single element may cause the entire network to fail because of their multiplicative interdependency (12,13,28,29). Thus, a prediction derived from such an inherent organization of mitochondria is that failures can scale to higher levels of organization (15,30). This has already been shown to be true at criticality in the case of the mitochondrial network of heart cells under oxidative stress (8,9) or the whole organ after ischemia reperfusion (31).

According to PSA, the mitochondrial network of heart cells does not show a dominant frequency. Consequently, whatever happens in one frequency range may reverberate on all frequency scales. This is reminiscent of heart rate regulation in a normal subject, suggesting the intriguing possibility that a change in mitochondrial network dynamics could entrain pathological consequences for the cell and the organism. With metabolic stress, the frequency spectrum for ΔΨm narrows and a dominant oscillatory frequency appears, indicating the transition from physiological to pathophysiological behavior in the mitochondrial network (Fig. 1). Interestingly, a “loss of spectral reserve” (32) for cardiac electrical activity occurs during the transition from normal to pathological states during the development of heart failure (33) or during postinfarction arrhythmias (34,35).

This raises the question of whether mitochondrial energetics could contribute to the mechanism underlying other scale invariant properties of the heart. The long-range correlations in the human heartbeat time series have been partly attributed to competition between parasympathetic and sympathetic stimuli on the pacemaker cells of the sinus node (4); however, the contribution of nonautonomic or cardiac cell processes has not been investigated. Fractal processes have also been recognized in the context of cardiac arrhythmias and used to define stimulation protocols to control chaos (36). It is worth noting that close links exist between mitochondrial energetics and action potential morphology, as exemplified in our recent study linking mitochondrial instability with postischemic arrhythmias (31), raising the possibility that the nonlinear properties of mitochondrial control could scale to produce cascades of feedback loops across coupled oscillatory systems (15,30). This possibility can be readily tested in future investigations.

Summarizing, we have described for the first time that the mitochondrial network of heart cells functions as a network of coupled oscillators under physiological conditions. The mechanism of the mitochondrial oscillator described experimentally and theoretically is shared by the physiological and pathophysiological domains of behavior, although differently. Under physiological conditions, the role of ROS would be more prominent for signaling intracellular processes rather than as in pathophysiology. These findings are in agreement with the highly structured, organized nature of the heart cell both from morphological and dynamic points of view.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

Supplementary Material

[Supplement]
biophysj_106.087817_index.html (834B, html)

Acknowledgments

We thank Dr. Ron Berger for helpful comments on the manuscript and fruitful discussions and Dr. Patrick Helm for advice in the calculation of pink noise.

This work was supported by National Institutes of Health grant R37-HL54598 to B.O'R.

References

  • 1.van der Pol, B., and J. van der Mark. 1928. The heartbeat considered as a relaxation oscillation, and an electrical model of the heart. Philos. Mag. 6:763–775. [Google Scholar]
  • 2.Bassingthwaighte, J. B., L. S. Liebovitch, and B. J. West. 1994. Fractal Physiology. Oxford University Press, New York. 64–94.
  • 3.Kobayashi, M., and T. Musha. 1982. 1/f fluctuation of heartbeat period. IEEE Trans. Biomed. Eng. 29:456–457. [DOI] [PubMed] [Google Scholar]
  • 4.Peng, C.-K., J. Mietus, J. M. Hausdorff, S. Havlin, H. E. Stanley, and A. L. Goldberger. 1993. Long-range anticorrelations and non-Gaussian behavior of the heartbeat. Phys. Rev. Lett. 70:1343–1346. [DOI] [PubMed] [Google Scholar]
  • 5.Goldberger, A. L., L. A. Amaral, J. M. Hausdorff, P. Ivanov, C. K. Peng, and H. E. Stanley. 2002. Fractal dynamics in physiology: alterations with disease and aging. Proc. Natl. Acad. Sci. USA. 99(Suppl. 1):2466–2472. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.West, B. J., R. Zhang, A. W. Sanders, S. Miniyar, J. H. Zuckerman, and B. D. Levine. 1999. Fractal fluctuations in cardiac time series. Physica A. 270:552–566. [DOI] [PubMed] [Google Scholar]
  • 7.Ivanov, P. C., L. A. Amaral, A. L. Goldberger, S. Havlin, M. G. Rosenblum, Z. R. Struzik, and H. E. Stanley. 1999. Multifractality in human heartbeat dynamics. Nature. 399:461–465. [DOI] [PubMed] [Google Scholar]
  • 8.Aon, M. A., S. Cortassa, E. Marban, and B. O'Rourke. 2003. Synchronized whole cell oscillations in mitochondrial metabolism triggered by a local release of reactive oxygen species in cardiac myocytes. J. Biol. Chem. 278:44735–44744. [DOI] [PubMed] [Google Scholar]
  • 9.Aon, M. A., S. Cortassa, and B. O'Rourke. 2004. Percolation and criticality in a mitochondrial network. Proc. Natl. Acad. Sci. USA. 101:4447–4452. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Cortassa, S., M. A. Aon, R. L. Winslow, and B. O'Rourke. 2004. A mitochondrial oscillator dependent on reactive oxygen species. Biophys. J. 87:2060–2073. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.O'Rourke, B., B. M. Ramza, and E. Marban. 1994. Oscillations of membrane current and excitability driven by metabolic oscillations in heart cells. Science. 265:962–966. [DOI] [PubMed] [Google Scholar]
  • 12.West, B. J. 1999. Physiology, Promiscuity and Prophecy at the Millennium: A Tale of Tails. World Scientific, Singapore. 161–193.
  • 13.West, B. J., and B. Deering. 1995. The Lure of Modern Science. Fractal Thinking. World Scientific, Singapore. 127–175.
  • 14.Cortassa, S., M. A. Aon, E. Marban, R. L. Winslow, and B. O'Rourke. 2003. An integrated model of cardiac mitochondrial energy metabolism and calcium dynamics. Biophys. J. 84:2734–2755. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Aon, M. A., S. Cortassa, F. G. Akar, and B. O'Rourke. 2006. Mitochondrial criticality: a new concept at the turning point of life or death. Biochim. Biophys. Acta. 1762:232–240. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Ingwall, J. S., and R. G. Weiss. 2004. Is the failing heart energy starved? On using chemical energy to support cardiac function. Circ. Res. 95:135–145. [DOI] [PubMed] [Google Scholar]
  • 17.Strogatz, S. H. 2003. Sync. The Emerging Science of Spontaneous Order. Hyperion Books, New York.
  • 18.Strogatz, S. H. 2001. Exploring complex networks. Nature. 410:268–276. [DOI] [PubMed] [Google Scholar]
  • 19.Lloyd, D. 1992. Intracellular time keeping: epigenetic oscillations reveal the functions of an ultradian clock. In Ultradian Rhythms in Life Processes: An Inquiry into Fundamental Principles of Chronobiology and Psychobiology. D. Lloyd and E. L. Rossi, editors. Springer-Verlag, Berlin. 5–22.
  • 20.Glass, L. 2001. Synchronization and rhythmic processes in physiology. Nature. 410:277–284. [DOI] [PubMed] [Google Scholar]
  • 21.Aon, M. A., and S. Cortassa. 1997. Dynamic Biological Organization. Fundamentals as Applied to Cellular Systems. Chapman & Hall, London.
  • 22.Winfree, A. T. 1967. Biological rhythms and the behavior of populations of coupled oscillators. J. Theor. Biol. 16:15–42. [DOI] [PubMed] [Google Scholar]
  • 23.Aon, M. A., B. O'Rourke, and S. Cortassa. 2004. The fractal architecture of cytoplasmic organization: scaling, kinetics and emergence in metabolic networks. Mol. Cell. Biochem. 256/257:169–184. [DOI] [PubMed] [Google Scholar]
  • 24.Gopalakrishna, R., and W. B. Anderson. 1989. Ca2+- and phospholipid-independent activation of protein kinase C by selective oxidative modification of the regulatory domain. Proc. Natl. Acad. Sci. USA. 86:6758–6762. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Ono, Y., T. Fujii, K. Igarashi, T. Kuno, C. Tanaka, U. Kikkawa, and Y. Nishizuka. 1989. Phorbol ester binding to protein kinase C requires a cysteine-rich zinc-finger-like sequence. Proc. Natl. Acad. Sci. USA. 86:4868–4871. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Quest, A. F., E. S. Bardes, and R. M. Bell. 1994. A phorbol ester binding domain of protein kinase C gamma. Deletion analysis of the Cys2 domain defines a minimal 43-amino acid peptide. J. Biol. Chem. 269:2961–2970. [PubMed] [Google Scholar]
  • 27.Guzy, R. D., B. Hoyos, E. Robin, H. Chen, L. Liu, K. D. Mansfield, M. C. Simon, U. Hammerling, and P. T. Schumacker. 2005. Mitochondrial complex III is required for hypoxia-induced ROS production and cellular oxygen sensing. Cell Metab. 1:401–408. [DOI] [PubMed] [Google Scholar]
  • 28.Barabasi, A. L. 2003. Linked: How Everything Is Connected to Everything Else and What It Means for Business, Science, and Everday Life. Plume, Penguin Group, New York.
  • 29.Barabasi, A. L., and Z. N. Oltvai. 2004. Network biology: understanding the cell's functional organization. Nat. Rev. Genet. 5:101–113. [DOI] [PubMed] [Google Scholar]
  • 30.O'Rourke, B., S. Cortassa, and M. A. Aon. 2005. Mitochondrial ion channels: gatekeepers of life and death. Physiology (Bethesda). 20:303–315. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Akar, F. G., M. A. Aon, G. F. Tomaselli, and B. O'Rourke. 2005. The mitochondrial origin of postischemic arrhythmias. J. Clin. Invest. 115:3527–3535. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Goldberger, A. L., V. Bhargava, B. J. West, and A. J. Mandell. 1985. On a mechanism of cardiac electrical stability. The fractal hypothesis. Biophys. J. 48:525–528. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Casolo, G., E. Balli, T. Taddei, J. Amuhasi, and C. Gori. 1989. Decreased spontaneous heart rate variability in congestive heart failure. Am. J. Cardiol. 64:1162–1167. [DOI] [PubMed] [Google Scholar]
  • 34.Ewing, D. J. 1991. Heart rate variability: an important new risk factor in patients following myocardial infarction. Clin. Cardiol. 14:683–685. [DOI] [PubMed] [Google Scholar]
  • 35.Skinner, J. E., C. M. Pratt, and T. Vybiral. 1993. A reduction in the correlation dimension of heartbeat intervals precedes imminent ventricular fibrillation in human subjects. Am. Heart J. 125:731–743. [DOI] [PubMed] [Google Scholar]
  • 36.Garfinkel, A., M. L. Spano, W. L. Ditto, and J. N. Weiss. 1992. Controlling cardiac chaos. Science. 257:1230–1235. [DOI] [PubMed] [Google Scholar]
  • 37.Kuramoto, Y. 1984. Chemical Oscillations, Waves and Turbulence. Springer-Verlag, Berlin.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplement]
biophysj_106.087817_index.html (834B, html)
biophysj_106.087817_1.pdf (1.1MB, pdf)
Download video file (11MB, avi)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES