Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2006 Sep 15;91(11):4230–4240. doi: 10.1529/biophysj.106.084608

Temperature-Dependence of Isometric Tension and Cross-Bridge Kinetics of Cardiac Muscle Fibers Reconstituted with a Tropomyosin Internal Deletion Mutant

Xiaoying Lu *, Larry S Tobacman †, Masataka Kawai *
PMCID: PMC1635655  PMID: 16980359

Abstract

The effect of temperature on isometric tension and cross-bridge kinetics was studied with a tropomyosin (Tm) internal deletion mutant AS-Δ23Tm (Ala-Ser-Tm Δ(47–123)) in bovine cardiac muscle fibers by using the thin filament extraction and reconstitution technique. The results are compared with those from actin reconstituted alone, cardiac muscle-derived control acetyl-Tm, and recombinant control AS-Tm. In all four reconstituted muscle groups, isometric tension and stiffness increased linearly with temperature in the range 5–40°C for fibers activated in the presence of saturating ATP and Ca2+. The slopes of the temperature-tension plots of the two controls were very similar, whereas the slope derived from fibers with actin alone had ∼40% the control value, and the slope from mutant Tm had ∼36% the control value. Sinusoidal analysis was performed to study the temperature dependence of cross-bridge kinetics. All three exponential processes A, B, and C were identified in the high temperature range (30–40°C); only processes B and C were identified in the mid-temperature range (15–25°C), and only process C was identified in the low temperature range (5–10°C). At a given temperature, similar apparent rate constants (2πa, 2πb, 2πc) were observed in all four muscle groups, whereas their magnitudes were markedly less in the order of AS-Δ23Tm < Actin < AS-Tm ≈ Acetyl-Tm groups. Our observations are consistent with the hypothesis that Tm enhances hydrophobic and stereospecific interactions (positive allosteric effect) between actin and myosin, but Δ23Tm decreases these interactions (negative allosteric effect). Our observations further indicate that tension/cross-bridge is increased by Tm, but is diminished by Δ23Tm. We conclude that Tm affects the conformation of actin so as to increase the area of hydrophobic interaction between actin and myosin molecules.

INTRODUCTION

Force generation is the result of a large-scale interaction between actin and myosin molecules. In striated muscles, this interaction is regulated by tropomyosin (Tm) and troponin (Tn). In the absence of Ca2+, Tm interferes with the actin-myosin interaction to hinder force generation (1–5). This is the “blocked state” as defined by functional studies in solution by McKillop and Geeves (6). This is the basic assumption of the steric blocking mechanism (1,2,7,8). In the presence of Ca2+, the signal of its binding to TnC is transmitted to TnI, TnT, and Tm. Tm then makes an azimuthal shift by 25° around the actin helix, and exposes most of the myosin binding site (1,9–11) forming the so-called “closed (or cocked) state” (6,12). Myosin cross-bridge binds to this state and causes a conformational change in actin (3,4), which in turn increases the actin-Tm affinity. This affinity increase causes a further 10° azimuthal shift of the Tm position as observed from EM image reconstruction studies (10,13). This structural state is tentatively assigned as equivalent to the functional “open state” (6), and the cross-bridge interaction with actin is now fully active. The interactions of Tm, actin, and myosin are cooperative and mutually interdependent (14).

With an increase in the temperature, active tension increases in mammalian skeletal (15–20) and cardiac muscle fibers (21,22). Subsequently, the role of Tm and Tn in the temperature effect of tension was reported (22), which demonstrated that the temperature effect was diminished if Tm and Tn were absent, but the effect came back when Tm and Tn were reconstituted in the actin filament reconstituted cardiac muscle fibers. Consequently, a new hypothesis was proposed which states that, in the presence of Ca2+, Tm and Tn modify the conformation of actin to increase the hydrophobic interaction between actin and myosin molecules, based on muscle fiber studies (22) and on solution studies of purified proteins (14). Our earlier results on the temperature effect in rabbit psoas fibers (18) and soleus fibers (20) are generally consistent with the hypothesis of the hydrophobic interaction.

The precise role of Tm in the temperature dependence of striated muscles is yet to be determined. Previous investigations using Tm-mutants have been helpful in understanding the regulatory function of the thin filament. A dimeric Tm molecule spans seven actin monomers and consists of seven quasi-repeating, loosely similar regions. Hitchcock-DeGregori and her colleagues synthesized Tm internal deletion mutants, and they reported that regions 2 and 3 contributed to Tm-Tn binding to actin by using Δ23Tm, which lacks the second and third regions (23,24). With an in vitro motility assay, Landis et al. (25) and Kawai et al. (26) found that thin filament motility was regulated by Ca2+ in the presence of Δ23Tm using heavy meromyosin (HMM) as the motor. One report (25) showed that while 90% of the control Tm filament moved continuously, only 67% of the Δ23Tm filament moved at 73% of the speed of the control filament. Another report (26) showed that, from control Tm to Δ23Tm, single molecular force was reduced to 43%, whereas the velocity was reduced to 52%.

The role of Tm and its mutant form Δ23Tm in the elementary steps of the cross-bridge cycle was also investigated by using sinusoidal analysis at 25°C (27). This investigation indicated that force and stiffness decreased significantly in Δ23Tm below the force generated by the actin-filament reconstituted fibers, but the cross-bridge number in force-generating states was not significantly decreased. From this study, it was concluded that force/cross-bridge and stiffness/cross-bridge of the mutant group were ∼40% of that of the control groups. Lu et al. (27) concluded that Δ23Tm did not significantly influence the equilibrium between cross-bridge states, but instead Δ23Tm decreased the force/cross-bridge. These results are consistent with the hypothesis that Tm modifies the actin-myosin interface for better hydrophobic and stereospecific interaction (positive allosteric effect), and that Δ23Tm diminishes the interaction (negative allosteric effect). If this is the case, and if a significant portion of the interface is made up of hydrophobic interaction, then it follows that the temperature effect would be diminished in Δ23Tm compared to the control or the one with unregulated actin filaments. Therefore, we performed the temperature study by using thin filament extraction and reconstitution technique (27,28) and found that the slope of the temperature-tension relationship of Δ23Tm group was 36% of the control groups, implying that the hydrophobic interaction between actin and myosin was reduced in the Δ23Tm group.

MATERIALS AND METHODS

Chemicals, solutions, and proteins

Adenosine 5′-triphosphate (Na2H2ATP), creatine phosphate (Na2CP), and 3-[N-morpholino] propane sulfonic acid (MOPS) were purchased from Sigma Chemical (St. Louis, MO); CaCO3, Triton X-100, KOH, K2HPO4, KH2PO4, Mg(OH)2, NaN3, NaOH, and propionic (Prop) acid were purchased from Fisher Scientific (Hanover Park, IL); ethylene glycol bis (2-aminoethyl ether)-N,N,N′,N′ tetraacetic acid (H4EGTA) was purchased from Amresco (Solon, OH); and creatine kinase was purchased from Boehringer Mannheim (Mannheim, Germany).

Solutions were prepared as described in Lu et al. (27). In brief, the relaxing solution (Rx) contained 5.03 mM EGTA, 0.97 mM CaEGTA (pCa 7.0), 2.2 mM MgATP, 5 mM free ATP, 74 mM KProp, 41 mM NaProp, and 10 mM MOPS. The standard activating solution (5S8P) contained 6 mM CaEGTA, 0.174 mM CaProp2 (pCa 4.40), 5.76 mM MgATP, 1.36 mM free ATP, 15 mM creatine phosphate (CP), 8 mM phosphate (Pi), 53 mM KProp, 1 mM NaProp, 10 mM MOPS, and 10 mM NaN3. The rigor solution contained 8 mM Pi, 55 mM NaProp, 122 mM Kprop, and 10 mM MOPS. The extraction solution contained 2.0 mM K2CaEGTA, 2.2 mM Na2K2ATP, 20 mM MOPS, 40 mM 2,3-butanedione 2-monoxime (BDM), 121 mM KCl, 4.25 mM MgCl2, 2 mM leupeptin, 2 mM diisopropyl fluorophosphate, and ∼0.3 mg/ml gelsolin. The actin reconstitution solution contained 4 mM K2EGTA, 4 mM Na2MgATP, 20 mM K1.5Pi, 40 mM BDM, 80 mM KI, 8 mM KCl, and 1 mg/ml G-actin. Tm and Tn reconstitution solution contained 6 mM K2EGTA, 2.2 mM Na2MgATP, 5.0 mM Na2K2ATP, 8 mM K1.5Pi, 41 mM NaProp, 74.5 mM KProp, 10 mM MOPS, 40 mM BDM, 0.6 mg/ml bovine Tm, and 0.6 mg/ml bovine Tn for the acetyl-Tm reconstitution group, 0.5 mg/ml AS-Tm and 0.6 mg/ml bovine Tn for the AS-Tm reconstitution group and 0.3 mg/ml AS-Δ23Tm and 0.5 mg/ml Tn for the mutant Tm reconstitution group. The pH of all solutions was adjusted to 7.00.

The source and preparation of actin, gelsolin, acetyl-Tm, AS-Tm, AS-Δ23Tm, and Tn are as described in Lu et al. (27). Acetyl-Tm (90% α, 10% β) was prepared from bovine cardiac muscle (29). AS-Tm and AS-Δ23Tm (100% α) were prepared from Escherichia coli by using rat α-Tm cDNA. Because E. coli proteins lack N-terminal acetylation, Ala (A) and Ser (S) were inserted at the N-terminus to correct for the lack of acetylation (30).

Fiber preparation

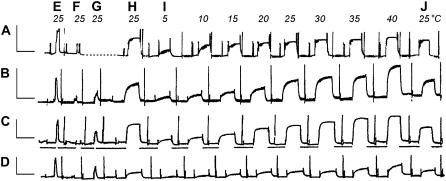
Bovine cardiac muscle fibers were obtained as described (27,28). In brief, a strip (fiber) of bovine cardiac muscle was dissected from the skinned muscle bundle under a dissection microscope. One end of the fiber was connected to a length driver and the other end to a tension transducer by a 210 μm-diameter stainless steel wire with a very small amount of nail polish. The fiber was stretched to give a small passive tension. At this time, the average sarcomere length was in the range 1.9–2.1 μm. The end-to-end distance of the fiber (L0) was 1.5–3.2 mm. The diameter was measured under a stereomicroscope (35×) and ranged 78–145 μm. The fiber was further skinned in the Rx solution containing 1% Triton X-100 for 20 min at 25°C. Triton X-100 was washed out with the Rx solution afterwards. The first active tension record was taken in the standard activating solution at 25°C (Fig. 1 E).

FIGURE 1.

FIGURE 1

Open in a new tab

Slow pen trace of isometric tension in the standard activating solution at different temperatures in reconstituted cardiac muscle fibers with actin alone (A) and with three kinds of Tm (B–D). A, actin-filament reconstituted fiber; B, Acetyl-Tm reconstituted fiber; C, AS-Tm reconstituted fiber; D, AS-Δ23 Tm reconstituted fiber; E, activation of native fibers; F, activation of thin filament extracted fibers after gelsolin treatment at 0°C for 50–90 min; G, activation of actin-filament reconstituted fibers; and H, activation of Tm and Tn reconstituted fibers (except for A) after actin filament reconstitution. I, activation at eight different temperatures as indicated; J, repeat of H to test for the reproducibility. AG is missing, but it is the same as AH. Between E, F, G, and H, the pen recorder was stopped to perform extraction and reconstitution at 0°C. Before each activation, the muscle fibers were washed in the standard activating solution at 0°C (first artifact), which did not induce tension. Tension was induced by switching the fibers to the higher temperature (indicated at top) bath (second artifact) containing the same solution. The fibers were relaxed (third artifact) in the Rx solution that contains 40 mM BDM at 0°C. In some cases the Rx solution was changed once again (fourth artifact). Horizontal bars below the pen trace in (C) indicate that the temperature was 0°C during relaxation. Calibrations are 1 min (abscissa) and 0.2 mN (ordinate).

Extraction and reconstitution of the thin filament in cardiac muscle fibers

The extraction and reconstitution was performed at 1 ± 1°C and as described (27,28,31,32). In brief, bovine cardiac muscle fibers (myocardium) were treated with the extraction solution until <10% active tension was left (Fig. 1 F). The actin filament was then reconstituted from G-actin with 4–6 solution changes of seven minutes each. Active tension was measured at 25°C after actin reconstitution (Fig. 1 G), and the fiber was relaxed at 0–2°C in the Rx solution to which 40 mM BDM was added. Tm/Tn reconstitution was then performed in the Tm and Tn Reconstitution Solution for 12–15 h (Fig. 1, G to H). We compared cardiac fibers reconstituted with 1), actin filament alone without regulatory proteins (Fig. 1 A); 2), actin filament, acetyl-Tm, and Tn (Fig. 1 B); 3), actin filament, AS-Tm, and Tn (Fig. 1 C); and 4), actin filament, AS-Δ23Tm, and Tn (Fig. 1 D). These are respectively called 1), actin-filament group; 2), acetyl-Tm group; 3), AS-Tm group; and 4), AS-Δ23Tm group. Groups 2 and 3 are also called the control groups.

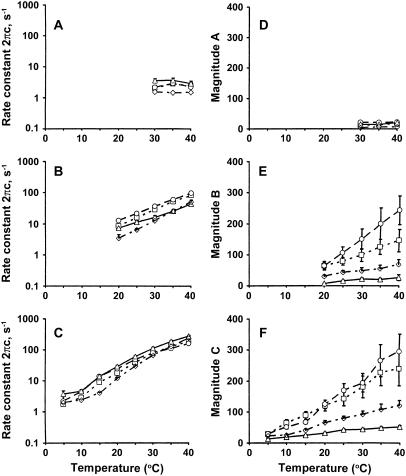
FIGURE 4.

FIGURE 4

Open in a new tab

The apparent rate constants and their magnitudes as functions of temperature. The apparent rate constants 2πa (in A), 2πb (in B), 2πc (in C), and their magnitudes A (in D), B (in E), and C (in F) are plotted against temperature for the standard activation. Actin filament reconstituted group (– - – -⋄– - – -), average of 6–26 experiments; acetyl-Tm group (……□……), average of 6–10 experiments; AS-Tm group (– – –○– – –), average of 7–10 experiments; and AS-Δ23Tm group ( ——▵—— ), average of 7–11 experiments. Error bars represent mean ± SE, and error bars smaller than the symbol size are not shown.

Experimental procedure and deduction of the rate constants

Four muscle groups were relaxed in the Rx solution at 1°C. The fibers were first activated in the standard activating solution at 25°C (Fig. 1 H). After a steady tension developed, sinusoidal analysis was performed and an experimental record of the complex modulus data together with isometric tension was collected. This is followed by a relaxation at 0°C. The same procedure was repeated at 5°C, 10°C, 15°C, 20°C, 25°C, 30°C, 35°C, and 40°C (Fig. 1 I). The fibers were once again activated in the standard activating solution at 25°C to measure the reproducibility of active tension (Fig. 1 J). If this tension was ≤85%, the data were excluded from analysis. Ten to eleven experiments were performed and the data were averaged for each group. The tension and complex modulus data were normalized to tension developed after the actin filament reconstitution (Fig. 1 AH or Fig. 1 G) at 25°C (this tension is called Tac), because in this way a scatter of the data caused by the error in the diameter measurement and by the length variation of the thin filament can be minimized.

The sinusoidal waveform at 18 discrete frequencies (f: 0.13–100 Hz) was digitally synthesized in a PC 386 and applied to the muscle length via a 16-bit D/A converter. The amplitude of the length oscillation was 0.125%. Tension and length signals were simultaneously digitized by two 16-bit A/D converters at the rate of ∼80 kHz. The signals were accumulated and averaged. From these, the complex modulus data [Y(f)] were calculated at each frequency. Y(f) is a function of frequency and is defined as the ratio of the stress change to the strain change. Y(f) was corrected for instrument response by using the complex modulus data of the rigor record as described (33). Y(f) is fitted to an equation consisting of three terms, each representing an exponential process (33).

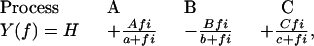graphic file with name M1.gif (1)
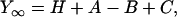graphic file with name M2.gif (2)

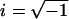where Inline graphic . Each term represents an exponential process. The characteristic frequencies are denoted as a, b, and c, and their magnitudes as A, B, and C, respectively. The apparent rate constants are the characteristic frequencies multiplied by 2π. H is the modulus extrapolated to the zero frequency (f → 0). Y∞ is the modulus extrapolated to the infinite frequency (f → ∞) and is often called stiffness. Details of sinusoidal analysis were described (33).

Statistical analysis

Data are expressed as means ± SE and analyzed by using multiple comparisons in ANOVA (Tukey-Kramer Method). The linear mixed model analysis for repeated measurements was used to test for differences in mean tension, stiffness, and the ratio. The fixed effects in the model were four muscle groups (actin-filament, acetyl-Tm, AS-Tm, and AS-Δ23Tm), temperature (5, 10, 15, 20, 25, 30, 35, and 40°C), and the muscle group-temperature interaction. A significant muscle group-temperature interaction would indicate that group differences varied across the temperature. To test for these pairwise group mean comparisons at the level of each temperature, test of the mean contrast was performed with the P-value that was adjusted by using Bonferroni's method to account for the number of tests (the total of 48 tests equals six pairwise group comparisons times eight temperatures). If there is no significant group-temperature interaction, the main effect of the groups is examined with the pairwise group comparison averaged across the group levels and Tukey's method used to adjust for the test of pairwise comparison between the group means.

RESULTS

Effect of temperature on isometric tension and stiffness of four muscle groups

Slow pen trace records of activations including the extraction and reconstitution of the thin filament, and activation with the standard activating solution at eight different temperatures, are shown in Fig. 1 for four muscle groups (A, actin-filament; B, acetyl-Tm; C, AS-Tm; and D, AS-Δ23Tm). In this figure, E is initial tension, F is tension after gelsolin treatment, G is tension after the actin filament reconstitution, and H is tension after Tm and Tn reconstitution. Tension of actin-filament reconstituted fibers (Fig. 1 G) was on the average 18.8 ± 2.1 kPa (n = 40) at 25°C. This value is defined as Tac, and all subsequent tension was normalized to this value. Tension increased further on reconstitution with acetyl-Tm (Fig. 1 BH) or AS-Tm (Fig. 1 CH), but decreased when reconstituted with AS-Δ23Tm (Fig. 1 DH). This result is consistent with in vitro motility studies using microneedles (25,34) or optical tweezers (26), and reconstituted muscle fibers (27). Between activations, the fibers were relaxed at 0°C with Rx to which 40 mM BDM was added, which is indicated by horizontal bars under Fig. 1 C. In the actin-filament reconstituted fibers (Fig. 1 A), active tension increased with an increase in the temperature. In the control groups (Fig. 1, B and C), active tension similarly increased with an increase in the temperature. In the AS-Δ23Tm group (Fig. 1 D), the increase of active tension was present, but less evident than the other three groups.

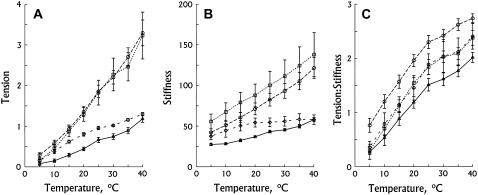
The temperature dependence of isometric tension for four muscle groups is summarized in Fig. 2 A. In all groups, isometric tension increased almost proportionately to the Celsius temperature. This is in close agreement with previous results using mammalian skeletal (15–20,35) and cardiac muscle fibers (21,22). Isometric tension at 25°C exerted by the acetyl-Tm fibers and AS-Tm fibers was the same (Table 1), while tension produced by the actin-filament fibers was 52% (= 0.96:1.835) of the two control groups; tension generated by the AS-Δ23Tm fibers was even less, just 36% (= 0.66:1.835) of the two control groups (Table 1). These results are consistent with our previous results (27). The test of the mean contrast was performed as described in Materials and Methods with the P-value that was adjusted by using Bonferroni's method. The results show that the AS-Δ23Tm group and the actin-filament group are significantly different (P < 0.05) from the control groups and from each other. These differences increase at higher temperature, except for the AS-Δ23Tm data and the actin-filament data which converge (Fig. 2 A). At 40°C, the isometric tension of the actin-filament fibers was 40%, and the isometric tension of the AS-Δ23Tm fibers was 36% of the two control groups. There was little difference in the slope of the temperature-tension plots between acetyl-Tm fibers (0.085 ± 0.015 Tac K−1, n = 10) and AS-Tm fibers (0.086 ± 0.008 TacK−1, n = 10). In contrast, the slope of the temperature-tension plots derived from the actin-filament data was 0.034 ± 0.003 TacK−1 (n = 9), which was 40% (= 0.034:0.085) of the control groups. The slope of the temperature-tension plots in the AS-Δ23Tm group was 0.031 ± 0.003 TacK−1 (n = 11), which was 36% (= 0.031:0.085) of the control groups and similar to the results with actin-only fibers.

FIGURE 2.

FIGURE 2

Open in a new tab

Isometric tension (A), stiffness (B), and tension/stiffness (C) plotted against temperature. Actin reconstituted (– – ⋄ – –) (n = 9); Acetyl-Tm reconstituted (……□……) (n = 10); AS-Tm reconstituted (– –○– –) (n = 10); and AS-Δ23Tm reconstituted (——▵——) (n = 11) in the standard activating solution. Experiments were carried out in the presence of 5 mM MgATP, and 8 mM Pi. Error bars represent mean ± SE. Tension and stiffness were normalized to the tension of actin-filament reconstituted group: Tac = 18.8 ± 2.1 kPa (n = 40) measured at 25°C.

TABLE 1.

Active tension and stiffness of thin filament reconstituted fibers at 25°C

Parameters Actin-filament Acetyl-Tm AS-Tm AS-Δ23Tm
Tension 0.96 ± 0.04 1.82 ± 0.30* 1.85 ± 0.15* 0.66 ± 0.06†‡
Stiffness 55 ± 5 100 ± 17* 83 ± 8 43 ± 2†‡
Ratio %L0 1.89 ± 0.19 1.84 ± 0.14 2.30 ± 0.12† 1.51 ± 0.11‡
N 9 10 10 11
Open in a new tab

Tension and stiffness (Y∞, Eq. 2) are measured in the standard activating solution and normalized to Tac (actin reconstituted tension), and compared among different muscle groups.

*

P < 0.05 compared with actin-filament.

†

P < 0.05 compared with acetyl-Tm.

‡

P < 0.05 compared with AS-Tm.

The temperature dependence of stiffness (Y∞) during activation is shown in Fig. 2 B in all four muscle groups. Similar to isometric tension, stiffness increased linearly with an increase in the temperature. The error bars of the stiffness in the two control groups overlapped with each other, indicating that there was no significant difference between the two groups. Stiffness at 25°C was 60% of the control for the actin filament group, and 47% for the AS-Δ23Tm group (Table 1). This is also consistent with previous findings (27). The test of the mean contrast demonstrates that the difference between the control groups and the actin-filament group or the AS-Δ23Tm group increases with an increase in the temperature, whereas the difference between the actin-filament group and the AS-Δ23Tm group decreases with an increase in the temperature (Fig. 2 B).

The temperature dependence of tension/stiffness during activation is shown in Fig. 2 C. With the increase of temperature, tension/stiffness increased linearly at low temperatures (5–25°C), and became less temperature-sensitive at high temperatures, which is consistent with previous results on rabbit psoas fibers (18). The test of the mean contrast demonstrates that there is no significant difference (P > 0.05) among the four muscle groups.

Stiffness during rigor and relaxation

The above results concerning active tension and stiffness suggest that actomyosin linkage is weaker in the actin-filament and AS-Δ23Tm groups than in the control groups. To test this possibility directly, each muscle fiber was brought into the high-rigor condition (rigor after high active tension: (36)) starting from the activation at 25°C (such as shown in Fig. 1 J), and rigor tension and stiffness were measured (Table 2). This table demonstrates that rigor stiffness was less in the AS-Δ23 Tm and actin-filament groups than in the control groups. This observation indicates that the actomyosin linkage is indeed weaker in the AS-Δ23Tm and actin-filament groups than in the control groups.

TABLE 2.

Rigor tension and stiffness of thin filament reconstituted fibers at 25°C

Parameters Actin-filament Acetyl-Tm AS-Tm AS-Δ23Tm
Tension 1.4 ± 0.1 2.7 ± 0.5* 3.2 ± 0.5* 2.2 ± 0.1
Stiffness 152 ± 13 252 ± 42* 178 ± 19† 142 ± 6†
Ratio %L0 0.97 ± 0.11 1.00 ± 0.06 1.75 ± 0.19 1.58 ± 0.09
N 8 10 9 11
Open in a new tab

“High rigor state” (36) was induced from the standard activation at 25°C (such as shown in Fig. 1 J), tension and stiffness at 100 Hz were measured and normalized to Tac (actin reconstituted tension).

*

P < 0.05 compared with actin.

†

P < 0.05 compared with acetyl-Tm.

There is a possibility that cross-bridges may contribute to resting stiffness, because some of them could be attached during relaxation. For this reason, resting stiffness was measured at 0°C, and the results were compared for the four muscle groups (Table 3). This table demonstrates that resting stiffness is not any different among the four muscle groups, indicating that there may not be any permanently attached cross-bridges.

TABLE 3.

Resting stiffness of thin filament reconstituted fibers at 0°C

Parameters Actin Acetyl-Tm AS-Tm AS-Δ23Tm
Stiffness 36.7 ± 6.5 37.3 ± 8.1 37.2 ± 9.9 38.8 ± 8.8
N 9 8 9 8
Open in a new tab

Resting stiffness was measured at 100 Hz while fibers were in the Rx solution containing 40 mM BDM at 0°C.

Effect of temperature on the complex modulus and exponential processes

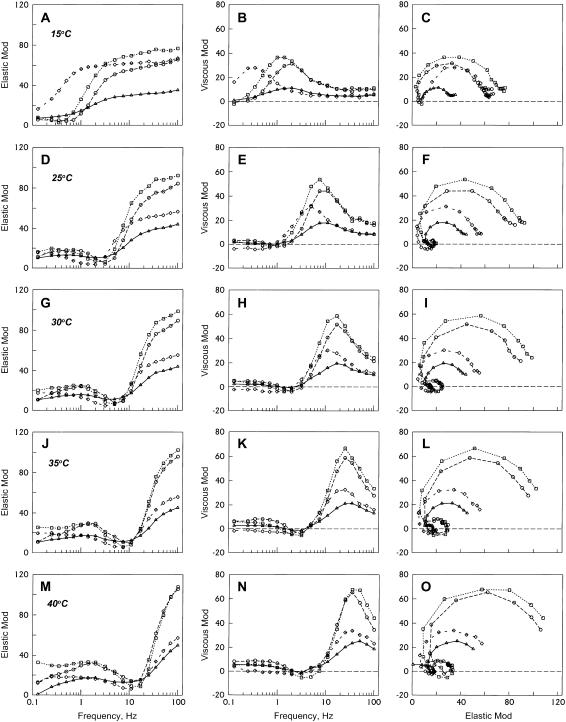
The temperature dependence of the complex modulus was studied in the four muscle groups by using sinusoidal analysis during the standard activation. In Fig. 3, the frequency dependence of elastic and viscous moduli and the Nyquist plot are shown at 15°C (Fig. 3, A–C), 25°C (D–F), 30°C (G–I), 35°C (J–L), and 40°C (M–O). In all muscle groups, frequency plots are shifted to the right as the temperature is increased, indicating that the cross-bridge kinetics become faster at higher temperatures (compare Fig. 3, A, D, G, J, and M; Fig. 3, B, E, H, K, and N). If the frequency plots are compared among the four muscle groups at the same temperature (i.e., within the same panel), plots of acetyl-Tm, AS-Tm, and AS-Δ23Tm have the maximum and minimum values at about the same frequency, indicating that the cross-bridge kinetics are almost the same, while a plot of the actin group has the maximum and minimum values shifted slightly to the left, indicating that the cross-bridge kinetics are slightly slower. What is different is the amplitude of each plot, and it is only about half with the AS-Δ23Tm group compared to the two control groups; amplitudes of acetyl-Tm and AS-Tm themselves do not differ much; the amplitude of actin group falls in between AS-Δ23Tm and the two controls groups. Consequently, the Nyquist plots have a shrunken appearance with actin and AS-Δ23Tm compared to acetyl-Tm or AS-Tm (see Fig. 3, C, F, I, L, and O). The Nyquist plots of the two control groups are just about the same.

FIGURE 3.

FIGURE 3

Open in a new tab

Complex modulus Y(f) of thin-filament reconstituted cardiac muscle fibers during standard activation at different temperatures. Actin-filament group (– – –⋄– – –), average of 22 experiments; acetyl-Tm group (……□……), average of 10 experiments; AS-Tm group (– – –○– – –), average of 10 experiments; and AS-Δ23Tm group (——▵——), average of 11 experiments. The units of both elastic and viscous modulus are Tac. (A, D, G, J, and M) Elastic modulus is plotted against frequency. (B, E, H, K, and N) Viscous modulus is plotted against frequency. (C, F, I, L, and O) Viscous modulus is plotted against elastic modulus (Nyquist plot). These data were obtained in the standard activating solution (5S8P).

The complex modulus data were fitted to Eq. 1, and the apparent rate constants and their magnitudes of the exponential processes were deduced. As it is seen in the Nyquist plots (Fig. 3, C, F, I, L, and O), only one exponential process C was identified in the low temperature range (5–15°C), two processes B and C were identified in the mid-temperature range (20–25°C), and all three processes A, B, and C were identified in the high temperature range (30–40°C): one exponential process is represented by one hemicircle in the Nyquist plots (33). The apparent rate constants were averaged for 6–10 experiments and plotted in the log scale in Fig. 4, A–C. This figure demonstrates that the rate constants 2πb and 2πc increased exponentially with an increase in the temperature. At the same time, it is seen from Fig. 4, A–C, that the rate constants did not differ much among the muscle groups at the same temperature, except that the rate constants were slower in the actin filament group. The magnitude parameters were similarly plotted in Fig. 4, D–F. These plots show that magnitudes B and C increase with an increase in the temperature. This profile is about the same for the two control groups, but the increase is very much reduced for actin-filament and AS-Δ23Tm groups. Their order was Acetyl-Tm ≈ AS-Tm > Actin-filament> AS-Δ23Tm. This order is the same as the tension and stiffness plots shown in Fig. 2, A and B.

On each apparent rate constant, Q5 was calculated for 5°C increments and averaged for the entire temperature range. This was then used to calculate Q10 as 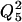Inline graphic. The activation energy (Ea) was calculated from Q10 by using Eq. 3,

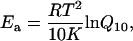graphic file with name M5.gif (3)

where T is the absolute temperature and R is the gas constant. Equation 3 is derived from the rate equation as the function of Ea and the temperature: r = r0 exp (−Ea/RT). The values of Q10 and Ea were then averaged for the same experiments and shown in Table 4. As seen in this table, both Q10 and Ea were in the order of 2πc ≥ 2πb > 2πa for all four muscle groups, but there were no significant differences among the four muscle groups.

TABLE 4.

Temperature sensitivity of the apparent rate constants

2πa (30–40°C)
2πb (20–40°C)
2πc (5–40°C)
Δ Q10 Ea (kJ mol−1) Q10 Ea (kJ mol−1) Q10 Ea (kJ mol−1)
Actin 1.75 ± 0.67 (4) 6 ± 20 (4) 4.03 ± 0.38 (13) 44 ± 3 (13) 4.92 ± 0.27 (17) 49 ± 2 (17)
Acetyl-Tm 1.67 ± 0.33 (6) 14 ± 6 (6) 3.38 ± 0.13 (10) 40 ± 1 (10) 4.50 ± 0.09 (10) 47 ± 1 (10)
AS-Tm 1.63 ± 0.45 (10) 10 ± 6 (10) 3.63 ± 0.27 (10) 42 ± 3 (10) 4.33 ± 0.19 (10) 46 ± 1 (10)
AS-Δ23Tm 1.16 ± 0.20 (10) 1 ± 6 (10) 3.36 ± 0.48 (11) 37 ± 5 (11) 4.72 ± 0.37 (11) 48 ± 2 (11)
Open in a new tab

Ea is the activation energy.

Quantification of muscle proteins by SDS-PAGE image

Muscle fibers at each stage of reconstitution were pooled and dissolved in a sample-diluting buffer (2% SDS, 25% glycerol, 5% β-mercaptoethanol, and 62.5 mM Tris-HCl, pH 6.8) and heated for 5 min at 90°C. SDS-PAGE was performed as described (32,39) with an 8–16% linear gradient running gel and a 4% stacking gel to examine the degree of thin filament protein reconstitution in five muscle groups. Proteins were stained using Coomassie Brilliant Blue R-250. The gel images (see Fig. 8 of our earlier article (27) for examples) were photographed by a digital camera and the intensity of the bands was quantified by UN-SCAN-IT (V. 5.1) software. The result is shown in Table 5. Since AS-Δ23Tm overlaps with TnI on the gel, the densities of Tm and TnI were added together. The total amount of Tm and TnI was analyzed against actin and α-actinin to obtain the relative amount of Tm and TnI in each reconstituted group. The result indicates that except for the actin-filament group, all of the three groups have no statistical difference compared with the native fiber group. Therefore, the difference in isometric force observed in Tm- and Tn-reconstituted muscle groups is inherent in the difference of the Tm molecule and does not reflect a difference in the extent of reconstitution.

TABLE 5.

Relative amount of Tm and TnI based on actin and α-actinin

Parameters Native Actin Acetyl-Tm AS-Tm AS-Δ23Tm
(Tm+TnI)/Actin 0.96 ± 0.10 0.19 ± 0.00* 1.11 ± 0.08 0.67 ± 0.04 0.93 ± 0.09
(Tm+TnI)/α-actinin 4.9 ± 0.3 1.4 ± 0.1* 4.7 ± 0.4 4.9 ± 1.2 3.8 ± 0.5
Actin/α-actinin 5.4 ± 0.8 7.3 ± 0.7 4.3 ± 1.1 7.5 ± 2.2 4.3 ± 0.6
N 5 3 7 3 10
Open in a new tab

The density of Tm, TnI, actin, and α-actinin was measured from SDS-PAGE. Means ± SE are shown. When compared with control group, there is no statistical difference except the actin-reconstituted group. Actin/α-actinin demonstrates the variability of the data. The average of the ratio actin/α-actinin for four reconstituted groups is 5.1 ± 0.5 (N = 23). The average of all the ratios is 5.2 ± 0.4 (N = 28).

*

P < 0.05.

DISCUSSION

Temperature effect on active tension and stiffness, and two proposed mechanisms

It has been reported that an increase in the temperature resulted in larger force in maximally activated mammalian skeletal (15–20) and cardiac (21,22) muscle fibers, which is called “endothermic force generation”. This is again confirmed in our thin-filament reconstituted system using bovine cardiac muscle fibers (Fig. 2 A). There are two possible mechanisms proposed for this temperature effect. One is a shift of equilibrium between the force-generating state(s) and the non-force-generating state(s) (18–20). The other is an increase in the force/cross-bridge, but the number of force-generating cross-bridges does not change (15,40–42). The first mechanism was proposed, because the equilibrium constant of the force generation step (K4) increased steeply with temperature, and the tension-temperature plot can be predicted based on equilibrium shift (18,20,43). The second mechanism was proposed because stiffness did not change much with the temperature. The first mechanism is consistent with the hydrophobic interaction (see below), and force measurements from single molecule experiments between the actin filament and HMM (44), the thin filament and HMM (26), or microtubule and kinesin (45), in which the single molecular force was found to be independent of the temperature change. There has been yet no explanation given for the second mechanism.

It has been found that in-series compliance plays a significant role in measured stiffness (46–51), and that the behavior of the stiffness-temperature plot can be predicted based on a series compliance model in which ∼50% of the compliance is in the in-series elements (43). The experiments which favored the second mechanism were performed in the absence of added Pi, in which more force-generating cross-bridges are formed than in its presence (52–54). In the absence of added Pi, the stiffness of the overlap region of the A-band becomes greater, which may be more than the stiffness of the I-band, hence I-band compliance would limit a further increase in the sarcomere stiffness even if more cross-bridges are formed by the increased temperature. Our observation of the linear increase in stiffness and no saturation with the temperature change (Fig. 2 B) implies that the number of force-generating cross-bridges is small under our activating conditions that included 8 mM Pi, and that the number of force-generating cross-bridges increases with an increase in the temperature.

Hydrophobic interaction

One possible mechanism for the endothermic reaction is the hydrophobic interaction between actin and myosin molecules. The hydrophobic effect is due primarily to unfavorable entropic effects when hydrophobic groups are exposed to water; therefore, it is often called an entropy-driven reaction (43,55,56). In this case, both the standard enthalpy change (ΔH°) and the standard entropy change (ΔS°) are large positive numbers. ΔH° > 0 (endothermic reaction) and ΔS° > 0 were observed for the force generation step in the muscle fiber system (18,20) and in the actin-myosin interaction in the solution system (57–59). In these studies it was found that ΔG°= ΔH° − TΔS° ≈ 0, which means that the absorbed heat is used for the increased Brownian motion with relatively little change in the free energy. This is additional evidence that the hydrophobic interaction is involved in the actomyosin interaction and force generation. Further evidence comes from the heat capacity change (ΔCP), which was measured to be negative (ΔCP < 0) for the force generation step in rabbit psoas (55) and soleus (20) fibers. This ΔCP pattern is another characteristic signature for the hydrophobic effect. As a whole, it can be concluded that the steepness of the temperature-tension plot can be taken as evidence of the degree of hydrophobic interaction between actin and myosin molecules (43). The fact that we observed only 40% steepness in the actin group and 36% steepness in the Δ23Tm group implies that less hydrophobic surface area becomes buried on force generation, perhaps down to 40% in the actin-filament group, and to 36% in the Δ23Tm group. If we start with the actin-filament group (no regulatory proteins), then we can conclude that normal Tm enhances the surface area of actomyosin interaction from 40% to 100%, whereas the mutant Tm (Δ23Tm) diminishes the surface area from 40% to 36%.

Allosteric effect of Tm on the actin-myosin interface

How then does a change in the Tm molecule affect the extent of hydrophobic interactions that accompany force generation? We suggest the answer is a conformational change in actin that is promoted by both myosin and Tm, involving hydrophobic residues in the actin-myosin interface. This proposed allosteric mechanism is supported by evidence that myosin greatly strengthens Tm binding to actin (60,61), and tropomyosin reciprocally strengthens myosin binding to actin (14,62,63). Of interest for this study, this myosin-tropomyosin interaction is an order-of-magnitude smaller for Δ23Tm than for control Tm (14,25). Because the tension developed between actin and myosin is largest with Tm (acetyl-Tm or AS-Tm), least with Δ23Tm, and intermediate without Tm (27), it can be concluded that normal Tm enhances the actomyosin interaction, and Δ23Tm diminishes the interaction. In other words, normal Tm has a positive allosteric effect on the actomyosin interface, whereas Δ23Tm has a negative allosteric effect on the interface. This mechanism is consistent with what was proposed earlier in the muscle fiber system (22,27,32) and in the solution system (14). The hypothesis that Tm and actin may interact to affect the actomyosin interface also has been proposed based on structural studies (13).

Alternate mechanisms

In solution studies, it has been reported that the ATP cleavage step is temperature-sensitive, and at higher temperatures, more cross-bridges would be populated at the cleaved state (AM·ADP·Pi) (64,65). This is a subset of the equilibrium shift mechanism, and it could partially explain the temperature effect on isometric tension. However, this is not a full explanation, because it is also known that the actin-myosin interaction becomes stronger (ΔSo>0, ΔHo>0) at higher temperatures (57,58). Because the cleavage step occurs mostly while cross-bridges are detached, it is not likely that this step is influenced by a variation in the Tm molecule. In other words, the observed difference in isometric tension among muscle groups (Tables 1 and 2; Fig. 2 A) must come from the thin filament-myosin interaction.

There may be yet another mechanism to explain the reduced force with Δ23Tm. With native Tm, tropomyosin dimer spreads over seven actin monomers and controls their interaction with myosin. However, not all seven actins may be available for interaction with myosin, because the troponin core domain spans approximately two actin monomers (66). Recent crystallographic results indicate the Tn core domain is located on the actin monomer outer domain, where it would sterically interfere with the myosin binding site on actin (12). Tn therefore may cause a steric hindrance for myosin to interact with actin. This subject was discussed in our earlier article (27), in which we concluded that the steric hindrance by Tn could not explain the large force reduction as we observed with Δ23Tm.

Ala-Ser substitution at the N-terminus of Tm

The N-terminus of Tm isolated from striated muscles is acetylated, whereas Tm synthesized by E. coli is not acetylated. This acetylation is essential for the head-to-tail interaction of the Tm molecule (38). To correct this shortfall, Ala and Ser are added to the N-terminus (AS-Tm and AS-Δ23 Tm) (25,30). In the current study we found that there is no significant difference between acetyl-Tm and AS-Tm in terms of their temperature sensitivity (Fig. 2) and cross-bridge kinetics (Figs. 3 and 4). Previously, we found that there was no difference in pCa50 (Ca sensitivity), Hill factor (cooperativity), and the kinetic constants of the elementary steps (27). These observations support the view that Ala-Ser substituted recombinant tropomyosins are well suited for structure-function studies.

CONCLUSION

We conclude that the hydrophobic interaction between actin and myosin is enhanced by Tm in the presence of Tn and Ca2+. This modulatory effect may be caused by a positive allosteric effect of Tm on actin, which recruits the increased number of hydrophobic amino-acid residues into the actin-myosin interface for better stereospecific matching between actin and myosin molecules. This modulatory effect of Tm is impaired in the Δ23Tm group (negative allosteric effect), perhaps by withdrawing some of the hydrophobic groups from the interface, resulting in a decreased temperature effect on tension and stiffness.

Acknowledgments

The contents of this work are solely the responsibility of the authors and do not necessarily represent the official view of an awarding organization.

We thank Mr. Luke Fraundorf for collecting the data from the actin-filament group used in this report.

This work was supported by National Institutes of Health grants No. HL70041 to M.K. and No. HL038834 to L.S.T., and American Heart Association Postdoctoral Fellowships No. 0320083Z and No. 0520084Z to X.L.

Abbreviations used: Acetyl-Tm, Tropomyosin synthesized by striated muscles, which typically have the N-terminal acetylation; AS, indicates that the N-terminus has instead Ala-Ser to compensate for the lack of acetylation; AS-Tm, Escherichia coli synthesized Tm, which lacks N-terminal acetylation; AS-Δ23Tm, E. coli synthesized Tm, lacking regions 2 and 3 (residues 47–123) of seven quasi repeat units of the Tm molecule.

References

  • 1.Huxley, H. E. 1972. Structural changes in the actin- and myosin-containing filaments during contraction. Cold Spring Harb. Symp. Quant. Biol. 37:361–376. [Google Scholar]
  • 2.Haselgrove, J. C. 1972. X-ray evidence for a conformational change in the actin-containing filaments of vertebrate striated muscle. Cold Spring Harb. Symp. Quant. Biol. 37:341–352. [Google Scholar]
  • 3.Chalovich, J. M. 1992. Actin-mediated regulation of muscle contraction. Pharmacol. Ther. 55:95–148. [DOI] [PubMed] [Google Scholar]
  • 4.Tobacman, L. S. 1996. Thin filament-mediated regulation of cardiac contraction. Annu. Rev. Physiol. 58:447–481. [DOI] [PubMed] [Google Scholar]
  • 5.Cooke, R. 1997. Actomyosin interaction in striated muscle. Physiol. Rev. 77:671–697. [DOI] [PubMed] [Google Scholar]
  • 6.McKillop, D. F., and M. A. Geeves. 1993. Regulation of the interaction between actin and myosin subfragment 1: evidence for three states of the thin filament. Biophys. J. 65:693–701. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Parry, D. A., and J. M. Squire. 1973. Structural role of tropomyosin in muscle regulation: analysis of the x-ray diffraction patterns from relaxed and contracting muscles. J. Mol. Biol. 75:33–55. [DOI] [PubMed] [Google Scholar]
  • 8.Wakabayashi, T., H. E. Huxley, L. A. Amos, and A. Klug. 1975. Three-dimensional image reconstruction of actin-tropomyosin complex and actin-tropomyosin-troponin T-troponin I complex. J. Mol. Biol. 93:477–497. [DOI] [PubMed] [Google Scholar]
  • 9.Kress, M., H. E. Huxley, A. R. Faruqi, and J. Hendrix. 1986. Structural changes during activation of frog muscle studied by time-resolved x-ray diffraction. J. Mol. Biol. 188:325–342. [DOI] [PubMed] [Google Scholar]
  • 10.Vibert, P., R. Craig, and W. Lehman. 1997. Steric-model for activation of muscle thin filaments. J. Mol. Biol. 266:8–14. [DOI] [PubMed] [Google Scholar]
  • 11.Xu, C., R. Craig, L. Tobacman, R. Horowitz, and W. Lehman. 1999. Tropomyosin positions in regulated thin filaments revealed by cryoelectron microscopy. Biophys. J. 77:985–992. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Pirani, A., C. Xu, V. Hatch, R. Craig, L. S. Tobacman, and W. Lehman. 2005. Single particle analysis of relaxed and activated muscle thin filaments. J. Mol. Biol. 346:761–772. [DOI] [PubMed] [Google Scholar]
  • 13.Rosol, M., W. Lehman, R. Craig, C. Landis, C. Butters, and L. S. Tobacman. 2000. Three-dimensional reconstruction of thin filaments containing mutant tropomyosin. Biophys. J. 78:908–917. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Tobacman, L. S., and C. A. Butters. 2000. A new model of cooperative myosin-thin filament binding. J. Biol. Chem. 275:27587–27593. [DOI] [PubMed] [Google Scholar]
  • 15.Goldman, Y. E., J. A. McCray, and K. W. Ranatunga. 1987. Transient tension changes initiated by laser temperature jumps in rabbit psoas muscle fibres. J. Physiol. 392:71–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Ranatunga, K. W., B. Sharpe, and B. Turnbull. 1987. Contraction of human skeletal muscle at different temperatures. J. Physiol. 390:383–395. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Rall, J. A., and R. C. Woledge. 1990. Influence of temperature on mechanics and energetics of muscle contraction. Am. J. Physiol. 259:197–203. [DOI] [PubMed] [Google Scholar]
  • 18.Zhao, Y., and M. Kawai. 1994. Kinetic and thermodynamic studies of the cross-bridge cycle in rabbit psoas muscle fibers. Biophys. J. 67:1655–1668. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Coupland, M. E., E. Puchert, and K. W. Ranatunga. 2001. Temperature dependence of active tension in mammalian (rabbit psoas) muscle fibres: effect of inorganic phosphate. J. Physiol. 536.3:879–891. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Wang, G., and M. Kawai. 2001. Effect of temperature on elementary steps of the cross-bridge cycle in rabbit soleus slow-twitch muscle fibres. J. Physiol. (Lond.). 531.1:219–234. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Ranatunga, K. W. 1999. Endothermic force generation in skinned cardiac muscle from rat. J. Muscle Res. Cell Motil. 20:489–496. [DOI] [PubMed] [Google Scholar]
  • 22.Fujita, H., and M. Kawai. 2002. Temperature effect on isometric tension is mediated by regulatory proteins tropomyosin and troponin in bovine myocardium. J. Physiol. (Lond.). 539.1:267–276. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Hitchcock-DeGregori, S. E., and T. A. Varnell. 1990. Tm has discrete actin-binding sites with sevenfold and 14-fold periodicities. J. Mol. Biol. 214:885–896. [DOI] [PubMed] [Google Scholar]
  • 24.Hitchcock-DeGregori, S. E., and Y. An. 1996. Integral repeats and a continuous coiled coil are required for binding of striated muscle tropomyosin to the regulated actin filament. J. Biol. Chem. 16:3600–3603. [DOI] [PubMed] [Google Scholar]
  • 25.Landis, C., N. Back, E. Homsher, and L. S. Tobacman. 1999. Effects of tropomyosin internal deletions on thin filament function. J. Biol. Chem. 274:31279–31285. [DOI] [PubMed] [Google Scholar]
  • 26.Kawai, M., T. Kido, M. Vogel, R. H. Fink, and S. Ishiwata. 2006. Temperature change does not affect force between regulated actin filaments and heavy meromyosin in single-molecule experiments. J. Physiol. (Lond.). 574.3:877–887. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Lu, X., L. S. Tobacman, and M. Kawai. 2003. Effect of tropomyosin internal deletion AS-Δ23 Tm on isometric tension and the cross-bridge kinetics in bovine myocardium. J. Physiol. (Lond.). 553.2:457–471. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Kawai, M., and S. Ishiwata. 2006. Use of thin-filament reconstituted muscle fibres to probe the mechanism of force generation. J. Muscle Res. Cell Motil. 27:455–468. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Tobacman, L. S., and R. S. Adelstein. 1986. Mechanism of regulation of cardiac actin-myosin subfragment 1 by troponin-tropomyosin. Biochem. Biophys. Res. Commun. 25:798–802. [DOI] [PubMed] [Google Scholar]
  • 30.Monteiro, P. B., R. C. Lataro, J. A. Ferro, and C. Reinach Fde. 1994. Functional α-tropomyosin produced in Escherichia coli. A dipeptide extension can substitute the amino-terminal acetyl group. J. Biol. Chem. 269:10461–10466. [PubMed] [Google Scholar]
  • 31.Fujita, H., K. Yasuda, S. Niitsu, T. Funatsu, and S. Ishiwata. 1996. Structural and functional reconstitution of thin filaments in the contractile apparatus of cardiac muscle. Biophys. J. 71:2307–2318. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Fujita, H., D. Sasaki, S. Ishiwata, and M. Kawai. 2002. Elementary steps of the cross-bridge cycle in bovine myocardium with and without regulatory proteins. Biophys. J. 82:915–928. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Kawai, M., and P. W. Brandt. 1980. Sinusoidal analysis: a high resolution method for correlating biochemical reactions with physiological processes in activated skeletal muscles of rabbit, frog and crayfish. J. Muscle Res. Cell Motil. 1:279–303. [DOI] [PubMed] [Google Scholar]
  • 34.Homsher, E., D. M. Lee, C. Morris, D. Pavlov, and L. S. Tobacman. 2000. Regulation of force and unloaded sliding speed in single thin filaments: effects of regulatory proteins and calcium. J. Physiol. (Lond.). 524.1:233–243. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Ranatunga, K. W., and S. R. Wylie. 1983. Temperature-dependent transition in isometric contraction of rat muscle. J. Physiol. 339:87–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Kawai, M., and P. W. Brandt. 1976. Two rigor states in skinned crayfish single muscle fibers. J. Gen. Physiol. 68:267–280. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.Reference deleted in proof.
  • 38.Heald, R. W., and S. E. Hitchcock-DeGregori. 1988. The structure of the amino terminus of tropomyosin is critical for binding to actin in the absence and presence of troponin. J. Biol. Chem. 263:5254–5259. [PubMed] [Google Scholar]
  • 39.Laemmli, U. K. 1970. Cleavage of structural proteins during the assembly of the head of bacteriophage T4. Nature. 227:680–685. [DOI] [PubMed] [Google Scholar]
  • 40.Kraft, T., and B. Brenner. 1997. Force enhancement without changes in cross-bridge turnover kinetics: the effect of EMD 57033. Biophys. J. 72:272–281. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Bershitsky, S. Y., and A. K. Tsaturyan. 2002. The elementary force generation process probed by temperature and length perturbations in muscle fibres from the rabbit. J. Physiol. 540.3:971–988. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 42.Piazzesi, G., M. Reconditi, N. Koubassova, V. Decostre, M. Linari, L. Lucii, and V. Lombardi. 2003. Temperature dependence of the force-generating process in single fibres from frog skeletal muscle. J. Physiol. 549.1:93–106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Kawai, M. 2003. What do we learn by studying the temperature effect on isometric tension and tension transients in mammalian striated muscle fibres? J. Muscle Res. Cell Mot. 24:127–138. [DOI] [PubMed] [Google Scholar]
  • 44.Kawai, M., K. Kawaguchi, M. Saito, and S. Ishiwata. 2000. Temperature change does not affect force between single actin filaments and HMM from rabbit muscles. Biophys. J. 78:3112–3119. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 45.Kawaguchi, K., and S. Ishiwata. 2000. Temperature dependence of force, velocity, and processivity of single kinesin molecules. Biochem. Biophys. Res. Commun. 272:895–899. [DOI] [PubMed] [Google Scholar]
  • 46.Oosawa, F., S. Fujime, S. Ishiwata, and K. Mihashi. 1972. Dynamic property of F-actin and thin filament. Cold Spr. Harbor Symp. Quant. Biol. 37:277–285. [Google Scholar]
  • 47.Bagni, M. A., G. Cecchi, F. Colomo, and C. Poggesi. 1990. Tension and stiffness of frog muscle fibres at full filament overlap. J. Muscle Res. Cell Motil. 11:371–377. [DOI] [PubMed] [Google Scholar]
  • 48.Kojima, H., A. Ishijima, and T. Yanagida. 1994. Free in PMC direct measurement of stiffness of single actin filaments with and without tropomyosin by in vitro nanomanipulation. Proc. Natl. Acad. Sci. USA. 91:12962–12966. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 49.Wakabayashi, K., Y. Sugimito, H. Tanaka, Y. Ueno, Y. Takezawa, and Y. Amemiya. 1994. X-ray diffraction evidence for the extensibility of actin and myosin filaments during muscle contraction. Biophys. J. 67:2422–2435. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 50.Huxley, H. E., A. Stewart, H. Sosa, and T. Irving. 1994. X-ray diffraction measurements of the extensibility of actin and myosin filaments in contracting muscle. Biophys. J. 67:2411–2421. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 51.Higuchi, H., T. Yanagida, and Y. E. Goldman. 1995. Compliance of thin filaments in skinned fibers of rabbit skeletal muscle. Biophys. J. 69:1000–1010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 52.Fortune, N. S., M. A. Geeves, and K. W. Ranatunga. 1991. Tension responses to rapid pressure release in glycerinated rabbit muscle fibres. Proc. Natl. Acad. Sci. USA. 80:7323–7327. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 53.Kawai, M., and H. R. Halvorson. 1991. Two step mechanism of phosphate release and the mechanism of force generation in chemically skinned fibers of rabbit psoas muscle. Biophys. J. 59:329–342. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 54.Dantzig, J. A., Y. E. Goldman, N. C. Millar, J. Lacktis, and E. Homsher. 1992. Reversal of the cross-bridge force-generating transition by photogeneration of phosphate in rabbit psoas muscle fibres. J. Physiol. (Lond.). 451:247–278. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 55.Murphy, K. P., Y. Zhao, and M. Kawai. 1996. Molecular forces involved in force generation during skeletal muscle contraction. J. Exp. Biol. 199:2565–2571. [DOI] [PubMed] [Google Scholar]
  • 56.Van Holde, K. E., W. C. Johnson, and P. S. Ho. 1998. Principles of Physical Biochemistry, 3rd Ed. Prentice Hall, Upper Saddle River, NJ.
  • 57.Tonomura, Y., S. Tokura, and K. Sekiya. 1962. Binding of myosin A to F-actin. J. Biol. Chem. 237:1074–1081. [PubMed] [Google Scholar]
  • 58.Highsmith, S. 1977. The effects of temperature and salts on myosin subfragment-1 and F-actin association. Arch. Biochem. Biophys. 180:404–408. [DOI] [PubMed] [Google Scholar]
  • 59.Ishiwata, S., B. A. Manuck, J. C. Seidel, and J. Gergely. 1986. Saturation transfer electron paramagnetic resonance study of the mobility of myosin heads in myofibrils under conditions of partial dissociation. Biophys. J. 49:821–828. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 60.Eaton, B. L. 1976. Tropomyosin binding to F-actin induced by myosin heads. Science. 192:1337–1339. [DOI] [PubMed] [Google Scholar]
  • 61.Cassell, M., and L. S. Tobacman. 1996. Opposite effects of myosin subfragment 1 on binding of cardiac troponin and tropomyosin to the thin filament. J. Biol. Chem. 271:12867–12872. [DOI] [PubMed] [Google Scholar]
  • 62.Geeves, M. A., and D. J. Halsall. 1986. The dynamics of the interaction between myosin subfragment 1 and pyrene-labelled thin filaments, from rabbit skeletal muscle. Proc. R. Soc. Lond. B Biol. Sci. 229:85–95. [DOI] [PubMed] [Google Scholar]
  • 63.Williams, D. L., and L. E. Greene. 1983. Comparison of the effects of tropomyosin and troponin-tropomyosin on the binding of myosin subfragment 1 to actin. Biochem. Biophys. Res. Commun. 22:2770–2774. [DOI] [PubMed] [Google Scholar]
  • 64.Malnasi-Csizmadia, A., D. S. Pearson, M. Kovacs, R. J. Woolley, M. A. Geeves, and C. R. Bagshaw. 2001. Kinetic resolution of a conformational transition and the ATP hydrolysis step using relaxation methods with a Dictyostelium myosin II mutant containing a single tryptophan residue. Biochemistry. 40:12727–12737. [DOI] [PubMed] [Google Scholar]
  • 65.Xu, S., G. Offer, J. Gu, H. D. White, and L. C. Yu. 2003. Temperature and ligand dependence of conformation and helical order in myosin filaments. Biochemistry. 42:390–401. [DOI] [PubMed] [Google Scholar]
  • 66.Takeda, S., A. Yamashita, K. Maeda, and Y. Maeda. 2003. Structure of the core domain of human cardiac troponin in the Ca2+-saturated form. Nature. 424:35–41. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES