Bio-Microrheology: A Frontier in Microrheology

Abstract

Cells continuously adapt to changing conditions through coordinated molecular and mechanical responses. This adaptation requires the transport of molecules and signaling through intracellular regions with differing material properties, such as variations in viscosity or elasticity. To determine the impact of regional variations on cell structure and physiology, an approach, termed bio-microrheology, or the study of deformation and flow of biological materials at small length scales has emerged. By tracking the thermal and driven motion of probe particles, organelles, or molecules, the local physical environment in distinct subcellular regions can be explored. On the surface or inside cells, tracking the motion of particles can reveal the rheological properties that influence cell features, such as shape and metastatic potential. Cellular microrheology promises to improve our concepts of regional and integrated properties, structures, and transport in live cells. Since bio-microrheology is an evolving methodology, many specific details, such as how to interpret complex combinations of thermally mediated and directed probe transport, remain to be fully explained. This work reviews the current state of the field and discusses the utility and challenges of this emerging approach.

INTRODUCTION

Animal cells rely on components, such as the nucleus, mitochondria, Golgi, and ribosomes, to perform tasks required for survival, self-renewal, and adaptation in changing conditions. Far from a homogeneous mixture, the intracellular environment is bounded by a flexible plasma membrane and is organized into locally distinct collections of molecules and structures within a dynamic, filamentous cytoskeletal scaffold. An integrated model of cell physiology that incorporates this complexity is required for understanding adaptive responses and for advancing areas of immediate concern, such as targeted drug and organelle replacement therapy in the emerging field of nanomedicine. An important challenge, therefore, is to assess and interpret the dynamic local mechanical properties of cells, which impact all trafficking and communication processes that coordinate functional responses. This brief review focuses on an up-and-coming approach for quantitative studies of the mechanical properties of live cells. This approach is bio-microrheology (BMR) and is based on an application of microrheology methodologies that were initially developed for the analysis of uniform complex fluids (1).

Many approaches have previously been used to determine the deformability and elasticity of cells by manipulating the plasma membrane and examining physical responses. Such measurements were usually intended to provide insight about membrane properties and often indirectly extracted information on internal cell structures that contributed to cell shape and rigidity. An advantage of cell surface methods is the relative technical ease of experiments. Direct and indirect biomembrane techniques are reviewed elsewhere and include atomic force microscopy (AFM) (2), optical laser tweezers (3), magnetic tweezers (4), biomembrane force probing with pipette suction (5), single-cell uniaxial stretching rheometry (6), hydrodynamic methods (7), and deformability-based flow cytometry (8). In many of these methods large deformations or strains are induced that can cause nonlinear responses, including unwanted contributions from regions neighboring the area of interest or from within the cell. The timescales for mapping entire cells using some of these methods are on the order of minutes, precluding the detection of rapidly evolving cellular responses. Moreover, most of these measurements actually probe a combination of cell surface and bulk properties that are difficult to decouple.

A conceptually distinct approach is to measure mechanical, rheological properties at specific regions inside live cells. Rheological measurements quantify the bulk or average physical responses of liquids and flexible macromolecules to deformation or mechanical forces. Rheological properties can vary as a function of time, temperature, concentration, and applied stress. For example, a basic rheological property is the viscosity, or resistance to flow, of a fluid (9). However, classical rheology equipment, even if miniaturized (6,10), cannot be used to probe the microenvironment within individual live cells because stresses are applied and responses are measured through mechanical fixtures that would have to be artificially inserted into a cell, thereby disrupting its structure. An optical method established for complex liquids and DNA solutions is particle tracking microrheology (11). Using this method, microscale studies of deformation and flow of complex fluids can be performed. When performed on living cells or in vitro reconstituted biomaterials, this technique is termed “bio-microrheology”.

BMR can potentially be used in vivo for linking mechanical and structural characteristics of a cell with its biochemical properties. In a typical microrheology experiment, the motion of an embedded probe is tracked and its relationship to the local microenvironment inferred. In cells, changing mechanical and cytoskeletal properties indicate ongoing processes, such as the modulation of proteins that affect the plasma membrane during cytokinesis (12), the stiffening of the cell furrow at division (13), or the increasing elasticity of certain cancer cells from induced changes in the perinuclear or cytokeratin networks (14). BMR techniques have been used to evaluate the material properties of DNA solutions (15), actin filaments (16–19), microtubule aggregates (20), and lipid vesicles as models of intracellular behavior (21,22). However, the relationship of these measurements to conditions within cells is unknown.

BMR holds great promise for correlating cell structure and function; however, many technical and interpretive challenges exist. In the following sections, the concepts and utility of BMR for determining real-time rheological and transport properties inside live cells are discussed. The goal of this review is to introduce the basic ideas, summarize many recent studies, and demonstrate the challenges of BMR within living cells.

Microrheology concepts and passive probe motion

In BMR, nanometer- or micrometer-sized particles, synthetic and endogenous, as well as fluorescently tagged molecules are used as local probes for live-cell measurements. The motions of appropriately sized probes embedded within cells provide an evaluation of the local, nonbulk, viscoelastic properties of heterogeneous cellular regions. The use of local probes for measuring rheological properties has motivated several kinds of experiments and theoretical interpretations. Whereas in macroscopic rheology stress-strain relationships are measured through mechanical deformation of bulk materials, in BMR embedded probe motion is tracked and its relationship to the local microenvironment inferred. Hence, distinct analytical concepts are employed in BMR, with the trajectories or time-dependent displacements of probe particles transformed into measurements of regional deformation (1,11). A recent review provides an introduction to cellular sensing and response to forces and gives several examples of linked mechanical and biochemical effects in cells (23).

In a system at thermodynamic equilibrium where no external forces are applied, particles suspended in a liquid undergo translational and rotational diffusion due to forces exerted by molecules in the surrounding medium (24). In other words, particles diffusing freely through a liquid typically exhibit a “random walk” that is nondirectional and characterized by a Gaussian distribution in step size. This random walk is propelled by thermal fluctuations as the probe particles interact with cellular structures and the liquid surrounding them.

Thermal, or passive, microrheology for viscoelastic materials is based on an extension of the concepts of Brownian (25) motion of particles in simple liquids. The motion of particles within a viscous liquid can be quantified with the diffusion coefficient, D, which is a measure of how rapidly particles execute a thermally driven random walk. Given the particle size, temperature, and viscosity, η, the diffusion coefficient in a viscous liquid can be determined by the Stokes-Einstein relation: 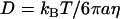(24,26–28). This relation is valid for thermal fluctuation-induced particle motion where no energy consumption, such as ATP-driven motion or convective flows of liquids, is present (1). In addition, it is assumed in the equation that particles are spherical and rigid and no heterogeneities exist. Therefore, in microrheological experiments, particle dynamics are related to the medium and probe properties and provide quantitative information about the local microenvironment.

The dynamics of particle motion are usually described by the time-dependent mean-square displacement (MSD), . An equivalent statistical representation is the position autocorrelation function, but since the MSD is a more physically based property we adhere to it. When particles diffuse through viscoelastic media or are transported in a nondiffusive manner the 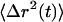becomes nonlinear with time and can be described with a time-dependent power law, 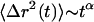. The slope of the log-log plot of the 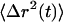, α, which is also referred to as the diffusive exponent (29), describes the mode of motion a particle is undergoing and is defined for physical processes between 0 ≤ α ≤ 2.

The MSD can be used to obtain rheological properties of a complex fluid microenvironment (1). The generalized Stokes-Einstein relation (GSER) correlates the particle radius, a, and the 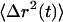to provide the creep compliance: , where k_B is Boltzmann's constant, and T is the absolute temperature (30,31). The time-dependent creep compliance (30,31), or material deformation under a step-increase in stress, can be directly obtained from the MSD. This provides a measure of the viscosity or the elastic modulus in viscous or elastic samples, respectively. In addition, a method was developed to estimate the elastic, storage modulus and the viscous, loss modulus algebraically based on the logarithmic slope of the MSD (30). This approach was later extended to provide more accurate estimates of the moduli, including rapidly changing MSDs (32). The material moduli provide equivalent rheological information to that obtained by the creep compliance and are typically used when comparisons to bulk macrorheology measurements are needed.

An example of a microrheological study in living cells is provided in Fig. 1. Adherent, NIH3T3 murine fibroblasts are incubated with 100-nm-diameter fluorescent polystyrene beads with a carboxylated surface (Molecular Probes, Eugene, OR) that are internalized by natural uptake (Fig. 1 A). The plane of examination is chosen so that it is some distance from the coverslip, as indicated by two out-of-focus particles attached to the surface (arrowheads in Fig. 1 A). The dynamics of particle transport inside the cells are studied by recording 20-s videos at 30 frames per second. Particle motion is then tracked in nanometer resolution (33) with a specially written program in MATLAB 7.0 (The MathWorks, Natick, MA). Trajectories of representative particles within the cell are presented in Fig. 1 B. All the particles moved directionally, as indicated by the start and end locations; however, transport speeds, on average 7.5 nm/s, were too low to be mediated by molecular motors (see Table 1). Hence, the underlying directionality is attributed to cell crawling on the coverslip surface. This is confirmed by examining the cell location at the start and end of the video by bright field microscopy. Particles either displayed small steps, 5–10 nm/frame (particles 1–4 in Fig. 1), or a broader distribution of step sizes, 5–40 nm/frame (particles 5–6). Particles with limited mobility or subdiffusive motion, as indicated by an α < 1 (Fig. 1 C), are spatially constrained in a small microdomain within the cell, most likely cavities in the cytoskeletal network. The MSDs of those particles never displayed an α = 0, indicating that these particles are never fully elastically trapped.

FIGURE 1.

Particle tracking microrheology on 100-nm-diameter fluorescent particles within living NIH3T3 murine fibroblast cells. (A) Phase contrast image of cells with internalized particles. Particles of interest are encircled and numbered. Note two, out-of-focus particles stuck to the coverslip (arrowheads). (B) Trajectories of the numbered particles in A. Note the consistent directionality of all the particles, which is less obvious in particles 5 and 6. (C) Time-dependent MSRs of the numbered particles in A: (1) ▾, (2) ▴, (3) •, (4) ▪, (5) , and (6) . The dashed line indicates the upper limit of data reliability due to lack of measurements. (D) Time-dependent creep compliances of the averaged MSDs: (1+2) ▾, (3+4) ▴, and (5+6) •. Dashed lines indicate where the compliance becomes nonphysical and active motion dominates.

TABLE 1.

Force application in active bio-microrheology

Method	Force	Applied force	Length scale	Speed
Molecular motors (ATP-driven single motors)	Active	Net force:	Step size:	Speed @ 2 nM ATP
		Kinesin: 5–6 pN (81)	Kinesin: 8.2 nm	Kinesin: 670 nm/s
		Dynein: 2–5 pN (82)	Dynein: 37 nm	Dynein: 4.2 μm/s
		Myosin: 3–4 pN (81)	Myosin: 11 nm	Myosin: 1.7 μm/s
Laser tweezers	Active	1–100 pN (83)	Can sense motion for <1 nm	Particle size and force dependent
Magnetic tweezers	Active	5–1000 pN (83)	Can sense motion for <1 nm	Particle size and force dependent

Convective motion revealed by an α > 1 at long lag times is attributed to cell motility. The particles with broader distribution of step sizes (particles 5 and 6 in Fig. 1) exhibited near-Brownian motion as indicated by the proximity of the diffusive exponent to 1 (Fig. 1 C). The MSD remained constant at ∼0.8 at all lag times, as the larger random steps masked the convective motion due to cell crawling. We divide the six particles in Fig. 1 into three categories: assuming that particles with similar diffusive exponents are undergoing comparable motion; spatially confined at short timescales with diffusive exponent 0.5 and 0.25 corresponding to particles 1,2 and 3,4, respectively; and nearly diffusive transport for particles 5 and 6. Each pair of particles is ensemble averaged, an operation typically performed on multiple trajectories, and the time-dependent creep compliance, J(t) given in Fig. 1 D, is found by using the GSER. The 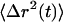data are only statistically reliable up to the last decade of time (dashed line in Fig. 1 C) as there are few long lag-time measurements to be averaged; hence, those data are not presented in Fig. 1 D. In addition, the compliance is only physical when its log slope ≤1, thus any instances where the slope is >1 are marked with dashed lines. Similar values have been obtained for microrheological measurements performed in vitro with reconstituted actin polymers (34). It is not currently possible to fully interpret the meaning of these data, as models explaining this complex behavior are lacking. This example also demonstrates that the concepts of microrheology cannot be directly applied to studies in cells.

Force-induced probe motion in cells

Thermal fluctuations induce particle motion, but are not the only forces acting within cells. Molecules or particles within a cell may diffuse to accumulation sites (18,35) or may be actively transported by molecular motors. Molecular motor transport processes, which expend ATP-stored energy, result in non-Brownian dynamics. This directed motion is typically saltatory (36), suggesting the simultaneous operation of several motors, and is a superposition of directed transport and Brownian motion (37). Molecular motors, in the presence of ATP, have been shown to transport organelles and particles at velocities as high as a few micrometers per second. A summary of forces and motion resulting from the three main molecular motors is given in Table 1. Molecular-motor driven probe displacement does not typically yield rheological data because particle motion is nonrandom, directional, and mediated by an ATP-driven force.

In addition to thermal fluctuation-driven and ATP-driven internal cell forces, probes may be externally manipulated using so-called “active” microrheology techniques. Externally applied forces acting on particles in cells result in local physical stress and movement of the particles through more elastic regions. Thermal fluctuation cannot excite soft materials out of equilibrium, necessitating active techniques to extend measurements to larger strains or deformations, often into the nonlinear range. However, active stress application may result in disruption of internal microstructures. Hence, BMR studies usually begin with passive experiments and proceed to active measurements if small deformations produced by thermal fluctuations are not enough to probe the material properties of stiff cellular regions. Similarly, experiments on stiff cells, or direct measurements of stiff structures such as the cytoskeleton, benefit from active force application techniques.

Forces applied to probes within cells and within ex vivo reconstituted bio-macromolecules must be highly localized so that they affect only the region of interest. For this purpose, magnetic or laser tweezers have mainly been used. Typical ranges of applicability for magnetic and laser tweezers are given in Table 1. A more detailed summary of the measurement applications for active methods is given elsewhere (38).

Active forces can be applied to particles on the surface and inside cells through magnetic and laser tweezers. Magnetic BMR has mainly been used for measurements of membrane elasticity (4,39,40). Magnetic particles have been functionalized to bind to a particular receptor type or region on the cell surface (4,39). Studies with paramagnetic or ferromagnetic microspheres have shown that displacement fields, or affected areas after force application on the cell surface (4) or in the cytoplasm (41), decay rapidly with distance from the magnetic microsphere. Hence, microspheres in one region can be manipulated (42) without mechanically affecting adjacent regions, and measured responses are therefore local. Similarly, laser tweezers have been used to manipulate particles, cells, and bacteria (43–45) by applying small forces to them and then measuring their displacements with high precision and accuracy. Trapped particles can be restricted to a specific region and passively monitored (46), or an active force can be locally applied and its effects on internal structure measured. For example, the force required to bend actin filaments (22,47) can be quantified. Laser tweezers have been used to trap spherical, polymeric particles (22,47) or naturally occurring granules within cells (46). They have also been used to stably trap thin, coin-like, wax microdisks (48) and examine the nonlinear rheological properties of liquids (49).

Bio-microrheology

Table 2 provides, to the best of our knowledge, a comprehensive summary of the microrheological studies done within live animal cells to date. We have grouped these studies into two main categories—force-induced (active) and thermally driven (passive) particle motion—and have organized these works by ascending dates and groupings of ongoing studies. Table 2 can be further categorized as evaluations of cytoskeletal mechanics and migration, mapping of heterogeneous viscoelastic regions in cells, and studies of the origin of particle motion within cells. In addition to animal cells, live amoeba (50) and yeast (46) cells have also been evaluated with BMR techniques.

TABLE 2.

Microrheological studies within live animal cells

Cell line	Cell substrate	Probe particles	Particle introduction
Active forces in live cells
J774 mouse macrophages	Glass	1.3 μm ferromagnetic	Phagocytosis
		2 μm carboxylated latex beads and 1 μm melamin-coated beads
	Main point: Magnetic pulse does not affect neighboring regions (41)
Vero African green monkey kidney fibroblasts	Glass coverslip	Lipid granules	Naturally occurring
		Cells were wounded by scraping dish with razor blade
	Main point: Microtubule removal hinders cell motility and organelle transport. Microtubule stabilization may create many free microtubules leading to poor organelle transport (59)
HeLa human cervical cancer cells	Glass coverslip	8 nm carboxylated CoFe2O4 magnetic beads	Internalized in endosomes
	Main point: Cell interior is a highly heterogeneous structure composed of stiff and soft viscoelastic regions (51)
Human neutrophils at room temperature	Glass coverslip	Lipid granules	Naturally occurring
		Manipulated by laser tweezers
	Main point: Leading edges of locomoting neutrophils were fluid-like, whereas body and trailing edges are more elastic. Intracellular pressure may be the origin of locomotion (60)
Swiss 3T3 fibroblasts	Glass with PDL and fibronectin	100 nm polystyrene carboxylated beads	Microinjection after cells wounding by scraping dish with syringe needle.
	Main point: Motility preferentially stiffens the leading lamella. This spatial orientation is partially regulated by microtubules (52)
Passive measurements in live cells
Human SV80 and mouse NIH3T3 fibroblasts	Glass coverslip	3 μm polystyrene beads, lectin concanavalin A coated	Phagocytosis
	Main point: Motion of probes is active (35) and results from random forces, from molecular motors, and movement of cytoskeletal filaments (47)
TC7 African green monkey kidney epithelial cell	Glass coverslip	Fluorescent proteins	Microinjection
	Main point: Diffusion constants for proteins in cells are broader than in a glycerol solution (57)
COS7 kidney epithelial cells	Glass	Spherical lipid granules	Naturally occurring
	Main point: Lamellar regions are more rigid than viscoelastic perinuclear regions, at low frequencies. High lamellar stiffness arises not only from F-actin (61)
Swiss 3T3 fibroblasts	Glass with PLL or PDL with or without fibronectin	100 or 200 nm polystyrene carboxylated or amine-modified beads	Microinjection or endocytosis
	Main point: The intranuclear region is elastic and highly viscous and is stiffer than the cytoplasm (54). ρ-kinase decreases the microheterogeneity of the cytoplasm (53). Synergistic activity of fascin and α-actinin highlights cooperative action of multiple actin-cross-linking proteins (56)
J774A.1 mouse macrophage F9 mouse carcinoma cells	Collagen-coated glass coverslips	Lipid granules and mitochondria	Naturally occurring
	Main point: First application of two-particle analysis microrheology (71) in cells. Cytoskeleton is a continuum with power-law rheology (62)
COS7 kidney epithelial cells	Glass coverslips	Polymer complex with salmon DNA	Endocytosis
	Main point: Active motor protein-driven transport of the complex through the cytoplasm toward the nucleus on microtubules (58)
SW13 human adrenal carcinoma cells	Glass coverslips	0.1 μm polystyrene carboxylated beads vimentin particles	Microinjection and stable transfection
	Main point: Particle movement is linked to chromatin reorganization. Chromatin density affects mobility of nuclear protein assemblies. Introduction of four-dimensional platform for study of particle transport in cells (55)
HeLa human cervical cancer cells	Cell culture dish	FTIC-labeled dextrans	Microinjection or electroporation
	Main point: Subdiffusion in cells is the result of spatial crowding (63)

PLL, poly-l-lysine; PDL, poly-d-lysine.

Probes used to study cell interiors have been magnetic (41,50,51) or polymeric (35,41,47,50,52–56) particles, fluorescently tagged molecules (57,58), and endogenous lipid granules and organelles (46,59–63). Synthetic particles are introduced into cells by cellular uptake, microinjection, or electroporation (see Table 2) depending on particle size, particle surface chemistry, cell size, and cell type. Cellular uptake mechanisms have been identified, but the process is not quantified or well understood at the molecular level. Particles introduced by natural cellular uptake processes, e.g., endocytosis and phagocytosis, may become trapped within membrane-bound vesicles. Particle-containing vesicles will be transported differently than “free” cytoplasmic particles within the cell interior, and their resulting environmental interactions will be unique. Thus, BMR of particles introduced by cellular uptake processes may provide a biased picture of internal cell structure. Also, exogenous particles can disrupt the local cell structure as they can bind to or push-and-pull internal structures, such as the cytoskeleton (64). Conversely, endogenous particles are naturally present and do not perturb the cell structure. However, since endogenous particle size and surface chemistry cannot be controlled their interactions also cannot be predicted, so that certain granules may, for example, unknowingly become transported by molecular motors. Thus, a compromise between control of particle and transport parameters and perturbation of the natural cell state is typically encountered in BMR studies, and a mixture of information about the rheological environment and about molecular motor activity is obtained.

The studies in Table 2 have focused on evaluations of probe transport in the cell cytoplasm. An interesting and important extension would be evaluations within the nucleus, particularly during mechanically intensive processes such as nuclear membrane assembly and disassembly, DNA replication, and nuclear division. A potential obstacle for nuclear BMR measurements is that introducing particles into the nucleus of small animal cells may be technically challenging. Fluorescently tagged molecules, such as proteins (65), transfected into the cell and targeted to the nucleus have typically been used to examine nuclear dynamics. However, tracking the precise motion of molecules directly is difficult because of their small size and resulting fast diffusion. In addition, several molecules may aggregate together, making accurate size determination impossible. The diffusion coefficients and MSD of molecules can be estimated by examining the concentration changes due to molecule motion through a stationary volume (66), as indicated by changes in fluorescent intensity; this approach is termed “fluorescence correlation spectroscopy” and may be a useful initial approach for nuclear BMR.

Probe displacement in cells can be tracked by video particle tracking, such as Nomarski optics (differential interference contrast, DIC) (33), fluorescence microscopy (67), laser particle tracking, or three-dimensional (3-D) confocal microscopy. In contrast, probe motion in biomaterials, where large sample volumes are available, is tracked by dynamic light scattering (1), diffusing-wave spectroscopy (11), interferometric microscopy (68), or x-ray photon correlation spectroscopy (69). The simplest and most common method in cells is video tracking by DIC or fluorescent microscopy. Each of these techniques has advantages and disadvantages, and selection of a method is usually based upon a compromise between spatial and temporal resolution and the desired number of simultaneously tracked particles. Digital video tracking is often sufficient to track several particles simultaneously with a reasonably high signal/noise ratio. Beads with a diameter larger than the cytoskeletal network mesh size push through surrounding filaments to move (47) and can provide an accurate measure of the viscoelasticity in the entire region (64). Particles smaller than the cell filament mesh size are sensitive to the viscosity of the solvent and hydrodynamic interactions within the network but do not reflect the bulk viscoelasticity of that region (64).

The internal microenvironments of cells are a complex, heterogeneous combination of flexible cytoskeletal macromolecules and viscous liquid containing small molecules and ions, molecular complexes, and organelles (70). Studies in Table 2 have shown that cell interiors are heterogeneous and can be viscous, elastic, or viscoelastic depending on the scale and on cell state. BMR can be used to mechanically “map” distinct regions in the cell under various conditions. In the following paragraphs, we briefly discuss two BMR studies, one within and one on the surface of cells, as examples of the utility of BMR approaches.

As discussed above, in microrheological studies the motion of probes embedded in the sample are tracked and used to infer the rheological properties of the sample. In addition to examining each particle separately, pairs of particles can be examined (71). In two-particle microrheology the correlated movements of pairs of neighboring particles are used to measure the relative viscoelastic response on the timescale of a single probe particle (72,73). This approach has been shown by Lau et al. (62) to be of particular interest for cell BMR studies, since they provide a more accurate, simplified view of the transport in the complex microenvironments of cells. In that study, the motion of endogenous lipid granules and mitochondria in cells were tracked using DIC microscopy. Probe motion was mostly random, but a few convective molecular motor induced trajectories were observed. Single particle trajectories suggested diffusive motion, whereas two-particle measurements showed convective motion. The reasoning for the apparent discrepancy between one- and two-particle trajectories is ascribed to the inability of single particle measurements to distinguish between convection of the network surrounding the probe, e.g., cell crawling on the surface as in Fig. 1, and active transport of a probe relative to a stationary network. The two-point MSD results unambiguously indicate that the cytoskeleton itself is actively fluctuating due to nonthermal forces, effectively causing the entire axis system to be moving. Hence, employing two-point microrheology in heterogeneous samples, such as cells, can aid in interpretation of complex trajectories and provide more accurate information about the motion of the probes and their origins.

A locally applied stress may link biochemical and mechanical cell properties by triggering or blocking specific signaling pathways (23,74) and can lead to receptor or protein clustering (75) and cytoskeleton-based mechanical deformation. A highly deformed but intact cell will likely not return to its original shape, since energy has been expended on rearranging the cytoskeleton and other molecules. The extent of elastic energy storage and the viscous energy dissipation define the elastic and viscous components of the cell response, respectively. In a recent study, Bursac et al. (76) examined cytoskeletal remodeling after application of a mechanical load to cells in the physiologic range of stress (e.g., from <1 Pa to >100 Pa) (77). Mechanical stress is felt by cells when, for example, lymphocytes squeeze through the endothelium during extravasation. Magnetic beads are used as a tool to apply local stress by coating with an Arg-Gly-Asp (RGD) peptide sequence that facilitated binding to the surface of human airway smooth muscle cells. In doing so, the beads are linked indirectly to the actin cytoskeleton through integrin receptors (39). This local approach was validated, as a magnetic pulse applied to the beads did not generate long-distance effects and responses were regional (41). Shear forces were used to disrupt the cell's cytoskeleton as local torque was applied through integrins. The cell compliance increased with the time of applied step stress, but its functional behavior was independent of the aging time. Thus, no distinct molecular relaxation time or time constant could characterize the process (77), implying that relaxation within a cell includes several simultaneous processes (6). Hence, mechanical aging and rejuvenation processes in live cells can be systematically studied by surface microrheology, providing an indication of the rate of aging and rejuvenation and the complexity of the involved processes.

CONCLUSIONS AND PERSPECTIVES

BMR is an emerging field that, in certain cases, may be used to quantify the rheology of heterogeneous regions on and within cells. Measurement techniques will guide the data gathering process and influence the data available for analysis, and specific probe types will determine which properties can be measured. Whereas surface properties can be compared to similar measurements made with other methods like AFM, there are no current comparisons for internal BMR measurements and we are just starting to learn how to apply microrheology for live cells. More work is needed to overcome hurdles in data acquisition and analysis procedures, especially of intermittent and superposed transport and diffusion processes (78), but a strong framework within the field already exists. Also, a challenge is to successfully apply this approach to the study of real-time complex biological processes where responses are not directly related only to changes in the cytoskeleton. For example, stem cell differentiation includes both cytoskeletal changes and complex alterations in biochemical pathway reactions that contribute to structural and cell shape changes.

Modeling collected and computed particle trajectories will improve our understanding of processes occurring in the cell. These models must account for the many elastic and viscous components of the system. The multi-component response of the cytoskeleton to applied stresses has been modeled by complex, 30-element tensegrity or tensional integrity models, with both twisting rheometry (D. Weihs, M. A. Teitell, and T. G. Mason, unpublished) and externally applied uniaxial extension or compression (80). Various phenomenological scaling laws have also been applied to the cell cytoplasm with passive measurements (35) and to the cell cytoskeleton with active measurements (39). However, easily employable models describing physical and functional cell states are still lacking. In addition, no universal theoretical model exists that can describe transport of molecules and larger structures within cells.

Many BMR-related studies have established the basic methodology and set a baseline for data interpretation (Table 2). Some major unresolved issues remain and include how to best insert particles into cells, how exactly probes interact with their microenvironment, and whether in vitro rheology of cell extracts is indicative of intracellular BMR properties. Most studies are currently carried out in two dimensions, whereas probe motion and the rheological properties of the cell are 3-D; hence tracking and analysis procedures for 3-D studies need to be developed. Accurate interpretation of intracellular data is an evolving science, as the interactions between tracers and the networks they probe are not yet fully established (64). The future lies in interpreting physical-mechanical data obtained from BMR to help explain biochemical processes and biological functions.

The time-dependent material rheological properties of the cell as evaluated from particle motion on the cell surface can be used as an indirect indication of dynamic, structural changes within the cell. Particle tracking using optical methods can be generalized for use with surface molecules that are bound strongly enough to allow forces to be applied to them, typically ones directly tied into the cytoskeleton. Perturbing actin filaments (76), which are concentrated just beneath the plasma membrane, through the cell surface can reveal changes in their structure; however, responses of cellular organelles or cytoskeletal elements located primarily in the cell center, such as microtubules and intermediate filaments, require study from within the cell. We suggest simultaneous evaluations of the responses of internal microenvironments in parallel with indirect surface measurements, utilizing the strengths of BMR. Hence, particles embedded within the cell cytoplasm can serve as indicators for internal, mechanical, and structural changes, whereas particles on the cell surface are used to apply local torques and examine surface- and near-surface structure remodeling.

BMR is a frontier science and is rapidly evolving. It provides the potential for an exciting new understanding of cell physiology and ensuing developments, such as monitoring the effects of drug delivery to specific cells. New technologies may arise from this type of approach, including microrheology lab-on-a-chip and high-throughput, real-time characterization of the internal rheology of live cells. We anticipate that this methodology will become more prevalent as researchers recognize the potential of BMR for quantitative studies in cell biology and medicine.