Electrostatic Potential Energy within a Protein Monitored by Metal Charge-Dependent Hydrogen Exchange

Abstract

Hydrogen exchange measurements on Zn(II)-, Ga(III)-, and Ge(IV)-substituted Pyrococcus furiosus rubredoxin demonstrate that the log ratio of the base-catalyzed rate constants (Δ log k_ex) varies inversely with the distance out to at least 12 Å from the metal. This pattern is consistent with the variation of the amide nitrogen pK values with the metal charge-dependent changes in the electrostatic potential. Fifteen monitored amides lie within this range, providing an opportunity to assess the strength of electrostatic interactions simultaneously at numerous positions within the structure. Poisson-Boltzmann calculations predict an optimal effective internal dielectric constant of 6. The largest deviations between the experimentally estimated and the predicted ΔpK values appear to result from the conformationally mobile charged side chains of Lys-7 and Glu-48 and from differential shielding of the peptide units arising from their orientation relative to the metal site.

Both theoretical modeling challenges and limitations in experimental characterization render the analysis of electrostatic interactions among the most problematic aspects of protein structural biology. Explicit ab initio representation for the protein, water and solvent ions is computationally prohibitive. Mixed quantum mechanics/molecular mechanics methods (1) and molecular dynamics free energy simulations (2) can be used for detailed analysis of a small region surrounding an ionization site. However, in practice, Poisson-Boltzmann analysis (3) remains the most commonly utilized treatment of protein electrostatic interactions.

Variations in the pK values of protein side-chain groups provide the main source of experimental data for comparing different electrostatic models and for optimizing the parameter values of those models, most notably the effective dielectric constant for the protein interior. Although hundreds of side-chain pK values have been reported (4), most of these residues are highly solvent-exposed, with modestly perturbed pK values that only weakly depend upon the assumed internal dielectric. Analysis of side chains that exhibit large shifts from the reference pK values provides the most effective distinction between models (5).

For most proteins studied, only one or two side-chain groups exhibit pK values that are shifted by substantially more than one unit. Since the internal dielectric is commonly treated as an adjustable parameter, the data from a single protein provide insufficient criteria to distinguish among differing electrostatic models. The need to compare data from multiple proteins, differing in structure and experimental conditions, decreases the precision and the resultant ability to distinguish between models. Simultaneous monitoring of large pK shifts at numerous sites in the same protein would enhance discrimination between electrostatic models and facilitate their optimization. Structurally conservative metal charge-dependent modulation of amide hydrogen exchange rates can offer such experimental data.

Rubredoxin is a small electron transfer protein bearing a tetracysteine-coordinated Fe(II)-Fe(III) redox couple. Zn²⁺ and Ga³⁺ can each substitute into the rubredoxin active site to form structures closely isomorphous with the analogous iron charge state (6,7). We recently found that Ge⁴⁺ can also be exchanged into the rubredoxin active site to form the first reported Ge(IV) biomacromolecular complex (8). Amide hydrogen exchange measurements were carried out on these three forms of Pyrococcus furiosus (Pf) rubredoxin, the most thermostable protein characterized to date (9). Within 12 Å of the metal, the metal charge-induced change in the log ratio of the base catalyzed rate constants (Δ log k_ex) varies inversely with the distance between the metal and the corresponding amide nitrogen (10). The distance dependence of these data is consistent with the electrostatic potential modulating the exchange rates, via alteration of the amide nitrogen pK values.

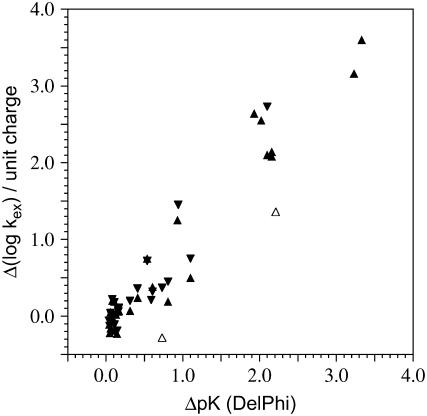
The single dielectric Coulomb model predicts an effective dielectric constant of 15 from the Pf rubredoxin differential exchange data (10). More physically realistic Poisson-Boltzmann calculations were applied to these metal charge-induced electrostatic interactions, using the DelPhi program (11). Atomic charge values for the metal and the four coordinating sulfur and cysteine C^β atoms for the Zn(II) and Ga(III) forms were taken from the corresponding Fe(II) and Fe(III) values for the rubredoxin metal cluster derived from unrestricted Hartree-Fock calculations (12). The corresponding charges for Ge(IV) and the coordinated sulfur and C^β atoms were estimated from the differential between the Fe(II) and Fe(III) calculations. Parse partial charges were used for the remainder of the protein (13). Illustrated in Fig. 1 is the correlation between the differential DelPhi potentials at the amide nitrogens with an internal dielectric of 6 and the log ratio of the base-catalyzed rate constants for Zn(II)- versus Ga(III)-substituted Pf rubredoxin (upward triangle) and Zn(II) vs. Ge(IV)-substituted Pf rubredoxin (downward triangle). Rapid hydrogen exchange of the Ge(IV)-substituted Pf rubredoxin amides nearest the metal precludes the determination of their base-catalyzed rates by the conventional exchange technique (10). This internal dielectric value is higher than for a nonpolar medium. This elevation likely reflects, in part, limited hydration of the deprotonated amide anion, analogous to the bound water observed for the buried Glu-66 residue in a staphylococcal nuclease variant (14).

FIGURE 1.

Metal charge-induced differential hydrogen exchange in the rubredoxin from Pf versus the Poisson-Boltzmann-derived differential pK values for the corresponding amide nitrogens. The log ratio of the base-catalyzed exchange rate constants of Zn(II)- versus Ga(III)-substituted Pf rubredoxin (▴) and Zn(II)- versus Ge(IV)-substituted Pf rubredoxin (▾) are compared to the electrostatic potential of the ionizing amide nitrogens predicted from nonlinear DelPhi calculations, assuming an internal dielectric constant of 6 and a solvent dielectric of 80 with 0.1 M NaCl. The conformationally mobile charged side chains Lys-7 and Glu-48 are indicated with open symbols. The Ge(IV) differential data are normalized by a factor of 2 to reflect the difference in the metal site charge. The electrostatic calculations were based on the N-terminal methionine containing wild-type sequence (16), whereas the NMR exchange data utilized a comparably stable variant containing an alanine-to-lysine mutation at the second residue (9).

The differential exchange rates for each amide along the backbone between the Zn(II)- and Ga(III)-substituted Pf rubredoxins predict apparent pK shifts within 1.0 pH unit of those estimated by the Poisson-Boltzmann calculations (Fig. 2). A positive differential corresponds to an effective dielectric constant larger than 6, whereas the converse applies to the negative differentials. The two most strongly positive differential values occur for residues Lys-7 and Glu-48. Conformationally mobile charged side chains have been proposed to provide the primary source of enhanced dielectric shielding within proteins (15). In rubredoxin, Lys-46 is the only other charged residue within 11 Å of the metal for the data of Fig. 2. However, the amino group of Lys-46 is tightly coordinated by hydrogen bonds to the backbone carbonyl oxygens of residues 30 and 33 (16).

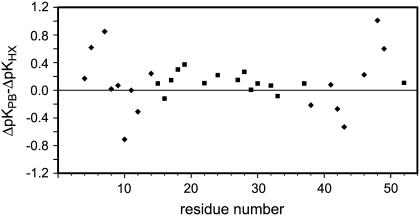
FIGURE 2.

Deviations between the Poisson-Boltzmann-estimated and hydrogen exchange-derived ΔpK values for the nitrogens along the peptide backbone of Zn(II)- versus Ga(III)-substituted Pf rubredoxin. Positions within 12 Å of the metal are denoted by diamonds. Excluding the conformationally mobile charged residues Lys-7 and Glu-48, DelPhi calculations for the indicated amides within 12 Å of the metal yielded a minimum deviation from the hydrogen exchange-derived ΔpK values at an internal dielectric constant of 6.

The assumption of a uniform internal protein dielectric in these calculations may contribute to the deviations from the apparent amide nitrogen pK values of Pf rubredoxin. Peptide linkages provide the largest and most common dipole within the protein interior. If the peptide dipole moment is oriented away from the metal site, the carbonyl group lies between the nitrogen and the metal and can be anticipated to provide increased dielectric shielding. For residues Val-5 and Phe-49, the differences between the DelPhi and hydrogen exchange-estimated amide nitrogen pK values of Fig. 2 are 0.62 and 0.59, respectively. In both cases, the angle between the peptide dipole and the peptide-metal vector is >90°. Conversely, the difference values of Fig. 2 for residues Gly-10 and Gly-43 are −0.75 and −0.55, respectively, and both residues form an acute angle between the peptide dipole and the peptide-metal vector.

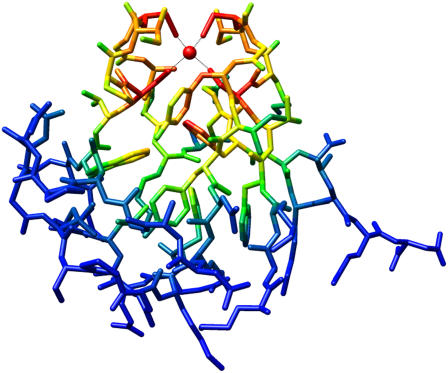
The mobile charged side chains and peptide bond orientations provide plausible explanations for all deviations >0.5 pH units between the exchange data and the Poisson-Boltzmann predictions for Zn(II)- versus Ga(III)-substituted Pf rubredoxin. The same conclusion holds for the corresponding Zn(II)- versus Ge(IV)-substituted Pf rubredoxin hydrogen exchange data. The precision in the agreement between the experimental estimates of the amide nitrogen pK values and the Poisson-Boltzmann-derived predictions is generally superior to that reported in various studies of ionizable side chains (4,5,17). This level of agreement likely reflects the differential character of the hydrogen exchange analysis, since experimental variations among the amide data are minimized. Similarly, through subtraction of the electrostatic potential values calculated for differing metal forms, various systematic errors in the Poisson-Boltzmann calculations are also likely to cancel. As a result, the pattern of how the differential electrostatic potential propagates through the rubredoxin structure (Fig. 3) will be more accurate than the corresponding predictions of the absolute potential.

FIGURE 3.

Differential electrostatic potential energy within Pf rubredoxin arising from the substitution of Ga³⁺ for Zn²⁺ in the active site. For an internal dielectric of 6, atoms bearing Poisson-Boltzmann-derived differential electrostatic potential above 8 kT/e are colored in red, 4–8 kT/e in orange, 2–4 kT/e in yellow, and 1–2 kT/e in green, with blue indicating differential potentials less than kT/e.

The analysis presented here assumes that the differential hydrogen exchange rates, induced by alteration of the charge at the metal site, arise solely from the electrostatic potential-induced change in the amide nitrogen pK values and its resultant effect on intrinsic exchange rates. In principle, changes in local conformational stability resulting from substitution of the different metal ions could also contribute to the observed differential hydrogen exchange behavior (18). However, as previously indicated, this is unlikely to account for a large proportion of the differential exchange behavior of Pf rubredoxin (10). The close agreement between the differential hydrogen exchange and these Poisson-Boltzmann predictions indicates that differential conformational stability makes little contribution. Hence, for this system, charge-dependent hydrogen exchange provides a useful monitor of the amide nitrogen ionization behavior within the protein interior.