TASSER-Lite: An Automated Tool for Protein Comparative Modeling

Abstract

This study involves the development of a rapid comparative modeling tool for homologous sequences by extension of the TASSER methodology, developed for tertiary structure prediction. This comparative modeling procedure was validated on a representative benchmark set of proteins in the Protein Data Bank composed of 901 single domain proteins (41–200 residues) having sequence identities between 35–90% with respect to the template. Using a Monte Carlo search scheme with the length of runs optimized for weakly/nonhomologous proteins, TASSER often provides appreciable improvement in structure quality over the initial template. However, on average, this requires ∼29 h of CPU time per sequence. Since homologous proteins are unlikely to require the extent of conformational search as weakly/nonhomologous proteins, TASSER's parameters were optimized to reduce the required CPU time to ∼17 min, while retaining TASSER's ability to improve structure quality. Using this optimized TASSER (TASSER-Lite), we find an average improvement in the aligned region of ∼10% in root mean-square deviation from native over the initial template. Comparison of TASSER-Lite with the widely used comparative modeling tool MODELLER showed that TASSER-Lite yields final models that are closer to the native. TASSER-Lite is provided on the web at http://cssb.biology.gatech.edu/skolnick/webservice/tasserlite/index.html.

INTRODUCTION

Knowledge of the native structure of a protein can provide insight into the molecular basis of protein function. Since the experimental determination of a protein's tertiary structure is both time consuming and expensive, the ability to predict the native conformation of a protein has become increasingly important, especially in the postgenomic era (1,2). There are three basic classes of protein prediction approaches (3): homology modeling (4,5), threading (6–8), and ab initio folding (9–11). Of these, homology or comparative modeling aims to find a clear evolutionary relationship between the template sequence (of known structure) and the target sequence (of unknown structure). Since evolutionarily related sequences have similar folds (12,13), a model of the target structure based on that of the template can be built (14). The usefulness of comparative modeling is steadily increasing because the number of unique structural folds that protein can adopt is limited (13) and the number of protein families where the structure of at least one member has been solved is increasing exponentially (12). Moreover, it has been recently shown that the PDB is complete for low-to-moderate resolution single domain protein structures (15). Hence, it is in principle possible to use comparative modeling to predict the tertiary structure of most single domain proteins, provided that a suitable template can be identified (15). If there is a clear evolutionary relationship between the template and target, as indicated above, this is relatively easy to do. However, if such a relationship cannot be detected or the folds are analogous (similar folds adopted by proteins with no apparent evolutionary relationship), then the identification of the analogous template structure can be quite difficult, and in general the resulting models are of poorer quality.

In practice, homology modeling proceeds as follows: First, an evolutionarily related template protein is identified. Second, an alignment between the target and template sequences is constructed. Third, a three-dimensional model including loops in the unaligned regions is built (5). A variety of methods could be used to construct the protein's three-dimensional structure. One involves modeling by rigid-body assembly as in COMPOSER (16,17). Another method uses segment matching, which relies on the approximate positions of the conserved template atoms (18–20); a representative approach is SEGMOD. The third group of methods incorporates modeling by satisfaction of the spatial restraints obtained from the alignment by using either distance geometry or optimization techniques (21–23); such an approach is implemented in MODELLER (24), one of the most widely used comparative modeling tools. Despite improvements in homology modeling procedures, the ability to accurately predict the conformation of the intervening loops between the aligned regions has been rather limited (25,26). Moreover, the accuracy of the resulting model depends mainly on the template selection and alignment accuracy between the target and the template. Indeed, the resulting models (in the aligned regions) are generally closer to the template structure than that of the target sequence being modeled. This is an essential problem that must be addressed; this forms the major focus of this work.

Recently, we developed a methodology, Threading/ASSembly/Refinement (TASSER) (27), for the automated tertiary structure prediction that proceeds in a two-step fashion: First, we employ the threading algorithm PROSPECTOR_3 to provide continuous aligned fragments and predicted tertiary restraints (28). TASSER uses PROSPECTOR_3 provided fragments and tertiary restraints to assemble the structure under the influence of a knowledge-based force field. TASSER has been benchmarked on a comprehensive set of weakly/nonhomologous single domain proteins (27) as well as medium to larger sized, possibly multi-domain, proteins (29). This benchmarking showed that TASSER could significantly refine the structures and provide final models that are often considerably closer to the native structure than the input templates, and it could generate good predictions for the unaligned (loop) regions. Moreover, the performance of TASSER in CASP6 (30) was consistent with that of the benchmark.

Although TASSER often generates good models for weakly/nonhomologous proteins, the procedure is rather CPU intensive, requiring several CPU hours to days/sequence for a complete run. However, when the sequence identity between the target and template is >35%, viz. in the comparative modeling regime, the alignment to the template is usually good and such long simulations might not be required; however, TASSER's ability to refine proteins over their initial template alignment in the comparative modeling regime where the initial alignments are in general quite good has not been systematically explored. Thus, this study systematically benchmarks TASSER in the comparative modeling regime. The benchmark set consists of representative single domain protein structures in the Protein Data Bank (PDB) (31) of the length between 41–200 residues having a sequence identity ≥35% with respect to the templates. We optimize the run time parameters of TASSER so that a single calculation gives essentially the same results as the original procedure but does so in considerably less computer time. The resulting fast and effective search version of TASSER, TASSER-Lite, is a rapid comparative modeling tool that is readily applicable to the large-scale comparative modeling.

METHODS AND MATERIALS

Construction of the benchmark set

TASSER has been previously benchmarked on a representative set of single domain proteins with sequence identities <35% (27). In this work, the benchmark set was constructed using all the PDB structures (with 41–200 amino acids and solved x-ray crystallography with a resolution of 2.5 Å or better) having pairwise sequence identity between 35–90% to their respective templates from the PDB template library of PROSPECTOR_3 (28).

We constructed an initial data set from which the benchmark set was derived. Each member of the PDB template library has its own cluster, which consists of the PDB sequences having sequence identity >35%. Those PDB sequences, which satisfy the criteria mentioned above, were selected from each of these template clusters to form the initial data set. In addition, sequences having sequence identity ≥98% among the cluster members were removed from each template cluster to reduce redundancy. From the initial data set, sequences having two or more domains were identified using the protein domain parser (32), scrutinized manually, and removed from the data set. For the systematic analysis, sequences in the 35–90% sequence identity range are subdivided into six categories: 35–40%, 40–50%, 50–60%, 60–70%, 70–80%, and 80–90%. From this initial data set, one representative target per template cluster was selected to form the benchmark set, except for the category 35–40%. For 35–40%, all members are included to form the benchmark set. The list of all proteins belonging to the six sets of cluster can be found at http://cssb.biology.gatech.edu/skolnick/files/tasserlite/tasserlite_data.html.

Overview of TASSER

Since TASSER has been previously described (27,28,33–36), here we just outline its essentials. Structural templates for a target sequence are selected from a representative PDB library using our iterative threading procedure PROSPECTOR_3 (28) designed to identify homologous as well as analogous templates. The scoring function of PROSPECTOR_3 includes sequence profiles, secondary structure propensities from PSIPRED (37), and consensus contact predictions from the previous threading iterations. A target sequence is classified into three categories based on the confidence of the template identification and likely alignment accuracy as “Easy”, both the template identification and alignments are likely to be quite accurate; “Medium”, the template is reasonable, viz., has a good structural alignment with the target structure, but the threading-based alignment may be quite inaccurate; and “Hard”, where the template selection is likely incorrect.

Based on the threading template, the target sequences are split into the continuous aligned regions and unaligned regions. For a given threading template, an initial full-length model is built by connecting the continuous template fragments (building blocks) by a random walk confined to lattice bond vectors. If a gap is too long to be spanned by the specified number of unaligned residues, a long C_α-C_α bond remains and a spring-like force that acts to draw sequential fragments together is used until a physically reasonable bond length is achieved. Parallel hyperbolic Monte Carlo (MC) sampling (38) samples conformational space by rearranging the continuous fragments excised from the template. During assembly, building blocks are kept rigid and are off-lattice to retain their geometric accuracy; unaligned regions are modeled on a cubic lattice by an ab initio procedure and serve as linkage points for rigid body fragment rotations. Conformations are selected using an optimized force field, which includes knowledge-based statistical potentials describing short-range backbone correlations, pairwise interactions, hydrogen-bonding, secondary structure propensities from PSIPRED (37), and consensus contact restraints extracted from the PROSPECTOR_3 identified template alignments.

In a standard TASSER run, for each protein, five MC runs (N_run) are performed. Each MC simulation contains 40–50 replicas (N_rep), depending on the size of the protein, with each replica simulated at a different temperature. The number of MC steps, N_step, before a temperature exchange or a swap is performed is 200. The total number of such swaps, N_swap, is 1000. After each MC swap, the structures of the 16 lowest temperature replicas are stored. Finally, the structures generated in these 16 lowest temperature replicas for all the five independent runs are submitted to an iterative clustering program, SPICKER (36). The final models are combined from the clustered structures and are ranked by the cluster density, and the five highest structural density clusters are selected. Thus, no knowledge of the native structure is used in either generation of the models or in their selection. Solely for the purpose of subsequent analysis, the final model is the one among the top five cluster centroids that has the lowest root mean-square deviation (RMSD) from the native structure in the aligned region. We construct a detailed atomic model using PULCHRA (unpublished) using the best cluster centroid model.

The set of parameters (N_run, N_rep, N_step, N_swap) described above are those of a standard TASSER simulation and were obtained based on the optimization of TASSER on a weakly/nonhomologous protein benchmark set of 1489 proteins (27). Since with the above-mentioned parameters TASSER takes hours/days of CPU time, our goal here is to develop TASSER into a reliable fast comparative modeling tool, which we achieve by tuning the run time parameters of TASSER. Although we found that the parameters N_run, N_step, and N_swap could be significantly reduced during the optimization, N_rep could not (data not shown).

We have used the template modeling score (TM-score) (39) as one means of comparing the improvement over the initial template, which is defined as

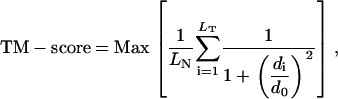where L_N is the length of the native structure, L_T is the length of the aligned residues to the template structure, d_i is the distance between the ith pair of aligned residues, and d₀ is the scale to normalize the match difference. Max denotes the maximum value after optimal superposition. The value of TM-score always lies between (0,1), with better templates having a higher TM-score.

RESULTS

The benchmark set consists of 901 homologous single domain PDB structures having pairwise sequence identities in the range of 35–90% with respect to the templates in the PDB template library of PROSPECTOR_3. The targets are classified into six categories, based on their sequence identity with the template, as discussed in the Methods section. The benchmark set encompasses various classes from the Structural Classification of Proteins (SCOP) database (40). Of 901 targets, 160 belong to the α-class, 248 targets are in the β-class, and 387 targets belong to either the α/β or α + β class. Of the rest, either they belong to peptides or membrane proteins or could not be classified into any of the above classes.

In general, the RMSD is used to assess the quality of the full-length models between the equivalent atoms in the model and the native structure (41). For the weakly/nonhomologous pairs of proteins where only substructures of the target and template may be related, the RMSD is a poor measure to estimate the quality of different initial templates because the alignment coverage could be very different even when the RMSD is the same (28,41,42). When the models are of low to moderate quality (say with an RMSD above 3 Å), the TM-score has a relatively good correlation between the initial template alignment and the final model (39). However, for very good full-length models without large local deviations, because of its greater sensitivity to details, the RMSD is the more appropriate measure. Hence, in this work, the RMSD from native of the Cα atoms has been used to assess the quality of the structure template and the predicted full-length model.

The threading results of PROSPECTOR_3 for the 901 targets are summarized in Table 1 under the columns labeled by T_ali. In the threading process, for each of the six categories (as mentioned in Methods), homologous templates with a sequence identity greater than the upper limit of identity ranges are excluded from the template library. Among the 901 target sequences, PROSPECTOR_3 assigns 897 to the Easy set with an average RMSD and TM-score to native of 2.1 Å and 0.86 respectively with an average alignment coverage of 97% (Table 1). Four targets are classified as belonging to the Medium set. Analysis of these cases, showed that either they are small proteins or have few secondary structures, which might have resulted in poor alignment and poor Z-scores. In further discussions, we focus on the Easy set of proteins. In general and not surprisingly, PROSPECTOR_3 identifies good templates with increasing sequence identity as shown by an average decrease in the RMSD of the template to native over the aligned region (Table 1). This is a minimal requirement for any acceptable threading algorithm.

TABLE 1.

Summary of results from PROSPECTOR_3, refinement by nonoptimized TASSER, and comparison with the best structural alignment between the template/model to native

				〈Coverage (in %)〉*			〈RMSD to native (in Å)〉†
Sequence Identity		N	Template selected	Tali	Taln	Maln	Tali	Mali	Ment	Taln	Maln
35–40%	Easy set	269	Top2 + consensus	96			2.5(1.6)	1.9(1.2)	2.2(1.4)
	TMalign A				94	95				1.7(0.4)	1.6(0.4)
	TMalign F				95	98				1.7(0.4)	1.7(0.4)
	Medium	1	Top five	55			1.3	2.7	7.6
	TMalign A				55	51				1.3	2.4
	TMalign F				55	63				1.3	3.2
40–50%	Easy set	219	Top2 + consensus	97			2.4(2.3)	2.0(2.1)	2.4(2.2)
	TMalign A				94	95				1.6(0.5)	1.5(0.5)
	TMalign F				95	98				1.5(0.5)	1.6(0.5)
50–60%	Easy set	150	Top2 + consensus	97			2.0(1.5)	1.9(1.7)	2.3(2.3)
	TMalign A				95	95				1.4(0.6)	1.4(0.5)
	TMalign F				95	97				1.4(0.6)	1.6(0.5)
60–70%	Easy set	111	Top2 + consensus	97			1.9(1.7)	1.8(1.6)	2.2(2.2)
	TMalign A				95	96				1.2(0.5)	1.4(0.5)
	TMalign F				96	98				1.2(0.5)	1.5(0.5)
70–80%‡	Easy set	60	Top2 + consensus	97			2.2(2.6)	2.0(1.9)	2.4(2.2)
	TMalign A				94	95				1.2(0.7)	1.5(0.6)
	TMalign F				95	97				1.2(0.7)	1.5(0.6)
	Medium	2	Top five	83			5.0	1.8	4.8
	TMalign A				73	83				2.2	1.6
	TMalign F				73	90				2.1	2.0
80–90%	Easy set	88	Top2 + consensus	97			1.8(2.0)	1.9(1.5)	2.1(1.6)
	TMalign A				95	95				1.1(0.6)	1.5(0.7)
	TMalign F				96	98				1.1(0.6)	1.6(0.7)
	Medium	1	Top five	86			2.4	7.0	11.5
	TMalign A				79	62				1.9	1.6
	TMalign F				81	64				2.0	1.7

N, number of targets in the category.

^*Alignment coverage on average for the best template that has highest TM-score to native is under the column T_ali. The coverage for the structural alignment of the best template to native and the final model to native is under columns T_aln and M_aln, respectively.

^†RMSD of the best initial template and best model among top five clusters, T_ali, template structure with RMSD calculated over aligned region; M_ali model with RMSD calculated over aligned residues; M_ent, model with the RMSD calculated over the entire chain. T_aln and M_aln refer to the structural alignment of the best template to native and the final model to native, respectively. TMalign (A) and TMalign (F) refer to the best structural alignment using TM-align for the aligned region of the template/model (by PROSPECTOR_3) to the native and full-length template/model to the native, respectively. T_aln and M_aln refer to the structural alignment of the best template to native and the final model to native, respectively. The number in parentheses is the standard deviation for the given average RMSD.

^‡Anomaly in the 70–80% range is because of two targets (1mvkA and 1tud_), which have a very high RMSD of 12.5 Å and 10.9 Å, respectively, from native. If we do not consider them, the average RMSD is reduced to 1.8 Å, and the trend of decreasing RMSD with increasing sequence identity is preserved. These two proteins have very few secondary structures and are small proteins.

The threading templates and alignments by PROSPECTOR_3 are taken as initial input into TASSER. Between the top two templates from PROSPECTOR_3, the one having the highest TM-score with respect to the native is selected as the best template for the subsequent calculation of the RMSD or TM-score. This step resulted in 162 targets with templates having pairwise sequence identity less than the lower limit of the sequence identity range in their respective category. Since most (75%) have sequence identities >30%, these are included in the analysis. Moreover, TASSER also uses the information from the other templates. As an initial step, a standard TASSER run (as discussed in Methods), which is not an optimized simulation, was performed. Table 1 presents the summary of final models produced by such a nonoptimized standard TASSER run, under columns M_ali and M_ent, for the various sequence identity ranges. For the Easy set of 897 proteins, TASSER yields final models with an average RMSD and TM-score of 1.9 Å and 0.85 in the aligned region, respectively. Thus, TASSER has the capacity to improve the model quality over that of the initial template alignment by 0.2 Å on average as assessed by the decrease in RMSD. Hence, TASSER improves the RMSD in the aligned region by ∼10%. When we compare the improvement in the average RMSD of the final model (M_ali) with respect to the initial template (T_ali) for the different sequence identity ranges, as is evident from Table 1, with the increase in sequence identity, there is no relative improvement in the RMSD. This suggests that when the sequence identity is high, while the room for further structure improvements is reduced, then refinement by TASSER with respect to the initial template is limited essentially because the distance between the target and template structures is below the inherent resolution of the TASSER potential.

In the above analysis, we have calculated the RMSD of the template or model to native with an a priori specified equivalence between pairs of residues provided by the threading method PROSPECTOR_3. To clarify the relationship between the threading alignments and the best structural alignments, we compare the above results with the RMSD calculated by finding the best structural alignment between the template/model to native using TM-align (43). We align the substructure identified by threading (using PROSPECTOR_3) to the native structure. The average RMSD of 897 proteins in the Easy set, for the template aligned region to native for the structural alignment is 1.4 Å (Table 1 under column T_aln in the row TMalign A) in comparison to the 2.1 Å RMSD given by PROSPECTOR_3. The average RMSD of the template to native becomes better by 0.7 Å, when we use the alignment provided TM-align instead of the threading alignment; however, the average alignment coverage drops by 2% (97–95%) for the structural alignment. For the full-length final models (897 proteins in the Easy set), a similar calculation shows that the average RMSD of the final models evaluated in the aligned region is 1.5 Å, (Table 1 under column M_aln in the row TMalign A) with TM-align, which is better than the RMSD obtained without using the structural alignment, 1.9 Å. In Table 1 (row TMalign A), comparison of the average RMSD for the template (under column T_aln), with the final model (under column M_aln) for the higher sequence identity range, shows marginal improvement in the RMSD for the model. This reflects the fact that models of this quality are at the limit of the resolution of TASSER.

Using the threading alignment of template to native and structural alignment of template (threading aligned region) to native, we extracted the residues of the target sequence that are identically aligned by both threading and structural alignment, with respect to the template. These common aligned residues cover ∼95% of the threading aligned region. Thus, as would be expected, there is good agreement between the threading and structural alignments. The other ∼5% of residues, which show disagreements in the alignment are, mostly, in the loop region at the start or end of the secondary structures and at the N- or C-termini of the protein. For these (∼5% of the residues that are aligned in threading), the average shift per residue between the structural and threading alignments is 2.1. Furthermore, using the set of residues that are aligned to the template by threading, we calculated the average RMSD between the final TASSER model to the native structure. The obtained average value is 1.9 Å. If we consider these residues in the structural alignment, 98.6% are aligned on average with an average RMSD of 1.5 Å. Of the residues that contribute to the structural alignment, 97% are identical to those of the TASSER model. For the remaining 3%, the average shift in alignment from the TASSER model is 1.7 residues.

Next, we have used TM-align for the structural alignment of the full-length template or full-length model to native (for the Easy set) to see if there is any improvement in the alignment by including all residues in the template whether or not they are aligned by PROSPECTOR_3. The result is listed in Table 1 in the row TMalign F under the columns T_aln and M_aln for template and final model, respectively. The structural alignment, using either the aligned region of the template or the full-length template to the native, results in an alignment coverage of ∼95% and an average RMSD of 1.4 Å. This implies that including the unaligned region of the template does not result in any improved alignment compared to the one that is restricted to the threading aligned region. The threading alignment has apparently extracted the best portion of the template proteins. In a similar comparison for the final models, when we include the unaligned region in the structural alignment, the average RMSD of the full-length model shows an increase of 0.1 Å (from 1.5 Å, only considering the aligned region) to 1.6 Å and an increase in average alignment coverage of ∼3% (from 95% to 98%) for the full-length model. We also looked at the standard deviation of the average RMSD from TM-align and the direct superposition of the threading aligned region. In general, TM-align shows less variation compared to the one obtained using direct superposition of equivalent residues. Most sequences in the Medium set show a trend similar to that observed for the Easy set of proteins.

On average, a standard TASSER run needs ∼29 h of CPU time on a 1.28-GHz PIII Pentium processor for the sequences with the lengths ranging between 41–200 residues. Longer sequences take more CPU time in comparison to the short sequence (a 200-residue protein needs ∼74 h, whereas a 43-residue protein takes ∼4 h). The clustering procedure, SPICKER, needs an additional average CPU time of ∼47 m on a 1.28-GHz PIII Pentium processor for one sequence. Hence, with the parameters used here, TASSER is not suitable for fast comparative modeling. To reduce the simulation time, we next turn to the optimization of the run time parameters.

Over a broad initial RMSD range, TASSER can refine the structure over the template

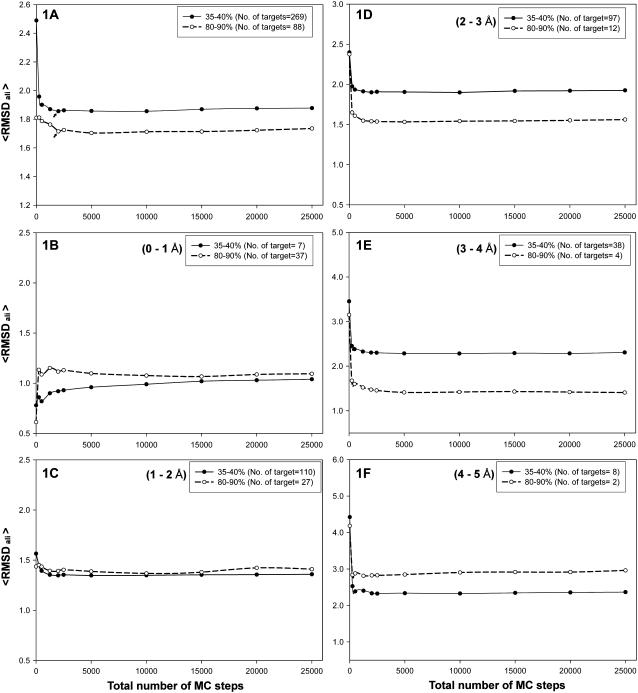
We explored the RMSD as a function of the number of total MC steps from 250 to 25000. A general decreasing trend could be observed which increases slightly after a certain number of MC steps (Fig. 1 A). We have investigated the reason for the minimum in RMSD. The targets are divided into five bins of 1 Å based on the RMSD of the template to the native, ranging from 0 to 5 Å. The dependence of average RMSD on total simulation time is shown in Fig. 1, B–F, for targets in the 35–40% and 80–90% sequence identity ranges. As shown in Fig. 1, B–F, except for the 0–1-Å bin (Fig. 1 B), the average RMSD of the final model (aligned region) to the native decreases with increasing number of MC steps and then reaches a plateau. For structures whose initial template has an RMSD from native in the range 0–1 Å, the RMSD does not improve—rather it becomes worse. This is simply due to the inherent resolution of the TASSER potential which is ∼1.2 Å. There are ∼16% of targets in this category and with, as would be expected, more such proteins in the high sequence identity range. The combined trend shown by targets in the 0–1-Å category and the other targets give rise to the observed trend of an average RMSD decrease followed by a slight increase with the total number of MC steps as in Fig. 1 A. Nevertheless, on average, the net trend is to improve the RMSD over the initial template alignment. A similar trend is observed for the other sequence identity ranges as well.

FIGURE 1.

(A) Representative plot of the average RMSD (aligned region) of the final model to the native versus the total number of MC steps in the TASSER run simulation (N_step = 25) for 35–40% and 80–90% sequence identity categories. The RMSD of the MC step = 0 corresponds to the average RMSD of the template to the native structure. The arrow indicates the minimum for each sequence identity range in A. The targets in the 35–40% and 80–90% categories are divided into five bins of 1 Å based on the RMSD of the template to the native, ranging from 0 to 5 Å. B–F show the same plot as in A for the five bins 0–1 Å, 1–2 Å, 2–3 Å, 3–4 Å, and 4–5 Å, respectively.

Optimization of TASSER parameters

As an initial step to find the minimum number of MC steps (N_swap × N_step), we proceeded to optimize TASSER using the RMSD calculated over the aligned region as the criterion to identify the minimum number of MC steps required to reach convergence. Based on a series of runs and the simulation time dependence of the RMSD, we fixed N_step at 25 and searched for an optimal N_swap. The selection of optimized N_swap was made empirically for the various sequence identity ranges based on the plot of RMSD as a function of the total number of MC steps and the approximate CPU time required for each run. We selected N_swap = 80 (MC steps = 2000) for all the six sequence identity categories. Using N_step = 25 and N_swap = 80 gives comparable average RMSD results in ∼17 min of CPU time as compared to the original 29 h, with the requisite CPU time, and the average CPU time for clustering using SPICKER is reduced to ∼7 min. Next, we examined the effect of reducing N_run from 5 to 1 On average, the RMSD with N_run = 1 is slightly worse by ∼2% in comparison to N_run = 5. Using this, N_run is set to 1, which resulted in nearly the same result as N_run = 5. This also resulted in reduction of the CPU time for structure clustering from ∼7 min (N_run = 5) to 16 s when N_run = 1. Thus, the various optimized parameters are N_run = 1, N_step = 25, and N_swap = 80 for homologous sequences, which on average requires a CPU time of 17.26 min per sequence.

Comparison of TASSER-Lite with MODELLER

We compared the results from TASSER-Lite refined models for the homologous sequences in the Easy set with the widely used homology modeling tool, MODELLER (version 8v0) (14,22). We provided MODELLER with the same input alignment from PROSPECTOR_3, and five models were generated per sequence. The best model for MODELLER is the one with the lowest RMSD from the native structure in the aligned region. The criterion shows the upper bound of refinement for both procedures. A summary of the RMSD for the final models obtained using MODELLER and TASSER-Lite is tabulated in Table 2. TASSER-Lite improves the RMSD in the aligned region by ∼10%, whereas MODELLER improves by ∼1.2%. This is mainly because MODELLER produces models by optimally satisfying tertiary restraints and threading templates govern the final model. However, TASSER allows movements in the relative orientation of template fragments that can generate a final model that could be significantly different from the initial template. TASSER does not improve the RMSD (in the aligned region) with respect to the initial templates for high sequence identity targets, where the distance between the target and template structure is below the inherent resolution of the TASSER potential. As observed before in Fig. 1 B, TASSER's ability to improve over the initial templates for targets with an RMSD of the template to native in the 0–1-Å range is limited. The number of cases increases in the high sequence identity ranges. For such targets, TASSER-Lite might not improve over the initial templates; however it will result in final models within ∼1 Å.

TABLE 2.

Summary of the comparison of the final model generated by either TASSER (using various parameters) or MODELLER with the initial template

	〈RMSD to native† (in Å)〉
Sequence identity and conditions used	Tali	Mali	Ment
35–40%
*Standard TASSER run	2.5	1.9	2.2
Nrun = 5 (Nswap = 80, Nstep = 25)	2.5	1.9	2.1
Nrun = 3 (Nswap = 80, Nstep = 25)	2.5	1.9	2.2
Nrun = 1 (Nswap = 80, Nstep = 25)	2.5	1.9	2.2
‡Nrun= 1 (Nswap = 80, Nstep = 25)	2.5	2.0	2.2
MODELLER	2.5	2.3	2.8
40–50%
*Standard TASSER run	2.4	2.0	2.4
Nrun = 5 (Nswap = 80, Nstep = 25)	2.4	1.9	2.3
Nrun = 3 (Nswap = 80, Nstep = 25)	2.4	1.9	2.3
Nrun = 1 (Nswap = 80, Nstep = 25)	2.4	2.0	2.3
‡Nrun= 1 (Nswap = 80, Nstep = 25)	2.4	2.2	2.5
MODELLER	2.4	2.3	3.0
50–60%
*Standard TASSER run	2.0	1.9	2.3
Nrun = 5 (Nswap = 80, Nstep = 25)	2.0	1.7	2.2
Nrun = 3 (Nswap = 80, Nstep = 25)	2.0	1.7	2.2
Nrun = 1 (Nswap = 80, Nstep = 25)	2.0	1.8	2.1
‡Nrun= 1 (Nswap = 80, Nstep = 25)	2.0	2.1	2.6
MODELLER	2.0	1.9	2.8
60–70%
*Standard TASSER run	1.9	1.8	2.2
Nrun = 5 (Nswap = 80, Nstep = 25)	1.9	1.8	2.1
Nrun = 3 (Nswap = 80, Nstep = 25)	1.9	1.8	2.1
Nrun = 1 (Nswap = 80, Nstep = 25)	1.9	1.8	2.2
‡Nrun= 1 (Nswap = 80, Nstep = 25)	1.9	2.1	2.5
MODELLER	1.9	1.9	2.7
70–80%
*Standard TASSER run	2.2	2.0	2.4
Nrun = 5 (Nswap = 80, Nstep = 25)	2.2	2.0	2.4
Nrun = 3 (Nswap = 80, Nstep = 25)	2.2	2.0	2.4
Nrun = 1 (Nswap = 80, Nstep = 25)	2.2	2.0	2.4
‡Nrun= 1 (Nswap = 80, Nstep = 25)	2.2	2.2	2.6
MODELLER	2.0	2.2	3.2
80–90%
*Standard TASSER run	1.8	1.9	2.1
Nrun = 5 (Nswap = 80, Nstep = 25)	1.8	1.7	1.9
Nrun = 3 (Nswap = 80, Nstep = 25)	1.8	1.7	1.9
Nrun = 1 (Nswap = 80, Nstep = 25)	1.8	1.7	1.9
‡Nrun= 1 (Nswap = 80, Nstep = 25)	1.8	2.0	2.2
MODELLER	1.8	2.0	2.5

^*Standard TASSER run has N_swap = 1000, N_step = 200, and N_run = 5.

^†RMSD of the best initial template and best model among top five clusters, T_ali, template structure with RMSD calculated over aligned region; M_ali model with RMSD calculated over the aligned residues; M_ent, model with RMSD calculated over the entire chain.

^‡The first rank models are used for calculation.

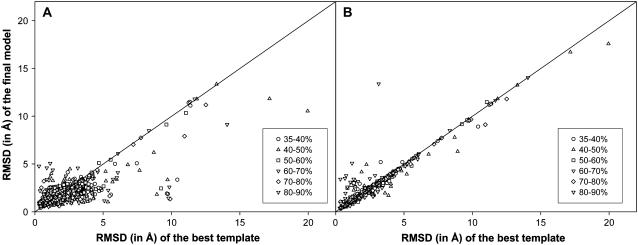
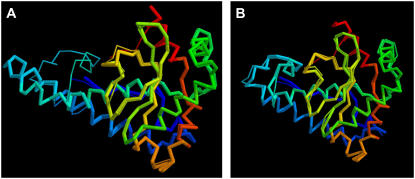
In Fig. 2, A and B, we show a detailed comparison of the RMSD over the set of residues initially aligned to the template to native of the final model compared to the initial alignment (from PROSPECTOR_3) provided by TASSER and MODELLER, respectively. As is evident, the RMSD of the final models relative to the initial template alignments improves more when TASSER is used as compared to MODELLER. In 551 cases, TASSER improves the quality of the aligned regions and moves them closer to native. For example, 1dt0A has an initial RMSD of 4.3 Å (template: 1ap5A) from threading in the aligned region (Fig. 3 A). After refinement by TASSER, the final model has an RMSD of 1.4 Å (2.2 Å) in the aligned region (over the entire chain) (Fig. 3 B), whereas in the case of MODELLER, the final model RMSD has not deviated from the initial template, with a final RMSD of 4.2 Å in the aligned region. However, a single case need not be representative, so we examine the more general case below.

FIGURE 2.

(A) Scatter plot of the RMSD of the final model (by TASSER) to native versus RMSD of the initial alignment (by PROSPECTOR_3) to native. The same aligned region is used in both the RMSD calculations. (B) Similar data as in A, but with the models from MODELLER. (Circle, triangle, square, downward triangle, diamond, and solid triangle correspond to data points for targets in the sequence identity range of 35–40%, 40–50%, 50–60%, 60–70%, 70–80%, and 80–90%, respectively.)

FIGURE 3.

Example of the improvement of the final model with respect to the initial template by TASSER. (A) Superimposition of the native structure 1dt0A with template (from 1ap5A) with an initial RMSD of 4.3 Å over the aligned region. (B) Final model of 1dt0A superimposed on the native structure with an RMSD of 2.2 Å (1.4 Å over aligned region). The thin lines are the native structure, and the thick line is either template or final model. Blue to red runs from the N- to the C-terminus.

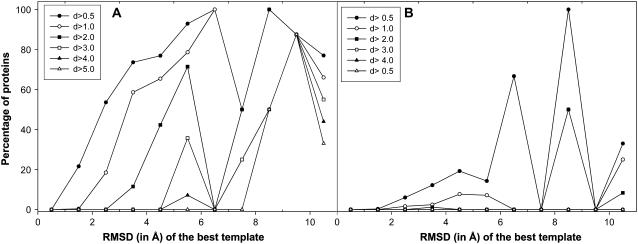
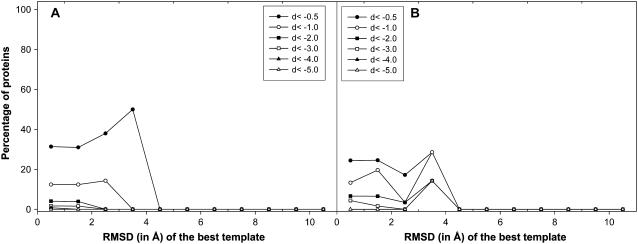
The fraction of the targets having an RMSD improvement, d_better, above a given threshold is plotted as a function of the initial RMSD of the aligned residues in Fig. 4 A. As evident from the figure, TASSER is able to improve the models for various initial RMSD values. For example, ∼54% of very good templates with an initial 2–3-Å RMSD improve by at least 0.5 Å. Even for an initial RMSD of ≈4–5 Å, 42% of the targets improve by at least 2 Å. However, as shown in Fig. 4 B, MODELLER does not show such an improvement in the RMSD. Furthermore, we compared the corresponding overall decrease in RMSD over the aligned region. Fig. 5 A shows the plot of the fraction of targets whose RMSD becomes worse by at least the given threshold, d_worse, against various initial RMSD values. In comparison to MODELLER (Fig. 5 B), the increase in RMSD is on average smaller for the TASSER models than for those generated by MODELLER. This indicates that even when TASSER is unable to refine some models over their initial template, in general, it does not make the final models worse. The investigation of 259 targets in which the RMSD over the aligned region has increased for the final model in comparison to the initial template by TASSER showed that in most of the cases (174), the native structures have extended tails, have a ligand bound, or are involved in a protein-protein interaction. The latter cases could need other partners to generate the native structure.

FIGURE 4.

(A) Fraction of the targets with an RMSD improvement d_better by TASSER greater than some threshold value. Here, d_better = (RMSD of template-RMSD of final model). Each point in A is calculated with a bin width of 1 Å; however, the last point includes all the templates with RMSD > 10 Å. (B) Similar data as in A but with the models from MODELLER.

FIGURE 5.

(A) Fraction of the targets with an increase in RMSD d_worse by TASSER lower than some threshold value. Here, d_worse = (RMSD of template-RMSD of final model). Each point in A is calculated with a bin width of 1 Å; however, the last point includes all the templates with RMSD > 10 Å. (B) Similar data as in A, but the models are from MODELLER.

A detailed comparison of the TM-score of the full-length final models to native compared with the initial threading aligned region for TASSER and MODELLER are shown in Fig. 6, A and B, respectively. The improvement in the TM-score of the final model over the initial aligned template is relatively greater for TASSER in comparison to MODELLER. Thus, as suggested before, the final models generated by TASSER are closer to the native.

FIGURE 6.

(A) Scatter plot of the TM-score to native for the final model (by TASSER) versus TM-score to native over the aligned region (given by PROSPECTOR_3). (B) Similar data as in A, but with the models from MODELLER. (Circle, triangle, square, downward triangle, diamond, and solid triangle correspond to data points for targets in the sequence identity range of 35–40%, 40–50%, 50–60%, 60–70%, 70–80%, and 80–90%, respectively.)

In the analysis here, the final best model selection among top five cluster centroids is based on the lowest RMSD over the aligned region (by PROSPRCTOR_3) between the model and native. However, in the real cases, when the structure of the target is unknown, the cluster centroid with the highest cluster density, usually the rank-one model, is reported as the final model if only one model can be chosen (36). The best of the top five models ranked on the basis of cluster density, the selected model has an average rank of 1.5, as is also evident from the fact that most of the targets (∼79%) have the rank-one model as the selected (best) model. Further, we compared the average RMSD in the aligned region of the rank-one model with the best model (Table 2). On average, in the aligned region the average RMSD of the rank-one model is worse (2.1 Å) than the best (1.9 Å) model. We calculated the RMSD difference (D) in the aligned region between the rank-one model and best model. The average (standard deviation) for D is 0.2 Å (1.9 Å). The high standard deviation suggests that for some of the targets the difference D is large. For 21 targets, D > 3 Å. This provides a plausible explanation for the observed poorer average RMSD with the rank-one model, despite the fact that the average rank is 1.5 for the best model.

Next, we considered the percentage of cases in which the RMSD shows an improvement in the aligned region over the initial template for the selected (best) model and rank-one model. For the selected (best) model, this is observed in 61% of cases, whereas for the rank-one model the improvement of RMSD (over the aligned region) is seen in 57% of the cases. For 10% of the targets, the best model is not the rank-one model; however, even the rank-one model shows an improvement in the RMSD over aligned region with respect to the initial template. This shows that the rank-one model shows an improvement in the RMSD with respect to the initial alignment. For both the rank-one model and best model comparison, in ∼10% of the cases, the RMSD for the final model remains invariant with respect to the initial template. A detailed table summarizing the results is provided at http://cssb.biology.gatech.edu/skolnick/files/tasserlite/tasserlite_data.html. Thus, the rank-one model is a reasonable choice for real world protein structure prediction.

In all the above calculations, the cluster centroid structures were used. Subsequently, we generated full-atom models using PULCHRA and compared it with the cluster centroid model, which shows an average deviation of 0.4 Å. This indicates that the above results could be used even for the full-atom models generated after PULCHRA.

The accurate modeling of loops has been a long-standing problem in comparative modeling (25). Here, we compare the results of the unaligned loop and tail regions generated by both TASSER and MODELLER. An unaligned loop (tail) region is defined as a piece of continuous sequence that has no coordinate assignments in the middle (terminus) of a target protein in the PROSPECTOR_3 threading alignments. There are 712 unaligned regions ranging from 1 to 31 residues in length in the 897 proteins. Most loops (∼97%) are ≤10 residues in length. We calculated two types of modeling errors for each loop (25): RMSD_local (the RMSD between the native and model after direct superposition of the unaligned region) and RMSD_global (the RMSD obtained after the superposition of up to five neighboring residues). The former provides the modeling accuracy of the local conformation of the loop, and the latter value examines both the local conformation and the global orientation of the loop regions. RMSD_local and RMSD_global increase with increasing length of the loop in the final models in both TASSER and MODELLER protocols. However, the average deviation of the RMSD_global from RMSD_local for the TASSER models (0.8 Å) is less in comparison to the average deviation (1.5 Å) than those generated using MODELLER. For example, the average deviation of RMSD_global from RMSD_local for seven residue loops is 0.9 Å for TASSER, whereas for MODELLER it is 1.7 Å. This suggests that the global loop orientations are relatively better predicted by TASSER.

There are 607 unaligned regions either at the N- or C-terminus as given by the alignment of PROSPECTOR_3 with lengths ranging from 1 to 46 residues. Most tails (∼94%) are shorter than or equal to 10 residues in length. On average, the RMSD_global is ∼14% greater than RMSD_local in the final TASSER models, whereas for the same comparison using MODELLER, the increase is ∼23%, which suggests that TASSER better predicts the overall tail orientation in comparison with MODELLER. For example, the TASSER final model for a 20-residue tail in 1qkkA has an RMSD_local of 2.3 Å and an RMSD_global of 3.6 Å, whereas the same 20-residue tail model from MODELLER has an RMSD_local and an RMSD_global of 7.2 Å and 9.5 Å, respectively.

On average, the CPU time for MODELLER is ∼1.8 min per sequence. Although TASSER requires more CPU time (∼17 min), the final models are more accurate in comparison to the models generated by MODELLER. Hence, such accurate models could be used for more precise protein function prediction such as identification of ligand binding substrate specificity.

With the optimized condition of TASSER, we have a fast and efficient modeling tool referred to as TASSER-Lite. This tool is publicly available on the world wide web (http://cssb.biology.gatech.edu/skolnick/webservice/tasserlite/index.html) for use by the scientific community.

CONCLUSIONS

We performed a systematic assessment of TASSER for modeling homologous sequences and showed that in many cases, TASSER could refine the initial template to generate models that are closer to the native structure. The CPU time for a standard TASSER run is reduced from ∼29 h to ∼17 min for one sequence. Furthermore, on comparing TASSER-Lite with the widely used modeling tool (MODELLER), we showed that TASSER performs, on average, better than MODELLER in improving both the aligned and unaligned regions of the targets. Hence, TASSER-Lite forms an effective and fast modeling tool for the homologous sequences.