Spatially Resolved Fluorescence Correlation Spectroscopy Using a Spinning Disk Confocal Microscope

Abstract

We develop an extension of fluorescence correlation spectroscopy (FCS) using a spinning disk confocal microscope. This approach can spatially map diffusion coefficients or flow velocities at up to ∼10⁵ independent locations simultaneously. Commercially available cameras with frame rates of 1000 Hz allow FCS measurements of systems with diffusion coefficients D∼10⁻⁷ cm²/s or smaller. This speed is adequate to measure small microspheres (200-nm diameter) diffusing in water, or hindered diffusion of macromolecules in complex media (e.g., tumors, cell nuclei, or the extracellular matrix). There have been a number of recent extensions to FCS based on laser scanning microscopy. Spinning disk confocal microscopy, however, has the potential for significantly higher speed at high spatial resolution. We show how to account for a pixel size effect encountered with spinning disk confocal FCS that is not present in standard or scanning FCS, and we introduce a new method to correct for photobleaching. Finally, we apply spinning disk confocal FCS to microspheres diffusing in Type I collagen, which show complex spatially varying diffusion caused by hydrodynamic and steric interactions with the collagen matrix.

INTRODUCTION

Fluorescence microscopy is a powerful technique that has given us a detailed view of the generation, maintenance, and function of cellular organization. As our understanding of subcellular and intercellular processes increases, there is a need for more quantitative approaches to measuring intra- and intercellular dynamics and transport, with high resolution in both space and time. A number of techniques based on fluorescence correlation spectroscopy (FCS) and scanning microscopy have been successful in addressing this need. Here we report an extension of FCS to spinning disk confocal microscopy, which can further push the limits of temporal and spatial resolution to 1000 frames per second at up to 10⁵ locations simultaneously.

FCS was developed in the 1970s and is widely used to study intracellular dynamics (1). Using confocal or two-photon techniques, light intensity fluctuations caused by fluorescent molecules or microparticles moving through a femtoliter measurement volume are recorded and analyzed. The temporal autocorrelation of these fluctuations can be used to determine the diffusion coefficients, concentrations, mobile fractions, and flow velocities of the fluorescent species.

FCS has been extended in many ways, including several very recent applications of laser scanning microscopy (LSM). In LSM, an image is constructed by collecting light from confocal or two-photon optics point-by-point (creating “pixels”) serially. We refer to the FCS techniques based on LSM as “scanning FCS.” Among the variations of scanning FCS are: image correlation spectroscopy (ICS) (2,3), image cross-correlation spectroscopy (ICCS) (3), scanning fluorescence correlation spectroscopy (SFCS) (4), raster image correlation spectroscopy (RICS) (5), spatiotemporal image correlation spectroscopy (STICS) (6), and position-sensitive scanning fluorescence correlation spectroscopy (PSFCS) (7).

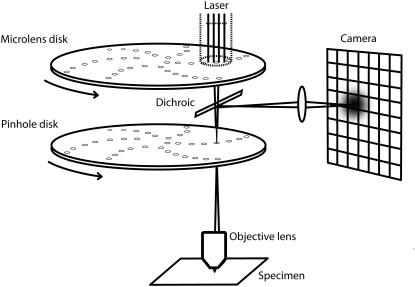
Spinning disk confocal microscopy (SDCM) is a widely-used extension of confocal LSM that allows for higher imaging speeds (8,9). (The speed limitation in the most common LSM implementation results from the time needed to repeatedly accelerate and decelerate the scanning mirror, which is eliminated in SDCM.) A rotating disk of ∼10,000 pinholes, together with a corotating disk of microlenses, produces an array of diffraction-limited spots that rapidly scans the image field (Fig. 1). The fluorescent light is refocused on the pinholes and then projected on a CCD camera.

FIGURE 1.

Spinning disk confocal microscopy. Aligned arrays of moving pinholes and microlenses scan a field of view in one camera exposure, giving lateral and axial resolutions typical of standard confocal microscopy (the densities of the arrays are much higher than shown). The image of a point source can then be approximated by a product of Gaussians (Eq. 3) and standard FCS analysis can be applied to each pixel time series.

ICS, ICCS, and STICS are approaches that can transfer directly to SDCM, since they all start with an image time series. ICS involves the calculation of either the spatial autocorrelation (e.g., to establish the distribution of molecules in a membrane) or the spatial average of the temporal autocorrelation (to improve statistics when the dynamics are slow and the region homogeneous). STICS extends ICS by analyzing the generalized spatiotemporal autocorrelation for an image or subimage. Both ICS and STICS have been used to spatially map dynamics in cells (but only on a few subimages) (10). ICCS extends ICS to situations with different fluorescent species. RICS, SFCS, and PSFCS, which use the time delay between pixels in scanning microscopy to extract more information, are not applicable to spinning disk microscopy.

In this article we describe the temporal version of ICS as applied to SDCM, but without spatially averaging the results. We address the effect of the pixel size on the FCS measurement and calculate a numerical correction factor, which we validate with a stochastic simulation. We also introduce an empirical method of minimizing the effect of photobleaching, which can be severe for slowly diffusing fluorescent species. Finally, we use spinning disk FCS to map hindered diffusion in hydrogels, a problem relevant to drug and gene delivery, such as the dispersal of high molecular weight agents in the tumor interstitium (11) or through the extracellular matrix (12). Hindered diffusion in hydrogels (e.g., collagen) is also a consideration in the design of tissue substitutes and controlled release devices (13). We obtain a spatial map at pixel resolution (128 × 128) of diffusion coefficients from diffusing fluorescent microspheres (210-nm diameter) in Type I collagen and find diffusion coefficient variation that is complex and directly related to the polymer network structure. In addition, we observe deviations from normal diffusion that are well described by spatially varying anomalous diffusion.

Other approaches have been applied to hindered diffusion in inhomogeneous media. NMR has been used to map effective diffusion coefficients and diffusion anisotropies (14). Fluorescence recovery after photobleaching has been used to measure diffusion coefficients of tracer molecules in various media, for example, Type I collagen (15), agarose gels (16), tumors (11), and the extracellular space in the central nervous system (17). Fluorescence recovery after photobleaching was also used to measure spatial inhomogeneities in diffusion (18). An FCS-based nonscanning approach, sampling-volume controlled FCS (19), was applied to diffusing fluorophores in an aqueous hyaluronic acid solution. None of these techniques provide the spatial resolution of spinning disk FCS. Theoretical approaches to hindered diffusion also typically spatially average, as for example the effective medium model (20,21). More involved calculations (22) and simulations (23), which are capable of incorporating microstructure, so far also have presented results as spatial averages. However, in complex biopolymer networks, diffusion can vary locally and dynamically, for example in “caging” effects (24). The fast, spatially resolved technique described here will provide a powerful new tool for studying hindered diffusion and other transport phenomena in complex media.

THEORY

FCS

Fluorescence correlation spectroscopy is based on the temporal autocorrelation function,

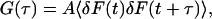(1)

where the angled brackets indicate an average over the time 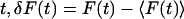, τ is the delay time, and A is a normalization constant. There are two common normalizations: A = 1/〈δF² 〉, so that G(τ) is in the range [1, −1]; and A = 1/〈F〉², in which case G(τ = 0) is the inverse of the average concentration.

The fluorescence fluctuation δF for a given detector position depends on the details of the optical system, which are incorporated in the point spread function PSF(r − r_d),

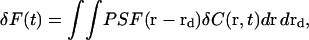(2)

where r is position in the object plane, r_d is a point on the detector mapped to the object plane, and 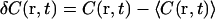is the zero-mean fluorophore concentration. (The analysis could be performed equivalently in any plane conjugate with the sample, with appropriate factors to account for magnification.) PSF(r − r_d) is the image of a point particle located at r and depends on the spatial variation of both the illumination and the light collection efficiency. The standard FCS analysis assumes that PSF(r − r_d) can be approximated as a separable product of Gaussians (25), which is generally true for confocal optics with a small pinhole:

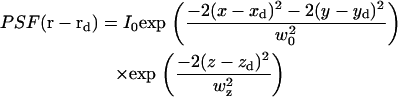(3)

The factor of 2 in the numerator is included for consistency with the FCS literature, where w₀ refers to the e⁻¹ radius of the illumination and the collection efficiency functions, the product of which give PSF(r − r_d). The image of a finite size microsphere can also be approximated by Eq. 3 (if the sphere diameter is not much larger than w₀), but w₀ will be larger than the diffraction-limited w₀.

In Eq. 2, the r integral is over all space, and for spinning disk FCS, the r_d integral is over one pixel. Substituting Eq. 3 and integrating over r_d gives the apparent intensity profile E(r). The x component, E(x), is (similarly for the y dimension),

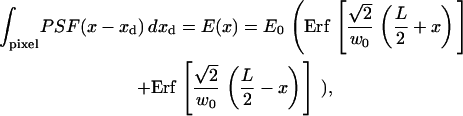(4)

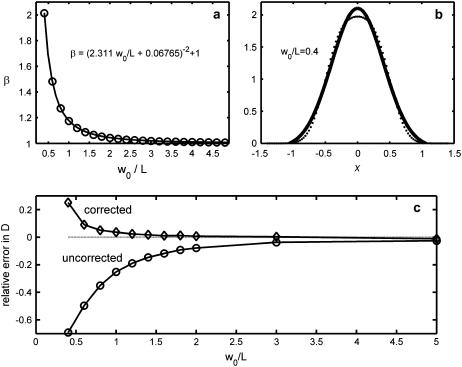
where L is the length of the pixel. When L is not too large compared to w₀, Eq. 4 can be approximated by a Gaussian, with an e⁻² radius given by w_eff = β w₀. The factor β depends only on the ratio w₀/L (see Materials and Methods and Fig. 2). In the limit of infinitesimal pixels (L → 0), β → 1 and the result of the r_d integral is E(r) = PSF(r) (i.e., Eq. 3 with r_d = 0).

FIGURE 2.

Adjusting the FCS e⁻² radius to account for the effect of finite pixels. (a) The correction factor β, which depends only on the ratio of the e⁻² radius w₀ to the pixel length L, relates w₀ to w_eff, the effective e⁻² length that accounts for finite pixel size. The solid line is a fit to the data given by the equation at the top of the figure. (b) When w₀/L is <0.5, the Gaussian approximation to Eq. 4 starts to break down, as seen by the best-fit Gaussian (line) to Eq. 4 (·) for w₀/L = 0.4. (c) Results of a stochastic simulation of spinning disk FCS measurements, showing the relative error with and without the finite pixel effect correction. The top curve is the bottom curve multiplied by β².

After integrating PSF(r − r_d) to yield E(r), Eq. 1 can be written as

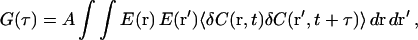(5)

where r and r′ are position at t and t+τ, respectively, and the brackets indicate a time average. With the Gaussian approximation to E(r), and the concentration autocorrelation function for normal diffusion,

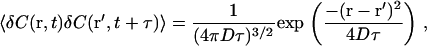Eq. 5 becomes (1)

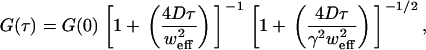(6)

where γ = w_z/w_eff is the ratio of axial to (effective) lateral e⁻² radii. (Correlations from dynamics of the fluorophore triplet state are usually considered in conventional FCS, but the timescale is much faster than our fastest frame rate and so they are not considered here.) The autocorrelation with the exact form of E(r) (Eq. 4) is too complicated (involving still more error functions) to use with fitting procedures.

Hindered and anomalous diffusion

For normal diffusion in three dimensions, the mean-square displacement of an ensemble of diffusers is proportional to time,

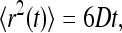(7)

where D is the diffusion coefficient. For a simple homogeneous solvent, D is given by the Stokes-Einstein equation,

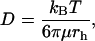(8)

where r_h is the solute hydrodynamic radius, μ is the solvent viscosity, and k_BT is the Boltzmann factor. Diffusion in a dilute polymer network will have a D lower than the value computed from Eq. 8 (using the solvent viscosity) because of hydrodynamic and steric interactions of the solute with the network. These interactions are said to hinder diffusion.

Hydrodynamic interactions with the polymer network increase the drag on the solute and slow diffusion, and can be calculated for a given configuration of fibers (23). These interactions are long range, but are only significant within a shielding length. Steric interactions occur only with direct contact between the solute and the network, and their effect depends on the geometry or structural properties of the network (22).

These interactions can also change the character of diffusion, such that Eq. 7 does not hold for any range of timescales. In hindered diffusion, the mean-square displacement is often proportional to time to an exponent α,

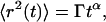(9)

where Γ is the anomalous transport coefficient (having α-dependent dimensions). When α ≠ 1, the diffusion is called “anomalous”, and when α < 1 (typical for hindered diffusion), it is called “subdiffusive”. The autocorrelation function for anomalous diffusion is (26)

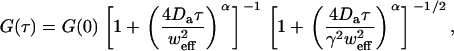(10)

where 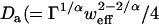) is an anomalous diffusion coefficient. Though fully characterizing anomalous diffusion requires two coefficients, a map of D_a alone can still characterize the time to diffuse the fixed distance w: τ ∼ w²/4D_a. Note that this generalization has normal diffusion as a special case (α = 1, D_a = D), but still does not describe all possible forms of diffusion in complex media.

MATERIALS AND METHODS

Spinning-disk confocal microscopy

Images were acquired with an inverted Nikon Eclipse TE2000-U microscope and Nikon 60× oil-immersion (1.4 NA) objective (Nikon, Tokyo, Japan), with 1.5× intermediate magnification (giving 90× total magnification). The spinning disk confocal unit is a Yokogawa CSU21 scan head (Yokogawa, Tokyo, Japan), part of a spinning-disk confocal package from PerkinElmer (Wellesley, MA). The package also includes a Hamamatsu cooled-CCD camera (ORCA-ER, Shimokanzo, Japan), a NEOS acoustic optical tunable filter (AOTF) (Melbourne, FL), a proprietary sync box, and software. Fluorescence excitation is provided by a Coherent Innova 300 gas laser (Santa Clara, CA), which replaced the laser provided by PerkinElmer. As described later in the section on imaging artifacts, the exposure of the CCD must be precisely synchronized to the rotation of the spinning disk. The PerkinElmer system achieves this with the AOTF, cutting the laser power to the sample during the camera's readout. The spinning disk spins at 1666.67 rpm, as controlled by a TTL pulse (at twice that frequency) generated by the PerkinElmer sync box and connected to the scan head's BNC sync port. The spinning disk scans the field of view in 1/12 of a rotation, so this rotation rate allows exposure times in steps of 3 ms. Only the microspheres in pure glycerin were imaged using the full PerkinElmer system.

The collagen and water-glycerin samples were imaged with a 512 × 512 Andor electron multiplied CCD (EMCCD) (DV-887, Andor Technology, Belfast, Northern Ireland), acquired using Andor's iXon software. With these measurements, the spinning disk was controlled to run at its maximum speed of 5000 rpm by a separate PC running Labview and a card with a 10 MHz timer (National Instruments, Austin, TX). The AOTF was controlled by the camera's TTL “exposure” signal, which was on only while the camera was exposing (and not reading out). Cutting the laser power when reading out is especially important for frame transfer cameras, like the Andor EMCCD, as explained in the imaging artifacts section.

The pure water samples were imaged with a Cooke pco.1200 hs (high speed) CMOS camera and Cooke's Camware 2.12 (Cooke, Romulus, MI). Here, the scan head was run at 5000 rpm and the AOTF allowed the laser through continuously, since the camera does not have appropriate outputs to synchronize illumination. Instead, the camera has a precise electronic shutter, so the exposure time was adjusted to match a multiple of 1/12 of the disk rotation rate.

Microspheres and PEGylation

Untreated and carboxylated microspheres adhere to collagen, so we employed spheres coated with polyethylene glycol (PEG), a molecule known for its nonreactivity with proteins. Carboxylated fluorescent microspheres (210-nm diameter, green-yellow FluoSpheres, Invitrogen, Carlsbad, CA) were coated with amine-terminated PEG (5 kDa, Nektar, Huntsville, AL) using a protein coupling kit (PolyLink Protein Coupling Kit for COOH Microparticles) and protocol (Technical Note No. 644) from Polysciences (Warrington, PA). In short, carboxylated beads were pelleted via centrifugation and resuspended in a coupling buffer (50 mM MES, pH 5.2, 0.05% Proclin-3). This step was repeated, and then EDAC (Carbodiimide) added to form a 200 mg/mL solution. Next PEG was added and incubated for 30 min to 1 h while gently mixing in coupling buffer. The beads were again centrifuged and resuspended in a washing/storage buffer (10 mM Tris, pH 8.0, 0.05% Bovine Serum Albumin, 0.05% Proclin-300). For beads with diameters below 1 μm, the protocol recommended using a Microkos microfilter (Spectrum, Rancho Dominguez, CA) instead of centrifuging. However, we found that many beads were lost in the filter, so we centrifuged instead. The concentration of the sphere mixture, estimated from images of an undiluted drop, was ∼5 × 10¹⁰ spheres/ml, or 10% of the stock sphere solution. Clumps were dispersed using continuous ultrasound for ∼1 min (Model 550 Sonic Dismembrator with 1/8" tip, Fisher Scientific, Pittsburgh, PA), though a few (<1% of total) larger clumps remained.

Sample preparation

All samples consist of 50 μl of solution mounted between a microslide and a No. 1.5 thickness glass coverslip, spaced with one layer of double-stick tape, making a ∼100-μm thick layer with low background fluorescence. The sphere solutions were sonicated before mounting. Immediately after mounting, the edges of the coverslip were sealed to the slide with nail polish to minimize evaporation.

Glycerin samples were made by adding a drop of aqueous microsphere solution (57-nm diameter, green fluorescent, G50, Duke Scientific, Palo Alto, CA) to ∼50 μL of glycerin on coverslips, which were left open to evaporate the water. The samples were placed periodically on a slightly warmed hot plate to speed evaporation. When the weight of the sample returned to within 1% of its glycerin-only weight (typically overnight), the evaporation was considered complete. The concentration of spheres was ∼2 × 10¹¹/ml.

Collagen samples were made from Type I Collagen stock derived from rat tail (BD Sciences, Bedford, MA), and diluted with water to give a final concentration of 2 mg/ml. Also added were 27 μl of a 7.5% sodium bicarbonate solution per ml of original collagen stock, and 1/10 final volume of 10× OptiMEM (Invitrogen). Last, the PEGylated sphere solution was added to give a 6% final concentration by volume. (The sphere solution was sonicated before adding to the mixture, since sonication damages collagen.) The collagen solution was allowed to gel at room temperature after mounting.

Water-glycerin samples were made with the same 210-nm diameter (un-PEGylated) spheres, added to a 40% water by weight water-glycerin mixture, which gives a diffusion coefficient similar to the collagen samples. The sphere solution was added to be 6% of the final volume. Pure water samples were made similarly.

Measurements

Samples were imaged ∼5 μm above the coverslip. The tensioner on the microscope focus was adjusted to minimize focus drift. Bright-field images of the collagen looked identical before and after runs, suggesting there was minimal sample drift during the measurement. Samples were measured at ambient temperature, which was monitored near the sample with a thermocouple. Except for movies taken with the PerkinElmer software (pure glycerin), all movies were taken on the same computer used for the autocorrelation analysis.

The water-glycerin and collagen samples were both imaged at 90× with the Andor EMCCD. 128 × 128 pixel (22.76 × 22.76 μm²) regions of interest were selected and exposed for 12 ms at a frame interval of 12.2 ms, for 8192 frames, and saved in a file (27), forming a “time chunk.” For each sample, 16 time chunks were recorded.

The same procedure was used for the pure water samples, except the images were recorded with a Cooke camera and a 3 ms frame interval. Also, only three time chunks were recorded, and the images were stored in .tif format. The pure glycerin samples were imaged at a frame interval of 50 ms using the PerkinElmer system with Hamamatsu camera.

Autocorrelation analysis

All computer analysis was performed in MatLab R14 (The MathWorks, Natick, MA) on a personal computer (3.0 GHz, 2GB RAM), using custom-written C code compiled to run in the MatLab environment (using mex). The mex C codes are ∼20 times faster than comparable MatLab scripts, and can use MatLab's built-in functions.

The analysis began with loading a time chunk, consisting of 8192 128 × 128 images, into memory. The time-average for each pixel was subtracted, and when the photobleaching correction was used, each time point was divided by the spatial mean of the image for that frame. The autocorrelation function was then calculated for each pixel and normalized by the variance of the (corrected) time series, giving a curve in the range [−1, 1]. The autocorrelation curves were then binned logarithmically. This procedure was repeated for each time chunk. The binned autocorrelation curves for each pixel were averaged, and then fit using the procedure described in the next section.

The ratio of the mean-squared intensity to the intensity variance, 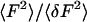, was averaged for each pixel over time chunks; this ratio divided by the extrapolated zero-time lag autocorrelation, G(0), gives the average concentration per observation volume of 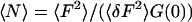. Since our experiments are performed at concentrations much less than one fluorescent sphere per observation volume, it is essential to remove the background intensity from the mean before constructing the ratio. We estimated the background for each pixel and time chunk as the peak of the histogram of intensity values for each time series.

Autocorrelation curve fitting procedure

The autocorrelations were performed using MatLab's fft function (which uses fftw) and the autocorrelation fits using MatLab's nlinfit function (which uses the Levenberg-Marquardt nonlinear least-squares fitting algorithm), to the model,

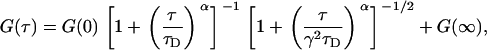(11)

where G(0), G(∞), τ_D and (sometimes) α were free parameters. When diffusion was treated as normal, α was fixed at one. The diffusion coefficient was found from the diffusion time, 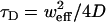. The ratio of the axial and (effective) lateral e⁻² radii of the Gaussian profiles, 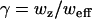, was found from empirical estimates of w_z and w_eff = βw₀. First, two-dimensional Gaussian fits (using fminsearch in MatLab) were performed on lateral slices of a three-dimensional image of a 210-nm-diameter sphere mounted in a viscous mounting medium (PS-Speck Microsphere Point Source Kit, P7220, Invitrogen). The peak value (from the fits) for each z slice was then fit to a one-dimensional Gaussian, giving w_z. The e⁻² radius weighted by the peak intensity was next averaged over slices, giving w₀. Finally, multiplying w₀ by the adjustment factor β (see Theory and Fig. 2 a) gave w_eff.

Photobleaching correction and pixel size adjustment

The analysis involves two steps that are unique to spinning disk FCS. First, to minimize the effect of photobleaching, which creates spurious time correlations, particularly for slow diffusion, each pixel intensity time point F_i(t) is divided by the spatial average of the image intensity, F_avg(t). The time dependence of F_avg(t) and F_i(t) result from the product of the average intensity per diffuser η(t)—which is generally a monotonically decreasing concave-up curve resulting from photobleaching (what we are trying to cancel)—and the fluctuating number of diffusers in the image N_avg(t) and pixel N_i(t), respectively:

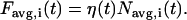To the extent that N_i(t) and N_avg(t) are uncorrelated, the ratio F_i(t)/ F_avg(t) is proportional to N_i(t). However, some number of diffusers leave the image within a diffusion time of leaving a pixel (especially for pixels near the image edge), meaning some diffusive fluctuations of N_i(t) will be spuriously cancelled in F_i(t)/ F_avg(t). For diffusers that leave the image in the lateral direction, this effect will be concentrated at the image edges, and uniform for the z direction. This effect fortunately becomes insignificant when the number of pixels N_p is large. Since N_avg(t) and N_i(t) both obey Poisson statistics and because not all diffusers leave the image within one diffusion time after leaving a given pixel, the relative importance of this effect is always 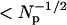. The image size cannot be too large, however, because spatial inhomogeneities in the illumination can cause η(t) to vary in space, causing other spurious correlations. We find that 128 × 128 images work well.

The second step in the analysis is to replace the lateral e⁻² radius w₀, with an effective length scale w_eff = βw₀ that takes into account the finite size of the pixels. Equation 4 (see Theory) is evaluated at 100 points over [−w₀ –L, w₀ + L] and fit to a Gaussian using nlinfit in MatLab, from which β is calculated (see Fig. 2 a). The accuracy of this approximation is quantified by a stochastic computer simulation.

Note that the ratio between the radius w_0, measured for a finite sphere size, and the theoretical radius for a point source can be given by an analogous β-value, where the pixel length L is replaced by the sphere diameter.

Computer simulations

A simulation of two-dimensional homogeneous diffusion and spinning disk FCS measurements was custom-written in C and compiled in MatLab using mex. The functions ran1, gassdev, and poidev were used to generate random numbers (28). A time series of all the fluorophore positions (as single precision floating-point numbers) was generated by adding random numbers picked from a zero mean Gaussian distribution with standard deviation 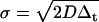, where 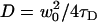is the diffusion coefficient and Δ_t is the time step. For each fluorophore, a random number of simulated photoelectrons (picked from a Poisson distribution, with mean η = 5 photoelectrons per fluorophore) were created with positions determined from a Gaussian probability distribution (with σ = w₀/2) centered at each fluorophore location. The photoelectrons were then binned on to a 128 × 128 matrix, which represented the CCD. Autocorrelations were performed on each pixel, and the binned autocorrelation curves were averaged and then fit to a two-dimensional FCS model: 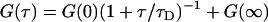. The extracted diffusion coefficient was compared to D, giving a relative error. This procedure was repeated for a range of w₀, fixing pixel size L = 1 and varying D to keep τ_D constant.

RESULTS AND DISCUSSION

Pixel correction accuracy from simulation

Fig. 2 shows the accuracy of simulated measurements of diffusion coefficient (Fig. 2 c), with and without the pixel size correction (Fig. 2 a). The first six data points in Fig. 2 c are the average of nine runs, and the last the average of 18. The error bars are smaller than the plot symbols. For w₀/L = 5, more runs were necessary because the large observation volume results in fewer independent measurements (29). The bottom curve in Fig. 2 c shows the error without pixel size correction. When w₀/L is large, no correction is necessary, but when the pixel size approaches the PSF size, the diffusion coefficient becomes increasingly underpredicted, since large pixels increase τ_D and thus decrease the apparent D. Multiplying the bottom curve by the correction β² gives the top curve. The corrected curve has a substantially improved accuracy, particularly at ∼w₀/L = 1, where the error is only a few percent (compared to ∼20% for the uncorrected estimate). The error in the corrected curve increases systematically at small w₀/L because the Gaussian approximation to Eq. 4 breaks down (Fig. 2 b).

Homogeneous samples

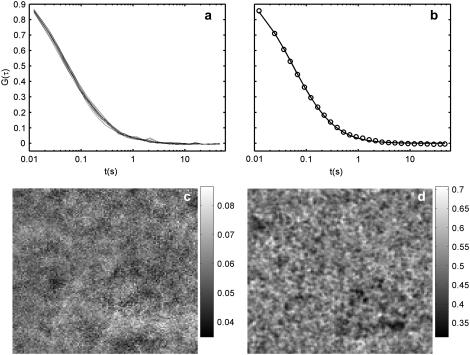
Fig. 3 shows the results of spinning disk FCS applied to a (homogeneous) water-glycerin sample. The top panels show autocorrelations for 16 individual pixels (Fig. 3 a) and their average together with a best fit to Eq. 11 with α fixed at 1 (Fig. 3 b). The circles in Fig. 3 b show the binning used, for both the water-glycerin and the collagen measurements. The bottom panels show the maps of 〈N〉 (Fig. 3 c) and D (Fig. 3 d). The means of 〈N〉 (0.04 particles per observation volume) and D (0.5 μm²/s) are consistent with independent estimations of both values. The two maps reflect the variation inherent in the measurements, and serves as a comparison for the collagen sample in Fig. 5.

FIGURE 3.

Spinning disk FCS applied to microspheres diffusing in (homogeneous) water-glycerin. The autocorrelation curves for 16 different pixels are plotted in panel a, and panel b shows their average, along with best fit curve to Eq. 11 with α, is fixed at 1. (c) 128 × 128 maps of the mean concentration 〈N〉 and (d) diffusion coefficient (in μm²/s). The pixel size is 178 nm. The variation is due primarily to statistical noise, but also deviant large particles (or clumps).

FIGURE 5.

Spinning disk FCS applied to PEGylated spheres diffusing in collagen. A bright-field image (a) and the average of all fluorescent images (16 chunks × 8192 frames per chunk) (b) show the filamentous structure of the collagen fibrils, which are reflected in the maps of 〈N〉 (c) and diffusion coefficient (in μm²/s) (d). Due to caged particles, bright spots appear in panels b and c. Some spots in panel b do not appear in panel c because of the background subtraction used in the FCS analysis. The imaging parameters and analysis are the same as for the water-glycerin sample (Fig. 3).

The variation is due to a combination of statistical noise, imaging and analysis artifacts, and variation in particle size (due to clumping and variation in the stock solution). The effect of the last is seen in the lower right quadrant of the diffusion map Fig. 3 d, where there is a ∼30 pixel region of low diffusion coefficient. In the movies of several time chunks, a larger and brighter particle can be seen spending a lot of time in that region. The feature disappears when the analysis is redone without those time chunks (though the overall variation is larger, since there is less data).

We tried to account for these larger particles by fitting the data to a two-population model,

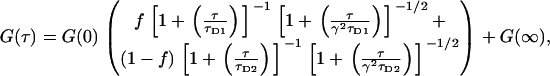where f is the fraction of particles having diffusion time τ_D1, and (1 − f) is the fraction of larger particles having diffusion time τ_D2. However, this procedure produced unphysical results, with extracted diffusion times that were negative or complex, or deviated by orders of magnitude from the mean. Including constraints in the fitting algorithm would probably improve the procedure, but this was not attempted. Lastly, we note that most of the variation in Fig. 3 d is due to statistical noise, and has a spatial autocorrelation that is very close to that of individual images.

To test the accuracy of our spinning disk FCS measurements, we also measured two samples with known diffusion coefficients. (The water-glycerin samples in principle also have a known diffusion coefficient, but the sample preparation produced uncertainty in D that is likely greater than uncertainty in the analysis.) With the same spheres in a pure water sample, we obtained an average diffusion coefficient D = 1.9 μm²/s, ∼18% below the expected value. With 57-nm-diameter spheres in pure glycerin, we obtained an average diffusion coefficient D = 8.9 × 10⁻³ μm²/s, ∼5% above the expected value. (The standard errors of these measurements are ∼1%.) The likely sources of the discrepancies are discussed below.

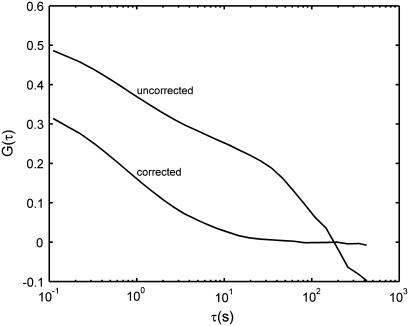
Photobleaching correction

Photobleaching causes an overall decrease in intensity, creating long-time correlations that can dominate the autocorrelation curve when the diffusion is slow. Fig. 4 shows autocorrelation curves from spheres (57-nm diameter) diffusing in glycerin, before and after the photobleaching correction. The uncorrected curve is completely unusable. The corrected curve yields a diffusion coefficient that (as mentioned above) is only 5% above the expected value. When the diffusion times are much faster, photobleaching modifies the data only slightly. For the water samples, which have the shortest diffusion times, we found that the photobleaching correction decreased the measured diffusion times by ∼7%. (This effect depends nontrivially on the rate of photobleaching relative to the diffusion time.) Note the 7% figure is different (and opposite in sign) from the spurious increase of diffusion time caused by the pixel size correction (see Theory).

FIGURE 4.

Effect of photobleaching and the photobleaching correction on (averaged) autocorrelation curves for pure glycerin. The frame interval is 110 ms. Photobleaching causes an intensity decay in time that contaminates the correlation, particularly for slow diffusion, but can be adequately corrected for.

The photobleaching correction also adds statistical noise. This noise could be eliminated if a smooth curve-fit to the decaying mean intensities were used in place of the means. Such a technique (with an exponentially decaying curve) was applied to scanning FCS in two dimensions (30). The functional form of the curve for diffusion in fully three-dimensional samples, however, may be different and not easy to determine. If the photobleaching deviates from the model used to derive the functional form, this technique would add systematic error. We found the noise from the correction used in this article to be negligible for our measurements. An added advantage of this approach is that it corrects for fluctuations in illumination intensity.

Hindered diffusion in collagen

Fig. 5 shows spinning disk FCS measurements in collagen, with the same imaging parameters as for the water-glycerin sample (Fig. 3). The collagen fibrils are clearly visible in a bright-field image of the region investigated (Fig. 5 a). Corresponding locations in the average of all fluorescent images (Fig. 5 b) and the map of 〈N〉 (Fig. 5 c) show dark filamentous structures where particles are excluded by the fibrils. In the average fluorescence image there are also bright spots, where spheres are trapped in the network. Some of these bright spots can be seen in the map of 〈N〉 also. However, other bright spots in the average fluorescent image show up in the map of 〈N〉 as dark or near the average. The discrepancy is likely due to the background subtraction algorithm, which can produce unphysical (and unpredictable) results when the number density is high (see Background Removal), as it is for regions with caged particles.

The most interesting panel of Fig. 5 is the map of the diffusion coefficient D, which also shows filamentous structures highly correlated with the bright-field image, but with less direct correspondence than Fig. 5, b and c. Not all features in the bright-field image show up in the FCS maps, and vice versa. As with the map of 〈N〉, the diffusion coefficient map has deviant regions corresponding to caged particles. Although caging can produce a lower apparent (normal) diffusion coefficient if particles can eventually leave the cage, the deviation at these locations results instead from the autocorrelation curves not conforming to Eq. 10, which produces instabilities in the fitting.

The mean of the 〈N〉 map is 0.08 particles per observation volume, which is comparable to an estimation based on counting particles in the field of view. The mean of the diffusion coefficient map is D_avg = 0.8 μm²/s, approximately three-times lower than the diffusion coefficient of these spheres in water, and comparable to other measurements of diffusion in collagen (15).

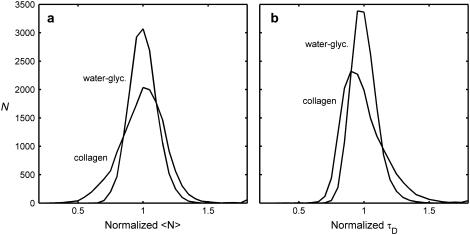
Fig. 6 shows the normalized distributions of 〈N〉 (Fig. 6 a) and τ_D (which is inversely proportional to D) (Fig. 6 b), for both collagen and water-glycerin. For both 〈N〉 and τ_D, the distribution is wider for the collagen sample. Furthermore, the distribution of τ_D is stretched more toward longer diffusion times, as expected from hindered diffusion, and the distribution of 〈N〉 is stretched more toward lower number densities, as expected from steric interactions.

FIGURE 6.

Comparison of normalized histograms for water-glycerin and collagen. The distributions of average number density (a), and diffusion time (b) are both broader for collagen than for water-glycerin, as the collagen fibrils make the concentration and diffusion more inhomogeneous.

Diffusion in complex media is often anomalous, at least over some range of length and timescales (see Theory, above, and Anomalous Diffusion, below). Fig. 7 shows the result of allowing for anomalous diffusion in the analysis of our collagen data. The map of the anomalous diffusion coefficient D_a (Fig. 7 a), analogous to Fig. 5 d except with α (in Eq. 10) allowed to vary, still shows filamentous structure, but with noticeable differences. In particular, there are dark regions on either side of the fibrils. These features also show up in the map of the best-fit values of α (Fig. 7 b), but are inverted (bright). Indeed, the maps of 1/D_a and α look nearly identical. The decrease in D_a adjacent to filaments may be the result of filaments blocking escape routes, thereby increasing the residence time, or of hydrodynamic interactions with the fibrils (see Anomalous Diffusion).

FIGURE 7.

Anomalous diffusion in collagen. (a) The map of diffusion coefficient D_a, as in Fig. 5 d, except with the anomalous parameter allowed to vary, giving (b) the corresponding map of best fit α. The units in panel a are μm²/s. (c) The summed square difference of the autocorrelation and the fit for α fixed at 1, and (d) with α allowed to vary. The scales in panels c and d have been multiplied by 10³. The mean of D_a is ∼80% bigger than the mean of D (in Fig. 5 d). The mean and standard deviation of panel c are both ∼5 times larger than those of panel d. Much—but not all—of the filamentous structure in the residuals is removed when α is allowed to vary.

The maps of the summed squared error (SSE) are shown for when α = 1 (Fig. 7 c) and for when α is allowed to vary (Fig. 7 d). In allowing α to vary, the mean SSE error decreased by a factor of 6, an unsurprising result given that an additional fitting parameter was introduced. More interestingly, much of the filamentous structure in Fig. 7 c is not present in Fig. 7 d, indicating that the diffusion in collagen is better described as anomalous.

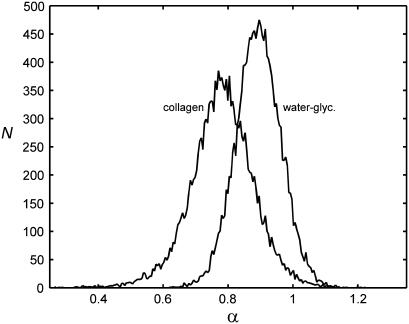
For comparison, the water-glycerin data were also analyzed for the possibility of anomalous diffusion. Fig. 8 shows the resulting distribution of α together with the same distribution for collagen. The collagen distribution, as expected, is both wider and more subdiffusive. However, the peak of the water-glycerin distribution is not centered at α = 1, the value for normal diffusion. This discrepancy may be due to some combination of imaging artifacts, as discussed below. Also, the SSE for the water-glycerin data decreased when α was allowed to vary, as it did for collagen, but only by a factor of 2.5.

FIGURE 8.

Histograms of the anomalous diffusion parameter. Diffusion in collagen is more subdiffusive, with more variation, than the homogeneous sample. The water-glycerin histogram has a finite width and a peak <1, probably due to noise and imaging artifacts.

Background removal

To obtain an accurate estimate of the number density, the background fluorescence—due to out-of-focus spheres, autofluorescence, and ambient light—must first be subtracted from the mean. Since our experiments are performed at concentrations much less than one fluorescent sphere per observation volume, the background is close to the mean and its subtraction is essential for an accurate measure of 〈N〉 (29). Increasing the fluorescent sphere concentration would increase the signal relative to autofluorescence and the ambient light background, but not out-of-focus spheres. We estimate the background for each pixel and time chunk as the peak intensity of an intensity histogram. This estimate only works for low concentration, however. We use a different estimate for each pixel and time chunk to account for spatially varying illumination and photobleaching. Another approach is to subtract the mean intensity of an image from just outside the fluorescent region (29). Our samples cover the entire region imaged, so that approach cannot be implemented easily. Use of a nonfluorescing region as background also cannot correct for a spatially varying background.

Anomalous diffusion

Hindered diffusion is known to be anomalous when the probed length scale contains a range of obstacle length scales. In a Monte Carlo simulation, for instance, anomalous diffusion was found for hard sphere diffusion (i.e., no hydrodynamic interactions) on a lattice with high densities of randomly placed immobile point obstacles (31). Normal diffusion was found at low densities. In our system, however, the probed length scale, ∼300 nm, is smaller than the obstacle length scale, 1 μm, the average pore size for 2 mg/ml collagen (15,32).

Theoretical analysis by Fradin et al. (33) of FCS measurements near a planar boundary may partially explain the apparent anomalous diffusion in collagen. In particular, they derive an analytical form for the autocorrelation function that is well approximated by anomalous diffusion (but is different from Eq. 11), giving a subdiffusive anomalous exponent for a range of distances from the boundary. The residence times over this range are increased, due to the blockage of escape routes by the boundary. When the boundary obstructs more than half of the measurement volume, the dominant effect is the decrease in volume available to the diffuser, resulting in decreased residence times. This description is consistent with bright lines sandwiched between dark lines centered on the fibrils in Fig. 7 a, the map of D_a (which is inversely proportional to the residence time). Far from the fibrils, however, the anomalous exponent remains, on average, around α = 0.8, rather than unity, as predicted for the planar boundary. This discrepancy might be explained by hydrodynamic coupling with the boundaries (fibrils), or crowding from unpolymerized collagen monomers (35), neither of which was considered by Fradin et al. (33). Lastly, though an anomalous diffusion autocorrelation fits our data reasonably well, we note that the underlying assumption of a power law mean-square displacement, used to derive Eq. 11, may not hold for any measurement volumes in our experiment.

The mean anomalous exponent for collagen α = 0.78 is similar to the expected exponent for semiflexible polymers, 3/4, which was also found in particle tracking experiments of microspheres in actin (34). To see such fluctuations reflected in measurements, however, the network fluctuation amplitudes must be at least comparable to the size of the measurement volume, which is not the case for our network, composed of relatively stiff collagen fibrils. Furthermore, a similar particle tracking experiment in actin only found anomalous diffusion when the spheres were comparable to the network mesh size. For the same sphere/pore-size ratio as our collagen experiments, the diffusion was normal. Anomalous diffusion has also been observed in a number of other biologically relevant environments, including the extracellular space of the central nervous system (17), extracellular matrices (19), solutions with high densities of globular proteins (35), and inside living cell nuclei (36).

Camera considerations

The collagen and water-glycerin samples were imaged with the Andor EMCCD, a camera with an excellent SNR and high speed. Both features benefit from the camera's “electron multiplying” gain stage, similar to the amplification in a photomultiplier tube, which effectively reduces read noise to <1 electron, even when the readout amplifier is noisy, as is typical for fast readout rates. Read noise is problematic when the photon count per exposure is low, so the EM stage is particularly valuable for high speed imaging. Because read noise can be neglected, the signal/noise analysis for spinning disk FCS with an EMCCD is essentially the same as for conventional and scanning FCS (29,30). (Similar to photomultiplier tubes, the EM process does add signal-dependent exponential noise.) Another SNR improving feature of the Andor EMCCD is back-illuminated pixels, which give a quantum efficiency of ∼90% (versus ∼60% for conventional front-illuminated pixels).

The fastest EMCCDs are still slower than the fastest conventional cameras. The Cooke camera used for the pure water measurements, for instance, can image a 128 × 128 at well over 1000 Hz. (By comparison, this resolution can be imaged at ∼120 Hz with the EMCCD camera and ∼40 Hz with the Hamamatsu.) The large read noise of the Cooke camera (∼100 electrons RMS) together with the low photon counts due to short exposure times limits the camera's usefulness to only the very brightest sources. To get autocorrelation data of similar quality to Fig. 3 with the Cooke camera at 333 Hz would require roughly 100-times more data. For reference, our laser intensity at 488 nm is ∼200 mW (at the laser exit aperture), and the 200-nm diameter spheres have a brightness equivalence of 10⁵ fluorescein molecules.

Lastly, the highest speed cameras typically impose movie size limitations, as the images must be stored in onboard RAM when the data rate is faster than hard-disk write speeds. The Cooke camera had 4 GB of RAM for this purpose, adequate to record 128 × 128 movies containing 8192 frames.

Imaging artifacts

There are several imaging artifacts that we have not included in the analysis. First, the lateral e⁻² radius, w₀, increases somewhat with axial distance from the focal plane, instead of being constant as implied in Eq. 3. This axial dependence increases with the pinhole size (37). Our disk has 50-μm diameter pinholes, which are optimized for 100× magnification, close to the 90× magnification used in these experiments. (One drawback to SDCM is that the pinhole size is fixed.) The axial dependence will cause the autocorrelations to deviate from Eq. 11, and is possibly a reason the water-glycerin data appears slightly subdiffusive (Fig. 8). The axial dependence will also increase the length scale w₀ compared to both the theoretical PSF and a two-dimensional Gaussian fit to a particle imaged in the focal plane. We account for this by estimating w₀ from an average of two-dimensional slices weighted by the peak intensity (see Materials and Methods). Another approach is to estimate w₀ from fitting the spatial autocorrelation of individual frames to a two-dimensional Gaussian (3). (Note that the autocorrelation radius is.)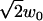

Second, if the spheres are significantly bigger than the PSF, then the lateral radial profile will deviate from a Gaussian. In fact, the profile will be given by the right-hand side of Eq. 4, except with x replaced by r, and the pixel size L replaced by the sphere diameter. Thus, the error in the extracted D will be similar to the top curve of Fig. 2 c. For the water-glycerin and collagen measurements, the microsphere diameter of 210 nm and the estimated PSF of 148 nm gives w₀/L = 0.7, which in Fig. 2 c gives an estimated error in D of 5%.

Third, if the spheres move an appreciable distance compared to w₀ in an exposure time, then the autocorrelation will deviate from Eq. 11. In particular, the resulting autocorrelation will be Eq. 11 convolved with a step function of width τ = t_exp, which will increase the apparent τ_D. To estimate the magnitude of this effect, convolved autocorrelations with α = 1 were synthesized (using appropriate exposure times) and then fit to Eq. 11. The extracted diffusion times were increased for the different experiments by 20% (collagen), 9% (water-glycerin), 7% (water), and 7% (glycerin). The extracted anomalous exponents were changed <1%. The spatial autocorrelation will also be increased by intraframe sphere movement, as the ensemble-averaged lateral profile of a single sphere should be the convolution of two Gaussians with e⁻² radii w₀ and the diffusion propagator, (8Dt_exp)^1/2.

Lastly, two imaging artifacts can be introduced by the spinning disk unit. First, misalignment of the disks causes the laser illumination at the sample to oscillate at the spinning disk rotation rate with a peak-to-peak amplitude ∼20% of the average output. These oscillations are evident in the time series and contaminate the autocorrelations. The photobleaching correction procedure partially cancels their effect. The oscillations can be eliminated if the exposure time is one full disk rotation, as it was for the collagen and water-glycerin experiments. Second, coherent streaks appear in the images if the exposure time is not within ∼10 μs of one scan time of the disk. Many cameras, like our Hamamatsu, cannot control their exposure time to this precision. However, the effective exposure time can be set by pulsing the laser illumination with an AOTF (having ∼1-μs rise and fall times). Streaks can also be induced by fluctuations in the laser power over a scan. These streaks are uncorrelated, however, unlike the streaks from poor synchronization, and do not add systematic error. Streaks also appear on frame transfer cameras, like our Andor EMCCD, when illuminated during readout. Synchronizing the AOTF to the camera exposure eliminates this problem too.

Analysis artifacts and error

The fitting procedure can become unstable, either because of noise, poor statistics, or dynamics that deviate from the assumed model. Deviation from the model likely happens for pixels with caged particles (the bright spots in Fig. 5 b) and for pixels that have deviant size particles, as mentioned earlier. Noise and poor statistics were found to be a problem (causing large outliers) when much fewer than 16 trials of 8192 time points were used, particularly for the collagen and pure water samples.

The uncertainty in the measured diffusion coefficient is due to uncertainty in w₀ and the measured τ_D. The uncertainties in w₀ give rise to an uncertainty in obtaining D for a given measured τ_D according to the relation 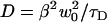. Since β depends on w₀, the sensitivity of D on w₀ is not simply quadratic, and will be largest when w₀/L is small, since 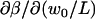is largest there (see Fig. 2 a). Uncertainty in w₀ also leads to uncertainty in the measured τ_D, through the ratio of lateral and axial diffusive timescales γ. Increasing γ² from 4.6 to 6.5 (a 50% increase) decreases τ_D by ∼10%. When γ is larger, as it was for the glycerin experiments (because the spheres and pixels were smaller), the fits are less sensitive to its value. There is also uncertainty in the true diffusion coefficient resulting from uncertainty in the solution viscosity, the microsphere radii, and temperature.

CONCLUSION

We have extended LSM-based spatially resolved FCS (scanning FCS) to SDCM (spinning disk FCS), which has the potential to image rapid dynamics at high spatial resolution. The speed advantage of SDCM over LSM will be further enhanced as EMCCD cameras reach higher speeds, which seems likely in the near future. We have shown how to correct for two problems in this technique: photobleaching, which occurs for scanning FCS as well, and a pixel size effect, which is unique to spinning disk FCS. We have measured, using spinning disk FCS, spatially resolved hindered diffusion of fluorescent microspheres in Type I collagen and found spatial variation in the diffusion coefficient that appears nontrivially correlated to the collagen microstructure. When anomalous diffusion is considered, the collagen structure is also apparent in the anomalous exponent α. As cellular environments are highly heterogeneous and show hindered diffusion at relatively fast timescales, spinning disk FCS should be a promising new approach to FCS and quantitative cell biology.