Filament Compliance Effects Can Explain Tension Overshoots during Force Development

Abstract

Spatially explicit stochastic simulations of myosin S1 heads attaching to a single actin filament were used to investigate the process of force development in contracting muscle. Filament compliance effects were incorporated by adjusting the spacing between adjacent actin binding sites and adjacent myosin heads in response to cross-bridge attachment/detachment events. Appropriate model parameters were determined by multi-dimensional optimization and used to simulate force development records corresponding to different levels of Ca²⁺ activation. Simulations in which the spacing between both adjacent actin binding sites and adjacent myosin S1 heads changed by ∼0.06 nm after cross-bridge attachment/detachment events 1), exhibited tension overshoots with a Ca²⁺ dependence similar to that measured experimentally and 2), mimicked the observed k_tr-relative tension relationship without invoking a Ca²⁺-dependent increase in the rate of cross-bridge state transitions. Tension did not overshoot its steady-state value in control simulations modeling rigid thick and thin filaments with otherwise identical parameters. These results underline the importance of filament geometry and actin binding site availability in quantitative theories of muscle contraction.

INTRODUCTION

Cross-bridge cycling kinetics in contracting muscle fibers are often assessed by measuring the rate at which force redevelops after a rapid shortening/restretch perturbation (1). Most subsequent analyses model the recovery as an exponential (or biexponential) process during which the population of attached cross-bridges recovers asymptotically toward a maximum value dictated by the relative level of Ca²⁺ activation. This approach has proved to be extremely useful (see review by Gordon et al. (2)), but recent measurements published by this author (3) show that the real situation is often more complicated. In submaximally activated rat soleus fibers for example, tension temporarily exceeds the steady-state level during recovery before gradually declining back to the original isometric level.

One way this could occur is if a subpopulation of cross-bridges remained attached between the myofilaments during restretch (4). Subsequent tension recovery would then involve two competing processes: 1), the gradual detachment of cross-bridges that remained bound during restretch, and 2), the asymptotic growth of a new population of cross-bridge links that formed after relengthening was complete. If the new population formed faster than the original population of bound cross-bridges detached, force could overshoot the steady-state level during recovery.

An alternative explanation is that the number of newly formed cross-bridge links itself overshoots. This does not happen in most conventional models of cross-bridge force generation, but it could occur if the probability of cross-bridge attachment temporarily increased during the recovery process. This work presents the results of computer simulations developed to investigate whether such an effect might arise from a “compliant realignment” of the thick and thin filaments similar to that first described by Daniel et al. (5).

METHODS

The model

A theoretical model of a half-sarcomere containing one actin and one myosin filament was developed (Fig. 1). The distance between the Z-line and the M-line was fixed at 1.3 μm to match the mean sarcomere length (2.6 μm) used in the author's recently reported experiments (3).

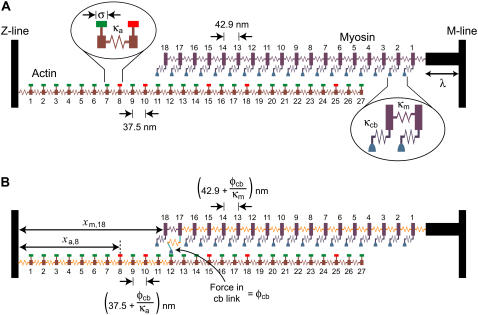
FIGURE 1.

Theoretical model. (A) A schematic diagram showing the linear arrays of S1 heads and actin binding sites at the beginning of a representative simulation. The width of the horizontal bar above each binding site indicates the effective range σ of the site. Sites that are available for S1 heads to attach to are marked in green; unavailable sites are marked in red. Some S1 heads (for example S1 head 7) fall between actin binding sites and cannot attach to the thin filament. Other S1 heads (for example, S1 head 4) are aligned with a binding site and could potentially attach. (B) The situation if S1 head 17 were to attach to binding site 12. The force (φ_cb) in the actomyosin link stretches all the myosin elastic elements distal (relative to the Z-line) to S1 head 17 and all the actin elastic elements proximal to binding site 12. This results in relative interfilamentary movement and potentially allows further S1 heads to come within range of available binding sites. The additional arrows show sample x_m and x_a displacements, in this case, for S1 head 18 and binding site 8, respectively.

The myosin filament was modeled as an array of 18 S1 heads connected together by identical elastic elements, each with a rest length of 42.9 nm and a spring constant denoted by κ_m. The thick filament was connected to the M-line by a rigid strut of length λ.

The actin filament was constructed in a similar way. It consisted of 27 binding sites joined by elastic elements with rest lengths of 37.5 nm and spring constants equal to κ_a. Each binding site had an effective range σ such that only S1 heads that fell within ±½ × σ of a binding-site's midposition could potentially attach. When such an attachment occurred, the force (φ_cb) in the resulting cross-bridge link was given by

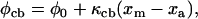(1)

where φ₀ is the force produced by an S1 head attached to a directly opposed binding site, κ_cb is the spring constant for an actomyosin link, and x_m and x_a are the respective displacements of the distal end of the actomyosin link and the actin binding site from the Z-line (Fig. 1).

Contractile activity was regulated by the prevailing free Ca²⁺ concentration via two distinct mechanisms. The first involved a Ca²⁺-dependent change in the effective range of each binding site such that

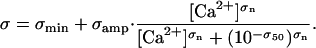(2)

Such an effect could result physically from, for example, S1 heads (not considered in these simulations) binding to the far side of the thin filament and displacing tropomyosin molecules and/or increased disorder of the S1 head array at high levels of Ca²⁺ activation. Mathematically, the effect increased the probability of cross-bridge attachment at high Ca²⁺ concentrations because S1 heads were more likely to fall within range of actin binding sites.

The second mechanism involved binding-site kinetics. Each actin site was assumed to cycle between “on” (available for cross-bridges to bind to) and “off” (unavailable) states. The rate k_off at which each binding site switched from the on to the off state was independent of the prevailing Ca²⁺ concentration but the transition was forbidden for occupied sites. In other words, the cross-bridge occupying the binding site had to detach before the site could revert to the off state.

The proportion of sites in the on state in the absence of attached cross-bridges increased with the prevailing free-Ca²⁺ concentration as

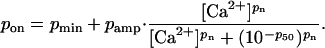(3)

In turn, this defined k_on as

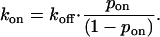(4)

The Ca²⁺ dependence of the p_on parameter further increased the chances of cross-bridge attachment at higher Ca²⁺ concentrations because a cross-bridge in range of a potential binding site was more likely to find the site in an on (or available) state.

S1 heads attached to suitably positioned available binding sites at a rate f. S1 detachment was considered strain-dependent and occurred at a rate g defined as

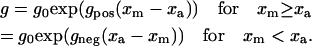(5)

The coefficients g_pos and g_neg were both constrained to be >0 and defined how quickly the cross-bridge detachment rate increased as the force φ_cb (Eq. 1) in a given cross-bridge link deviated from φ₀.

Filament compliance effects were incorporated by recalculating the position of each S1 head and each actin binding site after every cross-bridge attachment/detachment event. This was achieved by repetitive solution of the matrix equation

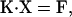(6)

previously described by Daniel et al. (5). In this equation, K is a matrix of spring constants, X is a vector of x_m and x_a values, and F is a vector of forces due to attached cross-bridges and/or elastic element rest lengths. Further details can be found in Daniel et al.'s manuscript.

Implementation

Force records showing the recovery toward steady-state isometric tension were simulated using a computer-based Monte Carlo algorithm. Individual trials corresponded to a fixed pCa value in the range 6.5 (low activation) to 4.5 (saturating effect), and consisted of 15 s of simulated actomyosin interactions. Stochastic noise was reduced by averaging up to 1500 such trials for each pCa value (see Fig. 3, B and C). Muscle force was calculated from the extension of the actin elastic element located closest to the Z-line.

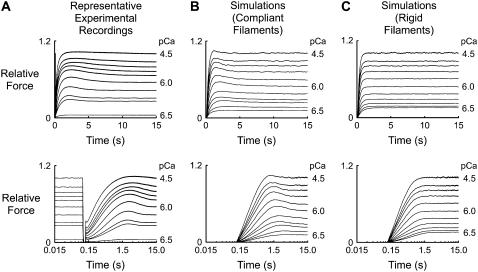
FIGURE 3.

Representative force records. Records are plotted using linear (top) and logarithmic (bottom) time axes to show the initial phases of force development on an enlarged timescale. (A) Experimental records for a soleus fiber subjected to a rapid shortening/restretch protocol in each of 10 pCa solutions. The fiber was shortened by 20% of its initial length at 0.10 s and restretched to its initial length (step time ∼0.6 ms) at 0.12 s. Records are replotted from Fig. 3 of Campbell (3). (B) Simulated records showing the recovery time course for the 10 levels of Ca²⁺ activation plotted in A and an additional pCa 6.4 activation, as computed using the parameters listed in Table 1. Each record is the average of 1000 individual trials and is normalized to the steady-state force (8.89 ± 0.01 φ₀) in the pCa 4.5 simulation. Note that the simulated records are plotted so that they start at 0.12 s (the same time that the muscle was restretched in the experimental records) and start from zero force rather than from the residual level measured experimentally. (C) Same as for B, but calculated using values of κ_a and κ_m 10⁶ times greater than those listed in Table 1. These calculations describe the model's behavior with effectively rigid thick and thin filaments. The steady-state pCa 4.5 force under these conditions was 8.20 ± 0.01 φ₀ (0.92 ± 0.01 of the corresponding value in the simulations modeling compliant filaments).

Each trial commenced with a random initialization of the thin filament using values of σ and p_on determined by the prevailing free-Ca²⁺ concentration (Eqs. 2 and 3). Potential filament registration artifacts were minimized by assigning λ to a randomly chosen value uniformly distributed between 80 and 123 nm (equivalent to the approximate length of the thick filament bare zone plus a random fraction of the S1 head separation). All cross-bridges were initially detached.

The simulation then advanced to the end of the record in a series of discrete time steps of fixed length Δt. The following calculations were performed sequentially between each step:

1. A different pseudorandom number ranging from 0 to 1 was assigned to each attached cross-bridge. If the number was more than exp(−g × Δt), the S1 head detached from the thin filament and the positions of each S1 head and each binding site were recalculated.

2. Additional randomly distributed numbers were assigned to each detached cross-bridge. If the cross-bridge's associated number exceeded exp(−f × Δt) the cross-bridge was deemed “primed”, that is, it would attach if it subsequently came within range of an available binding site during the time step.

3. The algorithm then cycled through the primed cross-bridges in random order checking to see if the relevant S1 head had come within ±½ × σ of an available binding site during the time step. If it had, the cross-bridge attached to the thin filament and the S1 head and actin binding site positions were recalculated before continuing.

4. Once all potential cross-bridge attachment/detachment events had been considered, random numbers were assigned to each unoccupied binding site. If the binding site was off (unavailable for cross-bridge attachment) it switched to the on state (available for S1 binding) if its assigned number was more than exp(−k_on × Δt). Available binding sites switched to the off state if their associated random number exceeded exp(−k_off × Δt).

The calculated value of muscle force was noted after each time step and the resulting record was saved to a computer file at the end of the simulation for subsequent averaging and analysis. The records presented in this work used a time step Δt of 1 ms. Reducing Δt to 0.1 ms did not affect the simulation results.

The simulations were implemented using custom-written MATLAB routines (The MathWorks, Natick, MA). Each single trial (simulating 15 s of actomyosin interactions for a single level of Ca²⁺ activation) required ∼5 s computation time on a 3.4-GHz Intel PC. Pseudorandom numbers were obtained using the MATLAB rand() command (version 7.1) that returns integer multiples of 2.2 × 10⁻¹⁶ uniformly distributed between 0 and 1 with a cycle length of 2¹⁴⁹² (6). Equation 6 was solved using the MATLAB command X = K\F that invokes Gaussian elimination and partial pivoting to return the vector solution.

Optimization

Automated procedures were used to search for sets of model parameters that produced simulated responses as close as possible to those in recently reported experimental records obtained by this author using rat soleus fibers (3). This process was initiated by generating a series of force records corresponding to activations in pCa 6.5, 6.3, 6.0, 5.7, and 4.5 solutions and calculating the predicted values of the P_ss/P₀, P_max/P_ss, k_tr, and t_ct parameters (Fig. 2). These simulated values were then compared to the equivalent experimental values (see Fig. 4 of Campbell (3)) using an error function defined as

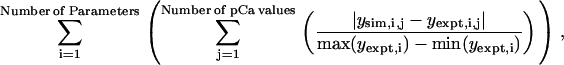(7)

where “min(y)” and “max(y)” return the minimum and maximum values from an array y and the subscripts “sim” and “expt” refer to values calculated from simulated and experimental traces, respectively. This function assigns equal weight to the relative tension (P_ss/P₀), relative overshoot (P_max/P_ss), k_tr, and t_ct indices, returns zero if the simulated traces fit the experimental data perfectly, and increases progressively as the simulations depart from the experimental records. The absolute value of the parameter deviation was used in preference to the squared deviation to minimize sensitivity to stochastic noise in the early stages of the fitting procedures.

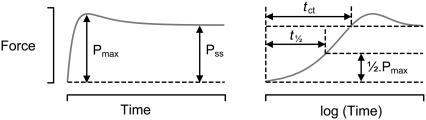
FIGURE 2.

Definitions. Panels show a schematic force record plotted using linear (left) and logarithmic (right) time axes. Parameters are defined as previously described (3), with the sole exception that the simulated records presented in this work do not exhibit the residual force measured experimentally. P_ss is the steady-state isometric force. P₀ is P_ss measured in pCa 4.5 solution. P_max is the maximum force attained in the first 5 s of the force recovery, and t_ct is the time required for force to rise to 0.97 P_ss. k_tr values were calculated as −ln(½)/(t_½), where t_½ is the time required for force to rise to 0.5 P_max. Adapted from Fig. 1 of Campbell (3).

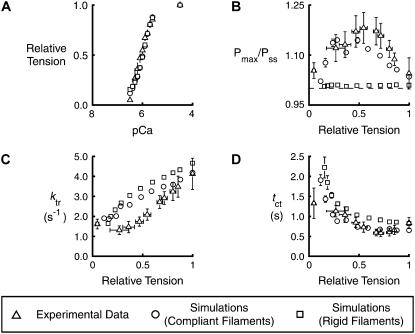
FIGURE 4.

Descriptive parameters measured from experimental and simulated records. Symbols show mean ± SD for the (A) relative tension, P_ss/P₀, (B) relative overshoot, P_max/P_ss, (C) rate of tension recovery, k_tr, and (D) crossing time, t_ct, parameters for individual pCa values ranging from 6.5 to 4.5. Experimental values (triangles) are replotted from Fig. 4 of Campbell (3). Simulated values computed with (φ₀/κ_m = φ₀/κ_a = 0.0645 nm (circles) (see Table 1)) and without (φ₀/κ_m = φ₀/κ_a = 6.45 × 10⁻⁸ nm (squares)) filament compliance were calculated as described for Fig. 2. The simulated data sets include points corresponding to pCa 6.4 activations. Equivalent experimental records were not available. pCa₅₀ values (indicative of the calcium concentration required to produce half-maximal force) differed by <0.01 for the data sets simulated with and without filament compliance.

Successive iterations repeated these calculations, gradually adjusting the individual model parameter values in an attempt to find successively lower error values (indicating better fits to the experimental data). Increasing numbers of trials were averaged together to produce the simulated records as the optimization converged to the final parameter set. The latter stages of the optimization procedure were performed using records that exhibited sufficiently low levels of stochastic noise that it is unlikely that random variation had a significant effect on the final parameter choice. Initial optimization attempts utilized simplex and/or direction-set minimization algorithms (7), but the parameter values listed in Table 1 (the set that produced the best fit to the experimental data determined during this work) were deduced using the particle swarm optimization technique first described by Eberhart and Kennedy (8).

TABLE 1.

Model parameters

Compliant extensions
φ0/κm = φ0/κa	0.0645 nm
φ0/κcb	50.0 nm
Actin filament
pmin	0.216
pamp	0.783
p50	6.25
pn	2.01
σmin	2.43 nm
σamp	24.5 nm
σ50	5.86
σn	2.14
koff	38.2 s−1
Myosin S1 heads
f	3.97 s−1
g0	0.0870 s−1
gpos	0.402 nm−1
gneg	0.140 nm−1

All parameter values are shown to three significant figures.

RESULTS

Table 1 shows the set of model parameters returned by the multi-dimensional optimization technique described in the Methods section. The simulated records produced by these parameters are the best fit to the previously reported experimental data (3) obtained during this work.

Stochastic simulations inevitably exhibit some amount of random noise. To quantify the effects of this noise, 10 separate records for 11 different pCa values were generated using the parameters from Table 1. Each record was the average of 1000 individual trials. Representative simulations for the different Ca²⁺ activations are shown in Fig. 3 B.

A second set of simulated records was then computed using values of φ₀/κ_m and φ₀/κ_a set equal to 6.45 × 10⁻⁸ nm (10⁶ times smaller than the value shown in Table 1) but with parameters otherwise identical to those used to generate the records shown in Fig. 3 B. These records illustrate the model's behavior with essentially rigid actin and myosin filaments. Sample records for this data set are shown in Fig. 3 C.

Mean and standard deviations were then calculated for the relative tension (P_ss/P₀, where P₀ is the steady-state isometric tension for the pCa 4.5 condition), relative overshoot (P_max/P_ss), k_tr, and t_ct parameters (Fig. 2) for each pCa value for each data set. The results are plotted, together with the corresponding experimental data, in Fig. 4. The error bars for the simulated data indicate the extent of the stochastic noise in the final records. In most cases, the error bars for the simulated data are smaller than the corresponding symbols.

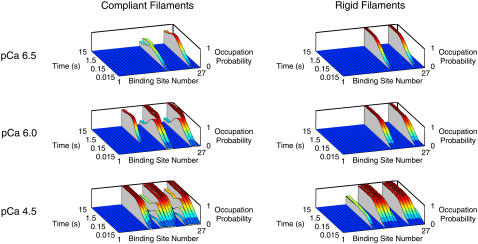
All of the stimulated records described above were calculated using randomly assigned values of the thick filament offset λ. An additional pair of data sets (one modeling compliant filaments, the other modeling rigid filaments) were generated with a fixed value of λ to illustrate the effects of compliant realignment. Fig. 5 shows distributions calculated from these simulations, indicating the probability of each binding site being occupied by an attached cross-bridge as a function of time.

FIGURE 5.

Compliant realignment. Distributions for three different levels of Ca²⁺ activation showing the probability of each actin binding site being occupied by an attached cross-bridge as a function of time. Left-hand panels show simulations performed using the parameters defined in Table 1. The simulations in the right-hand panels show the model's behavior with rigid thick and thin filaments. λ was 105 nm for all trials summarized in this figure. Since different values of λ result in distinct probability distributions, sweeping λ over the thick-filament repeat in successive trials (as was done for the simulated records summarized in Figs. 3 and 4) would have “smeared” the occupation-probability distributions and obscured the realignment effect.

DISCUSSION

Recent experimental results obtained using rat soleus fibers (3) show that tension overshoots its steady-state value during force development at submaximal levels of Ca²⁺ activation. This observation has been reproduced in this work using a spatially explicit model of stochastic cross-bridge binding. Overshoots are attributed to a filament compliance effect. Tension does not exceed its steady-state value in control simulations based on rigid filaments.

Tension overshoots

Overshoots occur in these simulations because compliant realignment of the actin and myosin filaments (5) allows S1 heads to interact with actin binding sites that they would not be able to reach if the filament lattice was rigid. The probability distributions shown in Fig. 5 illustrate the point. Each slice in these panels shows the probability of a specific binding site being occupied by an S1 head during a force-development time course. The left-hand panels show the situation with compliant filaments; the right-hand panels show the equivalent distributions for rigid actin and myosin structures.

Consider the right-hand panels first. Since λ (the offset between the first myosin elastic element and the M-line (Fig. 1)) was held constant for each of the trials illustrated in this figure, only some actin binding sites fell within interaction range of S1 heads during the simulations. Attachment events occurred where possible (but not at the inappropriately positioned sites) and the occupation probability for each favored location rose to a steady-state value reflecting the attachment-rate constant f and the detachment-rate constant g for an S1 head bound with the appropriate x_m-x_a strain.

The left-hand panels in Fig. 5 show simulations of acto-myosin interactions occurring between compliant filaments. The effects of filament strain are obvious. For example in the pCa 6.0 activation, the occupation probability of two of the binding sites rises quickly during the initial stages of force development and then drops to a lower level as the filaments realign and the sites pass almost out of range of their original S1 partners. This realignment allows three more sites (one clearly visible at position 11, and the other two partially hidden in this view at positions 19 and 27) to interact with S1 heads. Two other sites remain within range of S1 heads throughout the simulation. The net effect of this complicated redistribution is that force transiently exceeds its steady-state value during recovery, producing the characteristic overshoot observed experimentally.

Visualizing occupation-probability distributions in this way demonstrates why the predicted force-development records are critically dependent on the initial filament configurations. Altering λ by just a small fraction of the thick filament repeat changes which binding sites are initially in register. Test calculations showed that this modifies the final redistribution pattern and thus the predicted force response. Potential artifacts due to this behavior have been minimized in the simulated data sets by reassigning λ to a different value randomly staggered over the thick filament repeat at the beginning of each trial.

Thick and thin filament extensions

X-ray (9,10) and mechanical (11,12) measurements show that actin and myosin filaments elongate by ∼3 nm and by ∼2 nm, respectively, during a maximal isometric contraction. The corresponding extensions calculated in these simulations were larger. The actin filament extended by 10.8 ± 0.5 nm at steady state in pCa 4.5 solution. The thick filament stretched by 6.32 ± 0.3 nm.

Although the simulated filaments extend ∼3.5 times further than real actin and myosin structures, geometrical considerations imply that compliant realignment in the simulations could be very similar to that occurring in real muscle. Since the model incorporates only one actin and one myosin array, a relative interfilamentary movement equal to the binding site interaction range σ is required to double the probability of a cross-bridge interacting with a binding site. (This calculation assumes that σ is <½ of the binding-site repeat distance.) Real myosin filaments, on the other hand, have threefold radial symmetry with S1 heads protruding at different angles every 14 nm. The same relative filament displacement σ would double the probability of each of the S1 heads encountering an available binding site resulting in a potential sixfold increase in attachment probability.

This argument obviously holds only when the probability of cross-bridge attachment is quite low, but it suggests that filament extensions three times smaller than those computed here would be enough to produce appropriately sized tension overshoots if they occurred in a realistic three-dimensional lattice. That modification would put the simulated filament extensions very close to those measured experimentally.

Cross-bridge attachment and detachment

Relative filamentary movement always increased the probability of cross-bridge attachment in these simulations. Potential S1 binding events were never prevented because the actin site had been pulled out of range during the time step. Mathematically this was implemented by deciding at the beginning of each time step which cross-bridges were primed to attach. Physically this could correspond to a situation in which S1 heads attach very rapidly to suitably positioned available binding sites when they are oriented in a specific direction but cannot attach otherwise. The rate at which the cross-bridges reorient is the single-valued attachment parameter f.

Cross-bridge detachment was modeled as a strain-dependent process. The optimization procedure returned a value of g_pos that was >g_neg. This meant that cross-bridge links that were stretched by compliant realignment of the filaments detached more quickly than cross-bridge links that shortened an equivalent amount.

Ca²⁺ regulation

Soleus muscles develop more force at high levels of Ca²⁺ activation (Fig. 4 A). They also develop force more quickly (Fig. 4 C). This places quite severe constraints on a spatially explicit model with only two cross-bridge states. The effect of Ca²⁺ on steady-state force can be accommodated by increasing the proportion of binding sites in the on state in a Ca²⁺-dependent manner, but this increases only the steady-state number of bound cross-bridges and not the rate at which the cross-bridges attach.

Reproducing the activation-dependent k_tr requires at least one additional regulatory mechanism. One possibility is that the attachment rate f is Ca²⁺-dependent (1). Another idea (developed by Kenneth B. Campbell at Washington State University) is that k_tr is slowed at submaximal levels of Ca²⁺ activation because it requires additional time to recruit cross-bridges to the cycling pool (13). The activation dependence of k_tr in the current simulations is attributed to a third mechanism, similar to that described by Landesberg and Sideman (14); cross-bridges generate force more quickly at high levels of Ca²⁺ activation because the binding sites become available at a faster rate.

This effect depends on the fact that in a spatially explicit model not all cross-bridges have an equal chance of attaching to a binding site in a given time interval. Those juxtaposed to an unavailable site are (by definition) forbidden to attach. They must first wait until the relevant binding site has switched to its available state. The rate at which sites switch to the on state is set in these simulations by the k_on parameter (Eq. 4), which is rendered Ca²⁺-sensitive by its dependence on p_on (Eq. 3). k_tr values therefore increase at high levels of Ca²⁺ activation in this model, because S1 heads that are initially positioned opposite unavailable sites are more likely to find that the requisite sites have switched to their on state in some subsequent time interval.

Setting p_on and k_on as Ca²⁺-sensitive parameters therefore accounts for the observed Ca²⁺ dependence of steady-state tension and k_tr. Since crossing times (t_ct (Fig. 2)) are inversely related to k_tr values in situations where there are no overshoots, the Ca²⁺ dependence of these two model parameters can also explain why experimental t_ct values are generally lower at high free-Ca²⁺ concentrations. The remaining issue is how best to explain the experimental finding that the magnitude of the relative overshoot peaks at approximately half-maximal Ca²⁺ activation (3).

Tension overshoots occur in these simulations because relative movement of the thick and thin filaments during force development allows additional S1 heads to pass within interaction range of actin binding sites. The magnitude of the attachment-probability enhancement effect depends on the size of the binding-site interaction range σ becoming progressively smaller as σ approaches the binding-site repeat distance. The molecular mechanism underlying this effect is easy to understand. If most S1 heads are already aligned with binding sites, relative filamentary movement does not substantially increase the probability of actomyosin interactions.

This reasoning implies that simulated overshoots could be made smaller at high levels of Ca²⁺ activation by increasing the size of the binding site range σ in a Ca²⁺-dependent manner. When this mechanism was tested during the development of the model, it soon became apparent that the relative size of the overshoots was also small at low levels of Ca²⁺ activation simply because under these conditions not enough cross-bridge attachments were formed to substantially perturb the filament lattice. Intermediate levels of Ca²⁺ activation produce the largest relative overshoots in these simulations because they represent a balance between small numbers of bound cross-bridges and high values of σ.

The choice of a sigmoid Hill-type Ca²⁺ dependence for the p_on parameter (Eq. 3) can be justified on theoretical grounds as the predicted behavior for an array of regulatory units that activate cooperatively, that is, activation of one site increases the likelihood of another site becoming activated. The author is not aware of a formal justification for assigning the binding-site interaction range σ a similar Hill-type Ca²⁺ dependence (Eq. 2), but the relationship is practically convenient for these simulations and seems plausible for a biological system.

The σ parameter is modeled computationally as a property of individual binding sites but conceptually it incorporates myosin properties too. For example, σ could increase at high levels of Ca²⁺ activation because S1 heads are able to reach further from the thick-filament backbone. Such an effect could reflect increased Ca²⁺ binding to regulatory light chains (2) or the structural reorganization of the thick filament that x-ray measurements indicate occurs during force development (15). The Ca²⁺ dependence of the parameter could also be mediated through a variety of cooperative thin-filament effects (2). Given the complexity of the situation, it is difficult to say whether it is physiologically significant that the calculated value of p₅₀ is greater than that of σ₅₀. However, the shift would be consistent with the idea that the postulated Ca²⁺-dependent increase in σ occurs secondary to force development and is not the primary regulatory effect in soleus fibers.

Effects of compliance on tension recovery

Fig. 4 C shows that k_tr values calculated for the compliant system were lower for all but the very lowest level of Ca²⁺ activation than those calculated using the rigid filaments. This result is qualitatively similar to that described by Luo et al. (16). Their stochastic model of actomyosin interactions showed that a compliant extension of only ∼2 nm at the junction between the actin filament and the Z-line slowed tension transients induced by a simulated change in the cross-bridge detachment rate. The current work demonstrates that tension development kinetics are also slowed when compliant elements are distributed throughout the myofilament system.

This author has already pointed out (3) that crossing times t_ct (Fig. 2) represent an alternative way of quantifying the time course of tension recovery when substantial overshoots are evident. Interestingly, the t_ct values calculated for the rigid filaments were consistently higher than those calculated for the compliant filaments. This contradicts the straightforward expectation that an increase in the measured k_tr value would be accompanied by a reduced t_ct value and indicates that compliant realignment changes the qualitative time course of tension recovery, as well as its overall rate, in these simulations.

Physiological implications

Mathematical models are most useful in physiology when they help to provide insight into underlying physical mechanisms. The simulations presented in this work neglect many important features of muscle contraction but they reinforce four key points about the predicted behavior of linear arrays of actin binding sites and myosin S1 heads.

First, relative movement of misregistered binding sites and S1 heads allows additional actomyosin interactions to occur. If this effect occurs as a result of filament compliance at fixed muscle length, it may be regarded as a type of cooperative activation.

Second, compliant realignment will only produce substantial mechanical effects if the probability of an S1 head encountering an available binding site is rate-limiting for force development. If this were not the case, relative movement of the thick and thin filaments would not substantially increase the number of actomyosin interactions. A corollary to this argument is that S1 heads must be able to take advantage of what could be quite short-lived opportunities to attach to the thin filament. Consequently, the rate at which S1 heads proceed to force-generating states (the rate f in the current simulations) must be quite fast compared with other myosin transitions if substantial realignment effects are to be observed.

Third, the transient mechanical effects of compliant realignment only persist for a time period comparable to the mean attached lifetime of S1 heads. Once the heads have gone through a few attachment/detachment cycles, the filaments will have adopted their new configurations and the binding-site occupation-probability distributions will have reached steady state (Fig. 5). This suggests that the long-lived (∼10-s) tension overshoots observed in rat soleus fibers can only reflect filament compliance effects if the mean S1 detachment rate is very low (of the order 0.1 s⁻¹).

The final point highlighted by these simulations relates to the myosin duty ratio. In many models of muscle contraction, this ratio can be calculated either as the proportion of time that a single S1 head remains attached to actin or as the fraction of myosin heads bound to actin at any instant. These definitions are not equivalent in the current simulations because not all cross-bridges have the same probability of attaching to the actin filament.

Consider the probability distributions shown for the compliant filaments in Fig. 5. S1 heads that are able to bind to the thin filament spend, on average, 0.93 of their time attached at steady state in pCa 6.0 solution. (This duty ratio reflects the fact that the mean detachment rate g is higher than g₀, because compliant realignment dictates that cross-bridges are rarely attached with x_m equal to x_a (Eq. 5)). The mean number of attached cross-bridges, on the other hand, is 3.74, that is, 0.21 of the 18 S1 heads on the thick filament. Spatially explicit models therefore allow a situation in which the overall number of bound cross-bridges is quite low, even though a few S1 heads remain attached for extended periods of time.

Comparison with other models

This is not the first attempt to model a compliant myofilament system. Soon after the discovery of filament extensibility (9,10), Mijailovich et al. (17) presented a modification of A. F. Huxley's 1957 model (18) that included myofilament strain. This was followed by Daniel et al.'s stochastic two-filament system (5) which has now been extended to a spatially explicit three-dimensional form (19).

This work combined Daniel et al.'s innovative modeling technique with a simple actomyosin kinetic scheme and a novel system of thin filament Ca²⁺ regulation to test the specific hypothesis that tension overshoots could reflect filament compliance effects. The simulation results show that tension overshoots may indeed reflect compliant realignment of the thick and thin filaments and demonstrate that spatially explicit stochastic models can reproduce specific features of experimental records that cannot be readily explained using conventional cross-bridge models.

It would be interesting to know whether spatially explicit models can also account for some of muscle's other interesting mechanical properties. For example, it seems possible that compliant realignment effects might be able to explain residual force enhancement, that is, the increase in isometric force resulting from a stretch imposed during a sustained contraction (20) and/or the biphasic force-velocity relationship of contracting frog muscle described by Edman et al. (21). The author hopes to investigate these ideas in future work using more complex filament architectures and more realistic actomyosin kinetic schemes.