Alcohols Reduce Lateral Membrane Pressures: Predictions from Molecular Theory

Abstract

We explore the effects of alcohols on fluid lipid bilayers using a molecular theory with a coarse-grained model. We show that the trends predicted from the theory in the changes in area per lipid, alcohol concentration in the bilayer, and area compressibility modulus, as a function of alcohol chain length and of the alcohol concentration in the solvent far from the bilayer, follow those found experimentally. We then use the theory to study the effect of added alcohol on the lateral pressure profile across the membrane, and find that added alcohol reduces the surface tensions at both the headgroup/solvent and headgroup/tailgroup interfaces, as well as the lateral pressures in the headgroup and tailgroup regions. These changes in lateral pressures could affect the conformations of membrane proteins, providing a nonspecific mechanism for the biological effects of alcohols on cells.

INTRODUCTION

Short-chain alcohols have significant effects on the physical properties of biological membranes. These changes in the membrane properties, in turn, can lead to changes in the conformational states of intrinsic membrane proteins, thus leading to an indirect (nonspecific) mechanism for the modulation of protein behavior by alcohol adsorption into lipid membranes. It has been hypothesized that such indirect interactions are likely responsible for the role alcohols play in general anesthesia (1–3) and in alcohol toxicity in bacterial and yeast cells (4).

The detailed molecular mechanisms for these effects are not yet known, although various ideas have been put forth in the literature. Since short-chain alcohols are amphiphilic, perhaps not surprisingly they have been found to localize primarily in the headgroup region of the lipid bilayer (5–8). This disrupts the packing in the lipid bilayer and leads to a variety of changes, among them observed increases in membrane fluidity (9), in membrane permeability (10), and in lipid lateral mobility (11). Klemm provides a good review of the biological effects of alcohols (12). Recently, extensive experimental work on model membranes has examined the quantitative effect of alcohols on membrane structure and mechanical properties (4,13). Micropipette aspiration was used to directly measure the area compressibility modulus, bending modulus, lysis tension, lysis strain, and area expansion of 1-stearoyl, 2-oleoyl phosphatidylcholine (SOPC) fluid phase bilayers in aqueous alcohol solutions. Alcohol was found to increase the area per lipid and decrease the mechanical moduli of the bilayers, and these changes were larger for longer chain alcohols. After converting their area compressibility modulus data into interfacial tension values, Ly and Longo found that alcohol partitioning into SOPC lipid bilayers follows Traube's rule: for each additional alcohol CH₂ group, the concentration required to reach the same interfacial tension is reduced by a factor of three (14). The underlying phenomenon that gives rise to Traube's rule is that with each additional CH₂ group the amount of alcohol adsorbed in the bilayer is also higher by a factor of three (13).

One would expect that this reduction in interfacial tension could have a substantial impact on intrinsic membrane proteins. The functions of many membrane proteins, in particular mechanosensitive ion channels, are affected by bilayer tension (15,16). More generally, the mechanical properties of a lipid bilayer can be described by all the forces acting in the plane of the bilayer. In an equilibrium self-assembled bilayer, the bilayer adjusts the area per lipid so that these forces or lateral pressures sum to zero. However, they may vary as a function of depth in the bilayer as expressed by the lateral pressure profile across the bilayer, π(z). Cantor has proposed that changes in membrane composition and properties alter the shape of the lateral pressure profile, which then alters the amount of mechanical work associated with conformational changes in membrane proteins (1,17). It is thus of interest to determine the effect of alcohols on the lateral pressure profile and whether they might affect protein behavior. A recent experimental study of the dissociation of the tetrameric potassium channel KcsA by small alcohols suggested that the alcohols interacted with the protein via changes in the lateral pressure profile (18).

As of yet there are no direct experimental probes of lateral pressure profiles in membranes (19). The lateral pressure profile can be calculated from molecular dynamics (MD) simulations of lipid bilayers, although the calculation is computationally expensive for atomistic bilayers and thus has only been done recently (15,16,20,21). An alternative is to study coarse-grained models of bilayer-forming lipids. Although these models do not retain atomistic detail, they are still capable of describing trends such as the effects of different chain lengths, lipid interactions, temperature, and so forth. The lateral pressure profile of coarse-grained models has been calculated from both MD simulations (22) and from various molecular-level theories. Many groups have used self-consistent field (SCF) theories to study lipid bilayers. However, calculations of the lateral pressure profile from these theories have been restricted to the tail region of the lipids (2,23–25). Recently, we applied a classical density functional theory (DFT), originally developed for polymeric systems, to the self-assembly of coarse-grained lipids into bilayers (26,27). The lateral pressure profile of the entire lipid bilayer, including the headgroup and solvent regions, is a natural output of the theory, and the results compare favorably with MD simulations on the same model (27).

In this article we use the DFT to predict the effect of alcohols on the lateral pressure profile. There are relatively few computational studies of the effects of alcohols on lipid bilayers in the literature. Feller et al. studied the local interactions between ethanol and palmitoyleoylphosphatidylcholine (POPC) bilayers using atomistic MD simulations and NMR (7). Simulations of Kranenburg et al. used dissipative particle dynamics simulations of coarse-grained lipids and model alcohols to study the low temperature phase behavior of lipid/alcohol mixtures, below the main transition (28,29). Atomistic MD simulations of ethanol and methanol with POPC and dipalmitoylphosphatidylcholine (DPPC) lipid bilayers found, in agreement with experiment, an increase in the area per lipid and a decrease in the NMR order parameters for the acyl tails (8,30). Coarse-grained MD simulations on butanol and DPPC bilayers found similar results, and also that butanol penetrated further into the bilayer interior than the smaller alcohols (31). Meijer et al. studied the effect of dodecanol on the interactions between dimyristoylphosphatidylcholine (DMPC) bilayers using a lattice SCF theory (32). The theory was later applied to calculate the partition coefficients of various additives, including the homologous series of n-alcohols from butanol through octanol, and was found to be in good agreement with experiment (the partition coefficients roughly followed Traube's rule as described above) (33). Finally, Cantor has performed extensive lattice SCF theory studies of the effects of both short and long-chain alcohols on lipid bilayers (34), and particularly on their perturbation of the lateral pressure profile in the context of understanding the molecular mechanism of general anesthesia (1,2,25,35). However, these calculations of the lateral pressure profiles were restricted to the acyl tail region of the lipid bilayers, since the SCF theory did not treat the solvent and headgroups on the same footing as the lipid tails.

Here, we use our previously developed theory for lipid bilayers (26) to examine the effects of three short-chain alcohols, ethanol, butanol, and hexanol. We first calculate the changes in membrane structure and mechanical properties as a function of alcohol chain length and concentration to test whether the theory results in the same qualitative trends that are observed experimentally. We then go on to calculate the changes in the lateral pressure profiles. We describe our model system and very briefly review our methods in the next section, and then present our results.

MODEL SYSTEM AND METHODS

We restrict our calculations to the biologically relevant, fluid L_α phase of the bilayers. We use our previously developed coarse-grained (CG) model to describe the lipid molecules and solvent. The lipids consist of freely jointed tangent sites or “beads.” Our model lipid has two tails each with eight beads of size σ, and a headgroup comprised of two beads of size 1.44σ (see Fig. 1). Although not intended to map to a specific lipid, we can think of each tail bead as corresponding roughly to two CH₂ groups, so that our lipid has roughly 16 carbons per tail. We include an explicit solvent consisting of single beads also of size σ. The different beads interact with standard Lennard-Jones potentials,

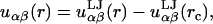(1)

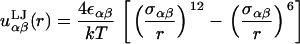(2)

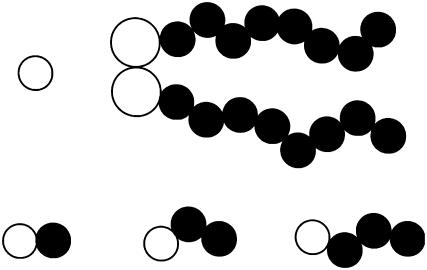
FIGURE 1.

Sketch of the coarse-grained model showing the solvent and lipid (top), and the model alcohols (bottom), with ethanol, butanol, and hexanol from left to right. Solid circles represent tail beads and open circles are head beads.

Here, r_c is the cutoff distance where the potential goes to zero, k is Boltzmann's constant, and T is the temperature. We set the cross-terms in the bead diameters from the usual Berthelot scaling rules, so that σ_αβ = 0.5(σ_α + σ_β). We have chosen the tail-solvent and tail-head interactions to be purely repulsive with r_c = 2^1/6σ_ts and r_c = 2^1/6σ_th, respectively. Solvent-solvent, solvent-head, head-head, and tail-tail interactions are all uniformly attractive with a cutoff of r_c = 3.5σ. Finally, we set all of ε_αβ ≡ ε = 1. This combination of parameters allows for a self-assembling bilayer to form. We report all lengths in units of σ and energies in units of ε/kT.

We model short-chain alcohols in the same way as the lipids. Each consists of a headgroup (the OH group) and a number of tail beads, and we take the sizes of both beads to be σ. The alcohol headgroup bead is thus somewhat smaller than that of the lipid headgroup, whereas the tail beads are the same size. We think of a two-site molecule consisting of a head and a tail as corresponding to ethanol, whereas butanol has two tail beads and hexanol has three, as depicted in Fig. 1. The tail and headgroup interactions are the same as for the lipid.

Because all the chains are treated as freely jointed, the model system has somewhat more configurational entropy than would a more accurate model that included some stiffness in the chains. This lack of chain stiffness prevents the lipids from forming a gel phase, so there is no fluid L_α to gel phase transition in our model (26,27). However, for the fluid phase it is unclear how serious the overestimation of the chain entropy is. Previous studies of fluid lipid phase behavior using fully flexible lipids found very good agreement with experiment (36,37). Based on this work, we expect the model to be useful for describing properties in the fluid phase since it captures the essential physics of the lipids and alcohols, namely that they are amphiphilic chain molecules. Since neither the Lennard-Jones interactions nor the details of the intramolecular interactions have been tuned to mimic real molecules, our predictions are purely qualitative. We were motivated to see if this very simple CG model could still be used to obtain trends in bilayer structure and properties as alcohol was added.

The details of the density functional theory, our numerical implementation of it, and its application to lipid self-assembly are described elsewhere (26,40,41). Briefly, the DFT is a mean-field theory for inhomogeneous liquids. It consists of an approximate free energy functional applied to our model system, which we minimize to find equilibrium, thermodynamic states of the system. The theory is formulated in an open (grand canonical) ensemble, and so a given thermodynamic state is specified by the temperature, the volume, and the chemical potentials of all the species in the system. The input to the theory is thus the model system and interactions, a temperature, and the relevant chemical potentials. The output consists of density profiles for all the species in the system (ρ_l, ρ_a, and ρ_s for the lipids, alcohols, and solvent, respectively) and the equilibrium grand free energy Ω. Note that we make no assumptions about the numbers of various molecules in the bilayer solution; rather, given a chemical potential the theory will find a minimum energy state and output the number of molecules in that state. The equilibrium area per lipid is thus an output of the theory. The model system is also compressible so the density of the system is not held constant but is determined by the inputs to the theory.

We perform calculations for a single lipid bilayer immersed in a large region of solvent, with a computational domain size of 40σ and reflective boundary conditions in the middle of the bilayer. We assume that the only spatial variations in the system occur perpendicular to the bilayer, so we calculate density profiles ρ_α(z) as functions of z, where z = 0 occurs at the bilayer midplane and is the direction normal to the bilayer. The reflective boundaries are used for computational convenience; their use constrains the two leaflets of the bilayer to be symmetric but does not prevent interpenetration of the two leaflets. In our previous work we found that the three sites closest to the ends of the lipid tails overlap between the leaflets, whereas the sites closer to the headgroups do not overlap so that the two leaflets are not fully interdigitated (27).

We ensure that our bilayer has a zero net tension by keeping it in equilibrium with a uniform fluid phase, as described in Frink and Frischknecht (26). This requires two solutions to the DFT equations at each state point—one solution containing the bilayer, and a second solution consisting of a uniform region of the aqueous solution (mixed solvent and alcohol) that is in equilibrium with the bilayer. The excess surface free energy Ω^ex, or equivalently the surface tension γ, is then defined as the free energy difference between the bilayer solution and the uniform aqueous fluid,

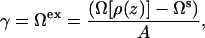(3)

where Ω is a functional of the density profiles, Ω^s is the free energy of the aqueous solution, and A is the total area. As discussed in our previous work (26,27), the lateral pressure profile emerges naturally from the theory as the excess grand free energy density,

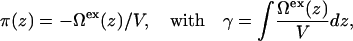(4)

where V is the volume, Ω^ex(z)/V is a surface tension density, and the lateral pressure is the negative of the surface tension. Additional details of the DFT calculations can be found in the Appendix.

RESULTS AND DISCUSSION

Trends and comparisons

The calculations presented here were done at a temperature of kT/ε = 1.3. We began with a converged bilayer solution that contained no alcohol. We then added the alcohol molecules into the system at very low densities and increased the densities gradually, by increasing the alcohol chemical potential. As the chemical potential increases, so do the alcohol concentrations both in the aqueous fluid region far from the bilayer and in the adsorbed amount of alcohol in the bilayer. Eventually at some higher concentration of alcohol, the bilayer phase becomes unstable and is no longer a solution to the DFT equations. We found that longer chain alcohols had a more dramatic effect on destabilizing the membrane at lower concentrations. Throughout the article, we will present data as a function of the concentration of alcohol molecules in the aqueous solution (far away from the bilayer), as a percentage of the total molecular density in the aqueous solution, x_a = ρ_{a, aq}/(ρ_{a, aq} + ρ_{s, aq}). This is equivalent to reporting mol % of alcohol.

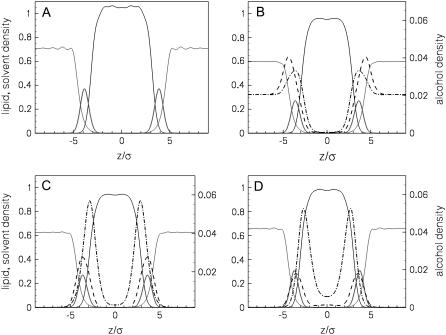
Fig. 2 shows density profiles for the unperturbed bilayer, and for bilayers at the upper limits of alcohol concentration. The left-hand axes correspond to the densities of the lipids and solvent, whereas the right-hand axes correspond to the alcohol densities. Note that these are number densities of the sites in our coarse-grained model, in units of ρσ³ (and not mass densities or volume fractions). As expected, all three alcohols are located preferentially in the headgroup region of the bilayers. The alcohol headgroups sit near the solvent-lipid headgroup interface, while the alcohol tails extend further toward the center of the bilayer. We see that the ethanol does not penetrate far into the tail region of the bilayer, whereas both the butanol and hexanol have nonzero densities of their tail beads in the middle of the bilayer, and the hexanol even has a small concentration of its headgroup in the interior of the bilayer.

FIGURE 2.

Density profiles: (A) pure lipid bilayer; (B) at 3.4% ethanol; (C) at 0.12% butanol; and (D) at 0.00048% hexanol. The curves show the lipid tailgroups (solid black curves), lipid headgroups (thick shaded curves), solvent (thin shaded curves), OH groups (dashed curves), and alcohol tails (dash-dotted curves).

In Fig. 2, the aqueous ethanol concentration is 3.4% and thus it has a significant contribution to the density in the aqueous solution outside the bilayer, whereas the other aqueous concentrations are much smaller, 0.12% for butanol and only 0.00048% for hexanol. These densities are so low because most of the longer alcohols adsorb into the bilayer, and once there is too much alcohol in the bilayer it becomes unstable and we no longer get solutions to the DFT equations. Density profiles at lower alcohol concentrations are similar to those shown in Fig. 2, with lower peaks in the alcohol density profile as x_a decreases. We find that the presence of the alcohols has essentially no effect on the amount of interdigitation between the two leaflets of the bilayer, a result consistent with recent MD simulations (8), so that the density profiles of the individual sites along the lipid tails are similar to those found previously (see Fig. 8 in (27)).

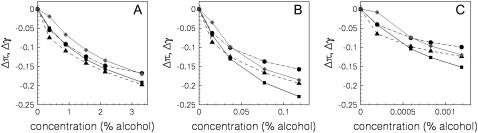
FIGURE 8.

Change in the magnitudes of the peaks in π(z) as a function of alcohol concentration for (A) ethanol, (B) butanol, and (C) hexanol. The different symbols correspond to the headgroup pressures π_hyd (diamonds), the headgroup-tailgroup surface tensions γ_HT (squares), the solvent-headgroup surface tensions (circles) γ_HS, and the tailgroup pressures π_int (triangles).

The density profiles we obtain for the lipids have shapes similar to those found in previous studies of CG lipid models that consist of chains of Lennard-Jones beads, including models incorporating chain stiffness through angle potentials (22,38). We note that unlike many previous mean-field theories for lipid bilayers (24,25,36), we do not constrain the density to be constant in the tail region of the bilayer. We thus obtain a small dip in density in the center of the bilayer, but in these CG models the dip is not nearly as pronounced as it is in experimental x-ray structures (39) or in atomistic MD simulations of lipid bilayers (e.g., (16)). This difference with atomistic systems could affect the alcohol partitioning into the bilayer, although, as we will see below, we obtain trends that are consistent with experiment.

In the remainder of this section we quantify the effects of the alcohol by calculating the area per lipid, the thickness of the bilayer, the partitioning of the alcohol into the bilayer, and the area compressibility modulus of the bilayer, as functions of both alcohol concentration and the acyl chain length. All of these quantities are experimentally measurable, and so we compare our results to those in the literature where possible.

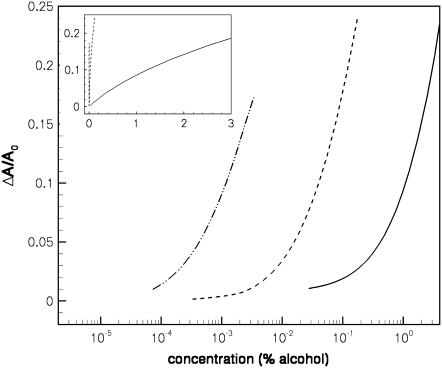
Since the alcohols are adsorbed in the interfacial region, one might expect that the area per lipid A_L would increase as alcohol is adsorbed in the bilayer. This is, in fact, what Longo et al. infer from their data on alcohol adsorption in SOPC vesicles (13). Atomistic MD simulations have also found that the area per lipid increases on addition of short alcohols (methanol, ethanol, and butanol) to bilayers (8,30,31). Fig. 3 shows the DFT result for the change in the area per lipid, ΔA_L = A_L – A_L0, relative to the area per lipid A_L0 at zero alcohol concentration, as a function of the aqueous alcohol concentration. We note that the DFT results are not consistent at very low alcohol concentrations due to sensitivity to approximations in the theory (see the Appendix), so this determines the lower bound for x_a in the data shown in Fig. 3. We find from the DFT that there is an increase in A_L as alcohol is added which is in qualitative agreement with experiment. It is difficult to compare number densities directly between our theory and experiment since our coarse-grained model does not map completely onto the physical system. However, experimentally there is a maximum concentration for which the vesicles are stable enough for micropipette aspiration. For comparison purposes, we compare values between this maximum experimental concentration and the maximum concentration at which we also obtain stable bilayer solutions to the DFT. Thus we see changes in ΔA_L/A_L0 between 16 and 24% at the upper limits of bilayer stability, which is similar to Ly and Longo's results of an ∼16% change for ethanol and a 27% change for butanol (13). The shape of the ΔA_L/A_L0 versus concentration curves shown in the inset of Fig. 3 is also qualitatively similar to Fig. 12 in Ly and Longo (13).

FIGURE 3.

Change in the area per lipid as a function of the concentration of alcohol in the aqueous solution outside the bilayer, showing results for ethanol (solid curve), butanol (dashed curve), and hexanol (dot-dashed curve); the area per lipid at zero alcohol concentration is A_L0 = 4.9σ². The inset shows the same results on a linear concentration scale.

Interestingly, the thickness of the lipid bilayer did not decrease as much as expected from the increase in A_L. We found a decrease in thickness of roughly 0.4σ at the maximum ethanol concentration and somewhat less for the butanol and hexanol, where we define the thickness as the distance between the peaks in the headgroup densities. The thickness of the pure bilayer at x_a = 0 is 7.7σ, so the change in thickness is at most ∼5%, which is considerably less than the change in A_L.

The result is that both the lipid and total site density in the bilayer decrease as alcohol is added (see Fig. 1). It is often assumed that lipid bilayers are essentially incompressible. We note, however, that in a MD simulation of methanol in DPPC bilayers, the bilayer density was found to decrease (30). We are not aware of any independent experimental data on the bilayer thickness as a function of alcohol concentration, so currently this issue is unresolved. In our calculations, the total site density in the aqueous solution far from the bilayer also decreases as alcohol is added. This is expected experimentally, since alcohol is less dense than water. However, our theory overpredicts the density decrease (e.g., we obtain a decrease in number density of ∼5.8% for 3.3 mol % ethanol, compared to an experimental value of ∼2.3% based on the same mol % of ethanol in aqueous solution).

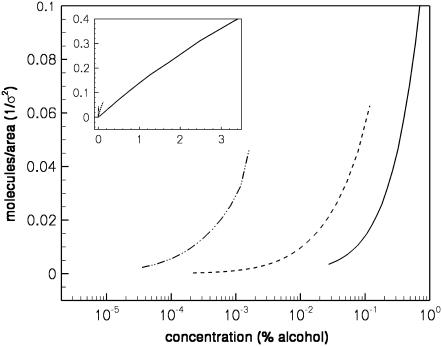
The amount of alcohol adsorbed into the bilayer is shown in Fig. 4 as a function of aqueous alcohol concentration. Calculation of the amount adsorbed requires a definition of which region of space is occupied by the bilayer. We define the edge of the bilayer as the point z_bi where the alcohol density first becomes higher than its value in the aqueous phase (coming in toward the bilayer from the aqueous region). We then calculate the number of alcohol molecules per unit area adsorbed in the bilayer as

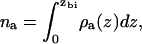(5)

where ρ_a(z) is the density profile for the alcohol molecules in the bilayer solution. Fig. 4 shows that, at the same aqueous concentration, the amount of alcohol adsorbed in the bilayer increases with alcohol chain length. This effect is also seen experimentally (13). The adsorption of our model alcohols does not, however, follow Traube's rule, in which we would expect nine times as much butanol as ethanol, and nine times as much hexanol as butanol adsorbed in the bilayer. The amount of butanol adsorbed in the bilayer is roughly five times that of ethanol at the same concentration, while something more on the order of ∼30 times as much hexanol is adsorbed than butanol at the same (very low) aqueous concentration. This is due to the coarseness of our model and to the fact that we did not tune the interaction parameters specifically for this system.

FIGURE 4.

Amount of alcohol adsorbed into the bilayer for ethanol (solid curve), butanol (dashed curve), and hexanol (dot-dashed curve), as a function of the log of the alcohol concentration in the bulk. The inset shows the same results on a linear concentration scale.

We can also calculate a partition coefficient K for the adsorption of alcohols into the bilayer, which we define as the zero concentration limit of K = x_{a, bi}/x_a, where the mole fraction of alcohol molecules in the bilayer is x_{a, bi} = n_a/(n_a + 1/A_L). We find that at low x_a, the partition coefficient is nonmonotonic, with a small maximum at a finite x_a. We therefore extrapolate the behavior at large x_a to x_a = 0 to obtain an estimate of K. This procedure gives K = 67.6, 573, and 34,470, for ethanol, butanol, and hexanol, respectively. These are larger than the values reported by Ly and Longo of K = 23.8 and 237.7 for ethanol and butanol in SOPC bilayers (13). Nevertheless, this is reasonable agreement given the simplicity and nonspecificity of our coarse-grained model and interactions. In DMPC liposomes, reported values of K were 16.6 and 119.0 for ethanol and butanol (42), whereas other published values of K for butanol range from 170 to 800 for DPPC measured by titration calorimetry (43), and from 186 to 600 for DMPC measured by NMR (44).

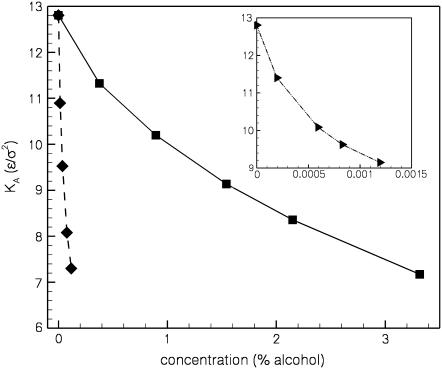
Finally, in Fig. 5 we show the effect of the alcohols on the area compressibility modulus K_A of the bilayer. This modulus can be obtained from the dependence of the surface tension on the area per lipid near the zero tension point,

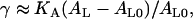(6)

for small deviations of A_L from its value A_L0 at γ = 0. K_A decreases with increasing alcohol concentration and also with increasing alcohol chain length. We see decreases in K_A at the highest x_a values of ∼44% for ethanol and butanol, and ∼29% for hexanol. The magnitude of the decrease is again similar to the 35% reduction in K_A measured by Ly and Longo (see Fig. 5 of (13)).

FIGURE 5.

Area compressibility modulus as a function of the alcohol concentration in the bulk, for ethanol (squares), butanol (diamonds), and hexanol (triangles, inset).

Thus, we find using our coarse-grained model that the DFT predicts the correct trends for the known effects of short-chain alcohols on lipid bilayers. The alcohol headgroups sit near the headgroup region of the lipid bilayer, causing the area per lipid to increase and the compressibility modulus to decrease with increasing alcohol concentration and chain length. The alcohols also partition into the bilayer more strongly as their tail length increases.

Lateral pressure profiles

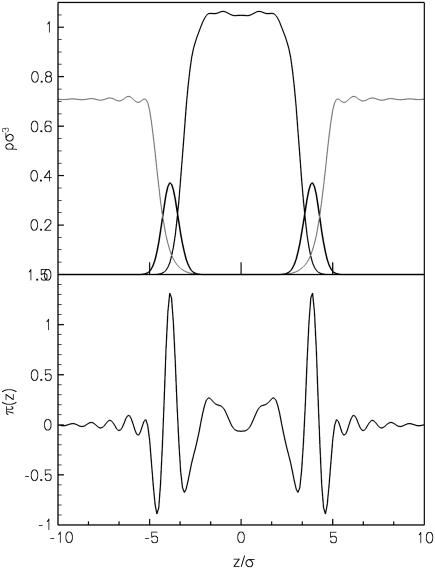
We now go on to examine the effect of the alcohols on the lateral pressure profile π(z). Fig. 6 shows the form of the lateral pressure profile for the unperturbed lipid bilayer in the absence of alcohol, along with the density profile on the same scale. Positive values of π(z) correspond to pressures while negative values correspond to interfacial tensions. Thus, for each leaflet of the bilayer there are two negative peaks, one corresponding to the solvent-headgroup interface and the other to the headgroup-tailgroup interface. The tall peak in between is due to the positive pressure in the headgroup region of the bilayer. In the tail region, we initially get a pressure as well due to packing in the tails, and in this case we have a slight tension in the middle of the bilayer at the ends of the lipid tails. The π(z) profiles calculated from the DFT are qualitatively similar to those calculated using MD on the same coarse-grained lipid model (27), as well as to previous MD simulations on similar models (22). The largest difference is in the center of the bilayer, where MD simulations on CG lipids showed less of a dip in π(z). The features of π(z) found from the DFT are also similar to those obtained from recent atomistic MD simulations, although in the atomistic systems the pressure typically has a peak in the center of the bilayer rather than a dip (16,21). This is presumably related to the difference in density profiles in the middle of the bilayer, as discussed above.

FIGURE 6.

Density (top) and lateral pressure (bottom) profiles for a pure lipid bilayer at kT/ε = 1.3.

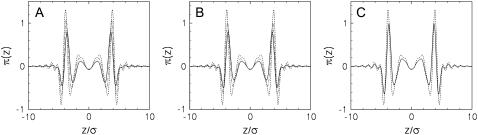
The profiles obtained upon varying the alcohol concentrations are shown in Fig. 7. All of these bilayers are still at zero net tension, γ = 0, so the area under all of the π(z) curves integrates to zero. Although the shape of π(z) remains similar, the alcohols reduce the magnitudes of all the peaks, both the pressures and the tensions, with increasing alcohol concentration. Because the thickness of the bilayer decreases somewhat, the profiles become somewhat more narrow so the peaks shift toward the center of the bilayer. The alcohols have almost no effect in the very center of the bilayer. We note that the pressure profile is related to the density profile of the bilayer (in the DFT it involves a nonlocal integral over the effective interactions between species and their densities, see Eq. A10 of (26)). As discussed above, our lipid density profiles are more homogeneous in the lipid tail region than what is typically found experimentally, which probably has some effect on π(z). This may not be important for the short-chain alcohols studied here since the largest effect is in the interfacial regions rather than the middle of the bilayer. Also, we see a fairly large change in π(z) with the addition of alcohol even though the density profile of the lipid is not much changed with added alcohols (note the difference in the scales for lipids versus alcohols in Fig. 2), so the effect of the alcohols may be decoupled from the effect of the lipid tail density on π(z).

FIGURE 7.

Lateral pressure profiles for bilayers with (A) ethanol at x_a = 0% (dashed), 0.89% (dash-dot-dot), and 3.32% (solid); (B) butanol at x_a = 0% (dashed), 0.037% (dash-dot-dot), and 0.12% (solid); and (C) hexanol at x_a = 0% (dashed) and 0.00119% (solid).

As we discussed in the Introduction, we would expect that a change in π(z) could lead to a change in membrane protein conformations, due to the change in pressures acting on the protein at different depths in the bilayer. To quantify the changes in π(z) due to the alcohols, we can separate π(z) into interfacial tensions and headgroup and tailgroup pressures. In fact, many theories of the free energy of membranes are constructed by adding contributions from the different bilayer regions separately. A good overview is given by Marsh (19). The main contributions are typically given by the interfacial tension γ_phob at the polar-nonpolar (headgroup-tail) interface, the pressure in the interior of the bilayer in the tailgroup region π_int, and the pressure due to headgroup and headgroup-solvent packing (or hydration) π_hyd. To obtain a bilayer with zero net tension, the two pressure contributions π_hyd and π_int must balance the interfacial tension γ_phob. Previous mean-field theories of the lateral pressure profile have typically calculated the spatial contribution of the lipid tails as π_int(z), and simply added the other two contributions as constants which act at the interface (assumed to be sharp) between the tails and headgroups (24,25).

We note that the interfacial tension that we predict at the headgroup-solvent interface is not typically discussed. Recent atomistic MD simulations of π(z) have found that the pressure profile is both complicated and difficult to compute in the headgroup region (16). At the atomistic level, the water penetrates further into the lipid acyl tail region than does the solvent in the coarse-grained models, and this apparently washes out the peak associated with the headgroup-solvent interface, since this interface is extremely broad in atomistic systems (see e.g., Fig. 7 in (16)).

Thus, here we assume that γ_phob corresponds to the headgroup-tailgroup tension γ_HT in the coarse-grained model. In the literature, “the surface tension” of a lipid bilayer takes two different meanings—either the integrated value of π(z) across the whole membrane, which we have termed γ; or, alternatively, the value of γ_phob. In an equilibrium lipid bilayer, γ = 0, whereas the value of γ_phob can be estimated by experiments on monolayers and is found to be of the order of 38 mN/m for typical phospholipids (19).

We now turn to the DFT-predicted values of these quantities. To obtain pressures and tensions we must define how to divide π(z) into different regions. This could be done in a variety of ways. One would be to define dividing surfaces based on the density profiles. A more simple way is to simply consider the areas under the various peaks in π(z), with the boundaries of the different regions defined by the points where π(z) = 0. We have followed this method to calculate four quantities from π(z), the tailgroup pressure π_int, the tailgroup-headgroup interfacial tension γ_HT, the headgroup pressure π_hyd, and the headgroup-solvent tension γ_HS. The change in the magnitude of these quantities as a function of alcohol concentration (relative to their values at x_a = 0) is shown in Fig. 8. The results are fairly similar for all three alcohols. The most change from the x_a = 0 values occurs in γ_HT and in the tailgroup pressures π_int. We note that the curves appear discontinuous at small x_a, in that they do not seem to extrapolate smoothly to the pure bilayer case, which is due to sensitivity of the DFT to approximations at small x_a. From the figure we see that the rate of change is largest for π_hyd and γ_HT, with γ_SH and π_int changing more slowly with increasing alcohol concentrations. In any case, the DFT predicts asymmetric changes in π(z) (in each bilayer leaflet) as alcohol is added. Cantor has argued that such asymmetric changes are necessary to affect protein conformational equilibria (17).

The decrease in γ_HT shows that the DFT does predict that the addition of alcohol reduces the polar-nonpolar interfacial tension. We find reductions in γ_HT of ∼48% for butanol and ∼40% for ethanol. Ly and Longo estimated values for γ_HT based on their area compressibility data (and some theory), and found reductions of ∼53% for butanol and 37% for ethanol (13).

We can also compare our results to previous theoretical work. Cantor has performed extensive calculations of the effects of alcohols and other additives on the lateral pressure profile using a lattice SCF theory (1,25,35). Our results differ somewhat, due to the different approximations in the two theories. In Cantor's work, only the lipid tail contribution to the spatial profile of π(z) is calculated. Both the lipid and alcohol tails are tethered at one end to a sharp aqueous interface, and the bilayer is assumed to be incompressible so that the density is constant in the hydrophobic tail region. The headgroup and interfacial tension contributions (π_hyd and γ_phob) to the free energy are added in separately as discussed above, although the equilibrium area (and hence the surface density) is calculated in a self-consistent way so as to obtain a tension-free bilayer. In general the SCF theory predicts that with the addition of short-chain alcohols, π(z) increases near the aqueous interface and then decreases a few layers into the acyl chain region, with no change in the very middle of the bilayer (25). The DFT predicts no change in the very middle of the bilayer and a decrease in π(z) in the rest of the tail region. However, we do not find an increase in π(z) in the tail region near the interface with the headgroups.

This difference is presumably related to the compressibility of the bilayer. As discussed above, the DFT calculations are for compressible fluids, and we find that as the alcohol concentration in the bilayer increases, the total site density decreases; although the thickness does decrease, it does not decrease sufficiently to counteract the increase in A_L. The lower density will lead to lower pressures in the tail region, since there is less entropic repulsion between the chains when they are at lower density. By contrast, Cantor imposes a constant density throughout the bilayer. The total density surely affects π(z), and neither theory obtains the density decrease in the middle of the bilayer seen experimentally. Also, as we noted above, the DFT overpredicts the density decrease in the aqueous region, which could also be affecting the lipid bilayer. We know that the coarse-grained solvent is not treated very accurately by the current DFT (27). Thus, it seems that more accurate models are required to be more confident of the predictions of the lateral pressure profile.

CONCLUSIONS

We have examined the effect of short-chain alcohols on lipid bilayers using a previously developed density functional theory. The theory treats all the components of the system on an equal footing, so that the self-assembly of the lipid bilayer and its properties are a direct output of the theory applied to any given model of the system. This is in contrast to many previous statistical mechanical theories of lipid bilayers, in which various contributions to the free energy were added in separately, some in a quite phenomenological way.

As expected, we find that the alcohols are located preferentially near the headgroup-tailgroup interface, with longer chain alcohols penetrating further into the bilayer interior. The theory predicts the correct qualitative trends for the changes in the area per lipid, the adsorption of alcohol into the bilayer, and the decreases in the area compressibility modulus and headgroup-tailgroup interfacial tension. For quantities that could be compared with experiment we generally obtained the right order of magnitude from the theory and in some cases even semiquantitative agreement. We calculated the lateral pressure profile π(z) for various aqueous alcohol concentrations and found that the alcohols have the effect of reducing the magnitudes of all the peaks in π(z). This is in part due to a reduction in the density of the lipid bilayer with the addition of alcohol. We found that the changes in π(z) induced by alcohol adsorption are asymmetric (in each leaflet), in that the change is greater in some regions of the bilayer than in others. These changes in the pressure profile could potentially influence the conformational state of intrinsic membrane proteins, and hence provide a nonspecific mechanism for the biological effects of alcohol.

Improvements to this work can be made in two areas. The first is in the coarse-grained models themselves; more accurate models could be developed and validated using simulations. Such models are available in the literature for some lipid systems (45,46), although currently they would be limited in which alcohols could be treated, since the “united atoms” in these models often incorporate as many as three or four real atoms in one bead. Second, improvements can be made in the approximations of the theory. There is a spectrum of density functional theories available in the literature, utilizing different approximations for the free energy functional. A DFT based on more accurate equations of state for the lipids, solvent, and alcohols (and their mixtures) would likely result in more quantitative predictions.

In general, density functional theory is a promising technique for investigating the effects of various additives on lipid bilayers, since it treats the full system in an internally consistent way. Further work on both the coarse-grained models and on the approximations in the free energy functional will lead to improvements in the theory and to more predictive results in the future.

APPENDIX

Here we describe some technical details of the DFT calculations that differ from our original work (26,27).

The DFT calculations are done in the grand canonical ensemble where the state variables are the volume V, the temperature T, and the chemical potentials of each molecular species in the system, μ_i. In our formulation, the chemical potentials are manipulated via the bulk densities in the homogeneous reference system, which is a bulk mixed fluid of all three species in equilibrium with our inhomogeneous solution of interest (the bilayer). In our previous lipid work (26,27), we set the chemical potentials through a total bulk site density ρ_b and the solvent number fraction x_s = ρ_{s, b}/ρ_b in the bulk reservoir fluid in equilibrium with the fluid in the computational domain. When the alcohols are added to the system, we have an additional chemical potential variable that must be set. Ideally, we would like the number densities of solvent and alcohol molecules in the bulk fluid region far from the bilayer to correspond to the values one would obtain experimentally, i.e., mostly constant with a small decrease in density as alcohol is added, following the correct equation of state for a water/alcohol mixture. However, we cannot set number densities in the open ensemble that we use here and additionally, we do not know the correct equation of state for our coarse-grained model. We must thus determine how to set the three “chemical potential” variables, ρ_{l, b}, ρ_{s, b}, and ρ_{a, b}, for the lipids, solvent, and alcohols, respectively.

For the calculations of bilayer structure, we are interested only in bilayers at zero net tension, γ = 0. This introduces one constraint on the chemical potentials. Thus at a fixed temperature in the absence of alcohols, setting γ = 0 defines a line in phase space. We enforce γ = 0 by always staying on the binodal line in which the bilayer solution is in thermodynamic coexistence with a uniform aqueous phase (either solvent or solvent + alcohols) (26). In our previous work, we kept the total site density ρ_b = ρ_{l, b} + ρ_{s, b} fixed at a constant value, which then picks out a single point on the binodal line, leading to a unique zero tension bilayer.

To introduce the alcohols, we begin with a very small concentration of alcohols added to the previous γ = 0 bilayer. We then locate bilayers at increasing concentrations of alcohols by increasing the alcohol chemical potential through increases in ρ_{a, b}. These calculations are performed using the phase transition-tracking algorithm in our DFT code (47). This algorithm works by first increasing ρ_{a, b}, and then finding the value of one of the remaining ρ_{i, b} necessary to maintain γ = 0. In our case we chose to adjust ρ_{s, b} in this stage. The third chemical potential parameter, ρ_{l, b}, is then a free parameter which we must set. To be consistent, we would like to again keep the total site density constant, in which case we would have

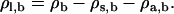(7)

Due to a subtlety in the algorithm, we can only fulfill this equation approximately. Essentially, the value of ρ_{s, b} must be adjusted to find the γ = 0 point, and so it cannot simultaneously be used in Eq. 7 as a fixed value. There are then various options for choosing the value of ρ_{l, b}, and each option corresponds to following a different binodal line on the phase-space surface defined by given values of T, V, and ρ_{a, b}.

We tried a few different options for this path. One option is to simply keep ρ_{l, b} at a fixed value. This led to large decreases in the densities in the aqueous fluid region away from the bilayer as we increased ρ_{a, b}, which is not physical. A more logical choice would be to decrease the value of ρ_{l, b} as we increase ρ_{a, b} so as to keep ρ_b approximately constant; physically, fluids are nearly incompressible so as we add one species, the site density of the others should decrease to keep the pressure roughly constant. We tried various phenomenological forms for ρ_{l, b} as a function of ρ_{a, b}, and evaluated the results based on the constancy of the site density in the uniform aqueous fluid region. We found that the best way to keep this density close to constant was to follow Eq. 7 as best we could. To do so, we use the following algorithm when performing phase transition tracking calculations:

• Step 0: Begin with a bilayer solution at some value of T and the ρ_{i, b}, say . We choose a solution with a small value of 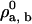= 0.001, close to the binodal point for the pure bilayer at T = 1.3 and ρ_bσ³ = 0.68.

• Step 1: Increase ρ_{a, b} by a fixed step to 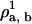. Set the lipid chemical potential variable 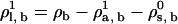. The algorithm will determine the new value of the solvent chemical potential, 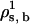, by requiring γ = 0.

• Step i: Repeat, using the new value of ρ_{s, b} in the next value of the lipid chemical potential, so that in step i, .

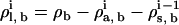This algorithm has the effect of approximating Eq. 7. Thus, the value of the total site density does not remain strictly constant but does not change by much. We found that we obtained better results at higher initial values of ρ_b compared to what we used previously, and in particular this allowed us to remain in the regime of liquidlike densities for all the calculations. We chose to perform all calculations in this article beginning with a total site density of ρ_bσ³ = 0.68. The value of ρ_b decreases somewhat as the amount of alcohol in the system is increased; at the highest aqueous alcohol concentrations, we obtained ρ_bσ³ = 0.652, 0.662, and 0.675 for the ethanol, butanol, and hexanol calculations, respectively. As noted in the text, the site densities in the aqueous region far from the bilayer also decrease somewhat as we increase ρ_{a, b}, from (ρ_s + ρ_a)σ³ = 0.71–0.64 for ethanol, from (ρ_s + ρ_a)σ³ = 0.7–0.63 for butanol, and from (ρ_s + ρ_a)σ³ = 0.71–0.66 for hexanol. These represent fairly small changes in the total and aqueous fluid site densities, although as described above, the decrease in the aqueous density is larger than seen experimentally for, say, ethanol/water mixtures.

These decreases in density do contribute to the lowering of all the peaks in π(z) as alcohol is added. For a comparison, we calculated π(z) for a pure lipid bilayer at the lower total site densities found at the maximum alcohol concentrations noted here. This is basically to attempt to make comparisons at roughly the same chemical potentials (although of course with the alcohols present, the values of ρ_{b, i} are different than for a pure bilayer, so it may not be meaningful to insist that the sum 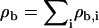be the same). We find that there is still a significant effect of the alcohols on π(z), so the decrease in ρ_b is not the only effect of the alcohols on π(z). Thus, the lowering of all the peaks in π(z) as we add alcohol is a prediction of the DFT, and not purely an artifact of our approximation scheme for setting the value of ρ_{b, l}.

One more consequence of using this algorithm to set ρ_{b, l} is that the DFT calculations appear to be quite sensitive to the initial choice of ρ_{b, l} and ρ_{b, s} at small alcohol concentrations. Slightly different choices of these initial parameters lead to different bilayer solutions with somewhat different values of A_L. However, at larger alcohol concentrations we find that solutions started with different initial values converge to the same results. This then determines the lower limit of alcohol concentration that we report in all of our results above. The results at larger values of x_a appear to extrapolate well back to the results for the pure lipid bilayer. For the pure lipid bilayer at ρ_bσ³ = 0.68 we obtain A_L = 4.848σ²; extrapolating our results with the alcohols back to x_a = 0 we obtain A_L = 4.898σ², 4.862σ², and 4.861σ² for ethanol, butanol, and hexanol, respectively.

The DFT requires input about the bulk thermodynamics of the system, in the form of the direct correlation functions c_αβ(r). As before, we obtain these from the polymer reference interaction site model (PRISM) theory (26). In principle, the c_αβ(r) values are functions of the different bulk site densities. To avoid recalculating these from PRISM every time we change one of the chemical potential variables, we again did an interpolation between four different c_αβ(r) values. For all the calculations presented here, we calculated the c_αβ(r) at fixed values of ρ_bσ³ = 0.68, and at four sets of values for ρ_{s, b} and ρ_{a, b}, namely {ρ_{s, b}, ρ_{a, b}} = {0.299, 0.00068}, {0.293, 0.0068}, {0.277, 0.022}, and {0.266, 0.034}.

Finally, we measured the area compressibility modulus as described previously (26,27). At each fixed value for the alcohol chemical potential, we varied the solvent and lipid chemical potentials (keeping ρ_b fixed to its value at the γ = 0 state point of interest) to vary the area per lipid A_L away from its value on the binodal at zero tension. The value of K_A was calculated by the best linear fit through the γ vs. ΔA_L/A_L0 data, for ΔA_L/A_L0 varying between −0.03 and 0.03.