A Computational Study of Nucleosomal DNA Flexibility

Abstract

Molecular dynamics simulations of the nucleosome core particle and its isolated DNA free in solution are reported. The simulations are based on the implicit solvent methodology and provide insights into the nature of large-scale structural fluctuations and flexibility of the nucleosomal DNA. In addition to the kinked regions previously identified in the x-ray structure of the nucleosome, the simulations support the existence of a biochemically identified distorted region of the DNA. Comparison of computed relative free energies shows that formation of the kinks is associated with little, if any, energy cost relative to a smooth, ideal conformation of the DNA superhelix. Isolated nucleosomal DNA is found to be considerably more flexible than expected for a 147 bp stretch of DNA based on its canonical persistence length of 500 Å. Notably, the significant bending of the DNA observed in our simulations occurs without breaking of Watson-Crick bonds. The computed relative stability of bent conformations is sensitive to the ionic strength of the solution in the physiological range; the sensitivity suggests possible experiments that might provide further insights into the structural origins of the unusual flexibility of the DNA.

INTRODUCTION

Evidence is now overwhelming that not only the sequence, but also the details of DNA packaging inside the cell are an important part of the genetic message. The primary level of DNA compaction in eukaryotic organisms in vivo is the nucleosome. At this level, a stretch of 147 basepairs of the DNA is tightly wrapped (∼1.65 times) around a set of eight proteins (histones) that carry the charge opposite to that of the DNA. Details of the nucleosome dynamics are vital for understanding key cellular processes such as DNA replication, repair, and transcription (1–5). Cell differentiation is also intimately linked with DNA compaction. Despite its importance, the nucleosome system is far from being fully understood. One of the key unanswered questions is the following: how can the whole nucleosome be highly stable, protective of its genetic material, while at the same time its tightly wrapped DNA be highly accessible, easily revealing its information content?

This dual nature of the DNA packaging in the nucleosome is supported by experimental studies; these reveal the high stability of the whole nucleosome at physiological conditions (6), and, at the same time, suggest that small fragments (∼50 bp) of the DNA helix can transiently peel off (7,8). The latter observation implies a relatively small free energy barrier associated with such partial unraveling and is suggestive of possible mechanisms behind processes such as transcription, in which fragments of the nucleosomal DNA become accessible sequentially (8). Since the atomic resolution structures of the nucleosome became available, there is likely not much ambiguity left about its static conformation; however, details of nucleosomal dynamics are not as clear, especially at atomic resolution. These are important for developing molecular mechanisms of the key biological processes involving the nucleosome. Theoretical studies using atomistic molecular dynamics simulations may provide much needed insights in this area.

A general question that can be addressed by such simulations: exactly how flexible is the DNA wrapped around the nucleosome? Severely restricted mobility of the double helix would be suggestive of tight binding, possibly inconsistent with the idea of transient DNA dissociation in processes such as transcription. A related question: what is the origin of structural distortions that arise when the straight DNA double-helix is forced to adopt the conformation found on the nucleosome? Past experimental studies have characterized the persistence length of DNA to be ∼500 Å, or 150 basepairs (9–11). Based on this finding, one would expect that considerable force would have to be exerted on the DNA for it to adopt the highly bent superhelical conformation of nucleosomal DNA. Not only would this force need to wrap the DNA around the histone core, but, based on experimental data, it would also have to locally distort the DNA itself. In particular, the histone core was shown to have a preference for DNA with an altered helical periodicity (12). Additionally, Hayes et al. (13) showed that DNA sequences with different structural properties in solution all adopt a similar, slightly perturbed conformation in the nucleosome. The 1.9 Å resolution nucleosome core particle crystal structure affirms that the structure of the DNA on the histone core deviates significantly from the best fit ideal superhelical DNA (14). Not only does nucleosomal DNA have twice the basepair-step curvature needed for the superhelical conformation, but it is kinked in several regions. Structurally distorted regions, or kinks, have also been identified biochemically. Regions ±1.5 helical turns from the dyad have been shown to be the sites of DNA distortion. Some of these kinked regions have been shown to have potential biological significance. For example, the DNA located at ±15 bp from the dyad have increased sensitivity to attack by singlet oxygen (15), which preferentially attacks denatured or wedge-shaped DNA structures. This region of the DNA is also recognized as being distorted by HIV integrase (16) and permanganate (17).

The idea that considerable force is needed to create the large overall bending and local distortions of the nucleosomal DNA appears to be common sense from the classical picture of the rather inflexible DNA. However, it may not be all that simple, according to recent intriguing experimental findings (18,19). Namely, on short length scales (∼100 bp), the DNA double helix was not found to behave as a relatively stiff rod, as might have been expected based on its classical (9–11) persistence length value of ∼150 bp. In contrast, short DNA fragments were found to cyclize spontaneously, with an appreciable probability. Exactly how this unusual flexibility is accommodated structurally is not known (19). Since relatively short, bent DNA fragments participate in many vital biological processes, the issue is important; it has already provoked considerable interest and debate in the community. Various, sometimes mutually exclusive (19–21) explanations for the phenomenon have been proposed. While the debate does not yet appear to have been settled (20), recent experimental evidence based on techniques such as FRET (22) and AFM (P. A. Wiggins, T. van der Heijden, F. Moreno-Herrero, A. Spakowitz, R. Philips, J. Widom, C. Dekker, and P. C. Nelson, Nature Nanotechnology, in press)—different from those used in the original study (18)—provide more evidence in support of enhanced DNA flexibility on short length scales.

To investigate the flexibility of nucleosomal DNA and examine the origins of possible structural distortions contributing to this flexibility, we have performed several all-atom molecular dynamics simulations. These simulations explore, at the full atomic resolution, the dynamics of the entire nucleosome core particle (histone core and the DNA) as well as its isolated DNA free in solution. In some of the simulations, constraints have been used to model the DNA winding around the nucleosome.

The key to our approach is the use of the implicit solvent (24,25) technique in which the effects of aqueous solvation are represented implicitly, via a continuum medium with the properties of bulk water. The electrostatic screening effects of the high dielectric medium as well as those of salt ions enter implicitly, via appropriate terms added to the system's configurational energy. The hydrophobicity is also included as a separate contribution. Within the approach, the system's configurational energy in the presence of solvent becomes an analytical function of the coordinates of the macromolecule only (and solvent parameters such as ionic strength), which contributes to the method's computational efficiency. The technique effectively eliminates the need to keep track of the individual water molecules, and focuses the computational power on the macromolecule of interest (e.g., the protein and the DNA), often resulting in considerable gains in computational efficiency. Also, compared to the traditional explicit solvent simulations, the implicit solvent methodology effectively eliminates the drag of viscosity, leading to greatly enhanced conformational sampling. The approach is also particularly well suited for estimations of relative free energies of various molecular conformations. Over the past decade the methodology has enjoyed considerable success, especially in such computationally challenging applications as the protein-folding problem (26,27).

The article has the following structure. First, we orient the reader by briefly describing the simulations we have performed. Then we present the results of the molecular dynamics simulation of the entire nucleosome, highlighting the structural fluctuations and kinking of the DNA. Next, we describe the simulations and energetic analyses of two superhelical DNA structures and show that, on average, formation of the kinked structures on the nucleosomal DNA are unlikely to entail considerable energetic costs. Finally, we discuss the flexibility of isolated nucleosomal DNA observed in our simulations. Analysis of the relative free energies of the conformations with various degrees of bending is presented. Computational protocols and comparative validation of the methodology are presented in Methods, below.

METHODS

Structures

The 1.9 Å crystal structure of the nucleosome core particle (PDB code 1KX5) (28) has been used as the initial structure for molecular dynamics of the NCP-DNA and WholeNCP-DNA simulations. The same sequence is used to build DNA in standard B-form and also the Ideal-DNA. The structures are built with NAB (29). The Free-DNA is built using standard B-form parameters of 35.87° as the twist value and 3.33 Å as the rise value. The parameters of the WholeNCP-DNA are first analyzed with X3DNA (30), and the corresponding parameter values of 34.65° for twist and 3.38 Å for rise are used to build the Ideal-DNA.

Molecular dynamics

All molecular dynamics (MD) trajectories have been obtained with AMBER 8 (31), using the ff99 force field. The SHAKE method is used to restrain hydrogen-heavy atom bond distances. The integration time-step is 2 fs. The average temperature of the system is maintained at 300 K by weak coupling (via the Berendsen algorithm) to a heat bath with coupling constant of 2 ps.

Simulations in implicit solvent

The implicit solvent methodology based on the modified Generalized Born model (25) (GB^OBC, igb = 5) is used to describe solvation effects in MD simulations of the WholeNCP-DNA, Free-DNA, NCP-DNA, and Ideal-DNA. The mbondi2 radii are set. The nonpolar contribution is computed via ΔG_surf = 0.005 [kcal/mol] × A [Ų], where A is the solvent-accessible surface of the molecule estimated by a fast analytical routine within AMBER. A reaction field cutoff (rgbmax = 15) is employed to speed-up the calculation of effective Born radii (32). No cutoff is used for the long-range interactions. The salt concentration is set to 0.2 M during the WholeNCP-DNA and the Free-DNA simulations. A salt concentration of 10 M is used for the NCP-DNA and Ideal-DNA simulations to dampen the electrostatic repulsions between the coils of the nucleosomal DNA and reduce possible artifacts associated with the use of the restraints. All simulations undergo 100 steps of minimization with a 5 kcal/mol all-atom constraint relative to the x-ray positions. Two 10 ps equilibration steps are performed, the first using a constraint of 1.0 kcal/mol/Ų, the second using a 0.1 kcal/mol constraint. After equilibration, the simulations continued without constraints, or with 0.1 or 0.001 kcal/mol/Ų constraints, as in the NCP-DNA and Ideal-DNA simulations. All simulations continue for 1 ns, except for the Free-DNA for which a total of 5 ns is performed.

Simulations in explicit solvent

Explicit simulations of the WholeNCP-DNA and Free-DNA have been performed to provide further validation and a reference point for implicit solvent simulations. Detailed comparisons are presented in Additional Validation, below.

The initial minimization steps are as follows. The systems are immersed in a box of TIP3 water and are neutralized with Na⁺ ions. The default particle mesh Ewald (PME) parameters of AMBER 8 are used (32). The water and ions are first equilibrated to 300 K for 100 ps while the solute is held frozen. Next the water and ions undergo 300 steps of minimization. Lastly, the solvent and solute are minimized for 300 steps. The system is then gradually heated to 300 K over 40 ps at constant volume and then an additional 40 ps of constant volume MD at 300 K is performed. The constant-pressure, explicit solvent MD simulations with PME of the WholeNCP-DNA and Free-DNA are performed. The following conditions are used: SHAKE on the hydrogen atoms; a 2 fs timestep; temperature of 300 K; and a 9 Å cutoff applied to the long-range interactions.

Calculation of structural signatures

The minor groove has been measured with the ptraj module of the AMBER package, using the same procedure as reported by El Hassan and Calladine (33). The DNA parameter values of roll, twist, and slide have been calculated with the software package, Curves (34).

The error margins are computed by dividing the 500 snapshots into five equal-sized bins in order of the time. The average of each bin is computed, and the error is computed from the standard deviations of the five averages.

Calculation of energies and forces in implicit solvent

All energies are calculated using the MM-GBSA module in AMBER 8, which uses the continuum solvent approximation. The same scheme is used to compute configurational energy E(x_i, y_i, z_i) as a function of atomic coordinates (x_i, y_i, z_i) for each step of molecular dynamics. The forces are computed as F_i = ∂E/∂x_i (see, e.g., (35)). Within the implicit solvent approach, the total energy E of the solvated system is calculated as the sum of gas-phase energy plus the free energy of solvation that includes the electrostatic and nonpolar parts. Namely, E = E_int + E_elec + E_vdw + E_surf. Here, E_int represents the additive bond, angular and dihedral degrees of freedom, respectively:

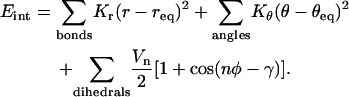(1)

The constants and their specific values are defined in the force field of Cornell et al. (36); a general discussion of this type of decomposition can be found in Schlick (35).

The van der Waals interactions between the atoms are described by E_vdw, and E_surf mimics the hydrophobic effect. We use [kcal/mol] E_surf = 0.005 A, where A [Ų] is the calculated solvent-accessible area of the molecule. The value E_elec is computed as E_elec = E_vac + E_solv, where E_vac is the protein's Coulomb energy in vacuum, and E_solv is the electrostatic component of the free energy of solvation, computed here within the GB approximation. All components of the total energy are computed for each snapshot using the AMBER force-field parameters. Note that the energy computed by the MM-GBSA approach includes the free energy of solvent rearrangement implicitly. For the MM-GBSA we use the same force field, GB model, and nonpolar surface parameters as described above in the MD simulation section. The differences are as follows. For the energetic analysis we do not use any reaction field cutoffs (when calculating effective Born radii we set rgbmax > system size). Also, we set the salt concentration to 0.2 M in all cases except in the calculation of the salt-dependence of the relative stability of the bent and straight conformations. Naturally, no restraining potentials are included for the post-MD analysis of the individual snapshots.

The relative stability is calculated as ΔΔG(salt) = ΔG(salt → ∞) + [ΔE_elec(salt) − ΔE_elec(salt→ ∞)]. Since we are interested only in how the destabilization effects of salt change as the salt concentration is decreased, we set ΔG(salt → ∞) = 0. The GB model we use here was demonstrated to describe the electrostatic effects of monovalent salt adequately (37).

Computational resources and times

All of the MD simulations have been performed on Virginia Tech's SYSTEM X, the 2200 CPU supercomputer (http://www.tcf.vt.edu/systemX.html). The computational times and CPUs used for each simulation are noted in Table 1. Clearly, for the large systems such as the entire nucleosome, the implicit simulations reported here appear to be more computationally expensive than the explicit simulations. This is due to the fact that we have not used any approximations to speed-up the calculation of the charge-charge interactions in order to avoid introducing any potential artifacts into the implicit solvent (GB) approach. As a result, the time complexity of the method is O(N²), where N is the number of atoms. On the other hand, the traditional explicit solvent simulations typically employ the PME approximation, which reduces the time complexity of computing the electrostatic interactions to O(Nlog(N)) by introducing an artificial periodicity into the system. Still, the seemingly unfavorable computational expense of the implicit simulations are completely offset by drastically enhanced conformational sampling: for the DNA system, the enhancement is believed to be a factor of 20 or even 100 (see (38,39)). Thus, a 5 ns implicit solvent simulation of a DNA fragment effectively corresponds to 0.1–0.5 μs in explicit solvent.

TABLE 1.

Computation time and processor utilization of the simulations

Simulation	No. Atoms	Simulation time	Computation time (hours)	No. CPUs
Implicit-WholeNCP-DNA	25,086	1 ns	720	16
Explicit-WholeNCP-DNA	223,132	500 ps	70	16
Implicit-NCP-DNA	9346	1 ns	122	32
Implicit-Free-DNA	9346	5 ns	115	128
Explicit-Free-DNA	111,629	500 ps	35	16
Explicit-DNA decamer	10,277	10 ns	56	16
Implicit-DNA decamer	632	10 ns	49	8

Additional validation

The structures from the implicit solvent MD simulations described above have been compared to the ones obtained by the traditional, explicit solvent approach. The latter, in conjunction with modern force fields, is known to provide a fairly good representation of nucleic acids as compared to experiment (40,41). In our implicit solvent simulation, the all-atom RMSD to the x-ray structure of the WholeNCP-DNA system stabilizes soon after equilibration to ∼4.0 Å and exhibits only minor fluctuations around this value for the rest of the simulation. The all-atom RMSD of the explicit solvent trajectory is 3.6 Å at the end of the 500 ps simulation. Flexible histone tails are excluded from the RMSD calculations in all cases.

To provide additional support for the use of the implicit solvent approach in the context of the nucleosomal DNA, the number of Watson-Crick basepairs have been calculated for each snapshot of the implicit-solvent-based WholeNCP-DNA and Free-DNA simulations (using the 3DNA software package (30)). The average number of pairs for the WholeNCP-DNA is 143. The average number of pairs for the Free-DNA simulation is 146. When the 10 basepairs from both ends are excluded from the calculation, on average, all included basepairs are persistent throughout both the WholeNCP-DNA and Free-DNA simulations.

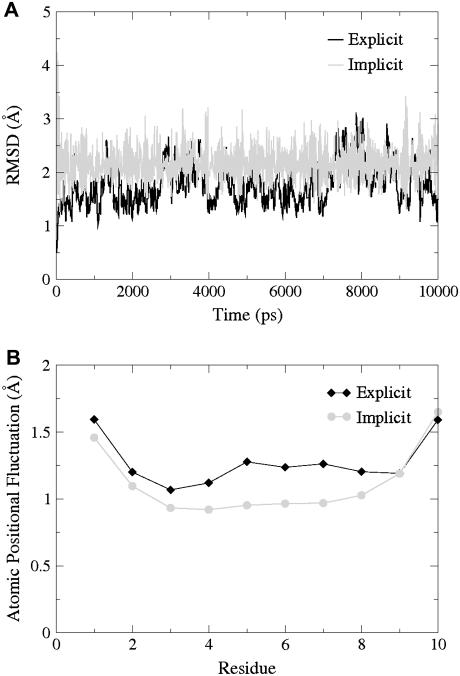
Relatively short DNA fragments present an opportunity to directly compare the explicit and the implicit solvent MD on multi-nanosecond timescales. To this end we have used a 10 bp fragment (decamer GCGCGCGCGC created with the NAB program using standard B-form DNA parameters). Both the implicit and explicit water simulations are run for 10 ns using the protocols described above. All Watson-Crick basepairs have persisted throughout both the implicit and explicit solvent trajectories. In the explicit solvent simulation, the backbone RMSD to the t = 0 conformation is 1.8 ± 0.4 Å, averaged over the last 5 ns; for the same timeframe, the RMSD of the implicit simulation is only slightly larger, 2.2 ± 0.4 Å. As is evident from Fig. 1, the decamer in the implicit simulation is as stable as in the explicit solvent simulation. We attribute the fluctuations to the shortness of the fragment, and note that similar results and RMSD values were reported earlier by Tsui and Case (38) for a DNA fragment of similar size. The agreement between the explicit and the implicit solvent results provides an additional support for the use of GB-based implicit solvent model for the DNA simulations, at least on the timescale of 10 ns.

FIGURE 1.

Plots of (A) RMSD versus time of every 10 ps and (B) atomic positional fluctuation by residue of the last 5 ns of the explicit (solid) and implicit (shaded) decamer simulations.

RESULTS AND DISCUSSION

The MD simulations we have performed can be divided into three groups: 1), MD of the whole nucleosome core particle; 2), MD of just the nucleosomal DNA constrained to the wound-up conformation found on the nucleosome; and 3), MD of the free nucleosomal DNA in solution, initially set in a straight, classical B-form. All structures used have the same sequence as the DNA in the 1.9 Å NCP crystal structure of Richmond and Davey (14). In this section we describe results and analysis of the simulations in each group identified above. In all simulations, an implicit solvent model based on the GB approximation has been used to represent solvent effects, including the screening effects of salt.

The whole nucleosome

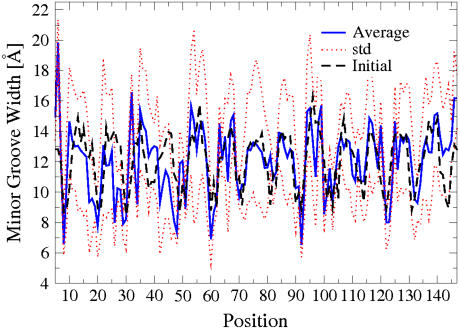
The 1-ns-long simulation of the whole nucleosome core particle (WholeNCP-DNA: histones + the DNA) is based on the x-ray structure of Richmond and Davey (14) as the starting conformation. The main motivation is to estimate the size of the DNA fluctuations and explore the nature of the kinked regions originally identified in the x-ray structure of the NCP. In particular, Richmond and Davey (14) identified six kinked basepair steps (16/17, 26/27, 38/39, 109/110, 121/122, and 131/132), three on either side of the dyad. Minor groove bending causes kinking of the DNA in the 1.9 Å crystal structure of the NCP and is defined by, relative to the classical B-form, increased slide values, increased twist values, and decreased roll values. The results of our simulation are summarized in Fig. 2. Our definition of a kink is slightly less stringent than Richmond and Davey's (roll < −11.8°; twist > 40°; and slide > 1.25 Å) to ensure the inclusion of all of the six kinked basepairs from the x-ray structure. Overall, during the course of the 1-ns-long MD simulation, the kinks do appear to persist predominantly at the locations found in the x-ray structure, providing support for the methodology we use. The simulation also reveals the presence of a kinked region (dashed line at basepair-step 90 in Fig. 2) previously not identified in the x-ray structure. This region corresponds with the biochemically identified distorted structure (15–17). Analysis of the minor groove width during the MD simulation supports the existence of a distorted structure located at ±15 bp from the dyad (Fig. 3). Near residues 60 and 90, the minor groove width decreases from ∼9 Å at the initial value in the crystal structure, to an average of ∼6.5 Å over the last 500 ps of the simulation. During DNA bending, the minor groove will become compressed when it faces the histone octamer. Sharp bending is evident ±15 bp from the dyad, as the width of the minor groove at this location is much less than the other minor grooves that also face the histone octamer.

FIGURE 2.

Localization of kinked basepair steps during the MD simulation of the whole nucleosome core particle (WholeNCP-DNA), represented here by 1000 equidistant snapshots. The solid lines (shown here to guide the eye), correspond to the kinks in the original structure identified by Richmond and Davey (14). We adopt a slightly more relaxed definition of a kink (open circles): roll <−11.8°; twist > 40°; and slide > 1.25 Å. Solid circles represent kinks at t = 0. The dashed line represents a region that has been identified as a spot of DNA distortion (biochemical kink).

FIGURE 3.

Minor groove width of the bases of the nucleosomal DNA (WholeNCP-DNA) during the 1 ns MD simulation. Thick blue solid line, values averaged over last 500 ns of the MD; the corresponding standard deviations are shown as red dotted lines. For reference, the initial values of minor grove width are also shown (black dashed line). An extreme narrowing of the minor groove occurs near a region located at ±15 basepairs from the dyad.

The superhelical DNA: energetics of the kink formation

Experimental determination of the amount of free energy stored in the kinks of the nucleosomal DNA is difficult, if not impossible; certainly, this information is not directly available from the x-ray structure of the nucleosome. At the same time, MD simulations based on implicit solvent offer an opportunity to estimate this additional conformational energy, relative to a hypothetical smooth superhelical DNA, in a fairly straightforward manner (24,38). To this end, we have performed MD simulations of two 147 bp fragments of DNA starting from the structures described below and illustrated in Fig. 4 A:

1. NCP-DNA. Nucleosome core particle DNA in the same conformation as in the core particle, but stripped of histones.

2. Ideal-DNA. An ideal (i.e., smooth, no kinks) superhelical DNA with structural parameters corresponding to the average values of NCP-DNA (see Methods, above, for details). No histones.

FIGURE 4.

Axes of curvature of the initial (A) and final (B) snapshots of the NCP-DNA (dark) and the Ideal-DNA (light) simulations. Both structures represent the winding of the DNA in the nucleosome, but the kinks are initially present only in the NCP-DNA; the Ideal-DNA is in an ideal, smooth superhelical conformation at the start of the simulation. No histone core is present in either case, but all-atom harmonic restraints (0.1 kcal/mol/Ų) are used to keep the structures close to their respective initial conformations.

The Ideal-DNA and NCP-DNA have each undergone 1 ns of MD in implicit solvent. Cartesian harmonic restraints (0.1 kcal/mol/Ų) have been used to hold all the atoms close to their original positions. The results are illustrated in Fig. 4 B, which shows the qualitative difference between the two structures at the beginning and at the end of the simulation. Clearly, the overall superhelical shape of the DNA found on the nucleosome is preserved by the constraints throughout the simulation. A detailed analysis reveals the persistence of most of the kinks in the NCP-DNA and almost a complete absence of those in the Ideal-DNA throughout the simulation. Namely, an average of 379 ± 27 kinked basepair steps occur in a 100 ps interval in the NCP-DNA while only an average of 2.6 ± 0.4 kinks occur in the Ideal-DNA during the same time interval. To put these numbers in perspective: if all six kinks identified by Richmond and Davey persisted in every snapshot throughout the entire simulation, the number of kinked basepair steps would be 600 per a 100 ps interval.

To determine whether an ideal, smooth superhelical conformation of the nucleosomal DNA is energetically preferred over the conformation (with kinks) found in the actual nucleosome, the difference in (free) energy of the two systems has been estimated on the ensemble of snapshots from the last 500 ps of the MD trajectories described above. The result is that the energy of the NCP-DNA is 172.42 ± 7.09 kcal/mol less than that of the Ideal-DNA. Therefore, it appears that, if anything, kinks do not cost additional energy relative to an ideal, smooth DNA constrained to the overall conformation found in the nucleosome. One has to be careful, though, as to the exact meaning of this finding. It does not guarantee that no extra energy (conformational strain) is stored locally in the kinked regions, but if the strain does build up, it is compensated for by conformational adjustments elsewhere on the structure so that the overall energy of the 147 bp fragment is still lowered. Of course, force-field artifacts are always a possibility, but we are reasonably confident that this is not the case; in an earlier work by Tsui and Case (38), a similar approach based on the AMBER force field was reported to be adequate to correctly describe the subtle free energy differences between A and B forms of the DNA.

To assess the effects of the strength of the harmonic constraints, we have performed another set of simulations, this time with the restraining force holding the DNA reduced by two orders of magnitude, from 0.1 to 0.001 kcal/mol/Ų. The same structures have again undergone 1 ns of MD with all other conditions being the same as described above. With these much softer restraints, the overall global shape of the DNA still remains superhelical and similar to what is shown in Fig. 4; however, the kinks practically disappear in the NCP-DNA during the course of the simulations. The structures become similar to each other; namely, an average of 2.4 ± 1.2 kinked basepair steps occur over a 100 ps interval of the NCP-DNA while an average of 4.8 ± 4.6 kinked basepair steps occur in a 100 ps interval of the Ideal-DNA. The structure that has evolved from the Ideal-DNA appears to be slightly more favorable energetically, by 21.96 ± 9.16 kcal/mol, than the one evolved from the NCP-DNA. Again, formation of the small local distortions (kinks) appear to be energetically favorable for the entire structure.

The free B-form nucleosomal DNA

Accepted theories of DNA flexibility (42,43) backed by classic experiments (9,11) predict the persistence length of DNA to be ∼150 bp (∼500 Å) at physiological conditions. Therefore, DNA fragments shorter than this perceived length, were, until very recently, believed to be generally inflexible. Nucleosome core particle DNA contains ∼147 bp of DNA that is wound ∼1.65 times around the histone core, and therefore one might expect that considerable force would be needed to bend the DNA to assume its orientation on the nucleosome. Recent experiments, however, suggested that DNA as short as 94 bp can spontaneously cyclize (18), indicating that at the length scales on an order of, or smaller than, 500 Å, the DNA may be much more flexible than previously thought.

To investigate the flexibility of nucleosomal DNA free in solution, we have performed a 5 ns MD simulation of the DNA segment 147 bp long (Free-DNA), with the same sequence as the DNA in the 1.9 Å NCP structure of Richmond and Davey (14). The main results are summarized in Fig. 5. A natural question arises: is it realistic to observe the large fluctuations seen in Fig. 5 on the seemingly short timescale of the MD reported here, that is, only 5 ns? Of course, in an experiment, the relevant timescale for the structural fluctuations of this size would be much larger, but note that in our simulations the drag of viscosity is eliminated through the use of the implicit solvent methodology, and so the Free-DNA can sample conformations on a much faster timescale than it would in an explicit solvent simulation or experiment. Therefore, while the simulations reported here are only several nanoseconds long, the conformational sampling for the DNA systems is expected to be enhanced 20–100 fold (38,39), which would make these simulations effectively correspond to hundreds of nanoseconds or more of real-time. The implicit solvent approach can be considered as a sampling enhancement technique, which preserves the thermodynamic properties of the system but changes its dynamic timescales. The presence of quasi-periodic motions (Fig. 5) on timescales atypical for traditional simulations in viscous solvents is therefore not surprising. In what follows, we will not discuss any dynamical properties of the system.

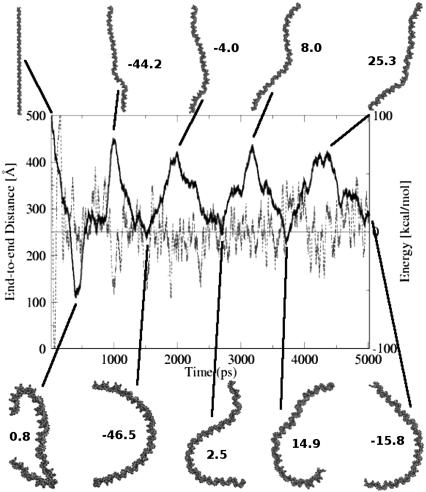
FIGURE 5.

End-to-end distance (thick solid line) of the free B-DNA during the course of the 5 ns MD simulation at room temperature. Horizontal line represents the average potential energy of the last 4 ns. Dashed line is a running average of the potential energy over a window of 25 data points; this energy includes the molecular mechanical energy and the free energy of solvent rearrangement (see Methods). Some of the structures and their corresponding energies relative to the 4 ns average are also shown. The DNA helix is shown as a VDW representation. (The complete MD trajectory is available as a movie at http://people.cs.vt.edu/%7Eonufriev/RESEARCH/DNA.html.)

Several qualitative conclusions can be made by inspecting Fig. 5. First, the nucleosomal DNA appears quite flexible on the length scale of 150 bp. Its shape undergoes substantial fluctuations, indicating that DNA that forms a nucleosome does not behave like a fairly rigid rod. Assuming contour length of the nucleosomal DNA to be roughly equal to its canonical persistence length of L_p ∼500 Å (∼150 bp), the standard polymer theory (44,45) predicts the average end-to-end distance to be 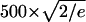∼ 425 Å. However, according to Fig. 5, the end-to-end distance barely reaches this value (apart from the starting point). These results are difficult to reconcile with the classic models of the DNA flexibility; they are in better qualitative agreement with experiments of Cloutier and Widom (19), who estimated the persistence length for a nucleosome positioning sequence to be ∼350 Å (105 bp). We avoid making quantitative comparisons here because, on one hand, the measured persistence length appears to be sequence-dependent (18,19), but also because its reliable estimation through computed end-to-end distance would require longer MD simulations than reported here. Still, we are confident that our qualitative conclusion—that the persistence length of the nucleosomal DNA is appreciably shorter than the classical value of 500 Å—is valid. Given the careful equilibration protocol, a relatively tight binding to the thermostat (see Methods) and the analysis of the energy fluctuations presented below, we are reasonably sure that during the simulated dynamics the system has not traveled far from the state of thermal equilibrium at 300 K, the simulation temperature.

A more detailed analysis of the relative free energies of the DNA snapshots will now be presented to confirm the qualitative observations made above. Again, the timescales are irrelevant here: the only requirement is that enough of the conformational space has been sampled to make a statistically meaningful analysis. The implicit solvent methodology (MM-GBSA) (46,47) allows straightforward calculation of the energy of each snapshot as a sum of the full molecular mechanics energy of the macromolecule plus the free energy of solvent rearrangement (see Methods).

As with the size of the conformational fluctuations, one may wonder whether the considerable energy fluctuations seen in Fig. 5 are reasonable to expect. In fact, they are quite reasonable for the system of this size. That is, if the DNA fragment used here is approximated by a classical solid with 3N degrees of freedom, general thermodynamics argument predict, in the Dulong-Petit limit, the size of the energy fluctuations 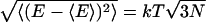∼100 kcal/mol at 300 K and for the number of atoms in the nucleosomal DNA, N ∼9000. This is in qualitative agreement with the value of 52 kcal/mol calculated directly from the MD trajectory.

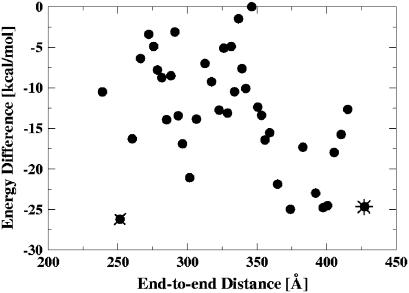
Looking at the conformational snapshots presented in Fig. 5 and their associated (free) energies, there appears to be no large penalty for significant (semicircle or even more) bending of nucleosomal DNA at room temperature. This conclusion is consistent with a recent theoretical model proposed by Wiggins et al. (48) and with experimental observations on the contours of DNA adsorbed to a surface (P. A. Wiggins, T. van der Heijden, F. Moreno-Herrero, A. Spakowitz, R. Philips, J. Widom, C. Dekker, and P. C. Nelson, Nature Nanotechnology in press). The point is investigated further in Fig. 6. Clearly, the expected trend is present: conformations with smaller end-to-end distances are generally less energetically favorable. The scatter is also not surprising, as more than one spatial conformation corresponds to a given end-to-end distance, with the exception of the completely straight polymer. At the same time, some obviously bent conformations (end-to-end distance as low as 250 Å) have virtually the same energy as relatively straight ones (those with end-to-end distances at ∼400 Å). In fact, among the five lowest energy conformations (all within the error margin from each other) in Fig. 6, one corresponds to snapshots with an end-to-end distance of ∼250 Å.

FIGURE 6.

Conformational energy as a function of the end-to-end distance of the nucleosomal DNA free in solution (Free-DNA). Each point represents an average over a bin of 100 structures: the average energy and distance for each bin is shown. The lowest-energy bent and straight conformations are denoted by an x and *, respectively. All the energies are offset by a constant (the highest energy).

It is worth mentioning that there appears to be no obvious sampling bias in our simulation due to possible dynamic effects. As evident from Fig. 6, the number of bent conformations (end-to-end distance <318 Å) is roughly equal to the number of stretched ones (end-to-end distance > 318 Å). It does not appear that highly bent conformations of the nucleosomal DNA are very rare, as one might expect from the classical picture of the stiff DNA on the length scale of 150 bp. A more accurate quantitative analysis of the relative populations would require considerably longer simulations to generate an adequate ensemble of states; and the numbers may still be somewhat dependent on the molecular mechanical force fields used.

Still, it is instructive to compare the relative energies of the snapshots in Fig. 6 with the predictions of the classical picture of DNA flexibility based on the semiflexible polymer model (45). The latter assumes that the DNA can be represented as an elastic rod with quadratic dependence of the elastic energy upon the bending degree of freedom. Within Landau's model of thin elastic rod, the bending energy is (49)

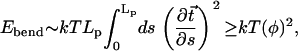(2)

where the rod's axis is given by parametric curve 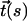( is the tangent unit vector at position s). The inequality reflects the fact that the quadratic function strongly penalizes sharp bends, and so the most energetically favorable conformation for a given end-to-end distance is that of a perfect circular arc of arc-length φ radians. The inequality becomes an equality only for an unbent rod. In the case of the nucleosomal DNA, contour length ∼L_p ∼500 Å, which gives ∼kT of elastic energy for the classical DNA bent into a circular arc of exactly 1 radian.

In Table 2 we compare predictions of the classical theory, Eq. 2, with the averages of points in Fig. 6 taken over three intervals: the two extremes of the observed range of end-to-end distances and the middle of the range. Due to a constant (unknown) offset of the energy of the snapshots in Fig. 6 relative to that of the completely straight conformation of the nucleosomal DNA, it is only meaningful to compare the differences in energies as the end-to-end distance changes. We start from the relatively lightly bent conformations. The extra cost in the DNA bending energy in going from the end-to-end distance of 411 Å to 318 Å, assuming bending through perfect circular arcs, is 5.8–2.3 = 3.5 kcal/mol according to the classical theory (Table 2). This is to be compared with −12.8–(−19.1) = 6.3 kcal/mol corresponding to the same change in end-to-end distance of the conformations observed in our simulation. In view of the inequality in Eq. 2, the latter value is reasonable, and does not contradict the classical picture. However, the classical picture predicts an almost equal increase in bending energy of 8.0–5.8 = 2.2 kcal/mol in going from the half-circle (318 Å or φ = π) to the most bent conformations in Fig. 6, with the average end-to-end distance of 257 Å. This predicted lower bound of the energy increment is more difficult to reconcile with the much smaller value observed in our simulation, −12.5–(−12.8) = 0.3 kcal/mol, especially since the strength of inequality in Eq. 2 is only expected to increase as the contour shape of the polymer deviates more and more from the straight line. We would like to stress, however, that generalizing this observation made for the specific nucleosomal sequence used in this work to arbitrary DNA may not be appropriate, as the flexibility of the DNA is known to be sequence-dependent.

TABLE 2.

Comparison of the nucleosomal DNA bending energies predicted within the classical elastic rod theory with those observed in the simulations reported here

Arc length, φ, rad	2.0	π	3.7
End-to-end distance, Å	411	318	257
Classical Ebend, kcal/mol	2.3	5.8	8.0
〈E〉 of snapshots in Fig. 6, Kcal/mol	−19.1	−12.8	−12.5

The classical values are computed assuming bending through perfectly circular arcs of specified end-to-end distance; Eq. 2 is used with the persistence length of L_p = 500 Å. Conformational energies are computed as averages over the following representative points in Fig. 6, as one moves along the horizontal axis: five rightmost points, five in the middle (interval [300, 325] Å), and five leftmost points. Their average energies 〈E〉 and end-to-end distances are reported. Note that each interval contains 500 of the original molecular dynamics conformations, 100 per each point. Since only the snapshots from the last 4 ns of the MD are included in the energy analysis, the energy of the initially fully stretched DNA conformation (end-to-end distance ∼500 Å, φ = 0) is not computed, and can be considered as an unknown constant offset.

Quantitative predictions can be made for the ionic-strength dependence of the relative free energies of conformers (Table 3). Success of the atomic-detail continuum electrostatics approach in describing the salt-dependent conformational changes was recently reported on various molecular systems such as proteins (50), the nucleosome (51), and chromatin fibers (52). The analysis can potentially provide clues into the nature of the enhanced DNA flexibility and how it is consistent with the strong repulsion between parts of this highly charged polymer.

TABLE 3.

Destabilization effects of monovalent salt on the bent DNA state relative to the straight one as a function of solvent salt concentration

Salt concentration, M	10.0	1.0	0.4	0.2	0.1	0.05	0.01
Debye screening length, Å	1.0	3.1	5.0	7.0	10.0	14.1	31.6
ΔΔG, kcal/mol	0.0	0.0	1.85	1.48	3.22	5.19	19.17

The bent state corresponds to an average of the 100 conformations represented by x and the straight state corresponds to the average of the 100 conformations represented by * in Fig. 6. Progressively higher values of ΔΔG indicate decreasing relative stability of the bent conformations as ionic strength of the solution decreases. Computational details are in Methods.

Note that the presence of salt introduces an important length scale into the system—the Debye screening length, 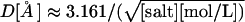; electrostatic interactions over distance L scale as ∼exp(−L/D). From Table 3 there is no apparent salt-dependence above 1 M salt concentration, or D < 3 Å, which makes sense given that the distance between consecutive negative charges along the backbone is ∼6.6 Å. In the physiological range of salt concentrations, there is a small, but noticeable difference in relative free energies of straight and bent conformations. For example, changing the salt concentration from 0.2 to 0.1 M will result in destabilization of the bent state by 1.74 kcal/mol, corresponding to an ∼18-fold decrease in the relative population. The observation suggests that particular care of ionic strength conditions must be taken when comparing quantitative results from experiments that measure end-to-end distance of DNA fragments comparable in length to the nucleosomal DNA. When the salt concentration is reduced to 0.01 M, the low end-to-end distance conformations become virtually nonexistent, separated by at least 10–15 kcal/mol barrier from the lowest-energy straight conformations. Interestingly, the 0.01 M salt corresponds to Debye length of only ∼30 Å ≪ lowest end-to-end distance observed in our simulations (250 Å). This suggests that electrostatic repulsion on length scales of ∼30 Å become important. The observation also suggests that salt-dependence of end-to-end distance fluctuations, or related experimentally accessible quantities such as salt-dependence of cyclization probability, may be used to gain insights into the mechanism of the unusual DNA flexibility discussed above.

The idea is that these salt-dependent quantities should be strongly affected by the details of the molecular mechanism behind the observed phenomenon of unusually high bending of short DNA fragments. In particular, if formation of sharp kinks (conformation 1 in Fig. 7 on left) is key, one should expect a noticeably stronger dependence on the screening effects of salt compared to the case of a more uniform bending, as in conformation 2 in the same figure. This is because, for a polyion, the electrostatic repulsion disfavors sharply bent conformations much more strongly than the uniformly bent.

FIGURE 7.

An example of two plausible structural scenarios of cyclization of short DNA fragments. Scenario 1 implies stronger electrostatic repulsion between the strands and is therefore expected to be more sensitive to the screening effects of salt.

The analysis presented above and Fig. 6 also suggest that the elastic energy component associated with the curvature of the nucleosomal DNA may be small. This, by itself, does not necessarily mean that the overall energy cost of creating the DNA in the conformation found in the nucleosome is small: the cost of bringing the two strands right on top of each other to create the 1.65 turns found in the nucleosome is unlikely to be small, due to strong electrostatic repulsion between the two strands at physiological conditions. This cost is expected to be compensated by the attractive interactions with the oppositely charged histone core.

Atomic-level MD simulations provide an opportunity to complement experiment in narrowing down the list of competing theories that claim to explain the unusual persistence length of the DNA. For example, in the literature (19), several different theoretical models were found consistent with the available experimental data on DNA cyclization, in particular the melted-bubble model of Yan and Marko (21). Note that the melted-bubble mechanism, as proposed, postulates the breaking of at least two consecutive WC bonds to create a sharp bend in the DNA. Analysis of our Free-DNA MD trajectory shows that two adjacent basepair unpairings never occur (and even single breaks occur rarely, and only at the ends of the fragment) in the simulation that nevertheless exhibits sharp bends. Therefore, the melted-bubble may not be an appropriate model to describe the unusually high flexibility of the DNA, at least on length scales of ∼150 bp. This conclusion is likely to be model-independent: the drastic conformational changes such as formation of bubbles of broken WC bonds should not be sensitive to details of modern force fields used here. Similarly, while the fine-grain conformational details may be forcefield-dependent, the salt dependence computed within the implicit solvent approach appears to be insensitive to them (50). This is because nonelectrostatic components cancel out, and what remains are “ΔΔ” estimates, which are typically more accurate than just “Δ” involved in computing of the electrostatic part of solvation energy. Our previous experience with a similar size system—unfolding apomyoglobin—shows that the computed salt dependence of free energy can be within kT of the experimental numbers (50).

Fluctuations of the DNA on the nucleosome

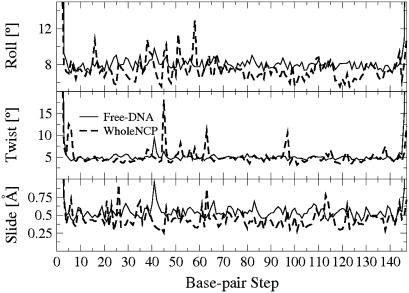
The many interactions between the histone core and the nucleosomal DNA are thought to severely constrain the motion of the DNA. Our MD simulations provide evidence that these interactions may not be so restrictive after all. To support our point, we compare structural fluctuations between the DNA on the nucleosome and fluctuations of the same fragment free in solution. Comparison of the standard deviation of the basepair step parameters roll, twist, and slide of the Free-DNA with those of the WholeNCP-DNA trajectory shows that these are similar (Fig. 8). That is, the degrees of freedom of the nucleosomal DNA determined by these parameters do not appear to be noticeably restricted by interactions with the core histones. The similarity of the structural fluctuations between the DNA bound in the nucleosome and the corresponding free DNA was also reported in a recent molecular dynamics study that used explicit solvent (53).

FIGURE 8.

Standard deviation of the basepair-step parameter roll, twist, and slide values for the WholeNCP-DNA (thick dashed line) and the Free-DNA (thin solid line) simulations. Values used to compute the standard deviation are from the last 500 ps of the WholeNCP-DNA simulation and that last 4.5 ns of the Free-DNA simulations.

CONCLUSIONS

This work is motivated by the biological importance of structural fluctuations in the nucleosome; these are related to the inherent flexibility of its DNA. Several multi-nanosecond molecular dynamics simulations of the nucleosome core particle and its corresponding DNA in isolated form in solution have been performed. Implicit solvent methodology has been used to represent effects of aqueous solvation at physiological conditions, including the electrostatic screening effects of monovalent salt. Despite the relatively large molecular size of the system, the use of the continuum solvent methodology has allowed us to observe considerable structural fluctuations, such as significant bending of the 147 bp stretch of isolated nucleosomal DNA. The implicit solvent approach (MM-GBSA) has also been used to estimate relative free energies of conformations observed in the simulation. The analysis of the computed structural signatures and energies has led to a number conclusions.

A biochemically identified region of DNA distortion localized at ±15 basepairs away from the dyad becomes apparent during the simulation of the entire nucleosome core particle. This region was not identified as distorted in the 1.9 Å crystal structure of the nucleosome, but, during the simulation the distortion of the DNA in this region becomes clear. This region may have importance in the binding of the DNA to the histones; short DNA sequences that can be easily distorted may indicate where DNA binds to the histones. At the same time, the six kinked basepair steps identified in the 1.9 Å crystal structure by Richmond and Davey (14), three on either side of the dyad, are not always present throughout the entire simulation. Rather, the six regions are the predominant regions of kink persistence, dynamically adapting to the fluctuations of the superhelical DNA. The result is consistent with our finding that the free energy cost of forming the kinks cannot be large: in fact, the formation of kinks is likely to be energetically favorable overall. This result follows from comparing free energy of kinked superhelical nucleosomal DNA conformation to the corresponding smooth conformation making the same number of turns around the histone core. Our finding does not exclude the possibility that additional conformational strain builds up locally in the kinked regions, but if it is the case, this extra energy appears to be compensated by structural adjustments elsewhere in the nucleosomal DNA that lower the overall energy of the fragment relative to the corresponding “smooth” conformation.

A related observation is that the nucleosomal DNA bound to the histones experiences substantial structural fluctuations. In particular, the fluctuations of the key structural parameters such as roll, twist, and tilt are essentially the same as those observed in the simulations of the isolated nucleosomal DNA. This observation supports the idea that the histone core does not impose strong structural constraints on the nucleosomal DNA. The histones most likely stabilize the superhelical structure of the DNA through electrostatic interactions, which are long-range and therefore more conducive of substantial structural rearrangements in the core particle compared to strong short-range van der Waals forces. Thus, the structure of the core particle appears to be more fluid than one might expect from its static x-ray representation. From a biological standpoint, an ability of the nucleosomal DNA to easily change conformation locally while preserving the overall global structure of the nucleosome may be important. In particular, it could hint at how the entire nucleosome can be highly stable, protective of its genetic material, while at the same time its tightly wrapped DNA be highly accessible, easily revealing its information content.

The simulations of the isolated nucleosomal DNA free in solution have provided interesting insights into the nature of its flexibility. First, we have found the nucleosomal DNA to be considerably more bendable than might be expected from the classical picture of a DNA polymer with a persistence length of ∼150 bp. The conclusion is further supported by the analysis of relative free energies of the conformers seen along the simulated trajectory: the energetic cost associated with substantial degrees of bending is smaller than expected from the classical picture. Our results are in qualitative agreement with the recent cyclization experiments of Cloutier and Widom (19), which suggest that small DNA fragments are capable of sharp bending unaccounted for by the classical models. Notably, no breaking of Watson-Crick bonds is observed in our simulations, suggesting that the unusual flexibility of nucleosomal DNA does not imply formation of local bubbles of single-stranded DNA. This conclusion relies on the observed absence of drastic conformational changes during the simulation, and is robust to subtle details of the methodology and the force fields used. Computed dependence of relative free energies of the simulated conformations upon ionic strength of the solution suggests that the relative population of the highly bent and relatively straight conformations is sensitive to the salt conditions in the physiological range. This relative population is also predicted to be sensitive to the structural details responsible for the enhanced DNA flexibility. This observation suggests that by measuring this dependence experimentally one might gain further insights into the molecular mechanism underlying this newly discovered phenomenon. For example, a scenario that involved formation of sharp bends would produce a much stronger salt-dependence of some experimentally accessible quantities (e.g., cyclization probability) than would a mechanism based on smooth, uniform bending. The methodology that we have used here to compute the salt effects was shown before to give quantitatively reliable predictions for molecular systems of similar size. Insight into the molecular mechanism underlying DNA flexibility can better our understanding of processes such as gene regulation and nucleosome positioning. Flexible DNA can form loops with much lower energetic consequence, thus providing some explanation for the many looped regulatory complexes, and regions of DNA that are of higher flexibility may be indicators for nucleosome positioning.

Perhaps one of the main methodological conclusions of this work is that the use of implicit solvent methodology allows one to observe and analyze conformational changes on a scale that would have been difficult or impossible with the traditional explicit solvent approach. This is mainly due to the fact that the implicit solvent approach eliminates the viscous forces, and so a considerably larger part of the available conformational space is explored. Also, since solvent degrees of freedom are taken into account implicitly, estimating free energies of solvated structures is much more straightforward than with explicit water models: for the systems as large as the nucleosome, an approach based on implicit solvation may be the only practical way to estimate relative stabilities of various conformations. Potential artifacts of periodic boundary conditions (often used to speed-up explicit solvent simulations) are also avoided. This may be important for free moving, highly charged systems such as the DNA in our simulation. While obtaining atomic-resolution pictures of conformational fluctuations in such large systems experimentally is difficult, they come within reach through the methodology described here.