Clusters: A bridge across the disciplines of physics and chemistry

Clusters in Physics

The properties of elements from atoms to bulk can be divided into two regimes: (i) a scalable regime where properties vary smoothly as some power law until they reach the bulk limit and (ii) a nonscalable regime where the variation is highly nonmonotonic (1). In this latter region, characterized by clusters, unusual things can and often do arise because of quantum confinement and boundary effects. Clusters of nonmagnetic elements become magnetic, semiconducting materials exhibit metallic properties, metallic systems become semiconducting, the color of particles changes with size, noble metals become reactive, and brittle materials become malleable. These properties arise because of the unusual structure of the clusters and because the electrons belong to molecular orbitals and exhibit an energy gap, referred to as the highest occupied molecular orbital–lowest unoccupied molecular orbital (HOMO-LUMO) gap. The magnitude of the HOMO-LUMO gap varies with both size and composition of the cluster, and the way these orbitals are filled determines not only the stability of the clusters but also their properties. A systematic study of the structure and properties of clusters composed of a variety of elements has bridged many fields of physics, particularly atomic, molecular, nuclear, and condensed-matter physics.

Clusters and Nuclear Physics.

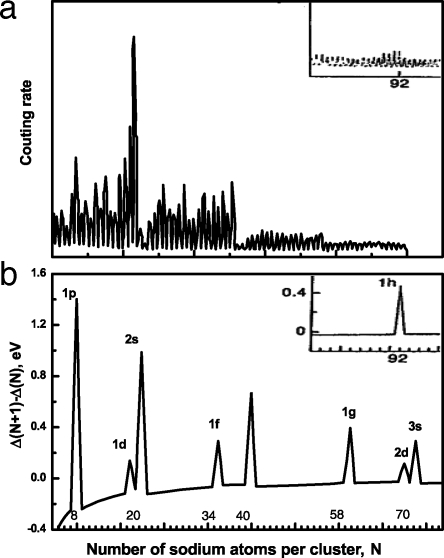
The pioneering of work of Knight et al. (2) on the mass spectra of Na clusters provided the first insight that clusters and nuclear physics may have something in common. They observed that Na clusters consisting of 2, 8, 20, 40, … atoms were unusually stable (Fig. 1) and coincided with the “magic numbers” in nuclear physics where nuclei with the same numbers of protons and/or neutrons were known to be very stable. Following the nuclear shell model, these authors assumed that a Na cluster can be modeled by a sphere of uniform positive charge density (commonly referred to as the jellium model), and the valence electrons of the cluster fill the energy levels in accordance with the Pauli principle. Each time an electronic shell is full, the corresponding cluster should exhibit pronounced stability, just as each time a nuclear shell became full, the nucleus became magic. A simple calculation of the energy levels of the electrons confined to a 3D square-well potential yields 1s², 1p⁶, 1d¹⁰, 2s², 1f¹⁴, 2p⁶, … shells. As these shells are filled, clusters containing 2, 8, 20, 40, … electrons become very stable.

Fig. 1.

Mass spectra and relativity stability of Na clusters. (a) Mass spectrum of sodium clusters, N = 4–75, exhibiting magic numbers. (b) Calculated change in electronic difference, Δ(N + 1) − Δ(N) vs. N. Labels of the peaks correspond to the closed-shell orbitals. This plot was an early illustration of shell effects in metal clusters demonstrating electron shell closure. Insets show results from a range outside of the larger mass spectra (2). [Reprinted with permission from ref. 2 (Copyright 1984, American Physical Society).]

The intensity distributions of metallic clusters showed that, in addition to the magic numbers that occur at 2, 8, 20, 40, … electrons, clusters with an even number of atoms are more stable than those containing an odd number of atoms (see Fig. 1). This odd–even alternation in the mass ion intensity distribution cannot be explained by using the simple spherical jellium picture described above, suggesting that the geometries of clusters, not corresponding to magic number species, may be deformed. The deformation of nuclei from spherical shape had been found earlier to be due to the nonvanishing quadrupole moments (3). By using the Nielssen model (4), originally developed for understanding the relative stability of quadrupole-deformed nuclei that lie between magic numbers, it was shown (5) that the energy of a cluster also can be lowered by structural distortion of the otherwise spherical jellium cluster. This effect, commonly known as the Jahn–Teller effect in condensed-matter and molecular physics, allows the energy levels of the clusters to further split by reducing their structural symmetry. Application of this concept provides a link between cluster, nuclear, and condensed-matter physics.

This observation led to the prediction (6) that Na clusters carrying a single positive charge (hence a cation) should exhibit magic numbers that are shifted by 1, namely at sizes containing 3, 9, 21, 41, … atoms as they respectively contain 2, 8, 20, 40, … valence electrons. This prediction was indeed later verified experimentally (7) and suggested that the stability of metal clusters can be altered by manipulating their number of valence electrons, just as the stability of nuclei can be altered by changing the number of protons and/or neutrons. The existence of magic clusters in neutral and charged metal clusters was later shown to have significance in the manner in which clusters fragment. It was predicted (8) and later verified (9) that the dominant channel in the fragmentation of a cluster, whether it is neutral or charged, will usually involve a magic cluster. This process is analogous to nuclear fission where magic nuclei appeared in the fission process.

The similarity between magic numbers in nuclei and atomic clusters at first was surprising because the forces that bind the nuclei are very different from those that bind the atoms in a cluster. Subsequent observations of discontinuities in the ionization potentials, electron affinities, and fragmentation energies of neutral and multiply charged clusters have shown that these results are strikingly similar to those observed in corresponding quantities (e.g., the separation energies of protons and neutrons) in nuclear physics. This finding also offered the first indication that clusters constitute a link between nuclear and condensed-matter physics. Indeed, metal clusters provide an avenue where concepts from nuclear structure and dynamics can be applied in the electronvolt (1 eV = 1.602 × 10⁻¹⁹ J) energy range. For example, the optical response of metal clusters exhibits substantial analogies with corresponding photonuclear processes (10). In particular, photoabsorption in metal clusters proceeds by means of the excitation of a dipole plasma mode where the valence electrons move collectively against the jellium positive background. This process is quite analogous to the well known giant dipole resonance in nuclei, where protons move against the neutrons (11). Detailed studies of the photoabsorption in alkali–metal clusters have been carried out using techniques familiar in condensed-matter physics such as time-dependent density functional theory and those related to the nuclear many-body problem. For specific mass numbers and species like neutral Na₂₀ and Na₄₀ (12), this method predicted multipeak photoabsorption profiles, which are more complex than simple one-peak profiles expected from the Mie theory of the charge oscillations of a classical metal sphere. Such profiles have been verified experimentally (13) and represent quantum size effects due to the discreteness of the single particle level and their bunching into electronic shells.

Another class of phenomena in clusters that is related to nuclear fission arises in cluster systems that can accommodate multiple charges (14). Because of the cohesive energy of a cluster at sizes above a certain critical limit, repelling charges can be accommodated, and multiply charged clusters can be observed. Notable examples include cation clusters of ammonia and, more recently, some anion systems where a coulomb barrier provides stabilization (15, 16). Fission of these metastable clusters usually occurs as they evaporate atoms and pass from the metastable to unstable region (17–20).

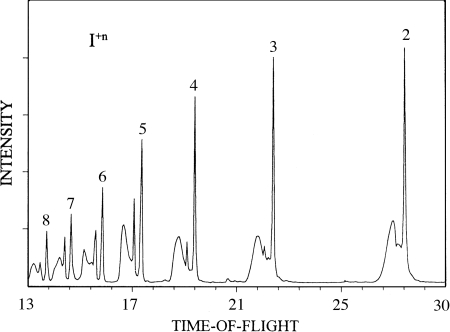
A related process was discovered to occur upon the exposure of clusters to intense laser fields (15, 21). High-flux femtosecond laser pulses provide short bursts of light up to 10¹⁵ W/cm², leading to the delivery of many photons to a cluster and an almost instantaneous loss of many electrons, in some cases all of the valence electrons (14, 22–25). These initially ionized free electrons can further ionize the inner-shell electrons of the atomic constituents of the cluster through intracluster inelastic electron-atom collisions. During the photon absorption and subsequent ionization processes, there is little time for nuclear motion (23–25). The highly charged atomic ions of the cluster are formed in very close proximity, and hence the system thereafter rapidly explodes because of the coulomb repulsion from like charges, releasing atomic ions with high kinetic energies (21, 26, 27). An example of the high-charge states that can be acquired, as well as the degree of coulomb explosion that can be generated, is evidenced by the splitting of mass-resolved peaks seen in Fig. 2. The exact mechanisms leading to the phenomenon are a subject of intense current interest among theoreticians as well as experimentalists and are not yet fully resolved.

Fig. 2.

TOF mass spectrum of multicharged iodine atoms resulting from the Coulomb explosion of HI monomer and HI clusters induced by strong femtosecond laser fields (21). [Reprinted with permission from ref. 21 (Copyright 1994, Elsevier).] Note that the degree of change state varies with the laser fluency.

Particularly interesting findings have come from a study of molecular clusters where, in the case of ammonia, highly charged nitrogen atoms up to N⁵⁺ have been found upon the irradiation of neutral ammonia clusters. In addition to the ejected nitrogen ions, intact ammonia clusters displaying peak splittings indicative of coulomb explosion have been well studied. Related work with HI clusters (21) has revealed the ejection of highly charged iodine atoms, with iodine up to +17 being observed, again only in the presence of clusters. Substantial kinetic energy releases with values of several thousand electronvolts have been measured (28), with related processes of x-ray emission (28–35) being reported. Another aspect of the coulomb explosion process has been learned from the study of acetone clusters (27) where highly charged carbon and oxygen atoms were found to be produced in pump–probe experiments. A unique feature of the work performed on this system was the utilization of pump–probe techniques in the ionization process as a test of theoretical predictions of the possible mechanisms involved, also demonstrating that a degree of quantum control in the production of highly charged ions can be acquired under intense laser conditions (27). The high energies of coulomb explosion for elemental and molecular clusters also have been studied extensively by Ditmire et al. (28). In this issue of PNAS, a new and exciting phenomenon of “table-top” nuclear fusion driven by cluster coulomb explosion that relates the field of clusters to “high-energy” nuclear physics is demonstrated by Jortner and coworkers (32). The stability of multicharged finite systems driven by long-range coulomb or pseudo-coulomb forces beyond the Rayleigh instability limit has been useful in unifying features of fragmentation channels in clusters, nuclei, droplets, and optical molasses (33). Studies of x-ray emission from Kr and Xe clusters in ultraintense laser fields have demonstrated an entirely new method where the multiphoton production of x-rays from clusters and high-intensity modes of channeled propagation in plasmas can produce conditions necessary for strong amplification in the multikilovolt range (34).

Clusters and Condensed-Matter Physics.

Although the success of the jellium model in explaining the stability of clusters of nearly free electron metals went a long way in bridging the gap between atomic, molecular, and nuclear physics, it does have limitations in accounting for the structural properties of clusters, such as their geometry and atomic arrangement. For such information, rigorous molecular orbital calculations based on quantum-chemical and density-functional techniques, where both the electronic and nuclear degrees of freedom are taken into account, are necessary (35).

The role of clusters in providing a bridge between atoms, molecules, and condensed matter should, in principle, be possible through a systematic study of the atomic and electronic structure as well as properties and dynamics of clusters as a function of size. The key questions are: when does a metal become a metal, and when does a cluster mimic the structure of a bulk solid? Despite considerable research in this area, no satisfactory answers are available at this stage. The difficulty lies in not being able to study the properties of clusters, one atom at a time, for sizes containing up to millions of atoms. Moreover, there is not a single answer, because varying materials display a different evolution of their properties with size. However, numerous studies of clusters of metallic, semiconducting, and insulating materials as a function of size have provided a wealth of data with wide-ranging interest in various areas of physics and chemistry.

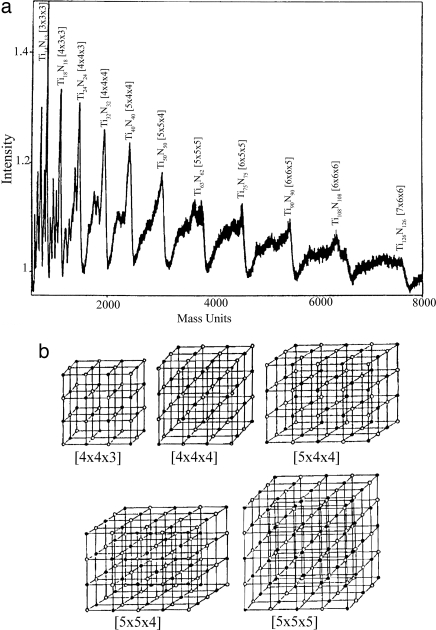
For metal clusters as well as those of elemental rare-gas clusters, one often sees clusters forming icosahedric structures, but crystals do not exhibit fivefold symmetry. In covalently bonded systems such as C and Si, the structures of clusters are very different from those in the bulk. In particular, a 60-atom carbon cluster exhibits the unique buckyball structure that is not characteristic of either graphite or diamond. However, in ionically bonded systems such as alkali halides and metal nitrides, carbides, and oxides, even small clusters bear the hallmarks of their crystalline structure (36, 37). Crystal-like growth patterns are often inferred from cluster distributions, as seen for the titanium nitride system shown in Fig. 3 (37). In clusters containing transition metals and carbon, the structures and stabilities have been found to depend strongly on whether the clusters were grown in a metal- or carbon-rich environment. In the former case, one finds clusters mimicking the bulk metal carbides, whereas in the latter, they form cage-like structures called metallo-carbohedrynes or “Met-Cars” (e.g., Ti₈C₁₂) (38–41).

Fig. 3.

Growth patterns of (TiN)_n⁺. (a) TOF mass spectrum of (TiN)_n⁺ clusters. Abundance patterns indicate the clusters have cubic structures resembling pieces of the fcc lattice of solid TiN. (b) Proposed structures of (TiN)_n⁺ clusters based on magic numbers observed in the mass spectrum (37). [Reprinted with permission from ref. 37 (Copyright 1993, American Institute of Physics).]

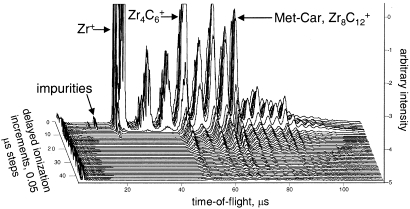
The phenomenon of delayed ionization in clusters can be linked to thermionic emission in the bulk, although the molecular aspects of the phenomenon are still under intense investigation (42–46). For a cluster to display delayed ionization, the ionization potential of the cluster must be less than its dissociation energy, and all of the phase space must be accessed by the system. The first requirement ensures that ionization, as an energy dissipation mechanism, will be more favorable than dissociation. Theoretical calculations and experimental results show that C₆₀ and Met-Car clusters meet this requirement, as do a few other systems, such as various transition metal carbides and oxides. The second requirement enables the system to temporarily store energy in excess of the cluster’s ionization potential through statistically sampling a large number of accessible vibrational and electronic states. Studies employing nanosecond lasers reveal that some degree of ionization occurs on a time scale orders of magnitude longer than that which is characteristic of normal photoionization responsible for the photoelectric effect. By contrast, prompt ionization usually dominates with femtosecond laser pulses. Met-Cars, with their low ionization potentials compared with the dissociation energies and the large density of electronic states, are ideal systems to exhibit this behavior because these clusters can “store” the energy gained during the excitation and delay ionize on a long time scale characteristic of the experiment. An interesting example of the delayed emission process is seen in Fig. 4 for the case of the zirconium Met-Car. At high laser fluences (>50 mJ/cm²), a second delayed channel that corresponds to an atomic ion emission has been observed (45, 47). Neither of these delayed ion channels, however, exhibit a substantial dependence on the laser excitation wavelengths, providing evidence that excitation to a specific (e.g., triplet) state is not likely to be responsible for the observed delayed ionization (48). The general process of delayed ionization is most readily treated through use of the Richardson–Dushman equation, which is an expression derived for the macroscopic bulk phenomenon often observed in metallic systems. Efforts have been made to reformulate the phenomenon by taking into account the finite size of the system under consideration and the collection of excited species having a distribution of internal energies.

Fig. 4.

3D data from delayed ionization study of zirconium–carbon system. The peaks that persist in the mass spectra represent those that are undergoing delayed ionizations (44). [Reprinted with permission from ref. 44 (Copyright 2003, American Institute of Physics).]

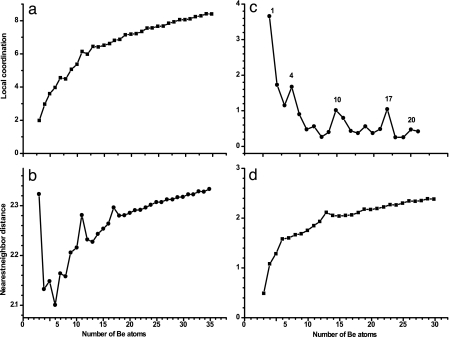
Other experiments, such as ones involving photoelectron spectroscopy, also have yielded valuable information on the evolution of the electronic structure of clusters. For example, in small clusters electrons form bonds, whereas in the bulk they form bands, although there are exceptions, such as in rare-gas clusters and small Hg_n clusters, where van der Waals binding prevails. The size at which the “bond” picture changes to the “band” picture is critical in our understanding of when a metal becomes a metal. In this context, see the work of von Issendorff and Cheshnovsky (49), who discuss the criterion for metallicity. Considerable amount of research has been carried out to study the evolution of the structure, interatomic distance, binding energies, ionization potentials, and electron affinities of metallic as well as nonmetallic elements (49–54). As an example, in Fig. 5 we show the evolution of some of the structural and electronic properties of Be clusters (54). Note that the evolution of properties toward bulk value depends on the property being investigated. Although the interatomic distance rapidly approaches the bulk value, the evolution of the binding energies toward the cohesive energies of the bulk and the evolution of the ionization potentials toward the work function are rather slow.

Fig. 5.

Be clusters. (a) Coordination number. (b) Nearest-neighbor distance. (c) HOMO-LUMO gap. (d) Binding energy per atom (54). [Reprinted with permission from ref. 54 (Copyright 2005, American Institute of Physics).]

Studies of the evolution of cluster properties with size, however, have led to some unexpected and spectacular results. One such property involves magnetism. Note that very few of the elements in the periodic table are magnetic, although half of these atoms contain an odd number of electrons and thus possess a net spin magnetic moment. An understanding of how magnetic moments are coupled is important for magnetism. Clusters provide an ideal medium where this phenomenon can be studied, not only by changing the size one atom at a time but also by changing geometry. A theoretical understanding of cluster magnetism involves spin-polarized quantum mechanical calculations of clusters and experiments measuring their deflection in a Stern–Gerlach field.

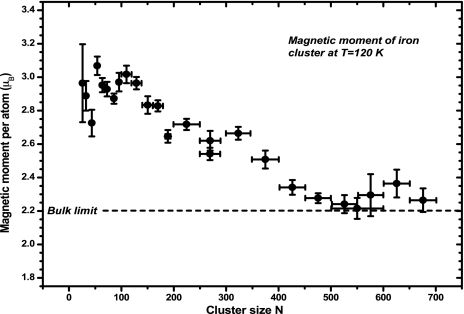
One of the early theoretical studies showed that magnetism of a cluster can depend on the cluster topology (55, 56). For example, the ground-state geometry of a Li₄ cluster is planar and spin singlet, whereas the preferred spin multiplicity of its 3D tetrahedron isomer is a triplet. This relationship between topology and spin of a cluster is also common in nuclear physics and suggests that one can use small clusters as magnetic storage media where their magnetism can be controlled by simply changing the atomic structure. Subsequent theoretical studies showed that clusters of nonmagnetic elements such as V, Rh, and Pd can become magnetic (57–59), and experiments on Rh clusters (60–62) verified some of the predictions. Studies of the magnetism of Mn clusters also have demonstrated that small clusters can be ferromagnetic, whereas the bulk is antiferromagetic, and as the clusters grow in size, ferrimagnetic order can set in (63–66). Clusters of ferromagnetic elements such as Fe, Co, and Ni also exhibit interesting properties. They not only behave as superparamagnets (67), but their magnetic moments are enhanced over their bulk value (68, 69) (Fig. 6). Studies show this enhancement results from the reduced symmetry and low coordination of the system (70, 71) and complement the well established studies of magnetism of surfaces.

Fig. 6.

Magnetic moments of Fe clusters (69). [Reprinted with permission from ref. 69 (Copyright 1993, American Physical Society).]

Clusters also have bridged our understanding between surface and bulk properties in the area of melting. It was shown quite some time ago (72–74) that atoms on a surface will melt much before the atoms in the bulk because of their low coordination number. Thus, clusters characterized by a large number of surface atoms will have lower melting points, which should increase as cluster size increases, eventually approaching the bulk value. Although this is the case in most systems, exceptions to this rule do exist. It was recently found that small clusters of Ga have melting points higher than their bulk (75)!

Clusters in Chemistry

Here, in this broad field of activity, we provide a few examples that demonstrate how clusters have helped in understanding complicated phenomena such as catalysis, reaction dynamics, solvation, metallorganic chemistry, and aromaticity.

Solvation: Energetics and Reaction Dynamics.

Elucidating factors that influence differences in the behavior of matter in the gaseous compared with the condensed state is a subject of major fundamental as well as practical importance. Such studies have implications in most areas of chemistry, including ones ranging from biological to environmental science, and wide-ranging industrial chemical processes. Indeed, determining the influence that solvation has on the properties and reactivity of both neutral and ionic systems is one of the challenging problems in the field of chemical physics (76–87). Studies of isolated gas-phase clusters are providing a wealth of new information that is serving to bridge an understanding of the influences that solvation has on the course of reactions. New insights at the molecular level are made possible through the large variety of techniques available for studying clusters of wide-ranging sizes. In the case of neutral systems, considerable insight into microscopic solvation (80–82) has been gained from spectroscopic studies of aromatic molecules embedded in rare-gas clusters, following seminal work on I₂–He complexes (83–85). Investigation of ultracold finite systems is an active field of endeavor with attention to spectroscopy (86, 87) and, in the case of ⁴He, superfluidity (88). A field that continues to remain very active involves electron solvation studies (89–93).

The study of cluster ion thermochemistry is a topic that has been actively pursued for several decades and has provided invaluable quantitative information on the energetics of interactions between ions and molecules (94–96). The development of high-pressure mass spectrometry enabled ion thermalization and the attainment of equilibrium cluster ion distributions at specified partial pressures of a clustering ligand (e.g., hydration) under well equilibrated source temperatures (97–99). This method has grown to be one of the most valuable in obtaining successive enthalpies and entropies of clustering (97, 98).

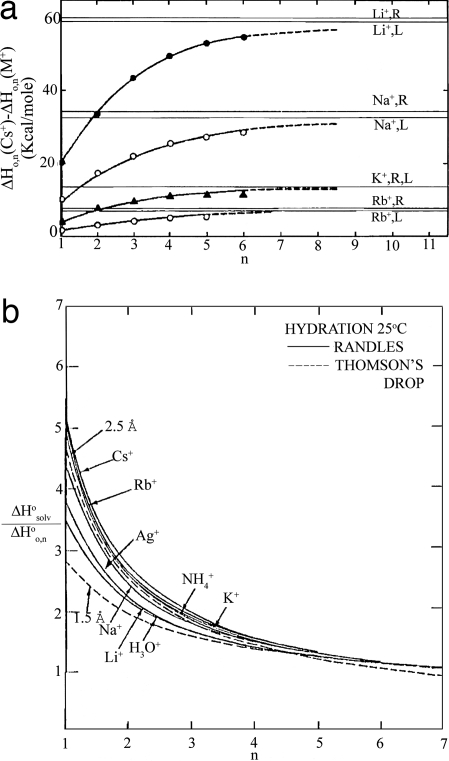
Researchers soon realized (99–101) that by a judicious comparison of the derived thermochemical values for gas-phase clustering onto a selected ion, it would be possible to gain direct information on solvation energies in the bulk liquid state of the solvent whose clustering was under study (102, 103) (see Fig. 7a).

Fig. 7.

Comparison of condensed phase with cluster data. (a) Plot of Δ(H_0,n(Cs⁺) − ΔH_0,n(M⁺) vs. n showing an asymptotic approach to differences in the total single ion heats of hydration obtained by Randles (R) and Latimer (L) (101). [Image in a reprinted with permission from ref. 101 (Copyright 1970, American Chemical Society).] (b) Ratio of Randles’ total enthalpy of solvation to the partial gas-phase enthalpy of hydration for positive ionic cluster size, n (103). [Image in b reprinted with permission from ref. 103 (Copyright 1986, American Chemical Society).]

One of the first attempts to predict solvation energies through connections between the gas and condensed states was based on the Born relationship (76, 101, 104, 105), where the ion is assumed to be a rigid charged sphere immersed in a structureless continuum with a dielectric constant. The Thomson equation is a version of the Born equation, where the size of the cluster “droplet” is taken into consideration, and concepts of bulk surface tension effects are incorporated. The Born relationship often yields an overestimation of the heat of solvation when typical values of crystalline radii are used for the ion size. This failure has led to proposed modifications based on structural considerations as well as other attempts to employ detailed ion–dipole, ion–quadrupole, and higher-order interactions (106–109). The general success of the model in relating clustering data to the condensed phase can be seen from data plotted in Fig. 7b.

A particularly important outcome of work in the area of cluster ions was the development of the electrospray technique, which has had such dramatic impact on basic as well as applied aspects of the mass spectroscopy of solvated and biological molecules (110). It enables ions of widely varying compositions and charge states to be introduced into the gas phase for study. The techniques have been especially valuable for analyzing biological molecules and gaining information on their structures through accompanying analytical separation and reactivity studies.

The study of acid dissolution is one of the most fundamental areas of solution phase chemistry, and the field of cluster science has had a large bearing on a basic understanding of a number of observed phenomena. Although thoroughly studied and understood in terms of bulk properties, the interaction between acids and accompanying solvents on the molecular scale continues to be an area of intense scientific study, driven by both scientific curiosity and practical importance. One question of longstanding interest concerns the number of water molecules required to dissolve an acid into its ion-pairs.

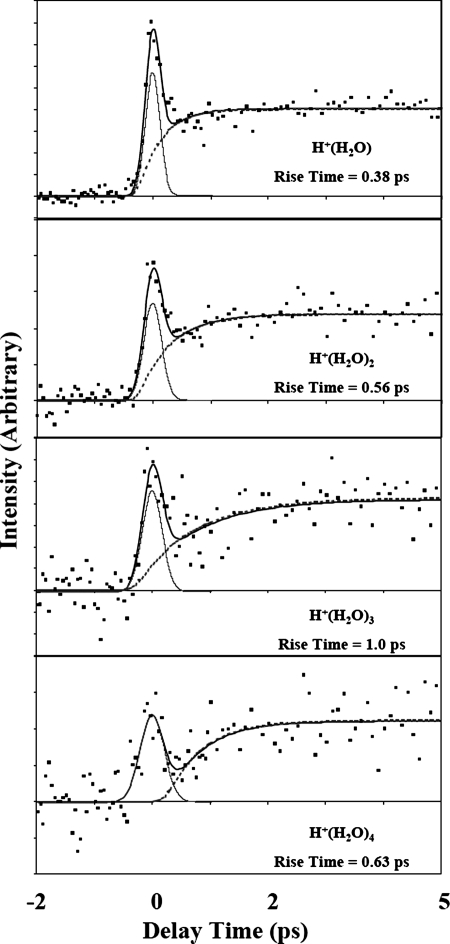
A recent investigation of the dynamics of HBr dissolution in mixed clusters with water (111, 112) has finally provided an answer for this system. Hydrated complexes formed by interacting water with clusters of HBr were subjected to femtosecond pump–probe spectroscopic investigation. The findings showed that the ground-state process is effected with five water molecules. Probing the excited-state population by multiphoton ionization, as a function of time, produces pump–probe transients that also contain temporal information about the ion-pair formation process (see Fig. 8). The signal resulting from ionization of the HBr_m(H₂O)_n clusters rose with increasing delay time, attributed to a reorganization of the solvent around the newly formed H⁺Br⁻ ion-pair. The influence of solute mass is seen for the case of HI clusters where the reorganization time is longer than that for HBr (113). Such studies are providing new insights of unprecedented detail into solvation phenomena.

Fig. 8.

Dynamics of protonated water clusters arising from femtosecond excitation of solvated HBr. The best fit of the data (squares) is shown by the solid line, where t_r is the rise time (112). [Reprinted with permission from ref. 112 (Copyright 2002, AAAS, http:www.sciencemag.org).]

In related work of HCl based on theoretical considerations (114), a stepwise proton transfer mechanism has been suggested, whereby a proton is first transferred from HCl to water, producing a so-called contact ion-pair; this step is visualized as being followed by subsequent transfer of a proton from the first to a second water, ultimately producing solvent-separated ion-pair complexes. Some spectroscopic evidence (111, 112, 115) for the interaction of four waters with HCl leading to ion-pair formation comes from matrix isolation studies, while related spectroscopic information for smaller water clusters in the gas phase is given in ref. 116. Theoretical studies (117, 118) have considered the energetics and also predicted the nature of the kinetics of dissolution and ion formation in hydrated systems of NH₃, H₂S, and HCl. Evidence of a concerted proton transfer mechanism for ammonia and hydrogen sulfide, which is predicted to differ greatly from the mechanism of solvation in the HCl system, has been reported.

Many processes in the condensed phase involve proton and hydrogen atom transfer mechanisms. Cluster science is providing a more complete understanding of these important mechanisms as well. Ever since the structure of DNA was determined, there has been interest in the potential role of proton-induced tautomerization and disfavored tautomers on mutagenesis in biological systems. The potential significance of such mismatches in tautomerization processes has sparked a great deal of interest and investigation of the dynamics of proton transfer in model-base pair systems. Particular interest has arisen in the double proton transfer that the 7-azaindole dimer undergoes upon excitation to the S₁ state, a process that has been extensively studied using pump–probe spectroscopy (119). The results confirm a stepwise process occurring in the isolated dimer pair, with evolution to a concerted reaction mechanism upon extensive hydration (120–122). Femtosecond pump–probe spectroscopy, in combination with cluster science, is giving considerable new understanding of the role that solvation plays on reaction dynamics (123–126).

Organometallics.

Studies of the chemistry of organometallic complexes consisting of metal atoms, metal clusters, and metal surfaces with organic molecules have been carried out for a long time by using conventional chemical synthesis procedures. A fundamental understanding of this interaction, however, is hampered by the fact that one must incorporate the effects of the solvent. In the past decade, laser vaporization techniques have provided an alternate route to produce complexes in the gas phase, thus eliminating the need to invoke solvation effects (127–130). Analysis of mass spectra, reactivity of mass selected species, and dissociation energies, combined with complementary theoretical calculations (131–138), provide information on atomic and electronic structures. For example, it is possible to determine the sites the metal atoms occupy on the organic molecule, the manner in which metal atoms cluster, and the changes in the structure as multiple organic molecules attach to these complexes.

Considerable amount of experimental efforts have been devoted to the study of 3D transition metal atoms (M = Sc, Ti, V, Cr, Mn, Fe, Co, Ni) interacting with benzene (Bz) (127) and larger organic molecules such as coronene (139). By varying the temperature and the partial pressure of organic molecules and the metal vapor, a large array of organometallic complexes have been produced and analyzed. These studies not only illustrate some novel structures of these complexes but also enable us to examine how the properties evolve as the organic molecules get larger, from a single benzene ring to coronene, which has six hexagons surrounding a central hexagon, analogous to graphite. In the following, we describe briefly some of the salient results in metal–benzene complexes.

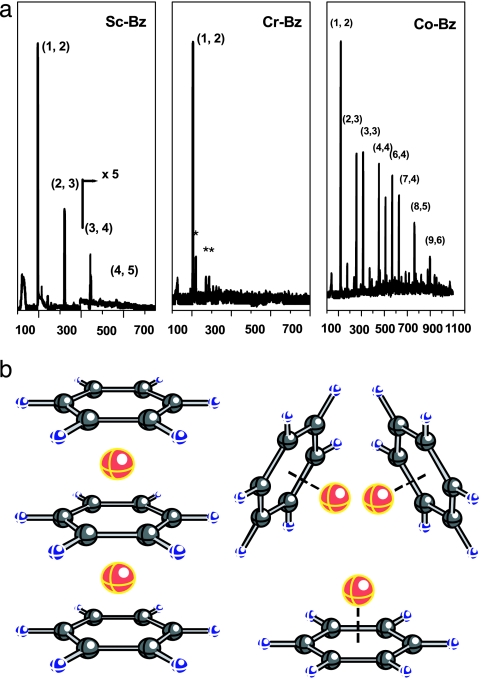
In Fig. 9a, we provide examples (Sc, Cr, Co) for the mass ion intensities of M_n(Bz)_m complexes (127). Note that the intensities of the peaks in the mass spectra exhibit three different characteristic patterns. For M_n(Bz)_m⁺ complexes (M = Sc, Ti, V), prominent peaks occur at m = n + 1, with peak intensities decreasing rapidly with increasing n. For Cr_nBz_m and Mn_nBz_m, only one major peak occurs at (n, m) = (1, 2). The above patterns indicate that the likely structure of M_n(Bz)_m (M = Sc to Mn) with m = n + 1 is that of a sandwich structure where metal atoms are intercalated between benzene molecules (see Fig. 9b). This hypothesis is further supported by the fact that these clusters are not reactive toward reagent molecules such as CO and NH₃ because metal atoms sandwiched between benzene molecules are not exposed to further reaction. Mobility experiments also support this conclusion (140). Co_nBz_m⁺ complexes, on the other hand, exhibit mass peaks at (n, m) = (1, 2), (2, 3), (3, 3), (4, 4), (5, 4), (6, 4), …, whereas peaks in Ni_nBz_m⁺ occur at (n, m) = (1, 2), (2, 2), (3, 2), (2, 3), (3, 3), (4, 3), (5, 3), (6, 3), (6, 4), … Note that, in these complexes, the number of metal atoms can exceed those of the benzene molecules, and, in particular, the maximum number of benzene molecules seldom exceeds m = 4. Equally important, the peaks beyond (n, m) = (1, 2) have similar intensities. It was suggested (127) that these complexes may have an entirely different structure where the metal atoms form a cluster and are coated by the organic molecules mimicking the shape of a “rice ball.” Recent mobility as well as reactivity experiments also support this structural assignment (140).

Fig. 9.

Mass ion intensity and structure of metal–benzene complexes. (a) Mass ion spectra of Sc-Bz (Left), Cr-Bz (Center), and Co-Bz (Right) complexes (127). [Image in a reprinted with permission from ref. 127 (Copyright 1999, American Chemical Society).] (b) Sandwich and rice ball structures of metal–Bz complexes (136). [Image in b reprinted with permission from ref. 136 (Copyright 2001, American Chemical Society).]

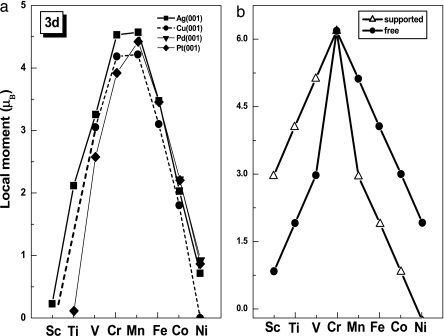
Extensive theoretical studies of the structure and electronic and magnetic properties of these complexes have been carried out (131–138, 141, 142). The geometries of these complexes suggested by the researchers have been borne out in theoretical studies. In addition, the theoretical studies also show that the magnetic properties of transition metal atoms can be significantly modified by the substrate. For example, the magnetic moments of Sc, V, Ti, Cr, Mn, Fe, Co, and Ni are 1μ_B, 2μ_B, 3μ_B, 6μ_B, 5μ_B, 4μ_B, 3μ_B, and 2μ_B, respectively. When these atoms are supported on a metal substrate such as Cu, Ag, and Pd, the trend in the magnetic moments remains unchanged, although their magnitudes are reduced by the overlap of the 3D electrons with those in the substrate (143) (Fig. 10a). However, when the same atoms are supported on a benzene molecule, the trend is very different (Fig. 10b) (135–137). Moments on Sc, V, and Ti are enhanced, whereas those on Mn, Fe, Co, and Ni are reduced. The moment on Cr remains unchanged. This unexpected result has been shown to be due to Pauli repulsion and provides clear evidence that the properties of metal clusters can be influenced by their support. A good example of this phenomenon is the prediction (138) that V atoms sandwiched between benzene molecules can become ferromagnetic with each V atom carrying a moment of 1μ_B. This prediction is particularly exciting because V is not ferromagnetic in the bulk. Recent magnetic deflection experiments have verified this prediction (146).

Fig. 10.

Dependence of magnetic moment of transitional metal atom on support. (a) Magnetic moment of 3d transition-metal atoms supported on metal substrates (144, 145). [Image in a reprinted in part from ref. 144 (Copyright 1996, American Physical Society) and in part from ref. 145 (Copyright 1994, Elsevier).] (b) Magnetic moments of neutral transition-metal atoms, free and supported on benzene (135, 137). [Image in b reprinted with permission from ref. 135 (Copyright 2000, Elsevier).]

Aromaticity.

Stability of a metallic cluster is traditionally understood from jellium models. Although this model works perfectly well for free-electron metallic clusters, the shell-model completely fails to predict the stability of magic clusters of transition metals and those bonded covalently. For these systems, rigorous quantum mechanical calculations are necessary for understanding their stability and electronic structure. There is a parallel theory, “aromaticity,” developed in chemistry to account for the unusual stability of σ/π-electron systems. Aromaticity is associated with extra stability arising from “electron delocalization” in complete circuits. Like the jellium model, the concept of aromaticity is also an electron-counting rule. The first and most used one was developed by Hückel and states that 4n + 2σ/π electrons (where n is an integer) impart extra stability, and 4nσ/π electrons, called antiaromatic, destabilize the system. The celebrated examples that follow these rules are benzene and cyclo-butadiene. Benzene has 6π electrons, forms a perfect planar-hexagon, and is extremely stable; cyclo-butadine has 4π electrons, has a distorted structure, and is very unstable. Although the Hückel rule is applicable for planar systems, Hirsch developed analogous rules for spherical systems. Based on spherical harmonics, Hirsch found that, when the valance shells are filled by 2(N + 1)² (N also being an integer) electrons, there is no distortion to spherical symmetry, and the system is very stable (147, 148).

Recently, based on similar aromatic principles, several metallic and nonmetallic clusters have been predicted and experimentally observed. Notably, Al₄²⁻, assuming it has 2π electrons, is aromatic and forms a perfect square, whereas Al₄⁴⁻ with 4π electrons is antiaromatic and has a rectangular shape. Both of these clusters have been characterized by anion photoelectron spectroscopy (149, 150). To illustrate the general usage of these rules, we give two representative examples for planar and spherical aromatic clusters (Fig. 11) comprised of both metals and nonmetals.

Fig. 11.

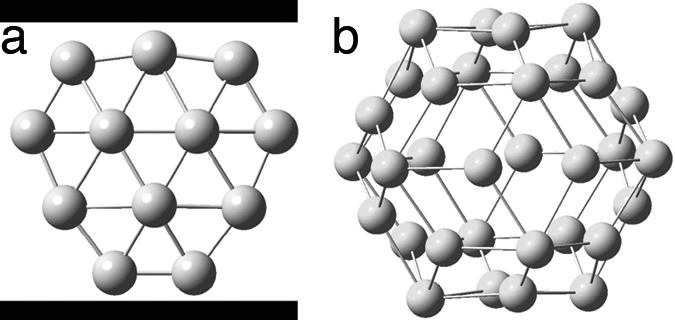
Structure of B₁₂ (a) (152) and Au₃₂ (b) clusters (153). [Image in a reprinted with permission from ref. 152 (Copyright 2003, Nature Publishing Group). Image in b reprinted with permission from ref. 153 (Copyright 2004, Wiley–VCH).]

Contrary to the bulk boron compounds, all of which have 3D structures, boron clusters, B_n with n < 20, prefer to be planar (151, 152). Among the boron clusters, B₁₂ occupies a special place; it has the biggest HOMO-LUMO gap (≈ 2.0 eV) and is therefore predicted to be very stable. The most stable structure for B₁₂ has circular shape (Fig. 11a) consistent with 6π electrons much like benzene, has a symmetrical bond distribution, and is highly aromatic. The planarity, shape, and electronic properties of boron clusters have been understood by applying the concept of aromaticity in both the σ/π domains (154).

Among the coinage metals, gold occupies a unique position. Relativistic density-functional theory predicts planar arrangements for neutral Au_n up to n = 13 (155). Au₂₀ is being observed and confirmed to have a pyramidal structure (156). Recently Johansson et al. (153) predicted a fullerene-like gold-cage, Au₃₂ (Fig. 11b). Jellinek, von Rague Schleyer, and coworkers (157), extending the fullerene analogy, calculated that Au₅₀ also prefers hollow cages compared with the space-filling isomers. Unusual stabilities of the gold cages Au₃₂ and Au₅₀ can be attributed to spherical aromaticity. Following Hirsch’s rule, both Au₃₂ and Au₅₀ have magic numbers of skeletal electrons, 32 with n = 3 and 50 with n = 4, respectively. On the other hand, Au₃₈, Au₄₄, and Au₅₆, which do not belong to the magic number family, are cage compounds and are less stable than the corresponding space-filling isomers.

Catalysis.

It would be difficult to overstate the impact that catalysis has on the economy and technology of industrialized countries, yet current knowledge of how to design catalysts that will lead to the facile formation of desired products with high selectivity and minimal environmental impact is still quite rudimentary (158–161). Although pioneering developments in surface science, such as those presented in the paper by Somorjai (162, 163), are having a major impact on the field, catalyst development often relies on empirical studies of the influence of various materials on the overall course of reactions. A promising complementary approach to conventional surface science involves the use of clusters as model systems to unravel the basic mechanisms of selected classes of reactions effected by heterogeneous catalysts (164–190) and elucidate the physical and chemical properties of condensed-phase catalysts. Notably, through advances in recent years, it is now possible to produce clusters of nearly any composition, size, stoichiometry, and oxidation and charge state and to investigate reactions of selected classes of molecules that are influenced by interactions with them.

Already some years ago, findings suggested that a metal oxide surface may be envisioned as a collection of clusters (191, 192), and subsequent experiments revealed that the identification of the reactive sites in heterogeneous catalysis can be aided by gas-phase studies of neutral and ionic clusters (193), in addition to studies of these materials in solids or solutions. As pointed out by Somorjai (162), surface chemical bonds have cluster-like properties, and in every case where a structure has been determined on a surface, there has been found to be a direct analogy to a comparable organometallic equivalent structure.

Especially significant are considerations and findings of Grzybowska-Swierkosz (194), who has considered in detail the physico-chemical properties of some vanadia containing catalysts and their effects on the selectivity toward certain products. The role of ionic centers that can arise at certain sites in heterogeneous catalysts has been identified, revealing that a study of charged clusters helps unravel the mechanisms that can occur at specific reactive centers in transition-metal oxide catalytic systems.

The potential significance of charge state and charge density in effecting oxidation reactions also has been discussed in the literature. For example, it has been proposed that OH⁻ and O²⁻ groups exist on γ-Al₂O₃ surfaces and that these sites are responsible for the nucleophilic behavior present in many catalytic oxidation processes (195). Others (196–198) have independently found ionic gold to be an integral part of CO oxidation on a gold-based surface. These studies have shown that using ionic clusters as models can prove beneficial toward unraveling mechanistic information. It also has been shown that through the study of clusters, complete catalytic cycles may be identified and investigated in the gas phase (161, 199, 200).

Significantly, in keeping with the ideas outlined above, there are numerous examples showing a direct similarity between reaction mechanisms involving clusters and similar ones effected by industrial catalysts. A few include investigations of cluster reactions (201–204) on gas-phase oxide clusters and extensive work on pure metal clusters (205–209). For example, it has been shown (210) that reactions of Mo_xO_y⁺ with methanol display close similarities with the reactions of methanol over heterogeneous and homogeneous catalysts containing molybdenum–oxygen sites (211). Experimental and theoretical studies of the reactivity of small gold clusters supported on magnesia provided evidence that Au₈ is a particularly reactive species for CO combustion (212, 213). Density-functional studies suggested that the reactivity observed experimentally is likely due to an anionic site originating from an F-center defect that anchors the octamer to the surface.

A few other notable examples that show a direct correspondence between gas-phase reactions and those known to function in condensed-phase heterogeneous processes include gas-phase studies of the reactions between V_xO_y⁺ clusters and CCl₄ (214), which display the production of phosgene as observed in the condensed phase (215). Studies of the reaction between (V₂O₅)_n⁺ and C₂H₄ (216) revealed the production of acetaldehyde, which is a major product over conventional vanadium oxide catalysts (217).

Few cluster studies, besides those summarized above, have been directed specifically toward elucidating the mechanisms involved in the catalytic chemistry of transition metal oxides, and there is a particular paucity of information on the related subject pertaining to the role of bimetallic interactions. In view of the insights that have been derived from the limited activities in the past, we may expect a considerable expansion of research efforts in this promising field of endeavor.

Abbreviation

HOMO-LUMO

highest occupied molecular orbital–lowest unoccupied molecular orbital.