Temperature Dependence of MinD Oscillation in Escherichia coli: Running Hot and Fast

Abstract

We observed that the oscillation period of MinD within rod-like and filamentous cells of Escherichia coli varied by a factor of 4 in the temperature range from 20°C to 40°C. The detailed dependence was Arrhenius, with a slope similar to the overall temperature-dependent growth curve of E. coli. The detailed pattern of oscillation, including the characteristic wavelength in filamentous cells, remained independent of temperature. A quantitative model of MinDE oscillation exhibited similar behavior, with an activated temperature dependence of the MinE-stimulated MinD-ATPase rate.

Minicelling of Escherichia coli is avoided during division through the oscillatory Min mechanism. The protein MinC is responsible for directly inhibiting the septation ring from forming, and it is targeted to the ends of cells by a subcellular spatiotemporal oscillation set up between MinD and MinE (reviewed in reference 30).

The MinDE oscillation cycle starts with cytoplasmic MinD:ATP, which binds to the membrane (15) and then recruits MinE (17). MinE stimulates the MinD ATPase, leading to the release of MinD:ADP and MinE to the cytoplasm (15, 17, 34), where nucleotide exchange can then occur to regenerate MinD:ATP. This binding/release cycle from the cytoplasmic membrane is thought to couple with reduced membrane-associated diffusivities (3, 14, 18, 21, 25, 26, 35) to generate a standing wave of concentration along the length of the cell. These standing waves have been observed in green fluorescent protein fusion studies for MinC (16, 28), MinD (29), and MinE (7, 10). The oscillation period has been reported to be approximately 40 s at room temperature, while a characteristic wavelength seen in filamentous cells is approximately 8 μm (29). It is not yet fully understood what microscopic factors determine the period and wavelength of MinDE oscillation, though many distinct quantitative models that exhibit similar oscillations have been proposed (3, 14, 18, 21, 25, 26, 35).

While E. coli has an optimal growth temperature attuned to a warm-blooded host, it is also viable outside the body at room temperature. The growth rate of E. coli as a function of temperature has been measured and increases approximately fourfold, in an Arrhenius manner, between 21°C and 37°C (13). This begs the following questions. Which subcellular processes of E. coli have temperature-dependent rates within the cell? How are they regulated? Do other aspects of their phenomenology, apart from the rate, vary with temperature? We know that the Min mechanism appears to function well over a broad range of culturing temperatures of E. coli, as reflected by the absence of reported minicells during division of wild-type cells (6). However, the temperature dependence of the Min oscillation has not been investigated previously. In this work, we report Arrhenius temperature dependence of the period of MinDE oscillation in E. coli, with a fourfold speedup in oscillation period between 20°C and 40°C.

What could be the molecular origin of the temperature dependence of the Min oscillation in E. coli? Approximately 9% of E. coli genes alter expression level at least twofold upon moderate temperature shifts, but the Min genes are not reported to vary their expression levels (8). While thermal Stokes-Einstein diffusivity of individual Min molecules is weakly temperature dependent (varying with absolute temperature in kelvin [T]), the variation is less than 10% over viable culturing temperatures and is unlikely to explain the large variation of period that we observe. While the MinDE oscillation is dependent on ATP and energy metabolism genes are differentially regulated with temperature (8), there is no evidence that subcellular ATP concentration depends on temperature; indeed, ATP concentration within E. coli is independent of growth medium (31). However, strong temperature dependence of the function of single enzymes, associated with the DnaK heat shock response (see reference 11 for a review), has been observed for E. coli. The rates of GrpE-induced nucleotide exchange vary strongly with temperature but in a non-Arrhenius manner, while DnaJ-induced hydrolysis of DnaK varies in an Arrhenius manner between 15°C and 45°C (9). While nucleotide exchange rates in the Min system have not been investigated, the Min oscillation period does depend on the MinE-stimulated MinD-ATPase rate (17). The hypothesis that temperature variation of nucleotide exchange and/or hydrolysis is the primary cause of the temperature dependence of the Min oscillation period is attractive, since similar mechanisms might also apply to the analogous Arrhenius temperature dependence observed for apparently unrelated biological phenomena, such as cricket chirps and firefly flashes (2), as well as to the many other subcellular processes leading to the temperature-dependent E. coli growth rate (13).

We used a relatively simple quantitative model of Min oscillation in E. coli, the model of Huang et al. (18), to examine the effects of varying the nucleotide exchange rate or the MinD-ATPase hydrolysis rate. While we do not have direct knowledge of the temperature dependence of the nucleotide exchange rate or the hydrolysis rate, we can see whether temperature dependences qualitatively similar to those in the DnaK/DnaJ/GrpE system (9) can lead, within the model, to the temperature dependences of the oscillation period that we observe experimentally. We can also see if the patterns of oscillation that we see experimentally correspond to the patterns seen in the model as we vary the parameters to reproduce the observed range of oscillation periods.

MATERIALS AND METHODS

Strains and growth conditions.

Strains PB103(λDR122) (P_lac::gfp-minDE) and PB114(λDR122)/pJE80 (ΔminCDE P_lac::gfp-minDE P_ara::sfiA) have been described previously (29) and were provided by Piet de Boer. Unless noted, all cells were grown overnight at 37°C in LB medium [chloramphenicol at 25 μg/ml was added for the PB114(λDR122)/pJE80 strain]. A portion (2 ml) of the bacterial suspension from the overnight cultures was diluted in a fresh M9 minimal salt medium supplemented with 50 g/ml of tryptophan, 0.2% Casamino Acids, 0.2% maltose, and 50 μM isopropyl-β-d-thiogalactopyranoside (IPTG) for the PB103(λDR122) strain or in LB plus chloramphenicol induced with 0.1% arabinose and 50 μM IPTG for the PB114(λDR122)/pJE80 strain. Bacterial cells were grown at 30°C in the new medium until the optical density (at 600 nm) reached 0.3. Immediately, a drop of this bacterial suspension was added to fresh medium for fluorescence microscopy.

Fluorescence measurements.

Cells were viewed on a Leica DMIRE2 inverted optical microscope outfitted with a Hamamatsu ORCA 285 digital charge-coupled-device camera and a 63× objective (numerical aperture, 0.9). A mercury arc lamp provided fluorescence excitation radiation via a 450- to 490-nm excitation filter, and a 500- to 550-nm barrier filter allowed green fluorescent protein fluorescence imaging. To automatically record several cycles of the MinD oscillations, shutters were placed in the path of the condenser light and the mercury excitation radiation. The shutters (MAC 5000) were controlled from a Macintosh iMac 1.8-GHz computer using Open Lab 4 software. Fluorescence images were captured at 1-s or longer intervals depending on the size of the oscillation period to be recorded. Bleaching was minimized by controlling the length of time that bacteria were exposed to excitation radiation. Exposure times were generally between 100 and 300 ms, although shorter times were used on occasion. With this arrangement, as many as eight MinD oscillation cycles could be recorded before photobleaching was significant.

Measurement of the oscillation period for strains PB103 and PB114 was done for bacteria that were immobilized at the bottom of the sample cell. The oscillation period was determined from a measurement of the average fluorescence intensity in a circular analysis region near one pole (illustrated in Fig. 1A). The diameter of this circular region was chosen to be approximately the same as the diameter of the bacteria so that most of the polar intensity was captured. To correct for fluorescence of the background medium, the average intensity in an equivalent circular region next to the bacterium was measured and subtracted from the oscillation signal.

FIG. 1.

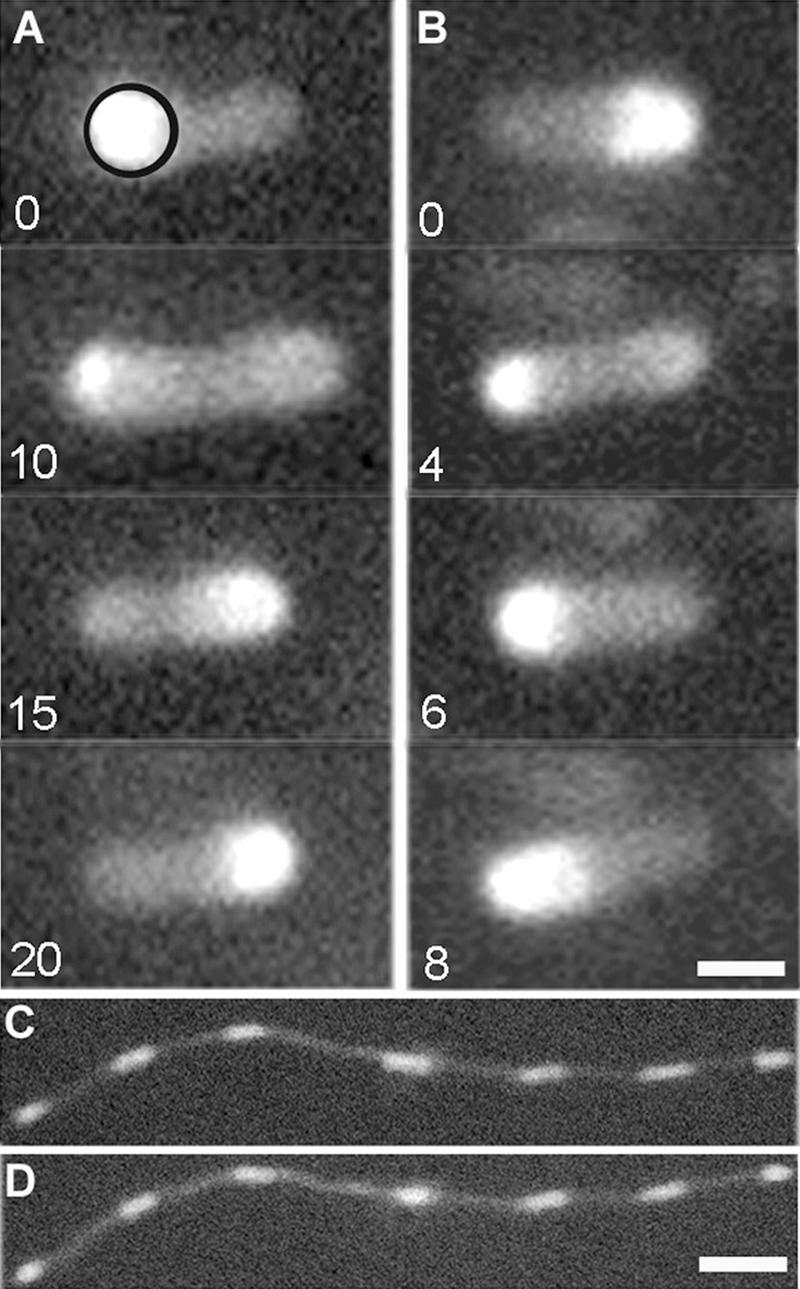
Oscillation of MinD concentration within E. coli bacteria. (A and B) (A) Fluorescence images of strain PB103 at 22°C at 0, 10, 15, and 20 s, giving an oscillation period of approximately 40 s. The circle in the top panel indicates the region over which the time dependence of the average polar fluorescence intensity was determined, as discussed in the text. (B) At 30°C, the oscillation period of the same strain (PB103) is now significantly shorter, approximately 16 s. Images at 0, 2, 4, and 8 s are shown. A temperature-independent pattern of growth and dissolution of the MinD polar caps can be seen. Bar, 1 μm. (C and D) Fluorescence patterns in filamentous strain PB114 at (C) 22°C and (D) 30°C. A temperature-independent characteristic wavelength of the MinD oscillations can be seen. Bar, 6 μm.

Temperature control.

The sample chamber consisted of a 10-mm-diameter and 5-mm-high quartz ring that was glued onto a coverslip. Several windings of a high-resistivity heater wire were varnished to the outside of the quartz ring, and a miniature chromel-alumel thermocouple placed inside the sample chamber and in contact with the coverslip acted as a temperature sensor. With the sample cell covered, the experimentally determined temperature profile along the bottom coverslip varied by less than 0.3°C within 3 mm of the center of the chamber. The thermocouple was placed in the immediate vicinity of the bacterium under investigation, and temperature stability during a measurement was better than 0.4°C. The overall temperature error for the oscillation measurements is estimated to be less than 0.5°C. The response time of the heater cell was slow, on the order of several minutes. The temperature was typically increased gradually to ensure that both thermocouple and bacteria were in thermal equilibrium with the suspending medium. Experimental results were essentially unchanged when the samples were allowed to cool from elevated temperatures.

To explore the speed with which the oscillation period could respond to a sudden increase in temperature, the oscillation period of a bacterium was first determined at room temperature. Then, a predetermined amount of suspending medium at 46°C was added to the sample chamber. This immediately raised the temperature at the thermocouple by 5 to 15°C, and this increase was then stabilized within 5 to 10 s by manually adjusting the heater current of the sample chamber. The thermocouple temperature could thereafter be maintained constantly to within 1°C for fluorescence images at the higher temperature.

Computational model.

We have implemented the computational model of Huang et al. (18) for MinCD oscillation in rod-shaped bacteria of 4 μm in length (but also for lengths of 10 μm, 20 μm, and 40 μm) as either the MinD nucleotide exchange rate, σ_D^ADP→ATP, or the MinD:ATP hydrolysis rate, σ_de, was systematically varied from the published values. We used a time step of 10⁻⁴ s and grid spacing of dr = dz = 0.05 μm. Initial conditions had MinE uniformly distributed in the cytoplasm and MinD:ATP uniformly distributed on the membrane of the peripheral bins, apart from a small random fraction (chosen uniformly between 0 and 1% of each bin) as MinD:ADP in the adjoining cytoplasm. Periods were measured as the intervals between times of maximal total MinD within 1 μm of the bacterial pole after at least 10⁴ s.

RESULTS

MinD oscillations were four times faster at 40°C than at room temperature.

As illustrated in Fig. 1, we observed strong MinD oscillations in a rod-shaped strain (PB103) and a filamentous strain (PB114) at both room and elevated temperatures. For strain PB103 at 22°C, the fluorescence intensity maximum shifted from one pole to the other in approximately 20 s (Fig. 1A), but the same process took approximately 8 s at a temperature of 30°C (Fig. 1B). For a single bacterium, Fig. 2 shows the time dependence of the fluorescence intensity averaged within a polar measurement circle (illustrated in Fig. 1A). Many oscillation periods could be recorded and evaluated easily with this method.

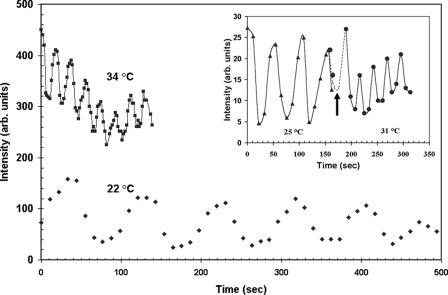
FIG. 2.

MinD polar intensity versus time for a single bacterium of strain PB114. The average intensity in a circular region (illustrated in Fig. 1A) initially placed over a fluorescence maximum is plotted as a function of time. Diamonds indicate the 22°C imaging temperature, while squares indicate 34°C (vertically offset for clarity). The lines through the data points are aids to the eye. The dramatic period reduction from 89 s to 18 s between the two temperatures is evident. The inset shows the rapid response of the oscillation period to a 6°C temperature step. A slower 51-s period at 25°C is illustrated by triangles before the arrow. At the time indicated by the arrow, but in an independent experiment, the temperature is raised within seconds to 31°C and a shorter period of 26 s is observed to occur immediately (circles). The two dots before the time of the arrow are from the bacterium that underwent the temperature increase. arb. units, arbitrary units.

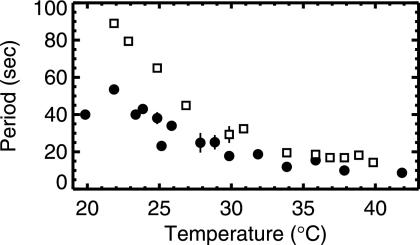
As shown in Fig. 3, the oscillation period decreased rapidly with increasing temperature for both rod-shaped and filamentous strains of E. coli. For both, we observed an approximately fourfold decrease in period between T of 20°C and 40°C. Significant variation within that trend is observed, which we attribute to variations of bacterial size, MinD/MinE stoichiometry, and possibly also other factors (e.g., ATP concentration, nucleotide exchange factors, or membrane phospholipid domains) of individual cells. Due to limitations imposed by photobleaching as well as insufficiently strong adhesion of bacteria to the substrate, the period of any particular bacterium could not be followed throughout the whole temperature range. The data in Fig. 3 represent results obtained from nine individual bacteria of strain PB103 and four bacteria of strain PB114. Although a period measurement was thus made only with a few stationary bacteria, all bacteria in the field of view showed the same decrease in the oscillation period with increasing temperature. The increase in the oscillation frequency with temperature was observed for strain PB103 in both rich (LB) and minimal (M9) media, although detailed analysis was done only in minimal medium.

FIG. 3.

Period of MinD oscillation versus temperature. Filled circles denote rod-shaped cells from strain PB103, while open squares indicate filamentous cells from strain PB114. The vertical bars indicate standard deviations when multiple measurements were taken at the same temperature. A strong and systematic decrease of oscillation period with increasing temperature is evident.

Oscillation period responded quickly to temperature changes.

By rapidly increasing the temperature in the sample chamber, we estimated the response time of the oscillation period to temperature changes of the bacteria. An example of such a measurement is shown in the inset in Fig. 2. The 51-s oscillation period at 25°C for strain PB114 changed within a few seconds to 26 s after a rapid temperature step of 6°C was applied at the time indicated. No subsequent drift of the period was observed, indicating that any heat shock response had little effect on the Min oscillation over the timescale of our measurements. For all filamentous and rod-shaped bacteria that we studied, the response time of the oscillations to a temperature step was found to be fast, less than one period, which was the limit of our resolution.

Complementing this result, we found that the oscillation period was independent of the culturing temperature, so that for a fixed imaging temperature no differences were observed for samples cultured at 30°C, 37°C, and 40°C (strain PB114) or at 37°C and 40°C (strain PB103) (data not shown). This indicates that there is no slow response of the oscillation period to temperature change.

Arrhenius behavior of oscillation period with temperature.

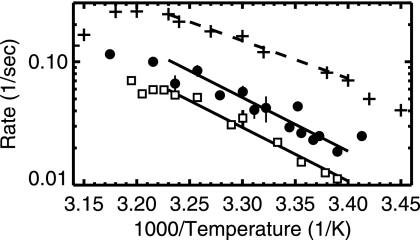
In Fig. 4, we show a log-linear Arrhenius plot of 1/period versus 1/T. Linear regimes in this plot correspond to activated processes with a constant activation energy, μ. The temperature dependence of the Min oscillation is consistent with an Arrhenius dependence. We obtained the same activation energy (μ ≈ 20 kcal/mol) for both rod-shaped and filamentous bacteria. For comparison, we show the reported growth rate temperature dependence along with its reported Arrhenius regime (corresponding to μ of 14 kcal/mol) between temperatures of 21°C and 37°C (13).

FIG. 4.

Arrhenius plot of the inverse of the MinD oscillation period versus the inverse absolute temperature (kelvin) scaled by 1,000. The filled circles and open squares are defined in the legend for Fig. 3. The solid line indicates the best-fit Arrhenius dependence, with activation energy (μ) of 20 kcal/mol, for the region between 21°C and 37°C. Pluses indicate growth rates of E. coli cultures (scaled by 500) (13). The dashed line is the best-fit Arrhenius dependence, with μ of 14 kcal/mol, to the growth rate (13).

Qualitative phenomenology of MinD oscillation was otherwise unchanged as temperature varied.

Apart from the oscillation period, we found no other phenomenology in the MinD oscillation that showed appreciable temperature dependence. For example, the wavelength exhibited by the MinD oscillation in filamentous bacteria was unchanged (compare Fig. 1C [22°C] and D [30°C]). For rod-shaped bacteria, we observed end caps form from MinD, growing from the bacterial pole, and then disassociate, shrinking to the bacterial pole (compare Fig. 1A [22°C] and B [30°C]), and this was qualitatively unchanged between 20°C and 40°C.

Increasing the nucleotide exchange rate slows the oscillation in silico.

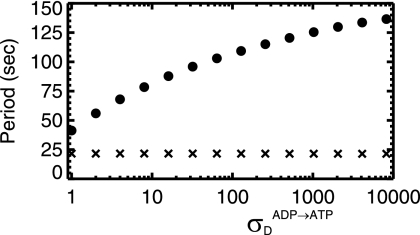
We systematically increased the nucleotide exchange rate, σ_D^ADP→ATP, in the model of Huang et al. (18) from the published value of 1/s. As shown in Fig. 5, we found that the oscillation slows as the nucleotide exchange rate increases. This has not been reported previously and represents a counterintuitive prediction of that model. Figure 5 also shows that the average time between MinD rebindings is independent of σ_D^ADP→ATP, which indicates that the increase of the period is due to an increase in the number of MinD bindings per period rather than the interval between bindings. The functional dependence of the period versus σ_D^ADP→ATP is weak, sublogarithmic, so that an enormous variation of σ_D^ADP→ATP would be necessary to recapitulate the fourfold variation in period that we see experimentally. Moreover, we would expect to see σ_D^ADP→ATP increase with temperature, as an activated enzymatic process and as seen for the action of GrpE in the DnaK system (9). This would lead to an increasing period with temperature, while we observe from Fig. 2 a strong decrease of the period with increasing temperature.

FIG. 5.

From the model of Huang et al. (18), the oscillation period versus the nucleotide exchange rate, σ_D^ADP→ATP, on a linear-log scale (filled circles) for a 4-μm-long bacterium. The period increases sublogarithmically as the nucleotide exchange rate is increased. Also shown (X's, scaled by a factor of 5) is the average time interval between every binding of MinD to the membrane. This is roughly constant as the nucleotide exchange rate increases, indicating that the period increases because the number of MinD bindings increases.

Increasing the hydrolysis rate speeds the oscillation in silico.

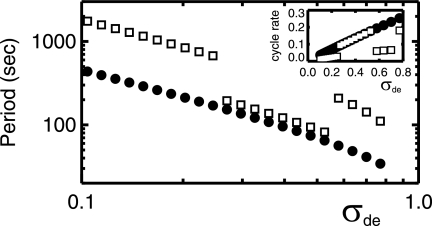
We also systematically investigated the parameter σ_de, corresponding to the action of the MinD-ATPase, i.e., the hydrolysis rate of MinD:ATP while membrane associated. As shown in Fig. 6, the period decreases approximately as the inverse of the hydrolysis rate (18). This agrees with experimental studies with mutant MinD in which a twofold increase in hydrolysis rate led to an approximately twofold decrease in period (17). It is also consistent with our observed decreasing period with increasing temperature combined with the increasing hydrolysis rate with temperature observed in the DnaJ/DnaK system (9). We see in the inset of Fig. 6 that the rate of MinD cycling between the membrane and cytoplasm depends linearly on σ_de for 4-μm-long bacteria.

FIG. 6.

From the model of Huang et al. (18), the oscillation period versus the MinE-stimulated MinD-ATPase rate, σ_de, on a log-log scale. Shown are results for a 4-μm-long bacterium and a 10-μm-long bacterium (filled circles and open squares, respectively). A strong decrease of oscillation period with increasing ATPase rate is seen. The longer periods for 10-μm-long bacteria with smaller or larger σ_de are associated with end-to-end oscillation, while intermediate σ_de values exhibit a symmetric breathing mode pattern. The inset shows the inverse time between MinD bindings (rebinding rate, in 1/s) versus σ_de.

We visually investigated the in silico patterns of MinD oscillation in both wild-type 4-μm-long bacteria and filamentous bacteria of lengths of 10 μm, 20 μm, and 40 μm for σ_de of 0.1, 0.3, and 0.7. The published value (18) is σ_de of 0.7. We found (see the supplemental material for oscillation patterns for 4-μm-long and 10-μm-long bacteria) that the 4-μm-long bacteria have oscillation patterns that are roughly independent of σ_de, though with stronger MinD end caps and MinE rings for smaller σ_de. The 10-μm-long bacteria show a symmetric (doubled) “breathing mode” oscillation pattern for σ_de of 0.3 but a significantly slower end-to-end oscillation for σ_de of both 0.1 and 0.7. For the published σ_de of 0.7, the breathing mode was unstable for 10-μm-long bacteria, in contradiction to previous results (18), though the end-to-end oscillation was not apparent until 8,000 s after the initial condition. (Similar results were obtained with a time step of 10⁻⁵ s.) Furthermore, we did not observe spatially or temporally periodic patterns for 20-μm-long or 40-μm-long bacteria up to 16,000 s after the initial conditions (data not shown), in disagreement with our experiment which shows regular oscillation patterns with a characteristic wavelength (Fig. 1C and D).

DISCUSSION

Temperature dependence of MinD oscillation.

We found a strong and systematic speedup of the MinD oscillation with increasing temperature between 20°C and 40°C, both in longer, filamentous bacteria and in shorter, rod-shaped bacteria. Surprisingly, we found that the characteristic wavelength of the oscillation in filamentous bacteria is unchanged in the same temperature range and so are other qualitative features of the shape of the oscillation. The first question that arises is the microscopic origin of our observed speedup with increasing temperature.

While significant variation of oscillation period with various relative expression levels of MinD and MinE has been observed previously (29), we do not believe that the ratio of MinD to MinE varies significantly with temperature. Earlier studies of chloramphenicol-treated cells (29) showed that oscillations persisted unchanged without protein synthesis and implied that both proteolysis and synthesis of Min proteins are slow in this system. We found that the oscillation completely responded to temperature changes within seconds, implying no significant changes in expression at longer times. This corroborates earlier studies with a culturing temperature of either 30°C (29) or 37°C (28) in which the oscillation period depended only on the imaging (room) temperature. This is also consistent with neither MinD nor MinE being identified in screens of E. coli for temperature-dependent protein expression (13) or mRNA expression (8). While direct assays of protein expression levels, comparable to that described in reference 32, of cells cultured at various temperatures are desirable, on the basis of our results we believe that no significant variation of the ratio of MinD to MinE per bacterial cell will be found in the temperature range that we considered.

Over the temperature range of our study, the Stokes-Einstein diffusivity of MinD or MinE varies by only 7%. This is unlikely to explain our observed fourfold variation in oscillation period over the same temperature interval and is indeed insufficient within existing models of Min oscillation where diffusivity does not play a critical role in determining the oscillation period (3, 14, 18, 21, 25, 26, 35).

We conclude that the temperature dependence of the Min oscillation period is caused largely by temperature dependence of interactions between the Min proteins or between the Min proteins and other cellular components, such as nucleotide exchange factors or the phospholipid membrane. The Arrhenius nature of the temperature dependence implies that it is an enzymatic (activated) process. The similarities with activated E. coli growth rates with temperature (13) and with activated temperature-dependent rates in disparate organisms, as with cricket chirps or firefly flashes (2), suggest that there may be an enzymatic process shared between Min and these other systems. We consider interactions involved in the energetics of the oscillation, in particular, nucleotide exchange and hydrolysis. While no nucleotide exchange factors have been implicated specifically for MinD:ADP, we do know from the GrpE/DnaK system (9) that their function can be strongly temperature dependent. Similarly, hydrolysis of MinD:ATP is activated (by MinE), and we know from the DnaJ/DnaK system that hydrolysis can also be strongly temperature dependent in E. coli (9). Remarkably, the biochemically determined Arrhenius constant for the DnaJ-induced hydrolysis of DnaK, 18 to 21 kcal/mol (from Fig. 6 of reference 9), is consistent with our Arrhenius constant, ≈20 kcal/mol, for the temperature dependence of the MinDE oscillation. We therefore expect that a temperature-dependent hydrolysis rate or perhaps a nucleotide exchange rate would be a natural candidate for causing the observed activated temperature dependence of the MinD oscillation.

Recapitulating our experimental results with the computational model of Huang et al.

While a number of numerical models have been proposed to describe MinDE oscillation, only a few of them include an explicit nucleotide exchange rate (3, 18, 26, 35). We examined the model of Huang et al. since it is relatively well studied (18, 19, 20, 22). We found that an increasing nucleotide exchange rate leads to an increasing oscillation period. However, we suspect that the nucleotide exchange rate would increase only with temperature, as an activated process and in analogy to the GrpE/DnaK system (9). Furthermore, the σ_D^ADP→ATP dependence is so small that a >10⁴-fold variation in this nucleotide exchange rate would be needed to recover the fourfold variation in period seen in our study. We conclude that within the context of the model of Huang et al. (18), variation of the nucleotide exchange rate with temperature cannot explain our results.

Increasing the MinE-induced MinD-ATPase rate (hydrolysis rate) leads to a decreasing period, both experimentally (17) and in the model of Huang et al. (18). Given that DnaJ-induced hydrolysis of DnaK has a strong Arrhenius dependence, increasing with increasing temperature, this provides an attractive picture for what may be causing most of the temperature dependence that we see. Nevertheless, significantly increasing the published hydrolysis rate of the Huang et al. model leads to no oscillation; the published value (σ_de = 0.7) is close to marginal. While we expect the other model parameters to have some temperature dependence, which may change the threshold for σ_de, we rather suspect that the published parameter values are underconstrained by experiment. We might therefore rescale all of the Huang et al. parameters by a factor of 1/4 to obtain a period four times faster, appropriate for T of 40°C, and leave plenty of room to decrease the rescaled σ_de at lower temperatures.

However, we did not find any range of σ_de values that both exhibited the experimentally consistent breathing-mode oscillation for 10-μm-long bacteria and was sufficiently wide to recover a fourfold variation of oscillation period. Furthermore, we found that none of the σ_de values led to a spatially or temporally periodic oscillation pattern for longer cells (lengths of 20 μm and 40 μm) with our initial conditions. This highlights the need for systematic data that could be used to constrain model parameters but may also point to missing components of the Huang et al. model, such as MinD polymerization effects (3, 26, 35) and/or periodically distributed phospholipid domains that might stabilize periodic Min patterns in filamentous cells (3). Indeed, we find it difficult to imagine how the spatial wavelength remains essentially unchanged as the temporal period varies fourfold without some sort of periodic template for the Min oscillation pattern.

Nevertheless, from our investigation of the Huang et al. model, a temperature-dependent hydrolysis rate appears to be a strong candidate for the dominant cause of the temperature dependence we observed with the MinD oscillation. Indeed, an assay of temperature dependence of the MinE-stimulated MinD-ATPase rate would complement our study of temperature dependence of the MinDE oscillation period to more specifically constrain this and other quantitative models of Min oscillation.

Possible implications for other time-dependent processes in E. coli.

For dividing cells of E. coli to avoid minicelling, the MinDE oscillation period that drives MinC to alternating poles must always be significantly faster than the FtsZ remodeling dynamics. At room temperature, the Min period is ≈40 s, the FtsZ remodeling timescale is ≈1 min (1, 33), and significant minicelling is reported when the proportion of MinD and MinE is changed to slow the Min oscillation period to ≈230 s (29). We do not know how the FtsZ remodeling timescale depends on temperature, but it should always be significantly slower than the Min oscillation in order to avoid minicelling. Since FtsZ is a GTPase, it might be surprising if its dynamics had temperature dependence similar to that of the MinD ATPase rate. Molecular mechanisms for coordinating the temperature dependence of individual dynamic processes in E. coli are not well understood and deserve further study.

MinD is a member of the deviant Walker A motif family of ATPases (23). A number of ParA-like members of this family are known to exhibit dynamic intracellular phenomena (see reference 12 for a review). Oscillations have been exhibited by ParA from the E. coli virulence factor pB171 (4, 5) and Soj from Bacillus subtilis (24, 27). It would be interesting to explore the temperature dependence of dynamic phenomena exhibited by the deviant Walker A motif family of ATPases and by ATPases more generally and to see if they are controlled by the temperature dependence of the ATPase activity.

For the MinDE oscillation, we have found a fast dynamic response to changing imaging temperatures in E. coli but no effect of culturing temperature. To assess the temperature dependence of other dynamic processes in the cell, both the imaging temperature and the culturing temperature should be controlled to independently probe fast activated responses and slow responses corresponding to changing expression levels. Even “room temperature” studies (20°C to 25°C) could expect significant variation if no temperature control is used.

For the Min oscillation system, imaging temperature is an easily, rapidly, and reversibly manipulable control parameter. It will be interesting to see how the details of other phenomena observed with MinCDE oscillation depend upon imaging temperature and to understand why.