Spontaneous sharp bending of DNA: role of melting bubbles

Abstract

The role of centrally located and distributed base pair mismatches (‘melting bubbles’) on localized bending and stiffness of short dsDNA fragments is evaluated using time-dependent fluorescence lifetime measurements. Distributed melting bubbles are found to induce larger bending angles and decreased levels of stiffness in DNA than centrally located ones of comparable overall size. Our results indicate that spontaneous local opening-up of the DNA duplex could facilitate sharp bending of short DNA strands even in the absence of DNA binding proteins. We also find that the occurrence of two closely spaced melting bubbles will generally be favored when a large energetic barrier must be overcome in forming the desired bent DNA structure.

INTRODUCTION

Gene expression often requires the interplay of two distant genetic regions and thus sharp bending of DNA is an essential component of gene functioning. Conventional thinking holds that bending of short DNA strands below the persistent length, N_p ≈ 150 bp, is facilitated by DNA binding proteins, such as integration host factor (IHF) and a histone-like protein (HU) (1). DNA cyclization experiments provide a convenient method for evaluating this hypothesis (2,3). In a typical cyclization experiment, DNA fragments are designed with two complementary sticky ends. A cyclization reaction is then performed by adding DNA ligase, e.g. T4 DNA ligase, to the DNA solution. The efficiency of the cyclization reaction (J), i.e. the relative yield of cyclized versus linear DNA product, is related to the bending rigidity of the DNA analyte. By analyzing the J factor using Zhang–Crothers (4) or Shimada–Yamakawa (5) theory, it is in fact possible to extract the intrinsic rigidity of short DNA fragments.

Fundamental understanding of how a short DNA fragment forms a complete cycle during the cyclization assay is then an important first step for developing a more complete understanding of how DNA is packaged and transcribed in cells. This information should also make it possible to determine how DNA achieves the required enhancement in flexibility to form sharp bends at minimum energetic cost.

Recent cyclization experiments by Widom's group using short DNA fragments below the persistence length indicate that even these fragments spontaneously form sharp bends (6,7). This finding simultaneously challenges conventional thinking about the role of DNA bending catalysts and questions the suitability of classical theories based on worm-like chain (WLC) models for interpreting bending stiffness of double-stranded DNA (dsDNA) (8,9).

It has long been suspected that local, spontaneous opening-up of the dsDNA duplex can dramatically enhance DNA flexibility, perhaps explaining its ability to form sharp bends. Treating DNA as a kinkable elastic chain, simple models have been proposed to describe this effect (8–10). Single or multiple bubble(s) on DNA backbone is/are capable of creating local kinks, and thus effectively reduce(s) its bending stiffness. Studies using these models conclude that two melting bubbles are essential (9,10), and indeed likely (10), for interpreting Widom's cyclization experimental data (6). A recent study by Du et al. (11), however, challenges the enhanced DNA flexibility observed in Widom's experiment. These authors attribute the exceptionally high cyclization efficiency to higher than normal ligase concentration, which they contend invalidates the kinetic assumptions used to relate J to the bending stiffness of DNA. This ongoing debate underscores the need for other types of experiments that complement cyclization measurements to elucidate the mechanism(s) by which DNA is bent in cells.

The spontaneous base pair flip-out rate for DNA has been determined experimentally to be ∼10⁻³ s⁻¹ (12). The rate of cyclization of 199 bp DNA fragments under normal experimental conditions (11), ranges from 10⁻³ to 10⁻² s⁻¹ with increasing ligase concentration. This means that cyclization of fragments containing flip-out bases will generally make a small to insignificant contribution to J. On the other hand, the cyclization rate of the short DNA fragments used by Widom et al., i.e. <106 bp, is in the range of 10⁻⁵ to 10⁻⁶ s⁻¹ and even lower (11). This means that as DNA fragment length is gradually reduced below the persistence length, fragments containing one or more transiently flipped-out bases become more probable during the lifetime of the cyclization assay. Furthermore, if these flip-out bases significantly enhance the cyclization rate, the population of fragments whose cyclization is assisted by base flip-out can become very large. For short DNA fragments well below N_p, this effect should become dominant, since the cyclization rate of DNA without base flip-out approaches zero. Indeed conventional cyclization measurements have already shown that internal base pair mismatches in DNA can significantly enhance the cyclization efficiency (13). Precise information about how the kink(s) form and about how their location(s) impact cyclization efficiency of DNA therefore seems required to use any theoretical model to quantitatively explain cyclization data for short DNA.

As a first step towards understanding the effect of flip-out bases on bending of short DNA, we investigate bending properties of idealized analytes containing one or more permanent base pair mismatch(s) or melting bubbles. Because the lifetime of base unpairing events in these analytes is effectively infinite, these systems best model short DNA fragments with ‘trapped’ base flip-out by the ligase-mediated cyclization reaction. Their bending properties therefore provide insight into a potential alternative reaction pathway for cyclization reactions involving short dsDNA fragments. The extent to which the detailed conformation of a melting bubble resembles that of a transient base pair flip-out is, however, presently unknown. The well-known ability of a base pair mismatch to disrupt local base pairing as well as stacking, nonetheless, makes it a reasonable analog of the base pair flip-out. Precisely how these bubbles change the conformation as well as the local stiffness of DNA remains an open question. To quantify these effects, time-dependent fluorescence resonance energy transfer (FRET) experiments will be used to measure the distance, and its fluctuation amplitude, between donor and acceptor fluorophores appended to the two ends of a short DNA fragment. Time dependent FRET measurements are preferable to single-molecule fluorescence experiments (14), for at least two reasons. First, they avoid inevitable complications in the analyte's conformation induced by its attachment to a surface. Second, the higher signal to noise levels possible with FRET permit direct correlation between DNA local flexibility and its conformational state.

MATERIALS AND METHODS

DNA samples

A series of short dsDNA analytes of fixed size (16 bp), containing single bubble and double-melting bubbles positioned at predetermined locations along the DNA backbone forms the focus of our study. Bubbles are introduced by non Watson–Crick base pairs at specific locations in the DNA backbone. All oligonucleotides used in the study were custom synthesized and high-performance liquid chromatography (HPLC) purified by Simga Genosys (Woodlands, TX). A single target strand with sequence 5′-GGACTCCAGGTCACCC-3′, is 5′-labeled with 6-FAM (donor) and 3′-labeled with TAMRA (acceptor). Complementary sequences (see Table 1) were designed to hybridize with the target to produce dsDNA structures containing: (i) no defects (bubbles); (ii) 1, 2 and 4 bp bubble(s) at the center; and (iii) two 1 bp bubbles symmetrically located 3, 4 and 5 bp away from the two ends, or in other words 8, 6 and 4 bp away from each other. Hybridization was performed under standard conditions (15), and all samples were purified using PAGE as described previously (15). A buffer solution containing 10 mM Tris–HCl, 500 mM NaCl and 1 mM EDTA (pH 8.0) is used for fluorescence measurements.

Table 1.

complementary DNA sequences used in the study

	Sequence (5′–3′) the mismatch sequence(s) is underlined
Centrally located melted bubble	GGGTGACCTGGAGTCC
	GGGTGACCAGGAGTCC
	GGGTGACAAGGAGTCC
	GGGTGAGAAAGAGTCC
Distributed melted bubbles	GGGTGTCCTGCAGTCC
	GGGTCACCTGGTGTCC
	GGGAGACCTGGACTCC

Time-dependent fluorescence measurements

A time-dependent fluorescence measurement technique is used to characterize the flexibility of the dsDNA fragments (16). All measurements were carried out at 20°C. The FRET efficiency E was determined by measuring the fluorescence life time of the donor molecule in absence (τ_d) and presence (τ_da) of acceptor molecule using a home-made device described in Ref. (15). E can be related to the distance between the fluorophore pairs, using the well-known formula,

$$E=1-\frac{{\tau }_{\text{da}}}{{\tau }_{\text{d}}}=\frac{1}{1+{(R/R_0)}^6}$$ 1

R₀ is the Förster radius, which has been previously characterized to be 5.0 nm for the 6-FAM/TAMRA pair (17). The anisotropy of 6-FAM and TAMRA was determined independently to be 0.08 and 0.20, supporting the usage of an orientation factor κ² = 2/3 in calculating the Förster distance. Alexa 488 was used as calibration dye. Measurements using our apparatus yield a lifetime of 4.1 ± 0.1 ns, which compares very well with the 4.1 ns value reported by the dye manufacturer.

All dsDNA samples used for these measurements are carefully purified using PAGE before measurements, and their purity rechecked by PAGE after FRET measurements. Given the relatively short fragment sizes used and the fact that these fragments contain one or more mismatched bases, it is possible that residual amounts of dual labeled single-stranded DNA (ssDNA) may contribute to the measured FRET efficiencies. Lifetime measurements provide a simple, direct means of ruling out this possibility. Specifically, because of the much higher flexibility of ssDNA the donor lifetime in the presence of acceptor is anticipated to be substantially smaller than for dye-pair labeled dsDNA. This effect was confirmed using control experiments with dual labeled ssDNA. In these experiments we independently measured the FRET efficiency of ssDNA using steady-state and time-dependent fluorescence data. The former experiments yielded high efficiencies in the range of 85–100%, which is consistent with the high flexibility of the ssDNA. The time dependent measurements, however, reveal no contribution from the donor–acceptor pair. This latter effect is easily traced to the small fluorescence lifetime, <400 ps, of the donor–acceptor pair attached to ssDNA. Such a fast decay time-scale is in fact comparable to the normal laser pulse rising time (∼200 ps), and therefore renders it inaccessible with the current equipment. As a result, residual amounts of dye-pair labeled ssDNA present in the FRET samples will make no contribution to the energy transfer efficiency deduced from the measured lifetimes.

RESULTS AND DISCUSSION

Centrally located melting bubbles

The energetic cost of introducing a single base pair mismatch in DNA is 1–2 kcal/mol (18). This value far exceeds the energetic penalty of interrupting local base pairing, i.e. 0–1 kcal/mol (19). This means that selective introduction base pair mismatches to dsDNA backbone, to create melting bubbles, will not only compromise local base paring, but also will interfere with local base stacking. It is known that base pairing and base stacking act to stiffen dsDNA (20). Therefore, in the vicinity of a melting bubble, dsDNA is expected to exhibit greatest flexibility, suggesting that these bubbles might act as de facto hinges or kinks in the DNA backbone. The structural characteristic of the bubble region are anticipated to resemble those of single stranded, rather than dsDNA (14).

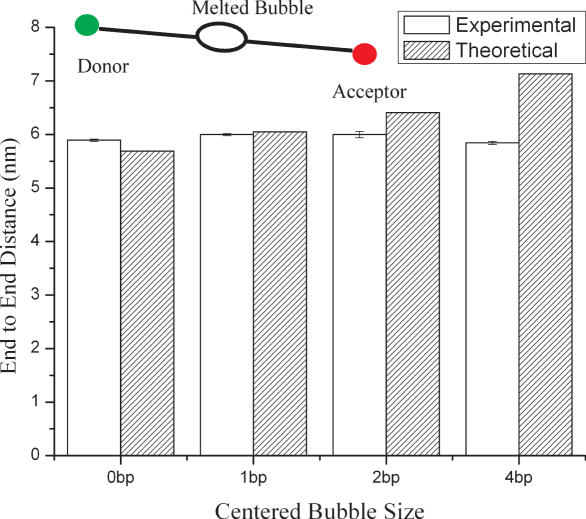
To quantify the effect of base pair mismatches/bubbles on dsDNA conformation, the average distance between 6-FAM and TAMRA appended to the ends of linear DNA fragments was determined from FRET efficiency data. By systematically varying the position(s) and number of bases contained in the bubbles, it is then possible to determine how these variables affect conformation of the DNA analyte. The simplest approach for extracting the size of the analyte from FRET efficiency data is the single component fitting method described in Ref. (15). End-to-end distances computed in this way are summarized in Figure 1 for a DNA analyte containing a single, centrally located melting bubble. The experimental values are compared with those obtained from theory (see Figure 1); theoretical end-to-end distance values in the figure were calculated by assuming that short DNA fragments assumes a linear rigid-rod structure and that dsDNA contributes 0.34 nm per base pair, while the melting bubble contributes 0.7 nm per base pair (14). These calculations are corrected for the extra distance [0.25 nm, (21)] due to dye labeling. The above calculation makes a key assumption about the ssDNA forming the melting bubble, namely that the unit length of each base of ssDNA is fixed at 0.7 nm. The unit length per base of ssDNA has in fact been determined using various approaches, including measuring the average distance between adjacent phosphorus atoms determined from crystal structures of ssDNA–protein complexes, in which case it has been determined to be (0.63 ± 0.08 nm) (22); stretching ssDNA (0.75 nm) (23); and the calculation of inter-phosphate distances based on a virtual bond scheme (0.59–0.69 nm) (24). Our choice of 0.7 nm per base is therefore justified by any of these approaches. Of course, based on the variation of the reported values other choices are possible (0.55–0.75 nm), which will change the specific values of bending angles and flexibility deduced, but should have no effect on the qualitative trends (see Table 3). The salt concentration used in this study is similar to the salt concentration used for typical cyclization reactions, the persistence length of ssDNA under these conditions is estimated to be ∼2.0 nm (22). This means that the length contribution from ssDNA in melting bubbles 2 bp and greater can be reasonably well modeled by summing over the single base contributions. However, when the two ssDNA strands are close to each other, inter-strand stacking may have an effect on the calculated lengths; this effect is discussed in the data analysis section of the paper.

Figure 1.

End-to-end distance of 16 bp dsDNA containing a fully complementary sequence and containing centrally located bubbles with varying size.

For the fully complementary DNA, the calculated end-to-end distance is almost identical to the theoretical value, indicating that it assumes an unbent, rigid rod-like structure. This result is expected because there are no (AT) or (CG) tracts in the sequence. As the melting bubble size gradually increases, the experimental values are observed to deviate systematically from the theoretical predictions. Specifically, for the 1, 2 and 4 bp melting bubbles/bubbles, the end-to-end distance decreases by 1, 7 and 19% relative to theoretically determined values. These deviations correspond to apparent bending angles of 16 ± 1°, 41 ± 1° and 71 ± 1°, respectively. Here, the position of the bend is taken to be in the center of DNA fragment.

Reduction in end-to-end distance of short dsDNA containing base pair mismatches does not necessarily imply that the structures exhibit permanent bends or kinks. Such reductions might also arise if the bubbles enhance the flexibility of the DNA backbone, which will also increase the FRET efficiency E above the values deduced from Equation 1, assuming a perfectly rigid-rod structure. To simultaneously consider the contribution from these two effects, we assume that fluctuations of the donor and acceptor dye separation about the mean value $\overline{r}$ are uncorrelated and small in comparison to the length of the fragment. In this case the probability distribution of end-to-end lengths can be represented analytically (25,26)

$$P\left(r\right)=\frac{1}{\sigma \sqrt{2\pi }}\text{exp}\left[-\frac{1}{2}{\left(\frac{\overline{r}-r}{\sigma }\right)}^2\right],$$ 2

where $\overline{r}$ and σ are the mean end-to-end distance and variance, respectively. The assumptions leading to Equation 2 are rigorously valid when the DNA fragment is long relative to its persistence length, and/or when dye-DNA bond fluctuations make a significant contribution to the end-to-end distance distribution (e.g. if the DNA fragment is short). The last condition has been corroborated using computer simulations of FRET from freely rotating dye pairs append to short DNA fragments (25). For intermediate size DNA, the end-to-end distance distribution of dsDNA, without considering dye-DNA bond fluctuations, can be calculated using a WLC model, which assumes an exponential form P(r_e) for materials in the size range of interest (27). The overall end-to-end distance reported by the FRET experiment is then a convolution over the distribution P(r_e) due to the bending stiffness of dsDNA and a Gaussian distribution P(r_g) due to dye-DNA bond fluctuations. When the dye-DNA bond fluctuations are either larger or comparable to the length fluctuations of the dsDNA analyte, as in this study, the convoluted distribution P(r) takes an approximate Gaussian form, and the variance is well approximated using the summation of the variances of P(r_g) and P(r_e). This approximation can be shown to become progressively worse when the variance in P(r) becomes two times or more greater than that of P(r_g); in which case an analysis of FRET data using the Gaussian form will lead to systematic underestimation of the contribution due to P(r_e).

The variance σ deduced from the above analysis therefore does not solely reflect the bending flexibility of DNA, but instead includes a significant contribution from DNA-dye bond fluctuation. Since DNA-dye bond fluctuations are independent of oligonucleotide content far from the dye labeling site, changes in the variance values produced by base pair mismatches in the DNA fragments are expected to provide a direct indication of changes in DNA flexibility.

The intensity decay curves obtained for an arbitrary DNA molecule labeled with a FRET pair is the convolution integral over this probability distribution (25–26,28–29)

$$I_{\text{DA}}\left(t\right)=I_{\text{D}}{\int }_0^{\infty }P\left(r\right)\text{exp}\left[-\frac{t}{{\tau }_{\text{D}}}-\frac{t}{{\tau }_{\text{D}}}{\left(\frac{R_0}{r}\right)}^6\right]\text{d}r.$$ 3

Here τ_D is the lifetime of the corresponding donor-only labeled molecule and is determined independently as described previously. I_D is a free fitting parameter reflecting the overall fluorescence intensity. Inserting Equation 2 in 3 yields a functional form for I_DA(t) that can be compared with the experimentally determined fluorescence decay data to extract the two unknown parameters $\overline{r}$ and σ. The donor decay curve can be directly fitted by Equation 3 to yield $\overline{r}$ and σ. However, this approach will yield undesirable coupling between the two parameters. An analytical procedure utilizing the method of moments (28,29) can be used to remove this coupling.

In this procedure, the fluorescence decay curves of the donor with and without acceptor molecules are first deconvoluted to remove the instrument response function. The resulting function is then analyzed using a multi-exponential fitting routine available in the SPC image software (Becker & Hickl GmbH). Based on a simple χ² minimization procedure, the fluorescence decay curve for the donor-only case was found to be best fit by a single exponential function I_D(t), while the donor–acceptor fluorescence decay is best fit by a bi-exponential function, I_DA(t).

These functions can be used to define a new function G(t) = I_DA(t)/I_D(t), which reflects only the pure energy transfer process between donor and acceptor (28,29). The zeroth and first moments of G(t) can be readily computed, allowing $\overline{r}$ and σ to be uniquely determined for any analyte. In addition to decoupling $\overline{r}$ and σ, this procedure also has the advantage of correcting for the effect of small amounts of residual donor-only labeled DNA present with the dye-pair labeled species during FRET measurements.

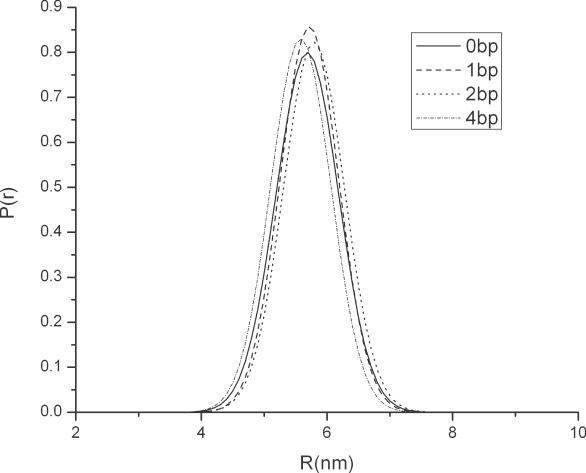
The fitted end-to-end distance distribution curves for DNA analytes containing centrally located bubbles of variable size are shown in Figure 2 and the results are summarized in Table 2. Bending angles calculated using the same procedure as described in the previous paragraph are found to be 39 ± 4°, 52 ± 2° and 78 ± 1° for melting bubble size of 1, 2 and 4 bp, respectively. These values are comparable to the value obtained using the one dominant conformation assumption, but are slightly higher since different analysis procedures are used. To evaluate the effect of ssDNA unit length on these values, bending angles are calculated using two other unit lengths, 0.55 nm and 0.75, and the results are summarized in Table 3. It is evident from the table that while different choices of ssDNA unit length do lead to different bending angles, the maximum relative error made by fixing the ssDNA unit length at 0.7 nm is in the range of 20–40%. As expected, however, changes in the unit length have no effect on the observed trends.

Figure 2.

End-to-end distance distribution of dsDNA containing centrally located bubbles with varying size.

Table 2.

Calculated contour length (including 0.25 nm extra length owing to dye labeling), experimentally measured mean end-to-end separation, $\overline{r}$, of FRET dye pair and the associated variance σ

Melted bubble size (bp)	rcontour(nm)	$\overline{r}$(nm)	σ(nm)
0	5.69	5.69 ± 0.02	0.50 ± 0.01
1	6.05	5.72 ± 0.03	0.46 ± 0.02
2	6.41	5.80 ± 0.02	0.49 ± 0.02
4	7.13	5.58 ± 0.02	0.48 ± 0.03

Results are for DNA containing one centrally located melting bubble with variable size.

Table 3.

Calculated bending angles of centrally located melting bubble with variable size using different unit lengths of ssDNA

Melted bubble size (bp)	0.55 nm	0.75 nm
0	0°	0°
1	29 ± 5°	41 ± 3°
2	37 ± 3°	52 ± 1°
4	64 ± 2°	88 ± 4°

Even from visual inspection of the curves in Figure 2, it is apparent that the variance σ is almost identical for all of the analytes studied. This result is quite unexpected because it means that for our experimental conditions, and time-scale resolution (∼100 ps), increasing the centrally located bubble size has only a negligible effect on analyte flexibility. This finding suggests that the primary difference between analytes containing centrally located melting bubbles is captured in $\overline{r}$, and therefore arise from permanent local bends/kinks in the DNA backbone. The closeness of the end-to-end distance of DNA with various bubble size nonetheless indicates that the formula used to estimate the melting bubble contribution to the contour length must be viewed with some care. Specifically, it could be argued that as a result of inter-strand stacking, two spatially close ssDNAs, forming the melting bubble, might fold in a similar way as a dsDNA, eliminating the need for a separate analysis of the single-strand contribution. The end-to-end distance of 22 bp dsDNA obtained in the single molecule fluorescence experiments by Schallhorn et al. (14) partially resolve this issue. These authors reported that the end-to-end distance of dsDNA is increased by 0.2 and 0.5 nm, respectively, when a 3 and 7 bp bubble is introduced; indicating that the ssDNA sections in the bubbles do enhance the end-to-end separation of short DNA duplexes.

Distributed melted bubbles

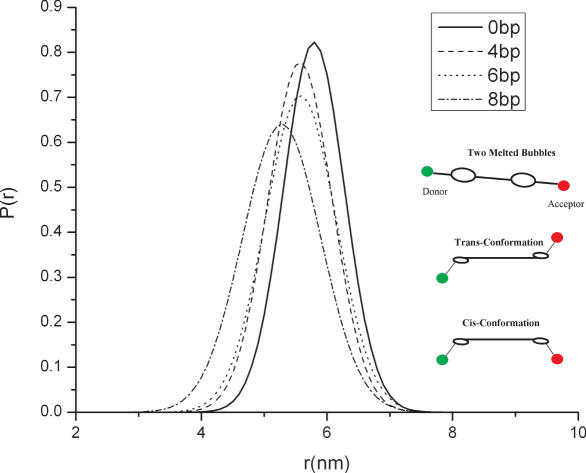
The FRET distance distribution for linear DNA containing two 1 bp melted bubbles, symmetrically located on its backbone was determined using a similar method as described in the previous paragraph. Figure 3 and Table 4 summarize results from this analysis. Two 1 bp bubbles distributed on the DNA backbone introduce two hinge points, which should result in many new molecular conformations. Since these two hinge points are placed symmetrically, they are essentially equivalent to each other. Also taking into account the electrostatic repulsion between DNA segments, which maximizes the inter-segment distance, trans-like conformation as illustrated in Figure 3 should be favored. The local bending angles calculated under the assumption of the trans-conformation are 47 ± 1°, 45 ± 1°, 47 ± 1° for base pair mismatches 4, 6 and 8 bp, respectively, away from each other. On the other hand, the local bending angle of the two hinges calculated based on the cis-conformation assumes a constant value close to 80° for each of these analytes. Bending angle values for the two-bubble analytes computed under the trans-dominant assumption, are evidently much larger than those computed for DNA containing a centrally located 1 bp bubble, but of similar magnitude to those obtained for analytes containing a central 2 bp bubble.

Figure 3.

End-to-end distance distribution of dsDNA containing two 1 bp bubbles symmetrically located on the backbone separated by varying distance.

Table 4.

Mean end-to-end distance, $\overline{r}$, of FRET dye-pair and the associated variance σ for DNA containing two symmetrically distributed 1 bp melted bubbles separated by varying distances

Distributed bubble distance (bp)	$\overline{r}$(nm)	σ(nm)
0	5.80 ± 0.02	0.49 ± 0.02
4	5.57 ± 0.03	0.51 ± 0.03
6	5.58 ± 0.01	0.57 ± 0.01
8	5.28 ± 0.01	0.62 ± 0.01

It is also evident from Figure 3 that the variance of the distance distribution is significantly larger for the two-bubble than for the one-bubble case. Taken together with the results from the previous section, this indicates that introducing two hinge points to the DNA backbone has a much larger effect on its flexibility, as well as on the amplitude of localized kinks or bends. The overall effect of introducing two hinge points is also substantially larger than what is expected if the hinges are assumed to act independently. Specifically, under the ‘independent action’ assumption, no change in local stiffness and smaller bending angles for each hinge are anticipated. This observation is most likely a manifestation of cooperative action by the two bubbles. In other words, when the two defects are spaced closely, i.e. less than the DNA helix twist length (<11 bp in our experiments), the two defects can sense each other, effectively softening the DNA. This means that in selecting multi-defect models for DNA bending the local stiffness parameters for closely located hinges should be selected with care because they will generally be quite different from stiffness parameters assigned to a single local defect. A surprising consequence of this result is that the flexibility of the DNA strand containing distributed 1 bp bubbles depends on the bubble separation distance. In particular, we find that the distributed bubbles act in concert to produce a cooperative enhancement in DNA's flexibility. This cooperative effect is typically large when the bubbles are positioned in equivalent phases of the helix.

CONCLUSIONS

There are at least two implications of our findings for interpreting cyclization data. First, our results show that spontaneous unpairing of DNA leading to localized or distributed bubbles, produces large permanent bends/kinks in short dsDNA analytes. Thus, although localized bubbles are found to have negligible effect on the overall flexibility of short DNA, the bends/kinks they produce can significantly impact cyclization efficiency and hence apparent flexibility of the analyte deduced from cyclization data. Second, our results suggest that multiple distributed bubbles provide a more efficient route to bend DNA than single multi-bp bubbles. This result stems from the fact that small distributed bubbles produce comparable overall levels of bending to large localized ones, but unlike localized bubbles also appear to increase the overall flexibility of the analyte. How this finding might impact model selection for fitting cyclization data depends both on the detailed sequences used and the degree of bending required to complete the cycle. Specifically, for the 2 bp bubble considered here, it can easily be shown that the energetic cost for initiating a second base unpairing event at the site of the first is ∼1–2 kcal/mol (18), while the alternative (two randomly located 1 bp bubbles) incurs an additional energetic cost in the same range, depending on the exact sequence (18).

Thus, at similar energetic cost, two closely spaced 1 bp bubbles can be formed with larger local bending and decreased levels of stiffness, as compared with a localized 2 bp bubble. In cyclization experiments requiring very sharp local bending of short dsDNA fragments, i.e. when the free energy cost of forming the required bended structure far exceeds that of forming two-melted bubbles, our experimental results indicate that the kinkable worm-like chain model including two closely spaced melting bubble is more plausible for explaining the spontaneous, sharp bending of DNA.