Abstract
Subcellular localization is one of the key functional characteristics of proteins. An automatic and efficient prediction method for the protein subcellular localization is highly required owing to the need for large-scale genome analysis. From a machine learning point of view, a dataset of protein localization has several characteristics: the dataset has too many classes (there are more than 10 localizations in a cell), it is a multi-label dataset (a protein may occur in several different subcellular locations), and it is too imbalanced (the number of proteins in each localization is remarkably different). Even though many previous works have been done for the prediction of protein subcellular localization, none of them tackles effectively these characteristics at the same time. Thus, a new computational method for protein localization is eventually needed for more reliable outcomes. To address the issue, we present a protein localization predictor based on D-SVDD (PLPD) for the prediction of protein localization, which can find the likelihood of a specific localization of a protein more easily and more correctly. Moreover, we introduce three measurements for the more precise evaluation of a protein localization predictor. As the results of various datasets which are made from the experiments of Huh et al. (2003), the proposed PLPD method represents a different approach that might play a complimentary role to the existing methods, such as Nearest Neighbor method and discriminate covariant method. Finally, after finding a good boundary for each localization using the 5184 classified proteins as training data, we predicted 138 proteins whose subcellular localizations could not be clearly observed by the experiments of Huh et al. (2003).
INTRODUCTION
Recent advances in large-scale genome sequencing have resulted in the huge accumulation of protein amino acid sequences (1). Currently, many researchers are trying either to discover or to clarify the unknown functions of these proteins. Since knowing the subcellular localization where a protein resides can give important insight into its possible functions (2), it is indispensable to identify the subcellular localization of a protein. However, it is time consuming and costly to identify the subcellular localizations of newly found proteins entirely by performing experimental tests. Thus, a reliable and efficient computational method is highly required to directly extract localization information.
From a machine learning point of view, a task that predicts the subcellular localizations of given proteins has several characteristics which demonstrate the task's complexity (see Table 1). First, there are too many localizations in a cell. For example, according to the work of Huh et al. (3), there are 22 distinct subcellular localization categories in budding yeast. It means that the possibility of correct prediction of one localization is <4.55% with a random guess. Second, the prediction task is a ‘multi-label’ classification problem; some proteins may have several different subcellular localizations (1). For instance, the YBR156C can be located either in ‘microtubule’ or ‘nucleus’ according to the work of Huh et al. (3). Thus, a computational method should be able to handle the multi-label problem. Finally, the number of proteins in each localization is too different making a protein localization data set highly ‘imbalanced’. It is generally accepted that proteins located in some organelles are much more abundant than in others (2). It also can be checked with the data of Huh et al. (3); the number of proteins in ‘cytoplasm’ is 1782, while the number of proteins in ‘ER to Golgi’ is only 6 (see the second column of Table 1). All these three characteristics make the task difficult. Thus, not only good features for a protein but also a good computational algorithm is ultimately needed for the reliable prediction of protein subcellular localization.
Table 1.
The number of proteins in the original Huh et al. Dataset (2003) and three training datasets
| Subcellular localization | Huh et al. Dataset | Dataset-I | Dataset-II | Dataset-III |
|---|---|---|---|---|
| 1. Actin | 32 | 32 | 27 | 27 |
| 2. Bud | 25 | 25 | 19 | 19 |
| 3. Bud neck | 61 | 61 | 48 | 48 |
| 4. Cell periphery | 130 | 130 | 98 | 98 |
| 5. Cytoplasm | 1782 | 1782 | 1472 | 1472 |
| 6. Early golgi | 54 | 54 | 39 | 39 |
| 7. Endosome | 46 | 46 | 37 | 37 |
| 8. ER | 292 | 292 | 207 | 207 |
| 9. ER to golgi | 6 | 6 | 5 | 5 |
| 10. Golgi | 41 | 41 | 30 | 30 |
| 11. Late golgi | 44 | 44 | 38 | 38 |
| 12. Lipid particle | 23 | 23 | 15 | 15 |
| 13. Microtubule | 20 | 20 | 17 | 17 |
| 14. Mitochondrion | 522 | 522 | 389 | 389 |
| 15. Nuclear periphery | 60 | 60 | 38 | 38 |
| 16. Nucleolus | 164 | 164 | 122 | 122 |
| 17. Nucleus | 1446 | 1446 | 1126 | 1126 |
| 18. Peroxisome | 21 | 21 | 16 | 16 |
| 19. Punctate composite | 137 | 137 | 91 | 91 |
| 20. Spindle pole | 61 | 61 | 27 | 27 |
| 21. Vacuolar membrane | 58 | 58 | 47 | 47 |
| 22. Vacuole | 159 | 159 | 124 | 124 |
| Total number of classified proteins, | 5184 | 5184 | 4032 | 4032 |
| Total number of different proteins, N | 3914 | 3914 | 3017 | 3017 |
| Dimension of features | 9620D | 2372D | 11992D | |
| Coverage | 100% | 77.08% | 77.08% |
Actually, many works have been done during the last decade or so in this field. The efforts in these works have followed several trends (see Table 2).
Table 2.
The previous researches in the prediction of protein subcellular localization
| Author(s) | Algorithm | Feature | # of Classes | Multi-label | Imbalance |
|---|---|---|---|---|---|
| Nakashima and Nishikawa (4) | Scoring System | AAk, PairAAl | 2 | x | x |
| Cedano et al. (13) | LDa (Mahalanobis) | AAk | 5 | x | x |
| Reinhardt and Hubbard (20) | ANNc Approach | AAk | 3, 4 | x | x |
| Chou and Elrod (2) | CDd | AAk | 12 | x | x |
| Yuan (21) | Markov Model | AAk | 3, 4 | x | x |
| Nakai and Horton (23) | k-NNe Approach | Signal Motif | 11 | x | x |
| Emanuelsson et al. (10) | Neural network | Signal Motif | 4 | x | x |
| Drawid et al. (27) | CDd | Gene Expression Pattern | 8 | x | x |
| Drawid and Gerstein (24) | BNb Approach | Signal Motif, HDEL motif | 5, 6 | x | x |
| Cai et al. (8) | SVMsi | AAk | 12 | x | x |
| Chou (6) | Augumented CDd | AAk, SOCn factor | 5, 7, 12 | x | x |
| Hua and Sun (16) | SVMsi | AAk | 4 | x | x |
| Chou and Cai (25) | SVMsi | SBASE-FunDo | 12 | x | x |
| Nair and Rost (26) | NNe Approach | functional annotation | 10 | x | x |
| Cai et al. (9) | SVMsi | SBASE-FunDo, PseAAm | 5 | x | x |
| Chou and Cai (11) | NNe Approach | GOp, InterPro-FunDq, PseAAm | 3, 4 | x | x |
| Chou and Cai (14) | LDa | PseAAm | 14 | x | x |
| Pan et al. (19) | Augmented CDd | PseAAm with filler | 12 | x | x |
| Park and Kanehisa (18) | SVMsi | AAk, PairAAm, GapAAk | 12 | x | x |
| Zhou and Doctor (22) | CDd | AAk | 4 | x | x |
| Gardy et al. (12) | SVMsi, HMMh, BNb | AAk, motif, homology analysis | 5 | x | x |
| Huang and Li (17) | fuzzy k-NNe | PairAAl | 4, 11 | x | x |
| Guo et al. (15) | p-ANNj | AAk | 8 | x | x |
| Bhasin and Raghava (7) | SVMsi | AAk, PairAAl | 4 | x | x |
| Chou and Cai (1) | NNe Approach | GOp, InterPro-FunDq, PseAAm | 22 | Considering | x |
aLD: Least Distance algorithm.
bBN: Bayesian Network.
cANN: Artificial Neural Network.
dCD: Covariant Discriminant algorithm.
eNN: Nearest Neighbor.
hHMM: Hidden Markov Model.
iSVMs: Support Vector Machines.
jp-ANN: probabilistic Artificial Neural Network.
kAA: amino acid composition.
lPairAA: amino acid pair composition.
mPseAA: pseudo amino acid composition.
nSOC: sequence-order correlation.
oSBASE-FunD: functional domain composition using SBASE.
pGO: gene ontology.
qInterPro-FunD: InterPro functional domain composition.
rFunDC: functional domain composition. (Here, ‘x’ means ‘Not Considering’.)
1) Feature Extraction: one trend is to try to extract good information (or features) from given proteins. One category of the features used is based on amino acid composition (AA) (1,2,4–14,15–22). Many works have used AA as the unique feature or the complementary feature of a protein owing to its simplicity and its high coverage. Prediction based on only AA features would lose sequence order information. Thus, to give sequential information to the AA, Nakashima and Nishikawa (4) also used amino acid pair composition (PairAA), Chou (5) used pseudo amino acid composition (PseAA) using sequence-order correlation (SOC) factor (6), and Park and Kanehisa (18) also used gapped amino acid composition (GapAA). For more sequence order effect, Pan et al. (19) used digital signal processing filter technique to the PseAA. These features based on AA have the advantage of achieving a very high coverage but may have limit on the high performance. Other researchers have used several kinds of motif information as the feature of proteins (1,9–12,23,24–26). Since Nakai and Horton (23) used protein sorting signal motifs in the N-terminal portion of a protein, some researchers (24) have used the motif in the prediction of localization. Using the 2005 functional domain sequences of SBASE-A which is a collection of well known structural and functional domain types (28), Chou and Cai (9,25) represented a protein as a vector with a 2005-dimensional functional domain composition (SBASE-FunD). They also introduced the dimensional functional domain composition (InterPro-FunD) (1,11) using the InterPro database (29). In contrast, Nair and Rost (26) represented a protein with functional annotations from the SWISS-PROT database (30). Recently, for higher prediction accuracy Cai and Chou (1,11) used Gene Ontology (GO) term as a auxiliary feature of a protein. Even though motif information and GO can improve the prediction accuracy, the information has a limited coverage of the proteins.
2) Class coverage extension: another trend is to increase the coverage of protein localization for practical use. At the beginning, Nakashima and Nishikawa (4) distinguished between intracellular proteins and extracellular proteins using the AA and the PairAA features. After that, many researchers enlarged the number of localization classes to 5 classes (13), to 8 classes (27), to 11 classes (23), to 12 classes (2), then to 14 classes (14). Recently Chou and Cai (1) used up to 22 localization classes using the dataset of Huh et al. (3), which is the biggest coverage of protein localization up to now.
3) Computational algorithm: to improve the prediction quality, another trend is to try to use an efficient computational algorithm in the prediction stage. Current computational methods include the following: a Least Distance Algorithm using various distance measures [a distance in PlotLock (31) that is modified from Mahalanobis distance originally introduced by Chou in predicting protein structural class (32), a Covariant discriminant algorithm (CD) in (2,27), and an augmented CD in (6)], an Artificial Neural Network approach in (15,20), a Nearest Neighbor approach in (1,11,17,23,26), a Markov Model (MM) in (21), a Bayesian Network (BN) approach in (24), and Support Vector Machines (SVMs) approach in (7,9,16,18,25). In (12), three algorithms, such as SVMs, a Hidden MM and a BN are used for improving prediction accuracy.
Even though many previous works have been done for the prediction of protein subcellular localization, none of them tackled effectively the three characteristics of protein localization prediction at the same time. For example, many existing predictors use only less than five different subcellular localizations. Moreover, very few predictors deal with the issue of multiple-localization proteins except for Chou and Cai (1). The majority only assumed that there is no multiple-localization protein. Furthermore, almost all previous methods did not consider the imbalanced problem in a given dataset. That means these methods achieve high accuracy only for the most populated localizations, such as the ‘nucleus’ and ‘cytosol’. They, however, are generally less accurate on the numerous localizations containing fewer individual proteins. Thus, a new computational method is eventually needed for more reliable prediction which should have the following characteristics: (i) it can show relatively good performance in case many classes exist, (ii) it can handle a multi-label problem and (iii) it should be robust in an imbalanced dataset. Our study is aimed to address these issues.
To achieve the purpose, we developed a PLPD method which can predict better the localization information of proteins using a Density-induced Support Vector Data Description (D-SVDD) approach. The PLPD stands for ‘Protein Localization Predictor based on D-SVDD’. The D-SVDD (33) is a general extension of conventional Support Vector Data Description (C-SVDD) (34–36) inspired by the SVMs (37). According to the work of Lee et al. (33), D-SVDD highly outperformed the C-SVDD. D-SVDD is one of one-class classification methods whose purpose is to give a compact description of a set of data referred to as target data. One-class classification methods are suitable for imbalanced datasets since find compact descriptions for target data independently from other data (33,36). Moreover, they are easily used for the dataset whose number of classes is big owing to linear complexity with regard to the number of classes. However, original D-SVDD is not for a multi-class and multi-label problem. For the protein localization problem, thus, we propose the PLPD method by extending the original D-SVDD method using the likelihood of a specific protein localization.
The structure of the paper is organized as follows: First, we briefly provide the information on the C-SVDD and the D-SVDD in Section 2. In this section, we also introduce the proposed PLPD method for protein localization prediction. Section 3 highlights the potentials of the proposed approach through experiments with datasets from the work of Huh et al. (3). Concluding remarks are presented in Section 4.
MATERIALS AND METHODS
Conventional support vector data description
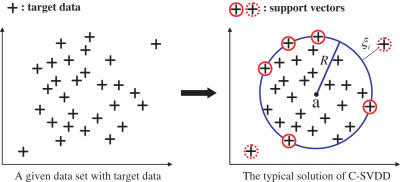
Since C-SVDD is not well introduced in bioinformatics fileds, we first briefly describe the basic ideas of the C-SVDD. Suppose a dataset containing n target data, {xi ∣ i = 1, … , n}, is given in the task of one-class classification. The basic idea of a C-SVDD (36) is to find the hypersphere (a, R) with minimum volume which includes most of the target data, where a and R are respectively the center and the radius of the solution (the hypersphere) as shown in Figure 1. To permit xi to be located in the outside of a hypersphere, the C-SVDD introduces a slack variable ξi ≥ 0 for each target data point analogous to SVMs (38). Thus the solution of the C-SVDD is obtained by minimizing the objective function O:
| (1) |
subject to (xi − a) · (xi − a) ≤ R2 + ξi where the parameter C+ > 0 gives the trade-off between volume of a hypersphere and the number of errors (number of target data rejected) (36).
Figure 1.
A typical solution of C-SVDD when outliers are permitted. The C-SVDD finds the minimum-volume hypersphere which includes most of target data. The data which resides on the boundary and outside the boundary are called support vectors which fully determine the compact boundary. Thus, the data with solid circle are the support vectors on the boundary, and the data with dotted circle are also support vectors which are the outliers.
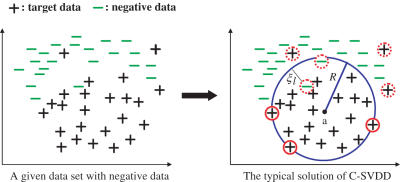
When negative data xl which should not be included in a compact description of target data are available during training, C-SVDD utilizes it. In this case, the C-SVDD finds the minimum-volume hypersphere that includes most of target data and at the same time, excludes most of negative data as shown in Figure 2. Suppose we have both n target data and m negative data. (Note: the total number of training data are N where N = n + m.) By using another slack variable ξl ≥ 0 for the permission of including negative data in a compact description, the objective function of this case is written as:
| (2) |
subject to (xi − a) · (xi − a) ≤ R2 + ξi and (xl − a) · (xl − a) > R2 − ξl where C− is another parameter which controls the trade-off between the volume of data description and the errors of negative data (36).
Figure 2.
A typical solution of C-SVDD when negative data are available. The C-SVDD finds the minimum-volume hypersphere which includes most of target data and at the same time, excludes most of negative data.
By using Lagrange Multipliers αk for xk, the dual problem of the C-SVDD is reduced to maximizing D(α):
| (3) |
subject to , 0 ≤ αi ≤ C+, and 0 ≤ αl ≤ C− where yk is the label of data xk. (Note: yk = 1 for a target data point, otherwise yk = −1.) After solving D(α) with regard to αk, the a of the optimal hypersphere can be calculated by , and the radius R can be obtained by the distance between a and any target data point xi that is located on the boundary of the hyperplane.
By comparing the distance between a test data point xt and a with R, the C-SVDD determines the decision whether xt is the same data type with the target data or not as:
| (4) |
where I is an indicator function (35). Thus, if the distance between xt and a is less than R, then we predict that xt is included in the given target dataset; otherwise, we predict that xt is not included.
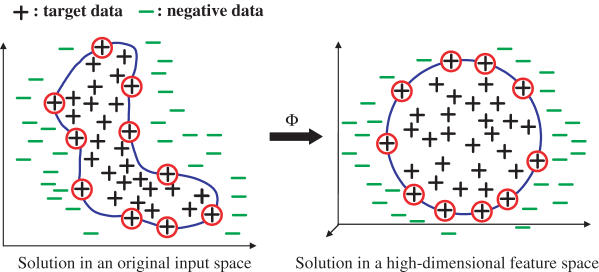
Similar to SVMs, the C-SVDD can find a more flexible data description in a high-dimensional feature space without directly mapping the space using a kernel function K(·,·) (38). As shown in Figure 3, the C-SVDD finds a solution by mapping the input training data into a possible high-dimensional feature space using a mapping function Φ, and seeking a hypersphere in the feature space. However, instead of explicitly mapping the training data into the feature space, C-SVDD directly finds the solution in the input space using the corresponding kernel K(xi, xj) between any two data xi and xj, defined by:
| (5) |
Thus, the kernelized form of Equation 3 is:
| (6) |
Using the kernel trick, the C-SVDD directly finds a more flexible boundary in an original input space as shown in the left figure of Figure 3 in an original input space.
Figure 3.
A typical solution of C-SVDD when a kernel function is used. The C-SVDD finds a more flexible solution in a high-dimensional feature space without mapping data into the feature space using some kernel function; C-SVDD finds a flexible solution directly in the original input space with a kernel function as shown in the left figure.
Density-induced support vector data description
As mentioned earlier, a C-SVDD finds a compact description that includes most of target data in a high-dimensional feature space, and the data that are not fully included in the hypersphere are called support vectors (36). In a C-SVDD, these support vectors completely determine the compact description (36) even though most target data can be non-support vectors. This can be a problem in data domain description especially when support vectors do not have the characteristics of a target dataset regarding its density distribution (33).
To address the problems outlined above and to identify the optimal description more easily, Lee et al. (33) recently proposed a D-SVDD which is a general extension of the C-SVDD by introducing the notion of a relative density degree for each data point. Using the relative density degree, Lee et al. defined a density-induced distance measurement for target data making data with higher density degrees give more influence on finding a compact description. By several experiments, the D-SVDD highly improved the performance of the C-SVDD (33). However, the original work of Lee et al. (33) only introduced the mechanism that can incorporate the density degrees of the target data, not negative data. Thus, in this study, we also introduce the mechanism of incorporating the density degrees of negative data by defining a density-induced distance measurement for negative data.
1) Relative density degree and density induced distance
to reflect the density distribution into searching the boundary of the C-SVDD, Lee et al. first introduced the notion of a relative density degree for each target data point which means the density of the region of the corresponding data point compared to other regions in a given dataset (33). Suppose we calculate a relative density degree for a target data point xi. By using , the distance between xi and (the Kth nearest neighborhood of xi), and the mean distance of Kth nearest neighborhoods of all target data, ℑK, they defined the local density degree ρi > 0 for xi as:
| (7) |
where , n is the number of data in a target class, and 0 ≤ ω ≤ 1 is a weighting factor. Note that the measure reports higher local density degree ρi for the data in a higher density region: the data with lower have higher ρi values. Moreover, a bigger ω produces higher local density degrees. In a similar manner, the relative density degrees for negative data are also calculated.
After calculating the relative density degrees, to incorporate the degrees into searching the optimal description in a C-SVDD, Lee et al. (33) proposed a new geometric distance called density-induced distance. They defined a positive density-induced distance between target data point xi and the center of a hyperspherical model (a, R) of a target dataset as:
| (8) |
where a and R are the center and the radius of the hypersphere, respectively. The basic idea is simple. To give higher influence on the search of the minimum-sized hypersphere, they made the distance between xi and the center a longer using relative density degre ρi. Note that to enclose the data point with increased distance owing to a higher relative density degree ρi, the radius of a minimum-sized hypersphere should be increased (a data point with higher ρi gives stronger influence on the boundary).
In a similar manner, we can incorporate the relative density degrees for negative data. After calculating the relative density degrees ρl for negative data xl using Equation 7, we define another density-induced distance between negative data and a, the center of the hyperspherical description of a target data set, as:
| (9) |
where a and R are the center and the radius of a hypersphere, respectively.
Note that decreases with increasing ρl. Hence, to exclude the negative data point with decreased owing to higher relative density degree ρl, the radius of a minimum-sized hypersphere should be decreased; the negative data point with higher relative density degree gives higher degree of penalty on the search of the minimum-sized hypersphere for a target dataset.
2) Mathematical formulation of D-SVDD
Using the density-induced distance measure for target data, Lee et al. reformulated the C-SVDD when only target data are available (33). Similar to C-SVDD, they permitted the possibility of training error using a slack variable ζi ≥ 0, which is the distance between the boundary Ω and xi outside Ω. Here, ζi equals for training error data, otherwise it is 0. It implies that ζi contains the information of a relative density degree of xi.
Using the slack variable for each target data point, they deduce Equation 10 from Equation 1:
| (10) |
subject to ρi(xi − a) · (xi − a) ≤ R2 + ζi.
By introducing Lagrange Multipliers, Lee et al. (33) could construct the dual problem: maximize D(α),
| (11) |
subject to , and .
After deriving αk that satisfy Equation 11, a of the optimal description can be calculated by:
| (12) |
Different from the C-SVDD (36), the center a of the optimal hypersphere is weighted by the relative density degree ρi (Equation 12) where the center is shifted to a higher dense region. Moreover, the R of optimal description is calculated by the distance between a and any Xi of which 0 < αk < C+ (33).
When negative data are available, D-SVDD can also utilize them to improve the description of the target dataset. In this case, we use negative density-induced distance for negative data in order to incorporating the density distribution of negative data. Using the negative density-induced distance and another slack variable ζl for possibility of training error for each negative data point, we find the optimal hypersphere that includes most target data and excludes most negative data. Here, ζl for each negative data point is the distance between the boundary Ω and xl inside Ω; that is, . Thus the new objective function is defined as:
| (13) |
subject to and where is a similar control parameter with that of the C-SVDD (34).
Similar to the previous case, after constructing the Lagrangian of Equation 13, the dual representation of this case is obtained as:
| (14) |
subject to and where yk is the label of xk (yk = 1 for a target data point, otherwise yk = −1), and N is the total number of data (N = n + m). Here, for target data xi and for negative data xl.
Note that using and (instead of ρk) the dual representation of negative version of D-SVDD becomes identical to the previous case of D-SVDD (Equation 11) except for the number of data considered (n becomes N = n + m). Therefore, when negative data are available, we can just use α′k and in the optimization problem and in the decision function of the precious case. That means there are no extra computational complications except the complication caused by the increased data size.
As seen in Equations 11 and 14, the dual forms of the objective functions of D-SVDD are represented entirely in terms of inner products of input vector pairs. Thus, we can kernelize D-SVDD where the kernelized version of the dual representation of the objective function when negative data are available is:
| (15) |
where T and constraints are the same as in Equation 14.
PLPD for prediction of protein subcellular localization
As mentioned earlier, the prediction of protein localization is a kind of multi-class and multi-label classification problem. However, D-SVDD including conventional SVDD is not for the multi-class and multi-label classification problems; it is for one-class and mono-label classification problems. Thus, we propose a new method for the prediction of protein localization by modifying the D-SVDD.
For a multi-class and multi-label classification problem, a predictor should answer two points. First, for a multi-class problem, a predictor should report the degree of being a member of each class for a test data point xt using some score function where f: ℵ × Ł → ℜ. (Here, ℵ is the domain of data, Ł is the domain of class labels, and ℜ is the domain of real numbers.) That is, a label l1 is considered to be ranked higher than l2 if . Second, owing to multi-label cases, the score function should be able to report multiple labels not a mono label, and the true positive labels of a protein should rank higher than any other labels. That is, if Łp is a set of the true positive labels of xt, then a successful learning system will tend to rank the labels in the Łp higher than any other labels not in Łp.
To address the requirements mentioned above, we adopt the following procedure.
if a training dataset is given, we divide it into a target dataset and a negative dataset by class. For a label li, for instance, a data point whose label set has li is included in the target data; otherwise, it is included in the negative dataset.
if a target dataset and a negative dataset are prepared for each class, we find the optimal boundary for the target data by using D-SVDD as formulated in Equation 15.
- we calculate the degree of being a member of each class li for a test data point xt using the following score function f:
where (ai, Ri) is the optimal hypersphere of target data which are included in the class label li. Note that this score function reports a higher value for a test data point with smaller distance between xt and ai regarding to the distance of Ri. If the distance between xt and ai, for example, is smaller than Ri, the score function reports higher values than 1; otherwise, the score function reports smaller values than 1. That means if the location of xt is closer to the center of the hypershpere, then the score function reports a higher degree of value.(16) Finally, according to the values of the score function for all classes, we rank the labels, and report them.
With this procedure, we can easily and intuitively modify the D-SVDD for a multi-class and multi-label classification problem like the prediction of protein localization by reflecting the overall characteristics of each class. We call the proposed method a PLPD.
RESULTS AND DISCUSSION
Data preparation and evaluation measures
1) Data preparation
To test the effectiveness of the proposed PLPD method, we experimented with the data of Huh et al. (3), which is currently the biggest class coverage and is a multi-label dataset. From the website http://yeastgfp.ucsf.edu, we get 3914 unique proteins whose locations are clearly identified. The breakdown of the original 3914 different proteins (N = 3914) is given in the second column of Table 1. Owing to some proteins may coexist several localizations, the so-called multi-label feature as mentioned earlier, the total sum of proteins in all localizations, denoted by , is 5184; In N = 3914 total different proteins, there are 2725 proteins in unique localization, 1117 proteins in two different localizations, 64 proteins in three different localizations, 7 proteins in four different localizations. And there is only 1 protein in five different localizations. Similar to the formulation by Chou and Cai (1),
| (17) |
Using the 3914 proteins, we represent a protein in three different ways, and make three datasets: Dataset-I, Dataset-II and Dataset-III to evaluate the performance of the proposed PLPD in various manners (see Table 1). In Dataset-I, we used AA-based features for a protein. After finding all amino acid sequences of 3914 proteins from the SWISS-PROT DataBank (30), we used PairAA features (400D; features from a21 to a420), and GapAA up to the maximal allowed gap (9200D = 400D × 23; the minimum length among all 3914 proteins is 25; features from a421 to a9620) for sequence information including the amino acid composition (20 Dimensions; features from a1 to a20). That is, a protein P is represented as a vector in a 9620-dimensional space (9620D = 20D + 400D + 9200D) as:
| (18) |
This dataset is described in the third column of Table 1. As you can see in the column, the coverage of this representation is 100%; that means, all of the 3914 proteins can be represented by this manner.
In Dataset-II, we adopted a similar manner with the Chou and Cai's approach (5) using the InterPro Motifs (29). Different from Chou and Cai, we first extracted 2372 unique motifs which are occurred only in the 3914 proteins in order to delete meaningless motifs. Using the unique motif set, we represent a protein as:
| (19) |
where bi = 1 if the protein has the ith motif in the unique motif set; otherwise, bi = 0. The coverage of each localization is depicted in the fourth column is Table 1. With this second manner, the overall coverage is 77.08% (3017 proteins among 3914 proteins).
For Dataset-III, we combined the previous two features only for the proteins which have more than one motif in the unique motif set. In this case, thus, a protein is characterized as:
| (20) |
where the elements from c1 to c9620 are derived from Equation 18, and the elements from c9621 to c11992 are derived from Equation 19. The coverage is same with the Dataset-II (see the fifth column is Table 1).
2) Evaluation measures
For multi-label learning paradigms, only one measurement is not sufficient to evaluate the performance of a predictor owing to the variety of correctness in prediction (39,40). Thus, we introduce three measurements (Measure-I, Measure-II and Measure-III) for the evaluation of a protein localization predictor. First, to check the overall success rate regarding to the total number of the unique proteins N, we define Measure-I as:
| (21) |
where L(Pi) is the true label set of a protein Pi, is the predicted top-k labels by a predictor, and
| (22) |
Note that owing to the multi-label protein localization problem, it is not sufficient to evaluate the performance of a predictor by checking only the topmost label predicted true. Thus, we check the real label set with the predicted top-k labels using the ψ[·, ·] function. The k value in Equation 22 is given by user, and we use 3 in this study since the numbers of true localization sites of most proteins are less than or equal to 3 (3).
Similar to the formulation by Chou and Cai (1), to check the overall success rate regarding to the total number of classified proteins, , we also evaluate the performance of a predict by using Measure-II:
| (23) |
where is the predicted top-ki labels by a predictor, and the Ψ[·, ·] function returns the number of labels which is predicted correctly. Note that the ki value determined by the number of true labels of a protein Pi, not by user.
As mentioned earlier, a dataset of protein localization is imbalanced in nature. Including overall success rate, thus, the information on the success rate of each class and the average rate of the success rates of each class is useful to evaluate the performance of a predictor. To achieve this, we define Measure-III as:
| (24) |
where μ = 22 is total number of labels or classes, l is a label index, is the number of proteins in the lth label, and
| (25) |
Performance comparison
To investigate the success of the proposed PLPD method and analyze it, we conducted several tests with the three datasets (Dataset-I, Dataset-II and Dataset-III). For comparative analysis we also experimented with the ISort method (1). To the best of our knowledge, ISort method showed the best performance for the prediction of yeast protein multiple localization up to now (1). Even though the jackknife cross-validation is one of most rigorous and objective validation measures (41,42), we did a 2-fold cross-validation approach to prevent the overfitting problem to a given training dataset. For a more flexible boundary of the PLPD, we used a Gaussian RBF function for kernelization in Equation 15 owing to the Gaussian RBF function is one of most suitable functions for kernelization (36,37). In addition, we selected the model parameters, such as C+ and C−, and the width parameter of the Gaussian RBF kernel function by using cross-validation approach (38,43) to identify the solutions of the PLPD.
The results of the ISort Method and the PLPD method for the three datasets are given in Table 3–5. As we can see in Table 3, ISort method showed 65.14, 35.91 and 10.02% according to Measure-I, Measure-II and Measure-III for the Dataset-I. For the same dataset, the PLPD method showed 73.89, 53.09 and 11.43% performance for the three measurements, respectively. This implies that the success rates of PLPD were 8.75, 17.18 and 1.41% higher than the ISort method regarding the Measure-I, the Measure-II and the Measure-III, respectively. Even though PLPD method showed better scores than the ISort method with regard to Measure-III, the two methods showed low degrees of average prediction accuracies for all localizations. For instance, ISort showed zero prediction accuracies at 10 localizations and PLPD at 9 localizations. As you can see in Table 1, those localizations whose prediction accuracies were zero have relatively small number of proteins in themselves. Thus, the prediction of localization based on only AA-based features has limitation to correctly predict all the localizations on average.
Table 3.
Prediction performance (%) of ISort and PLPD to the Dataset-I
| Measure | ISort method (%) | PLPD method (%) | |
|---|---|---|---|
| Measure-I | 65.14 | 73.89 | |
| Measure-II | 35.91 | 53.09 | |
| 1. Actin | 0.00 | 0.00 | |
| 2. Bud | 0.00 | 0.00 | |
| 3. Bud neck | 0.00 | 0.00 | |
| 4. Cell periphery | 0.00 | 0.00 | |
| 5. Cytoplasm | 77.55 | 99.89 | |
| 6. Early golgi | 5.56 | 5.56 | |
| 7. Endosome | 6.52 | 6.52 | |
| 8. ER | 0.00 | 0.00 | |
| 9. ER to golgi | 16.67 | 16.67 | |
| 10. Golgi | 0.00 | 4.88 | |
| 11. Late golgi | 2.27 | 6.82 | |
| Measure-III | 12. Lipid particle | 8.70 | 21.74 |
| 13. Microtubule | 10.00 | 10.00 | |
| 14. Mitochondrion | 0.77 | 1.15 | |
| 15. Nuclear periphery | 0.00 | 0.00 | |
| 16. Nucleolus | 6.10 | 1.83 | |
| 17. Nucleus | 83.82 | 65.08 | |
| 18. Peroxisome | 0.00 | 9.52 | |
| 19. Punctate composite | 0.73 | 0.00 | |
| 20. Spindle pole | 0.00 | 0.00 | |
| 21. Vacuolar membrane | 1.72 | 1.72 | |
| 22. Vacuole | 0.00 | 0.00 | |
| Average | 10.02 | 11.43 |
Table 5.
Prediction performance (%) of ISort and PLPD to the Dataset-III
| Measure | ISort method (%) | PLPD method (%) | |
|---|---|---|---|
| Measure-I | 75.90 | 83.49 | |
| Measure-II | 49.16 | 57.24 | |
| 1. Actin | 3.70 | 18.52 | |
| 2. Bud | 5.26 | 57.89 | |
| 3. Bud neck | 4.17 | 33.33 | |
| 4. Cell periphery | 30.61 | 33.67 | |
| 5. Cytoplasm | 73.30 | 77.04 | |
| 6. Early golgi | 12.82 | 25.64 | |
| 7. Endosome | 24.32 | 35.14 | |
| 8. ER | 22.71 | 21.26 | |
| 9. ER to golgi | 0.00 | 60.00 | |
| 10. Golgi | 13.33 | 43.33 | |
| 11. Late golgi | 10.53 | 26.32 | |
| Measure-III | 12. Lipid particle | 0.00 | 53.33 |
| 13. Microtubule | 29.41 | 52.94 | |
| 14. Mitochondrion | 27.51 | 33.16 | |
| 15. Nuclear periphery | 15.79 | 23.68 | |
| 16. Nucleolus | 28.69 | 31.97 | |
| 17. Nucleus | 51.07 | 66.96 | |
| 18. Peroxisome | 6.25 | 68.75 | |
| 19. Punctate composite | 10.99 | 12.09 | |
| 20. Spindle pole | 29.63 | 40.74 | |
| 21. Vacuolar membrane | 4.26 | 14.89 | |
| 22. Vacuole | 41.13 | 22.58 | |
| Average | 20.25 | 38.78 |
When the Dataset-II was used, the prediction accuracies of each method were higher than those of the two methods with Dataset-I. As you can see in Table 4, the ISort method showed 69.94, 44.27 and 15.33% accuracies for three measurements. On the contrary, the PLPD method showed 82.40, 56.32 and 32.41% accuracies for the three measurements. These improvements of the PLPD over the ISort were more conspicuous. Moreover, there was no zero performance for each localization in the PLPD method. In ISort method, however, there were 6 localizations(Actin, ER to Golgi, Lipid particle, Nuclear periphery, Peroxisome and Vacuolar membrane) whose prediction accuracies were zero. This means that the proposed method showed promising results even though a dataset is imbalanced when Dataset-II was used.
The best performance of each method was achieved when Dataset-III was used. Similarly, the PLPD method outperformed all the three measurements considered as shown in Table 5. The PLPD, for example, showed up to 83.49% accuracy with Measure-I, while the ISort method showed 75.90% accuracy. In regard to Measure-III, the PLPD method showed 38.78% average accuracy for all 22 localizations; it was 18.53% higher than the ISort method on average of all prediction accuracies for each localization.
In order to check the performance of PLPD with regard to Measure-III without considering the other two measurements, we did tests for the same data sets with similar manner to the previous tests. This means that we did parameter fitting process only regarding Measure-III for PLPD method. The results for Dataset-I, Dataset-II, and Dataset-III are depicted in Table 6. As you can see in Table 6, the average accuracies were highly increased. When the Dataset-III was used, for example, the average accuracy for all localization was up to 46.50%; it was 7.72% higher than the previous result of PLPD and 26.25% higher than the result of ISort method for the same dataset. It was remarkable.
Table 6.
The performance (%) of the proposed PLPD to the Dataset-I, Dataset-II, and Dataset-III only with regard to the Measure-III
| Measure | Dataset-I | Dataset-II | Dataset-III |
|---|---|---|---|
| Measure-III Average | 19.10% | 44.61% | 46.50% |
From Tables 3–6, we could conclude that the proposed PLPD method outperformed the ISort method regardless of the kind of evaluation measurement and regardless of the dataset used. Moreover, Motif information could increase the prediction accuracies of the two methods considered even though its coverage is lower than AA-based information. Furthermore, the best performance was obtained when both the features were used.
Similar to the work of Cai and Chou (44), to avoid homology bias, we removed all the sequences with >40% sequence homology and after then, we performed similar experiments to the previous cases. The new datasets are depicted in Table 1 in the Supplementary Data and the results of this experiments are described in Tables 2–4 in Supplementary Data. As we can see in the tables, we observed similar phenomena with previous results that were depicted in Tables 3–5, which means that the PLPD method can play a complimentary role to existing methods, regardless of the existence of sequence homology.
Table 4.
Prediction performance (%) of ISort and PLPD to the Dataset-II
| Measure | ISort method (%) | PLPD method (%) | |
|---|---|---|---|
| Measure-I | 69.94 | 82.40 | |
| Measure-II | 44.27 | 56.32 | |
| 1. Actin | 0.00 | 22.22 | |
| 2. Bud | 5.26 | 42.11 | |
| 3. Bud neck | 10.42 | 31.25 | |
| 4. Cell periphery | 41.84 | 26.53 | |
| 5. Cytoplasm | 71.13 | 84.58 | |
| 6. Early golgi | 7.69 | 25.64 | |
| 7. Endosome | 10.81 | 21.62 | |
| 8. ER | 16.43 | 12.56 | |
| 9. ER to golgi | 0.00 | 60.00 | |
| 10. Golgi | 6.67 | 33.33 | |
| 11. Late golgi | 5.26 | 21.05 | |
| Measure-III | 12. Lipid particle | 0.00 | 46.67 |
| 13. Microtubule | 29.41 | 41.18 | |
| 14. Mitochondrion | 18.77 | 16.20 | |
| 15. Nuclear periphery | 0.00 | 13.16 | |
| 16. Nucleolus | 17.21 | 26.23 | |
| 17. Nucleus | 44.32 | 65.36 | |
| 18. Peroxisome | 0.00 | 50.00 | |
| 19. Punctate composite | 6.59 | 7.69 | |
| 20. Spindle pole | 14.81 | 33.33 | |
| 21. Vacuolar membrane | 0.00 | 10.64 | |
| 22. Vacuole | 30.65 | 21.77 | |
| Average | 15.33 | 32.41 |
Using the 5184 classified proteins as training data we predicted 138 proteins whose subcellular localizations could not be clearly observed by the experiments of Huh et al. (3). Since the prediction accuracies were highest when both AA-based features and the unique InterPro Motif set were used as features of a protein, we used the information together. Actually we could not know the number of true localizations of a protein whose localization is not known yet, we enlist top three localizations which have the highest likelihood to be the true localization. In some cases, proteins have similar degrees in the likelihood. Thus, to treat this issue, we quantize the degrees of likelihood and treat them in the same rank. The predicted results of first 35 unknown localization proteins are given in the Table 7, where the roman numerals indicate the rank of likelihood of the corresponding localization. (See Supplementary Data for all results.)
Table 7.
The first 35 prediction results of proteins whose localizations are not clearly observed by the experiments.
| Protein | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| YAL029C | I | II | III | |||||||||||||||||||
| YAL053W | III | I | I | III | II | II | II | II | II | |||||||||||||
| YAR019C | III | I | II | |||||||||||||||||||
| YAR027W | II | I | II | II | III | II | ||||||||||||||||
| YAR028W | II | I | II | II | III | I | ||||||||||||||||
| YBL034C | I | III | II | III | II | III | ||||||||||||||||
| YBL067C | I | III | III | I | II | |||||||||||||||||
| YBL105C | III | II | II | I | III | |||||||||||||||||
| YBR007C | I | II | II | III | ||||||||||||||||||
| YBR072W | III | I | II | I | III | |||||||||||||||||
| YBR168W | III | I | III | II | ||||||||||||||||||
| YBR200W | II | III | I | II | ||||||||||||||||||
| YBR235W | I | III | III | II | ||||||||||||||||||
| YBR260C | I | II | II | III | ||||||||||||||||||
| YCL024W | III | II | III | I | ||||||||||||||||||
| YCR021C | I | II | III | III | III | |||||||||||||||||
| YCR023C | I | III | III | III | II | |||||||||||||||||
| YCR037C | I | III | III | II | III | III | III | |||||||||||||||
| YDL025C | II | I | III | I | III | |||||||||||||||||
| YDL171C | III | II | I | II | III | I | III | III | ||||||||||||||
| YDL203C | I | III | II | II | III | |||||||||||||||||
| YDL238C | I | III | II | I | III | |||||||||||||||||
| YDL248W | II | I | II | II | III | I | ||||||||||||||||
| YDR069C | I | III | II | III | ||||||||||||||||||
| YDR072C | III | I | II | II | III | I | ||||||||||||||||
| YDR089W | I | I | III | I | II | II | II | |||||||||||||||
| YDR093W | II | I | II | III | III | III | ||||||||||||||||
| YDR164C | II | I | II | II | III | II | I | |||||||||||||||
| YDR181C | I | II | I | III | ||||||||||||||||||
| YDR182W | I | III | II | I | I | |||||||||||||||||
| YDR251W | II | III | I | II | III | III | ||||||||||||||||
| YDR261C | I | III | III | III | III | II | II | |||||||||||||||
| YDR276C | III | II | II | II | III | II | I | I | II | |||||||||||||
| YDR309C | I | III | I | I | II | III | ||||||||||||||||
| YDR313C | III | II | II | III | I |
The numbers in the first row indicate the specific localizations listed in Table 2.
Among the predicted protein localizations, YBL105C, YBR072W and YDR313C are analyzed for validation as an example. As shown in Table 7, YBL105C is predicted to localize to ‘cytoplasm’ as the first rank, to ‘bud neck’ and ‘cell periphery’ as the second ranks. YBL105C (PKC1) is a Ser/Thr kinase and controls signaling pathway for cell wall integrity, for instance bud emergence and cell wall remodelling during growth (45,46). PKC1 contains C1, C2 and HR1 domains. HR1 domain targets PKC1 to bud tip and C1 domain targets it to cell periphery (47). Thus, PKC1 localizes to the ‘bud neck’ for its function. Those indicate that the localizations of YBL105C found from literature are consistent with our prediction results; ‘bud neck’ and ‘cell periphery’.
YBR072W (HSP26) is a heat shock protein which transforms into high molecular weight aggregate on heat shock and binds to non-native proteins (48,49). Depending on cellular physiological conditions, HSP26 localizes differently; accumulation in the ‘nucleus’ or wide-spread throughout the cell (48). The localizations of YBR072W found from literature, ‘nucleus’ and ‘cytoplasm’, are predicted correctly by our method.
Finally, YDR313C (PIB1) is a RING-type ubiquitin ligase containing FYVE finger domain. PIB1 binds specifically to phosphatidylinositol(3)-phosphate. Phosphatidylinositol(3)-phosphate is a product of phosphoinositide 3-kinase which is an important regulator of signaling cascade and intracellular membrane trafficking (50). The FYVE domain targets PIB1 to ‘endosome’ and ‘vacuolar membrane’ (51). The localizations of YDR313C found from literature, ‘endosome’ and ‘vacuolar membrane’, are consistent with our prediction results.
CONCLUSION
Subcellular localization is one of the most basic functional characteristics of a protein, and an automatic and efficient prediction method for the localization is highly required owing to the need for large-scale genome analysis. Even though many previous works have been done for the task of protein subcellular localization prediction, none of them tackles effectively all the characteristics of the task: a multiple class problem (there are too many localizations), a multi-label classification problem (a protein may have several different localizations), and an imbalanced dataset (a protein dataset is too imbalanced in nature). To get more reliable results, thus, a new computational method is eventually needed.
In this paper, we developed a PLPD method for the prediction of protein localization, which can find the likelihood of the specific localization for a protein more easily and more correctly. PLPD method is developed by using the Density-induced Support Vector Data Description (D-SVDD) (33). D-SVDD is one of one-class classification methods which is suitable for imbalanced datasets since they finds a compact description of a target data independently from other data (33,36). Moreover, it is easily used for the dataset whose number of classes is big owing to linear complexity with regard to the number of classes. However, D-SVDD is originally not for a multi-class and multi-label problem. Thus, we extended the D-SVDD for the prediction of protein subcellular localization. Moreover, we have introduced three measurements (Measure-I, Measure-II and Measure-III) for the evaluation of a protein localization predictor to more precisely evaluate the predictor. As the results of three datasets which are made by the experimental results of Huh et al. (3), the proposed PLPD method represents a different approach that might play a complimentary role to the existing methods, such as Nearest Neighbor method and discriminate covariant method. Finally, after finding the good boundary of each localization using the 5184 classified proteins as training data, we predicted 138 proteins whose subcellular localizations could not be clearly observed by the experiments of Huh et al. (3).
For the reliable prediction of subcellular localizations of proteins, both good features for a protein and a good computational algorithm are ultimately needed. Actually, this study mainly focused on a good computational algorithm for protein localization prediction. In this paper, we represented proteins in three different ways: AA-based features in Dataset-I, Motif-based features in Dataset-II and AA-and-Motif-based features in Dataset-III. From this study we observed that Motif-based features are more informative than AA-based features in protein localization prediction even though Motif-based features have lower coverage than AA-based features. Moreover, best performance was achieved when both AA-based features and Motif-based features are used simultaneously. In the current study we achieved relatively high performance in the protein localization prediction problem. However, it is not sufficient yet and for better results, further study should focus on a mechanism that can extract better information from given proteins.
SUPPLEMENTARY DATA
Supplementary data are available at NAR online.
Acknowledgments
The authors thank the anonymous reviewers for their helpful comments. This work was supported by National Research Laboratory Grant (2005–01450) and the Korean Systems Biology Research Grant (2005–00343) from the Ministry of Science and Technology. The authors would like to thank CHUNG Moon Soul Center for supporting BioInformation and BioElectronics and the IBM SUR program for providing research and computing facilities. Funding to pay the Open Access publication charges for this article was provided by Korean Science and Engineering Foundation (KOSEF).
Conflict of interest statement. None declared.
REFERENCES
- 1.Chou K.C., Cai Y.D. Predicting protein localizaiton in budding yeast. Bioinformatics. 2005;21:944–950. doi: 10.1093/bioinformatics/bti104. [DOI] [PubMed] [Google Scholar]
- 2.Chou K.C., Elrod D.W. Protein subcellular location prediction. Protein Eng. 1999;12:107–118. doi: 10.1093/protein/12.2.107. [DOI] [PubMed] [Google Scholar]
- 3.Huh W.K., Falvo J.V., Gerke L.C., Carroll A.S., Howson R.W., Weissman J.S., O'Shea E.K. Global analysis of protein localization in budding yeast. Nature. 2003;425:686–691. doi: 10.1038/nature02026. [DOI] [PubMed] [Google Scholar]
- 4.Nakashima H., Nishikawa K. Discrimination of intracellular and extracellular proteins using amino acid composition and residue-pair frequencies. J. Mol. Biol. 1994;238:54–61. doi: 10.1006/jmbi.1994.1267. [DOI] [PubMed] [Google Scholar]
- 5.Chou K.C. Prediction of protein cellular attributes using pseudo-amino-acid-composition. Proteins. 2001;43:246–255. doi: 10.1002/prot.1035. [DOI] [PubMed] [Google Scholar]
- 6.Chou K.C. Prediction of protein subcellular locations by incorporating quasi-sequence-order effect. Biochem. Biophys. Res. Commun. 2000;278:477–483. doi: 10.1006/bbrc.2000.3815. [DOI] [PubMed] [Google Scholar]
- 7.Bhasin M., Raghava G.P. ESLpred: SVM-based method for subcellular localization of eukaryotic proteins using dipeptide composition and PSI-BLAST. Nucleic Acids Res. 2004;32:414–419. doi: 10.1093/nar/gkh350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cai Y.D., Liu X.J., Xu X.B., Chou K.C. Support vector machines for prediction of protein subcellular location. Mol. Cell. Biol. Res. Commun. 2000;4:230–233. doi: 10.1006/mcbr.2001.0285. [DOI] [PubMed] [Google Scholar]
- 9.Cai Y.D., Zhou G.P., Chou K.C. Support vector machines for predicting membrane protein types by using functional domain compostion. Biophys. J. 2003;84:3257–3263. doi: 10.1016/S0006-3495(03)70050-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Emanuelsson O., Nielsen H., Brunak S., von Heijne G. Predicting subcellular localization of proteins based on their N-terminal amino acid sequence. J. Mol. Biol. 2000;300:1005–1016. doi: 10.1006/jmbi.2000.3903. [DOI] [PubMed] [Google Scholar]
- 11.Chou K.C., Cai Y.D. A new hybrid approach to predict subcellular localization of proteins by incorporating Gene ontology. Biochem. Biophys. Res. Commun. 2003;311:743–747. doi: 10.1016/j.bbrc.2003.10.062. [DOI] [PubMed] [Google Scholar]
- 12.Gardy J.L., Spencer C., Wang K., Ester M., Tusnády G.E., Simon I., Hua S., deFays K., Lambert C., Nakai K., et al. PSORT-B: improving protein subcellular localization prediction for Gram-negative bacteria. Nucleic Acids Res. 2003;31:3613–3617. doi: 10.1093/nar/gkg602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Cedano J., Aloy P., P'erez-Pons J.A., Querol E. Relation between amino acid composition and cellular location of proteins. J. Mol. Biol. 1997;266:594–600. doi: 10.1006/jmbi.1996.0804. [DOI] [PubMed] [Google Scholar]
- 14.Chou K.C., Cai Y.D. Prediction and classificaiton of protein subcellular location: sequence-order effect and pseudo amino acid composition. J. Cell. Biochem. 2003;90:1250–1260. doi: 10.1002/jcb.10719. [DOI] [PubMed] [Google Scholar]
- 15.Guo J., Lin Y., Sun Z. A novel method for protein subcellular localization based on boosting and probabilistic neural network. Proceedings of the second conference on Asia-Pacific bioinformatics. 2004;29:21–27. [Google Scholar]
- 16.Hua S., Sun Z. Support vector mahcine approach for protrein subcellularlocalization prediction. Bioinformatics. 2001;17:721–728. doi: 10.1093/bioinformatics/17.8.721. [DOI] [PubMed] [Google Scholar]
- 17.Huang Y., Li Y. Prediciton of protein subcellular locations using fuzzy k-NN method. Bioinformatics. 2004;20:21–28. doi: 10.1093/bioinformatics/btg366. [DOI] [PubMed] [Google Scholar]
- 18.Park K.J., Kanehisa M. Prediction of protein subcellular locations by support vector machines suing compositions of amino acid and amino acid paris. Bioinformatics. 2003;19:1656–1663. doi: 10.1093/bioinformatics/btg222. [DOI] [PubMed] [Google Scholar]
- 19.Pan Y.X., Shang Z.Z., Guo Z.M., Feng G.Y., Huang Z.D., He L. Application of pseudo amino acid composition for predicting protein subcellular location: stochastic signal processing approach. J. Protein Chem. 2003;22:395–402. doi: 10.1023/a:1025350409648. [DOI] [PubMed] [Google Scholar]
- 20.Reinhardt A., Hubbard T. Using neural networks for prediction of the subcellular location of proteins. Nucleic Acids Res. 1998;26:2230–2236. doi: 10.1093/nar/26.9.2230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Yuan Z. Prediction of protein subcellular locations using Markov chain models. FEBS Lett. 1999;451:23–26. doi: 10.1016/s0014-5793(99)00506-2. [DOI] [PubMed] [Google Scholar]
- 22.Zhou G.P., Doctor K. Subcellular location prediction of apoptosis proteins. Proteins. 2003;50:44–48. doi: 10.1002/prot.10251. [DOI] [PubMed] [Google Scholar]
- 23.Nakai K., Horton P. PSORT: a program for detecting sorting signals in proteins and predicting their subcellular localization. Trends Biochem Sci. 1999;24:34–35. doi: 10.1016/s0968-0004(98)01336-x. [DOI] [PubMed] [Google Scholar]
- 24.Drawid A., Gerstein M. A Bayesian system integrating expression data with sequence patterns for localizing proteins: comprehensive application to the yeast genome. J. Mol. Biol. 2000;301:1059–1075. doi: 10.1006/jmbi.2000.3968. [DOI] [PubMed] [Google Scholar]
- 25.Chou K.C., Cai Y.D. Using funcitonal domain composition and support vector machines for prediction of protein subcellular location. J. Biol. Chem. 2002;277:45765–45769. doi: 10.1074/jbc.M204161200. [DOI] [PubMed] [Google Scholar]
- 26.Nair R., Rost B. Inferring sub-cellular localization through automated lexical analysis. Bioinformatics. 2002;18:S78–S86. doi: 10.1093/bioinformatics/18.suppl_1.s78. [DOI] [PubMed] [Google Scholar]
- 27.Drawid A., Jansen R., Gerstein M. Genome-wide analysis relating expression level with protein subcellular localization. Trends Genet. 2000;16:426–430. doi: 10.1016/s0168-9525(00)02108-9. [DOI] [PubMed] [Google Scholar]
- 28.Murvai J., Vlahovicek K., Barta E., Pongor S. The SBASE protein domain library, release 8.0: a collection of annotated protein sequence segments. Nucleic Acids Res. 2001;29:58–60. doi: 10.1093/nar/29.1.58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Apweiler R., Attwood T.K., Bairoch A., Bateman A., Birney E., Biswas M., Bucher P., Cerutti L., Corpet F., Croning M.D.R., et al. The InterPro database, an integrated documentation resource for protein families, domains and functional sites. Nucleic Acids Res. 2001;29:37–40. doi: 10.1093/nar/29.1.37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bairoch A., Apweiler R. The SWISS-PROT protein sequence database and its supplement TrEMBL in 2000. Nucleic Acids Res. 2000;28:45–48. doi: 10.1093/nar/28.1.45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wang M., Yang J., Xu Z.J., Chou K.C. SLLE for predicting membrane protein types. J. Theor. Biol. 2005;232:7–15. doi: 10.1016/j.jtbi.2004.07.023. [DOI] [PubMed] [Google Scholar]
- 32.Chou K.C. A novel approach to predicting protein structural classes in a (20-1)-D amino acid composition space. Proteins. 1995;21:319–344. doi: 10.1002/prot.340210406. [DOI] [PubMed] [Google Scholar]
- 33.Lee K., Kim D.-W., Lee D., Lee K.H. Imporoving Support Vector data description using local density degree. Pattern Recognition. 2005;38:1768–1771. [Google Scholar]
- 34.Tax D.M.J., Duin R.P.W. Support vector domain description. Pattern Recognition Lett. 1999;20:1191–1199. [Google Scholar]
- 35.Tax D.M.J. 2001. One-class classification: Concept-learning in the absence of counter-examples. PhD Thesis, Delft University of Technology, June 2001, ISBN: 90-75691-05-x. [Google Scholar]
- 36.Tax D.M.J., Duin R.P.W. Support Vector Data Description. Machine Learning. 2004;54:45–66. [Google Scholar]
- 37.Vapnik V. NY: Wiley; 1998. Statistical Learning Theory: Section II Support Vector Estimation of Functions; pp. 375–567. [Google Scholar]
- 38.Schölkopf B., Smola A.J. Cambridge, MA, London: MIT Press; 2002. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond. [Google Scholar]
- 39.Thabtah F.A., Cowling P., Peng Y. MMAC: a new multi-class, multi-label associative classification approach. Fourth IEEE Int'l Conf. on Data Mining. 2004;4:217–224. [Google Scholar]
- 40.Zhang M.-L., Zhou Z.-H. A k-nearest neighbor based algorithm for multi-label classification. First Int'l Conf. on Granular Computing. 2005;1:718–721. [Google Scholar]
- 41.Mardia K.V., Kent J.T., Bibby J.M. London: Academic Press; 1979. Multivariate Analysis: Chapter 11 Discriminatnt Analysis; Chapter 12 Multivariate Analysis of Variance; Chapter 13 Cluster Analysis; pp. 300–386. [Google Scholar]
- 42.Chou K.C., Zhang C.T. Prediction of protein structural classes. Crit. Rev. Biochem. Mol. Biol. 1995;30:275–349. doi: 10.3109/10409239509083488. [DOI] [PubMed] [Google Scholar]
- 43.Chapelle O., Vapnik V. Advances in Neural Information Processing Systems 12. MA: MIT Press; 2000. Model selection for Support Vector Machines. [Google Scholar]
- 44.Cai Y.D., Chou K.C. Predicting 22 protein localizaitons in budding yeast. Biochem. Biophys. Res. Comm. 2004;323:425–428. doi: 10.1016/j.bbrc.2004.08.113. [DOI] [PubMed] [Google Scholar]
- 45.Gray J.V., Ogas J.P., Kamada Y., Stone M., Levin D.E., Herskowitz I. A role for the Pkc1 MAP kinase pathway of Saccharomyces cerevisiae in bud emergence and identification of a putative upstream regulator. EMBO J. 1997;16:4924–4937. doi: 10.1093/emboj/16.16.4924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Sussman A., Huss K., Chio L.C., Heidler S., Shaw M., Ma D., Zhu G., Campbell R.M., Park T.S., Kulanthaivel P., et al. Discovery of Cercosporamide, a known antifungal natural product, as a selective Pkc1 kinase inhibitor through high-throughput screening. Eukaryotic Cell. 2004;3:932–943. doi: 10.1128/EC.3.4.932-943.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Denis V., Cyert M.S. Molecular analysis reveals localization of Saccharomyces cerevisiae protein kinase C to sites of polarized growth and Pkc1p targeting to the nucleus and mitotic spindle. Eukaryotic Cell. 2005;4:36–45. doi: 10.1128/EC.4.1.36-45.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Rossi J.M., Lindquist S. The intracellular location of yeast heat-shock protein 26 varies with metabolism. J. Cell Biol. 1989;108:425–439. doi: 10.1083/jcb.108.2.425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Stromer T., Fischer E., Richter K., Haslbeck M., Buchner J. Analysis of the regulation of the molecular chaperone Hsp26 by temperature-induced dissociation: the N-terminal domain is important for oligomer assembly and the binding of unfolding proteins. J. Biol. Chem. 2004;279:11222–11228. doi: 10.1074/jbc.M310149200. [DOI] [PubMed] [Google Scholar]
- 50.Burd C.G., Emr S.D. Phosphatidylinositol(3)-phosphate signaling mediated by specific binding to RING FYVE domains. Cell. 1998;2:157–162. doi: 10.1016/s1097-2765(00)80125-2. [DOI] [PubMed] [Google Scholar]
- 51.Shin M.E., Ogburn K.D., Varban O.A., Gilbert P.M., Burd C.G. FYVE domain targets Pib1p ubiquitin ligase to endosome and vacuolar membranes. J. Biol. Chem. 2001;276:41388–41393. doi: 10.1074/jbc.M105665200. [DOI] [PubMed] [Google Scholar]