Abstract
A significant problem in biological motif analysis arises when the background symbol distribution is biased (e.g. high/low GC content in the case of DNA sequences). This can lead to overestimation of the amount of information encoded in a motif. A motif can be depicted as a signal using information theory (IT). We apply two concepts from IT, distortion and patterned interference (a type of noise), to model genomic and codon bias respectively. This modeling approach allows us to correct a raw signal to recover signals that are weakened by compositional bias. The corrected signal is more likely to be discriminated from a biased background by a macromolecule. We apply this correction technique to recover ribosome-binding site (RBS) signals from available sequenced and annotated prokaryotic genomes having diverse compositional biases. We observed that linear correction was sufficient for recovering signals even at the extremes of these biases. Further comparative genomics studies were made possible upon correction of these signals. We find that the average Euclidian distance between RBS signal frequency matrices of different genomes can be significantly reduced by using the correction technique. Within this reduced average distance, we can find examples of class-specific RBS signals. Our results have implications for motif-based prediction, particularly with regards to the estimation of reliable inter-genomic model parameters.
INTRODUCTION
Modelling biological signals with information theory
Information theory (IT) constitutes a branch of mathematics that describes the communication of symbols through a channel (1). This approach has been extended to the study of DNA and protein sequences with the most notable impact being the ability to measure the amount of sequence conservation at a given position in an alignment (2–6). This quantity is represented as information measured in bits and can be visualized neatly as sequence logos (e.g. c.f.u., Figure 3) (7). Measurement in bits provides a universal scale and allows information from independent sources to be summed together.
Perturbations in genomic signals
The information in DNA and RNA sequences can be encoded using four symbols but in most genomes, these symbols are not observed at equal frequencies (see Figure 1). These skewed distributions have consequences on the ability to predict features on one genome from another. Korf (8) highlighted these issues while comparing the prediction accuracy of eukaryotic gene finders that were trained on foreign genomes:
‘Gene prediction accuracy with foreign genome parameters appears to follow GC content more than phylogenetic relationships. This implies that choosing the best foreign gene finder is not simply a matter of using parameters from the closest relative’.
‘The GC-rich genomes prefer G and C in the third position and the AT-rich genomes prefer A or T. But even between genomes with similar GC content, there are significant differences among equivalent codons’.
Figure 1.
Compositional biases of major prokaryotic classes represented by %GC. The data are grouped and sorted in ascending order by the average GC content of the class.
Korf observed that these compositional differences between the various signals caused a high level of inaccuracy in predicting genes with foreign gene finders. Schreiber and Brown (9), however, proposed an application, extended from IT, which aims to overcome the problems caused by such compositional biases. This approach portrays the above two perturbations in genomic signals as distortion and patterned interference:
Distortion is described as a constant bias in a signal. This was used to model background GC content.
Patterned interference is a type of noise which is non-random and can be corrected. It can be depicted as a state-dependent distortion process and was used to model periodicity caused by codon bias.
Schreiber and Brown's modeling technique provides a method to correct these respective perturbation effects to recover the original signal that was transmitted. This approach assumed that linearity exists between compositional bias and the total information in the motif.
Prokaryotic classes and background %GC
To date, there are 17 bacterial classes and three archaeal classes that are represented by completely sequenced genomes (Figure 1). This classification is based on their branching patterns in 16S rRNA trees (http://www.bacterialphylogeny.com/taxonomic_ranks.htm) (10). Of the prokaryotic classes, only the Actinobacteria (high GC gram+) and Firmicutes (low GC gram+) have been described as being comprised of skewed GC-content members.
Ribosome-binding sites in prokaryotes
Ribosome-binding sites (RBS) in prokaryotes comprise ∼30 bp of mRNA roughly centered around the translation initiation codon (usually AUG). RBS may also contain a Shine-Dalgarno (SD) motif [usually ‘GGRGG’ where R = Adenine or Guanine (11)] that can lie between 5 and 13 bp upstream of the initiation codon (12,13). The SD motif is understood to be involved in complementary base-pairing to a short anti-SD sequence near the 3′ end of the ribosome's 16S rRNA [the anti-SD sequence on the 16S rRNA is highly conserved in prokaryotes (14)]. However, recent opinions on the essentiality of the SD motif argue that it may play a role in recognition that is secondary to factors such as steric hindrance and fold state of the mRNA (15). These may play a role in blocking accessibility of the ribosome to the initiation codon. This raises important questions such as: ‘Could specific mechanisms of translation initiation have evolved in different organisms and can these mechanisms be identified?’. The coding region, just downstream from the initiation codon, is also protected by the ribosome (16) so this is also important when modeling RBS.
Aim
The aim of our work was to firstly correct the effects of distortion and patterned interference (9) in the RBS signals of all available prokaryotic genomes. This would allow for further comparative genomics studies. We expected the distances between the corrected signals to (i) become significantly minimized when compared to the distances between the raw signals and (ii) lack correlation with the actual GC content of the genome. Comparisons between the corrected signals of prokaryotic classes could also help to indicate whether signal evolution occurs in the presence of a distorted compositional bias.
MATERIALS AND METHODS
Extraction of available prokaryotic translation initiation sites
Of the 311 fully completed prokaryotic genomes available in the GenBank database (December 2005), multiple strains of the same organism were first removed until each prokaryotic organism was represented only once. This resulted in a list of 208 prokaryotic genomes. For each genome, 49 bp ribosome-binding contexts were extracted. These extracted contexts included 25 bases upstream and 21 bases downstream of the start codon. Binding-contexts that overlapped coding DNA were removed in this step.
Accounting for variation in SD distance and its relation to total information
An additional step, prior to correcting the RBS signal, was carried out to account for the variation in the distance of the SD motif to the initiation codon. Gibbs alignment was used to find the most represented 7 nt-window motif in the upstream sequences. The software used to perform the Gibbs alignment is part of the Biojava toolkit (http://biojava.org/) (17). The motif thus found is expected to be the SD motif. All upstream sequences were shifted (including padding with gap symbols) such that the motif found was aligned at position −13. The shifted distances were recorded to yield a distribution over distances between the SD and the initiation codon. When calculating total information (Figure 5), the measurement was taken over (i) this distance distribution, (ii) the upstream matrix containing the SD motif and (iii) the N-terminal coding region matrix. This procedure was described earlier (18). A maximum of 500 sequences was sampled from each genome for practical reasons.
Distortion and noise correction
Distortion and noise correction steps of the RBS signals were then performed as previously described (9). The signals were stored as weight matrices for further analysis and graphically drawn as sequence logos using a modified version of Weblogo (7,19). The remaining analysis packages were all implemented using the Biojava toolkit (17). An example of signal correction of a low GC organism, Baccilus anthracis (35% GC; GenBank accession no. NC_007530), is shown in Figure 2. The high AT background becomes significantly reduced revealing the SD motif.
Figure 2.
Sequence logo of Baccilus anthracis (GenBank accession no. NC_007530) RBS signal (a) before and (b) after correction.
Principal components analysis of translation initiation signals
Principal components analysis (PCA) was performed on all raw and corrected signals by taking (i) the probabilities of each of the 4 nt at each of the 49 columns (196 variables) and (ii) the distribution over SD-initiation codon distances. This was reduced to two major principal components. The PCA analysis was carried out using the Spotfire Decision Site software (http://www.spotfire.com/). The output was then indexed by bacterial class and colour-coded by %GC as in Figure 6.
RESULTS
The distance to a raw Escherichia coli RBS signal was diminished upon correction
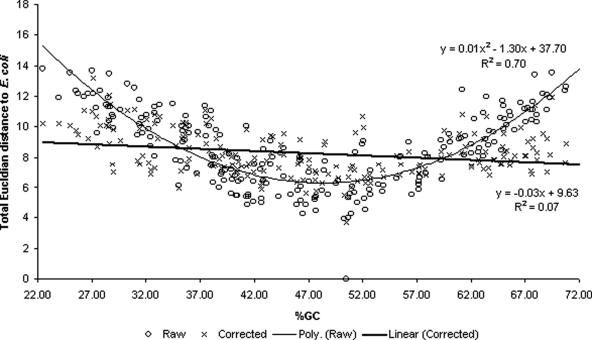
All the E.coli strains completely sequenced till now (GenBank accession nos NC_004431, NC_000913, NC_002695, NC_002655) have a uniform background nt distribution (50% GC). Therefore, we used the RBS signal of E.coli as a reference to assess the effects of correcting extremely biased raw signals. The summed Euclidian distance between the reference raw signal of E.coli strain CFT073 (Figure 3; GenBank accession no. NC_004431) to all other genomes was thus measured (Figure 4). This measurement also included the distribution of SD motif-initiation codon distances. At increasing or decreasing background GC content, there was a significant tendency for raw signals to diverge from the reference signal. Fitting a polynomial line to the raw data yielded a strong squared correlation co-efficient (R2)of 0.70 with the lowest peak of the graph roughly at 50% GC. One of the effects of correction was a significant reduction in the average total Euclidian distance from μ = 8.25 to 8.60 this was shown using a paired t-test (α = 0.05). An f-test (α = 0.05) was also performed and showed that the variation in the distances had also significantly reduced from 6.36 to 2.23 upon correction. Correction was also expected to remove any correlation between %GC and total Euclidian distance. This was observed as the relationship between these two variables was successfully flattened (Figure 4: a minor slope of −0.03 was seen when regressing a linear model). This showed that linear correction was sufficient for removing correlation caused by compositional bias.
Figure 3.
RBS reference signal from E.coli strain CFT073.
Figure 4.
Total Euclidian distance of raw and corrected RBS signals to the E.coli raw signal.
Signal correction reduces the distance between total information and ideal information
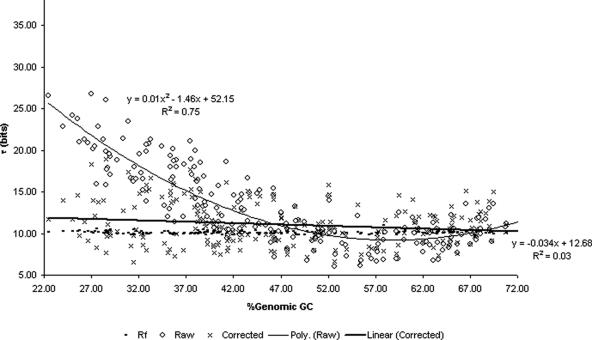
The information content (Rs) of a signal was calculated as the sum of the total information at all 49 positions of the extracted translation initiation model and the information of the SD-initiation codon distance distribution (see Materials and Methods). Therefore, it was possible to record a maximum value for Rs of 100.0 bits (49 × 2.0 bits + 2.0 bits) for a given signal (Figure 5). The value of Rfrequency (Rf), required to discriminate the occurrence of the observed number of RBS's with respect to its genome size, was calculated using the formula of Schneider et al. in (6). This came to 10.1 bits on average with a narrow variation (σ = 0.2) (Figure 5).
Figure 5.
Total information (Rs) in RBS signals.
The Rs of raw signals was seen to have a strong polynomial relationship with respect to the GC content of the genome (R2 = 0.75). As seen in Figure 5, <47%GC, Rs increases steeply until a maximum observation of 26.80 bits. This is far higher than the average Rf of 10.1 conserved bits of information for these binding sites. Towards the higher extreme of %GC content (>67%), there is again a tendency for Rs to increase over the ideal conserved information but not as sharply as moving <47%GC. This suggests that it would be desirable to correct signals in genomes that have background GC levels <47% or >67% but that the expected value of correction would be higher for low GC content genomes.
Upon signal correction, the average Rs was significantly reduced from 13.03 (σ = 4.61) to 11.07 (σ = 2.55) (α = 0.05using a paired t-test). This is significantly closer to the ideal information content (α = 0.05): average difference of 2.11 bits (σ = 1.78) compared to 10.09 bits (σ = 0.16). The relationship between Rs and %GC content was also diminished upon signal correction (Figure 5).
Corrected signals have reduced variation and can be sub-clustered by phylogenetic class
PCA of raw RBS signals can be explained mainly by non-coding and codon bias but also weakly by the SD motif
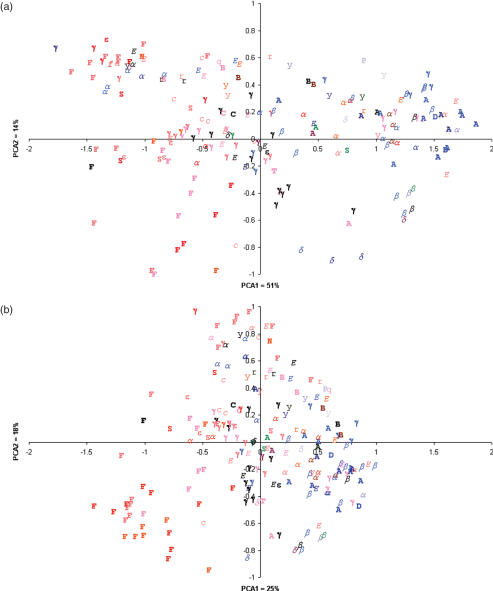
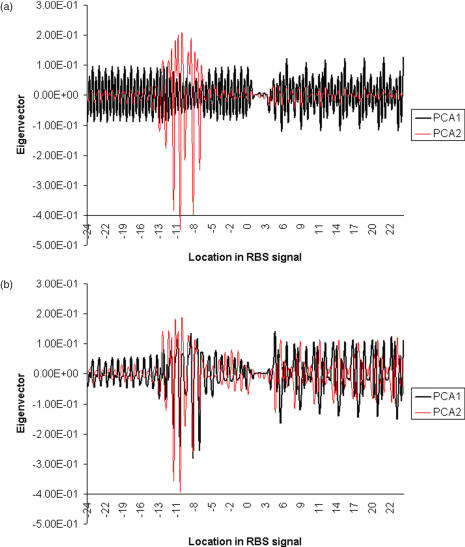
Performing PCA on the raw signals showed only a weak tendency for the results to be sorted by %GC on the PCA1 axis (linear R2 = 0.53) and this accounted for 51% of the variation (Figure 6a). Comparison of the eigenvectors of these two principal components showed that PCA1 was accounted for by variation in both non-coding and triplet bias whereas PCA2 was accounted for by variation in the SD motif (Figure 7a).
Figure 6.
Principal components analysis of RBS signals (a) before and (b) after correction. Each prokaryotic class is symbolized using the legend below and coloured by the %GC scale below.
Figure 7.
Eigenvectors of the two major principal components of (a) raw and (b) corrected RBS signals. The co-ordinates on the x-axis correspond to the co-ordinates of the example motif in Figure 2.
PCA of corrected RBS signals can be explained by SD motif and triplet noise
The effect of correction was a significant reduction (α = 0.05) in the average Euclidian distance and variation to the centroid from 1.12 (σ = 0.89) to 0.51 (σ = 0.46) (Figure 6b). After correction, PCA1 accounted for only 25% of the variation and lack of correlation to %GC was observed (linear R2 = 0.57). The regions of the RBS signal that caused the most variation on the two principal components were analyzed further (Figure 7b). This showed that after correction, both PCA1 and PCA2 mainly explained the variation caused by the SD motif and corrected triplet bias.
The corrected RBS signals of most phylogenetic classes form sub-clusters
We describe a prokaryotic class as forming a ‘sub-cluster’ if the variation of its RBS signals is less than or equal to half the variation of all datapoints along a principal component of Figure 6b. Therefore, in order to identify which prokaryotic classes sub-clustered, the distribution of their locations along both principal components (Figure 6b) was examined (Table 1). Only classes, having >5 representative sequenced genomes, were analyzed.
Table 1.
Average location of prokaryotic classes on the two major principal components of Figure6b shaded by standard deviation (σ)
| Phylogenetic class | Symbol in Figure 6b | No. of genomes | PCA1 | PCA2 |
|---|---|---|---|---|
| Actinobacteria | A | 17 | 0.47 (±0.29) | −0.15 (±0.25) |
| α-proteobacteria | A | 25 | 0.17 (±0.44) | 0.13 (±0.43) |
| Bacteroidetes | B | 5 | 0.49 (±0.22) | 0.26 (±0.17) |
| β-proteobacteria | B | 15 | 0.58 (±0.22) | −0.38 (±0.28) |
| Chlamydiae | C | 6 | −0.25 (±0.20) | 0.17 (±0.47) |
| Crenarchaeota | R | 5 | 0.19 (±0.23) | 0.41 (±0.18) |
| Cyanobacteria | Y | 8 | 0.20 (±0.28) | 0.31 (±0.29) |
| δ-proteobacteria | D | 7 | 0.08 (±0.18) | −0.60 (±0.44) |
| ε-proteobacteria | E | 5 | −0.27 (±0.32) | 0.26 (±0.52) |
| Euryarchaeota | E | 18 | 0.27 (±0.33) | 0.03 (±0.39) |
| Firmicutes | F | 41 | −0.70 (±0.44) | −0.12 (±0.59) |
| γ-proteobacteria | G | 42 | 0.00 (±0.38) | 0.05 (±0.40) |
| Spirochaetes | S | 5 | −0.30 (±0.36) | 0.14 (±0.22) |
The shading ranges from a maximum σ of 1.0 (white) to the lowest observed σ for each PCA axis (dark grey). Bold + underlined text represents formation of a sub-cluster along a principal component.
It was observed that only two classes (Crenarchaeota and Bacteroidetes) sub-clustered along both principal components (Table 1). These classes had a standard deviation (σ) that was lower than or equal to half the σ of all datapoints on either principal component (σ/2 = 0.27 on PCA1; σ/2 = 0.23 on PCA2). Because PCA1 and PCA2 are primarily accounted for by SD motif and corrected triplet noise, it indicates that the corrected RBS signals of these two classes sub-cluster largely by these two properties.
DISCUSSION
The value of correcting genomic signals
Being able to correct genomic signals is important for performing comparative genomics and for constructing predictive models based on inter-genomic parameters. We showed here that raw RBS signals have a strong correlation with the GC content of the genome (Figures 4 and 5). Correction removed this correlation and significantly reduced the average inter-genomic distance between RBS signals (Figures 4–6). The total information in corrected signals was also shown to be significantly closer to the average Rf (Figure 5). Correction also allows inter-genomic comparisons to be made between signals.
Using signal correction for inter-genomic feature prediction
We only observed two prokaryotic classes that sub-cluster based on the pattern of their corrected RBS signals (Figure 6b, Table 1). In such cases, predicting genes in a foreign genome, with parameters trained on a close phylogenetic neighbour (8) seems plausible using the signal correction approach. A typical approach might be when gene predictions are required for the freshly sequenced genome of organism X and the annotated genome of a close phylogenetic neighbour Y is available. If X is 40% GC and Y is 60% GC, then the distortion in a signal from Y may be corrected to a distortion level of 40% GC as in genome X. Similarly, the noise caused by codon bias in the two genomes can also be corrected to the same level. This corrected signal is more likely to represent an accurate predictive model. The approach could be extended to any kind of comparative motif-based search applications such as predictors of promoter and transcription factor binding sites.
Conservation of RBS signals in prokaryotes
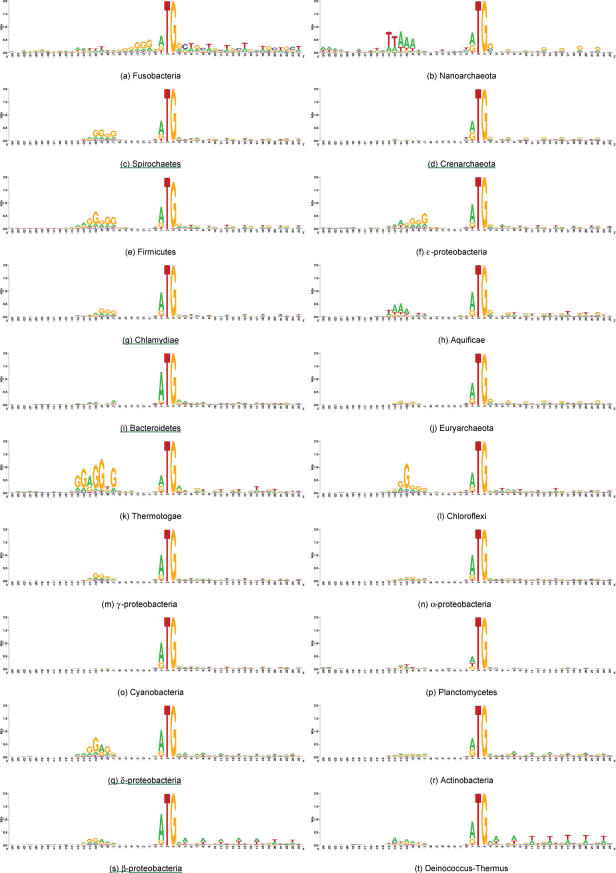
We observed four bacterial classes (Figure 8g,i,q,s) and one archaeal class (Figure 8d) that tend to conserve their RBS signal both in terms of SD motif and corrected triplet noise. These form sub-clusters on PCA1 (Table 1) and PCA1 can be explained largely by SD motif and corrected triplet noise (Figure 7b).
Figure 8.
Corrected and averaged RBS sequence logos of prokaryotic classes. The sequence logos are ordered here by ascending average GC-content of the class. Classes that form sub-clusters on either of the two major principal components (Figure 6b), based on their RBS signal similarity (Table 1), are underlined.
In general, however, the RBS signal was not expected to vary significantly between prokaryotic classes because the anti-SD sequence on the 16S rRNA is highly conserved (14). Therefore, it should be difficult to predict which organism an unknown RBS signal came from. Our findings show that the average inter-genomic distance between RBS signals is significantly decreased using correction. Within this decreased space, however, we observe that sub-clustering by class is possible. This suggests that only subtle RBS motif properties may help to distinguish one organism from another. These subtle differences, however, may account for different or uncharacterized signals required for initiating translation. For example, they may be required for mechanisms involved in unraveling mRNA secondary structure or overcoming steric hindrance to allow the fMet-tRNA to access the initiation codon (15).
Of the sampled classes, the actual GC content of Crenarchaeota and Bacteriodetes genomes are widely distributed (Figure 1) but their corrected RBS signals were seen to sub-cluster (Table 1). Therefore, correcting these signals was able to extract subtle motifs that were otherwise clouded by the actual genomic-GC distortion. This observation suggests that some aspect of the mechanism of translation initiation might be conserved in these classes.
The fact that the distances between corrected RBS signals is significantly smaller than raw signals lends support to the view that the binding ribosome must have evolved means to correct genome and codon bias. Furthermore, because sub-clustering classes by corrected RBS signals is possible, it makes it reasonable to model the evolution of motifs as a distortion process.
Sources of error in this analysis
Theoretically, organisms in the same phylogenetic class should have more morphological characteristics in common with each other than they do with organisms in other classes. However, this is not always the case as subsets of unique characteristics are often shared between taxonomic branches (10). Thus, there are inherent inaccuracies of taxonomic ranking, which affects our inter-class comparisons. Further sources of error in this analysis may have come from the presence of incorrectly annotated initiation codons and the fact that many genes do not require a SD region for translation initiation (20).
CONCLUSION
We demonstrated the usefulness of signal correction, a method derived from IT, in extracting motifs that can be compared between genomes. The results demonstrate that this approach has potential for enabling motif prediction on a newly sequenced genome using parameters derived from an available close phylogenetic neighbour. This is possible even when the compositional bias between the two genomes is very different.
Acknowledgments
Funding to pay the Open Access publication charges for this article was provided by the Novartis Institute for Tropical Diseases.
Conflict of interest statement. None declared.
REFERENCES
- 1.Shannon C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948;27:379–423. 623–656. [Google Scholar]
- 2.Shultzaberger R.K., Schneider T.D. Using sequence logos and information analysis of Lrp DNA binding sites to investigate discrepancies between natural selection and SELEX. Nucleic Acids Res. 1999;27:882–887. doi: 10.1093/nar/27.3.882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Zheng M., Doan B., Schneider T.D., Storz G. OxyR and SoxRS regulation of fur. J. Bacteriol. 1999;181:4639–4643. doi: 10.1128/jb.181.15.4639-4643.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Schneider T.D. Measuring molecular information. J. Theor. Biol. 1999;201:87–92. doi: 10.1006/jtbi.1999.1012. [DOI] [PubMed] [Google Scholar]
- 5.Hengen P.N., Bartram S.L., Stewart L.E., Schneider T.D. Information analysis of Fis binding sites. Nucleic Acids Res. 1997;25:4994–5002. doi: 10.1093/nar/25.24.4994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Schneider T.D., Stormo G.D., Gold L., Ehrenfeucht A. Information content of binding sites on nucleotide sequences. J. Mol. Biol. 1986;188:415–431. doi: 10.1016/0022-2836(86)90165-8. [DOI] [PubMed] [Google Scholar]
- 7.Schneider T.D., Stephens R.M. Sequence logos: a new way to display consensus sequences. Nucleic Acids Res. 1990;18:6097–6100. doi: 10.1093/nar/18.20.6097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Korf I. Gene finding in novel genomes. BMC Bioinformatics. 2004;5:59. doi: 10.1186/1471-2105-5-59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Schreiber M., Brown C. Compensation for nucleotide bias in a genome by representation as a discrete channel with noise. Bioinformatics. 2002;18:507–512. doi: 10.1093/bioinformatics/18.4.507. [DOI] [PubMed] [Google Scholar]
- 10.Gupta R. Criteria for the Major Taxonomic Ranks within Bacteria. 2005 [Google Scholar]
- 11.Cornish-Bowden A. Nomenclature for incompletely specified bases in nucleic acid sequences: recommendations 1984. Nucleic Acids Res. 1985;13:3021–3030. doi: 10.1093/nar/13.9.3021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ringquist S., Shinedling S., Barrick D., Green L., Binkley J., Stormo G.D., Gold L. Translation initiation in Escherichia coli: sequences within the ribosome-binding site. Mol. Microbiol. 1992;6:1219–1229. doi: 10.1111/j.1365-2958.1992.tb01561.x. [DOI] [PubMed] [Google Scholar]
- 13.Chen H., Bjerknes M., Kumar R., Jay E. Determination of the optimal aligned spacing between the Shine-Dalgarno sequence and the translation initiation codon of Escherichia coli mRNAs. Nucleic Acids Res. 1994;22:4953–4957. doi: 10.1093/nar/22.23.4953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Mikkonen M., Vuoristo J., Alatossava T. Ribosome binding site consensus sequence of Lactobacillus delbrueckii subsp. lactis bacteriophage LL-H. FEMS Microbiol. Lett. 1994;116:315–320. doi: 10.1111/j.1574-6968.1994.tb06721.x. [DOI] [PubMed] [Google Scholar]
- 15.Nakamoto T. A unified view of the initiation of protein synthesis. Biochem. Biophys. Res. Commun. 2006;341:675–678. doi: 10.1016/j.bbrc.2006.01.019. [DOI] [PubMed] [Google Scholar]
- 16.Hartz D., McPheeters D.S., Gold L. Influence of mRNA determinants on translation initiation in Escherichia coli. J. Mol. Biol. 1991;218:83–97. doi: 10.1016/0022-2836(91)90875-7. [DOI] [PubMed] [Google Scholar]
- 17.Pocock M., Down T., Schreiber M. The Biojava Project. 2006 July 7. [Google Scholar]
- 18.Shultzaberger R.K., Bucheimer R.E., Rudd K.E., Schneider T.D. Anatomy of Escherichia coli ribosome binding sites. J. Mol. Biol. 2001;313:215–228. doi: 10.1006/jmbi.2001.5040. [DOI] [PubMed] [Google Scholar]
- 19.Crooks G.E., Hon G., Chandonia J.M., Brenner S.E. WebLogo: a sequence logo generator. Genome Res. 2004;14:1188–1190. doi: 10.1101/gr.849004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ma J., Campbell A., Karlin S. Correlations between Shine-Dalgarno sequences and gene features such as predicted expression levels and operon structures. J. Bacteriol. 2002;184:5733–5745. doi: 10.1128/JB.184.20.5733-5745.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]