Indirect readout: detection of optimized subsequences and calculation of relative binding affinities using different DNA elastic potentials

Abstract

Essential biological processes require that proteins bind to a set of specific DNA sites with tuned relative affinities. We focus on the indirect readout mechanism and discuss its theoretical description in relation to the present understanding of DNA elasticity on the rigid base pair level. Combining existing parametrizations of elastic potentials for DNA, we derive elastic free energies directly related to competitive binding experiments, and propose a computationally inexpensive local marker for elastically optimized subsequences in protein–DNA co-crystals. We test our approach in an application to the bacteriophage 434 repressor. In agreement with known results we find that indirect readout dominates at the central, non-contacted bases of the binding site. Elastic optimization involves all deformation modes and is mainly due to the adapted equilibrium structure of the operator, while sequence-dependent elasticity plays a minor role. These qualitative observations are robust with respect to current parametrization uncertainties. Predictions for relative affinities mediated by indirect readout depend sensitively on the chosen parametrization. Their quantitative comparison with experimental data allows for a critical evaluation of DNA elastic potentials and of the correspondence between crystal and solution structures. The software written for the presented analysis is included as Supplementary Data.

INTRODUCTION

Besides encoding for the identity of proteins in a living cell, the DNA base pair sequence carries information which is read out by proteins that bind to specific sites on DNA with remarkable selectivity. Sequence-specific binding is essential in gene regulation, DNA replication and compaction, and there has been much effort to understand its mechanism. In contrast to the genetic code, it has proven impossible to describe specific protein–DNA interactions entirely by a simple ‘recognition code’, based on direct chemical contacts of amino acid side chains to bases (1). Even when taking the 3D arrangement of protein–DNA contacts into account (2,3), the observed specificity cannot always be explained.

In general, complexation free energies also depend on the deformation required to distort both the protein and the DNA binding site into their 3D structure in the complex. In this way, sequence-dependent structure and deformability of DNA contribute to sequence-specific binding, an effect called indirect readout.

The bacteriophage 434 repressor, Figure 1, is a well-studied example. It was shown that mutations in the non-contacted region affect binding affinities 50-fold (4), and a correlation of affinity to the twisting rigidity and intrinsic twist of these mutations was found (5–7).

Figure 1.

Representation of 434 repressor–O_R3 complex structure (4). The outer 5 + 5 and the inner 4 bp are shaded differently. Together they form the 14 bp binding site. The O_R sequences are indicated.

The importance of direct and indirect readout and protein–DNA binding affinities have been addressed computationally by sequence-structure threading. The elastic models considered range from a combination of fixed coarse-grained protein structure with DNA rigid rod (8,9), rigid base pair (10,11) and rigid base (12) models, to all-atom force fields with sequence-independent partial protein structure relaxation (13,14) and more recently, with sequence-dependent protein side chain relaxation (15,16), leading to high computational requirements.

In this article we focus on indirect readout and discuss its theoretical description in relation to the present understanding of DNA elasticity on the rigid base pair level. Available computational tools allow the convenient analysis of the base pair geometry in protein–DNA co-crystal structures (17,18). Here we add the calculation of elastic (free) energies which quantify elastic optimization and have a well-defined relation to competitive binding experiments. To estimate accuracy, we calculate all quantities for a set of five different (hybrid) DNA elastic potentials, which we obtained from parametrizations based on MD simulation (19) and structural data (20). This allows us to evaluate the robustness of our qualitative and quantitative conclusions with respect to inevitable parametrization uncertainties. The results are relevant also for coarse-grained models that include direct readout.

Using the 434 repressor as a test case we address the following general questions: (i) Given a protein–DNA co-crystal structure, can we detect regions of dominant indirect readout based on a local marker for elastic optimization of DNA? (ii) Is specificity dominated by particular degrees of freedom (twist, bend, …)? (iii) Is specificity predominately due to the structure or to the deformability of the optimal sub-sequences? (iv) Does current knowledge of the elastic properties of DNA suffice to predict the relative binding affinities of sequences which are mutated in regions of indirect readout? (v) Can we a posteriori evaluate different parameterizations of the DNA elastic potential, by comparing predicted and measured relative binding affinities? Given that there exist three different high-resolution X-ray structures of the 434 repressor complex, we can ask further, (vi) How strongly do the results of the analysis vary for different structural templates? (vii) Among the three solved co-crystal structures, is there one which seems to provide a better model of the solution complex?

The article is structured as follows: in the Materials and Methods section, we first derive the relevant elastic free energies starting from existing parametrizations of the rigid base pair DNA elastic potential, and considering the approximations involved in sequence-structure threading. Form these we then construct markers for indirect readout. In the Results and Discussion section, we apply our approach to a detailed re-investigation of elastic specificity in the 434 repressor complex. We discuss the robustness of our qualitative and quantitative observations to parametrization uncertainty and compare them to experimental data.

MATERIALS AND METHODS

Rigid base pair model of DNA

We describe DNA elasticity at the level of rigid base pairs, see e.g. (21). The deformations in this model are given by a set of 3 + 3 variables specifying the relative position and orientation of two adjacent base pairs. We use the 6 bp step variables ξ = (Sh, Sl, Ri, Ti, Ro, Tw), where Sh, Sl, Ri are the three translations Shift, Slide and Rise, and Ti, Ro, Tw are the three angles Tilt, Roll and Twist needed to specify the relative orientation, as defined in (17). To characterize a base pair step (bps) completely, we also need to give the sequence step σ formed by the bases (b₁, b₂) along one chosen strand from 5′ to 3′, e.g. σ = (b₁, b₂) = (A, C) = AC. Due to symmetry, there exist only 10 different sequence steps. A bps is written as (ξ, σ).

The general quadratic energy function for a bps with sequence σ is

$$E_{\sigma }\left(\xi \right)=\frac{1}{2}{(\xi -{\xi }_0\left(\sigma \right))}^{T}S\left(\sigma \right)(\xi -{\xi }_0\left(\sigma \right)),$$ 1

where ξ−ξ₀ are the six strain variables. ξ₀ gives the equilibrium or static step conformation, and S is the symmetric, positive definite, 6 × 6 stiffness matrix. Both depend on the sequence σ of the step. Note that as ξ has mixed dimensions of length and angle, S has mixed dimensions of linear, angular and linear-angular-coupling stiffness.

The deformation fluctuations of base pairs in our model are taken to be independent, which is a simplification. Since adjacent rbp steps are coupled through the DNA sugar –phosphate backbones, their fluctuations are correlated to some extent. To overcome this limitation, two refinements of the model are possible. One is the inclusion of nearest-neighbor step cross-correlation terms in the rbp elastic energy, leading to tetranucleotide stiffness matrices. Their corrections to a dinucleotide model were recently investigated (22) using MD simulation. We checked that in most cases these are much smaller than the difference between the dinucleotide potentials we used for the same step. We conclude that at the level of parametrization precision available, fluctuation correlations are a secondary effect. Another possible refinement is to consider a rigid base model. There are indications form MD simulation that this improves the quality of a purely local description (J. H. Maddocks, personal communication). However, a corresponding parameter set is not yet available.

Base pair step potentials

To parametrize a quadratic elastic energy one has to specify the stiffness matrix S and the equilibrium value ξ₀ for every sequence step σ. There exist two conceptually different parametrization methods (19,20).

Lankaš et al. (19) obtained a thermal ensemble of fluctuating base pair steps at a temperature T = 300 K from MD simulation of oligonucleotides. The fluctuating bps are Boltzmann distributed and by fitting a 6D Gaussian, one obtains the equilibrium values (23) and stiffness matrices (19), $\left\{{\xi }_{0,MD}{S}_{MD}\right\}$ in a standard way. If C_MD(σ) is the correlation matrix of step fluctuations, then $S_{MD}\left(\sigma \right)=k_{B}T{C}_{MD}^{-1}\left(\sigma \right)$ is the corresponding stiffness matrix, due to equipartition of energy at temperature T. The partition sum $Z(\sigma ,T)=\text{det}{\left[S\right(\sigma )/(k_{B}T\left)\right]}^{-1/2}$ gives a natural measure for the overall strength of fluctuations of a harmonic bps at temperature T, counting all six degrees of freedom.

Olson et al. (20) used crystal ensembles of deformed bps. Their B-DNA ensemble consists of B-form DNA oligonucleotides, while their P-DNA ensemble is obtained from protein–DNA co-crystals. Again, a Gaussian can be fitted to the data, giving directly the equilibrium values and the ensemble covariance matrices $\widehat{C}$. Stiffness matrices can be extracted under the assumption that equipartition of energy at some effective temperature occurs also in crystal ensembles.

To determine the effective temperature, we require that the fluctuation strength of the MD ensemble and that of a crystal ensemble X = B, P be equal, i.e. $Z_X(\sigma ,T)=Z_{MD}(\sigma ,T)$. We consequently define the crystal stiffness matrices by $S_X\left(\sigma \right)=k_B{T}_X{{\displaystyle \widehat{C}}}_X{\left(\sigma \right)}^{-1}$. Here, the average of effective temperatures needed to reach equal fluctuation strength for each sequence is the ensemble's effective temperature,

$$T_X=300\text{K}{〈{\left(\frac{\text{det}{{\displaystyle \widehat{C}}}_X\left(\sigma \right)}{\text{det}{C}_{MD}\left(\sigma \right)}\right)}^{\frac{1}{6}}〉}_{\sigma }.$$ 2

We obtain T_B = 107 K and T_P = 233 K. Our B and P ensembles then have equilibrium values and stiffness matrices $\{{\xi }_{0,B},S_B\}$ and $\{{\xi }_{0,P},S_P\}$, respectively. In summary, the observed fluctuations in the crystal appear as strong as if they were thermally excited at their respective effective temperature, judging by the MD simulation.

In (19), the effective temperature for the P-DNA ensemble (20) was computed by comparing the persistence lengths for DNA oligomers as extrapolated from a normal mode analysis of oligomers without temperature scale (24), to experimental values for B-DNA in solution. This yielded a value of T_P = 295 K. While our microscopic approach matches fluctuations of all six rigid bp degrees of freedom to an MD simulation, this mesoscopic method (19) effectively matches the bending fluctuations only, to experimental data. For comparison, we have repeated our determination of effective temperatures using only the bending (i.e. Roll and Tilt) stiffness submatrices. This gives effective temperatures of T_B′ = 166 K and T_P′ = 232 K, the latter value surprisingly unchanged from T_P. We denote the resulting crystal ensembles by B′ and P′.

If we were to introduce multiple effective temperatures, matching all sequences and degrees of freedom separately to the MD stiffness matrices, we would finally end up with the B and P equilibrium values combined with the MD stiffness matrices $\{{\xi }_{0,B},S_{MD}\}$ and $\{{\xi }_{0,P},S_{MD}\}$. Since the equilibrium values obtained from MD using the parm94 force field (25) generally have a Twist that is lower than commonly accepted on the basis of structural data (26), we also included these two hybrid parametrizations, denoted MB and MP.

For the plots in the Results section, all quantities were calculated separately for the parametrizations MD, B, P, MB and MP. The mean and error bar of these lists are shown, giving an overview of the agreement between the available parametrizations. The B′ and P′ parametrizations are used only where indicated, for comparison.

When the effective temperature is set, we replace the observed distribution of deformations, ${{\displaystyle \widehat{p}}}_X(\xi \mid \sigma )$, by the corresponding Boltzmann distribution $p_X(\xi \mid \sigma )$ at T = 300 K, given by (27) below. This distribution has covariance C_X(σ), which is a rescaled version of ${{\displaystyle \widehat{C}}}_X\left(\sigma \right)$. The rescaled joint distribution $p_X(\xi ,\sigma )=p_X(\xi \mid \sigma )p\left(\sigma \right)$ is the starting point of the discussion in the section on free energies below.

Detecting indirect readout

When some protein binds a specific sequence, it is because this sequence has optimal binding free energy. It is interesting to ask which part of the binding free energy is most important for specificity. Certainly, if DNA elasticity were the dominant part, the operator would be optimal with respect to DNA elasticity. Our working hypothesis is the converse: we assume that indirect readout dominates at positions where the operator sequence is optimal with respect to DNA elasticity. Otherwise, elastic optimization would be coincidental. To systematically exclude false positive detections, additional information on direct readout is required, which is beyond the scope of this work. We can still greatly reduce the probability of false positives by a high threshold for optimization and by considering simultaneous optimization of subsequences.

The question whether an operator is elastically optimal can be given two different precise meanings. Consider a known structure of some stretch of DNA in a co-crystal. We may ask

1. Is the structure optimal for the observed sequence? i.e. how relaxed is this sequence in the given structure?

2. Is the sequence optimal for the observed structure? In other words, are other sequences distorted more strongly?

These questions can be answered by considering two different thermodynamic potentials or free energies. In the following two, more technical subsections, we introduce a deformation free energy F_σ(ξ) and a sequence potential G_ξ(σ), both defined for single as well as for multiple bps. F is relevant when comparing different structures, and answers question (i) above. G is the relevant free energy when comparing different sequences in the same structure, and answers question (ii). We then relate these free energies to competitive binding experiments and indirect readout.

Free energies derived from a bps ensemble

Suppose we are given some (MD or crystal) ensemble ${\left\{\right({\xi }_i,{\sigma }_i\left)\right\}}_{1\le i\le N}$ of elastically fluctuating, single bps. The step deformations and sequences are jointly distributed according to some normalized probability density function (pdf) p(ξ, σ), which contains all available statistical information.

At a temperature T (300 K in our case) we can associate to the joint pdf a free energy K,

$$\beta K(\xi ,\sigma )=-\text{ln}\left[vp\right(\xi ,\sigma \left)\right],$$ 3

where $\beta =1/\left(k_{B}T\right)$. The constant v is a volume scale in ξ space needed to fix dimensions, and drops out in all free energy differences. Differences in K correspond to relative probabilities in the ensemble, of bps that differ in sequence and structure.

Taking partial averages, we get the marginal pdf's: $p\left(\sigma \right)=\int p(\xi ,\sigma )d\xi$ gives the frequency of a sequence step in the ensemble while $p\left(\xi \right)={\sum }_{\sigma }p(\xi ,\sigma )$ is the pdf to find the deformation ξ in any sequence step.

The deformations of a chosen sequence step σ follow the conditional pdf $p(\xi \mid \sigma )$ to find ξ, given σ. Since in DNA the angular distributions are quite sharply peaked, it is safe to neglect the curvature and finite boundaries of ξ-space. A fit of $p(\xi \mid \sigma )$ with a 6D Gaussian, which is the maximum entropy distribution with the mean and covariance of the data,

$$p(\xi \mid \sigma )=\frac{p(\xi ,\sigma )}{p\left(\sigma \right)}={\left(2\pi \right)}^{-3}Z{\left(\sigma \right)}^{-1}{e}^{-\beta E_{\sigma }\left(\xi \right)},$$ 4

defines the parameters ξ₀ and S of the quadratic elastic energy E_σ(ξ), Equation 1. The partition sum $Z\left(\sigma \right)=\text{det}{\left[S\right(\sigma )/(k_{B}T\left)\right]}^{-1/2}$ gives the overall fluctuation strength (20). This Gaussian fit is by no means necessary to define the elastic free energies below. We use it here since the parameter sets we consider are given to this approximation. With more detailed (multi-modal) energy functions, conformation space integrals would get more involved but the formalism would not change. We associate a deformation free energy,

$$\beta F_{\sigma }\left(\xi \right)=-\text{ln}\left[vp\right(\xi \mid \sigma \left)\right]=\beta K(\xi ,\sigma )+\text{ln}\left[p\right(\sigma \left)\right].$$ 5

A free energy difference $F_{\sigma }\left(\xi \right)-F_{\sigma }\left({\xi }^{\prime }\right)=E_{\sigma }\left(\xi \right)-E_{\sigma }\left({\xi }^{\prime }\right)$ expresses the relative probability to find the deformation ξ rather than ξ′ in the data, given that we are looking at a fixed sequence σ. F corresponds to a canonical potential (or Helmholtz free energy) at fixed sequence, depending on the state variable ξ. Using Equation 4 one can see that up to a constant, we have the relation $F=E-T\Delta \Sigma$. Here

$$\begin{array}{l}\Delta \Sigma \left(\sigma \right)=+k_B\int p(\xi \mid \sigma )\text{ln}\left[vp\right(\xi \mid \sigma \left)\right]d\xi \\ =-k_B\text{ln}\left[v^{-1}Z\right(\sigma \left)\right]+\text{const}\end{array}$$ 6

is the entropy change upon binding of the fluctuating harmonic bps. Softer steps loose more entropy when forming a complex. The difference in TΔΣ between sequence steps is up to 2 $k_{B}T$. Here we do not assume that the fluctuations are fixed completely, but only that for all sequence steps σ they are fixed to the same degree upon binding. One way to see this is to consider an additional, sequence-independent harmonic potential representing the protein elastic energy, with stiffness matrix S_prot, say. In the stiff protein limit $S_{\text{prot}}\gg S\left(\sigma \right)$, the leading term is $F=E-T\Delta \Sigma$, independent of S_prot.

Similarly, we may ask for the probability to find the sequence step σ among all steps at fixed deformation ξ. It is given by the (discrete) conditional pdf

$$p(\sigma \mid \xi )=\frac{p(\xi ,\sigma )}{p\left(\xi \right)},$$ 7

and we associate a sequence potential

$$\beta G_{\xi }\left(\sigma \right)=-\text{ln}p(\sigma \mid \xi )=\beta K(\xi ,\sigma )+\text{ln}\left[vp\right(\xi \left)\right].$$ 8

A potential difference $G_{\xi }\left(\sigma \right)-G_{\xi }\left({\sigma }^{\prime }\right)$ expresses the relative probability to find the sequence σ rather than σ′, given we are looking at a fixed deformation ξ. A value G_ξ(σ) = 0 at deformation ξ, the sequence σ occurs with certainty in the ensemble. G_ξ(σ) corresponds to the Gibbs free energy in the grand canonical ensemble, at fixed deformation ξ.

Often, it is interesting to compare sequences in an unbiased ensemble where each sequence step is equally probable, so p(σ) = const. In this situation, the formulas look simpler. We obtain

$$\beta G_{\xi }\left(\sigma \right)=\beta F_{\sigma }\left(\xi \right)+\text{ln}{\displaystyle \sum _{{\sigma }^{\prime }}}{e}^{-\beta F_{{\sigma }^{\prime }}\left(\xi \right)}.$$ 9

In fact, since now $G_{\xi }\left(\sigma \right)-G_{\xi }\left({\sigma }^{\prime }\right)=F_{\sigma }\left(\xi \right)-F_{{\sigma }^{\prime }}\left(\xi \right)$ the relative probabilities of sequences are in this case expressed by their F differences. Still, E differences (10) cannot be used instead, since they lack the term TΔΣ (see Equation 6).

Multiple steps

We extend the free energies introduced above for single steps to a sequence of consecutive steps. These may be efficiently calculated without making the approximation (12) of additive single step free energies.

By assumption, the deformations in our model fluctuate independently. However, we have to make sure that consecutive steps form a meaningful sequence, e.g. AC can be followed by CG but not by GC. This clearly correlates the sequence steps. To get the correct free energies for a stretch of multiple bps, we go back to the probabilities.

Extending previous notation, we now denote a base pair step sequence (bpss) by (ξ, σ). It consists of l bps $({\xi }_j,{\sigma }_j)$ with the additional requirement that the sequence steps match, ${\sigma }_j=(b_j,b_{j+1})$, where $\sigma =(b_1,\dots ,b_{l+1})$ is a sequence of l + 1 bases.

Computing the pdf's, we have $p(\xi \mid \sigma )={\prod }_{j}p({\xi }_j\mid {\sigma }_j)$ since the deformations are independent. Consequently, $\beta F_{\sigma }\left(\xi \right)=\beta {\sum }_j{F}_{{\sigma }_j}\left({\xi }_j\right).$ The sequence pdf p(σ) has to be renormalized so that its sum over matching sequences is unity. Define

10

where the primed sum runs only over matching sequences with l steps. Then clearly $p\left(\sigma \right)=W_l^{-1}{\prod }_{j}p\left({\sigma }_j\right)$ and $p(\xi ,\sigma )=W_l^{-1}{\prod }_{j}p({\xi }_j,{\sigma }_j)$ are properly normalized. In the case where all sequences are equally likely, one can check that $p\left(\sigma \right)=4^{-(l+1)}$. The joint free energy K is not additive because of the renormalization,

$$\beta K(\xi ,\sigma )=-ln\left[v^{l}p(\xi ,\sigma )\right]=\beta {\displaystyle \sum _{j=1}^l}K({\xi }_j,{\sigma }_j)+ln{W}_l.$$ 11

For the sequence potential we obtain

$$\beta G_{\xi }\left(\sigma \right)=-ln\left[p(\sigma \mid \xi )\right]=\beta K(\xi ,\sigma )+ln\left[v^l{{\displaystyle \sum _{{\sigma }^{\prime }}}}^{\prime }p(\xi ,{\sigma }^{\prime })\right].$$ 12

Noting that

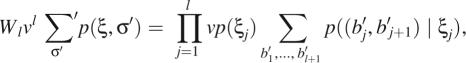13

we can introduce the 4 × 4 transfer matrix $T\left({\xi }_j\right)$ with entries

$${\left(T\right({\xi }_j\left)\right)}_{b^{\prime },b^{″}}=p\left(\right(b^{\prime },b^{″})\mid {\xi }_j)=e^{-\beta G_{{\xi }_j}\left(\right(b^{\prime },b^{″}\left)\right)}$$ 14

and rewrite the primed sum as a matrix multiplication. With ${\mathrm{l}}^{\text{T}}=(1,1,1,1)$, the sequence potential of a bpss finally acquires the compact form

$$\beta G_{\xi }\left(\sigma \right)=\beta {\displaystyle \sum _{j=1}^l}{G}_{{\xi }_j}\left({\sigma }_j\right)+\left[{\mathrm{l}}^{\text{T}}T\right({\xi }_1)\dots T({\xi }_l\left)\mathrm{l}\right],$$ 15

which is again not additive. Even though there are 4^{l + 1} possible sequence mutations, G can be computed in a time ∝ l. Note that for l = 1, the formula reduces to the single step result since $p(\sigma \mid \xi )$ is normalized.

Whenever the steps are equidistributed, p(σ) = const, the formulas become simpler. In particular, one can see from Equations 14 and 15 that, as in the single step case, $G_{\xi }\left(\sigma \right)-G_{\xi }\left({\sigma }^{\prime }\right)=F_{\sigma }\left(\xi \right)-F_{{\sigma }^{\prime }}\left(\xi \right)$, while E differences would give a different result.

Competitive binding

The free energies just derived in the context of freely fluctuating bps, have a direct relation to an idealized competitive binding experiment. Consider a protein that can bind any operator sequence σ in some corresponding structure ξ, but has no intrinsic sequence preference. That is direct readout that drives complex formation has the same strength for all operators, and is absent for non-operator sequences. This protein may be put in contact with a bpss ensemble, such as a genome containing operators with relative frequencies p(σ) (different from the frequencies in the reference ensemble above). Then the relative occupancies of the protein with different sequences are determined only by elastic free energy differences.

Binding the sequence σ in a structure ξ costs a deformation free energy F_σ(ξ). Multiplying the probability p(σ) to find σ at all in the ensemble gives the relative occupancy of (σ, ξ) compared to (σ′, ξ′) as $\text{exp}\{-\beta [K(\xi ,\sigma )-K({\xi }^{\prime },{\sigma }^{\prime })\left]\right\}=p(\sigma ,\xi )/p({\sigma }^{\prime },{\xi }^{\prime })$. In two different situations this general result simplifies.

A complex structure that minimizes F_σ(ξ) is optimal in the sense of question 1. above, i.e. it is the most relaxed structure for σ. Whenever all steps in the bps ensemble are equally frequent, those sequences will bind whose bound structures are most relaxed. We get $p(\sigma ,\xi )/p({\sigma }^{\prime },{\xi }^{\prime })=\text{exp}\{-\beta [F_{\sigma }\left(\xi \right)-F_{{\sigma }^{\prime }}\left({\xi }^{\prime }\right)\left]\right\}$, see (4). Protein–DNA binding can be driven by enthalpy or by entropy or by a combination thereof (28). While the total entropy of complex formation has more contributions, F accounts at least for the entropic cost of fixing the deformation fluctuations to a value ξ in the complex, and softer steps acquire a higher entropic contribution that counteracts complexation. This trend persists also if the suppression of fluctuations upon binding is only partial.

Consider a binding experiment as above, in which now the protein is very stiff. Here, the sequence distribution p(σ) may be nonuniform, but all sequences bind in one fixed deformation ξ. In this situation, we see from Equation 8 that $p(\sigma ,\xi )/p({\sigma }^{\prime },\xi )=\text{exp}\{-\beta [G_{\xi }\left(\sigma \right)-G_{\xi }\left({\sigma }^{\prime }\right)\left]\right\}$. The sequence that minimizes G is optimal in the sense of question 2. above, i.e. it is the sequence that fits best with the prescribed structure, taking into account its frequency in the ensemble.

If both special cases occur at the same time, we have a fixed ξ and constant p(σ). Then indeed F and G differ only by a constant, so they give the same relative occupancies. However, the elastic energy E will still give different results.

Measures of elastic optimization

For some stretch (ξ, σ) of DNA in a given co-crystal structure, we would like to tell whether it is specifically bound because of DNA elasticity. Naively, one might assume that this is the case if it carries a small elastic energy, but this not correct. We are really asking: compared to all mutated sequences, is σ elastically optimal? In general, this is the case if $K(\xi ,\sigma )<K({\xi }^{\prime },{\sigma }^{\prime })$ for all other (ξ′, σ′).

Most of the time however, there is only one crystal structure ξ available as a model for the solution complex. We can still plug all possible sequence mutations into that structure and calculate their free energies. For sequence-structure threading, we therefore make the additional simplifying approximation that the experimentally inaccessible complexes (ξ′, σ′) of the protein with any other DNA sequence σ′ will force the DNA into essentially the same structure ${\xi }^{\prime }\simeq \xi$. One can check that

$$K(\xi ,\sigma )-K({\xi }^{\prime },{\sigma }^{\prime })=G_{\xi }\left(\sigma \right)-G_{\xi }\left({\sigma }^{\prime }\right)+F_{{\sigma }^{\prime }}\left(\xi \right)-F_{{\sigma }^{\prime }}\left({\xi }^{\prime }\right).$$ 16

Then our approximation is that $\left|F_{{\sigma }^{\prime }}\right(\xi )-F_{{\sigma }^{\prime }}({\xi }^{\prime }\left)\right|\ll \left|G_{\xi }\right(\sigma )-G_{\xi }({\sigma }^{\prime }\left)\right|$, which could be called the stiff protein limit, and we disregard the F difference between structures. The same approximation is effectively made in (13), where after an initial partial structure relaxation the structure was kept fixed, and in the static model of (12). The validity of the stiff protein limit depends on the protein in question. However, when only one structure is known, it is a reasonable first approximation to consider only the known part of the free energy difference. As an aside we note that when the protein is stiffer than DNA, it will itself store less elastic energy, making the protein elastic energy contribution to the total binding energy less important.

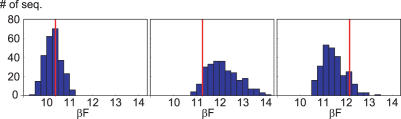
Consider a competitive binding experiment where all possible mutated sequences occur with equal probability p(σ′) = const. To find an optimal sequence, we can then look for minimal $F_{\sigma }\left(\xi \right)$. An example of an F histogram of all sequence mutations is shown in Figure 4. One widely used (11,22) way to quantify optimization of the native sequence is the Z-score, given by the difference of the mean F to the native F, normalized by the width of the F histogram. We add another option: Looking only at the low F tail, we consider the normalized difference of the native F to the minimal F. For an example of both quantities see Figure 3. Any Z-score disregards information on the global scale of free energy differences in a histogram. The normalization with the histogram width makes quantitative comparison with experiments impossible.

Figure 4.

Histograms of the free energy per bps of mutated sequences, in k_BT units. All possible mutations inside a 5 bps window were generated, around bps 3, 7 and 11 from left to right. The structure is O_R2, and the MD parameter set combined with P-DNA equilibrium values is used. The vertical line indicates the F value of the native sequence.

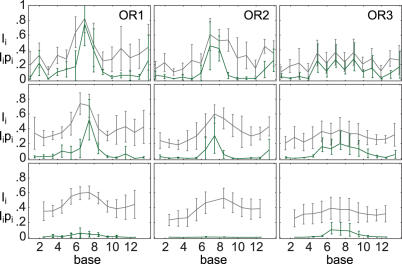
Figure 3.

Elastic optimization in 434 repressor structures O_R1, 2, 3. Deformation energy E and free energy F, first and second rows. Z-scores of mean (green) and minimum (gray), third row. The fourth row shows the sequence potential G together with the random G level. All energies are given in k_BT. E and F are per bps while G is per bp. The moving window length is 3 bps. Error bars indicate parametrization uncertainty, and lighter shading marks the inner 4 bp.

A more direct way to quantify optimization is to consider just the free energy $G_{\xi }\left(\sigma \right)$ of the native sequence. Since this is the logarithm of a normalized pdf, σ has a higher-than-random probability of occurring if $G_{\xi }\left(\sigma \right)$ is lower than that of an ensemble with $p({\sigma }^{\prime }\mid \xi )=\text{const}$. By normalization, a value $G_{\xi }\left(\sigma \right)=0$ means that σ occurs with certainty at that deformation, $G_{\xi }\left(\sigma \right)\le \text{ln}2$ means that σ has half of the total probability, and $G_{\xi }\left(\sigma \right)=(l+1)\text{ln}4$ is the random value for a bpss with l bps. It is clear that the value of G(σ) alone contains information about how low-lying the corresponding F_σ is in the F histogram. In fact, the sequence potential $G_{\xi }\left(\sigma \right)$ is similar to a Z-score, but computed for the Boltzmann factors: In the case p(σ′) = const, by rewriting Equation 9, we get $G_{\xi }\left(\sigma \right)=F_{\sigma }\left(\xi \right)-\overline{F}\left(\xi \right)$, where

$$\beta \overline{F}\left(\xi \right)=-\text{ln}\sum _{{\sigma }^{\prime }}{e}^{-\beta F_{{\sigma }^{\prime }}\left(\xi \right)}.$$ 17

This can be interpreted as the difference of F_σ to an ‘exponential mean’ $\overline{F}$ over all mutations, where sequences with high F value are exponentially suppressed, according to their statistical weight.

Since G is a true free energy, it is directly related to relative affinities in a competitive binding experiment, unlike a Z-score. By normalizing G to the length of the considered window, an unbiased comparison of specificity for different subsequence window lengths is possible. The expected dependence of a Z-score on window length is less clear (22).

Elastic consensus sequences

Assuming a stiff protein with structure ξ, and regarding only DNA elasticity, any mutated subsequence σ′ of length l binds with a probability $p({\sigma }^{\prime }\mid \xi )=e^{-\beta G_{\xi }\left({\sigma }^{\prime }\right)}$. Instead of looking at an entire subsequence one can ask for the probability to find just one base b at a certain position i in all length l subsequences. This probability p_i(b) is given by the expectation

$$p_i\left(b\right)={{\displaystyle \sum _{{\sigma }^{\prime }}}}^{\prime }{\delta }_{b_i^{\prime }b}{e}^{-\beta G_{\xi }\left({\sigma }^{\prime }\right)},$$ 18

where δ is the Kronecker delta. Using Equation 15, we obtain

$$p_i\left(b\right)=\frac{{\mathrm{l}}^{\text{T}}T\left({\xi }_1\right)\dots T\left({\xi }_{i-1}\right)P_{b}T\left({\xi }_i\right)\dots T\left({\xi }_l\right)\mathrm{l}}{{\mathrm{l}}^{\text{T}}T\left({\xi }_1\right)\dots T\left({\xi }_l\right)\mathrm{l}}.$$ 19

Here the matrix ${\left(P_b\right)}_{b^{\prime }{b}^{″}}={\delta }_{b^{\prime }b}{\delta }_{b{b}^{″}}$ is a projector onto the base b. This expression takes into account sequence correlations up to the window length l. Calculating p_i(b) for all bases $b=A,T,C,G$ along a given structure, using centered windows of constant length, gives a complete base-per-base picture of elastic preference in the structure. To check for elastic preference for the native sequence, one can just set b equal to the native base at each position.

Similarly, we can ask for the joint probability $p_{i,i+k}\left(\sigma \right)$ to find k bases $(b_i,\dots ,b_{i+k})=\sigma$ at positions $(i,\dots ,i+k)$ in all length l subsequences. To calculate it, we have to insert projectors at all base positions in question,

$$p_{i,i+k}\left(\sigma \right)=\frac{{\mathrm{l}}^{\text{T}}T\left({\xi }_1\right)\dots T\left({\xi }_{i-1}\right)P_{b_i}T\left({\xi }_i\right)P_{b_{i+1}}T\left({\xi }_{i+1}\right)\dots P_{b_{l+k}}T\left({\xi }_{i+k}\right)\dots T\left({\xi }_l\right)\mathrm{l}}{{\mathrm{l}}^{\text{T}}T\left({\xi }_{\mathrm{l}}\right)\dots T\left({\xi }_l\right)\mathrm{l}}.$$ 20

The difference of this expression to the probability $p(\sigma \mid \xi )$ of the k + 1 bp sequence σ is that $p_{i,i+k}\left(\sigma \right)$ takes sequence correlations up to the boundary of the length l subsequences into account, while $p(\sigma \mid ({\xi }_i,\dots ,{\xi }_k\left)\right)$ cuts them off at length k. Whenever k = l, there are projectors to the left and right of all transfer matrices and both expressions agree. Note that in general $p_{i,i+k}\left(\sigma \right)$ is a function of the window length l up to arbitrary l. In practice, one can simply choose for l the complete binding site length, since the computational cost is ∝ l only. We remark that no approximation of base-wise or step-wise additivity (12) is necessary here.

It has been pointed out (29) that different distributions p_i(b) contain varying amounts of information. For example, a position i at which all bases are equally probable has no information and should be considered as carrying no elastic specificity. Extending this to the case of k + 1 bases, we need to calculate the entropy of the distribution $p_{i,i+k}\left(\sigma \right)$,

$${\Sigma }_{i,i+k}=-{{\displaystyle \sum _{{\sigma }^{\prime }}}}^{\prime }{p}_{i,i+k}\left({\sigma }^{\prime }\right)\text{ln}\left[p_{i,i+k}\right({\sigma }^{\prime }\left)\right]\le (k+1)\text{ln}4.$$ 21

A measure for the information content of the distribution that ranges from 0 to 1 is given by $I_{i,i+k}=1-{\Sigma }_{i,i+k}/\left[\right(k+1\left)\text{ln}4\right]$. An extension of a sequence logo (29) for length k + 1 subsequences can then be constructed by plotting the relative frequency of each subsequence, scaled with the information content, along the complex. For k > 0, the subsequences overlap, so the usual letter scaling notation cannot be used. However, the most interesting information can be shown by plotting $I_{i,i+k}{p}_{i,i+k}\left(\sigma \right)$ for native subsequences only, see Figure 6 below. Such a plot shows directly how well the native sequence coincides with an elastic consensus sequence, and gives a local marker for which significantly nonzero values point to elastic specificity. Again, since the subsequence length of interest is usually just a few base pairs, computation is cheap.

Figure 6.

Similarity to elastic consensus for native subsequences in the O_R complexes. Information (gray) and scaled native probability (green) are shown for 1, 2 and 4 bp subsequences, from top to bottom.

RESULTS AND DISCUSSION

Indirect readout in 434 repressor

The 434 repressor is a viral transcription factor that forms part of a genetic switch between the lytic and lysogenic states in the bacteriophage 434 virus. There exist two operator regions O_R, O_L with three binding sites of 14 bp in each region (4). The protein dimer binds in a helix–turn–helix motif, making the structure (27,30,31) approximately 2-fold rotationally symmetric. The outermost 5 + 5 bases on each binding site are directly contacted by the protein, and the sequence of the outermost 4 + 4 bases is conserved with a single base exception in all six binding sites. The consensus sequence of the contacted outer 5 + 5 bases shows the 2-fold symmetry expected from the structural symmetry. In contrast, the inner four bases are not contacted directly. Their sequence is neither conserved nor rotationally symmetric. Interestingly, binding affinities of the native binding sites vary 40-fold, and those of synthetic binding sites vary as much as 200-fold, depending only on the sequence of the inner four bases (4,30). This is true even though in the existing structures none of the individual bps is kinked strongly, and the overall bend is between 25 and 40 degrees. In gel shift experiments (32), the overall bend was found to be small and sequence-independent, supporting the idea that the protein is stiffer than DNA.

Together these facts indicate that indirect readout in the central part is important in tuning the relative affinities of 434 repressor for different operators. For the contacted outer 5 + 5 base pairs we expect no elastic specificity, since protein–DNA contacts are likely to dominate interaction energies there. DNA distortion is moderate and the protein is reasonably stiff, so quadratic bps potentials should reflect this behavior.

Elastic energies

For an overview over DNA elastic energy in the 434 repressor, we plot elastic energies $E_{\sigma }\left(\xi \right)$ versus base pair number in Figure 2. Here, σ denotes the sequence of a bps or a bpss, and ξ denotes the corresponding step deformations. The bps deformations were extracted from the structure data using the program 3DNA (17). The energy per step in a moving window of length three steps around each bps was computed, using the five hybrid potentials introduced in Materials and Methods. The mean and SD of these five values give a data point and error bar in the plot, respectively.

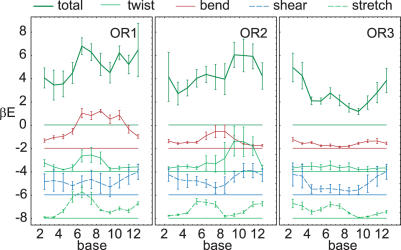
Figure 2.

Elastic energy E along O_R1, 2, 3. A 3 bps window was used. The elastic energy and parametrization uncertainty per bps are shown in units of k_BT. The top curve shows the full elastic energy, while partial energies are shown subsequently shifted down by 2 k_BT for clarity.

Partial energies for bend, twist, shear and stretch are also shown. These are calculated by replacing the full correlation matrix $C=S^{-1}$ by its (Ti,Ro), (Tw), (Sh,Sl) and (Ri) submatrices, respectively. This corresponds to integrating out the other variables. In each case, the correlation 1 × 1 or 2 × 2 submatrix is inverted to give the partial energy stiffness matrix. Since all coupling stiffnesses are averaged out, the partial energies obtained in this way do not sum up to the full energy.

The full and partial energies for the three crystal structures show variation along the structure that is well above the parametrization uncertainty. However, all curves look remarkably different and show no common features at the central non-contacted bases. Elastic energy is not strongly dominated by any one of the partial energies. Rather, the identity of the most important partial energy varies between the structures and even within each structure. In O_R1 and O_R3, bend and stretch appear most important, respectively. In O_R2 there is a remarkable balance between all four partial energies. We checked that the main contributions to the twist energy at bases 6 to 10 result from overtwisting, in accord with experimental results that indicate overtwisting of the central region (5). However, twist does not appear more important than other partial energies. The overall bending angles for O_R1, 2, 3 are around 25, 40 and 30 degrees, respectively. Although O_R1 has the lowest overall bend, O_R3 clearly is the most relaxed structure.

Free energies and specificity

We now return to the full elastic energies. For an overview of elastic optimization in the three 434 repressor complex structures, the upper two rows in Figure 3 show the elastic energy E and the deformation free energy F of the native sequence, normalized per bps. They are computed in a centered moving window of length 3 bps, which gives sufficient spatial resolution to distinguish the central from the outer base pairs while smoothing the curves. Although, the deformation free energy F includes conformational entropy of the bps, this contribution is smoothed by the moving window, resulting in an almost constant difference of E and F. Both energies show no features that are special to the inner four bases (bases 6 to 9). While in the O_R1 case the inner four bases have high F, they lie low in O_R3, i.e. there is no common trend in all structures.

Overall, the E or F profiles give no clear signal that would correspond to the experimentally observed specificity in the central 4 bp. This is not surprising since only the value of F compared to the whole F distribution of all mutated sequences is relevant for sequence optimization, see Materials and Methods. What is the distribution of mutation free energies? In Figure 4 we show a typical example, the F histograms of sets of mutated sequences in three consecutive 5 bps windows along the O_R2 structure.

One sees that the free energies follow a skewed, Gamma-like distribution which varies in both mean and width. Only in the central window, the native sequence lies significantly below average and close to the minimum of the distribution. Note that although the native value of F is lowest in the left window position, the native sequence is not optimal there.

Quantifying these observations, we return to Figure 3. The third row shows the F difference of the native sequence to the mean (Z_mean) and to the minimum (Z_min), computed from F histograms of all mutated sequences in the same moving windows as in the rest of the panel, and normalized by the width of the histograms. In line with Figure 4, the O_R2 plot shows a maximum in the cental region. The corresponding maxima in the other Z-score plots showthat also in O_R1, 3 the native sequence is especially low-lying at the central base positions. Generally, the constant difference $Z_{\text{mean}}-Z_{\text{min}}$ indicates that while the width of the histograms may change, the shape of the distribution stays the same. Note that through its normalization by the width of the histogram, any Z-score discards information about the width of the F histogram, which as illustrated by Figure 4, may vary with the window position. The native sequence comes close to the minimal F only in a small region which coincides well with the four central base pairs.

The fourth row of Figure 3 shows the sequence potential G, given per bp, together with the random G level. It is computed in a 3 bps window and assuming a uniform sequence probability p(σ). In contrast, to the deformation energies, G shows a significant dip below the random value close to the center, in all structures. Since G is normalized per bp, a value G = 0.5 corresponds to 8% probability of the native 4 bp subsequence, which is 20 times the random value of $4^{-4}\simeq 0.4$% The G dip shows that subsequences around the central, but not the outer, base pairs of the binding site occur with a probability above chance, when accounting only for DNA elasticity. In this sense the native sequence of the central base pairs is optimized, in each of the three available structures. The minimum in G agrees well with the maximum of Z_min, which can be explained with the exponentially high weight of the sequences with low F. Following the reasoning in the Materials and Methods section, these measures give a clear indication for indirect readout mediated by DNA elasticity in the central region of the 434 repressor. The fact that all available structures show the same feature lends support to the method of inferring the presence of indirect readout from one representative crystal structure in general.

In the above results, the moving window length is not crucial for the central dip. While any window from 1 to 5 bps will show the same trend, there is a tradeoff between spatial resolution and noise.

Native versus elastic consensus sequences in 434 repressor

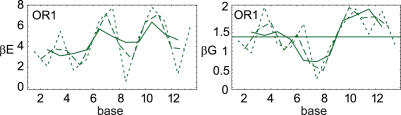
We have shown that the central 4 bp native subsequences are elastically optimized in the 434 repressor structures. But how strongly is the identity of each individual base of the native sequence preferred? When using very short subsequences to calculate G, the results get noisy. We show one typical example of the tradeoff between spatial resolution and noise in Figure 5.

Figure 5.

Elastic energy (E) and sequence free energy (G) in the O_R1 structure, using the MP potential. The moving window lengths 1, 2 and 3 bps are shown with short, long and no dashes, respectively. E and G are given per bps and per bp, respectively.

We stress that while using a moving window for E is exactly the same as a simple moving average of the single bps energies, this is not the case for G; as can be seen from Equation 15, the difference is an additional term that account for sequence continuity.

A way around the large local free energy variations is to check how similar the native base is to an elastic consensus sequence, at each position, see Materials and Methods. This is quantified by first obtaining the probability p_i(b_i) to find the native base b_i at position i, in the full distribution of sequence free energies for the complete binding site. This probability can then be scaled by the information I_i contained in the probabilities p_i of all four bases at position i. The information I_i is the height at position i of a sequence logo (29) constructed from DNA elasticity, while the scaled probability $I_i{p}_i\left(b_i\right)$ gives the height of the native base in such a logo. In the same way, the similarity of small native subsequences with a elastic consensus subsequences may be defined Methods.

In Figure 6 the similarity to elastic consensus is shown for native subsequences of 1, 2 and 4 bases. The information is scaled to range from 0 (equidistribution) to 1 (total concentration to a single subsequence). The scaled native probability indicates elastic specificity of the native sequence on the level of single bases, dimers, and tetramers, from top to bottom. Interestingly, in the O_R1, 2 complex structures, elastic specificity is concentrated on two central bases, and while the information still has a maximum in the center for the 4 bp logo, the native 4 bp subsequences have a very small part of the total probability. In contrast, in the O_R3 structure, specificity is not as strong as expected from the G plots, Figure 3, for the one base and two base subsequences. Instead, specificity for the native sequence is distributed over several bases, as can be seen in the 4 bp row, where the native sequence still has high probability. It appears that the more relaxed structure of O_R3 achieves selectivity by a combination of several smaller base preferences.

Origins of specificity

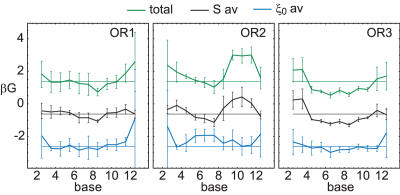
Indirect readout is caused by the sequence dependence of both DNA structure and DNA stiffness. Does the structure or the stiffness dependence have a stronger effect? We can selectively switch off either one, by averaging either the equilibrium values or the covariance matrices of the bps potential over all possible sequence steps. The profiles of the resulting averaged sequence free energies in 434 repressor are shown in Figure 7. The characteristic G dip at the central bases persists when the stiffness matrices are averaged, and the G curve roughly traces the original one. However, averaging the equilibrium values and retaining sequence dependent stiffness, does alter the shape of the curves, and the central G dip is lost. This indicates that sequence dependent structure is more important for indirect readout than sequence dependent stiffness, at least in the present example.

Figure 7.

Sequence potential G for O_R1, 2, 3. The curves show the fully sequence-dependent potential, the potential with averaged equilibrium values ξ₀, and the potential with averaged stiffness matrix S, from top to bottom and shifted in 2 k_BT steps. The zero line corresponds to random sequences.

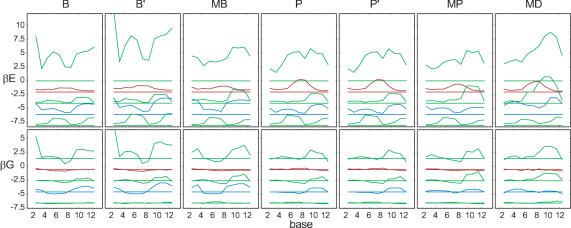
Is it possible to explain sequence specificity by a reduced set of variables? For example, can twisting alone explain indirect readout in the 434 repressor, as suggested by the fact (5) that operators with higher twist in the central region have higher affinity for 434 repressor than those with lower twist? We investigated this question using partial sequence free energies derived from the partial elastic energies in the same way as the full G is derived from the full E. In Figure 8 we show both full and partial sequence free energies (compare Figure 2). The result is ambiguous. In O_R2, twist and shear together do account for the characteristic G minimum in the center. In the other structures, sequence specificity appears to arise from an interplay between all deformation modes.

Figure 8.

Sequence potential G along O_R1, 2, 3, analogous to Figure 2. The partial free energies are shifted down by 2 k_BT successively for clarity, and each one is shown together with the level of random probability. A 3 bps moving window was used.

Comparison of parametrizations

In order to emphasize the features in the energy profiles that are robust with respect to parametrization, we have so far shown mean values and standard deviations of our set of five parametrizations. In the present section we compare these results for different elastic potentials in more detail, using the 434 structures as an example. In Figure 9 we show plots of the elastic energy E and of the sequence free energy G of all mentioned parametrizations, and in addition the crystal ensembles rescaled using effective temperatures for bending only, B′ and P′ (see Materials and Methods).

Figure 9.

Elastic energy E and sequence free energy G in the O_R2 complex, for all parametrizations used. Full and partial energies are shown, with color coding and offsets as in Figures 2 and 8.

When comparing B′ and P′ to B and P, the elastic energy is simply scaled by the effective temperature ratio and thus depends quite sensitively on the choice of this parameter. However, the sequence free energy depends much less on variations in effective temperature. In particular, the predicted regions of elastic optimization are remarkably insensitive to effective temperature uncertainty.

Comparing the O_R2 elastic energy profiles for different parametrizations, the overall shape generally agrees better for the partial energies than for the total energy, suggesting that the coupling terms vary more strongly. The main contribution to the twist energy comes from overtwisting. Consequently, the MD parametrization which has low equilibrium twist values, gives the highest twist energy. In contrast, the overall shape of the total sequence free energy profiles is less affected by the choice of parameters. In particular, the dip in the central region always appears. The robustness of this qualitative feature is also directly evident from the parametrization error bars that we used throughout the article.

Binding affinities

Experimental evidence for indirect readout in 434 repressor comes from the dependence of binding affinity on the sequence of the central, non-contacted bases (4). Does DNA elasticity alone already capture the observed affinities?If DNA elasticity dominates over chemical effects, and if in addition the protein forces all of the artificial sequences into a common structure ξ, then one expects that

$$\beta \left[F_{\sigma }\right(\xi )-F_{{\sigma }^{\prime }}(\xi \left)\right]=\text{ln}\left[c_{1/2}\right(\sigma )/c_{1/2}({\sigma }^{\prime }\left)\right].$$ 22

Here $c_{1/2}\left(\sigma \right)$ is the affinity, given by the (normalized) repressor concentration needed to occupy half of the operators σ. Note that the mere existence of three different 434–operator co-crystals implies that the above equation is an approximation.

In Figure 10 we plot left hand side versus right hand side of this equation. We used affinity data of ten 14 bp artificial sequences, which differ only in the central base pairs (4). The experimental affinities for the R1–R69 subdomain of the repressor were used, since this eliminates cooperative binding effects and corresponds to the domain that was crystallized (30). The F differences are computed as the total deformation free energy for the same sequences in each of the 14 bp O_R structures. Out of the two possible orientations in which the repressor can bind, we used the one with lower F value. This makes a difference only for those three artificial sequences that are not self-complementary. All possible combinations of σ and σ′ are shown, so the plots are inversion symmetric.

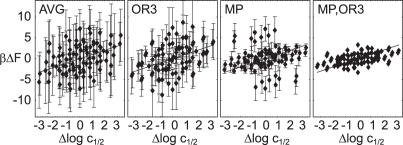
Figure 10.

Computed deformation free energy differences versus measured log affinity differences. From left to right, we used ΔF values for all structures and parametrizations (AVG), the O_R3 structure and all parametrizations (OR3), all structures and the MP parametrization (MP) and O_R3 together with MP (MP, OR3). Error bars indicate the spread in ΔF, and the line indicates equality.

Clearly there is a positive correlation between the log affinity and F differences in all panels. A priori, we have no way to single out one of the crystal structures or one of the parametrization as corresponding best to the experiment. When we consequently plot error bars resulting from all possible combinations of structure and parametrization (AVG), the result is compatible with the data but has no predictive power. Possible reasons are (i) our basic assumptions (independent bps, stiff proteins, elasticity dominating binding in 434) are not justified, (ii) the crystal structures do not correspond to the relevant structures in solution closely enough and (iii) the parametrizations of the potential are inexact.

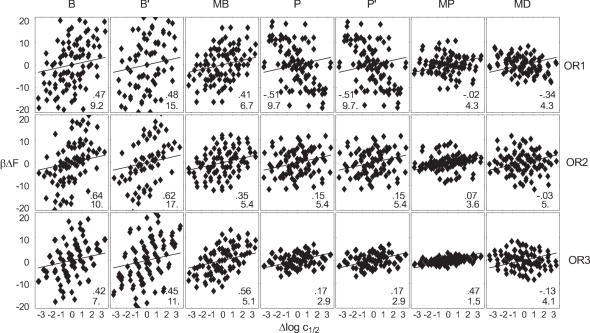
A posteriori, we can check whether one combination of parametrization and crystal structure stands out as the best model for the measured solution affinities. Figure 11 gives an overview of affinity-free energy plots for all such combinations. They show widely varying RMS deviation, ranging from 1.5 k_BT to 26 k_BT depending on the parametrization and structure used. Note that the global energy scales agree for all potentials except B′. Only for the rescaled ensembles B′ and P′ is it higher, increasing the spread of computed affinities.

Figure 11.

Computed deformation free energy differences versus measured log affinity differences, for all combinations of crystal structure and employed parametrization, see also Figure 10. Linear correlation coefficients (upper number) and the RMSD from the line $\beta \Delta F=\Delta \text{log}{c}_{1/2}$ (lower number) are inset.

The shown linear correlation coefficients vary between −0.52 and 0.64. They measure quality of a linear regression of the points with arbitrary slope. Although a negative correlation does identify bad correspondence, the correlation coefficients are clearly insufficient as indicators of fit quality. For example, B′ has higher correlation than B but is far off the correct energy scale. Interestingly, high correlation coefficients often coincide with large absolute errors. Indeed, our model is a line of slope one. The shown RMSD from this model together with the linear correlation indicate clearly that overall, the combination of the MP potential and the O_R3 structure agree best with measured affinities, at RMS error 1.5 k_BT and correlation 0.47.

When this choice is partially relaxed (Figure 10), one sees that the variation among parametrizations in the best structure (OR3), is greater than that among structures for the MP parametrization (MP), as summarized in Figure 10. A ${\chi }^2$-test using the respective error bars reveals that the model $\beta \Delta F=\Delta \text{log}{c}_{1/2}$ is compatible with the (OR3) data, while it is rejected for (MP) at a 5% confidence level. This is in accord with the observation that MP together with O_R1, 2 give no positive correlation, while O_R3 together with B, MB, P and MP results in acceptable correlation with affinities.

These observations give some hope that the parametrization error (c) is more important than the basic approximations (a) made in the model, and that improvements in the determination of a harmonic base pair potential will eventually lead to quantitative affinity predictions. If we accept the MP potential as a valid representation of solution DNA elasticity based on its small RMS deviation, we can then identify the O_R3 structure as the only co-crystal structure that is a good representative of the affinities in solution. In Table 1 we list some corresponding binding affinity predictions. For all possible mutations of the inner four bases we calculated free energies relative to the experimental reference sequence (4). For complementary sequences, we used the lower F value, in the same way as in Figure 11. One can see that the range of computed free energies is bigger than that of the measured ones, which lie in the high affinity half. Note that the highest affinity sequence AAAA coincides with the central part of the native sequence of O_R3, which however differs in the outer parts, see Figure 1. To test improved rbp potentials, it appears helpful to extend the experiments to the sequences with extreme affinities.

Table 1.

Computed free energy differences for mutations of the inner four bases of the sequence ACAATNNNNATTGT

Rank	βΔF	Δ log c	NNNN	Rank	βΔF	Δ log c	NNNN
1	−1.9		AAAA	39	0.9	2.7	ACGT
2	−1.5		AAAG	51	1.3	1.1	GTAC
3	−1.4		ATAA	55	1.5	2.8	AGCT
4	−1.2	0.3	TTAA	75	2.2	0.3	AATT
5	−1		ATAG	132	5.7		CATA
8	−0.5	−0.5	AAAT	133	6.2		TGCA
17	0.0	0.0	ATAT	134	6.8		CACA
21	0.1	1.1	CTAG	135	7.0		CATC
25	0.3	0.6	GTAT	136	8.6		CATG
37	0.9	1.4	AGAT

Sequences used in (4) are shown with the experimental log affinity difference Δ log c. In addition to these, the five highest and lowest affinity random sequences are shown.

SUMMARY AND CONCLUSION

We have developed a theoretical framework for modeling indirect readout based on appropriate elastic free energies. The resulting markers detect sites of dominant indirect readout by locating elastically optimized subsequences in protein–DNA co-crystals. They are linked to experimentally measurable relative binding affinities of operators mutated at these sites. In particular, we propose the similarity $I_{i,i+k}{p}_{i,i+k}\left(\sigma \right)$ of the length k native subsequence to the corresponding elastic consensus subsequence as a non-additive local marker for indirect readout. Unlike a Z-score, this marker can be computed with little numerical effort for arbitrary lengths of the total binding site, and has a direct probabilistic interpretation.

Obviously, the success of our approach depends on the applicability of the model used to describe DNA elasticity as well as on the quality of the parametrization. Here we have chosen a description on the rigid-base pair level, as a sensible compromise between computationally much more expensive all-atom models and rigid rod representations. We have combined state–of–the–art parametrizations from MD simulation and from structural data analysis, using a new, microscopic method of adapting the effective temperature scale. The resulting error bars allow an estimation of the effect of parametrization uncertainty. Qualitative observations appear quite robust with respect to the parametrization uncertainty. Examples are the location of indirect readout sites, the relative importance of structure and elasticity for specificity, or the distinction of contributions from different elastic degrees of freedom. Quantitative predictions for relative binding affinities depend more sensitively on the choice of parametrization. In the case of the 434 repressor, results averaged over the available elastic potentials and structural templates are compatible with measured binding affinities, but the margins of error are too wide to allow quantitative predictions. Closer inspection shows that our MP hybrid potential performs significantly better than alternative parameterizations. These observations underscore the importance of ongoing efforts to improve DNA elastic potentials (26), and suggest the quantitative prediction of indirect readout-mediated relative affinities as an efficient way to benchmark them.

For our test case, the 434 repressor complex, the detailed analysis of the elastic energy (Figure 2) and specificity (Figure 8) profiles reveals differences between the co-crystal structures of the three operator sequences $O_{R}1,2,3$. However, in all three cases we find that agreement between the native and the elastic consensus sequence is confined to the central, not directly contacted part of the operator. On a qualitative level, this supports our working hypothesis that strong elastic optimization in protein–DNA co-crystals is an indicator for dominant indirect readout in real protein–DNA solution complexes. Our results suggest that twist (7) alone cannot account for specificity of the 434 repressor. Rather, the effect seems to due to a coupling of bend, twist, and shear. Furthermore, we find in our relatively weakly distorted example that sequence dependent structure plays a larger role for the tuning of binding affinities than sequence dependent elasticity (Figure 7). Finally, the comparison of predicted and measured relative binding affinities identifies the O_R3 structure as the best available structural template for the solution complexes of 434 repressor.

While the computational cost of the present analysis is negligible, we believe that DNA deformation (free) energies in protein–DNA co-crystals substantially extend the insights that can be gained from structural data. To encourage the application to other systems, we have included the required Mathematica (33) scripts as Supplementary Data.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR online.