Using DNA pools for genotyping trios

Abstract

The genotyping of mother–father–child trios is a very useful tool in disease association studies, as trios eliminate population stratification effects and increase the accuracy of haplotype inference. Unfortunately, the use of trios for association studies may reduce power, since it requires the genotyping of three individuals where only four independent haplotypes are involved. We describe here a method for genotyping a trio using two DNA pools, thus reducing the cost of genotyping trios to that of genotyping two individuals. Furthermore, we present extensions to the method that exploit the linkage disequilibrium structure to compensate for missing data and genotyping errors. We evaluated our method on trios from CEPH pedigree 66 of the Coriell Institute. We demonstrate that the error rates in the genotype calls of the proposed protocol are comparable to those of standard genotyping techniques, although the cost is reduced considerably. The approach described is generic and it can be applied to any genotyping platform that achieves a reasonable precision of allele frequency estimates from pools of two individuals. Using this approach, future trio-based association studies may be able to increase the sample size by 50% for the same cost and thereby increase the power to detect associations.

INTRODUCTION

Most genetic variation in humans can be characterized by single nucleotide polymorphisms (SNPs) and recent progress in the technology for high-throughput SNP genotyping has now provided an unprecedented opportunity to understand the genetic basis of complex disease through whole genome association studies (1–3). Unfortunately, even with these advances association studies remain very expensive due to the need to genotype thousands of individuals in order to compensate for the increased burden of multiple hypotheses. One of the challenges in case–control disease association studies is to eliminate the potentially confounding effect of population stratification, which may lead to false identification of association (4). One way to avoid these effects is to genotype mother–father–child trios in combination with statistical tests such as the transmission disequilibrium test (TDT) (5). In TDT, a set of affected children is genotyped along with their parents, in order to test for a deviation from a random transmission of alleles from heterozygous parents to their children. The main advantage of the TDT test is that it is not affected by population stratification or any other population-wide mating patterns (6). In addition, the genotyping of trios reduces uncertainties in haplotype inference (7). When unrelated individuals are genotyped, the genotype information is obtained and not the haplotypes; the subsequent determination of the haplotype information then becomes an error-prone and a computationally difficult task. With mother–father–child trio genotypes, haplotype inference becomes much easier and the prediction error rate is reduced considerably; this is especially useful in studies that test haplotypes for association.

Unfortunately, the extraction of genotype information from trios requires genotyping of three individuals, whereas the effective size of the sample only consists of two independent individuals, as the child's genotypes are transmitted from the mother and the father. As a result, the power of trio-based studies is reduced, given fixed resources for genotyping, as fully two-thirds of the genotyping effort is expended on unaffected individuals (the parents). Here, we describe a generic protocol to reconstruct the individual genotypes of trios, using two DNA pools per trio, which reduces the genotyping effort of TDT studies to that of case–control studies.

In our approach, rather than genotypes, SNP allele frequencies are determined from mother–child and father–child DNA pools and genotypes of all three individuals are inferred from these pool allelic frequencies. The method thereby increases the sample size by 50% for the same amount of work, by employing two measurements for each trio (allelic frequency estimates of mother–child and father–child pools) compared to three measurements (genotypes of mother, father and child). Our use of pooled trio DNA is unlike other pooling approaches that have been published recently, in which pools of hundreds of cases versus controls are employed (8–11). Whereas in our approach, pool allele frequencies result in inferred genotypes, in studies using large pools, allele frequencies are the goal per se and are not resolved to the genotypes of the individuals who make up the pool. Thus, using our approach, no information is lost, while the cost of the experiment is reduced considerably. Furthermore, our approach is generic in the sense that any genotyping platform that achieves a reasonable precision (≈12.5%) of allele frequency estimates from two individuals may be used.

In this proof-of-principle study we have evaluated Triophase using a population of 12 previously genotyped individuals comprising a single three-generation lineage of 8 trios, from which all pairwise parent–child pools (16 pools) were assembled (Supplementary Table 1). These pools were allelotyped with a high degree of replication (32 replicate allelotypes per pool per SNP) across 12 SNPs in order to generate a large body of data (6144 allelotypes) in which technical variation from the construction of pools and from the instrumentation itself would be the primary source of error. Even though a high degree of replication was used, in our analysis, the genotypes of each trio are predicted from data of two pools without replication. In other words, the dual goals of this study were (i) to establish that technical error does not rule out the use of the method and (ii) to develop and benchmark an algorithm, which we have called Triophase, for use in inferring genotypes from parent–child pools, without replications. The results demonstrate that under these model circumstances, both the approach and algorithm compare very favorable with standard genotyping.

MATERIALS AND METHODS

Triophase algorithm

Given two DNA pools, one consisting of the mother and the child, and another consisting of the father and the child, there are 16 possible configurations of alleles, depending on the assignments to the four chromosomes involved. The pair of allele frequencies creates a signature in the sense that when the allele frequencies of the two pools are given, there is exactly one genotype configuration that corresponds to it (Table 1). When all three individuals are heterozygous, there are two different possible configurations of the alleles, but both configurations result in the same pair of allele frequencies.

Table 1.

The table illustrates the 16 possible trio configurations of parent and child alleles at a biallelic SNP, using A and G as an example

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Mother	AA	AA	AA	AA	AG	AG	AG	AG	GA	GA	GA	GA	GG	GG	GG	GG
Father	AA	AG	GA	GG	AA	AG	GA	GG	AA	AG	GA	GG	AA	AG	GA	GG
Child	AA	AA	AG	AG	AA	AA	AG	AG	GA	GA	GG	GG	GA	GA	GG	GG
Mother + Child Pool	AA	AA	AA	AA	AG	AG	AG	AG	GA	GA	GA	GA	GG	GG	GG	GG
	AA	AA	AG	AG	AA	AA	AG	AG	GA	GA	GG	GG	GA	GA	GG	GG
M + C Pool G Freq.	0	0	0.25	0.25	0.25	0.25	0.50	0.50	0.50	0.50	0.75	0.75	0.75	0.75	1	1
Father + Child Pool	AA	AG	GA	GG	AA	AG	GA	GG	AA	AG	GA	GG	AA	AG	GA	GG
	AA	AA	AG	AG	AA	AA	AG	AG	GA	GA	GG	GG	GA	GA	GG	GG
F + C Pool G Freq.	0	0.25	0.50	0.75	0	0.25	0.50	0.75	0.25	0.50	0.75	1	0.25	0.50	0.75	1
Paired Pool Freq.	0	0	0.25	0.25	0.25	0.25	0.50	0.50	0.50	0.50	0.75	0.75	0.75	0.75	1	1
	0	0.25	0.50	0.75	0	0.25	0.50	0.75	0.25	0.50	0.75	1	0.25	0.50	0.75	1

The first three rows correspond to the genotypes of the mother (normal font), father (italics) and child (one allele from each parent). The allele that is transmitted to the child from each parent is underlined. Rows 4 and 6 show the composition of pools consisting of equimolar amounts of DNA from mother + child and father + child, respectively. Rows 5 and 7 tabulate the frequency of G in these pools [the frequencies of A are = 1 − Freq (G)]. The final row shows the pair of pool frequencies for each configuration and illustrates that this pair of values uniquely identifies the genotype of mother, father and child (configurations 7 and 10, the only two with the same pair of pool frequencies, correspond to the same genotypes of heterozygous mother, father and child).

In practice, there are technical issues that complicate theoretical calculations. To begin with, when preparing pools, it is never the case that the two individuals' DNA are absolutely equimolar. Owing to imprecision in quantification, normalization and liquid handling, one of the individuals has a larger representation than the other. Furthermore, in allele frequency estimates using a technology such as single-base extension/MALDI-TOF mass spectrometry (as well as most other technology platforms), the accuracy of the allele frequency estimate may vary from SNP to SNP. For most SNPs, estimates of allele frequency are skewed due to differential hybridization of allele-specific oligonucleotides, with the direction and magnitude of the shift depend on the genotyping platform, the specific SNP and on the actual allele frequency (8,12,13).

To resolve these technical problems, we have implemented an algorithm, Triophase, which relies on the fact that the allele frequency for an ideal pool must be equal to one of five values: 0, 25, 50, 75 or 100%. If the imprecision introduced by technical considerations is significantly less than half the difference in frequency between these bins (i.e. 12.5%), one could use clustering methods to accurately assign the observed allelic frequencies into one of these five bins. Furthermore, the algorithm derives power from the fact that a biased distribution due to an asymmetrical contribution of DNA from two individuals in a pool will affect the observed allelic frequencies of all SNPs in the assay in the same way. This allows the algorithm to normalize the allele frequency estimates in silico.

The Triophase algorithm models the behavior of the allele frequency estimate of each SNP by a polynomial of degree three. Specifically, the algorithm begins by finding a new set of centers that minimizes the least squares distance between the allele frequency estimates and the corresponding centers (ideally, the centers will be close to 0, 25, 50, 75 and 100%). We map every possible cluster center to a new allele frequency using a polynomial $g\left(x\right)=a{x}^3+b{x}^2+(1-a-b)x$. This map satisfies that g(0) = 0 and g(1) = 1. Furthermore, we restrict the polynomial to satisfy that g(0.25) ∼ 0.25, g(0.5) ∼ 0.5 and g(0.75) ∼ 0.75. As a result, the polynomial will only slightly change the clustering centers; these changes in the clustering centers correspond to the skewness of the allele frequency estimates, as demonstrated in Figure 1 (and Supplementary Figures 1 and 2). As can be seen in these figures, skewness is normally eliminated for allele frequencies that are close to zero and one, and this fact is modeled by the mapping function by to constraints that g(0) = 0 and g(1) = 1.

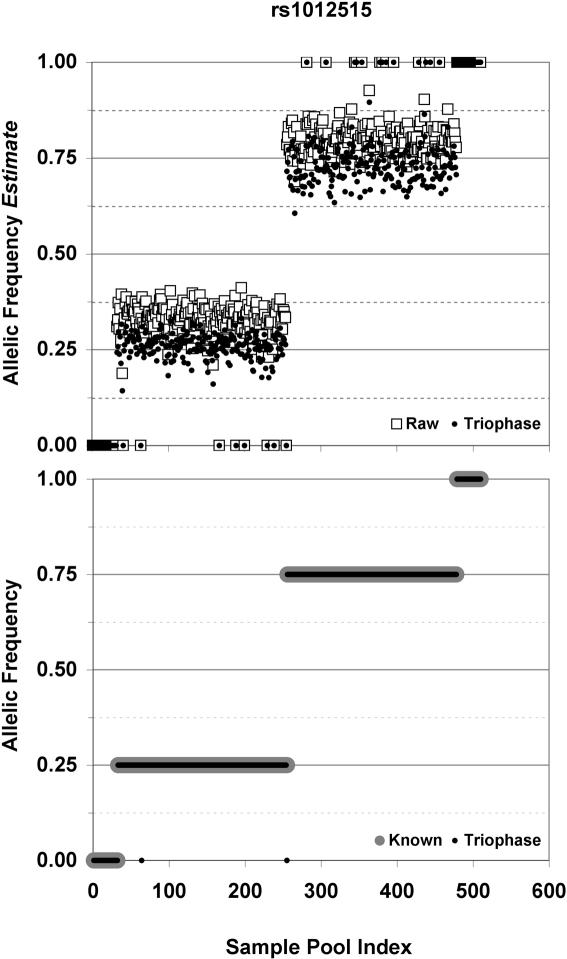
Figure 1.

Allelic frequencies of pools for SNP assay ID rs1012515. The x-axes correspond to pool index, ordered by increasing known pool allelic frequency. Upper panel: the pools' allelic frequency estimate as measured by MassARRAY genotyping (raw data, open boxes) versus the Triophase-corrected estimates (closed circles). Lower panel: the pools' known allelic frequency bin (large gray circles) versus Triophase-assigned frequency bins (small dark circles). Two errors in pool frequency estimation are evident in the lower panel as lone small dark circles.

To deal with pool asymmetries, we incorporate the DNA quantities of the individuals to the calculation above. Even though the sample quantities are not provided to the algorithm, we use the fact that non-normalized pools will affect all SNPs in the same manner. More formally, our model assumes that for every SNP i and trio j, the following equations would be satisfied if no other error sources existed:

$$\begin{array}{l}{p}_{ij}^{mc}\approx g_i\left(\frac{q_i^m{m}_{ij}+c_{ij}}{2(q_i^m+1)}\right)=a_i{\left(\frac{q_i^m{m}_{ij}+c_{ij}}{2(q_i^m+1)}\right)}^3+b_i{\left(\frac{q_i^m{m}_{ij}+c_{ij}}{2(q_i^m+1)}\right)}^2+(1-a_i-b_i)\left(\frac{q_i^m{m}_{ij}+c_{ij}}{2(q_i^m+1)}\right)\\ p_{ij}^{fc}\approx g_i\left(\frac{q_i^f{f}_{ij}+c_{ij}}{2(q_i^f+1)}\right)=a_i{\left(\frac{q_i^f{f}_{ij}+c_{ij}}{2(q_i^f+1)}\right)}^3+b_i{\left(\frac{q_i^f{f}_{ij}+c_{ij}}{2(q_i^f+1)}\right)}^2+(1-a_i-b_i)\left(\frac{q_i^f{f}_{ij}+c_{ij}}{2(q_i^f+1)}\right)\end{array}$$

, where $p_{ij}^{mc}$ and $p_{ij}^{fc}$ are the allele frequency estimated from the genotyping platform, $f_{ij},m_{ij},c_{ij}$ are the actual genotypes of the father, mother and child, and $q_i^f,q_i^m$ are the DNA quantity ratios for the father–child and mother–child pools. Other error sources are then incorporated into the model by minimizing the sum over the squares of deviations from these equations (minimizing the least squares distance).

In order to find the minimum least squares distance, we run Triophase in iterations. In the first iteration, the algorithm assumes that all pools are equimolar and the mapping functions g(x) are calculated for each SNP based on the least squares distance, as described above. Given these mappings, we search for sample quantities that will minimize the least squares distance between the mapped clustering centers and the allele frequency estimates. We compare the mapped frequencies to the actual allele frequency estimates and pick the sample quantities that minimize the sum of least squares. We then iterate by searching for new mapping functions based on the estimated sample quantities. The algorithm terminates when there is no substantial improvement in the least squares sense (for a formal discussion of the algorithm see Supplementary Data).

Triophase with missing data

The quantification of the DNA product is a nontrivial process that may result in some uncertainties in the allele frequency calls. In most cases, the genotyping platform can derive a confidence interval [x,y], within which the actual allele frequency is likely to lie. In the case where the pools are of size two, the confidence intervals may be viewed as integer intervals, where x and y are both integers that represent bounds on the possible allele count in these two individuals.

SNPs in close proximity to each other are usually correlated and are said to be in linkage disequilibrium (LD). If the genotyped SNPs are in high LD, Triophase uses the LD structure to infer the missing data. In particular, Triophase first estimates haplotypes from the confidence intervals and then infers genotypes from haplotypes. The haplotypes are estimated based on local prediction. We use a sliding window of varying length and the haplotypes are inferred for each of these windows using an approach similar to the greedy algorithm suggested for genotype phasing (14). For a given window and trio, there is a confidence interval associated with each of the SNPs in that window. These confidence intervals can be viewed as constraints on the possible four haplotypes (mother and father haplotypes) that appear in the trio. The algorithm searches for a haplotype that can be assigned to as many trios as possible within this window. Once this haplotype is assigned to these trios, the algorithm updates the constraints that are set by the confidence intervals accordingly. This is done repeatedly until all trios have been assigned four haplotypes in the window. The final result for each of the SNPs is based on a majority rule, which takes into account all windows overlapping with that SNP (for additional details see Supplementary Data).

We use chromosome 22 of the Yoruban population available from the HapMap dataset (denoted YRI) to evaluate Triophase. This dataset is composed of 30 trios taken from a Yoruban population from Nigeria and it spans 19 738 SNPs, in an average distance of 5 kb. We used the phasing algorithm HAP (15) to resolve the missing data that was present in this dataset. As explained below, we simulated errors and confidence intervals from this dataset in order to test our algorithms.

We simulated the confidence intervals for each of the pools. The simulations depend on a parameter p, which we define as the missing data rate. For each DNA pool with an allele count of k, we simulated a confidence interval [x,y] such that x ≤ k ≤ y. The bounds x and y are chosen according to a bounded geometric distribution with parameter p. That is, we pick x and y so that $k-x\sim G\left(p\right),y-k\sim G\left(p\right)$; if x < 0 we set x = 0 and if y > 4 we set y = 4. Under the resulting simulation, the fraction of ambiguous pools (when x < y) is ∼2p. As seen from our experiments, a realistic value of p would be on the order of 0.01.

DNA quantification and construction of pools

DNA samples were of CEPH/Pedigree 66, purchased as purified DNA from the Coriell Collection (details found at http://locus.umdnj.edu/nigms/nigms_cgi/cells.flat.cgi?id=7&query=66). This pedigree of 13 individuals is composed of both pairs of maternal and paternal grandparents, parents and seven children. Owing to constraints of available material, one of the children (repository number GM12550) was excluded. The remaining 12 individuals permitted the construction of 16 independent mother–child and father–child pools. Prior to pooling, DNA was quantified by three different methods: UV spectroscopy using the NanoDrop instrument (NanoDrop Technologies, Wilmington, DE), fluorimetry using the Picogreen DNA-binding dye (Invitrogen, San Diego) and quantitative-PCR using real-time quantitative-PCR and a sequence-specific Taqman probe. Samples were carefully normalized to a uniform concentration, re-quantified using all three methods to confirm the accuracy of normalization and equimolar pools assembled at a concentration of 1.25 ng/μl of each individual sample (2.5 ng/μl total [DNA]). The details of the pools are shown in Supplementary Table 1.

Allelotyping

Genotyping of individual samples and allelotyping of DNA pools were both performed using the same chemistry and laboratory protocols for multiplex PCR, single-base primer extension (SBE) and generation of mass spectra (for complete details see iPLEX Application Note, Sequenom, San Diego). For the purpose of this proof-of-principle experiment we used a single multiplex assay containing 14 SNPs selected for their high minor allele frequencies in HapMap populations (>0.4) and absence of LD. These included two SNPs on chromosome 3, three on chromosome 6, two on chromosome 8, one each on chromosomes 7, 10, 12, 17 and 21, and two mapping to the sex chromosomes (data not included in the analysis). Briefly, initial 14-plex PCR was performed using 28 primers in 5 μl reactions on 384-well plates containing 5 ng of genomic DNA, either a pure sample from a single individual (genotyping) or a 1:1 pool of 2.5 ng DNA of each of two samples (allelotyping). Reactions contained 0.5 U HotStar Taq polymerase (QIAGEN), 100 nM primers, 1.25× HotStar Taq buffer, 1.625 mM MgCl₂ and 500 μM dNTPs. Following enzyme activation at 94°C for 15 min, DNA was amplified with 45 cycles of 94°C for 20 s, 56°C for 30 s, 72°C for 1 min, followed by a 3 min extension at 72°C. Unincorporated dNTPs were removed using shrimp alkaline phosphatase (0.3 U, Sequenom). Single-base extension was carried out by addition of 14 SBE primers at concentrations from 0.625 μM (low MW primers) to 1.25 μM (high MW primers) using iPLEX enzyme and buffers (Sequenom) in 9 μl reactions. Reactions were desalted and SBE products measured using the MassARRAY Compact system and mass spectra were analyzed using TYPER software (Sequenom), in order to generate genotype calls and allele frequencies. Allelotyping of the 16 parent–child DNA pools was replicated completely (from initial PCR) 32 times, resulting in a dataset of size 512 allelotypes for each pool. Although these data do not represent 512 independent pools, the purpose of this experiment was to test whether or not technical variance from the platform would rule out the use of the proposed methodology and the benchmark the Triophase algorithm on real-world data; for the purpose of estimating technical variance these data represent independent analyses.

RESULTS

Evaluation of Triophase

In order to illustrate the feasibility of the protocol, we evaluated the genotyping protocol together with Triophase, by applying them to pedigree 66 of the Coriell Institute. The pedigree consists of 12 individuals from three different generations and it provides a set of 8 different, partially overlapping trios. We treated the trios as independent. We prepared the two pools for each of the trios, using equivalent DNA quantities as used for standard genotyping (2.5 ng per individual). We measured allelic frequency for 12 SNPs for each of the pools using multiplexed quantitative MALDI-TOF mass spectrometry and inferred the genotypes using Triophase. We have replicated this experiment 32 times and thereby modeled the performance of the method over 512 trios and 12 SNPs or 6144 allelotypes in all (see Materials and Methods for details). Our goal in carrying out such exhaustive replication was to generate a large dataset in which an accurate measure of the population variance from the technology platform could be ascertained. We measured the discordance rate between inferred genotypes from pooling to the actual genotypes (known from prior genotyping on the same platform, using the same chemistry). In Table 2, the discordance rate resulting from the use of parent–child pools is shown for all 12 SNPs, with or without the use of the Triophase algorithm and in the latter case, permitting a no-call rate of 0, 2 or 5%. We allow for no-calls (missing data) based on the signal to ratio (SNR) values of the mass spectra (values are discarded in order from lowest SNR) and on the least squares distance resulting from the Triophase algorithm (Materials and Methods).

Table 2.

The observed genotyping error (discordance) rates of the proposed parent–child pool-based protocol, under four conditions: (i) using simple rounding of frequencies into the nearest bin, (ii) with Triophase and a 0% no-call rate, (iii) with Triophase and a 2% no-call rate and (iv) with Triophase and 5% no-call rate

SNP ID	Simple bins	Triophase-correction
	100% Call rate	100% Call rate	98% Call rate	95% Call rate
rs1012515 (%)	2.08	0.26	0.27	0.28
rs1029687 (%)	0.39	0.26	0.13	0.13
rs1228988 (%)	0.26	0.26	0.26	0.26
rs12415456 (%)	0.52	0.26	0.13	0.13
rs1472343 (%)	1.69	1.43	0.94	0.68
rs1669703 (%)	0.00	0.00	0.00	0.00
rs2289300 (%)	0.52	0.52	0.13	0.13
rs2560643 (%)	0.13	0.13	0.00	0.00
rs4382469 (%)	0.78	1.04	1.01	1.04
rs6550139 (%)	15.76	1.04	0.79	0.79
rs6550503 (%)	0.39	0.39	0.26	0.26
rs6569474 (%)	3.13	2.95	2.34	2.63
Mean (%)	2.12	0.66	0.47	0.45

In theory, the use of parent–child pools is not dependent upon an algorithm such as Triophase; one might simply use uncorrected allelic frequencies rounded to the nearest frequency bin (e.g. a pool allelic frequency of 0.124 would resolve to zero and of 0.126 would resolve to 0.25). As illustrated in Figure 1 and Supplementary Figures 1 and 2, however, many assays are skewed from the expected allelic frequency binds, with the result that such rounding would result in unacceptably large error. In this pilot experiment, the genotyping error rate from such simple rounding was estimated at 2.12%.

The use of Triophase, in contrast, results in a discordance rate of 0.66%, assuming that all data are included. Clearly, there is a tradeoff between the no-call rate and the discordance rate. Discordance could be decreased to 0.47% with a 2% no-call rate. It appears that allowing >2% no-calls does not reduce the discordance rate considerably (Table 2).

In most genotyping platforms, the error rate is higher for heterozygous individuals than for homozygous individuals. This is detrimental to TDT, in which the false association of rare alleles is highly sensitive to errors in heterozygous SNPs. Therefore, for this study we only considered SNPs with minor allele frequency >0.45, so that the vast majority of the trios has at least one heterozygous individual. Surprisingly, we find that when restricting the evaluation to heterozygous trios, for which not all four alleles are identical, we get a discordance rate of only 0.17% with 2% no-call rate. This phenomenon can be explained intuitively by the following argument. Unlike standard genotyping, where the number of homozygous genotypes is always larger than the number of heterozygous genotypes (under Hardy–Weinberg Equilibrium), in the case of pools of size two, the number of pools where all four alleles are identical is relatively small. Therefore, our algorithm has more data points for heterozygous SNPs than for homozygous, resulting in an increased accuracy for heterozygous SNPs. In the context of an association study, where 100–1000 of samples are genotyped, the number of data points will increase dramatically and we expect the resulting discordance rate to decrease accordingly.

Power evaluation

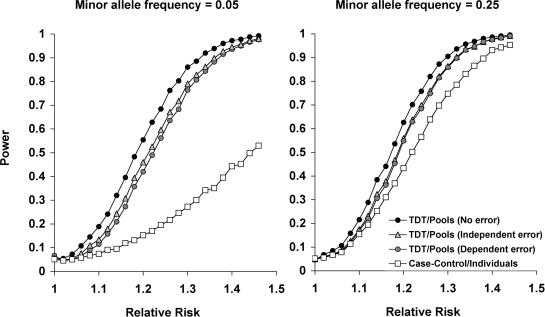
Even though our approach allows for the genotyping of trios using 50% less of the effort, it is not clear whether there is a substantial gain in power due to the dependencies between the genotyping errors of the children and their parents. To test the effect of these dependencies, we simulated sets of 500 trios each, in which we genotype a causal SNP with allele frequency ranging from 5 to 35%. In each of the simulations we used a different disease model that is characterized by the prevalence that was set to 0.05 and the relative risk ranging from 1 to 1.5. For each such disease model and allele frequency, we ran 5000 simulations and compared four different approaches for analysis: the TDT test when no genotyping errors are present, the TDT test when the Triophase is used and the genotyping errors are dependent, the TDT test when standard genotyping is used and the genotyping errors are independent and a χ²-test for a case–control scenario that was simulated for a set of 500 cases and 500 controls under the same disease model and allele frequency. The error rate used for the three latter analyses was 0.6%. As demonstrated in Figure 2, there is a slight loss in power when there are dependencies in the genotyping errors, but this is negligible compared to the gain in power over the case–control scenario.

Figure 2.

The increase in power resulting from the use of pairwise parent–child pools in genotyping trios. We compared the power of four different scenarios under a multiplicative disease model for a SNP with minor allele frequencies of 5 and 25%. In the first three scenarios, 500 trios are genotyped and the TDT test is performed. The first scenario assumes no genotyping errors, the second assumes that the trios were pooled using the Triophase approach and thus the errors of the child and its parents are dependent and the third one assumes that the errors for different individuals are independent, In the fourth scenario, we assume that 500 cases and 500 controls are genotyped and that a χ²-test is performed. Notably, the Triophase approach does not lose much power due to dependencies in the errors and for low allele frequencies, there is a considerable gain of power compared to a non-family-based case–control study.

Missing data

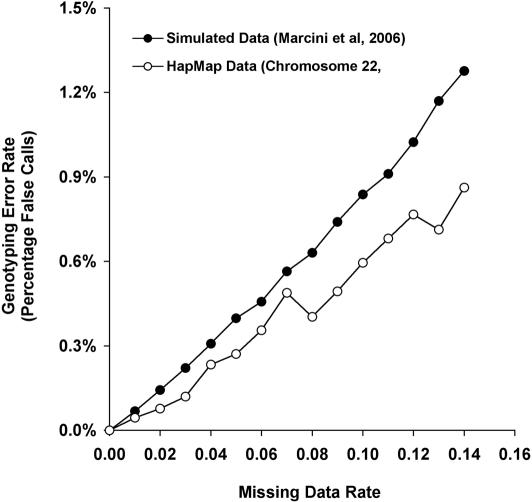
We evaluated the performance of Triophase with missing data on the set of 30 trios of the Yoruban population available from the HapMap dataset (HapMap Consortium, 2005). We simulated confidence intervals for the pools resulting from this dataset across chromosome 22. The simulated confidence intervals depend on an ambiguous data rate p (for details see Materials and Methods). We evaluated Triophase for ambiguous data rate p ranging from 0 to 14% with 1% increments. The simulation study shows that the error rate is kept 15-fold lower than the rate of ambiguity (Figure 3). Thus, when random SNPs are genotyped in a similar density to the one given in the first phase of HapMap (every 5 kb on the average), standard rates of missing data can be filled in with high accuracy using Triophase. We note the errors in the inference in the missing data decrease the power of the TDT test. This however is also true when missing data is inferred from data generated by standard genotyping. Evidently, the power lost due to the resulting errors is negligible compared to the power gained by the ability to type 50% more trios.

Figure 3.

The error rate of the predicted genotypes using multiplexing pools in trios and the greedy algorithm for missing data estimation. The x-axis is the missing data rate and the y-axis is the resulting genotyping error rate. The pools and the corresponding confidence intervals were simulated on two datasets: The first is a dataset simulated from the coalescent model, taken from the dataset publicly available by (7). The second is chromosome 22, taken from 30 Yoruban trios collected by the HapMap consortium, (15).

DISCUSSION

The genotyping of trios is still a common practice due to its robustness to effects of population stratification (6) and to the improved accuracy of trio phasing methods (7). Additionally, trios were used recently to find deletions variants in silico (16). Using the methods suggested in this paper, many of these tasks could be performed on larger datasets or for a lower cost. In particular, in the HAPMAP project (17), a genome-wide analysis was performed across 60 trios, half from a Yoruban population and half from Utah residents with European ancestry (CEPH trios). Using the methods described in this paper, future trio-based projects such as the HAPMAP project or other family-based association studies would be able to increase the sample size by 50% for the same cost.

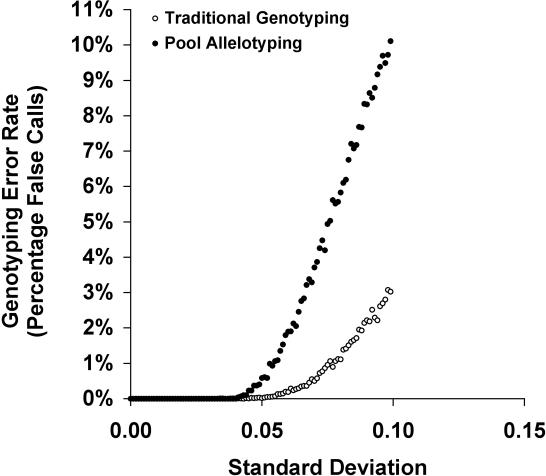
Current association studies only use pooled DNA data when the individual information is not needed, for instance, for the screening of potential linked SNPs as a first step of a multistage association study (8–10,18–20). In contrast to previous methods, the techniques presented here provide a new application for DNA pooling, namely the individual genotyping of trios. We have demonstrated that our method considerably increases the power of an association study when compared to a case–control based association study with an equivalent budget. The methodology used for this protocol is limited to trios and it assumes that the SNPs are biallelic and that there is no copy number variation. It may be possible to extend our methods to other scenarios in which more complex pedigree configurations are genotyped or even when unrelated individuals are genotyped. We emphasize that our choice of the genotyping platform for the evaluation of our method is arbitrary and is only used as a proof-of-principle. We expect the method to have similar performance on genotyping platforms that allows for reasonably accurate quantitative DNA pools measurements. In order to demonstrate this point, we used the HapMap CEU population to simulate scenarios in which the allele frequencies are read with errors. The simulations were performed over 200 SNPs in chromosome 22. The error was introduced by adding to the correct allele frequency a Gaussian distribution with mean 0 and standard deviation (SD) of allelic frequency estimation ranging from 0 to 10%. As can be seen in Figure 4, as long as the SD < 6%, the results are comparable to genotyping error rates. This is encouraging, since it implies that it may be possible to extend the approach to other genotyping platforms. In this study, empirical pool frequency determination using MALDI-TOF-based allelotyping across 12 SNPs resulted in a range of SDs (Min SD = 2.0%, Max SD = 10.0%, mean SD = 4.8 ± 2.3%, Supplementary Figure 3). For the current platform, at least, genotyping using parent–child pools in combination with Triophase should produce similar error rates to standard genotyping.

Figure 4.

The error rate of the parent–child pool genotyping versus standard genotyping as a function of increasing imprecision in allele frequency determination. All datasets are based on 200 SNPs in chromosome 22, taken from the HapMap CEU population, which includes 30 trios. For each allele frequency read (per SNP and pool), we added an error component, normally distributed with mean 0 and SD ranging from 0 to 10% (on the x-axis).

This proposed method is not without some drawbacks. Although Triophase includes an algorithm for using frequency estimates to correct, in silico, asymmetries in the contributions of parent versus child genomic DNA to a pool, it is likely that large asymmetries would interfere with the method. Hence, the accurate normalization of DNA samples is a prerequisite to the adoption of this method. Measuring and normalizing DNA samples is not trivial, involving an expense of both time and resources. In our hands, the cost (in labor and reagents) of accurately normalizing a standard 96-well plate of DNA to the standard of the current study is roughly $500 or $5 per sample. Thus, this cost is negligible compared to the current genotyping costs, in studies where hundreds of SNPs are genotyped.

Lastly, our study also provides an extensive measurement of allele frequency estimates for pools of size two. The study shows that for pools of this size, the clustering structure of the five possible allele frequency values can be exploited in order to provide accurate estimates of the actual allele frequencies (Figure 1 and Supplementary Figures 1 and 2). Therefore, it is conceivable that other methods involving pools of size two will be used for other applications, including those that are not based on trios.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.