Nonlinear auditory mechanism enhances female sounds for male mosquitoes

Abstract

Sound plays an important role in the life history of mosquitoes. Male mosquitoes detect females by the sound generated by their wingbeat. Because female wings are weak acoustic radiators, males have been driven by sexual selection to evolve sensitive acoustic sensors. Mosquito antennae are very sensitive acoustic receivers, featuring up to 16,000 sensory cells, a number comparable with that contained in the human cochlea. The antennal sound receiver exhibits frequency selectivity, input amplification, and self-generated oscillations, features that parallel the functional sophistication of the cochlear amplifier. Although arguably the male antenna is well suited to receiving weak female sounds, the role of active mechanisms in mosquito hearing is far from understood. Previous mechanical studies on mosquito hearing largely focused on the steady-state antennal response to harmonic sounds, mostly evaluating the data through conventional Fourier transforms. Here, we report on the time-resolved mechanical behavior of the male antenna in response to female sounds. Crucially, stimuli were designed to reflect the temporal acoustic profile of a female flying by. With these stimuli, several previously unreported nonlinear features were unveiled, involving amplification, compression, and hysteresis. The time-resolved analysis reveals that, through the active participation of the sensory neurons, the antenna mechanically responds to enlarge its own range of detection. This behavior augments the capacity of the antennal receiver to detect female sounds, enhancing the male's chance to successfully pursue a passing female.

In the vast majority of insect species, the antennae are endowed with a sensory organ sensitive to mechanical stimuli (1), Johnston's organ (2). In mosquitoes, this organ has evolved to be larger and more complex than in other insects (3) and comprises up to 16,000 sensory cells (4), just as many as in the human cochlea (5). As part of the mating behavior, male mosquitoes locate conspecific females by detecting the particle velocity component of the sound produced by their beating wings (3, 6–8). But males also detect the acoustic emissions of male conspecifics (9). In effect, males and females can alter their flight frequency with respect to each other, intriguingly as part of sexual recognition (9). Flying females, however, emit very faint sounds; their wingspan is much shorter (2–3 mm) than the wavelength (≈800 mm) of the sound they produce (350–450 Hz). Because of their small size, females are thus far below the length scale ratio of 1:6 (source size/wavelength) required for efficient sound radiation (10, 11). This mismatch results in female mosquitoes being very inefficient, faint sound emitters, for the same reason that a tweeter loudspeaker is too small to radiate low-frequency sound (11). The weak acoustic radiation power of female mosquitoes is likely to constitute a key evolutionary pressure that promoted the development of sensitive hearing in male mosquitoes. It was shown, by recording compound potentials generated by the activity of mechanosensory neurons in Johnston's organ, that deflections of the tip of the antenna by a mere 14 nm in magnitude are sufficient to elicit neural signaling (8). A key question resides in understanding the relationship between the antenna, acting as a purely mechanical oscillator, and the mechanoreceptive neurons, acting as an ensemble of mechanical sensors and actuators. This problem is formally similar to that still outstanding in mammalian hearing, that is to understand the passive and active contribution of the outer hair cells of cochlea to the mechanical behavior of the basilar membrane.

In insects, a breakthrough was achieved when it was shown in the mosquito Toxorhynchites brevipalpis that the mechanical response of the antenna is nonlinear, reflecting the active participation of the sensory neurons in the process of hearing (12). Structurally, the distal part of the male antenna, the flagellum, is well adapted to the detection of acoustic particle velocity (Fig. 1); it is highly verticillate, harboring a brush of thin hairs rigidly coupled to the flagellum (7, 8). This anatomical feature ensures a viscous coupling to the surrounding air, making the antenna mechanically extremely sensitive to the particle velocity component of impinging sound waves (7). Functionally, the antennal response to sound seems at first similar to a simple damped harmonic oscillator. Yet, several key nonlinear response characteristics reveal the active nature of the mosquito's auditory system. Interestingly, these characteristics are reminiscent of those found in vertebrate ears (5, 13–15); they encompass the variation of the response gain with stimulus amplitude, the amplitude-dependent response bandwidth, and notably, the presence of self-generated mechanical oscillations (5, 16).

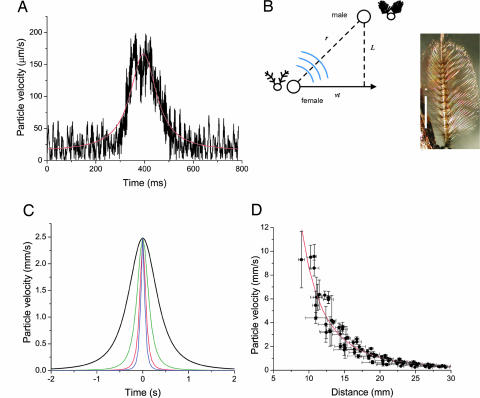
Fig. 1.

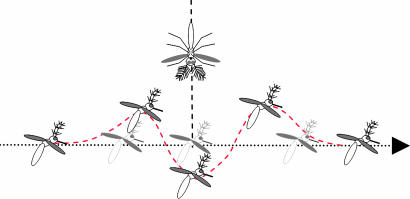
Female flight sounds and flyby simulation. (A) Sound recording of a single female passing a particle velocity microphone. The general shape of the curve is reminiscent of a Lorentzian profile. The dip seen at the maximum particle velocity reflects the response characteristics of the microphone to sound impinging parallel to its membrane. (B) (Left) Geometrical argument for a flying female passing a stationary male. Female flies on a straight line trajectory at speed v, with closest approach L. (Right) The plumose male antennal receiver is shown. (Scale bar: 1 mm.) (C) Simulated amplitude envelope of flyby sound in time for speeds 3.33 (black), 8.33 (green), 16.66 (red), and 25 (blue) cm·s⁻¹. (D) Particle velocity attenuation from a flying female, with fitted inverse-cube law (red line).

To date, the nonlinear mechanical response characteristics of an intact auditory system in response to evolutionarily relevant acoustic inputs have not been explored. The aim of this study is to explore how the amplificatory action, such as that supplied by the cochlear amplifier (13–15) or the antennal amplifier (12, 17), contributes to the process of capturing sound from the environment. So, from an acoustic ecological standpoint, what effect does the sound of a nearby flying female have on the mechanical response of the male antenna? Here, we establish the acoustic profile of a female flyby and generate a mathematical description, a Lorentzian function, that allows the synthesis of a model signal mimicking a female flyby at various flight velocities. The response to these acoustic profiles reveals the amplitude dependence of the gain function; active mechanisms modulate the mechanical response of the antenna. Characterized in time, the mechanical responses comprise three distinct phases: an initial gain, a compression at higher amplitudes, and a final, large gain. These three phases are typical of nonlinear oscillators responding to varying stimulus amplitude. As such, the response enhances the male's capacity to hear a passing female. This mechanism serves to sustain and amplify female signals, which are, by their very nature, weak and transient. The present analysis reveals the dynamic action of a nonlinear oscillator in an intact biological system and links it to its behavioral function.

Results and Discussion

Acoustics and Geometry of Female Sound.

As she flies past a male, a female mosquito is generating sound with an amplitude that, at the position of the male antenna, greatly varies with time. One way to measure this time-varying intensity profile is to use a microphone detecting the incident particle velocity from a free flying female passing by. Relying on the chance passing of females near the microphone, recordings were obtained that reveal a bell-shaped acoustic profile (Fig. 1). This measurement technique, however, does not provide information on flight speed or trajectory, and as such cannot be used for any quantitative measurements. On the basis of the free-flight recordings, a complementary theoretical approach was chosen to construct an idealized intensity profile. This profile is a function of both the geometry of the approach and the degree of spatial attenuation of sound waves in the near field.

In its simplest form, a female flyby can be approximated by a straight line trajectory past a male (Fig. 1). The absolute distance between female sound source and male receiver, r, coupled with the spatial inverse power law expected from a sound source constituted by two beating wings (18), indicates that the absolute distance from male receiver to female emitter should have a Lorentzian distribution. Although the spatial attenuation for the particle velocity component of near-field sound is known theoretically for simple sources (monopoles, dipoles, etc.), it is not known for more complex sound radiators, such as the two flapping wings of a mosquito. Attenuation as a function of distance had thus to be first experimentally determined. Furthermore, analysis of the strength of emitted sound from females was required to calibrate the amplitude of a simulated flyby to ensure biological relevance. Thus, stimuli were faithful to natural female sounds, both in amplitude and time profile.

To determine amplitudes, the sounds of tethered females were recorded in fictive flight. Sound particle velocity could thus be measured for various known distances between the female and the microphone. The sound produced from flying Dipteran flies is purported to be akin to sound produced by an acoustic dipole (18, 19). The intensity of sound radiated by that dipole source depends greatly on the receiver's distance to the source. Indeed, in the near-field, particle velocity decreases as 1/r³, where r is the distance from the dipole acoustic center (18–20). Sound particle velocity radiated from tethered female T. brevipalpis decays very rapidly with distance (Fig. 1). The characteristic attenuation that a dipole source produces is shown by the fitted curve, which depicts this dipole law of spatial attenuation A/r³, with A = 8,606 ± 222 mm⁴·s⁻¹.

The flight frequency was also determined from these recordings as a function of time. The frequency of the signal, corresponding to the wingbeat frequency, is remarkably stable, and averages 405.7 ± 43.5 Hz (n = 10). Both the amplitude modulation in time and the carrier frequency of the signal were used to generate model sounds with the key signatures of female flying by with different approach velocities, the Lorentzian amplitude distribution, and the carrier frequency of the sound (Fig. 1).

Antennal Response.

Flyby sounds elicit a remarkable response in the male antenna of T. brevipalpis. Deviation from linearity can clearly be seen in time from the marked amplification occurring as sound level increases (Fig. 2). This finding shows that, as the female approaches, the antenna becomes more sensitive to female sounds. This amplification does not take place when the female sound magnitude is too low. Past a certain amplitude threshold, the male antenna deflects more than what the acoustic input alone predicts (Fig. 3), a sign that signal amplification occurs (12). Interestingly, the amplification threshold is higher than the detection threshold. Thus, this effect appears to be related to a pursuit, rather than the initial detection of female sounds. The extent of the active process can be seen more clearly when considering the gain of the system. Male antennae respond linearly for low amplitude stimuli, i.e., when the female is still far away. In this case, the gain is constant (Fig. 3). As she approaches, gain increases. As sound amplitude further increases, gain decreases, to become a steady compression (negative gain) until the female is closest to the male. As the female passes by, stimulus amplitude decreases and the amplification process resumes. Notably, the gain associated with the decreasing sound amplitude is more pronounced than that obtained from the increasing amplitude. Finally, with increasing distance between male and female, the system returns to a linear response. These three phases, a primary amplification, a compression, and a secondary amplification, occur to varying extents in all live males. In effect, during the span of a flyby, the antennal response spends more time in the nonlinear regime than in the linear regime. Increasing the flyby velocity appears to soften the effect, as witnessed by the less pronounced amplifications and compression events. These antennal responses are highly repeatable; each image in Fig. 3 consists of five consecutive flybys that match very closely. Such peculiar nonlinear behavior is absent in the postmortem antennal response, suggesting that, in this regime, putative passive structural nonlinearities are not responsible for the observed effects (Fig. 3).

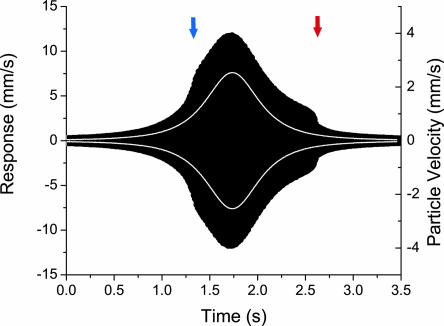
Fig. 2.

Time-resolved antennal response to a simulated flyby. The stimulus (white lined envelope) elicits a marked, asymmetric response in antennal motion (black envelope). Antennal motion appears to deviate from the expected trajectory at ≈1.25 s (blue marker). A marked loss of amplification occurs at ≈2.6 s (red marker). The asymmetry indicates a large amount of hysteresis in antennal motion.

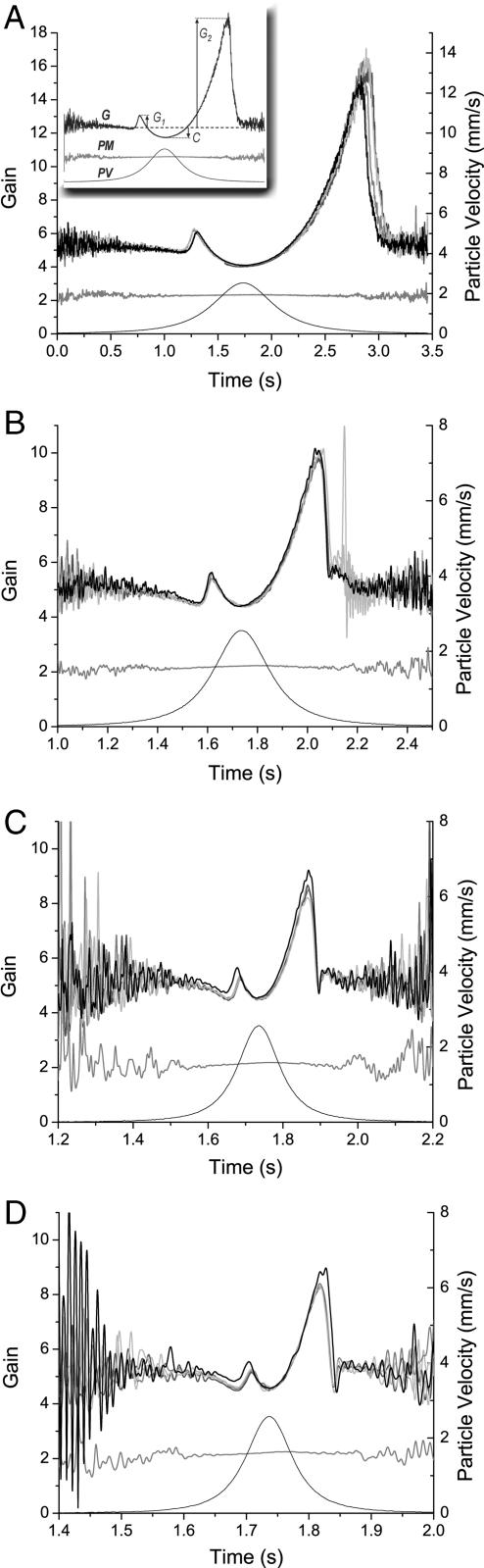
Fig. 3.

Nonlinear antennal gain (G) caused by simulated flybys [particle velocity (PV)]. Several different flyby speeds are presented: 3.33 (A), 8.33 (B), 16.66 (C), and 25 (D) cm·s⁻¹. Flybys are characterized by three distinct gain changes: primary amplification G₁, compression C, and secondary amplification G₂ (A Inset). These are absent in the postmortem response (PM). Each image shows five repeated sound stimuli, indicating a high level of repeatability. Across all speeds, these phenomena are qualitatively similar, although, as indicated by the changing scales, they are less pronounced for higher flyby speeds.

This mechanical response is thus clearly characterized by primary and secondary amplification and compression. Quantitatively, gain and compression vary from animal to animal but invariably occur in all mosquitoes investigated (n = 12 males). Gain and compression could not be observed in dead animals. It is worth noting here that, although this report focuses on T. brevipalpis, similar gain and compression responses have been measured in the culicid Aedes aegypti. In effect, a wide range of magnitudes have been observed for amplification, including none at all (gain range: 0–2,300% increase). To document the interindividual variation in the antennal response, three characteristic points were defined along the time-resolved response curve: maximum gain of primary amplification G₁, minimum compression C, and maximum gain of secondary amplification G₂, all relative to the standard gain in the linear regime (Fig. 3A Inset). The responses of different animals vary greatly (Fig. 4). Primary amplification appears to be the most variable; sometimes no primary amplification could be discerned. Quantitatively, the average value for G₁ was 0.365 (n = 12; SD = 0.338), or a 7.81% increase from average onset gain. In contrast, compression was always present; on average, C = −0.832 (n = 12; SD = 0.430), corresponding to a 17.78% decrease from onset gain. Likewise, the secondary amplification G₂ occurred on average 1.186 (n = 12; SD = 1.14) above onset gain, or 25.37% above initial gain, although some animals were able to amplify well over 50% of their initial gain. The enhancement of antennal vibrations highlights the ability of the mechanosensory system to increase the overall energy of oscillation. This evidence provides a biologically relevant manifestation of the active participation of mechanosensory neurons in mosquito hearing (12).

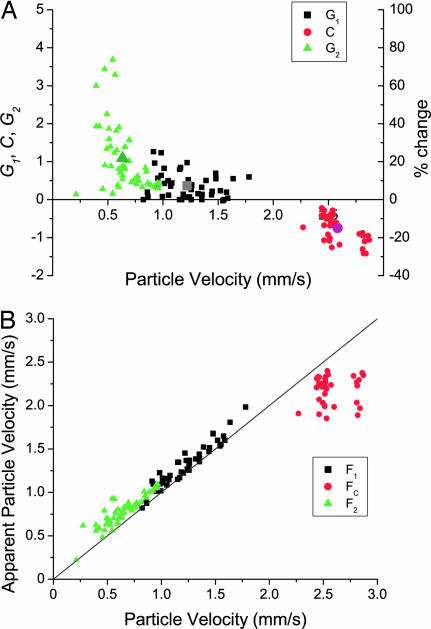
Fig. 4.

Nonlinearity in the male antenna. (A) Interindividual variation of the amplification and compression (n = 12). Average values are indicated by the larger symbols. Primary amplification G₁ is smaller on average than secondary amplification G₂, which varies and can exceed 50%. Importantly, there are occasions where G₁ = 0, i.e., there is no primary amplification. Compression, C, occurs always. G₂ occurs at quieter sound levels than G_1. (B) Change in apparent sound amplitude caused by antennal nonlinearity. Black line indicates where real and apparent particle velocities are equal: above this line, the sound appears louder, below it the sound appears quieter than would be for a passive response. Sound particle velocity for G₁, C, and G₂ are denoted by F₁, F_C, and F₂, respectively.

Much insight can be obtained from evaluating the timing (in relation to sound amplitude) at which maximum G₁, C, and G₂, take place. Primary amplification G₁ was maximum, on average, at sound particle velocity v_p = 1.22 ± 0.23 mm·s⁻¹. From the fitted curve for particle velocity emission from flying females (Fig. 1), this particle velocity corresponds to a male–female distance of ≈19 mm. Similarly, for maximum G₂, sound particle velocity was 0.63 ± 0.17 mm·s⁻¹, that is, a distance of ≈24 mm. Accordingly, the nonlinear active antennal response is fully present when the female is ≈2 cm from the male. As such, this response may coincide with, or trigger, a pursuit behavior. Furthermore, once the female has flown past, the male continues to amplify her sound by an additional 5 mm, in excess of that expected from the primary amplification. Although this extension in distance does not appear to be large, it can be noted that the secondary amplification ceases at half the amplitude of the primary amplification. Collectively, this analysis highlights the rapid attenuation of female sound, the difficulties associated with the detection of such a variable signal, and the strength of the antennal amplifier.

All along the female flyby, and in particular at times G₁, G₂, and C, the variations in gain mean that the apparent loudness of the female keeps changing. The apparent particle velocity (should the antenna respond linearly) can be calculated and compared with the actual (stimulus) particle velocity (Fig. 4). Put in behavioral terms, such analysis reveals the effects of the nonlinearity: both G₁ and G₂ serve to render the female louder than her actual sound output, a very useful effect in improving the male's ability to detect the female. In the amplification regime, the female thus appears to be closer (Fig. 5). Conversely, the compression C actually softens the female sound, making her appear quieter (Fig. 5). In essence, such a compression could be a mechanism to dampen down antennal oscillations that, when the female is close, may reduce the dynamic range. Compressive power laws are common in nonlinear systems. High amplitude compression is always related to nonlinear amplificatory mechanisms, and as such is a natural by-product. The compressive nature of the response restricts antennal motion and may serve to avoid overstimulation.

Fig. 5.

Schematic of the apparent motion of the female. As the female passes from left to right, the male antenna behaves as to modulate her apparent position. This modulation is hysteretic: the male actively sustains her signal for an additional period of time, and thus distance, focusing on her sound (not to scale in vertical direction).

How does this peculiar nonlinear auditory response contribute to detecting the elusive sounds of a female passing by? From electrophysiological recordings, male T. brevipalpis are predicted to hear female flight sounds from distances up to 10 cm (12). Yet, the nonlinear response described in this article is shown to take effect at ≈2 cm, which indicates that these nonlinear amplificatory and compressive effects are not effective in the amplitude range near neuronal detection thresholds. Instead, the entire sequence of nonlinear response takes place at a higher amplitude regime, where female mosquitoes are well within earshot. In effect, the nonlinear response modulates the perceived loudness of the close passing female. Speculatively, the nonlinear antennal response may serve the function of an autofocus auditory telescope that “snaps” to the sound source: it brings the female in focus, and makes her appear closer than she is (Fig. 5). Occurring for sounds well within detection range, this additional function highlights the extent to which active behavior can enhance the sensor's capabilities.

Temporal dynamics of the male antenna to biologically relevant sounds has revealed a remarkable and unexpected function in this auditory system, a mechanism that occurs not for detection but to serve a further purpose in the life history of mosquitoes. The nonlinear dynamics unfold in the time domain, revealing a further aspect of active auditory mechanisms. It is tempting to surmise that such time-domain analysis could uncover unsuspected functionality in sensory systems other than auditory.

Materials and Methods

Animals.

The Tanzanian mosquitoes T. brevipalpis were obtained as eggs from the London School of Tropical Hygiene and Medicine. The carnivorous larvae were fed liver powder and A. aegypti larvae during all stages until emergence. Adults were fed 5% sugar water. Animals were kept at 25–27°C and 70% relative humidity. Experiments were performed at room temperature within the range 22–25°C. Females were used to measure their sound emission in free flight and tethered flight (n = 10), while males were used for mechanical measurements on their antennae (n = 12).

Female Sound Emission.

Females were tethered to wood splints by the pronotum by using low-melting point dental wax. Care was taken to use a minimal amount of wax to avoid mechanical restriction of the thoracic box responsible for wing movements. Females were then held in a position consistent with flight behavior. Sound particle velocity behind the female in the horizontal plane was measured at various distances by using a particle velocity microphone (NR-3158; Knowles, Itasca, IL), powered at 9-V bias voltage by using a custom-made amplifier (21). The microphone signal was linear across all sound levels. The smallest distance between the mosquito and the microphone (distance zero) was defined as the point where the microphone and the female abdomen were touching. This distance, however, does not represent the actual distance from the microphone to the acoustic center of the sound source, as wings are located ≈0.5 cm away from the abdomen. To take this uncertainty into account, sounds were fitted to the function A(r + b)⁻³, with a constant b to allow for an offset in microphone position r. Each animal thus had separate fitted values for the parameters A and b; the average value of A used as the constant for the ideal female flyby.

Modeling Female Flight Sounds.

Idealized sound profiles of a female passing a male were constructed under the following assumptions: (i) the female wingbeat as a source of sound is a dipole (18) and has both constant radiation amplitude and frequency, and (ii) females pass males at a constant relative velocity. Sound particle velocity, v_p, at the receiver depends on relative distance r by

The constants A and ω (angular frequency of sound emitted) were determined directly from tethered females. In a flyby, when the female passes the male with a relative velocity v and a closest approach L (Fig. 2), Eq. 1 becomes

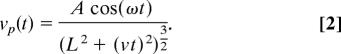As the velocity v between male and female is relative, the model is general and not specific to any behavioral flight dynamic. In practice, the source dipole approximation breaks down when very close (millimeter range) to the female. This breakdown has the effect of “softening” the divergence of the sound field, i.e., particle velocity begins to deviate from the 1/r³ law to lower powers. We can ignore this deviation, however, as the sound field is still diverging, and the modeled intensity profiles are qualitatively equivalent to a “flyby” in their characteristic shape (Fig. 2).

Sound Files.

Flyby sound was created by using the program Mathematica (v.5.1; Wolfram Research, Champaign, IL) and Eq. 2 and sampled at 10 kHz. Four sound files were used in total for four different flyby velocities. The closest approach parameter L was chosen to be 15 mm, corresponding to a maximum amplitude of ≈2.5 mm·s⁻¹ (Fig. 1). Files were played from the loudspeaker output of a laptop computer (Tecra; Toshiba, Tokyo, Japan) using the program GoldWave v.5.14 (GoldWave Inc., St. John's, Canada). This signal was passed through an attenuator (50BR-009; JFW Industries, Essex, U.K.), amplified by using an amplifier (TA-FE570; Sony, Tokyo, Japan), and broadcast through a loudspeaker (AP100MO, diameter: 117 mm; AUDAX, Chateau du Loir, France).

Mechanical Measurements.

Males were mounted in low-melting point wax, with head and antennae protruding well above the mounting wax. The mechanical response of male antennae was measured by using a microscanning laser Doppler vibrometer (PSV 300-F, OFV-056 measurement head with close-up attachment, PSV v.7.4 software; Polytec, Waldbronn, Germany) mounted on a vibration isolation table (TMC 784-443-12R; Technical Manufacturing Corp., Peabody, MA). In brief, this technique uses the Doppler-modulated laser signal backscattered from the moving object to compare it to the reference coherent laser beam to calculate the vibration velocity of that object. For postmortem experiments, animals were killed by CO₂-induced hypoxia and/or decapitation, ensuring that experiments were performed before the onset of rigor mortis (10). Only one antenna was measured per animal; 12 males were used in total.

Data Analysis.

Data from all experiments, sampled at 10.24 kHz, were analyzed by using both Mathematica v.5.1 and LabView v.8.0 (National Instruments, Austin, TX). Analytic signals were constructed from the time series s(t) to extract the amplitudes of oscillation (and, for tethered female sounds, their frequency). The analytic signal is defined as ξ(t) = s(t) + is_H(t), where s_H(t) is the Hilbert transform of s(t), defined as

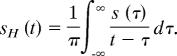The amplitude of the signal A(t) was computed from the analytical signal by A(t) = |ξ(t)|, giving an instantaneous amplitude (22). To ensure the accuracy of the transform, time series were filtered about the stimulus frequency to ensure a narrow-band signal. Instantaneous frequency of tethered female flight sounds was determined by ω(t) = dφ(t)/dt, where phase φ(t) = Arg(ξ(t)). The rms values of both A(t) and ω(t) were used for tethered flight experiments.