Discovery of principles of nature from mathematical modeling of DNA microarray data

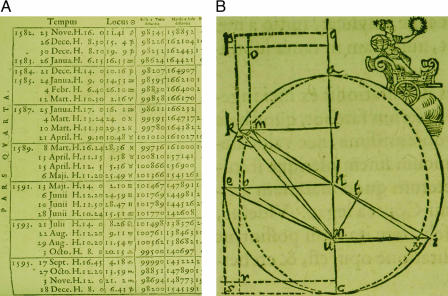
Recent advances in DNA microarray hybridization technology make it possible to record the molecular biological signals, e.g., mRNA expression levels and proteins' DNA-binding occupancy levels, that guide the progression of cellular processes on genomic scales (1, 2). Biology and medicine today may be at a point similar to where physics was after the advent of the telescope (3). The rapidly growing number of DNA microarray data sets holds the key to the discovery of previously unknown molecular biological principles, just as the astronomical tables compiled by Galileo and Brahe (Fig. 1A) enabled accurate predictions of planetary motions and, later, the discovery of universal gravitation. Just as Kepler and Newton made these predictions and discoveries by using mathematical frameworks to describe trends in astronomical data (Fig. 1B), so future predictive power, discovery, and control in biology and medicine will come from the mathematical modeling of DNA microarray data, where the mathematical variables and operations represent biological reality: The variables, patterns uncovered in the data, might correlate with activities of cellular elements, such as regulators or transcription factors, that drive the measured signals. The operations, such as data classification and reconstruction in subspaces of selected patterns, might simulate experimental observation of the correlations and possibly also causal coordination of these activities. Such models were recently created from DNA microarray data by using singular value decomposition (SVD) (4) and generalized SVD (GSVD) (5), and their ability to predict previously unknown biological as well as physical principles was demonstrated (6, 7).

Fig. 1.

Kepler' discovery of his first law of planetary motion from mathematical modeling of Brahe's astronomical data. (A) Astronomical table of positions of the sun, Earth, and Mars at different times. (B) Geometrical reconstruction of the orbit of Mars from these data reveals an ellipse with the sun located at one focus. [Images from ref. 3 (reproduced by permission of the Harry Ransom Humanities Research Center of the University of Texas, Austin, TX).]

In this issue of PNAS, Li and Klevecz (8) go from the discovery of patterns in DNA microarray data to the discovery of a chaotic genome-wide cellular oscillator that parallels the Rössler oscillator (9, 10). Li and Klevecz use DNA microarrays to monitor genome-wide mRNA expression levels in a culture of the yeast Saccharomyces cerevisiae, in which the cells were initially synchronized to follow the same transcriptional respiratory cycle and which was perturbed by the antidepressant drug phenelzine (PZ). Klevecz et al. (11) recently showed that, during the unperturbed cycle, >95% of the yeast genes exhibit mRNA expression oscillations, which correlate with an oscillation with a period of 40 min in the measured levels of dissolved oxygen (DO) in the culture. It is known that, in response to the PZ perturbation, the reductive phase of the DO oscillations, which corresponds to maximal DO and minimal oxygen utilization, doubles in duration, whereas the respiratory phase, which corresponds to minimal DO, remains unchanged (12).

Li and Klevecz use discrete Fourier transform (DFT) to show that the PZ perturbed transcriptional respiratory cycle remains characterized by genome-wide expression oscillations, further supporting the hypothesis that the interconnected cell division cycle (13, 14) is also characterized by genome-wide rather than genome-scale expression oscillations (4, 5, 11). DFT is commonly used in selections of genes that exhibit large amplitudes of expression oscillation during progressions of cellular clocks (15, 16). Here DFT is used to quantify the amplitude of the 40-min-period oscillation of each gene relative to this gene's overall expression rather than to the amplitudes of oscillation of all other genes; thus, Li and Klevecz ensure the selection of genes for which overall expression is oscillating with a 40-min period, yet their amplitudes of oscillations are small, as might be expected for, e.g., genes with regulatory roles.

Li and Klevecz (8) use SVD to discover global, decorrelated, and decoupled patterns of gene expression, i.e., “eigengenes,” in the data from the PZ perturbed transcriptional respiratory cycle. Significant eigengenes uncovered in genome-wide expression data from yeast during its cell cycle were recently shown to correlate with measured activities and genome-wide effects of known cell-cycle regulators (4). Reconstruction and classification of the data in the subspace spanned by these eigengenes was shown to simulate approximately the experimental observation of the cell-cycle progression alone, without concurrent biological processes and experimental artifacts. Now, Li and Klevecz show that three significant eigengenes correlate with the PZ perturbed DO: The second and third eigengenes correlate with the late and early reductive phases, respectively. The fourth eigengene exhibits sharp peaks of expression that coincide with the respiratory phase. Classification of the genes, based on the phase at which their expression levels peak, reveals three clusters of genes, the expression patterns of which are similar to these three eigengenes, and the gene compositions of which are similar to these of the three clusters uncovered in the data from the unperturbed cycle. For example, the late reductive cluster of genes, which corresponds to the third eigengene, is enriched with genes involved in mitochondrial function. The PZ perturbation does not seem to affect the classification of the genes significantly, but rather affects the expression pattern that each cluster follows. This finding suggests that the observed gating of DNA replication by the unperturbed transcriptional respiratory cycle might be maintained under the PZ perturbation (11).

Next, Li and Klevecz (8) use SVD to reconstruct the dynamics of the perturbed transcriptional respiratory cycle. Recent studies examined the use of SVD for reverse-engineering of genetic and biochemical networks from large-scale molecular biological data (17–20). SVD is a primary tool in the analysis of the dynamic responses of engineering systems and the design of their controls (21). SVD is also widely used in reconstruction of the phase-space descriptions of natural dynamical systems from experimental data (22). The SVD-reconstructed phase-space of mRNA expression during the cell cycle in yeast was recently shown to appoximate the “limit cycle,” which corresponds to an underlying genetic network that parallels the harmonic oscillator (4). The GSVD comparative reconstruction of the phase-space that is common to mRNA expression from yeast and human during their cell-cycle programs was shown to parallel the digital three-inverters ring oscillator (5). A synthetic genetic circuit analogous in its design to this oscillator was demonstrated recently (23). The picture of mRNA expression oscillations that emerges from the phase-space description of the perturbed transcriptional respiratory cycle, i.e., the “strange attractor,” suggests an underlying genetic network that parallels the chaotic Rössler oscillator. Li and Klevecz also show that the phase-space of the unperturbed transcriptional respiratory cycle is approximately the limit cycle, where the harmonic oscillator is a special case of the Rössler oscillator.

The interplay between mathematical modeling and experimental measurement is at the basis of the “effectiveness of mathematics” in physics.

Thanks to this discovery, the well known mathematical framework of the Rössler oscillator might be used to make predictions regarding the dynamics of the transcriptional respiratory cycle, which could then be tested experimentally. This mathematical framework could also guide the design of synthetic genetic networks (24), which might be engineered to control the transcriptional respiratory cycle or perhaps even the interconnected cell cycle.

The interplay between mathematical modeling and experimental measurement is at the basis of the “effectiveness of mathematics” in physics (25). Several recent studies illustrate how the mathematical modeling of DNA microarray data could lead beyond classification of genes and cellular samples to the discovery and ultimately also control of molecular biological mechanisms. One study found a chromosome-wide pattern of correlation between DNA binding of cohesin, a protein that holds together sister chromatids, and convergent transcription of genes, suggesting a mechanism for the relocation of cohesion during DNA replication (26). Another study discovered a genome-wide pattern of correlation between the activation of replication origins and minima or even shutdown of the transcription of adjacent genes during the cell-cycle stage G₁, by using pseudoinverse projection to map DNA-binding of replication initiation proteins onto the SVD- and GSVD-reconstructed phase-spaces of yeast cell-cycle mRNA expression (6). This pattern might be explained by a previously unknown mechanism of regulation, which is in agreement with current understanding of replication initiation (27) and is supported by recent experimental results (28). In a third study, SVD was used to uncover “asymmetric Hermite functions,” a generalization of the eigenfunctions of the quantum harmonic oscillator, in genome-wide mRNA lengths distribution data measured with DNA microarrays (7). These patterns of mRNA abundance levels across gel migration lengths might be explained by a previously undiscovered asymmetry in RNA gel electrophoresis thermal band broadening. These patterns also hint at two competing evolutionary forces that determine the lengths of mRNA gene transcripts, which act in the manner of the restoring force of the harmonic oscillator.

Such studies, together with the work of Li and Klevecz, may form the basis of a future where molecular biological systems are modeled and controlled as physical systems are today.