Pathogens, density dependence and the coexistence of tropical trees

Abstract

There is increasing interest in the role played by density-dependent mortality from natural enemies, particularly plant pathogens, in promoting the coexistence and diversity of tropical trees. Here, we review four issues in the analysis of pathogen-induced density dependence that have been overlooked or inadequately addressed. First, the methodology for detecting density dependence must be robust to potential biases. Observational studies, in particular, require a careful analysis to avoid biases generated by measurement error, and existing studies could be criticized on these grounds. Experimental studies manipulating plant density and pathogen incidence will often be preferable, or should be run in parallel. Second, the form of density dependence is not well understood and, in particular, there are no data indicating whether pathogens cause compensating or overcompensating density responses. Owing to this, we argue that the potential for pathogen-induced density dependence to generate diversity-enhancing outcomes, such as the Janzen–Connell effect, remains uncertain, as coexistence is far more probable if density dependence is overcompensating. Third, there have been few studies examining the relative importance of intra- or interspecific density dependence resulting from pathogens (or, more widely, natural enemies). This is essentially equivalent to asking to what extent pathogens are host-specific. If pathogens are generalists, then mortality rates will respond to overall plant density, irrespective of plant species identity. This will weaken the intraspecific density dependence and reduce the diversity-promoting effects of pathogens. Finally, we highlight the need for studies that integrate observations and experiments on pathogens and density dependence into the whole life cycle of trees, because as yet it is not possible to be certain of the degree to which pathogens contribute to observed dynamics.

1. Introduction

The past decade has seen several important advances in the search for explanations for the high diversity of tropical forests. These have included the development and testing of neutral theory (Bell 2000; Hubbell 2000), and the realization that plant natural enemies, particularly pathogens, may play an important role in limiting the degree to which one or a few species can competitively dominate a community (Harms et al. 2000; Wright 2002; Gilbert 2005). While neutral theory has proved contentious (e.g. Nee 2003; Purves & Pacala 2005; Volkov et al. 2005), the empirical evidence for the importance of pathogens has been growing, and recent interest in this mechanism is underpinned by a long history of field study in tropical forests (e.g. Augspurger 1984a,b, 1990; Augspurger & Kelly 1984; Dalling et al. 1998).

The basis for believing that natural enemies may be important in promoting coexistence concerns the level of mortality in relation to plant densities and distributions. The argument, originally proposed by Janzen (1970) and Connell (1971) (see also Gillett 1962), is that mortality from natural enemies will become increasingly intense at high plant densities. Broadly speaking, this will disadvantage common species relative to locally rare ones, slowing or preventing competitive exclusion.

These initial theories concerned natural enemies, such as insect seed predators and herbivores, the key element being that mortality affected seeds and seedlings. These stages of growth are important because they are the most numerous, and during these stages mortality can be very high. It now seems probable that intense mortality at the seed-to-seedling transition is frequently caused by plant pathogens, particularly Oomycota, which cause damping-off diseases in young seedlings (Augspurger 1983a,b, 1990; Dobson & Crawley 1994; Gilbert et al. 1994; Gilbert & Hubbell 1996; Packer & Clay 2000; Gilbert 2005). In the rest of this paper, we will concentrate on the effects of pathogens on coexistence through seedling mortality, although many of the points that we make are equally applicable to other natural enemies.

The diversity-promoting effect of natural enemies such as pathogens requires that their effects on mortality are density dependent, i.e. mortality must be greater at high host densities (in particular, close to parent trees) than at low host densities (in particular, far from parent trees), making it less probable that individuals of any given species reach maturity close to conspecific adults. In the context of this paper, we focus specifically on the densities of seeds and seedlings, rather than on the adult stage of the life cycle.

The recent literature on mortality in tropical trees has begun to exploit extensive forest plot datasets to quantify how widespread such density-dependent effects are (e.g. Wills et al. 1997; Harms et al. 2000), and the spatial scale over which they propagate (e.g. Peters 2003). A growing body of evidence suggests that large numbers of species are affected by density dependence in tropical forests (Gilbert et al. 1994; Wills et al. 1997; Wills & Condit 1999; Harms et al. 2000; Peters 2003), although it is unclear whether this density dependence is brought about by pathogens or other agents.

There is a large and growing literature on pathogen effects in tropical forests, and numerous studies are consistent with the hypothesis that pathogens generate density dependence in a variety of tropical forests (e.g. Augspurger 1984a,b, 1990; Augspurger & Kelly 1984; Dalling et al. 1998; reviewed by Gilbert 2005). This body of work is extremely suggestive, but by no means conclusive. For example, it has not been demonstrated that the strength of pathogen effects is sufficiently high, and that pathogens are sufficiently host-specific to allow coexistence (Gilbert 2005).

In this paper, we wish to highlight four issues that need to be addressed in such studies. First, we discuss the need for methodologically robust tests to detect density dependence in these systems and elsewhere. Second, we consider the importance of the precise nature of the relationship between density and mortality. Third, we discuss the importance of pathogen specificity and its consequences for whether density responses are species-specific, or whether density dependence acts interspecifically on the wider plant community. Finally, we highlight a limitation of existing studies: they frequently consider the impacts of interactions at a single stage of the life cycle, and do not address the issue of how density-dependent effects at one stage of the life cycle translate into long-term population and community dynamics.

(a) Detecting density dependence

In animal ecology, the search for density dependence has been extremely contentious (e.g. Hassell 1986; Hassell et al. 1989; Wolda & Dennis 1993; Shenk et al. 1998), as well as becoming increasingly technically complex (e.g. Bjornstad et al. 1999; Williams et al. 2003). In large part, the problems identified in this literature result because researchers attempt to infer whether or not density dependence is occurring using time-series data from unmanipulated populations. As a consequence, confounding factors cannot always be ruled out, and the complex nature of time-series data requires that the sophisticated statistical methods be developed (Freckleton et al. 2006).

Similarly, the literature on density-dependent pathogen effects on mortality in tropical trees has also tended to involve ‘natural experiments’, where the observed levels of mortality are correlated with the local densities or the distance from adult trees (e.g. Gilbert et al. 1994; Wills et al. 1997; Wills & Condit 1999; Harms et al. 2000; Peters 2003). Although there have been numerous demonstrations of distance and density-dependent effects, some multispecies analyses have yielded mixed evidence (e.g. Augspurger & Kelly 1984), and meta-analysis has failed to support some of the broad predictions of the theory (e.g. Hyatt et al. 2003).

One of the key methodological problems in testing for density dependence is that ecological censuses usually contain measurement error (Shenk et al. 1998; Dennis et al. 2006; Freckleton et al. 2006). This will influence the tests for density dependence in a number of ways. First, if per capita rates of population change (i.e. N_t+1/N_t, where N_t+1 and N_t are population sizes in successive censuses) are calculated using densities subject to census error, negative density dependence may be detected as an artefact. This is because the census error is present in both the density and the denominator of the population estimate of growth rate. A similar argument may be made for any vital rate which is calculated with density in the denominator, e.g. mortality rates. The potential for this kind of effect to bias tests for density dependence has been pointed out in the literature on density dependence in tropical trees, although not explicitly ascribed to census error (Wright 2002). The possibility of controlling such effects exists, particularly if the measurement error has been quantified e.g. reviewed by Freckleton et al. (2006), although tests that do not explicitly require census errors to be assessed also exist (Dennis et al. 2006).

The second problem arises when error-prone densities are compared directly. For example, one test of density dependence might be to compare densities of seeds falling from adult trees, or densities of adults, with subsequent seedling densities (e.g. Welden et al. 1991; Harms et al. 2000). A positive relationship with a slope of 1 on a log–log scale would indicate that recruitment is density-independent, whereas a slope less than 1 would indicate density dependence. However, if the density used as the independent variable in the analysis contains measurement error, then such an analysis would be invalid because the slope of a least-squares regression would be biased (e.g. Carroll et al. 2001). If density dependence were in fact weak, this bias would tend to indicate that density dependence is stronger than it actually is. This problem is well known in the fisheries literature in the context of stock–recruitment curves, and techniques have been developed to deal with the problem if the variances of the measurement errors are known (Walters & Ludwig 1981). In such analyses, it should be noted that the error may be the consequence of census errors, but may also result from censusing ‘open’ populations. For example, if one were comparing seed rain with seedling population size in order to demonstrate density dependence, if seeds disperse over a wider area than that used to census seedling populations, then an error would result. This issue is dealt with in more detail by Freckleton et al. (2006). A number of studies could be criticized on these grounds, as these two sources of measurement errors have not been explicitly recognized and controlled for appropriately.

Such problems do not arise when densities or pathogen levels have been manipulated experimentally. For example, a recent study by Bell et al. (2006) provided strong experimental support for the role of pathogens in generating density dependence in one tropical tree species. In this study, densities were manipulated experimentally (through thinning), in combination with the application of fungicides to exclude oomycete pathogens. Density dependence was very strong in unsprayed plots, but in plots subject to fungicide application there was no evidence for density dependence.

This situation highlights a tension between manipulative and non-manipulative approaches in plant population and community ecology (Emlen et al. 1989; Law et al. 1997; Freckleton & Watkinson 2001b). The advantage of studies conducted in unmanipulated communities is that they can reveal the strength of underlying processes over natural density ranges. On the other hand, the potential for biases and confounding is great. A fruitful route for future developments in this area will be the use of manipulative and experimental approaches alongside observational studies in the field.

(b) The form of density dependence

To date, studies on pathogen effects in tropical forests have considered whether or not density dependence occurs, but have not considered the form of the density response (i.e. the precise nature of the relationship relating mortality to density). Theoretical studies have shown that density responses describing competitive interactions vary depending on the precise nature of the interactions between individuals (e.g. Pacala 1986; Royama 1992; Freckleton & Watkinson 2001a), and the same will be true of pathogen-mediated interactions. For example, the mode of pathogen transmission might be one important factor (see Fenton et al. 2002 and references therein).

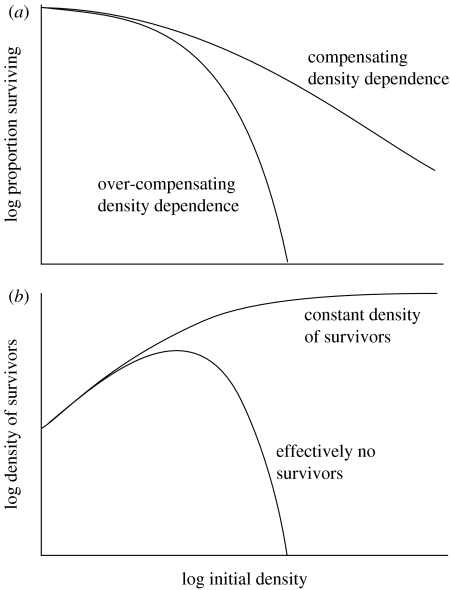
The form of density dependence is important because some density-dependent relationships are likely to have more dramatic effects on coexistence than others. Figure 1 illustrates two theoretical possibilities. The curves in figure 1a represent compensating density dependence, where mortality at high densities increases proportionately with density, and overcompensating density dependence, where mortality increases more than proportionately with density. The consequence of these responses for densities of survivors is shown in figure 1b.

Figure 1.

Theoretical density-dependent relationships. (a) Possible relationships between the proportion of individuals surviving and density. The relationships illustrated are compensating and overcompensating. (b) The relationship between the total number of survivors and density generated by the survival curves in (a).

Of the two responses, the overcompensating density response would generate a much stronger effect on coexistence than the compensating density response. This is because when density dependence is compensating, the density of survivors may be high, even if mortality is high. In contrast, when density dependence is overcompensating, the number of survivors tends towards zero at very high densities, generating competitor-free space for rarer species.

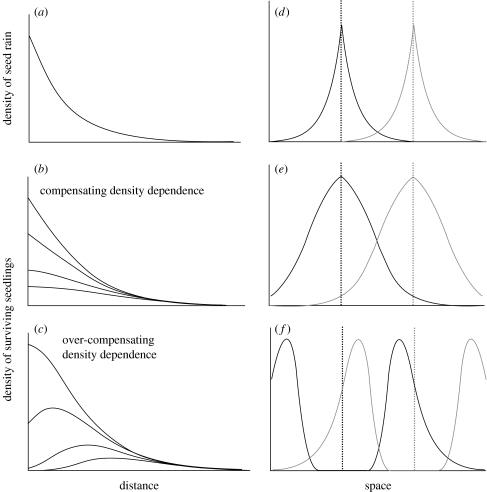
This difference is shown graphically in figure 2. Figure 2a shows a typical seed dispersal kernel, which is left-skewed, resulting in most seeds landing close to the parent plant. Figure 2b shows the resultant density of surviving seedlings following the action of compensating density dependence, with the curves showing differing intensities of density dependence (increasing density dependence results in decreased survival). The result of compensating density dependence is a progressive flattening of the recruitment curve, relative to the dispersal kernel. However, despite this flattening, the highest densities of survivors occur in the vicinity of the adult tree. In contrast, when density dependence is overcompensating, there is a peak of recruitment some distance from the parent, with the position of this peak moving further away from the adult with increasingly intense density dependence (figure 2c).

Figure 2.

(a) A hypothetical dispersal kernel, showing characteristic right skew. The line shows the density at which the seeds land at a given distance from the parent positioned at the origin. (b) The resultant density of surviving seedlings following the action of compensating density dependence. The maximum density of seedlings is always at the origin. The different lines show the effects of increasing the strength of density dependence. (c) The resultant density of seedlings following overcompensating density dependence. The maximum density of seedlings is at some distance away from the origin, depending on the strength of density dependence. (d) Dispersal in space of seeds from two individuals of different species of trees (indicated by different line shadings). (e) Assuming that the density-dependent effects of pathogens are host-specific, the resultant density of surviving seedlings through space following strong compensating density dependence is shown. (f) The resultant density of seedlings following strong overcompensating density dependence. Note that in this latter example, the highest densities of seedlings are closest to heterospecific parents, in line with the predictions of the Janzen–Connell hypothesis.

The consequences of these differing density responses for spatial patterns of recruitment are shown in figure 2d–f, assuming that the effects of pathogens are host-specific. These figures show dispersal and probability of recruitment of seeds from two hypothetical plants of different species, which are at some distance from each other. The dispersal kernels of each are leptokurtic and symmetrical (figure 2d). When density dependence is strong and compensating, the density of recruits is somewhat evened out when compared with the density of seed rain. However, the density of recruits is nevertheless highest immediately underneath the parent plant for each species. In contrast, when density dependence is overcompensating, the recruitment of seedlings is greatest at some distance from the parent, in this case near a heterospecific plant. Therefore, in this example, the diversity-enhancing effects of pathogens are clearly much greater if density dependence is overcompensating.

In his original paper, Janzen (1970) envisaged that the responses generated by the mechanism he proposed would look like those shown in figure 2c,f. Moreover, the basis for these responses was local density dependence, i.e. natural enemies aggregating and attacking as a function of seedling density. It is therefore clear that for these effects to generate the response envisaged by Janzen (1970), the underlying density response would have to be overcompensating.

In general, overcompensating density dependence is thought to be uncommon in plant populations (Rees & Crawley 1989, Freckleton & Watkinson 2002; but see Silvertown 1991; Gonzalez-Andujar & Hughes 2000). However, there are reasons to believe that in the case of pathogen-induced mortality, overcompensating responses may be more frequent. One reason is that, at high densities, pathogens may transmit more efficiently, with the consequence that all individuals become infected and die (Burdon & Chilvers 1982). However, it is also possible that compensating responses might occur, for example, if pathogens only affect the smallest or latest emerging individuals in the population in a manner analogous to asymmetric competition (sensu Weiner 1988).

As yet, there appear to be no data in the literature that permit an unequivocal test of the form of the density response resulting from pathogen-induced mortality in tropical forests. Testing the form of the relationship should be relatively straightforward through experimental density manipulations (e.g. Gibson et al. 1999), provided that a sufficiently wide range of densities is used.

(c) Intra- and interspecific density dependence

(i) Importance of pathogen specificity

Classic ecological theory, for example based on simple Lotka–Volterra models, tells us that intraspecific competition must exert a greater per capita effect than interspecific competition for a set of species to coexist (e.g. Maynard Smith 1973). In terms of pathogen-induced density dependence, this observation implies that coexistence is more probable if the mortality of a species responds more strongly to its own density than to the combined density of all species. This is equivalent to stating that species-specific pathogens will have a greater diversity-enhancing effect than generalists (e.g. Gilbert 2005).

Many of the pathogens that are likely to affect trees in tropical forests might be expected to have fairly wide host ranges. One group of pathogens that has frequently been implicated in generating density-dependent seedling mortality in tropical forests is the Oomycota, including taxa such as Pythium and Phytophthora, which are widespread pathogens of agricultural crops and forestry plantations. In agricultural systems, Pythium spp. are opportunists with wide host ranges, whereas Phytophthora spp. are said to be more host-specific (Augspurger 1990); however, data for these taxa and other oomycetes from tropical forest environments are lacking and host ranges may be extremely variable (Gilbert 2005). Molecular approaches will be required in order to identify genetically distinct pathogen taxa; however, these will have to be combined with reciprocal infectivity and pathogenicity experiments in order to assess the specificity of pathogen species and strains isolated from seedlings of individual tropical tree species.

(ii) Relative magnitude of inter- and intraspecific effects

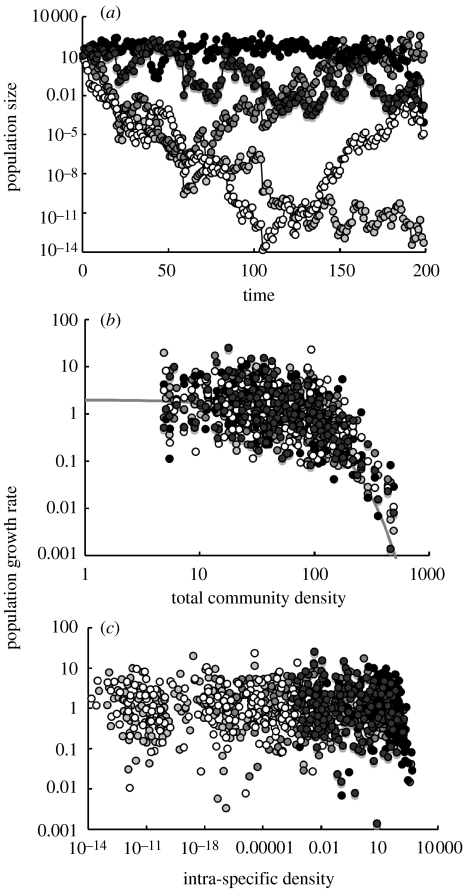
If rates of pathogen-induced mortality respond to the combined densities of all species, then intraspecific density responses might be weak or even absent. Figure 3 shows an extreme example of this, based on a simple model of five species in which the effect of density dependence is brought about through the total density of the whole community rather than through species-specific intraspecific density dependence (see figure legend for details of the model). In figure 3a, the dynamics of the system are shown. The first important point is the wide range of variation in the densities of the species, indicating the essentially weak effect of interspecific density dependence in bringing about coexistence. The relationship between population growth rate and interspecific density is relatively strong (figure 3b), but it is weak between population growth rate and intraspecific density. The weak intraspecific response results because it is generally masked by the wide variations in the interspecific densities.

Figure 3.

Example of the dynamics of a community in which density dependence acts through total community density. The five-species community was simulated using a simple model, in which the dynamics of each species was generated by a simple recurrence relationship assuming linear density dependence. Annually, densities of each species were subject to a random perturbation (lognormally distributed with geometric mean and variance of 0 and 1, respectively). (a) The dynamics of the whole community. (b) The relationship between the population growth rate of each species and the total density of the community. (c) The relationship between the population growth rate and the intraspecific density for each species.

As noted above, (§1c(i)) coexistence of species is far more probable if intraspecific density dependence is stronger than interspecific effects. In this example, the community is extremely unstable and, in reality, the stochastic fluctuations in density would lead to species becoming extinct, unless immigration to the community occurs, and diversity would eventually decline until only a fraction of the original community remained.

One potential prediction of the theories of Connell & Janzen is that species with high abundance may have greater mortality rates than the rarer ones (e.g. Connell et al. 1984). This relationship has been termed the community-level compensation trend (CCT; Webb & Peart 1999). If a CCT exists, there should be an interspecific negative correlation between mortality rates or population growth rates and abundance. In figure 3c, in which annual rate of population change is plotted against intraspecific density, this is not the case. This is despite the fact that, in figure 3b, population growth rates are a function of total interspecific density, rather than intraspecific density. On this basis, it seems unlikely that a CCT effect occurs through the action of generalist pathogens.

Indeed, the existing empirical evidence for a CCT effect appears weak (Connell et al. 1984; Welden et al. 1991; Webb & Peart 1999). Figure 3 illustrates why this may be the case in communities in which species share generalist pathogens. In the case of communities in which density dependence is brought about through specialist pathogens, the existence of such a relationship might be unlikely or difficult to demonstrate for three reasons. First, the Janzen–Connell effect results from the action of density dependence on local distributions of seeds and seedlings. Owing to leptokurtic dispersal kernels (e.g. figure 2a), local densities may frequently be very high, even if a species is globally scarce. Indeed, if dispersal is too localized, strong density dependence could conceivably restrict the spread of a species and make it rare. Second, species will vary in the values of their deterministic equilibrium density; for instance, some may have a low equilibrium, while others have a high density for reasons unrelated to the actions of natural enemies. Third, variation in seed production among species will also be important. For example, a rare species with restricted seed dispersal would be expected to have high mortality through the action of density dependence. For these reasons, we suggest that, although the notion of a CCT is initially appealing, this pattern may be too naive an expectation in real communities.

An important but neglected line of study is to determine whether pathogen-induced mortality in tropical forests is more closely related to intra- or interspecific densities, although one recent plot-based study quantifies the relative importance of con- and heterospecific neighbours on sapling growth (Uriarte et al. 2004). This study suggested that intraspecific competitive effects were stronger than interspecific ones. Similar analyses are now required for mortality and growth of small seedlings, where pathogens may mediate both intra- and interspecific density effects.

(d) Integrating pathogen effects into population dynamics

(iii) Smallest size classes

Because mortality resulting from pathogens may occur very early in the life cycle, one of the main problems in studying the effects of density dependence in tropical forests is that the dynamics of host–pathogen interactions may be very rapid. For instance, Bell et al. (2006) found that in one species more than 90% mortality of newly emerged seedlings resulted from the effects of pathogens, but this occurred within a period of just four weeks. Unless great care is taken, this mortality could be missed, and the effects of pathogens could be greatly underestimated. More significantly, many studies do not consider seedlings at all: the smallest size class considered in plot-based studies is frequently 1 cm in diameter at breast height, or larger. Plants of this size are better described as saplings rather than seedlings, and (particularly, in shade-tolerant species) may be several decades old. It is possible that ecologically important density-dependent effects have occurred by the time the plants recruit into these size classes. Therefore, censuses that use a minimum size threshold may provide an incomplete picture of the extent and importance of density dependence. Although difficult to identify and census, the fates of small seedlings may be the key to understand pathogen-mediated density dependence.

(iv) Whole life cycle studies

The highest mortality in tropical trees occurs at the seed and seedling stages (Harms et al. 2000; Connell et al. 2005). Typical densities of seeds (hundreds per square metre) exceed the densities of seedlings or saplings (tens per square metre) and adults (hundreds per hectare at most) by orders of magnitude. An important and unresolved issue is whether density dependence acting on seedlings is strong enough to determine the diversity and composition of mature trees, or whether density dependence (or other processes) acting later in the life cycle is also important, or even override density dependence acting on seedlings.

Although relevant long-term observational data are rare, as an alternative models can be used to assess the relative impacts of processes operating at different stages. Silva Matos et al. (1999) found that density-dependent effects were strong during seedling recruitment and seed–seedling transitions of a tropical palm (Euterpe edulis). In a model developed for the population dynamics of this species, this density dependence was capable of bringing about population regulation. It was not possible, however, to attribute density dependence to a specific cause, so it is not certain whether pathogens were the cause in this example. However, one important result from the modelling presented in this paper was that density dependence acting on seedlings overrode potential density-dependent effects later in the life cycle. Silva Matos et al. (1999) contrasted the results of a model in which density dependence acted only on seedlings with the one in which seed production was density dependent, and found that the results of these models were almost identical.

Studies that attempt to integrate information from the whole life cycle of tropical trees are rare, especially those including density dependence. None of the studies have explicitly included density dependence resulting from pathogens, and the consequences of such density dependence for communities are therefore uncertain.

Even if pathogen-mediated density dependence can be shown to be widespread and strong in tropical forests, an important outstanding issue concerns how pathogen-mediated density dependence might interact with other processes that are known to influence population and community dynamics. For instance, gap creation is the cue for regeneration in many species, and species-specific regeneration requirements play a role in generating tropical tree species diversity (Grubb 1977; Brokaw 1987; Denslow 1987; Brokaw & Busing 2000). Gaps occur when a canopy tree (or several neighbouring trees) dies. At that time, a variable density of seedlings, saplings and juvenile trees will be present in the sub-canopy, and it is from these cohorts that the successful colonist of the gap will be recruited. One effect of pathogen-mediated density dependence might be to ensure that the diversity of potential gap colonists is maximized (Connell et al. 2005). For pathogens to exert a marked effect on composition, a significant element of chance will be required to determine which individual eventually recruits into a gap. If the identity of the successful colonist were entirely driven by species traits and not to some extent a lottery, the diversity-promoting effects of pathogens would be negated. Similarly, if interactions between individuals are significant, either during gap colonization or prior to this, then even if pathogens generate strong density-dependent mortality during the early stages of plant growth, the consequences of this could be negated by non-random recruitment into gaps. Tropical tree species may show distinct habitat segregation indicating that recruitment and growth are not entirely random (e.g. Webb & Peart 2000). Thus, even if significant effects of pathogens are detected during the seedling and early growth stages, further data and analysis will be required to determine whether these effects actually translate into enhanced diversity of mature trees.

2. Conclusions

We have summarized several important areas in which further analysis of the community consequences of pathogen-mediated density dependence is required. Natural enemies, other than pathogens, may produce effects consistent with the Janzen–Connell hypothesis (e.g. phytophagous insects; Coley & Barone 1996, Marquis 2005), and many of the arguments we have presented are equally applicable to herbivores or seed predators. We have concentrated on pathogens owing to the growing body of circumstantial evidence that they cause major mortality in the early stages of growth in tropical forests, and yet have been the subject of relatively few manipulative studies. The aim of this review is to outline some directions in which the study of density-dependent seedling mortality in tropical forest might develop in the future. The underlying theory is well developed and indicates that density dependence may play a key role in maintaining community diversity and composition. However, as we have outlined, methodological issues need to be addressed, the form of density dependence and levels of pathogen specificity need to be documented, and the whole life cycle studies are required. Although pathogen specificity has been highlighted as a key area for future research (Gilbert 2005), the remaining issues have not been dealt with directly. It is our hope that this paper will stimulate ecologists to think further about density dependence and how it can be measured and characterized in tropical forests.