Ecological correlates of population genetic structure: a comparative approach using a vertebrate metacommunity

Abstract

Identifying ecological factors associated with population genetic differentiation is important for understanding microevolutionary processes and guiding the management of threatened populations. We identified ecological correlates of several population genetic parameters for three interacting species (two garter snakes and an anuran) that occupy a common landscape. Using multiple regression analysis, we found that species interactions were more important in explaining variation in population genetic parameters than habitat and nearest-neighbour characteristics. Effective population size was best explained by census size, while migration was associated with differences in species abundance. In contrast, genetic distance was poorly explained by the ecological correlates that we tested, but geographical distance was prominent in models for all species. We found substantially different population dynamics for the prey species relative to the two predators, characterized by larger effective sizes, lower gene flow and a state of migration-drift equilibrium. We also identified an escarpment formed by a series of block faults that serves as a barrier to dispersal for the predators. Our results suggest that successful landscape-level management should incorporate genetic and ecological data for all relevant species, because even closely associated species can exhibit very different population genetic dynamics on the same landscape.

1. Introduction

Identification of ecological and evolutionary factors that control local differentiation of populations is crucial for understanding fine-scale microevolutionary processes. This knowledge also allows more accurate prediction of the impact of conservation policy on genetic structure and evolutionary potential. Molecular genetic data typically average population structure over long time periods, while ecological studies usually sample populations over relatively shorter time-intervals. A combination of these two approaches can illuminate the processes driving genetic differentiation. Such a combined framework can then be used as a basis for sound management on landscape and ecosystem scales.

Recent analyses of population structure have incorporated landscape features in a variety of ways (e.g. Jacquemyn et al. 2004; Whiteley et al. 2004; Namroud et al. 2005; Spear et al. 2005). However, despite the growing prominence of landscape features as causal factors, most studies focus on a single species or on a group of closely related species (Hirau & Kudo 2004; Petren et al. 2005). In this study, we analyse the response of three species to a common landscape. Because these three species interact as competitors and predator-and-prey, we can explore the role of various ecological factors, including species interactions, as determinants of population genetic structure. Our results highlight the role of habitat characteristics and biological interactions, as well as landscape features, in the determination of population genetic structure.

In this study system (in Lassen County, CA, USA), the western toad (Bufo boreas), the terrestrial garter snake (Thamnophis elegans) and the common garter snake (Thamnophis sirtalis) occupy ponds, lakes and flooded meadows. Bufo boreas breeds in shallow water, and its tadpoles and metamorphs are eaten by both snake species (Kephart 1982; Kephart & Arnold 1982). The two snake species exhibit source–sink dynamics in this study system and show correlated genetic structure among the sites where they coexist (Manier & Arnold 2005). If the shared landscape played a major role in the observed pattern, one would expect an unrelated but ecologically relevant species that coexists on the landscape (e.g. B. boreas) to exhibit a similar pattern of genetic differentiation and isolation by distance.

We looked for barriers to dispersal using a clustering analysis that detected genetically similar groups of geographically proximate populations. We also used stepwise regression to identify ecological factors that influence genetic differentiation as expressed by effective population size (N_e), migration rate (m) and genetic distance for each species. Explanatory variables used in the analyses included habitat features, species abundance and nearest-neighbour characteristics.

2. Material and methods

(a) Microsatellite analysis

Genetic methods for T. elegans and T. sirtalis were reported by Manier & Arnold (2005). We evaluated variation at nine microsatellite loci for T. elegans and at seven for T. sirtalis. Analysis of 16 B. boreas microsatellite loci followed the same procedures, which are briefly outlined below. We collected a hind toe tip from 150 adult B. boreas at five sites (table 1) within an area of 1000 km² (figure 1), and stored them in Drierite, an anhydrous calcium sulphate desiccant. Simandle (2005) provided genotypic data for the Pikes Point locality. Sixteen microsatellite primer sets were obtained from Simandle et al. (2006). PCR profiles consisted of 94°C for 2 min followed by 36 cycles of 94, 55 and 72°C for 30 s each, ending with 72°C for 2 min.

Table 1.

Names, abbreviations and characteristics of study sites. (Type refers to relative depth: M, meadow; L, lake and LS, Eagle Lake shoreline. Sampling effort is the number of collector trips over 5 years. N_c is the number of individuals caught over 5 years. d and n indicate sampling during the day for snakes and at night for toads. N is the sample size for the microsatellite analysis. Asterisk denotes informal name, not official geographical place name.)

site	code	elevation (m)	perimeter (km)	type	sampling effort	B. boreas		T. elegans		T. sirtalis
Nc	N	Nc	N	Nc	N
Antelope Mountain Pond*	AMP	1920	0.52	M	15	0	—	32	30	20	19
Ashurst Lake	ASH	1950	3.5	M	9d, 4n	7	—	30	30	39	38
Blue Water	BLW	1770	0.425	L	11d, 10n	18	18	25	27	2	—
Bullard Lake	BUL	1860	3.3	M	13	0	—	67	67	35	35
Cleghorn Reservoir	CLG	1880	3.6	M	15	1	—	34	44	4	—
Colman Lake	COL	1965	2.2	L	28	0	—	49	24	35	27
Deans Meadow	DNS	1980	0.95	L	18	1	—	32	26	29	27
Feather Lake	FEA	1740	5.3	L	15	0	—	3	—	25	24
Gallatin Shoreline*	GAL	1575	2.3	LS	27	0	—	113	56	0	—
Gordon Lake	GOR	1850	3.1	M	4	0	—	2	—	43	42
Jacks Lake	JCK	1690	2	L	9	0	—	28	27	1	—
Little Cleghorn Reservoir	LTC	1880	3	M	15	0	—	40	18	8	—
Mahogany Lake	MAH	2065	1.7	L	39	0	—	167	91	94	26
McCoy Flat Reservoir	MCY	1700	18.9	M	25	0	—	20	16	3	—
Mosquito Flat	MOS	1890	1.6	M	2d, 2n	24	24	9	—	1	—
Nameless Meadow*	NML	1915	1.5	M	33	0	—	95	29	30	29
Papoose Meadows	PAP	1645	5	M	45	7	—	306	140	16	—
Pikes Point	PIK	1555	3.2	LS	53d, 4n	32	32	108	48	0	—
Pine Valley Meadow*	PVM	1730	9.1	M	9	0	—	72	70	83	83
Rocky Point	RKY	1580	4.1	LS	21	0	—	13	19	1	—
Roney Corral	RON	1825	1.2	L	28d, 8n	28	28	26	24	25	29
Camp Stanford	STF	1870	0.458	L	8d, 8n	15	15	47	45	31	32
Summit Lake	SUM	1890	2.5	M	13	0	—	27	27	27	22
Upper Gooch Valley Pond*	UGV	1920	0.2	M	7d, 8n	33	33	0	—	0	—

Figure 1.

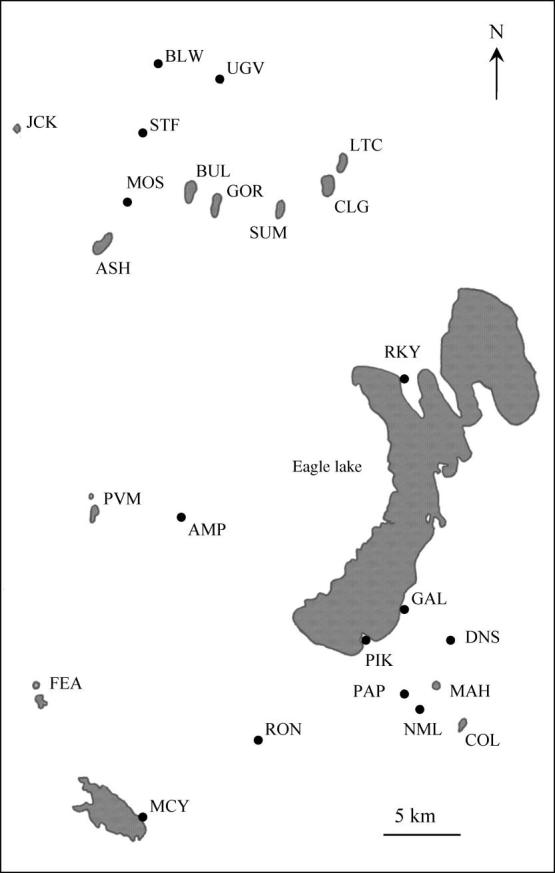
Map of the study area showing sampled sites. (For a key to the site codes, see table 1.)

All statistical analyses for B. boreas genetic data were as described by Manier & Arnold (2005). These analyses included exact tests for departure from Hardy–Weinberg equilibrium (Guo & Thompson 1992; Markov chain parameters: 5000 dememorizations, 500 000 steps per chain) calculated in Arlequin v. 2.000 (Schneider et al. 2000) and tests for linkage disequilibrium (Slatkin & Excoffier 1996; Markov chain parameters: 5000 dememorizations, 1000 batches, 5000 iterations per batch) performed in Genepop (Raymond & Rousset 1995). Significance levels were adjusted for multiple comparisons (Rice 1989). Number of alleles and observed and expected heterozygosities in each population and in all populations were calculated in Genepop (Raymond & Rousset 1995).

Overall and population pairwise estimates of F_ST were calculated using analysis of molecular variance (AMOVA; Excoffier et al. 1992) in Arlequin v. 2.000. Significance was assessed after 16 000 permutations for global estimates and 3000 permutations for pairwise estimates, with p-values adjusted with the sequential Bonferroni correction. We regressed genetic distance (F_ST/(1−F_ST); Rousset 1997) on log geographical distance to look for patterns of migration-drift equilibrium (Hutchison & Templeton 1999). A Mantel test (Mantel 1967; Mantel & Valand 1970; Manly 1997) implemented in Arlequin v. 2.000 was used to estimate the correlation between genetic distance and log geographical distance (significance over 10 000 permutations).

Estimates of effective population size and migration rate were obtained with Migrate v. 1.7.6.1 (Beerli & Felsenstein 2001). Assumptions, protocols and parameters used for the analysis are as outlined by Manier & Arnold (2005). F_ST estimates were used as starting values for the initial analysis. For all other analyses, ending parameters of the previous run were used as starting values for the next run until the results equilibrated at approximately the same values. Ten short chains with 10 000 sampled genealogies each and two long chains with 100 000 sampled genealogies each were run for each analysis. One of every 20 constructed genealogies was sampled and multiple long chains were combined for estimates. We used adaptive heating with temperature specifications of 1.0, 1.2, 1.5 and 3.0.

Effective population size was expressed as Θ=4N_eμ, where N_e is effective population size and μ is mutation rate. Assuming a mutation rate typical for vertebrates of 10⁻⁴ per locus per generation (Dallas 1992; Edwards et al. 1992; Weber & Wong 1993; Banchs et al. 1994; Ellegren 1995), N_e was obtained from Θ. Estimates of migration were expressed as 4N_em, where m is migration rate and N_e refers to the receiving population. Using N_e estimates from the previous step, m from each population into all other populations was calculated.

(b) Barriers to gene flow

For each species, spatial clustering of variation at microsatellite loci and, hence, potential barriers to dispersal were identified by partitioning genetic variation within and among populations and regions using AMOVA. The program SAMOVA v. 1.0 (spatial analysis of molecular variance; Dupanloup et al. 2002) was used to identify clusters of populations. For each species, SAMOVA used decimal degree latitude and longitude for each population (obtained using Maptech Terrain Navigator v. 3.02) to create a user-defined number of maximally differentiated groups of geographically proximate populations. For example, if three groups were defined, SAMOVA chose three spatially clustered groups of populations with the highest within-group relatedness and among-group divergence. Since SAMOVA sets the missing value threshold for rejecting a locus relatively low (5%), we tested the groups again using Arlequin v. 2.000 (rejection threshold of 50%). Thus, we used SAMOVA to generate hypotheses about population clusters and tested these hypotheses in Arlequin. For each hypothesis, we confirmed that the proposed groupings were spatially realistic and, if necessary, regrouped the sites to reflect reality. The F-statistic analogues, Φ_ST, Φ_SC and Φ_CT, were estimated for each hypothesis and their significance levels were determined with 16 000 permutations (Excoffier et al. 1992). Φ_ST represents the correlation between randomly drawn pairs of alleles within populations relative to the whole array of populations, Φ_CT is the correlation between randomly drawn pairs of alleles within a group of populations relative to the whole array of populations and Φ_SC is the correlation between randomly drawn pairs of alleles within populations relative to a group of populations (Excoffier et al. 1992).

(c) Ecological analysis

Multiple linear regression was used to identify ecological variables that best predicted population differentiation (F_ST), effective population size (N_e) and one-way migration rate (m). Independent variables (table 2) described habitat characteristics (site perimeter, site type and elevation) and census size of the focal and/or interacting species for each of 24 sites and its nearest neighbour (table 1). Log pairwise distance between sites or nearest-neighbour distance was also included to describe spatial structure. Site perimeter (km), elevation (m) and pairwise distances between sites (km) were estimated using Maptech Terrain Navigator v. 3.02. Site perimeter represented the maximum circumference of a pond or meadow or the length of Eagle Lake shoreline. This variable approximated a biologically relevant measure of habitat size, because shallow water is important to all the three species for breeding, foraging and/or thermoregulation. Snakes in this system are most often found around pond or meadow edges, and toad egg masses and larvae are likewise usually situated in shallow water. Meadow perimeter was defined as the maximum flooded waterline. Site type was characterized as meadow, lake or Eagle Lake shoreline (lakeshore) based on average depth and resulting degree of annual change in water level. Abundance represented all individuals caught in the months of June and July from 1999 to 2004, adjusted by sampling effort (number of collectors over all sampling trips). Garter snakes were caught by hand while searching at water edges and under cover objects, typically between midmorning and late afternoon. Ponds harbouring breeding toad populations were identified by the presence of tadpoles and metamorphs, and adult toads were captured by hand or net at night. Since toads were not sampled during the breeding season, these estimates probably underestimate true census sizes. However, since all populations were sampled within the same time period every year, these numbers probably accurately reflect the sizes of populations relative to one another.

Table 2.

Abbreviations and descriptions of variables used in stepwise regression analysis.

abbreviation	variable description
PERIM	site perimeter (km)
TYPE	site type (1, meadow; 2, lake; 3, lakeshore)
ELEV	elevation (m)
BUFO	census size of B. boreas
ELEG	census size of T. elegans
SIRT	census size of T. sirtalis
SNAKES	summed census size of T. elegans and T. sirtalis
NN-DIST	distance to nearest neighbour (km)
NN-PERIM	nearest-neighbour site perimeter (km)
NN-TYPE	nearest-neighbour site type (1, meadow; 2, lake; 3, lakeshore)
NN-ELEV	nearest-neighbour elevation (m)
NN-BUFO	nearest-neighbour B. boreas census size
NN-ELEG	nearest-neighbour T. elegans census size
NN-SIRT	nearest-neighbour T. sirtalis census size
NN-SNAKES	nearest-neighbour summed census size of T. elegans and T. sirtalis
PERIMDIFF	difference in perimeter between two sites (km)
TYPEDIFF	difference in type between two sites
ELEVDIFF	difference in elevation between two sites (m)
BUFODIFF	difference in B. boreas census sizes between two sites
ELEGDIFF	difference in T. elegans census sizes between two sites
SIRTDIFF	difference in T. sirtalis census sizes between two sites
SNAKEDIFF	difference in summed T. elegans and T. sirtalis census sizes between two sites
DIST	distance between sites (km)

Regression models included abundance of the focal and interacting species. Since the two garter snake species eat the same prey (Kephart 1982; Kephart & Arnold 1982), they were viewed as interacting species. Bufo boreas was not included in the snake models, because the diets of both predators can include other more abundant prey species, decreasing the ecological importance of B. boreas. For B. boreas, the interacting species variable was total garter snake abundance. Study sites whose nearest neighbour was not sampled for genetic variation were excluded from the analysis (FEA, JCK and MCY). The stepwise regression procedure selected the final model.

Of the three population genetic parameters used as response variables, m and genetic distance were expressed as pairwise matrices, while N_e had a single value per population. Regression models describing the matrix response variables consisted of pairwise population differences in each of the independent variables described previously. For example, ELEVDIFF was a matrix describing pairwise differences in elevation between sites. Since migration measures similarity between two populations (e.g. the proportion of population A that originated from population B), it was converted to a measure of dissimilarity (the proportion of population A that did not originate from population B) using the formula ρ=1−m (Sokal & Rohlf 1995). Elements of the genetic distance matrix, representing the distance between two populations, were calculated as F_ST/(1−F_ST) (Rousset 1997). Explanatory matrix variables of the F_ST/(1−F_ST) response matrix represented absolute differences between population pairs, because F_ST/(1−F_ST) is a symmetrical matrix that characterizes the overall genetic distance between two populations. For example, ELEVDIFF, in this case, was a symmetrical matrix of absolute differences in elevation between sites. In contrast, explanatory matrix variables of the ρ response matrix contained information on the directionality of the difference, because the ρ matrix was an asymmetrical full matrix of bi-directional dissimilarities. Each element of the asymmetrical variable matrices represented the value of the receiving population minus the value of the source population. In this model, ELEVDIFF was an asymmetrical matrix of differences, with negative values indicating that the receiving site was lower in elevation than the source site.

Stepwise regression of N_e was performed in SAS v. 9.2 (SAS Institute 2002). Analyses of ρ or F_ST/(1−F_ST) matrices were implemented using forward and backward selections in PERMUTE! v. 3.4 alpha 9 (Legendre et al. 1994) with a p to enter or remove of 0.1. In all cases, forward selection and backward elimination chose the same variables. Significance of the coefficients and associated R² values were determined using a permutation method for distance matrices (Legendre et al. 1994). PERMUTE! gives p-value and R² for forward-selected variables and backward-eliminated models but does not provide coefficients and standard errors for selected variables. These statistics were obtained using SAS, which identified the same models as PERMUTE!

3. Results

(a) Population genetics

One B. boreas locus deviated significantly from Hardy–Weinberg equilibrium in one population (MOS) after sequential Bonferroni correction (Rice 1989). All loci were in linkage equilibrium in all populations. Numbers of alleles ranged from 6 to 27 per locus with 4–16 per population per locus. Population averages for numbers of alleles over all loci ranged from 7 to 10 (see table 5 in the electronic supplementary material). Genetic differentiation of B. boreas populations was low but significant (F_ST=0.024; p<0.0001). Pairwise F_ST values are given in table 6 in the electronic supplementary material. We found significant isolation by distance (Mantel r=0.678; p=0.016), with a regression plot suggesting a migration-drift equilibrium (Hutchison & Templeton 1999; see figure 2 in the electronic supplementary material).

Bufo boreas N_e's were high relative to the garter snakes (Manier & Arnold 2005) with an average Θ=4N_eμ of 0.497 (see table 7 in the electronic supplementary material). This Θ yields an N_e of approximately 1240. UGV had the largest N_e (1765), followed by PIK (1560), while STF had the smallest N_e (765). Despite high N_e, m was very low. The average 4N_em between populations was 3.12 or 0.0007 migrants per generation. UGV was the largest source of migrants (0.005), implying that 0.5% of individuals in other populations originated from UGV. We found no evidence of a large source population driving migration in B. boreas as observed in both garter snakes (Manier & Arnold 2005).

(b) Barriers to dispersal

Thamnophis elegans populations clustered into at most three groups by separation of COL and DNS (p=0.010), then BLW (p=0.019) from the other populations. Thamnophis sirtalis populations formed a maximum of six groups with COL, DNS and MAH splitting off first (p=0.006), followed by COL splitting from this smaller group (p=0.019). Next ASH (p=0.007), SUM (p=0.018), and BUL and GOR (p=0.013) broke from the main cluster. Thus, population structure of both snakes was characterized by strong differentiation of a group that included COL and DNS. These two populations are separated from the others by a 300 m escarpment formed by a series of block faults. Structuring of B. boreas populations was not statistically significant but suggested a weak separation of northern (BLW, UGV, MOS and STF) and southern (PIK and RON) populations (p=0.066). The two clusters of points at smaller and larger geographical distances in figure 2 in the electronic supplementary material correspond with distances within and between the groups of populations identified by SAMOVA, respectively (table 3).

Table 3.

Results of genetic clustering analysis. (Best results for each pre-defined number of groups are shown. Only the number of groups which gave significant or almost significant Φ_CT is shown.)

number of groups	structure tested	total variance	Φ-statistic	s.e.	p-value
B. boreas
1	(BLW, MAR, MOS, PIK, RON, STF)	58.43	ΦST=0.024	<0.0001	<0.0001
2	(BLW, MAR, MOS, STF) (PIK, RON)	58.96	ΦST=0.035	<0.0001	<0.0001
			ΦSC=0.007	<0.0001	<0.0001
			ΦCT=0.028	0.0019	0.066
T. elegans
1	(ANT, ANS, ASH, BLW, BUL, CLG, COL, DNS, GAL, JCK, LTC, MAH, MCY, NML, PAP, PIK, RKY, RON, STF, SUM)	24.49	ΦST=0.024	<0.0001	<0.0001
2	(ANT, ANS, ASH, BLW, BUL, CLG, GAL,	25.52	ΦST=0.039	<0.0001	<0.0001
	JCK, LTC, MAH, MCY, NML, PAP, PIK,		ΦSC=0.022	<0.0001	<0.0001
	RKY, RON, STF, SUM) (COL, DNS)		ΦCT=0.018	0.0008	0.010
3	(ANT, ANS, ASH, BLW, BUL, CLG, GAL,	25.35	ΦST=0.033	<0.0001	<0.0001
	JCK, MAH, MCY, NML, PAP, PIK, RKY,		ΦSC=0.022	<0.0001	<0.0001
	RON, STF, SUM) (COL, DNS) (BLW)		ΦCT=0.011	0.0011	0.019
T. sirtalis
1	(ANT, ANS, ASH, BUL, COL, DNS, FEA, GOR, MAH, NML, RON, STF, SUM)	21.12	ΦST=0.035	<0.0001	<0.0001
2	(ANT, ANS, ASH, BUL, FEA, GOR, NML,	21.44	ΦST=0.054	<0.0001	<0.0001
	RON, STF, SUM) (COL, DNS, MAH)		ΦSC=0.025	<0.0001	<0.0001
			ΦCT=0.029	0.0007	0.006
3	(ANT, ANS, ASH, BUL, DNS, FEA, GOR,	21.44	ΦST=0.049	<0.0001	<0.0001
	NML, RON, STF, SUM) (DNS, MAH) (COL)		ΦSC=0.027	<0.0001	<0.0001
			ΦCT=0.023	0.0011	0.019
4	(ANT, ANS, ASH, BUL, DNS, FEA, GOR, NML,	21.40	ΦST=0.048	<0.0001	<0.0001
	RON, STF, SUM) (DNS, MAH) (COL) (ASH)		ΦSC=0.023	<0.0001	<0.0001
			ΦCT=0.026	0.0006	0.007
5	(ANT, ANS, ASH, BUL, DNS, FEA, GOR, NML,	21.30	ΦST=0.044	<0.0001	<0.0001
	RON, STF, SUM) (DNS, MAH) (COL) (ASH) (SUM)		ΦSC=0.024	<0.0001	<0.0001
			ΦCT=0.020	0.0011	0.018
6	(ANT, ANS, ASH, FEA, NML, RON, STF, SUM)	21.23	ΦST=0.041	<0.0001	<0.0001
	(DNS, MAH) (COL) (ASH) (SUM) (BUL, GOR)		ΦSC=0.020	<0.0001	<0.0001
			ΦCT=0.022	0.0009	0.013

(c) Ecological correlates

Stepwise regression results are shown in table 4. For T. elegans, variation in N_e was explained only by abundance (F_1,20=24.72, p<0.0001, R²=0.57). For T. sirtalis, N_e was explained first by abundance, then by a positive correlation with elevation and a negative correlation with nearest-neighbour elevation (F_3,20=24.78, p<0.0001, R²=0.81). In other words, T. sirtalis populations with higher N_e were characterized by higher census sizes, higher elevations and lower elevation neighbours. For B. boreas, N_e was larger when the nearest neighbour was deeper (F_2,20=31.92, p<0.0001, R²=0.78).

Table 4.

Results of stepwise regression analysis. (Effective population size (N_e), residency or 1−m (ρ) and genetic distance (F_ST/1−F_ST) for each species, showing variables as X1, X2, etc. with parameter estimates (s.e.), R² contribution and p-values for each explanatory variable.)

Y	species	X1	X2	X3	X4	X5	R2	p-value
Ne	T. elegans	ELEG					0.565	<0.0001
	62.73 (12.62)
	<0.0001; 0.565
T. sirtalis	SIRT	ELEV	NN-ELEV			0.814	<0.0001
	19.92 (2.43)	0.62 (0.17)	−0.30 (0.17)
	<0.0001; 0.671	0.002; 0.109	0.097; 0.034
B. boreas	BUFO	NN-TYPE				0.781	<0.0001
	148.22 (24.10)	394.68 (89.53)
	<0.0001; 0.543	0.0003; 0.238
ρ	T. elegans	ELEGDIFF	SIRTDIFF	DIST	ELEVDIFF	TYPEDIFF	0.342	0.001
	−2.16×10−4 (1.76×10−5)	2.04×10−5 (4.05×10−6)	2.12×10−4 (5.54×10−5)	8.31×10−7 (2.43×10−7)	2.01×10−4 (4.93×10−5)
	0.001; 0.252	0.001; 0.030	0.001; 0.026	0.001; 0.021	0.001; 0.013
T. sirtalis	SIRTDIFF					0.449	0.001
	−6.64×10−5 (5.93×10−6)
	0.001; 0.449
B. boreas	TYPEDIFF	SNAKEDIFF	ELEVDIFF	PERIMDIFF	DIST	0.659	0.001
	−3.42×10−4 (9.00×10−5)	2.46×10−5 (7.19×10−6)	−3.01×10−6 (6.40×10−7)	−2.70×10−4 (5.16×10−5)	1.22×10−4 (4.67×10−5)
	0.001; 0.207	0.003; 0.145	0.001; 0.108	0.001; 0.102	0.011; 0.097
FST/(1−FST)	T. elegans	DIST	ELEVDIFF				0.114	0.002
	6.23×10−3 (1.78×10−3)	4.74×10−5 (1.13×10−5)
	0.001; 0.058	0.002; 0.056
T. sirtalis	DIST	ELEGDIFF	PERIMDIFF			0.352	0.001
	1.28×10−3 (2.58×10−4)	−4.01×10−3 (1.30×10−3)	−6.82×10−3 (2.36×10−3)
	0.001; 0.158	0.001; 0.139	0.009; 0.055
B. boreas	DIST					0.464	0.007
	8.86×10−4 (2.39×10−4)
	0.003; 0.464

Interpretation of migration associations is facilitated by the fact that variable estimates are identical for ρ and m, but with signs reversed. For example, in T. elegans, the parameter estimate for ELEGDIFF is −2.16×10⁻⁴ when ρ is the dependent variable (table 4) and 2.16×10⁻⁴ when m is the dependent variable (data not shown). m for T. elegans was most associated with differences in abundance of T. elegans, then abundance of T. sirtalis, geographical distance, elevation and habitat type (p=0.001, R²=0.34). In short, T. elegans migrates to sites that primarily have more conspecifics, but also have fewer T. sirtalis, are nearby, lower in elevation and shallower. Thamnophis sirtalis migration occurs more to populations with higher T. sirtalis abundance (p=0.001, R²=0.46). Bufo boreas migrated towards sites that were deeper, had fewer snakes, were at higher elevation and were larger and nearby (p=0.001, R²=0.66).

Variation in genetic distance was explained primarily by geographical distance. After accounting for this variable, genetic distance between T. elegans populations increased with larger differences in elevation (p=0.002, R²=0.14). Genetic distance of T. sirtalis populations was greater with smaller differences in T. elegans abundance and more similar site perimeter sizes (p=0.001, R²=0.35), and B. boreas genetic distance was related only to geographical distance (p=0.007, R²=0.46).

Relative to their representation, habitat descriptors were more important than species abundances and nearest-neighbour characteristics. Regression models of N_e always included abundance and were explained by 1–3 variables that explained 57–81% of the variation. Interspecific interactions did not influence N_e for any species. Overall, m was determined by 1–5 variables of habitat features, abundance and interspecific interactions. In particular, migration occurred from sites with higher densities to sites with lower densities of both the focal and interacting species, and the selected models explained 34–66% of the variation. Genetic distance was explained by 1–3 variables, which accounted for 14–46% of the variation.

4. Discussion

(a) Ecological genetics

Multiple regression analysis identified habitat variables, biotic features and nearest-neighbour distances as elements that were statistically important in explaining population genetic parameters for the three study species. Models for T. elegans explained much less of the variation in population genetic parameters than for the other species (table 4), suggesting that factors other than those examined here are more important for genetic differentiation in that species. One possible explanation is that selection plays a major role in driving divergence of T. elegans populations. In separate work, we show that phenotypic differentiation between lakeshore and meadow populations is a key aspect of adaptation in this study system but is not reflected in microsatellite loci (M. K. Manier, C. M. Seyler and S. J. Arnold, unpublished data; see also Bronikowski & Arnold 1999).

Physical barriers to dispersal play an important role in this study system. Spatial clustering of both snake species identified a genetically distinct group of populations that included COL and DNS. A series of block faults have created a 300 m escarpment that separates these sites from NML and PAP to the west. This landscape feature appears to be a significant barrier to dispersal for both snake species, driving landscape-level patterns of migration-drift disequilibrium and similarity in genetic structure (Manier & Arnold 2005). Removing COL and DNS from the analysis restored migration-drift equilibrium (data not shown) and reduced the correlation in pairwise F_ST between the two species (p=0.06). Clustering of B. boreas populations, though not statistically significant, differs from that of its predators in suggesting a north–south division.

Multiple regression analysis identified different ecological correlates, as well as some commonalities, for each species. Population census size best predicted N_e for all three species, suggesting an N_e–N_c association. Migration rates were generally explained by species abundance as well as by census size for the garter snakes and predator abundance for the toad. The trend for both snakes to migrate to sites with higher snake abundance may reflect convergence on a common resource. Nevertheless, this result is unexpected, given a historical signal of source–sink dynamics in both snake species (Manier & Arnold 2005). This discrepancy may reflect inaccuracies in the abundance estimates or, most probably, it may simply result from trying to account for historical population divergence using contemporary measurements of ecological factors. Escape from predation may cause B. boreas to emigrate from sites with more snakes. Genetic distance for all the species was most explained by geographical distance, though R² values were relatively low. These results reflect the growing realization that F_ST alone may lack important information that is present in independent estimates N_e and m. For example, biological associations (both intra- and interspecific) seem to play a larger role than environmental variables in explaining the variation in N_e and m. This pattern is not found in F_ST.

The amount of variation that can be explained in studies of ecological and evolutionary processes is an issue of current debate (Møller & Jennions 2002; Peek et al. 2003). The R² values obtained in this study are consistent with the findings of Peek et al. (2003), who argue that the proportion of explained variance can be relatively high, up to 50%. The regression models from this study explained between 11 and 81% of the variance in population genetic parameters, with an average of 50%. Although higher R² values can result from the inclusion of more explanatory variables, we observed no relationship between the number of variables selected by the stepwise regression procedure and the total amount of variation explained (r=0.128, p=0.743).

(b) Bufo boreas population genetics

We found low but significant genetic structuring of B. boreas populations, with an F_ST of 0.024, comparable to those previously reported for T. elegans (0.024) and T. sirtalis (0.035; Manier & Arnold 2005). However, populations of B. boreas had effective sizes that were substantially larger than those for the garter snakes (average N_e=1240 for B. boreas, 375 for T. elegans and 325 for T. sirtalis), while bi-directional migration rates were much lower (average m=0.0007 for B. boreas, 0.0012 for T. elegans and 0.0017 for T. sirtalis). Thus, comparable F_ST values among all species masked differences in N_e and m.

Genetic structuring observed for B. boreas is consistent with the common observation of philopatry in anurans (e.g. Berven & Grudzien 1990) and low juvenile dispersal, despite a high capacity for vagility in juveniles and adults (e.g. Goater et al. 1993; Sinsch 1997). These life-history observations, along with our results, support a general observation of population differentiation over short geographical distances in anurans (e.g. Rowe et al. 2000; Brede & Beebee 2004).

Several lines of evidence point to a more stable population structure for B. boreas than for the garter snakes. Bufo boreas had a higher expected heterozygosity (average H_e=0.77) than T. elegans (0.54) and T. sirtalis (0.59), which could reflect larger stochastic fluctuations in garter snake population size or more extreme extinction–recolonization dynamics (Newman & Squire 2001). Higher B. boreas effective sizes and lower migration rates indicate that populations are relatively closed, with very little gene flow. Previous research revealed source–sink metapopulation dynamics in our garter snake populations (Manier & Arnold 2005). Other studies have found stable genetic structure in anurans (Hoffman et al. 2004; Rowe & Beebee 2004). Although population sizes can fluctuate widely (Berven & Grudzien 1990), they can be very large (Crawford 2003). These results are consistent with the general observation that source–sink dynamics in anurans are rare (Berven & Grudzien 1990).

This study represents the first comparative examination of landscape genetics in a metacommunity spanning two trophic levels. Our results contribute to an understanding of how ecological processes at smaller spatio-temporal scales shape population genetic and evolutionary trajectories at larger scales and across species. Conservation management of ecosystems will benefit from these types of studies through more accurate predictions of population structure and connectivity based on both community interactions and habitat features.

Supplementary Material

Supplement 1–4

Supplement 1, study populations of B. boreas and their sample sizes, average observed heterozygosity, average expected heterozygosity and average number of alleles per locus; Supplement 2, pairwise FST values for B. boreas populations and associated P-values; Supplement 3, genetic distance (FST/(1-FST)) as a function of log geographic distance for B. boreas; Supplement 4, estimates of 4Nem and 4Neu for B. boreas.