Cervical Spine Stenosis Measures in Normal Subjects

Abstract

Objective: To compare 2 methods of determining cervical spinal stenosis (Torg ratio, space available for the cord [SAC]); determine which of the components of the Torg ratio and the SAC account for more of the variability in the measures; and present standardized SAC values for normal subjects using magnetic resonance imaging (MRI).

Design and Setting: The research design consisted of a posttest-only, comparison-group design. The independent variable was method of measurement (Torg ratio and SAC). The dependent variables were Torg ratio and SAC scores.

Subjects: Fourteen men (age = 24.4 ± 2.5 years, height = 181.0 ± 5.8 cm, weight = 90 ± 13.5 kg) participated in this study. The C3 to C7 vertebrae were examined in each subject (n = 70).

Measurements: The Torg ratio was determined by dividing the sagittal spinal-canal diameter by the corresponding sagittal vertebral-body diameter. The SAC was determined by subtracting the sagittal spinal-cord diameter from the corresponding sagittal spinal-canal diameter. The Torg ratio and SAC were measured in millimeters.

Results: The SAC ranged from 2.5 to 10.4 mm and was greatest at C7 in 71% (10 of 14) of the subjects. The SAC was least at C3 or C5 in 71% (10 of 14) of the subjects. A Pearson product moment correlation revealed a significant relationship between the Torg ratio and SAC (r = .53, P < .01). Regression analyses revealed the vertebral body (r ² = .58) accounted for more variability in the Torg ratio than the spinal canal (r ² = .48). Also, the spinal canal (r ² = .66) accounted for more variability in the SAC than the spinal cord (r ² = .23).

Conclusions: The SAC measure relies more on the spinal canal compared with the Torg ratio and, therefore, may be a more effective indicator of spinal stenosis. This is relevant clinically because neurologic injury related to stenosis is a function of the spinal canal and the spinal cord (not the vertebral body). Further research must be done, however, to validate the SAC measure.

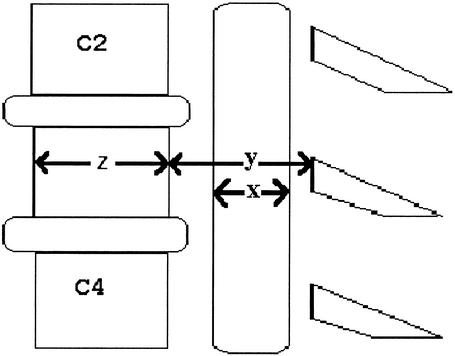
Stenosis, or narrowing, of the spinal canal has been previously associated with neurologic injury.^1–6 The spinal canal-to-vertebral body, or Torg, ratio is one method used to determine the presence of spinal stenosis in athletes.⁷ The Torg ratio is determined by dividing the sagittal diameter of the spinal canal by the sagittal diameter of the vertebral body.⁷ The sagittal spinal-canal diameter is measured from the middle of the posterior vertebral body to the laminar line (Figure). The sagittal vertebral-body diameter is measured at its midpoint. A ratio of less than .80⁷ or .70⁸ indicates significant spinal stenosis and an increased risk for neurologic injury.¹

Fig. 1.

Sagital-diameter spinal-cord, spinal-canal, and vertebral-body diameter measurments. x = sagittal spinal-cord diameter, y = sagittal spinal-canal diameter, z = sagittal vertebral-body diameter.

The Torg ratio is a more accurate indicator of spinal stenosis when radiographs are used compared with previous methods (eg, spinal-canal diameter).^7,8 This is because the ratio avoids measurement differences caused by different target distances, object-to-film distance, and magnification errors common with radiographs;^7,8 the spinal canal is compared with the vertebral body at the same spinal level. However, use of the vertebral body has been indicated as a possible reason for the ratio's poor positive predictive value in athletes.⁹ Therefore, because athletes tend to have larger vertebral bodies than nonathletes, they also have smaller Torg ratios and, thus, are overdiagnosed with stenosis. A stenosis measure that uses magnetic resonance imaging (MRI) would be of benefit because MRI avoids the magnification errors common with radiographs.

The space available for the cord (SAC) measurement has been performed previously using MRI.^1,9,10 The SAC is determined by subtracting the sagittal diameter of the spinal cord from the sagittal diameter of the spinal canal (Figure). Because stenosis is the spinal canal's encroachment on the spinal cord and spinal-cord size varies among individuals,^11,12 we believe this measurement technique may be best for identifying stenosis. To date, no study has compared the SAC measurement for determining stenosis with the Torg ratio. The first purpose of our study was to examine the relationship between the Torg ratio and the SAC in normal subjects and to determine which components of the Torg ratio and the SAC account for more of the variability in the measures. The second purpose was to present standardized SAC values for an asymptomatic sample.

MATERIALS AND METHODS

Research Design

The research design consisted of a posttest–only, comparison-group design. The independent variable was method of measurement (Torg ratio and SAC). The dependent variables were Torg ratio and SAC scores. The Torg ratio and SAC were measured in millimeters.

Subjects

Data from 14 male subjects (age = 24.4 ± 2.5 years, height = 181.0 ± 5.8 cm, weight = 90 ± 13.5 kg) were analyzed in this study. (Data on 12 of these subjects are also reported in Tierney RT, Mattacola CG, Sitler MR, Maldjian C. Head position and football equipment influence cervical spinal-cord space during immobilization. J Athl Train. 2002;37:185–189.) Potential subjects were recruited from a university by word of mouth. Subjects who reported a history of cervical spine injury or disease or a condition for which MRI was contraindicated (eg, claustrophobia, size restrictions in the MRI bore, ferromagnetic implantation) were excluded from the study. An institutional review board approved the study. All subjects signed a written informed consent before participating. Subjects also completed an injury and health history questionnaire.

Instrumentation

A polycarbonate board (182.88 cm × 39.37 cm × 1.27 cm) was custom manufactured (Rohm & Haas, Bristol, PA) for use in the MRI scanner. It simulated a wooden spine board but contained no metal supports that would otherwise create “noise” in the MRI scanner. A 1.5-Tesla superconducting MRI scanner (Signa, software 4.7, General Electric Medical Systems, Milwaukee, WI) with body coil was used to collect the data. MRI consisted of a volume 3-dimensional, T2-weighted, fast spin-echo pulse sequence (TR = 3000 ms; TE = 105 ms; FOV = 32 cm; 1.3-mm slice thickness; 10 slabs and 6 slices per slab; 256 × 256 matrix; 2 NEX; 62.5-kHz bandwidth; image time = 9 minutes, 50 seconds). This pulse sequence was selected because the 3-dimensional, fast spin-echo pulse sequence provides a higher resolution and signal-to-noise ratio than conventional 2-dimensional, fast spin-echo imaging and has been successfully used in the clinical setting for the assessment of spinal stenosis and degenerative disc disease.^13,14 All imaging was performed and evaluated by the same member of the research team (C.M.), a diagnostic radiologist. Torg ratio measurements were assessed no less than 3 weeks after SAC measurements.

Data Collection

Subjects reported to a university hospital radiology department for the MRI. Subjects were positioned supine on a spine board with no occipital padding for the MRI. Head position was standardized such that the lateral canthus of the eye and the top of the ear formed a line perpendicular to the horizontal. The MRI scans were evaluated midsagittally at each spinal level (C3 to C7). Sagittal-diameter vertebral-body, spinal-canal, and spinal-cord measurements were traced manually and assessed using the General Electric software that accompanies the Signa Scanner. The sagittal vertebral-body diameter was measured at the midpoint between the superior and inferior endplates (Figure). The sagittal spinal-canal diameter was measured as the shortest distance from the midpoint between the vertebral body's superior and inferior endplates to the spinolaminar line. The sagittal spinal-cord diameter was measured at the midline of the vertebral body at the appropriate level. The average of 3 measurements was reported. Intratester reliability was an intraclass correlation coefficient (ICC) (3, k) of .81 (from 3 spinal-canal measurements, standard error of the mean = .56). The SAC was determined by subtracting the sagittal-cord diameter from the corresponding sagittal-canal diameter.

Statistical Analyses

A Pearson product moment correlation was calculated to determine if a significant relationship existed among the selected variables. Regression analyses were performed with the Torg ratio and SAC scores as the criterion variables. The Statistical Package for the Social Sciences (version 7.5, SPSS Inc, Chicago, IL) was used for all statistical analyses. All statistical analyses were conducted in the null form, and the alpha level of 0.05 was determined a priori as statistically significant.

RESULTS

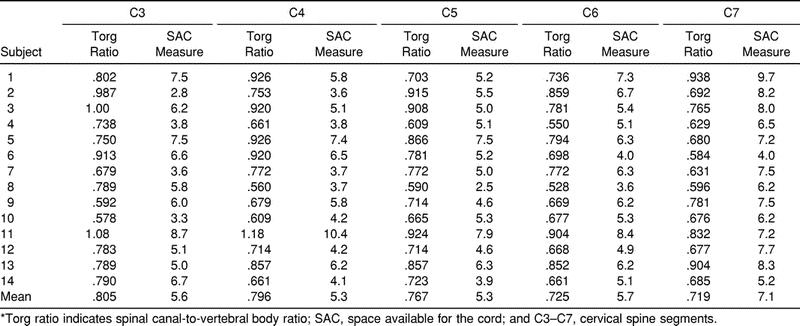
Average SAC and Torg ratio scores are reported by spinal level (C3 to C7) for each subject. SAC data ranged from 2.5 to 10.4 mm and was greatest at C7 in 71% (10 of 14) of the subjects (Table 1). The SAC was least at C3 or C5 in 71% (10 of 14) of the subjects. A Torg ratio less than .80 existed in at least one vertebral level in 93% (13 of 14) of subjects. Also, a Torg ratio less than .80 existed in 69% (48 of 70) of the total vertebral levels. There was a significant relationship (P < .01) between the Torg ratio and the SAC (r = .53). Regression analyses revealed that the vertebral body (r ² = .58) accounted for more variability in the Torg ratio values then the spinal canal (r ² = .48). Also, the spinal canal (r ² = .66) accounted for more variability in the SAC values than the spinal cord (r ² = .23).

Table 1. Torg Ratios and SAC Values for C3 to C7*

DISCUSSION

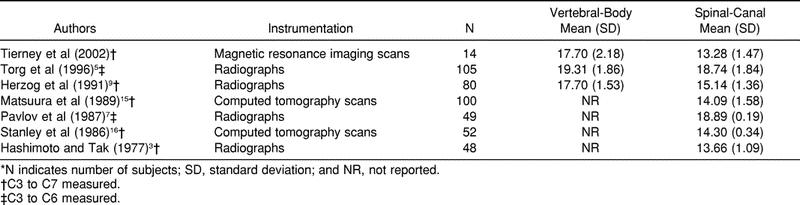
In reviewing the literature, we found that our sagittal vertebral-body and spinal-canal diameters were, on average, 1 to 2 mm smaller than measurements reported in several studies (Table 2).^9,15,16 In some cases,^5,7 the difference is as much as 5 mm. These differences can be attributed to the fact that we used MRI in determining measurements, and previous authors used radiographs or computed tomography scans. Compared with radiography, MRI avoids magnification error, allowing for the direct measure of the spinal cord. The differences cannot be attributed to differences in subject population, as all data extracted from previous studies were on normal male subjects. Our canal values were most closely related to those of Hashimoto and Tak,³ who compared their radiographic measurements with measurements made in dried specimens.

Table 2. Average Sagittal Vertebral-Body and Spinal-Canal Sizes*

We found a significant relationship (r = .53) between the Torg ratio and the SAC. A stronger relationship (for example, r = ≥80) was expected because the spinal canal is a component of both measures. However, the spinal canal accounted for more of the variability in SAC values (r ² = .66) than in Torg ratios (r ² = .44). In contrast, the vertebral body accounted for the most variability (r ² = .58) in the Torg ratios.

The vertebral body is used in the Torg ratio as a way of controlling for magnification errors. Previous authors have noted problems using the vertebral body in an athletic population.^5,9 Herzog et al⁹ explained that the Torg ratio relies on both the spinal-canal size and vertebral-body size. Their athletes had significantly larger vertebral bodies than did normal subjects in a previous study; the authors noted that the significantly larger vertebral bodies of the athletes could result in low Torg ratios.⁹ Even though we analyzed normal subjects, 93% of our subjects exhibited a Torg ratio below .80 at a minimum of one spinal level. These data and our finding that the Torg ratio relied more on vertebral body than on the spinal canal supports the hypothesis presented by Herzog et al.⁹

Our SAC measurement relied most heavily on the spinal canal and the spinal cord. These components are directly involved in neurologic injury occurring at the cervical spine and related to stenosis. Previous research analyzing a similar SAC measure revealed that risk of recurrence of a cervical-cord neurapraxia episode increased with less SAC.¹ Also, Herzog et al⁹ recommended that the “functional reserve” (SAC) be analyzed if symptomatic athletes had a Torg ratio less than .80 or a sagittal spinal-canal diameter value less than 12.5 mm. Unfortunately, an SAC value indicative of stenosis was never determined in the previous studies.

In the aforementioned studies assessing the SAC,^5,9 head position was not standardized. Torg et al⁵ did not indicate a standard head position during the MRI, and Herzog et al⁹ examined subjects with the neck in the neutral position. In the literature, the neutral position has been reported differently. Curran et al,¹⁷ in a study of children, defined cervical spine neutral as a Cobb angle of 0°. A Cobb angle of 0° would be equivalent to a position of 30° of flexion from the anatomical position and result in a straight alignment of the cervical vertebrae.¹⁸ Palumbo et al¹⁹ defined cervical spine neutral as the position of the cervical spine when one is immobilized on a spine board. The authors assumed this position to be neutral “because this is the standard position of immobilization for patients with a suspected cervical spine injury.”¹⁹ Schriger et al²⁰ and Nypaver and Treloar²¹ defined cervical spine neutral as the normal anatomical position of the head and torso that one assumes when standing and looking straight ahead at a distant object placed at eye level (12° of cervical spine extension).^20,21 Our subjects' head positions were standardized because head position affects spinal-cord size^22,23 and spinal-cord size varies among individuals.^11,12 Using this head-positioning method is important to ensure standard, reliable SAC measurements.

One limitation of our study included a small number of normal subjects. We analyzed 70 normal spinal levels in 14 subjects, so we acknowledge that it is difficult to generalize to an athletic or injured population. However, we believe that our regression findings are a naturally occurring phenomenon applicable to all populations. Although this must be verified, we believe our SAC measurement could be a better indicator of spinal-canal stenosis then the Torg ratio and should be used in an athletic population.

Another limitation of this study is its clinical relevance because radiographs may be more routinely included as a screening mechanism than MRI. We were not concerned with this because a preparticipation radiograph is rarely performed as a screening tool. Examinations are normally performed after an athlete makes a complaint. In this instance, use of an MRI scan to calculate our SAC value would be a viable option, rather than a radiograph and an MRI scan as previously recommended.⁹ If the MRI was performed and a precise stenosis indicator (such as the SAC) was determined, then future athletes could be better counseled on the possible risks of returning to play.

Future research should examine the SAC measure as an indicator of spinal stenosis. Prospective research on athletes can pinpoint a critical SAC value below which there is significant stenosis and an increased risk of neurologic injury. Also, if a true indicator of stenosis is determined, then prevention research could begin using athletes with and without stenosis. This research should focus on why some athletes develop stenosis and others do not.