Sympatric speciation as a consequence of male pregnancy in seahorses

Abstract

The phenomenon of male pregnancy in the family Syngnathidae (seahorses, pipefishes, and sea dragons) undeniably has sculpted the course of behavioral evolution in these fishes. Here we explore another potentially important but previously unrecognized consequence of male pregnancy: a predisposition for sympatric speciation. We present microsatellite data on genetic parentage that show that seahorses mate size-assortatively in nature. We then develop a quantitative genetic model based on these empirical findings to demonstrate that sympatric speciation indeed can occur under this mating regime in response to weak disruptive selection on body size. We also evaluate phylogenetic evidence bearing on sympatric speciation by asking whether tiny seahorse species are sister taxa to large sympatric relatives. Overall, our results indicate that sympatric speciation is a plausible mechanism for the diversification of seahorses, and that assortative mating (in this case as a result of male parental care) may warrant broader attention in the speciation process for some other taxonomic groups as well.

Since the modern synthesis of evolutionary biology, the prevailing belief has been that most speciation events occur as a consequence of geographic barriers to gene flow (1, 2). However, in recent years a growing body of theoretical studies has established that sympatric speciation is possible and may be more common than thought previously (3–8). Nevertheless, there still exists a dearth of empirical systems in which sympatric speciation seems a likely explanatory mechanism (reviewed in ref. 8). The most convincing examples of sympatric speciation involve host-race formation by species such as Rhagoletis flies (9, 10) or pea aphids (8, 11) and ecological speciation in closed environments by taxa such as sticklebacks (12) or cichlids (13). Speciation in these types of systems probably involves the simultaneous evolution of assortative mating and phenotypic divergence through disruptive selection. Recent theoretical models show that such complex scenarios are plausible under biologically realistic conditions (5, 6, 14–16).

The simplest situation favoring sympatric divergence occurs when both assortative mating and disruptive selection operate on the same phenotypic character (3, 17–19). Thus, if assortative mating appears in a population, even for reasons entirely unrelated to the speciation process, a lineage may in principle become predisposed to speciate whenever appropriate selective conditions arise. This model seems particularly feasible when mate choice involves ecologically important traits, which are likely to be the targets of selection, such as body size or habitat preference (3). This simplest scenario of sympatric speciation has not been empirically documented yet. Here we investigate the possibility that such a situation may have been important in the diversification of seahorses.

This line of research was inspired by empirical field observations suggesting that seahorses mate assortatively by body size (20). Such mating behavior is thought to have arisen as a result of male pregnancy and monogamy (20). In seahorses, the female deposits unfertilized eggs into a pouch on the ventral surface of the male, where he fertilizes them and enjoys complete confidence of paternity (21, 22). Because seahorses are monogamous (20, 22–25), individuals of both sexes must place a high premium on finding a partner with a similar reproductive capacity. Otherwise, eggs or brood pouch space will be wasted. Reproductive output is positively correlated with size for both sexes (20), and selection therefore favors size-assortative mating. Our goal was to evaluate the potential importance of assortative mating to the evolutionary legacy of this group. Specifically, our approaches were to (i) document genetically that assortative pairing by similarly sized adults underlies progeny production in a natural population, (ii) determine, using a quantitative genetic model, whether this mating preference in conjunction with modest disruptive selection is strong enough to produce phenotypic divergence in sympatry, and (iii) evaluate further the evidence for sympatric speciation in light of a molecular phylogeny for seahorses.

Materials and Methods

Field and Molecular Methods. Our study of assortative mating focused on a population of the Western Australian seahorse, Hippocampus subelongatus, in shallow marine waters 45 km south of Perth, Australia. The study area and the molecular techniques documenting genetic monogamy in this species are described in detail elsewhere (25). Briefly, the fish were monitored by scuba diving from the end of January to late March 1999. We fastened unique tags loosely around the necks of all encountered seahorses (25), and small fin clips were taken from adults. From the brood of each pregnant male, a sample of embryos (mean n = 17.6) was taken by using a capillary tube and bulb, and the male was released unharmed (25).

The father and his offspring then were genotyped by using three microsatellite loci. The sequences of two of the microsatellite primer pairs (Han03 and Han05) have been published (22). The third microsatellite locus, Han16 (forward primer, 5′-gcttagaggtcacattaagttca-3′; reverse primer, 5′-aagtttttattaaaataagtacgactg-3′), was identified by using the same procedures (22). All loci were amplified by using typical PCR conditions (22) with one fluorescently labeled primer, and fragments were sized on an ABI377 automated sequencer. Maternal alleles were deduced by subtracting the known paternal allele from each embryo's genotype, and the maternal genotypes thereby reconstructed were compared with those observed in sampled females. The microsatellite loci were highly polymorphic, with 24–42 alleles per locus (in samples of N ≅ 100 adults) and expected multilocus genotypic frequencies ranging from 2.7 × 10^–10 to 2.4 × 10^–6. Thus, we were able to match mothers to clutches with very high confidence.

Quantitative Model of Speciation. We developed a quantitative genetic model to investigate whether the observed magnitude of assortative mating in this natural population of H. subelongatus was sufficient to produce speciation in the absence of physical barriers to gene flow. For these analyses we focus on head length, because its measurement is more repeatable than total length, which can be affected by the position of the seahorse when it is measured.

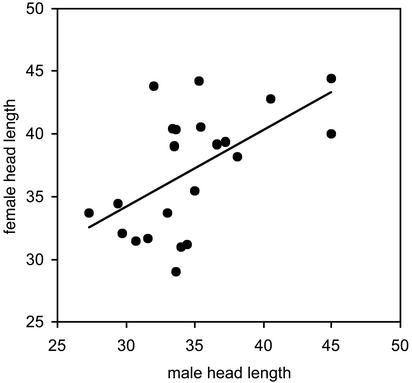
We first used a Monte Carlo approach to estimate the shape of a preference function necessary to generate the pattern of assortative mating revealed by our genetic study of parentage. We assumed that the probability of a male mating followed a Gaussian-shaped function given by exp[–y²/(2σ²)], where y is the difference in size between him and his prospective mate, and σ² specifies the steepness of the peak. We used Monte Carlo simulations to estimate σ² as well as F, defined here as the number of females a male can investigate before running out of breeding opportunities. In the simulations, males and females were randomly assigned phenotypes from a normal distribution with a variance equal to the observed head-length variation in the natural population. Each male then encountered unpaired females at random and mated with a probability specified by the mating preference function under consideration. Males that encountered F females without finding an acceptable mate remained unpaired. Twenty-two mated pairs then were drawn from the simulated population, and a linear regression of female size on male size was performed. Averaged over 10,000 runs, the values of σ² and F that minimized the cumulative percent deviation of the simulated regression (its slope, intercept, and correlation) from the empirically estimated regression (Fig. 1) were considered the best estimates. We estimated preference functions for populations of 200 (σ² = 24.0, F = 36) and 1,000 breeding adults (σ² = 26.0, F = 50). In either case, the preference functions tended to be rather wide; thus, for example, a size difference of one phenotypic standard deviation would lead to mating with a probability of ≈0.6 (or for two standard deviations, with a probability of ≈0.16).

Fig. 1.

Head lengths (in mm) of successfully mated partners (mothers and fathers of the seahorse broods). The regression is significant (n = 22, r = 0.56, P = 0.007), indicating positive size-assortative mating. Head length is reported here because its measurement is precise and repeatable. Nonetheless, head length is highly correlated with total body length (regression: n = 44, r = 0.90, P < 0.001), which also yielded similar evidence of assortative mating (regression: n = 22, r = 0.47, P = 0.03).

We then used this preference function in a multilocus quantitative genetic model of phenotypic evolution. Our model was essentially identical to a model used to investigate several aspects of quantitative genetics theory (26–28), with the addition of assortative mating and disruptive selection. The model involved direct simulation of each locus and every individual in a diploid, sexually reproducing population. The life cycle consisted of (i) production of offspring, including mutation, (ii) viability selection according to either Gaussian stabilizing selection (27) or disruptive selection, (iii) random selection of breeding adults from the survivors of selection, and (iv) monogamous pairing. We assumed that size was determined by 50 unlinked, additive loci, and allelic effects were drawn from a Gaussian distribution according to the continuum-of-alleles model (29). We determined the phenotype of each individual by summing additive effects across all loci and then adding environmental variation from a normal distribution with a mean of 0 and variance 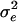. Initial parameters were chosen to yield a heritability for size close to 0.5 (with a phenotypic variance close to the observed value of 22.6) at mutation-selection-drift equilibrium under weak stabilizing selection (ω² = 100). We ran the simulations under two basic parameter sets corresponding to small (n = 200) and large (n = 1,000) populations. For both populations, the sex ratio was unity, 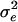was 11.3, the mutation rate was 0.001 per locus, and each breeding pair produced 10 offspring. The mutational variance (α²) was 0.80 for n = 200 and 0.25 for n = 1,000. To address the influence of heritability on the results of these analyses, we repeated our analyses with a combination of parameters that yielded a heritability of ≈0.3. The basic parameters were unchanged except that we used 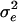and α² = 0.40 for n = 200 and 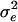and α² = 0.12 for n = 1,000. After 5,000 generations of stabilizing selection and random mating, the population was shifted to assortative mating according to the estimated mate-searching parameters and disruptive selection. We used a disruptive selection regime used by other models of sympatric speciation (6, 17), in which the top and bottom 10% of phenotypes have a fitness of 1.0, whereas intermediates have a constant fitness of <1, which varied among different runs of the simulation.

Phylogenetic Methods. We obtained 1,141 bp of cytochrome b sequence for 22 of the 32 recognized seahorse species from GenBank (accession nos. AF192638–AF192706; S. Casey, unpublished data). One sequence from each species was used for this analysis. The sister genus to Hippocampus is Syngnathus (30), thus we chose sequences from two Syngnathus species (S. floridae and S. acus) to use as outgroups (GenBank accession nos. AF356069 and AF356073, respectively). Neighbor-joining and maximum-parsimony trees were reconstructed by using PAUP* 4.0b6 (31) with similar parameters to those used in the investigation of a broader phylogeny of seahorses and pipefishes (30). We used the Hasegawa–Kishino–Yano model of substitution (30, 32). Bootstrapping was based on 100 replicates. The parsimony analysis used heuristic searches with random addition (10 replicates) and tree bisection-reconnection branch swapping.

Results

We tagged and monitored 43 seahorse males and successfully collected brood samples from 25 of them. In each case the genotypes of progeny within a brood were compatible with the genetic profile of the father and displayed at most two maternal alleles per locus, an expected pattern for this monogamous species (22–25). For 12 males, we obtained embryos from more than one pregnancy, but by genetic evidence nine of these males had remained faithful to a single female. Thus, 28 different mothers had produced the 37 broods examined. From a pool of 60 tagged and sampled females, 24 of these 28 dams were identified genetically, allowing us to designate at least one mate for 22 of the 25 fathers. For each of two focal adults (one male and one female), we identified two mates with whom the individual produced offspring during different parts of the breeding season; in subsequent analyses, we used the average phenotypes of these two mates.

The genetic results on parentage combined with the body-size measurements verified the occurrence of strong size-assortative mating in this seahorse population (Fig. 1). This result holds for our most repeatable measure, head length (Fig. 1), as well as for overall body length (regression: n = 22, r = 0.47, P = 0.03). We also confirmed that head length and body length are highly correlated (regression: n = 44; r = 0.90; P < 0.001), which justifies the use of head length in the models.

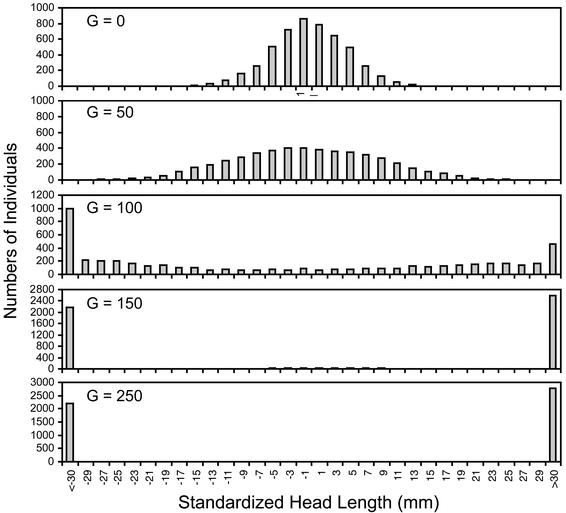
Our next question was whether the strength of assortative mating seen in this seahorse population would be sufficient to produce sympatric speciation. The results of our genetic model indicate that the tendency for seahorses to mate with similarly sized individuals, coupled with modest disruptive selection on body size, can produce sympatric speciation over quite short time scales. We deemed sympatric speciation to have occurred when the distribution of adult phenotypic values in the population had two distinct peaks with no intermediates (Fig. 2). Relatively weak disruptive selection typically led to speciation within hundreds of generations, whereas stronger disruptive selection produced sympatric speciation in tens of generations (Table 1). Not surprisingly, larger population size increased the efficiency of disruptive selection (particularly with high-fitness intermediates) and made sympatric speciation more likely (Table 1). A decrease in the heritability of size increased the time to speciation but did not dramatically affect the proportion of runs culminating in speciation under most parameter combinations (Table 1).

Fig. 2.

Phenotypic distributions of simulated seahorse populations evolving under assortative mating and disruptive selection. Head length is given as the deviation from the initial mean. (Top) Phenotypic distribution (in the progeny before selection) under stabilizing selection. The bottom four panels show the distribution of phenotypes after G generations of disruptive selection. Results are shown for a population of 1,000 adults, in which the fitness of intermediates under disruptive selection was 0.80 and heritability of size was 0.50.

Table 1. Number of generations to sympatric speciation under various strengths of disruptive selection for computer-simulated seahorse populations of two different sizes with either moderate (≈0.5) or low (≈0.3) heritability of size.

	Mean time to speciation				Proportion of runs resulting in speciation
	n = 200		n = 1,000		n = 200		n = 1,000
Fitness of intermediates	h2 = 0.34	h2 = 0.53	h2 = 0.32	h2 = 0.50	h2 = 0.34	h2 = 0.53	h2 = 0.32	h2 = 0.50
0.50	59.0	40.0	62.6	36.9	1.00	1.00	1.00	1.00
0.70	181.8	77.0	223.8	75.1	1.00	1.00	1.00	1.00
0.80	784.2	238.2	495.2	150.0	0.80	1.00	1.00	1.00
0.85	709.0	1,160.3	786.7	238.6	0.05	0.60	1.00	1.00
0.90	Never	Never	1,775.3	537.6	0	0	0.75	0.95
0.95	Never	Never	Never	Never	0	0	0	0

On the left we show the mean number of generations to speciation for those simulation runs in which speciation occurred. These results are based on 20 simulation runs for each parameter combination. An entry of “Never” indicates that speciation did not occur in any of the runs in ≤3,000 generations for a particular combination of parameters. In the columns on the right, we show the proportion of runs in which speciation did occur in ≤3,000 generations. In these simulations, individuals mated size-assortatively according to the preference function estimated from our empirical data on seahorse parentage.

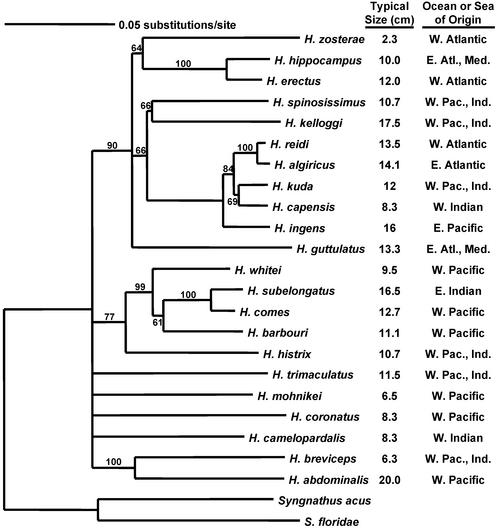
Finally, we investigated the extent to which biogeographic and phylogenetic evidence support the hypothesis that sympatric speciation may have played a role in the history of seahorses. Fig. 3 shows the neighbor-joining tree for these seahorse taxa. Regardless of the reconstruction method used, the phylogeny for seahorses based on cytochrome b sequence data were not well supported. Because our goal was to evaluate the specific hypothesis of sympatric speciation, however, the phylogeny still can serve as a valuable source of information. One important result is that the extremely small species of seahorses, of which three (Hippocampus breviceps, Hippocampus mohnikei, and Hippocampus zosterae) are represented in our data set, do not form a monophyletic group. This result is corroborated by both tree-reconstruction methods. Thus, each small seahorse must have shared a most-recent common ancestor with a larger species. The phylogeny also serves to pinpoint some possible cases of sympatric speciation. One case, involving the sister taxa H. breviceps and Hippocampus abdominalis, enjoys good support from both trees. The other putative case of sympatric speciation involves H. zosterae and Hippocampus erectus. Although the position of H. zosterae in the phylogeny is not well resolved, the phylogeny does not rule out the possibility that H. zosterae and H. erectus shared a fairly recent common ancestor.

Fig. 3.

Molecular phylogeny of seahorses based on 1,141 bp of mitochondrial DNA cytochrome b sequence. The numerals near branches indicate bootstrap values. For each species we also indicate the typical adult size for each species (midpoint of adult size range) (36) and general geographic distribution (36). Although much of this phylogeny is poorly resolved, it does pinpoint at least two candidate cases of sympatric speciation in which closely related species differ dramatically in size yet overlap in geographic range (see Discussion and Fig. 4).

Discussion

Our microsatellite-based study of mating patterns in this natural population confirms that the genetic mating system of seahorses involves the production of offspring by size-matched pairs. This result extends the previous visual observations that the seahorse Hippocampus whitei forms pair bonds size-assortatively (20). Specifically, our study shows that size-assortative pairing occurs in a second seahorse, H. subelongatus, and that such pairing results in the production of offspring. Because size-assortative mating probably arose as a consequence of selective constraints imposed by male pregnancy in a monogamous mating system (20), and all studied seahorse species have proved to be monogamous (20, 22, 23, 24, 25), size-assortative mating may be a common feature of seahorse mating systems. A broader question then becomes whether mating by size has had extended evolutionary consequences for this taxonomic group. Our evidence suggests that assortative mating indeed may have played a special role in seahorse diversification.

We used a quantitative genetic model of nonrandom mating and disruptive selection to test the hypothesis that the strength of assortative mating seen in seahorses was adequate to produce sympatric speciation over relatively short periods of evolutionary time. Our results clearly demonstrate that the observed patterns of assortative mating in H. subelongatus are sufficient to result in a bimodal phenotypic distribution without intermediates, given the appropriate regime of disruptive selection. In addition, speciation in our model usually occurs rapidly, sometimes in tens of generations. Although reasonably strong disruptive selection is necessary for sympatric speciation to occur in small populations, the required strength of disruptive selection drops substantially in larger populations.

One key unanswered question is whether disruptive selection of the appropriate magnitude has occurred in the history of some seahorse lineages. Further research will be necessary to establish to what extent disruptive selection has played a role in seahorse evolution. However, a recent review of selection intensities in nature showed that disruptive selection is as common as stabilizing selection on quantitative traits (33). This observation, coupled with the knowledge that sympatric speciation probably occurs rapidly, suggests that disruptive selection may be an important diversity-producing process in many organisms including seahorses. In addition, for organisms such as seahorses and pipefish one can readily imagine multiple adaptive peaks for body size, because species differing in size commonly occupy the same seagrass habitat (34). Disruptive selection may be particularly likely during the colonization of a new habitat or periods of environmental change. Thus, there is a reasonable probability that transient disruptive selection of sufficient strength has occurred over adequate time periods to produce sympatric speciation in syngnathid fishes that mate assortatively with respect to body size.

One other consideration with respect to our quantitative model of sympatric divergence is that many key life-history and demographic features of seahorses are not well documented. As a result, the model may make some unrealistic assumptions, which will be impossible to evaluate without more data on the natural histories of seahorses. One particular feature of the model that may cause concern is the fact that it uses a population with nonoverlapping generations, which permits each individual to mate only once. In reality seahorses mate multiple times within a season and may survive to breed in successive years. Depending on the extent to which mature adults grow during their reproductive life spans, our model may be more or less valid. However, indeterminate growth can be interpreted as environmental phenotypic variation, which is incorporated into the model as a heritability of less than one. We ran additional simulations to investigate the impact of a lower heritability (i.e., more indeterminate growth) on the propensity for phenotypes to diverge and found that sympatric speciation was still possible with lower heritabilities. For example with a heritability of size ≈0.3 in a population of 200 seahorses, a fitness of intermediates of 0.7 produced sympatric speciation in all runs in an average of 181.8 generations (Table 1). Results for other parameter combinations support this idea that speciation is still possible even with quite low heritability of the trait involved in assortative mating. Other features of the model such as the genetic architecture of size are also based on untested assumptions but probably have a smaller effect on the outcome of the model than the life-history assumptions. Nevertheless, future studies of seahorse ecology and life history, evaluated in terms of quantitative models, no doubt will provide additional insights into seahorse speciation and evolution.

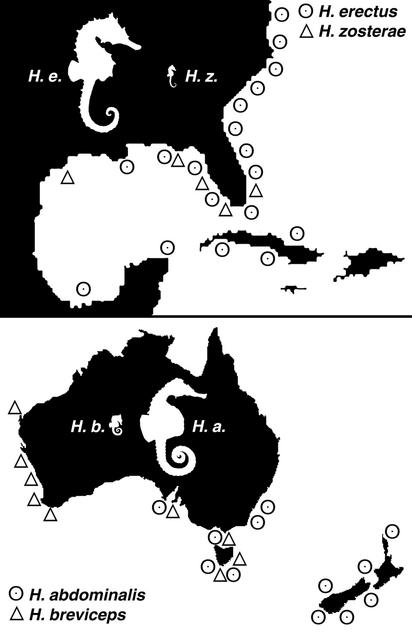
A second line of evidence consistent with sympatric speciation in some seahorse lineages comes from our phylogenetic analysis. Most-plausible candidates for sympatric speciation are species pairs that differ dramatically in size and are sympatric over all or part of their ranges (8). At least two such groupings may occur in the seahorse radiation (Fig. 4). The first example involves H. abdominalis (one of the largest seahorse species) and H. breviceps (one of the smallest), which are sister taxa sympatric in southeastern Australia. This species pair is well supported by our phylogeny (Fig. 3). The second example is less well supported but involves the very small H. zosterae, which may be a sister species to the clade comprising Hippocampus hippocampus and H. erectus (two medium-sized species), with the range of the latter entirely encompassing the range of H. zosterae.

Fig. 4.

Two pairs of seahorse species that might have diverged as a result of sympatric speciation. The maps show approximate ranges for the species, and the silhouettes (adapted from ref. 36) show relative body sizes. The two images are drawn on different scales, however, so in actuality H. abdominalis is considerably larger than H. erectus. The range of H. erectus extends from Canada to South America and fully encompasses the range of its close relative, H. zosterae. H. abdominalis is sympatric with its sister species, H. breviceps,in Southeastern Australia and Tasmania.

Additional examples of possible sympatric speciation may be identified with more research. For example, H. mohnikei is a small seahorse, the position in the phylogeny of which is almost completely unresolved. In addition, four other species of tiny seahorses (Hippocampus bargibanti, Hippocampus lichtensteinii, Hippocampus minotaur, and Hippocampus sindonis) are not represented in our data set. A better-resolved phylogeny with greater coverage of species could reveal additional examples of putative sympatric speciation. The two examples of sympatric speciation presented in Fig. 4 involve relatively old speciation events. The identification of more recent examples of possible sympatric speciation (which probably would be less striking with respect to size differences among species than the examples presented here) would provide opportunities to study this phenomenon in greater detail.

Another indirect line of evidence that assortative mating may have played a role in seahorse diversification is the sheer richness of the syngnathid radiation. The family is composed of >200 living species (35), which contrasts with closely related families such as Solenostomidae (ghost pipefish), Pegasidae (sea moths), Aulostomidae (trumpetfish), and Macrorhamphosidae (snipe-fish), none of which contain more than ≈12 recognized species (36). Assortative mating has not been studied yet in pipefishes or sea dragons, but if a similar process is at work in these taxa, then a propensity to speciate sympatrically may have increased the rate of speciation in the male-pregnant Syngnathidae relative to these other groups. Such an increase in speciation rates may also occur as a result of the effect of assortative mating on rates of allopatric speciation (37), because among-population divergence in mean size, as a consequence of selection or drift, will lead quickly to reproductive isolation under such a mating pattern. Regardless of whether most of the speciations were sympatric or allopatric, assortative mating as a consequence of male pregnancy could represent a key innovation leading to the rapid diversification of syngnathid fishes (30).

Although our results show that sympatric speciation may have occurred in the evolutionary history of seahorses, rapid speciation in sympatry is exceedingly difficult to document directly in sexual taxa even in the most favorable of natural evolutionary settings (38, 39). Hence, arguments must rely on plausibility assessments and circumstantial evidence (8). Seahorses represent one of only a few vertebrate groups in which sympatric speciation appears eminently plausible (8). We are not suggesting that all seahorse speciation has occurred in sympatry. Indeed, assortative mating increases the probability of both allopatric and sympatric speciation. Thus, most speciation in seahorses has no doubt been due to geographic isolation, but the balance of evidence suggests that particular species pairs that differ dramatically in size may have diverged as a consequence of sympatric speciation.

In summary, constraints imposed by male pregnancy may create a situation in which seahorse lineages will bifurcate quickly whenever appropriate selective conditions arise. Thus, male pregnancy represents an unusual form of parental care with extraordinary evolutionary consequences not only in terms of a reversal in the direction of sexual selection (21, 40) but also in a likely predisposition for sympatric speciation. Other taxa with male parental care or other social constraints that lead to assortative mating may provide fruitful opportunities to discover additional examples of lineages in which assortative mating has been important to the speciation process (41, 42). Future research involving seahorses and pipefish will be necessary to resolve the relative importance of sympatric versus allopatric speciation in the diversification of the speciose family Syngnathidae.