Global perception in small brains: Topological pattern recognition in honey bees

Abstract

A series of experiments with honey bees demonstrate that their small brains nevertheless possess the ability for topological perception. Bees rapidly learned to discriminate patterns that are topologically different, and they generalized the learned cue to other novel patterns. By contrast, discrimination of topologically equivalent patterns was learned much more slowly and not as well. Thus, although the global nature of topological properties makes their computation difficult, topology may be a fundamental component of the vocabulary by which visual systems represent and characterize objects.

In contemporary studies of vision, the primitives of visual perception remain a central issue of debate (1–5). In human visual perception, early pattern recognition engages later, cognitive, stages, which may make the primitives of perception more difficult to discern. Studies of pattern recognition in small creatures, such as honey bees with their relatively simple nervous systems, might reveal certain visual capacities that are shared across species, which may therefore represent elementary and general underlying functions for any visual system.

Recent work has revealed that honey bees can be trained to distinguish between patterns on the basis of general characteristics such as orientation (6–8) and symmetry (9). However, the visual form primitives for small creatures, like bees, remain an unsolved mystery. One important factor in evaluating potential primitives for perceptual representation is their relative stability (5, 10). An object in the natural environment, say a flying bird, is often subjected to shape changes due to, for example, its nonrigidity and changes of illumination. Among other form properties of an object, topological properties, such as connectivity and holes, are structurally most stable under changes; i.e., smooth deformations (in mathematical terms, one-to-one and continuous transformations) cannot create or destroy connected objects and holes, whereas they alter other form properties, such as orientation, length, parallelism, and collinearity. (Topology can be imaged as a “rubber-sheet” geometry. Under an arbitrary rubber-sheet distortion without breaking or fusion, i.e., smooth deformations, the number of holes remains constant, despite changes in shape. The number of holes is, therefore, a topological invariant.)

A hypothesis of topological perception was, therefore, put forward that topological properties constitute a formal description of fundamental perceptual organizations, such as distinguishing figure from background, parsing visual scenes into potential objects, and performing other global, Gestalt-like operations (3–5). Recent neuroimaging studies (5), together with behavioral studies (4), provide strong evidence supporting the notion that topological properties (such as the number of holes) are primitives of visual representation in humans. If topological perception is indeed a fundamental property of vision, one might expect topological properties to be extracted by all visual systems, including the relatively simple ones possessed by insects. Thus, a rudimentary visual system may not be good at discriminating patterns that are topologically equivalent, such as a disk and a solid square, but be able to discriminate patterns that are topologically different, such as a disk and a ring that contains a hole.

Methods

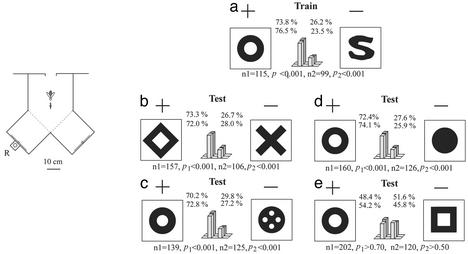
General Procedure. A Y-maze paradigm (ref. 6; shown in Fig. 1 Left) was used to train bees to distinguish between patterns. In each experiment, a fresh group of 8–10 bees was marked and trained to enter the Y-maze apparatus that presented two stimuli, one on the vertical end wall of each tunnel (Fig. 1 Left). One stimulus (termed “positive”) offered a reward of sugar water, R, which the bees could reach through a tube. The other stimulus (termed “negative”) carried no reward. The positions of the positive and negative stimuli were interchanged every 10 min (spanning approximately two rewards per bee). The reward was moved with the positive stimulus throughout the experiment to prevent the bees from developing a preference for one of the two tunnels, and to cancel the effect of any residual side preferences when learning performance was assessed. A bee's choice was determined by noting which tunnel the bee entered first when it arrived at the apparatus. Bees were first trained to discriminate training stimuli, then tested with each of the testing stimuli. The bees' performance was measured in a series of tests, in which the percentage of choices in favor of the correct stimulus was determined. The reward was present at the positive stimulus during the training as well as in the tests. In tests that examined the bees' preferences for stimuli other than the training stimuli (such as in Figs. 1 Right b–e and 3b), the duration of each testing session was restricted to 10 min (allowing two rewards per bee, on average). Control experiments, using identical stimuli and rewards in both tunnels, assured us that the bees' choices were not influenced by olfactory cues. (For further details of training and testing, see refs. 6–9).

Fig. 1.

(Left) Y-maze apparatus for training and testing bees. Scale applies to the apparatus. (Right) Stimuli and results of experiments 1 and 2. (a) Training stimulus pair. (b–f) Test stimulus pairs. Bars and numbers show relative frequencies of choices in favor of the positive (+) and negative (-) stimuli, as measured after training and in various transfer tests. Light and dark bars depict results from experiments 1 and 2, respectively. n1 and n2 are the numbers of choices analyzed in experiments 1 and 2, respectively, and p1 and p2 are the respective values associated with a χ² test for significant difference from random-choice behavior.

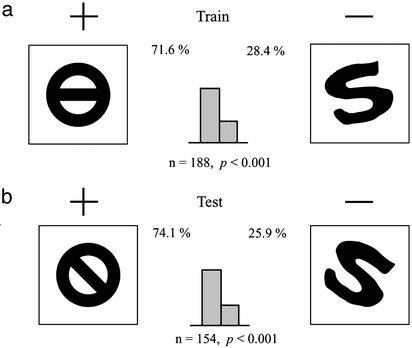
Fig. 3.

Training (a) and test stimulus (b) pairs used in experiment 4. They were rotated to control the possible role of local differences in pattern intensity on discrimination. See text for details. The choice frequencies, number of choices (n), and P value in a χ² test for significant differences from random choice are given in the figure.

A modified Y-maze apparatus was also used in the present study. The Y-maze apparatus was modified by adding a transparent baffle, with a central hole 5 cm in diameter at the entrance to each arm (11). This forced the bees to slow down and inspect the stimuli more carefully before making a decision. It also allowed the bees' choices to be monitored more precisely.

Stimuli. The outer and inner diameters of the ring (in Figs. 1 Right, 2, and 4) were 16.6 and 9 cm, respectively. In Fig. 1, the outer and inner lengths of each side of the hollow diamond were 16 and 8.8 cm, respectively, and the length and the width of one arm of the cross were 22.5 and 4.4 cm, respectively. In Fig. 1 Right c, the outer diameters of the ring and the disk with 4 holes were identical (16.6 cm); and the diameters of the large hole and each small hole were 8 and 4 cm, respectively. In Fig. 1 Right d, the outer diameter of the disk was the same as that of the ring (16.6 cm). The hollow square in Fig. 1 Right e was the same size as the hollow diamond in Fig. 1 Right b, but was rotated by 45°. The theta-shaped figure (hereafter referred to as θ) and the S-shaped figure (12) (hereafter referred to as S) in Fig. 3 were scaled to have the same area. The outer diameter of the θ was the same as that of the ring (16.6 cm); the diameter of its inner circle was 10.9 cm; and the width of its central line-segment was 2.8 cm, similar to that of the oriented central line-segment of the S. In experiments 5 and 6, the S, the ring, and the disk used are the same as those shown in Fig. 1 Right, and the size of the solid square is the same as outer size of the hollow square in Fig. 1 Right.

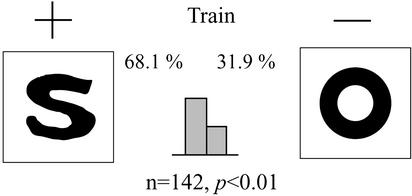
Fig. 2.

Stimulus and results of experiment 3, in which bees were trained to distinguish between an S and a ring with the S as the positive stimulus.

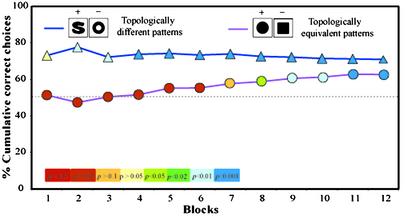
Fig. 4.

Learning curves for experiment 5 a and b. Triangles depict performance in distinguishing between two topologically different stimuli (an S and a ring, as in Fig. 2). Circles depict performance in distinguishing between two topologically equivalent stimuli (a disk and a square). The dashed line depicts the random choice level (50%). Twelve blocks were run for each pair of stimuli to attain the plateaus of the learning curves. Total choices in each block range from 28 to 43.

Results

We explored topological perception in bees by using the Y-maze paradigm. Six sets of experiments were conducted.

Experiment 1 investigated topologically based discrimination by using five pairs of stimuli, shown in Fig. 1 Right. The patterns were designed to present topological differences, and to exclude the use of nontopological cues in making the discriminations. They were: a ring and an S (Fig. 1 Right a); a hollow diamond and a cross-like figure (hereafter referred to as a cross) (Fig. 1 Right b); a ring and a disk with four holes (Fig. 1 Right c); a ring and a solid disk (3) (Fig. 1 Right d); and a ring and a hollow square (Fig. 1 Right e). The two figures in each of the first four pairs (Fig. 1 Right a–d) differ topologically in the number of holes. The ring and hollow diamond each contain a hole, whereas the S, cross, and disk do not, and the ring and four-hole disk also differ in the number of holes they contain. At the same time, these stimulus pairs were designed to control carefully for nontopological features. In Fig. 1 Right a, the ring and S were made to have equal area (and therefore luminous flux), very nearly the same spatial frequency components and perimeter length, and equal averaged edge crossings. The shape of the S was also made to be irregular to eliminate possible effects of subjective contours. In Fig. 1 Right b, the hollow diamond and the cross were oriented with their edges parallel to eliminate potential use of orientation cues, and also made to have equal area. In Fig. 1 Right c, the total area of the four smaller holes contained within the four-hole disk was made equal to the area of the larger hole contained within the ring, and their spatial-frequency spectrum and perimeter length were nearly equal. Although phenomenally they look quite different, the ring and hollow square in Fig. 1 Right e are topologically equivalent to each other, because each of them contains the same number of holes, specifically one hole in this case.

Bees were first trained to discriminate between the ring and the S, by rewarding them on the ring. Despite the fact that the ring and the S possess the same area and nearly the same spatial-frequency spectrum, this task was learned well. The choice frequency in favor of the positive stimulus is 73.8% [number of choices (n1) = 115, P < 0.001].

The trained bees were then tested with each of the stimulus pairs b–e, in turn, as shown in Fig. 1 Right. The bees were immediately able to distinguish between the patterns presented in the test pairs b, c, and d, without any training on these specific patterns. The choice frequencies in favor of the positive stimulus are 73.8% (n1 = 157, P < 0.001), 70.2% (n1 = 139, P < 0.001), and 72.4% (n1 = 160, P < 0.001), respectively. That is, bees that had been trained to distinguish between the ring and the S could immediately distinguish between a hollow diamond and a cross, a ring and a four-hole disk, and a ring and a disk. In other words, the bees behaved as although they perceived and learned the topological difference between the ring and the S and were using this as a cue to distinguish between the other patterns, which they had never previously encountered. This occurred despite the fact that the patterns in each of pairs b–d differ from those in pair a with regard to various local features. By contrast, this discrimination capacity did not transfer to the testing stimulus of Fig. 1 Right e. That is, the bees were unable to distinguish between the ring and the hollow square, which are topologically equivalent, even though they appear more different from the ring and the disk, and differ in local features such as orientation and curvature. The choice frequency in favor of the positive stimulus was 48.4% (n1 = 202, P > 0.70).

The above results were replicated in experiment 2, in which the modified Y-maze was used to force the bees to slow down and inspect the stimuli more carefully before making a decision and to allow the bees' choices to be monitored more precisely. The results are also shown in Fig. 1 Right. These findings in experiments 1 and 2 consistently suggest that the visual system of honey bees is capable of perceiving (abstracting) topological differences in the number of holes.

In the above experiments, the ring was used as the positive stimulus during training. Previous studies have suggested that bees possess innate preferences for certain naturally shaped objects, such as flowers (13). Because the ring, in some sense, is a more common and regular form (that might stimulate, for example, an on-center or off-center cell) than the S, cross, or 4-hole disk, it could be argued that at least some of the above results were simply caused by an innate or spontaneous preference for the ring, rather than an ability to discriminate topological differences between the figures per se. Even though the fact that the bees were unable to discriminate between the ring and the hollow square made this counterexplanation unlikely, we further examined this possibility in experiment 3, in which bees were still trained to distinguish between a ring and an S, but where the S was now the positive stimulus (Fig. 2). Nevertheless, the bees were able to learn this discrimination too. The choice frequency in favor of the positive stimulus of the S is 68.1% (n = 142, P < 0.01). Thus, the ability to distinguish between the ring and the S is not caused by an innate preference for one stimulus over the other.

One of the primary concerns in the study of pattern recognition in bees is the role played by local cues in distinguishing visual patterns (14, 15). Thus, it could be argued that the discrimination capacity observed in at least some of the above experiments may have arisen from differences in local, nontopological cues rather than global, topological difference. For instance, the ring could have been distinguished from the S on the basis of the fact that the ring carries a white part at the middle (e.g., stimulating an on-center cell), or the S could have been distinguished from the ring on the basis that the S carries an oriented, straight-line segment in the middle. To address these possibilities, we conducted experiment 4, in which a fresh group of bees was trained to discriminate between a θ and an S (Fig. 3). Neither of these stimuli contains a white region at the middle, but they are topologically different because the θ contains two holes whereas the S contains none. The θ and the S were made to have the same area. To prevent the possible use of local orientation cues in making the discrimination, the two stimuli were always oriented such that the central line segments of the S and the θ were parallel. Furthermore, to prevent the possible use of other local cues such as black areas, the stimuli were both rotated by 90° at regular intervals during the training period. The rotation was performed each time the positions of the positive and negative stimuli were interchanged in the Y-maze. After training, the bees were tested with the same pair of stimuli, but each stimulus was rotated by 45° relative to its orientations during training (Fig. 3b). In other words, during the tests, the stimuli were both oriented at +45° or -45°, each orientation being presented for half the duration of the test. This procedure for training and testing rendered the use of local intensity and orientation cues very unlikely. Nonetheless, the bees were clearly able to distinguish the θ from the S in the training as well as in the tests. The choice frequencies in favor of the positive stimulus of the θ, are 76.1% (n = 188, P < 0.001) in the training duration, and 74.1% (n = 154, P < 0.001) in testing duration, respectively. This finding suggests that the bees were discriminating the training stimuli on the basis of their topological difference, and transferring this discrimination capacity to stimuli of other orientations.

Measurements of learning curves collected in experiment 5a and 5b indicate that bees learn to recognize topological differences very rapidly (Fig. 4). One block represents approximately four rewards per bee, on average. Twelve blocks (≈28 rewards per block) were run for each pair of stimuli to attain the plateaus of the learning curves. In each case, the choice frequencies are accumulated from the start of the experiment, and averaged over all participating bees. In experiment 5a, when bees are trained to distinguish between the S and the ring, the plateau of the learning curve is attained very quickly. In fact, learning occurs so rapidly that it is difficult trace its development in the initial part of the curve. From block 1 onwards, the preference for the correct stimulus is already significantly different from the random-choice level. In contrast, in experiment 5b, when trained to distinguish between shapes that are topologically equivalent, a disk and a solid square, despite their apparent differences in local features (such as extended horizontals and verticals), the plateau is attained only after 11 blocks (≈44 rewards per block), and performance departs from random choice only after block 7.

The learning curves (Fig. 4) represent data pooled over several individuals and several visits of each individual, which might obscure individual learning performance and the development of the learning process at its very beginning. We further examined the speed of individual learning by tracking the choices of individual bees from the commencement of the training. In experiment 6a, a fresh group of bees was trained to distinguish between the S and the ring. For each of the bees, its sequence of choices was monitored and recorded for the first two blocks, starting immediately after the bee received the first reward. As Table 1 shows, it is clear that for the task of distinguishing the S from the ring, individual bees perform well by the end of the first training block, typically within the first one or two rewards. Table 2 shows, for comparison, data for bees trained to distinguish between the disk and the solid square in experiment 6b, which are topologically equivalent. Here, the bees are still choosing randomly between the two stimuli at the end of the second training block. Thus, the evolution of individual performance demonstrates that although a long learning process is necessary to discriminate local features, such as terminator (16) or the end of bars (the square could be considered to be a thick bar), as reported in earlier studies of discriminating ends of bars (17), the bees learned to discriminate topological differences between forms so quickly even within the first one or two rewards.

Table 1. Sequences of choices of individual bees in learning to distinguish between the S and the ring.

			Cumulative choices
Bee no.	Block/tunnel (the first reward)	Sequence of choices + or -* (block/tunnel)	+	-
04	1/R	+ (1/R), + (1/L), + (2/R), + (2/L), - (2/L), + (2/L)	5	1
01	1/R	- (1/L), + (2/R), + (2/L), + (2/L), + (3/R), + (3/R)	5	1
02	1/R	+ (1/L), + (2/R), + (2/L), + (2/L), + (3/L)	4	0
11	2/R	+ (2/L), - (2/L), + (3/R), + (3/L), - (3/L), - (4/L)	3	3
12	2/L	- (3/R), + (4/L), + (4/R), + (4/R)	3	1
05	2/L	- (3/R), + (4/L), + (6/L), + (6/L), - (7/R)	3	2
20	3/R	+ (3/R), - (3/R), + (4/L), + (4/L), + (5/R), + (5/R), + (5/R), + (6/L)	7	2
14	3/L	+ (3/R), - (4/L), + (4/L), + (4/L), + (5/R), + (5/R), + (7/R)	5	1
		Cumulative percent of correct choices: 76.1% (n = 46, P < 0.05)	35	11

^*+ and - denote correct and wrong choices, respectively.

Table 2. Sequences of choices of individual bees in learning to distinguish between the disk and solid square.

			Cumulative choices
Bee no.	Block/tunnel (the first reward)	Sequence of choices + or -* (block/tunnel)	+	-
12	1/R	+ (1/R), + (1/R), - (2/R), - (2/R), + (3/R), + (3/R), - (3/L)	4	3
20	1/R	+ (1/R), - (1/L), - (1/L), - (2/R), - (2/R), + (3/R), + (3/R)	3	4
10	1/R	- (1/L), - (1/L), + (2/L), + (2/L), + (2/R), + (2/R), - (3/L)	4	3
51	2/R	- (2/R), + (3/R), + (3/R), + (3/L), - (4/R)	3	2
06	2/L	- (2/R), - (3/L), - (4/R), - (4/R), + (5/R), + (5/R)	2	4
41	2/L	+ (3/R), + (3/R), + (4/R), + (4/L), - (4/L), + (5/R), + (5/R)	5	2
01	3/R	- (4/R), - (4/R), - (4/R), + (5/R), - (6/R), + (7/L), + (7/L), - (7/L)	3	5
11	4/L	+ (4/L), - (4/R), + (4/R), - (4/R), + (5/R), - (5/L)	3	3
		Cumulative percent of correct choices: 49.1% (n = 53, P > 0.80)	26	27

^*+ and - denote correct and wrong choices, respectively.

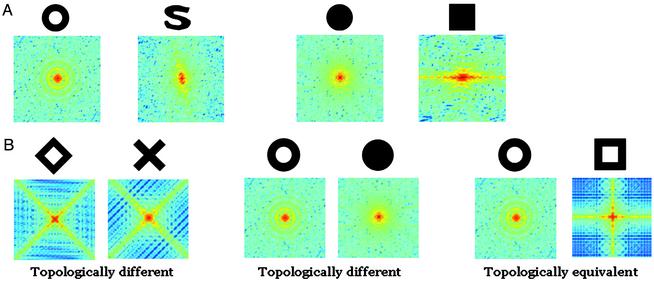
We also considered whether the behavioral results may have been determined by the spatial frequency characteristics of the stimuli, such as in experiments 5 and 6, for example. We therefore conducted spatial frequency analyses of stimulus patterns used in the present study (Fig. 5). The power spectra (2D Fourier transformation) together with the calculations of differences in power spectra (illustrated in Fig. 5A) revealed that the differences in power spectra between the ring vs. the S are much smaller than those between the disk vs. the solid square. The results of these Fourier analysis therefore demonstrated that topological distinctions, rather than variations in spatial frequency components, were much better at predicting differences in the speed of form discrimination learning.

Fig. 5.

(A) The power spectra (2D Fourier transformation) of the S vs. the ring, and of the disk vs. solid square, used in experiments 5 and 6. The differences in power spectra between the S and the ring and between the disk and the square {Sum [(X - Y)²]} are 2.10 and 19.63, respectively. (B) The power spectra of three pairs of stimulus figures used in experiment 1.

Discussion

The main conclusions from these bee experiments are that (i) bees are able to abstract the general property of topological invariance, namely, the number of holes; and (ii) bees are capable of learning topologically based discriminations very rapidly.

However, a major challenge to the study of the topological discrimination is that there seem to be, in principle, no two geometric figures that differ only in topological properties, without any differences in local features. Thus, one cannot test for the role of topological differences in form perception in complete isolation, by designing stimuli that differ only topologically, without any differences in nontopological features (12, 18). We believe that we minimized this problem and ruled out obvious explanation based on nontopological features through careful design of the stimuli and by adding additional control experiments, which are described in the sections below.

First, the stimuli, and the training and testing paradigms were carefully designed to prevent the bees from using various nontopological cues that are usually considered to be important in tasks of pattern discrimination. The pairs of stimuli were designed to exclude the use of orientation cues (e.g., Figs. 1 Right b and 3), spatial frequency components (e.g., Fig. 1 Right a–c), luminous flux (e.g., Figs. 1 Right a–c and 3), perimeter length (e.g., Fig. 1 Right a and c), and the number of edges crossed while scanning the figure (e.g., Figs. 1 Right a and b and 3). Across all of these stimulus pairs, the topological explanation is the only one that explains all of our results in a unified manner. In contrast, nontopological features, such as orientation, luminous flux, spatial frequency components, and size commonly considered in the study of vision, cannot explain all of the results in a consistent manner.

A second approach that we took to ruling out explanations based on local feature differences was to test for generalization to novel stimuli. The ability to transfer learned discriminations to novel stimuli is not readily measurable with humans, but is particularly easy to carry out with bees. Such transfer tests are particularly powerful in excluding the possible use of local cues. In experiment 1, the bees that had been trained to distinguish between the ring and the S (Fig. 1 Right a) were tested on a number of novel pairs of test stimuli: a hollow diamond vs. a cross (Fig. 1 Right b), a ring vs. a four-hole disk (Fig. 1 Right c), a ring vs. a disk (Fig. 1 Right d), and a ring and a hollow square (Fig. 1 Right e). The bees were immediately able to distinguish between the two members of novel pairs b, c, and d without being trained specifically on them. In other words, the bees behaved as though they were abstracting the topological difference between the ring and the S, and using this as a cue to distinguish between the other patterns, which they had never previously encountered. However, the bees were unable to distinguish pair e, the ring and the hollow square, which represents topological equivalent forms, even though the same ring was used.

Two more points about the stimulus patterns used in testing generalization are worth noting. First, the ring and the disk (Fig. 1 Right d), which are topologically different, appear more similar than the ring and the hollow square (Fig. 1 Right e), which are topologically equivalent. These contrasting results strengthen the hypothesis that the topological difference, rather than subjective similarity, was better at predicting differences in form discrimination learning. Second, the bees trained to distinguish between the ring (the rewarded stimulus) and the S were immediately able to distinguish between the hollow diamond (the rewarded stimulus) and the cross. This result indicated that in such transfer test, the hollow diamond and the ring (both containing a hole), in comparing with the cross and the S, respectively, served as metamers for these discriminating tasks, despite that they appear very different. Thus, the bees' capacity for topological discrimination was revealed not only by performance in a single training task, but also, more importantly, by the ease of transfer of this capacity to a number of novel test stimuli. The immediate transfer of the learning to other pairs indicates that topology is the only distinguishing feature that is common to all of the stimuli, and that the local cues specific to individual stimuli are not relevant.

Another approach to testing the relative roles of topological and nontopological features was based on inspection of learning curves. Learning curves, particularly the evolution of individual performance from the very beginning of the training, are not readily measurable with human subjects, but they are readily measured for bees. They provide an additional means by which one can distinguish between the use of topological and nontopological cues. Although previous studies have found that bees can learn to distinguish between stimuli based on nontopological features, such as orientation, symmetry or the end of bars, such learning is, by comparison, very slow, requiring hundreds of trials (reinforcements) (6–9, 11, 13–15, 17). This stands in the sharp contrast to the extreme rapidity with which bees learn to distinguish between stimuli that are topologically distinct (experiments 5 and 6). The extreme rapidity of topological learning suggests a unique mechanism for topological discrimination, and may serve a criterion for distinguishing topological discrimination from discriminations based on nontopological features.

Another approach to testing the role of topological and nontopological features was to test for transfer of learning to rotated patterns. The paradigm of rotation of training and test figures was used in experiment 3: (i) the stimuli were frequently rotated by 90° during the training, and (ii) in the test, the stimuli were also rotated and presented at a novel orientation (45°). Therefore, it would be difficult to invoke local cues (related to orientation and location) or a template-based model to explain the discrimination between the θ and the S, when the two stimuli are rotated frequently during the training, and presented at a novel orientation in the tests. On the other hand, a model invoking the topological difference between the two stimuli provides a straightforward explanation.

These tests of learning transfer, such as experiments 1 and 3, may also be considered as a kind of concept learning experiment. In experiment 1, the stimuli change with every test: after training, the bees were tested with different stimuli shown in Fig. 1 Right b–e. In experiment 3, the stimuli changed with every training and test session (allowed only two rewards per bee, on average): the θ and the S were rotated with every training session as well as testing session. But all that remains constant as a predictor of where the reward will be found is one unvarying topological property of the number of holes. Such kind of concept learning experiment provided a strong version of the hypothesis that bees are able to abstract the general property of topological invariance, namely, the number of holes.

In experiments 1, 3, 5, and 6, symmetrical learning tests were carried out by the separate experiments in which we trained bees to distinguish between the ring and the S. In one case, the ring was the positive (rewarded) stimulus, and in the other case the S was the positive stimulus. The fact that the bees could learn the discrimination equally well in either case, together with the fact that the bees could not discriminate the ring and the hollow square (Fig. 1 Right e), indicates that the bees' ability to distinguish between the ring and the S was not simply caused by a rigid template-based preference for the ring over the S.

Finally, in the eight pairs of stimuli used in the present study, we not only made the metric distortions great enough and varied enough (they share no common local feature) but also tested the bees on a large spectrum of topologically different stimuli. The bees were able to learn rapidly and transfer topological differences represented by “one hole vs. no hole,” “two holes vs. no hole,” and “four holes vs. one hole;” on the other hand, they were unable to discriminate patterns that contain “no hole vs. no hole” and “one hole vs. one hole.” This paradigm of varying the topological difference in the number of holes provides support for the more general version of the topological hypothesis with respect to hole; that is, bees' discrimination is sensitive to the number of holes.

One of the principal goals of research in visual perception is to discover the primitives that underlie the representation and recognition of objects (1–5). These experiments using the above paradigms demonstrate that bees can rapidly learn and abstract the general property of topological invariance. These results of topological discrimination in bees are particularly useful in revealing the topological primitives of visual representation. The holes in the testing stimuli were designed to be different from those in the training stimuli in widely varied local features. The transferability demonstrates the abstract nature of holes, independent of the local features. It is therefore quite difficult to explain the topological discrimination in terms of confounds of such nontopological features. In addition, the learning curves and the sequences of choices in performance evolution provide a unique criterion for distinguishing topological discrimination from discriminations based on nontopological features. Thus, topological pattern recognition may be a fundamental aspect of bees' visual processing. It is well known that computational theories of vision tend to assume that the primitive elements of computation are local geometrical features (1). With respect to such local primitives, topological properties have high computational complexity (19). Existing computational models, therefore, lead one to expect that discriminations based on topological properties would occur at a higher level of perception than those based on local geometrical properties. We have shown here, however, that topological perception is displayed by a creature with a brain weighing less than a tenth of a milligram and carrying fewer than 0.01% as many neurons as the human brain. We also find that bees are quicker at learning discrimination tasks if the discrimination was based on topological cues. These findings contradict prevailing notions of computational complexity, and highlight the need to readdress some of the fundamental questions in the study of vision, such as “where does visual processing begin?” (2) or “what are the primitives of visual perception?” (3, 4, 5).