Human and mouse genomic sequences reveal extensive breakpoint reuse in mammalian evolution

Abstract

The human and mouse genomic sequences provide evidence for a larger number of rearrangements than previously thought and reveal extensive reuse of breakpoints from the same short fragile regions. Breakpoint clustering in regions implicated in cancer and infertility have been reported in previous studies; we report here on breakpoint clustering in chromosome evolution. This clustering reveals limitations of the widely accepted random breakage theory that has remained unchallenged since the mid-1980s. The genome rearrangement analysis of the human and mouse genomes implies the existence of a large number of very short “hidden” synteny blocks that were invisible in the comparative mapping data and ignored in the random breakage model. These blocks are defined by closely located breakpoints and are often hard to detect. Our results suggest a model of chromosome evolution that postulates that mammalian genomes are mosaics of fragile regions with high propensity for rearrangements and solid regions with low propensity for rearrangements.

In a landmark paper, Nadeau and Taylor (1) introduced the notion of conserved segments (i.e., segments with preserved gene orders without disruption by rearrangements) and estimated that there are ≈180 conserved segments in human and mouse. In the same paper they provided convincing arguments in favor of the random breakage model of genomic evolution postulated by Ohno (2). The model assumes a random (i.e., uniform and independent) distribution of chromosome rearrangement breakpoints and is supported by the observation that the lengths of synteny blocks shared by human and mouse are well fitted by the predicted distribution imposed by the random breakage model. Since the model was first introduced, it has been analyzed by Nadeau and others (1, 3–6), and it has become widely accepted. It was further supported by studies of significantly larger datasets that confirmed that newly discovered synteny blocks still fit the predicted exponential distribution very well (7–11). These studies, with progressively increasing levels of resolution, made the random breakage model the de facto theory of chromosome evolution.

The arguments in favor of the random breakage model usually proceed as follows. One first constructs the distribution of lengths of conserved segments and fits the resulting histogram with the theoretical distribution predicted by the random breakage model. An important implication of this model is that the segment lengths approximate an exponential distribution with density function f(x) = 1/L e^-x/L, where L is the average length of all segments. Nadeau and Taylor (1) did not have information about all segments because most of them were still undiscovered in 1984. However, they were able to estimate L (and therefore the number of still undiscovered segments) from the small set of already discovered segments. The relatively small departure from an exponential distribution was attributed to missing information about some conserved segments. Of course, there was always a danger that newly discovered segments would shift this estimate and even deviate from the exponential distribution predicted by the model. However, this did not happen in the past, and the random breakage model was reinforced in a number of influential studies in the last decade (7, 9, 12, 13). Sankoff et al. (14, 15) analyzed the accuracy of the random breakage model and further reinforced it despite some deviations, particularly for relatively short conserved segments. These deviations are often attributed to mapping errors, statistical noise, or other evolutionary processes like frequent short inversions (16). As a result, the Nadeau–Taylor predictions are viewed as among the most significant results in “... the history and development of the mouse as a research tool” (17).

The Nadeau and Taylor (1) result laid the foundation of the statistical approach to studies of chromosomal history that was further advanced by Nadeau and Sankoff (3, 4) and others. The statistical approach is not concerned with the details of rearrangement history. Sankoff and colleagues (18, 19) pioneered a combinatorial approach to studies of genome rearrangements that attempts to infer the rearrangement scenario explaining the differences between genomic organizations. They also raised the problem of integrating the statistical and combinatorial approaches, something that never was done in the past (20). In this article, we demonstrate that such combined analysis reveals limitations of the random breakage model and leads to a fragile breakage model.

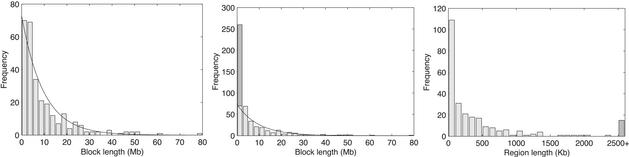
The draft human and mouse sequences reveal many previously undiscovered synteny blocks and put the random breakage model to a new test. We (21) identified 281 synteny blocks shared by human and mouse of size at least 1 Mb (Tables 1 and 2, which are published as supporting information on the PNAS web site, www.pnas.org). Although the number of synteny blocks is higher than the Nadeau–Taylor predictions, the lengths of the blocks still fit the exponential distribution (Fig. 1 Left), another argument in favor of the random breakage model. However, a different type of evidence derived from genome rearrangements studies reveals an unexpectedly large number of closely located breakpoints that cannot be explained by the random breakage model. This analysis implies that in addition to the segments shown in Fig. 1 Left, another 190 “short” synteny blocks, typically <1 Mb in length, exist. These blocks were never discovered in the comparative mapping studies, and moreover, most of them are hard to find even with available human and mouse sequences. If the breakpoints are located very close to each other (e.g., within a few nucleotides or even at the same position), the corresponding very short blocks may be undetectable by alignment analysis. Moreover, some short blocks may be deleted in the course of evolution. However, the rearrangement analysis confirms the existence of such breakpoints, even in the absence of statistically significant sequence alignments. The existence of these short blocks immediately implies that an exponential distribution is not a good fit to reality, thus pointing to limitations of the random breakage model (Fig. 1 Center). In other words, the rearrangement analysis of human and mouse genomes reveals clumps of closely located breakpoints that cannot be explained by the random breakage model.

Fig. 1.

(Left) Histogram of synteny block lengths in human for N_b = 281 synteny blocks of length at least 1 Mb, fitted by an exponential distribution with mean block length L = G_bN_b = 9.6 Mb, where G_b = 2,707 Mb is the overall length of syntenic blocks. The bin size is 2.5 Mb. (Center) The same histogram superimposed with the 190 hidden synteny blocks revealed by genome rearrangement analysis, under the assumption that all hidden blocks are short, i.e., <1 Mb in length. (Right) Histogram of breakpoint region lengths in the human genome (bin size is 100 kb). Most breakpoint regions are very short, with 109 of 258 regions being <100 kb. However, there is a small number of long breakpoint regions: 17 regions are between 1 and 2.5 Mb, and 15 are <2.5 Mb (shown by a single bar at the right end). Chromosome ends can also host breakpoints, but are not included.

The surprisingly large number of breakpoint clumps is an argument in favor of a different model of chromosome evolution that we call the fragile breakage model. This model postulates that the breakpoints occur mainly within relatively short fragile regions (hot spots of rearrangements). The existence of some fragile regions at the population level was supported by previous studies of cancer and infertility (22, 23), but the extent of this phenomenon in molecular evolution became clear only after the human and mouse DNA sequences became available. Although many clinical rearrangement breakpoints form clusters (24, 25), there were no previous reports of evolutionary breakpoint clustering, and the relationships between the cytogenetic processes and evolution remain unclear. Moreover, previous evolutionary studies implicitly (and wrongly) assumed that there exists a single rearrangement site between any two consecutive conserved segments shared by human and mouse, and therefore overlooked potential breakpoint clustering. Our understanding of fragility is still incomplete; in particular, there are reports of correlations between some common fragile sites and evolutionary breakpoints (26) and lack of correlation for other ones (27). A recent study (28) of some breakpoints on chromosome 19 and corresponding repeats suggested that clinical and evolutionary rearrangements may be driven by similar forces. Our study opens the possibility of correlating the detailed cancer breakpoint maps recently generated by Volik et al. (29) with breakpoint reuse affecting evolutionary fragile sites, despite the vastly different time scales.

If one assumes that the fragile regions are uniformly distributed through the genome then the fragile and random breakage models lead to identical estimates for the number of long segments (e.g., segments >1–2 Mb). In some sense, the random breakage model can be viewed as an excellent null hypothesis for a certain level of resolution and genome heterogeneities. However, the random breakage and fragile breakage models generate very different predictions when it comes to short segments that were below the granularity level of comparative mapping studies.

Synteny Blocks

The genomic sequences provide evidence that the human and mouse genomes are significantly more rearranged than previously thought. A large proportion of previously identified conserved segments turned out not to be really conserved, because there is evidence of multiple microrearrangements in many of them (10). These microrearrangements were not visible in the comparative genetic maps that were used for defining ≈180 conserved segments in the past. The draft human and mouse genomic sequences reveal a few thousand conserved segments; many of them may be caused by microrearrangements whereas others may be artifacts of assembly errors. We therefore developed the GRIMM-Synteny algorithm (21) to detect synteny blocks, i.e., fragments that can be converted into conserved segments by microrearrangements. The blocks generated by GRIMM-Synteny are similar to the blocks generated in ref. 30 and are based on the same versions of the draft human and mouse genomic sequences. GRIMM-Synteny detected N_b = 281 synteny blocks shared by human and mouse of size at least 1 Mb in human, and N_b - N_c = 281 - 23 = 258 breakpoint regions, i.e., regions between consecutive synteny blocks, where N_c is the number of chromosomes. Many of these synteny blocks were previously viewed as “conserved segments” by Nadeau and Taylor (1), because microrearrangements within these blocks were beyond the resolution of comparative human–mouse maps. Because of insufficient sequencing data, we ignore the breakpoint regions at the ends of the chromosomes. Our estimates need to be revisited when more sequencing data from chromosome ends become available. We do not exclude the possibility that chromosome ends may host multiple rearrangement hot spots.

Errors in draft human and mouse genomic sequences raise the question of whether imperfections of the sequence assemblies affect our estimate of breakpoint reuse. Although the draft genomic sequences indeed contain many errors, these errors are local rather than global. For example, the draft human sequence may include some misassembled bacterial artificial chromosomes, resulting in the appearance of microrearrangements with spans <200 kb. Such local errors typically result in microrearrangements that are sequencing artifacts rather than real evolutionary events. We identified 3,170 microrearrangements between draft human and mouse sequences and it is expected that only a portion of them correspond to real evolutionary rearrangements whereas the rest are caused by assembly errors (21). However, there is little doubt that large synteny blocks (e.g., blocks >1 Mb) are placed correctly because their arrangement is consistent with existing genetic and physical maps (30). Our breakpoint analysis is based only on the arrangement of such large synteny blocks and therefore the existing local assembly errors do not affect our conclusions.

These large synteny blocks were rigorously derived from the same 558,678 small-scale orthologous landmarks as in ref. 30 and are largely consistent with other recent studies of human–mouse synteny blocks (21). See ref. 30 for discussion of the quality of these 558,678 small-scale orthologous landmarks. We emphasize that even if smaller synteny blocks (e.g., <1 Mb in length) and breakpoint regions are corrupted because of assembly errors, it does not affect our conclusions; information about short synteny blocks is not used in establishing the breakpoint reuse phenomenon.

We emphasize that in contrast to previous approaches to analyzing gene orders, our approach takes into account similarities in both coding and noncoding sequences. This allows us to bypass the problem of unreliable gene annotations and take into account overwhelming evidence that similarities are well preserved in noncoding regions as well. Although most synteny blocks contain a large number of annotated genes (see Tables 1 and 2), some blocks contain very few genes and would be hard to find with the traditional gene order approaches. In particular, there is a synteny block with just one annotated human gene, and another with just one annotated mouse gene. We emphasize that these findings refer to annotated genes and more accurate gene predictions may prove that these synteny blocks contain more genes. We also found a number of genes residing within breakpoint regions and even some genes spanning entire breakpoint regions. Such “spanning genes” are likely examples of the genes that were disrupted by rearrangements in the course of evolution. Gene disruption in clinical rearrangements was discovered in the past; for example, the Abelson gene on chromosome 9 and the BCR gene on chromosome 22 are both disrupted and fused together in many leukemia patients (31). Our finding indicates that similar gene disruption effects happen in the course of evolution, contrary to the existing point of view that evolutionary genome rearrangements are neutral speciation events.

Fig. 1 Left presents a histogram of the lengths of these 281 synteny blocks (in human) fitted by an exponential distribution. However, the empirical distribution in Fig. 1 Left does not include the lengths of short synteny blocks (i.e., blocks <1 Mb), which are hard to detect even with available human and mouse sequences. Nadeau and Taylor (1) bypassed this problem by declaring such short blocks as still undiscovered and even estimated the number of such blocks via the predicted curve (4). Our key insight is that although most of these blocks are still undiscovered, the number of such blocks can be reliably estimated with genome rearrangement analysis. Each such short block creates an impression of breakpoint reuse because the breakpoints flanking short synteny blocks are hard to separate. The genome rearrangement analysis implies that there is a very large number N_r (N_r is at least 190) of such breakpoint reuses (and, therefore, short synteny blocks), thus adding an extra bar to the empirical distribution of block length (Fig. 1 Center).

This new distribution cannot be fitted with the exponential one, thus providing a solid argument against the random breakage model. Most breakpoint regions are short (<1 Mb) with very few exceptions like a 23.2-Mb breakpoint region in human and a 6.7-Mb breakpoint region in mouse (the distribution of breakpoint region lengths in human is shown in Fig. 1 Right). However, the average size of breakpoint regions is only 668 kb in human and 458 kb in mouse, and each of them contains on average 1.9 breakpoints (rather than a single breakpoint as was implicitly assumed in the previous studies). The overall size of the breakpoint regions equals 172.5 Mb in human (5.7% of the genome length) and 119 Mb in mouse (4.7% of the genome length). Intuitively, the random breakage model contradicts the fact that 5.7% of the genome is populated by such a large number of closely located breakpoints (1.9 breakpoints per breakpoint region on average if the chromosome ends are excluded). The 190 breakpoint reuses revealed by rearrangement analysis and the 258 breakpoint regions revealed by GRIMM-Synteny imply an estimate of n = N_b - N_c + N_r = 281 - 23 + 190 = 448 for the overall number of breakpoints.† We assume that these breakpoints are located in breakpoint regions and we ignore chromosome ends (see above). One can estimate the expected number of clumps [e.g., pairs of consecutive points that are within a “small” distance w from each other) in the positions of n uniformly distributed points in the interval‡ [0,1] as (n - 1)(1 - (1 - w)ⁿ] (34). If we are interested in the number of clumps of n breakpoints within a distance of 0.668 Mb (average size of breakpoint regions in human) in the genome of total length§ G = 2,983 Mb, then w = 0.668/2,983, and the number of clumps is ≈43. This is in sharp contrast with the estimate of N_r = 190 breakpoint reuses, a strong argument against the random breakage model.¶

We emphasize that this insight has only become possible with human and mouse genomic sequences available. It turned out that most breakpoint regions are rather short, thus implying that still undiscovered synteny blocks (residing within breakpoint regions) are short and making it impossible to fit the empirical distribution by the exponential one.

Genome Rearrangements and Breakpoint Reuse

The evidence for existence of 190 closely located breakpoints is provided by genome rearrangement analysis. Every genome rearrangement study involves solving a combinatorial puzzle to find a series of genome rearrangements to transform one genome into another. For multichromosomal genomes, the most common rearrangements are inversions (also known as reversals), translocations, fusions, and fissions, and the number of such rearrangements in a most parsimonious scenario is known as the genomic distance. Following Nadeau and Taylor (1), we assume that transpositions are rare and therefore can be ignored. Finding the genomic distance is a difficult combinatorial problem. In the very first computational studies of genome rearrangements, Watterson et al. (35) and Nadeau and Taylor (1) introduced the notion of a breakpoint (disruption of gene order) and noticed some correlations between the genomic distance and the number of breakpoints. The shortcoming of early genome rearrangement studies is that they considered breakpoints independently without revealing combinatorial dependencies between related breakpoints. The simplest example of related breakpoints are two breakpoints formed by a single inversion or translocation. Hannenhalli and Pevzner (36, 37) and Tesler (38) developed a polynomial-time algorithm for the genomic distance problem. We used a fast implementation of the Hannenhalli–Pevzner algorithm (39) to analyze the human–mouse rearrangement scenario (available via the GRIMM web server at www-cse.ucsd.edu/groups/bioinformatics/GRIMM). Our analysis implies that at least 245 rearrangements of 281 synteny blocks occurred because the divergence of human and mouse. This result, combined with formulas to compute the number of breakpoint reuses, implies that any human–mouse rearrangement scenario requires at least 190 breakpoint reuses.

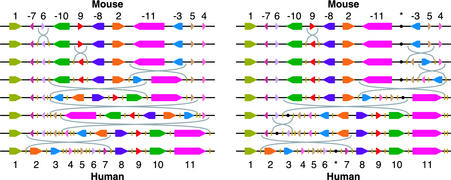
Fig. 2 presents two different most parsimonious scenarios that transform the order of the 11 synteny blocks on the mouse X chromosome into the order on the human X chromosome. Although the scenarios are very different, they both have three breakpoint region reuses.

Fig. 2.

Two different most parsimonious scenarios that transform the order of the 11 synteny blocks on the mouse X chromosome into the order on the human X chromosome. The arrangement of synteny blocks in the ancestor is unspecified (and is assumed to coincide with one of intermediate arrangements) because it cannot be inferred without availability of a third genome (33, 41). Breakpoint uses are shown as short vertical yellow lines, and breakpoint region reuses are shown as double yellow lines. In the first scenario (Left) the breakpoint reuses are located in human in breakpoint regions (3,4), (4,5), and (5,6), whereas in the second one (Right) they are located in (5,6), (6,7), and after block 11. In the second scenario, a potential hidden block is shown as a black dot; it restricts the set of possible most parsimonious scenarios, and it separates two breakpoint uses that would have been a breakpoint region reuse. Our theory implies that any rearrangement scenario based on these 11 blocks has at least three reuses of breakpoint regions (possibly including chromosome ends).

Our extension of the Hannenhalli–Pevzner theory implies that any rearrangement scenario based on these 11 blocks has at least three reuses of breakpoint regions (although we cannot unambiguously infer where these breakpoint reuses happened). This indicates that there are at least three more “hidden” synteny blocks in addition to our 11 “large” synteny blocks. Some of these blocks may be detected by lowering the threshold for synteny block detection, whereas others may escape such detection. Our analysis further reveals at least 190 breakpoint region reuses over the whole genome on the evolutionary path from mouse to human.

Identifying the exact position of hidden blocks is a difficult problem. If the consecutive breakpoints are very close (e.g., within tens of nucleotides of each other) then the resulting very short hidden synteny blocks will escape detection because the similarity between them is insignificant at the genome scale. In addition, even longer hidden blocks (e.g., tens of thousands of nucleotides) may escape detection because these blocks may not host genes and therefore the similarity between them may be quickly dissolved by frequent mutation in noncoding regions. Despite these difficulties we were able to point to some potential hidden blocks. The black dot flanked by double yellow lines in Fig. 2 Right shows the position of such a potential hidden block on the human X chromosome. Backtracking the position of this block to mouse implies that it resides between blocks 11 and 3 on the mouse X chromosome. There is indeed an area of significant similarity (≈350 bp) between the breakpoint regions in human and mouse indicated by black dots in Fig. 2 Right. We emphasize that it is not a repeat-induced similarity but rather a significant alignment hit that does not extend to any other regions.

Two similar segments in the breakpoint regions of mouse and human form a potential hidden block if one of them can be backtracked into the other within some most parsimonious evolutionary scenario on the existing blocks, but these do not merely lengthen an existing block. For technical details, see the definition of (g, b)-splits in ref. 37.

We have developed an algorithm to find all such potential hidden blocks, given our list of 281 synteny blocks and a separate list of candidate regions. It identified 111 potential hidden blocks between breakpoint regions in human and mouse (see Appendix, which is published as supporting information on the PNAS web site). Moreover, we found 81 orthologous gene pairs in the breakpoint regions satisfying the potential hidden block requirements. We emphasize that most orthologous gene pairs falling into breakpoint regions are not potential hidden blocks because there is no rearrangement scenario in which they satisfy the combinatorial constraints imposed by the backtracking procedure illustrated in Fig. 2 Right. However, the question of which of these 81 orthologous genes correspond to real hidden synteny blocks remains open because the backtracking procedure assumes that the evolutionary scenario is known. Although this is not the case yet, sequencing other mammalian species will reveal the likely rearrangement scenario and will point us to real hidden synteny blocks.

Because every rearrangement creates at most two new breakpoints, the genomic distance is at most half the number of the breakpoints in the genome. If there is no breakpoint reuse then the real evolutionary scenario is a most parsimonious one as computed by the Hannenhalli–Pevzner algorithm (36). However, the estimate of genomic distance in terms of breakpoints is inaccurate because it assumes that the breakpoints are not reused in evolution. In most genome rearrangement studies, there is evidence of breakpoint reuse (at least at a certain level of synteny block resolution), thus indicating that breakpoint reuse is the rule rather than the exception. We emphasize that by reusing breakpoints we do not mean multiple use of exactly the same genomic position as an endpoint of rearrangements, but rather the fact that the breakpoint regions host endpoints for multiple rearrangement events. Therefore our estimate of 190 breakpoint reuse events in human–mouse evolution does not imply that there were 190 reuses of exactly the same nucleotides as rearrangement endpoints.

Fragile Breakage Model Versus Random Breakage Model

Below we describe our tests of the random breakage model and introduce the alternative fragile breakage model. If positions of n breakpoints in the genome are given by random variables u_i in [0, 1], the segment sizes are y_i = u_i - u_i - 1. For the following analysis, n = N_b - 1 = 280, because we ignore the chromosome endpoints (see above) and, similarly to Nadeau and Taylor (1), do not consider short blocks (<1 Mb). We also discard any other genomic material not observed to be within the synteny blocks. To test the random breakage model, we follow the approach described in Churchill et al. (40) and use the Kolmogorov– Smirnov test, which measures the largest difference between the empirical and theoretical distribution functions:

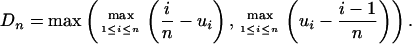The computed Kolmogorov–Smirnov statistic is D₂₈₀ = 0.085, which comes close to the estimate of 0.095 computed by Sankoff et al. (14) based on comparative mapping data for 1,423 genes and only 130 blocks. The probability (P value) that the Kolmogorov–Smirnov statistic D₂₈₀ is >0.085 for the uniform distribution is 0.032. We also found that there is a reasonably good fit between the largest synteny block of length 79.6 Mb and the expected maximum fragment length L[γ + ln(n + 1)] = 59.8 Mb, where L is the mean fragment length and γ = 0.5772 is Euler's constant.

Ideally, these inferences should be based on complete data about segment lengths. However, the information about short segments may be hard to obtain even with available draft human and mouse sequences. Churchill et al. (40) model the missing data by assuming that if two breakpoint sites are within locking distance a then the conserved segment remains undetected. However, even this more flexible model is unable to explain the very large number N_r = 190 of short unobserved segments that are revealed by our genome rearrangement studies.

In summary, the tests of the random breakage model reveal its inability to explain a large number of short synteny blocks found by genome rearrangement analysis. At the same time, the truncated exponential density function 1/L e^x-a/L fits the experimental data for synteny blocks longer than a = 1 Mb well. The question therefore arises as to whether there exists a different model of chromosomal rearrangements that (i) explains the fit between the distribution of long synteny blocks and the truncated exponential density function observed by Nadeau and Taylor (1), and (ii) explains a large number of short blocks that the Nadeau–Taylor statistics failed to explain. Below we describe a natural fragile breakage model that explains both good fit of long blocks and a large number of short blocks.

In the fragile breakage model, the genome consists of (short) fragile and (long) solid regions with different propensities to breakpoints. For expository purposes we assume that the probability of a breakpoint in a fragile region follows the Poisson process, while the probability of a breakpoint in a solid region is zero (extreme case). The overall size of fragile regions may be very small, e.g., 5% of the genome, in sharp contrast to the random breakage model. However, if fragile regions are distributed randomly in the genome, both the random breakage and the fragile breakage models predict the same distribution of long synteny blocks. This may be the reason for the prophetic predictive power of the random breakage model in the past. However, the random breakage model does not perform well in a test with the sequencing data that has recently became available, whereas the fragile breakage model easily explains the large number of short blocks, thus reinforcing our belief that the fragile breakage model may be a better approximation of reality than the random breakage model. In addition, the fragile breakage model allows one to estimate the number of still unobserved fragile regions that may be revealed by sequencing efforts in other mammalian species. Assume there are m fragile regions in the genome and n = N_b - N_c + N_r = 448 random breakages, of which N_b - N_c = 258 are observed. The probability that a given fragile region is not affected by any breakage is (1 - 1/m)ⁿ. Therefore, the expected number of observed fragile regions (i.e., fragile regions that are broken by breakages) is m[1 - (1 - 1/m)ⁿ]. Solving m[1 - (1 - 1/m)⁴⁴⁸] = 258 gives m ≈364. The estimate for the number of still undiscovered fragile regions is m -(N_b - N_c) ≈106, most of which probably reside within existing synteny blocks. This high estimate of the number of still undiscovered fragile regions may explain the recently observed phenomenon that the highly recombinogenic FRA3B locus was never disrupted in the course of mouse–human evolution (27).

Conclusion

The visionary insights of Nadeau and Taylor (1) and prophetic accuracy of their estimates survived many comparative mapping studies and (at a certain level of granularity) still remain in good fit with available human and mouse genomic sequences. The random breakage model proved to be an extremely valuable evolutionary theory, particularly when contrasted against random gene scrambling and other models that were considered in the early 1980s. However, the available human and mouse genomic sequences dramatically increased the level of resolution at which we can analyze the genomes and reveal that, with a new level of granularity, the random breakage model is unable to explain the very large number of breakpoint clumps. Therefore, a new more accurate model is needed for comparative studies of the many mammalian genomes that are about to be sequenced.

We remark that our conclusions about breakpoint reuse are based on the assumption (made in ref. 1) that transpositions are relatively rare. Although inversions and translocations are believed to be more common than transpositions, we do not entirely rule out the possibility that a significant fraction of breakpoint reuses is caused by transpositions (because every transposition can be modeled by three inversions that reuse three breakpoints).