Connectivity optimization and the positioning of cortical areas

Abstract

By examining many alternative arrangements of cortical areas, we have found that the arrangement actually present in the brain minimizes the volume of the axons required for interconnecting the areas. Our observations support the notion that the organization of cortical areas has evolved to optimize interareal connections.

In his classic 1909 study of cortical organization, Brodmann (1) defined 47 distinct areas in human cortex and provided a classification scheme, based on the microscopic structure of cortex, that still forms the basis for contemporary work concerned with cortical structure and function. Later studies have discovered that many of Brodmann's original areas should be subdivided, and other work has demonstrated that his architectonically distinct regions do, as Brodmann believed, carry out different functions. The utility of Brodmann's areal classification scheme arises from the remarkable fact that the different Brodmann areas bear the same adjacency relationships to each other from one individual's brain to the next, despite variations in absolute size and cortical position of the various areas (2–4). For example, even though the size of Brodmann's area 17 (now called V1) can vary from one individual to the next by 2- to 3-fold (3, 5), area 17 (V1) is always next to area 18 (V2) and never has area 19 (V3) as a nearest neighbor. Why are the many recognizable cortical areas arranged the way they are?

Because cortical areas participate in information-processing circuits through rich interareal connections (6) (each area connects to something like 10 other areas) one plausible organizing principle for the arrangement of cortical areas is that they are positioned to minimize the volume of the axons that relay information between the various areas (7). We have tested this hypothesis by examining many thousands of possible alternative arrangements of 11 distinct areas in macaque prefrontal cortex and find that every alternative arrangement would require more axonal volume than the one actually found.

Methods

Cortical Maps and Area Parameters. Brain maps (Fig. 1) were generated from the surface-based atlas of macaque brain by using the program CARET (8, 9). In localization and assignment of prefrontal cortical areas we followed the description of Carmichael and Price (10). Area sizes were determined from the control (uninflated) brain. The surface-based coordinates of the area centers were determined from both the map of the very inflated cortex and its flattened version to minimize the error in determining the distances caused by the brain folding. The interareal distances calculated from the two sets of coordinates differ on average by 9%. Calculations were performed with each set of coordinates and yielded identical results. The interareal distances directly determined from the folded brain differ from those calculated from the very inflated brain by ≈14%. This error is well within the allowed distortion limits of interareal distances that produce identical results (see Fig. 4 for details).

Fig. 1.

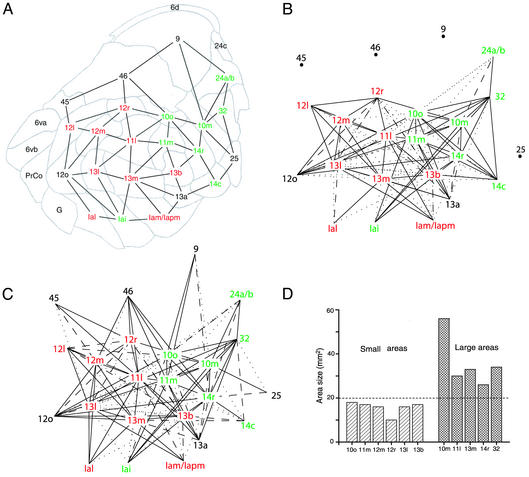
Identification of prefrontal cortical areas. (Inset) Lateral view of macaque cerebral cortex showing the general location of prefrontal cortical areas. (A) Ventromedial view of the right macaque cerebral cortex with the areas of the prefrontal cortex identified in color (10). The 11 selected areas (see text for details) are shown in colors other than yellow. Borders are also shown for some of the adjacent cortical areas identified in Carmichael and Price (10) that were not included in our calculations. (B) The same view as in A of the inflated cortex. This map and its flattened version were used to determine the surface-based coordinates of the area centers. Area color assignment is the same as in A and Inset.

Fig. 4.

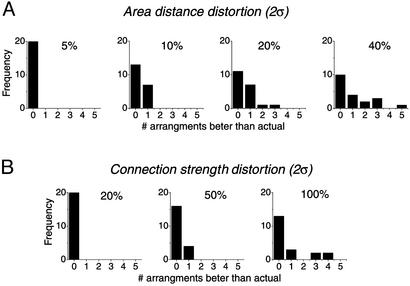
Robustness of connectivity optimization. A set of random, Gaussian-distributed numbers [with a mean of 0, and various SDs (σ), see Methods for details] was added to the matrix of interareal distances or to the matrix of connection weights. For each σ, 20 different randomly perturbed sets of areal positions or connection strengths were generated, and all possible permutations within the small and large area groups (this set of permutations is identical to that described in Fig. 3A) were examined. The frequency of appearance of arrangements better than control was plotted for distances (A) and for connection strengths (B) for each σ examined [2σ is shown above each plot as a percent of the average interareal distance (A) or connection strength (B)].

Axon Volume Calculations. Axon volume for interareal connections (V) was calculated as a sum over all areas of the Euclidian distances between area centers (x_i and y_i for the ith area) multiplied by the strength of their connection [ranked 0–3 (10)]:

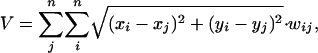where w_ij is the weight of connection from area i to area j; n = 24 is the number of prefrontal cortical areas considered in the calculation. We assume that the axon diameter does not depend significantly on length so that volume is proportional to axonal length. Note that, because connections between two areas generally have different weights in the forward and reverse direction (see Fig. 2 B and C), both directions were included in axon volume calculations.

Fig. 2.

Connectivity between prefrontal cortical areas. (A) A map of the inflated prefrontal cortex (same view as in Fig. 1B) with 10 areas of the medial network identified in red and 8 areas of the orbital network identified in green. Other cortical areas that are not a part of the orbital–medial network are shown in black. The edges connect the areas of the prefrontal cortex that share a common border and appear in the connection matrix (see text for details). (B and C) The connection matrix for connections from B and to C for the 11 selected areas. From and to matrices contain 125 and 145 connections, respectively. The strength of connection, ranked from 0 (no connection) to 3 (strongest connection), is shown as follows: 0, no line; 1, dotted line; 2, dashed line; and 3, solid line. (D) A histogram of selected area sizes as determined from the control (uniflated) cortex. The selected areas were subdivided according to the histogram into two size groups: six small areas (<20 mm²) and five large areas (>20 mm²).

Area Permutation. We systematically generated all possible permutations of area positions within groups of selected areas (see below) by using algorithms written in MATLAB. Axon volume was calculated for each configuration, assuming the weight of connections between the same areas remained unchanged. The control total axon volume was subtracted and the result was ranked so that configurations with smaller additional axonal volumes were assigned a smaller index.

We selected areas to be eligible for rearrangement if (i) they belonged to orbital–medial prefrontal cortex and (ii) all connections with their neighbors were known; 11 such areas were identified within the orbital–medial network. Four separate calculations were made that included all possible permutations within the following groups of areas: small (10o, 11m, 12m, 12r, 13l, 13b) and large (10m, 11l, 13m, 14r, 32) areas for a total of n = 6!·5! = 86,400 permutations; orbital (11l, 12r, 12m, 13b, 13l, 13m) and medial (10o, 10m, 11m, 14r, 32) areas for a total of n = 6!·5! = 86,400 permutations (the results of this calculation were qualitatively identical to that shown in Fig. 3 A and B and therefore not further discussed in the text); all selected areas with the exception of the largest (10m), for a total of n = 10! = 3,628,800 permutations; and, all selected areas without exceptions, for a total of n = 11! ≅ 39.9 million permutations.

Fig. 3.

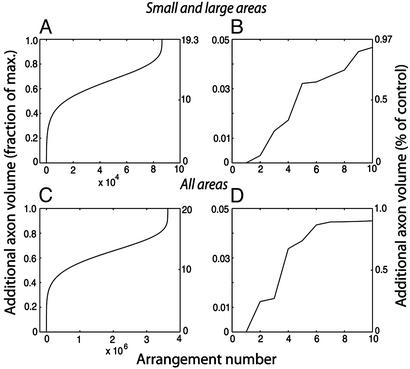
Additional axonal volume in alternative cortical configurations. Additional interareal axonal volume (compared with the axonal volume for the actual cortex) for all possible arrangements was ranked in ascending order and plotted versus its rank. Scales on the left are normalized and scales on the right give the percent change from actual cortex. (A) Six small and five large areas were permuted within each group and all possible combinations were considered for a total of 6!·5! = 86,400 alternative configurations. (B) Ten best configurations from A. The best configuration has 0 additional axonal volume and corresponds to the actual arrangement of areas. The second-best and third-best alternatives correspond to the exchange of areas 10m ↔ 32 and 10o ↔ 11m, respectively. In the worst alternative, all areas were misplaced from their positions. (C and D) Same as A and B, respectively, for all selected areas except for 10m. All possible permutations of 10 areas give 10! = 3.629 million alternative configurations. As in A, C shows the best configuration has 0 additional axonal volume and corresponds to the areal configuration of the actual cortex. Because area 10m is not moved in this calculation, the second-best alternative corresponds to the third best of A and B: exchange of areas 10o ↔ 11m. Third-best and fourth-best alternatives correspond to exchange of areas 11m ↔ 14r and 12m ↔ 13l, respectively. As in A, C shows that in the worst alternative configuration all areas were misplaced from their positions.

Robustness Test. To examine the sensitivity of our results to the distances and interconnection weights used, we introduced random perturbations of nonzero elements in the matrix of interareal distances and the matrix of connection weights. Matrix elements were perturbed by adding random, Gaussian-distributed numbers with a mean of 0 and a SD of σ = 2.5%, 5%, 10%, or 20% of the average interareal distance (15.5 mm) or σ = 10%, 25%, or 50% of the average connection strength (2.18), respectively, to all nonzero entries in the matrices. For each σ examined, 20 different randomly perturbed matrices of areal locations and connection strengths were generated, and the 86,400 possible permutations within small and large area groups were evaluated and plotted as described. Note that because the average interareal distance is about three times the typical distance between the centers of neighboring areas, a Gaussian distributed pertubation with σ = 2.5% of the average distance is equivalent to ≈15% error in determining the distance between the neighboring areas; similarly pertubation with σ = 20% corresponds to an error of ≈120%.

Results and Discussion

To determine which particular arrangement of cortical areas is optimal in the sense that areal interconnections have a minimal volume, one must have a clear definition of the cortical areas considered and must know essentially all pathways to and from each of the areas, together with the relative size of each interareal pathway. We have focused on the 11 areas in macaque orbital–medial prefrontal cortex that meet these criteria (10). Fig. 1 A presents views of the right macaque cerebral cortex with 24 areas (indicated in color) identified by Carmichael and Price (10); in Fig. 1B, the cortex has been inflated and viewed from the same ventromedial position as the uninflated cortex that appears in Fig. 1 A. The 11 selected areas, in colors other than yellow, occupy 2.73 cm², ≈1 1/3 × 2 cm, and the entire colored region amounts to ≈7.8 cm².

The Price and colleagues prefrontal cortex parcelation (11) is based on the original Walker assignment of areas (12), but has been extended and refined by consideration of cytoartectectonic, myelinatectonic, immunohistochemical, and interareal connectional properties. From areal connection patterns, Price and colleagues (11) have identified two major clusters of areas in the orbital–medial prefrontal cortex: the orbital network with 10 areas and the medial network consisting of 8 areas. Furthermore, interareal connections, and their relative size, between members of these two networks and five other prefrontal cortical areas not included in the two networks are available as a connection matrix (table 1 in ref. 10). From the representation in Fig. 1, we also know the distance from the center of each colored area to all others.

We have schematized the arrangement of the prefrontal cortical areas as a graph, illustrated in Fig. 2 A, in which the vertices indicate the various cortical areas that appear in the Carmichael and Price connection matrix (10), and the edges indicate that the two joined vertices share a common areal border. The 11 areas whose arrangement we study appear in color (nonyellow) in Fig. 1, and the Price and colleagues (11) designations for these areas, together with the surrounding areas (shown in yellow in Fig. 1) that make connections to our 11 selected areas, are seen in Fig. 2 A. These 11 areas were chosen because all or most of their connections to other areas have been established; the connections between the yellow areas and the members of the two networks are known, but these yellow areas presumably also have connections to adjacent (uncolored) regions that are not represented in the connection matrix. The connection matrix is presented graphically in Fig. 2B for the connections from, and Fig. 2C for the connections to, the selected 11 areas. Each of the 11 areas sends outputs to ≈11 areas (Fig. 2B) and receives its inputs from ≈13 areas (Fig. 2C).

To explore various possible rearrangements of the 11 selected areas, we have permuted the areal assignments to the vertices in the graph in Fig. 2 A. For example, we would interchange the labels on the vertices corresponding to areas 12m and the adjacent 13l, and then, using the connection matrix (Fig. 2 B and C) and the distances between the centers of all of the areas (measured from Fig. 2 A), we would add up all of the contributions to the volume of axonal interconnections made by the interareal pathways. Axonal volume is found as the sum, across all interconnections, of connection length (center to center of the connected areas) times its strength (on a scale of 1 to 3, table 1 of ref. 10). In these calculations we assume that axon diameter is independent of the connection length (13). Our 11 areas have different sizes (Fig. 2D), and we started by permuting areas of similar sizes.

The 11 selected areas fall into two distinct size groups, large and small, as illustrated in Fig. 2D, with one area (10m) that is much larger than the next smaller one. Except perhaps for area 10m, the differences in sizes and shapes within both the small and large classes are less than the differences between the brains of different individuals (4). To restrict rearrangements to similar sized areas, we have studied 17,280 arrangements in which positions within the small group and within the large group (excluding area 10m, whose position is kept fixed) are permuted; we also have examined the 86,400 arrangements that result when the location of area 10m can also be moved. We ordered the arrangements according to their connection optimality and plotted the results in Fig. 3 A and B for the 86,400 arrangements (including moving the especially large area 10m); the results were not different if area 10m was kept fixed or moved. We found that the actual arrangement was optimal, and any rearrangement of area positions required a greater volume of interconnecting axons.

The small and large areas in Fig. 2 A and B do not differ very much in size, except perhaps for area 10m, and we therefore also considered rearrangements of positions for all but the largest of the areas even though this would require some distortions of area shape and, perhaps, also of area size. We have kept the position of the largest area (10m) fixed and examined the consequences of 3.629 million arrangements that result from permuting the locations of the remaining 10 areas. As before, the actual arrangement is optimal and the other possible arrangements rapidly become worse, as is seen in Fig. 3 C and D. Note that the previous 17,280 permutations are a subset of the ones considered here, so that this result implies the optimality of the actual arrangement for the earlier smaller set of permutations.

Finally, we examine all possible permutations of 11 areas without any exceptions for a total of 39.9 million arrangements, a calculation that contains the preceding ones. As in all previous cases, we found that the actual arrangement is optimal and any reassignment of area positions requires additional axonal volume (data are qualitatively identical to that of Fig. 3C and therefore not shown).

Two aspects of our calculations particularly concerned us. First, we recognize that neither the positions of the areas nor the strengths of the connections between them are known with great precision. Is our conclusion robust in the sense that it does not depend on the precise areal positions and connection strengths we used? The second worry is the other side of this coin: is our conclusion unsurprising in the sense that it is the inevitable consequence of the neighbor relations and the fact that most connections are to neighboring and next-to-neighboring areas? If our result is robust, it should not depend on the precise values of interareal distances and connection strengths we have used. On the other hand, changing area sizes (that is, interareal distances) and connection strengths should matter if the optimal arrangement of areas depends on more than just the pattern of neighbor relations and connections. To address these concerns, we have randomly perturbed the positions of areas in Fig. 2 A by altering the coordinates of the vertices (keeping the adjacency relations as shown) and have randomly perturbed the connection strengths (represented in Fig. 2 B and C). We find that the actual arrangement of cortical areas is optimal for perturbations in interareal distances up to ≈15% for neighboring areas (Fig. 4A, see Methods for details) and connection strengths up to ≈20% (Fig. 4B), but that larger perturbations start giving alternative area arrangements that are better than the actual one. We conclude that the arrangement of cortical areas does not depend on the precise position (and size) of areas and strength of connections between them, but that the actual arrangement is not an inevitable result of the pattern of neighbor relations and connections.

Prefrontal cortex makes connections to subcortical and transcortical structures (14), and we have not included these pathways in our calculations for two reasons. First, the subcortical interconnections are generally less massive than the interareal pathways. Second, the freedom for choosing paths in three dimensions, as compared with essentially two dimensions available to the interaeral pathways, is greater so that rearrangements of area positions would require less additional volume for the subcortical and transcortical pathways. Nevertheless, the possible contribution of cortical–subcortical connections should be examined in future studies.

Several previous workers have proposed theories for why areas are arranged as they are. Van Essen (15) has argued that, given an arrangement of areas on the cortical sheet, the interareal distances in three dimensions are determined by mechanical forces related to interareal connection strength. This theory explains the pattern of convolutions, given connection patterns, but cannot fully account for the relative placement of areas on the cortical sheet, nor can it explain why area neighbor relations are maintained across species with varying degrees of cortical folding. Young (16) has previously used multidimensional scaling to find a “nearness” of visual cortical areas from a connection matrix similar to the one illustrated here in Fig. 2 B and C. The difference between this earlier analysis and the present one is that Young did not take the sizes of cortical areas and their physical position into account so his interareal “distances” depended only on connection pattern and not on the actual distance axons have to travel (as is the case in our calculations). Furthermore, we have considered the consequences of every alternative arrangement, whereas Young's method yielded only a “best” arrangement based on the pattern of connections. Indeed, the conclusion of this earlier work is that minimizing the volume of axonal connections does not account for the positioning of cortical areas (17), but rather the connections are determined by nearest-neighbor and next-nearest-neighbor relations. Our work provides, then, a quantitative test for a theory of areal arrangement.

The notion that neurons are arranged to minimize the volume of axonal interconnections has been used to explain why separate cortical areas exist (18), why ocular dominance columns (18–20) and orientation columns (21, 22) occur in primary visual cortex, and why the cortical areas in mammalian brain and the ganglia of Caenorhabditis elegans have the arrangement they do (7, 23). Even for the balance of the various elements making up neuropil, the idea that one should minimize the components that conduct information has important consequences (24).

Because the rules that govern cortical organization are unknown, we have pursued what we believe to be a conservative approach to the question of why areas are arranged the way they are. For the calculations presented in Fig. 3A, we have required only slight changes in areal size and shape, changes that are well within natural variations from one brain to another (25, 26). Using several approaches for examining the consequences of possible rearrangements, we have consistently found that the actual arrangement of areas is the optimal one. We certainly cannot claim that the actual arrangement produces a global minimum for the volume of interareal axonal connections because we have not explored such variables as the shape and orientation of the various areas. Nevertheless, given that cortical regions are constrained to have approximately the size and shape found in actual brains, we have produced strong evidence that cortical areas are arranged in a way that minimizes the volume of interconnecting axons. Because the volume of white matter in neocortex of large brains, such as the human brain, is almost the same as that of gray matter (27), developmental rules that minimize the white matter contribution clearly leave more room in the head for circuits that carry out the brain's computations and thus maximize our brain's computational power. If our conclusions can, as we believe, be generalized to the entire cortex, Brodmann's map of cortical areas and modern versions of it give strong clues about the strength of cortical interconnections.