An analysis of reaction pathways for proton tunnelling in methylamine dehydrogenase

Abstract

Computational methods have now become a valuable tool to understand the way in which enzymes catalyse chemical reactions and to aid the interpretation of a diverse set of experimental data. This study focuses on the influence of the condensed-phase environment structure on proton transfer mechanisms, with an aim to understand how C–H bond cleavage is mediated in enzymatic reactions. We shall use a combination of molecular simulation, ab initio or semi-empirical quantum chemistry and semi-classical multidimensional tunnelling methods to consider the primary kinetic isotope effects of the enzyme methylamine dehydrogenase (MADH), with reference to an analogous application to triosephosphate isomerase. Analysis of potentially reactive conformations of the system, and correlation with experimental isotope effects, have highlighted that a quantum tunnelling mechanism in MADH may be modulated by specific amino acid residues, such as Asp428, Thr474 and Asp384.

1. Introduction

Proton, hydride or hydrogen tunnelling has now been proposed for a range of enzymes in which C–H bond activation plays an important role in the enzyme catalytic mechanism. Although it is now becoming widely accepted that hydron tunnelling does indeed occur in some of these enzymes (e.g. Ball 2004; Liang & Klinman 2004), it is not clear how widespread it is, or how important the phenomenon may be to catalysis (Bahnson et al. 1997; Doll et al. 2003; Warshel 2003). To contribute to this discussion, we have studied the enzyme methylamine dehydrogenase (MADH, EC 1.4.99.3) with the aim of understanding its structural features which promote or enhance the tunnelling mechanism.

There has also been considerable recent debate over the role of protein dynamics in the mediation of enzyme reaction and tunnelling events, and a number of related theories have been proposed to explain the experimental kinetic data (Antoniou et al. 2002; Sutcliffe & Scrutton 2002; Kim & Hammes-Schiffer 2003; Klinman 2003; Knapp & Klinman 2003; Schwartz 2003; Warshel & Villa-Freixa 2003; Mincer & Schwartz 2004). Both molecular simulation and experimental kinetics have been used to study the role of promoting vibrations in a range of enzymes, mainly concentrating on liver alcohol dehydrogenase, dihydrofolate reductase and soybean lipoxygenase, and to ask if key amino acid residues may be involved to enhance catalysis (Billeter et al. 2001; Kalyanaraman & Schwartz (2002); Mincer & Schwartz 2003; Sikorski et al. 2004).

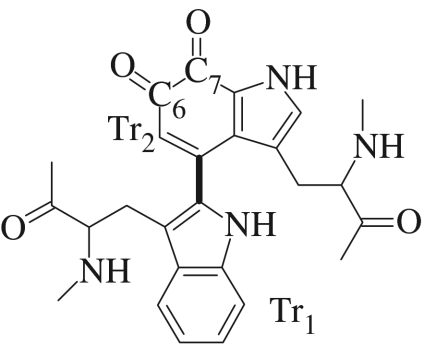
The quinoprotein enzymes, particularly the amine dehydrogenases, also exhibit some interesting kinetic properties (Masgrau et al. 2004). One of these enzymes, MADH, catalyses the oxidative deamination of methylamine to formaldehyde, allowing certain methylotrophic bacteria to grow using methylamine as their sole carbon and energy source. MADH is a hetero-tetramer containing two heavy subunits and two light subunits, α₂β₂ (Shirai et al. 1978; Chen et al. 1998). Each β-subunit of MADH has a tryptophan tryptophylquinone (TTQ) prosthetic group (figure 1), which is formed by post-translational modifications of Trp57 and Trp108 of the heavy subunit. The redox cofactor, TTQ, is located in each light subunit and is positioned close to the interface between heavy and light subunits of the same αβ unit. The active site of MADH includes the side chains of the residues Thr382, Ile383, Asp384, Asp428 and Thr474 in the light subunit. There are 20 residues from the light subunit within 4 Å of the TTQ moiety, but in only eight cases (Ser408, Val410, Tyr426, Asp428, Ile458, Phe462, Asp384 and Thr474) do any side-chain atoms beyond C_β approach this closely. Phe462 acts as a potential ‘gate’, separating the closed active-site cavity from a water-containing channel. The surroundings of the TTQ are mostly hydrophobic, and the active-site pocket of MADH, which exhibits a strong preference for methylamine over longer carbon chain amines, is a closed cavity inaccessible to bulk solvent, although two solvent molecules were proposed in the crystal structure, that were likely to be readily displaced by a large cation or by the substrate.

Figure 1.

The tryptophan tryptophylquinone (TTQ) cofactor in MADH.

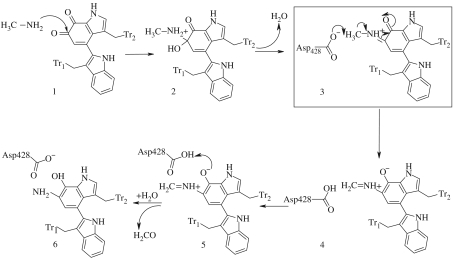
In determining the mechanism, site-directed mutagenesis was used to alter the active-site residues of MADH from Paracoccus denitrificans (Sun et al. 2001), and four residues in the active site (β-subunit) were modified. The crystal structure of the protein revealed that each of these residues participated in hydrogen-bonding interactions with other active-site residues, TTQ or water. Thus, relatively conservative mutations, which removed the potentially reactive oxygen in the side chains of Thr474, Asp428 and Asp384, each resulted in greatly reduced or undetectable levels of MADH turnover; no activity or cross-reactive protein was detected in experiments with cells expressing D428N, T474A and T474C MADH mutants. Thus, possible roles of these amino acid residues in stabilizing unusual structural features of the MADH β-subunit, protein folding and TTQ biosynthesis were proposed (Sun et al. 2001). Figure 2 summarizes the proposed mechanism and highlights the third step, which is rate limiting, involving deprotonation of the iminoquinone intermediate. These key residues are also conserved in the Methylophilus methyltrophus variant of the enzyme and will form the basis for further discussion in this study.

Figure 2.

The mechanism of the reductive half-reaction catalysed by MADH. The deprotonation step (3), outlined in the box, is the experimentally determined rate-limiting step.

The kinetic isotope effects (KIEs) for MADH, from M. methyltrophus, have been studied experimentally by Basran et al. (1999), and a large primary deuterium isotope effect, 16.8±0.5 at 298 K, and a proton reaction activation barrier of 10.7 kcal mol⁻¹, were reported for the rate-limiting step. In addition, the KIEs were found to be temperature-independent, and the Arrhenius constants for the proton and deuterated experiments were found to be very similar. These data were attributed to an extreme proton tunnelling mechanism, since the large KIE value is greatly in excess of an upper limit of approximately 7, predicted for the classical zero-point energy difference for C–H bond activation. We have previously studied the KIE for this reaction using computational methods (Faulder et al. 2001; Tresadern et al. 2002a, 2003) and have shown that the large KIE could indeed be obtained by tunnelling of the proton through the multidimensional barrier. Other similar theoretical studies found this effect for the reaction in MADH taken from P. denitrificans (Alhambra et al. 2002). Although the importance of concerted motion of the enzyme structure has been suggested to promote the tunnelling mechanism in MADH, the computational studies have not been able to explain the apparent temperature independence of the KIEs observed in the experimental studies, perhaps due to the limitations of the methodology employed.

Further investigation of the mechanism (Tresadern et al. 2002a), enhancing the computational models used in the initial study (Faulder et al. 2001), indicated that the degree of tunnelling was particularly sensitive to the enzyme conformation and to the solvation of the base within the active site. Here, we shall present new results obtained with these models of the enzyme and discuss some interesting observations from the data, which may imply that Thr474, Asp428 and Asp384 play important roles in promoting a catalytic tunnelling mechanism.

2. Computational details

The study of the kinetic properties of enzymes is a major challenge for computational chemistry, since the reaction events are rare and the size of the systems can be very large, so the use of pure quantum chemistry methods is often prohibitive. Quantum mechanical and molecular mechanical (QM/MM) methods (Harrison et al. 1997; Burton et al. 1998) with semi-classical transition state theory (TST) (Truhlar et al. 1996; Alhambra et al. 1999; Gao & Truhlar 2002) are particularly appropriate for studying the enzymatic reactions, since a small reactive region of a molecular system can be treated quantum mechanically, while the remainder of the enzyme and solvent can be described at a less computationally demanding level by a MM potential. A particularly important consideration when employing QM/MM methods for the study of condensed-phase systems is that the potential energies of the QM region will be extremely dependent upon the conformation of the surrounding environment. To properly quantify the energy changes involved in enzyme catalysis, it is often necessary to sample the phase space of the entire system properly, and thus to consider ensembles of structures in order to determine the free-energy barriers of reactions, rather than to use potential energy (PE) differences of stationary points. Gao & Truhlar (2002) have recently reviewed a range of approaches available to study enzyme catalysis and to include the important quantum effects. As an alternative to a full quantum treatment of the systems, it has been shown that free-energy methods, such as umbrella sampling, can now be usefully combined with QM/MM potentials and semi-classical corrections to TST to account for quantum tunnelling (Truhlar et al. 2004). However, with the inherent theoretical limitations and the considerable computational cost of such approaches, we have chosen here a more approximate way to study the conformational effects of the enzyme structure on the reaction event which will decouple the sampling of QM and MM regions (Tresadern et al. 2002a). Using a classical equilibrium molecular dynamics (MD) trajectory, generated with an MM potential, we shall generate an ensemble of enzyme structures which can be used to represent the environment. For a sample of these structures, the effect that the enzyme environment has on the reaction will be approximated by studying the minimum PE path of the proton transfer reaction with the QM/MM model, but within a fixed configuration of the enzyme environment. The minimum reaction paths were accurately determined using a reaction path following method (Page & McIver 1988), starting from an optimized QM/MM transition state (TS) stationary structure for each enzyme configuration. Primary deuterium KIEs were subsequently obtained for each reaction pathway. The activation energies, which will be presented for each reaction event, are obtained directly from the temperature dependence of the rate constants, and thus include the contribution from through-barrier tunnelling as well as classical over-barrier motion.

A clear restriction of this approach is that the active site is constrained by the junction between the QM and MM regions and the interactions are with fixed MM coordinates which are not averaged in any way and do not respond to the reaction event. The approximation does, however, allow us to consider a range of reaction events which are representative of the true TS ensemble. We acknowledge that relatively few structures will be considered, insufficient to be statistically meaningful, and that there is limited coupling between the environment and the electronic structural changes, so unusual temperature effects proposed from enzyme dynamics cannot be estimated quantitatively. The major benefit of this approach is that it allows specific electrostatic and steric effects of the enzyme conformation on the curvature of the reaction barrier to be efficiently identified.

In this study, the PM3 semi-empirical Hamiltonian (Stewart 1989) and Amber force field (Cornell et al. 1995) were chosen for the QM and MM regions, respectively. While the limitations of the PM3 method are well documented, previous studies on this system have clearly shown that this potential is appropriate to describe this reaction. Studies on related model systems (Tresadern et al. 2002b) have shown that the PE barrier to deprotonation may be slightly underestimated in comparison with some higher level methods, but that the method well reproduces the shape and general features of the PE surface. It should also be noted that higher level quantum methods are not a practical proposition, since over 500 second derivative evaluations are required to generate the adiabatic PE curve for each enzyme configuration. The QM/MM program employed here uses the Gaussian (Frisch et al. 1995) and Amber (Case et al. 1999) program. Amber was also used for the classical MD simulations to generate our ensemble of enzyme structures.

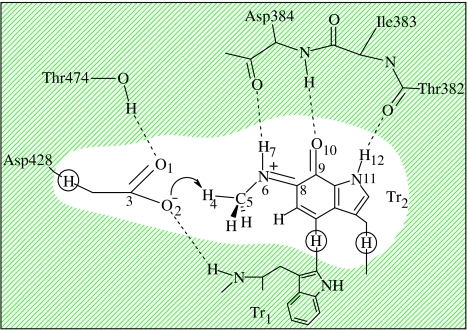
We have followed a previous model of the enzyme and active site (Tresadern et al. 2002a), which we shall review here briefly. The QM region consisted of the iminoquinone cofactor, and the side chain of Asp428 as shown in figure 3. A link-atom approach (Hall et al. 2000) was chosen to terminate the quantum region (hydrogen link atoms are shown circled in figure 3) when partitioning between QM and MM atoms which are formally covalently bound.

Figure 3.

The active site in MADH depicting a typical reactant configuration. The QM region used in the QM/MM calculations is shown unshaded with link atoms circled.

To predict the rates of proton/deuteron transfer, and hence the primary deuterium KIEs, we shall specifically employ the canonical variational transition state theory (CVT) method with a multidimensional small-curvature tunnelling (SCT) correction (Liu et al. 1993a) as implemented in the Polyrate code (Corchado et al. 2000) and interfaced to our QM/MM program via a modified version of the Gaussrate (Corchado et al. 1999) interface (Nichol et al. 2001). As noted earlier, these methods have been particularly successful in reproducing the large experimental KIEs observed experimentally in a range of enzymes.

To generate an enzyme model for the iminoquinone intermediate reactant state (structure 3 in figure 2), the X-ray structure of the oxidized form of the dimer of M. methyltrophus MADH (resolved at 2.5 Å) was used and the oxygen of carbonyl C₆ was replaced by –N⁺HCH₃. The C₆ carbonyl of the tryptophylquinone cofactor (figure 1) has been shown previously to be the site of attack by nucleophilic inhibitors (Moenne-Loccoz et al. 1996). The active-site residues, Asp428, Trp460, Trp409, Asp384, Val410, Ser408 and Thr474 were given standard protonation states according to the pH and pK_a values of their titratable groups, and the 224 waters in the crystal structure were retained. The two ring systems of the TTQ cofactor formed from Trp460 and Trp409 will be referred to as Tr₁ and Tr₂, respectively, throughout the text and figures (figure 2). ChelpG charges were developed for the non-standard TTQ residue at the HF/6-31G(d,p) level of theory. The enzyme–substrate complex was then solvated in a cubic box of 18503 TIP3P waters and neutralized with 10 chloride anions. An improper torsion was applied to the cofactor/substrate to maintain the planarity of the methylamine nitrogen with the conjugated ring system of the indole of Tr₂. The solvent was first minimized, and then the entire complex was minimized for 40 000 cycles until the root mean square of the energy fell below 10⁻² kcal mol⁻¹ Å⁻¹. It was at this stage, during the unrestrained minimization, that the three active-site water molecules that were near the Asp428 residue in the crystal structure drifted slightly away from Asp428 in the active site. Additionally, the methyl moiety of the substrate rotated by 60° and Asp428 moved towards the Tr₂ ring, sitting on top of it. Despite the structural changes that occurred to the solvent molecules, the geometry of the active site showed good agreement with the initial crystal structure.

In order to generate the ensemble of structures for study with the QM/MM method, classical MD simulations of the enzyme–substrate complex were performed at this stage with the Sander program included in the Amber package (Case et al. 1999). The temperature of the system was controlled during the simulations with Berendsen's method using a single scaling factor for all atoms. Starting with the minimized enzyme structure, the system was restrained with a harmonic potential of 20 kcal mol⁻¹, heated gradually to 300 K over a period of 12.5 ps and maintained at this temperature for a further 12.5 ps. The harmonic potential on the entire enzyme–substrate complex was then released, constraining only the iminoquinone intermediate and the three active-site waters, and the simulation continued for a further 30 ps. Finally, all restraints were removed and MD was performed for 300 ps at 300 K, recording the enzyme configuration every 0.1 ps for later study at the QM/MM level. The simulation was carried out at constant volume and temperature (NVT) conditions using an integration time-step of 1 fs. The particle mesh Ewald algorithm was used to simulate the remaining bulk water, a van der Waals cut-off of 9 Å was used, and the SHAKE algorithm was applied to constrain bonds containing hydrogen atoms to their equilibrium lengths. The non-bonded pair list was updated each time any atom moved by more than 0.5 Å.

3. Coordination of Asp428

In our initial studies (Faulder et al. 2001), using an enzyme structure based on crystal structure data, the importance of the pK_a of the Asp428 group was highlighted. A clear energetic preference for protonation at the most basic O1 site (figure 3) resulted when O2 was hydrogen bonded to a water molecule and when there was no direct H-bonding interaction of O1 with Thr474. Following equilibration at 298 K (with the iminoquinone intermediate-cofactor present), discussed in §2, an alternative stable conformation of the enzyme active site resulted, with coordination of Asp428 to the OH-group of Thr474 (figure 3) and complete displacement of water from the vicinity of the Asp group. It is particularly pleasing to note that these important structural changes, which we predict, with the resulting strong interaction between Thr474 and the Asp428 base, are now evident in the experimental structure of the analogous intermediate in aromatic amine dehydrogenase (Masgrau et al. 2004).

In order to investigate the energetic and kinetic consequences of this Thr-coordinated conformation of the active site, a further MD simulation was performed for 300 ps to generate an ensemble of structures for analysis. The preliminary details of this ensemble showed that a variation of KIE with respect to enzyme environment was particularly evident. Here, we discuss some further results from this simulation. When evaluating the importance of specific contributions of the overall enzyme structure to catalysis, it is usually appropriate to compare the reaction to the equivalent reaction in aqueous solution. It is interesting to note that our attempts to model this reaction in solution were unsuccessful since explicit solvation of Asp428 effectively lowered its basicity so that proton transfer did not occur. It is likely that one of the reasons for the successful catalysis of the proton transfer reaction in the enzyme is through limiting the adverse affects of solvent.

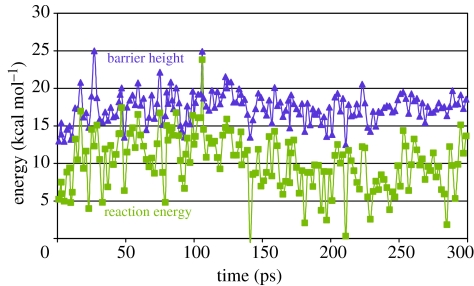
For each configuration of the enzyme, stationary points corresponding to the reactant, product and TS were calculated at the QM/MM level, typically with the uncoordinated O2 group as the proton-accepting group. Reaction barriers corresponding to each of these configurations are plotted in figure 4 against the reaction PE difference between product (protonated Asp) and reactant. It is evident from figure 4 that the reaction energies are, on average, endothermic by 10.2±3.8 kcal mol⁻¹. We have selected five configurations, A, B, C, D and E, from this simulation, randomly selected at 2.9, 9.9, 45.9, 134.4 and 188.1 ps, and have given the values for the PE barriers and reaction energies in table 1. In each case, rate constants were computed at the CVT/SCT level using an adiabatic PE surface propagated from each TS structure. Primary deuterium KIEs were then calculated and are presented in table 2 together with their representative tunnelling energies (RTEs) (Liu et al. 1993b) below the peak of the classical adiabatic PE barrier. Unexpectedly, since a large KIE is observed experimentally, very few of the configurations resulted in a large KIE, e.g. configuration B, and low tunnelling transmission coefficients, τ. In several cases, e.g. A and E, non-physical values of the KIEs of less than 1 are computed due to breakdown of the CVT/SCT model for reactions with very small backward barriers. We ascribe the generally low KIEs to be a result of the endothermic nature of the reactions, resulting in low curvature in the TS region, and thus significant tunnelling is not favoured. Returning to other configurations described in figure 4, it is clear that the vast majority will not promote a tunnelling mechanism due to the lower barriers and relatively high reaction energies.

Figure 4.

Potential energy barriers (filled triangles) and reaction energies (filled squares) (kcal mol⁻¹) for an ensemble of enzyme configurations with proton transfer to O2 of Asp428.

Table 1.

Selected potential energy barriers, ΔV^≠, and energies of reaction, Δ_rV (kcal mol⁻¹) corresponding to the proton transfer to O1 or O2 of Asp428.

	transfer to O2					transfer to O1
structure	A	B	C	D	E	A	B	C	D	E
ΔV≠	15.4	13.2	19.2	19.2	16.6	16.5	20.4	16.2	17.0	17.4
ΔrV	7.5	4.8	14.0	14.2	9.8	5.1	2.3	9.7	9.2	2.1

Table 2.

QM(PM3)/MM potential energy barriers, ΔV^≠, and reaction energies, Δ_rV (kcal mol⁻¹); TS imaginary frequencies, υ_TS (cm⁻¹); SCT transmission coefficients, κ^SCT; the representative tunnelling energies, RTEs (kcal mol⁻¹); activation energies including tunnelling, E_a (kcal mol⁻¹), at 300 K; and KIEs for selected enzyme configurations for proton transfer to O2.

structure	ΔV≠	ΔrV	υTS	κSCT	RTE	$E_{\text{a}}^{\text{CVT}/\text{SCT}}$	kH/kD
CVT	CVT/SCT
A	15.4	7.5	1999i	8	2.58	9.9	5.3	0.2
B	13.2	4.8	1996i	14	3.14	7.3	5.3	7.2
C	19.2	14.0	1935i	1	0.35	15.3	5.0	2.2
D	19.2	14.2	1922i	1	0.43	15.6	4.9	2.2
E	16.6	9.8	1986i	5	1.87	11.5	5.1	0.2

For comparison, new TSs and products were computed for each of these five selected configurations with transfer to the alternative oxygen atom of Asp428, O1 (figure 3). For each configuration, transfer to the alternative O1 atom gave a consistently larger PE barrier than the transfer to the uncoordinated O2 atom. However, in each case, the reaction energy is clearly less endothermic and in some of these cases, notably configurations B and D, and to some extent A, the reaction is almost isoenergetic. To illustrate the kinetic differences which would arise from these energetic differences for transfer to O1 rather than to O2, minimum energy paths and adiabatic PE surfaces were computed for each case, and kinetic data and KIEs at the CVT/SCT level are presented in table 3.

Table 3.

QM(PM3)/MM potential energy barriers, ΔV^≠, and reaction energies, Δ_rV (kcal mol⁻¹); TS imaginary frequencies, υ_TS (cm⁻¹); SCT transmission coefficients, κ^SCT; activation energies including tunnelling, E_a (kcal mol⁻¹); and primary deuterium KIEs at 300 K, for selected enzyme configurations for proton transfer to O1.

structure	ΔV≠	ΔrV	υTS	κSCT	RTE	$E_{\text{a}}^{\text{CVT}/\text{SCT}}$	kH/kD
CVT	CVT/SCT
A	16.5	5.1	2039i	43	3.33	9.8	8.3	11.0
B	20.4	2.4	2060i	32	3.70	13.8	9.6	13.4
C	16.2	9.7	1959i	4	1.15	11.3	3.4	4.0
D	17.0	9.2	1977i	5	1.28	12.2	3.7	4.5
E	17.4	2.1	2064i	29	3.44	10.5	8.8	13.6

Since the curvatures of the reaction paths for endothermic and isoenergetic reactions differ greatly, the KIEs computed using the CVT/SCT model corresponding to transfer to O1 are larger than for transfer to O2, and for A, B and E are larger than 7. Without the tunnelling correction, using the CVT method alone, the KIEs are consistently lower than 7. Indeed, for each of these configurations, the transmission coefficient with the SCT model ranges from 29 to 43 with correspondingly larger RTEs, indicating that each of these cases undergo considerable proton tunnelling through the barrier.

Overall it is clear that, although the lower PE barrier would be expected to favour a mechanism for proton transfer to O2, a tunnelling mechanism is possible for transfer to O1, resulting in a lower free energy of activation and a large KIE.

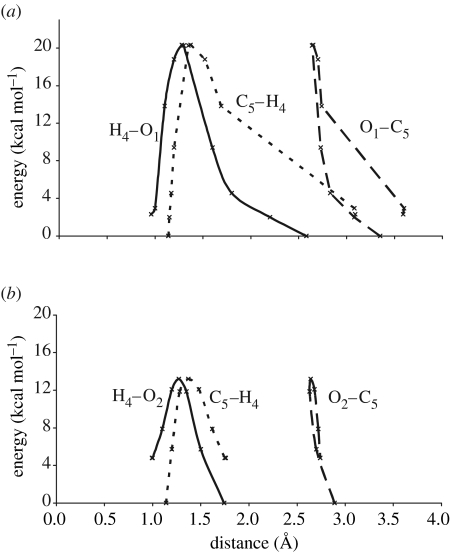
It is interesting to observe the relationship between the donor–acceptor motions and PE profile during the proton transfer reaction in configuration B, which shows both classical proton transfer and tunnelling behaviour. Figure 5b corresponds to a classical over-the-barrier mechanism when transfer takes place to O2 and the PE is plotted against the C5–H4, C5–O2 and O2–H4 internuclear distances, respectively. The PE profile for the corresponding distances when transfer to O1 can occur by tunnelling through the barrier is shown in figure 5a. In both cases, the proton donor atom (C5) and the acceptor atom (O2 or O1) approach to within 2.6–2.7 Å before a rapid change in the C–H distance is observed, indicating C–H bond breaking. Figure 5a shows that for the higher PE barrier O1 transfer reaction, there is a more distinct region of rising PE when the donor and acceptor have reached their closest approach. The reaction coordinate for this region of the PE profile is thus mainly the motion of the proton only and there is little heavy atom motion, so that tunnelling through this region of the PE barrier is favourable. However, there is no such PE rise corresponding to light atom motion in the case of transfer to O2 and thus little tunnelling would be observed. In this example, we might expect the reaction to proceed via a classical mechanism, but in other cases where the PE barrier heights are more similar, such as configuration A, the tunnelling mechanism would result in lower activation energies.

Figure 5.

Plot of potential energy (kcal mol⁻¹), corresponding to conformation B, against (a) the change in the O₁–C₅, O₁–H₄ and C₅–H₄ distances (Å) for proton transfer to O1 and (b) the change in the O₂–C₅, O₂–H₄ and C₅–H₄ distances (Å) for proton transfer to O2.

4. Product stabilization and the roles of Thr474 and Asp384

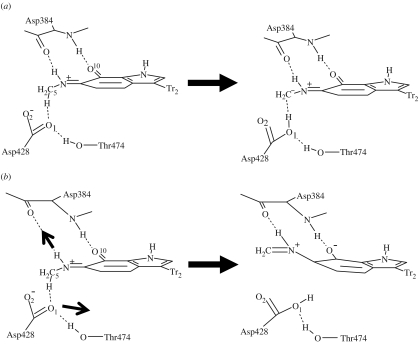
In this section, we shall consider how the amino acid residues Thr474 and Asp384 may affect the probability of a tunnelling event. Close inspection of the reaction energetics and kinetic parameters in tables 2 and 3 reveals that proton transfer to O1 does not always result in a large KIE and tunnelling mechanism. For example, configurations C and D have KIEs of 4.0 and 4.5, respectively. Although the structural differences between each of the configurations are small, one interesting feature does consistently emerge for all proton transfer profiles to O1 or O2. Enzyme configurations which result in a low KIE, and thus do not promote a tunnelling mechanism, are generally very endothermic. The endothermicity of the reaction is due to the relative instability of the product structure and orientation of Asp428. This residue is relatively immobile during the reaction and after proton abstraction it remains in alignment with the methylene carbon, C5, with a direct H-bond interaction. The coordinated structure at this carbon is found to deviate from planarity, with the improper torsion HHC5N6 tending to 150°, indicating significant sp³ anionic character at C5. The partial charge obtained from a Mulliken analysis for C5 is approximately −0.26. A schematic of this reaction configuration is shown in figure 6a.

Figure 6.

Competing proton transfer mechanisms in MADH: (a) carbanion formation resulting in a classical reaction and (b) delocalization of the anion resulting in proton tunnelling (the arrows indicate significant changes in structure).

On the other hand, for the enzyme configurations which show significant tunnelling, the product is stable relative to the reactant, with Asp428 no longer directly interacting with the methyl/methylene group, having rotated away from C5. This appears to be as a result of its stronger interaction with Thr484. The improper torsion at the C5 donor atom now tends towards planarity, indicating a lower energy delocalized π-system and considerably less anionic character at the methylene carbon as shown by a partial charge of −0.04. The position and interactions of Asp384 are also important in this configuration. Although Asp384 is involved in the stabilization of the developing oxyanion at O10 of this resonance structure, the Asp384 to O10 distance is not remarkably different from the previous endothermic case. However, here there is a significant interaction with N6H7 of the TTQ cofactor which assists in separating the proton donor C5 and Asp428 O1 atoms as the product forms. A structural scheme for this tunnelling promoted reaction is shown in figure 6b.

We may rationalize these two cases by considering the two resonance forms of the deprotonated product (figure 7), and that form II gives an endothermic product while formation of III, a structurally distinct state in the condensed phase, would give an isoenergetic reaction. In the latter case, stabilization of the product would suggest a steeper, and hence narrower, PE barrier. The subtlety of the interactions in MADH of the Asp428 and the substrate in the active site, especially with Thr474 and Asp384 respectively, determine which resonance form predominates during each reaction event.

Figure 7.

Carbanion formation and delocalization of anionic character during the proton transfer mechanism in MADH.

This effect is very reminiscent of the nitroalkane anomaly (Kresge 1974; Keefe et al. 1979), where the deprotonation of the nitroalkanes is slower than of other carbon acids with similar pK_a values. This decreased reactivity has been attributed to the delocalization of the anionic charge onto the nitro group during deprotonation, and the mediation of this resonance stabilization process by explicit solvation effects, as encapsulated in the concept of non-perfect synchronization (Bernasconi 1992). The potential relationship of the barrier shape to explain the unusual kinetic behaviour has also been recently highlighted for several quinoprotein enzymes (Basran et al. 2001).

We are aware that in these calculations the position of the Thr group is fixed, possibly in a relatively extreme position, so that it cannot achieve full relaxation to maintain an optimally favourable interaction with Asp428. However, the interactions of Thr484, Asp384 and Asp428 would be expected to vary over time, and since proton transfer is fast and most probable when the donor and acceptor have approached within a critical distance, we may still anticipate the effect indicated in the calculations. When the important interactions with Thr474 and Asp384 allow the product to achieve full delocalization of the anionic charge, large curvature on the product side of the PE curve would promote significant tunnelling probability. Furthermore, the rapid loss of sp³ character of the carbon would disfavour any backward reaction. However, when the donor–acceptor positions favour charge localization as a carbanion and continued interaction between the protonated base and the carbanion, the product-like states will be less stable leading to decreased curvature of the PE surface and lower tunnelling transmission coefficients.

5. Comparison with triosephosphate isomerase

It is interesting to compare the proton tunnelling mechanism of MADH to that of triosephosphate isomerase (TIM). TIM is a homodimeric enzyme that catalyses the conversion between dihydroxyacetone phosphate (DHAP) and glyceraldehydes-3-phosphate, an important step in the glycolytic cycle. The mechanism has been extensively studied, both experimentally (e.g. Albery & Knowles 1976; Knowles 1991; Lodi & Knowles 1991) and via computational techniques (Bash et al. 1991; Alagona et al. 1995; Aaqvist & Fothergill 1996; Cui & Karplus 2001, 2002a), and it is widely accepted that the first step is rate-limiting C–H bond activation, involving a proton transfer of the pro-R hydrogen from the DHAP substrate to Glu165 to form an enediolate intermediate, EDT1. This proton transfer step, shown in figure 8, has been recently studied using QM/MM and TST methods (Cui & Karplus 2002b), including semi-classical tunnelling corrections, to compute the primary KIEs. Overall, tunnelling does not appear to play a significant role in the mechanism, even though the chemical mechanism is fundamentally similar to that of MADH. A free-energy barrier, 13.9 kcal mol⁻¹, has been estimated for TIM from the rate constant (2000 s⁻¹; Albery & Knowles 1976), which is similar to the activation barrier found in MADH. However, contrary to our predictions for MADH, the reaction in TIM is proposed to be quite endothermic, with an estimated reaction energy of 6–7 kcal mol⁻¹ (Cui & Karplus 2001).

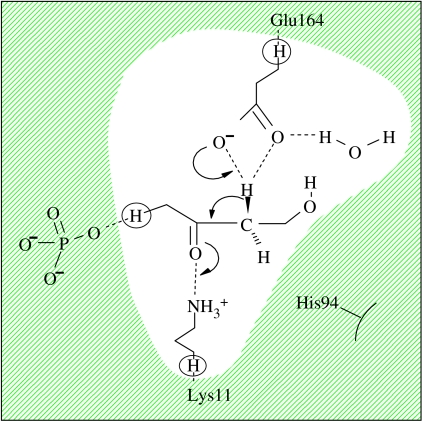
Figure 8.

Active-site and proton transfer mechanism in TIM (QM region is shown unshaded).

To investigate the different behaviour of MADH and TIM, we have followed a similar computational protocol to that used for MADH and a MD simulation was performed on TIM with the DHAP substrate for 1 ns after initial equilibration at 300 K. Structures were selected every 1 ps and stationary points were obtained using the QM/MM method, again with the PM3 Hamiltonian, in an analogous way to the MADH study. The QM region in the QM/MM calculation consisted of the Glu164 side chain, an active-site water molecule, the side chain of Lys11 and the main chain of the DHAP substrate (figure 8). Lys11 has previously been predicted to play a vital role in the enzyme reaction (Lodi et al. 1994), reducing the endothermicity relative to the uncatalysed reaction in solution by 23.4 kcal mol⁻¹ (Cui & Karplus 2001). In this case, the average PE barriers and the average reaction potential energies obtained using the QM/MM method on TIM were found to be 17.6±3.4 and 13.4±4.3 kcal mol⁻¹, respectively, which may appear a little high on average largely as a result of the small sample and the limitations of the standard PM3 method which we have employed. In table 4, we have summarized the energetic and kinetic parameters predicted for three enzyme configurations, TA, TB and TC, with reaction barriers less than 10, 15 and 20 kcal mol⁻¹, respectively. Unlike the proton transfer mechanism in MADH, no significant proton tunnelling was predicted for these configurations and no difference in kinetic behaviour was evident between protonation of the different O atoms of the Glu164 base.

Table 4.

QM(PM3)/MM potential energy barriers, ΔV^≠, and reaction energies, Δ_rV (kcal mol⁻¹); SCT transmission coefficients, κ^SCT; representative tunnelling energies, RTEs (kcal mol⁻¹); activation energies including tunnelling, E_a (kcal mol¹); and primary deuterium KIEs at 300 K, for selected enzyme configurations, TA, TB and TC, of TIM.

structure	ΔV≠	ΔrV	κSCT	RTE	Ea	kH/kD
CVT	CVT/SCT
TA	9.5	4.0	3.2	1.3	4.3	4.6	4.8
TB	12.7	7.0	4.8	1.6	7.2	4.7	5.0
TC	15.2	10.6	2.3	0.3	10.8	2.6	2.8

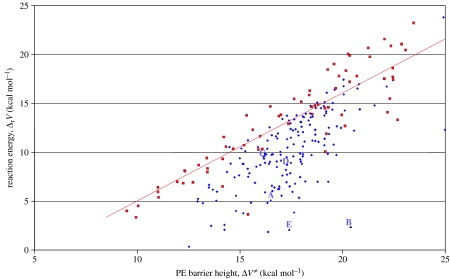
In order to illustrate the main differences between the reaction energetics in TIM and MADH, the reaction potential energies are plotted in figure 9 against the PE barriers for the various enzyme configurations. Within the limits of the methodology, it is evident that there is a marked difference in the distribution of the points corresponding to TIM compared to transfer to O2 in MADH. Perhaps the most striking difference is that there is an approximate correlation between the reaction barrier and reaction energies in TIM where an endothermic reaction is accompanied by a high barrier; however, for MADH, there are a significant number of configurations in which the reaction energy is low despite relatively high barriers. The configurations A–E, with transfer to O1 analysed in §4, are also marked. In TIM, there are very few configurations with energetics similar to A, B and E of MADH, where significant tunnelling occurs. We might expect this region of the distribution to be more populated for MADH should further reactions with transfer to O1 be included, although these data are not available.

Figure 9.

Potential energy barriers, ΔV^≠, and reaction energies, Δ_rV, for proton transfer in an ensemble of enzyme configurations to O2 in MADH (filled diamonds) and TIM (filled squares). Five configurations corresponding to transfer to O1 in MADH are indicated by A–E (filled triangles).

These data suggest that in general TIM is unable to stabilize the product states relative to the TS and thus the curvature of the reaction surfaces does not favour significant tunnelling and very large KIEs. This trend was also evident in other semi-classical profiles of proton tunnelling in TIM. Although Lys11 in TIM, like Asp384 in MADH, is important in stabilizing the developing oxyanion and lowering the PE barrier, it appears to be unable to narrow it sufficiently for tunnelling to become a dominant mechanism. In contrast, the extensive delocalization of the anionic charge into the rings of the TTQ cofactor in MADH appears to be a dominant factor in forming a narrow PE barrier and promoting an extreme tunnelling mechanism.

6. Concluding remarks

We have studied the proton transfer step associated with C–H bond activation in the rate-limiting step of the mechanism of MADH with its natural substrate methylamine. By using TST with a semi-classical tunnelling correction for a range of enzyme conformations, we have been able to investigate the important features of the mechanism and to determine the important factors responsible for catalysis and tunnelling mechanism. Unfortunately, the computational strategy employed in this study is not appropriate to directly address the temperature independence of the KIEs suggested by experiment or directly couple specific dynamical effects suggested to explain it, such as modes involving compression of the donor and acceptor. However, within the limitations of our strategy, we have shown that large KIEs can be reproduced computationally, but only when the product structures can be stabilized.

In a similar study of TIM with its natural substrate DHAP, significant product stabilization in the analogous C–H activation step appears to be rare, and thus a tunnelling mechanism is not favoured, as noted by other workers (Cui & Karplus 2002b). For both TIM and MADH, there is a general mechanism to stabilize the developing anionic charge in the deprotonated carbon acid, but it is the additional resonance stabilization of the product states in MADH which acts to narrow the barrier and ultimately promotes the tunnelling behaviour. As a consequence of these interactions in MADH, a significant proportion of the classical reaction coordinate in the transition region can be attributed to proton motion with little contribution from heavy atom motion. The combined effect is a significant through-barrier contribution to the mechanism, resulting in large transmission coefficients and large primary KIE.

We have shown that an interesting feature of the mechanism for MADH is that there can be two resonance forms in the product state, with either localized or delocalized anionic character, but that tunnelling was only evident when the latter form predominates. It is likely that the amino acid residues Thr474 and Asp384 may play significant roles in stabilizing this delocalized form and thus can be attributed to modulating the tunnelling behaviour. Although our approach may not model the true dynamical role of these interactions during a reaction event, our study does illustrate the effect that their relative positions can play in promoting quantum tunnelling of the proton rather than a classical over-the-barrier coordinate.

Another important aspect of the mechanism that has been illustrated by this study is that of the solvent environment around the Asp428 base. Initial studies revealed that specific solvation by active-site water molecules could strongly affect the relative basicity of the two oxygen atoms of the Asp. Subsequent simulation has shown that Thr474 can displace these waters and may thus play an important role. Although higher classical PE barriers for deprotonation of the carbon acid may result for abstraction by the oxygen coordinated to Thr474, this will be accompanied by an increased probability of tunnelling. Again, this behaviour can be explained within the semi-classical model since greater curvature of the PE surface, and hence smaller barrier widths, are associated with the higher classical barriers. Since a large primary kinetic isotope is observed, it is likely that significant proton transfer does indeed occur to the coordinated oxygen, but it is also likely that transfer via a classical over-the-barrier mechanism would also occur to the other oxygen atom.

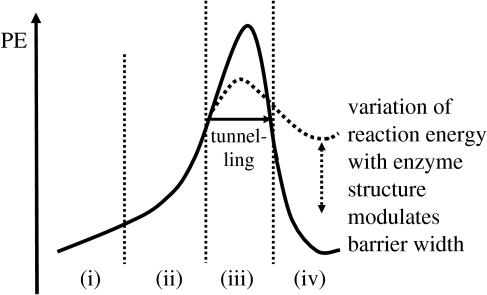
We have found it useful to summarize the reaction coordinates of these reactions in terms of the reaction profile shown in figure 10. We note four distinct regions in the classical reaction profile: (i) the alignment of Asp428 with the C–H bond to be activated; (ii) predominantly heavy atom motion due to donor–acceptor approach (either by thermal or promoting vibrations); (iii) proton motion via a classical TS which may be circumvented via quantum tunnelling; and (iv) product formation. For simplicity, only the RTE is illustrated on the diagram, but tunnelling may occur at all other energies. We would like to stress that stabilization of the product state is not directly related to increased tunnelling, but that less endothermic reactions encourage a greater probability of tunnelling via the shape of the PE barrier. Isoenergetic and exothermic reactions tend to have greater curvature on the product side of a reaction PE profile, and thus narrower barriers and greater transmission coefficients can be observed at lower energies. The possible modulation of this barrier shape is rather reminiscent of passive gating mechanisms which have been proposed in the context of an environmental coupling mechanism to explain possible temperature-independent KIEs (Klinman 2003).

Figure 10.

Potential energy profile for proton transfer in MADH.

Clearly, there is the need to clarify these observations with improved computational methods, improved potentials, and to employ models which will allow better dynamic coupling between the enzyme environment and the proton transfer event. However, the complexity of the enzyme system and many features which may contribute to the mechanism, also highlight the need to find simpler intramolecular chemical models which can mimic the various features and can be studied with a higher degree of certainty, both experimentally and computationally.