Abstract
For almost 15 years, our Pathway model has been the most powerful model in terms of predicting the tunnelling mechanism for electron transfer (ET) in biological systems, particularly proteins. Going beyond the conventional Pathway models, we have generalized our method to understand how protein dynamics modulate not only the Franck–Condon factor, but also the tunnelling matrix element. We have demonstrated that when interference among pathways modulates the electron tunnelling interactions in proteins (particularly destructive interference), dynamical effects are of critical importance. Tunnelling can be controlled by protein conformations that lie far from equilibrium—those that minimize the effect of destructive interference during tunnelling, for example. In the opposite regime, electron tunnelling is mediated by one (or a few) constructively interfering pathway tubes and dynamical effects are modest. This new mechanism for dynamical modulation of the ET rate has been able to explain and/or predict several rates that were later confirmed by experiment. However, thermal fluctuations can also affect these molecular machines in many other ways. For example, we show how global transformations, which control protein functions such as allostery, may involve large-scale motion and possibly partial unfolding during the reaction event.
Keywords: electron transfer, protein folding, energy landscape, quantum interference, anharmonic normal modes, allostery and signalling
1. Introduction
Biomolecular machines of living cells are made from soft materials—biopolymers like proteins and RNA. As opposed to macroscopic machines, biomolecular machines experience thermal motions that play an important role in their function. In this paper, we discuss two aspects of these machines. First, we comment on how such constructs can control quantum details of chemical reactions with particular emphasis on electron transfer (ET). Second, we discuss how these machines experience global motions that may be necessary for long-range control of chemical reactions. The goal of these two examples is to demonstrate that protein dynamics in completely different time and length scales may modulate function in different contexts. For example, in the ET case discussed below, structural fluctuations in the picosecond time-scale and sub-angstrom structural fluctuations may be sufficient for substantial changes in quantum interference. On the other hand, large-scale motions involving fluctuations of several angstroms and time-scales of nano- to microseconds may be involved in catalysis, signalling or allosteric reactions.
ET reactions play a key role in living systems, particularly in bioenergetic pathways. Most ET reactions in biological systems take place over large separations (5–20 Å), and consequently have very weak tunnelling coupling between the donor (D) and the acceptor (A) sites. This coupling is represented as the electronic matrix element (TDA). In this weak coupling regime, the ET rates are the product of the square of TDA, as expected from perturbation theory, and the probability of the donor and acceptor forming a resonant-activated complex (Marcus theory). About a decade ago, Beratan and Onuchic developed the Pathway Method to estimate these TDAs and to understand the tunnelling mechanism in proteins (Beratan et al. 1991). The Pathway Method assumes that tunnelling occurs via a dominant pathway tube (a family of similar pathways), and that the decay through this tube can be quantified as a product of contributions from covalent bonds, hydrogen bonds and through-space jumps.
The above description works well when a single tube dominates the reaction. Five years ago, we showed in the case of ET reactions that are dominated by a single pathway tube (or a few tubes that interfere constructively), corrections due to protein dynamics are minor (Balabin & Onuchic 2000). The situation reverses when the assumption of a single pathway tube breaks down, and ET involves multiple tubes with destructive interference, which are now known to be sensitive to conformational details and nuclear dynamics. Calculations with a single frozen conformation provide incorrect results; tunnelling is controlled by far-from-equilibrium protein conformations, where one or few tubes dominate, thereby minimizing destructive interference. Marcus theory explains how thermal nuclear motions modulate the energy gap between donor and acceptor sites in protein ET reactions. In this case, we have shown that this thermal control goes beyond Marcus theory and can actually control the tunnelling matrix element. Here, we demonstrate this effect for detailed calculations of tunnelling matrix elements in the protein Azurin.
A second interesting situation is when large-scale motions are involved in controlling biological function. We present a model for global structural transformations such as allostery that involves large-scale motion and possible partial unfolding, illustrating the method for the case of adenylate kinase. We conclude by showing how a similar approach can be applied for more interesting reactions such as function of the C-terminal Src kinase (Csk).
2. Computing tunnelling matrix elements in Azurin
By utilizing a combination of molecular dynamics with semi-empirical and ab initio (Hartree–Fock) quantum chemistry calculations, we are able to quantify how dynamics and the quality of the electronic Hamiltonian affect the tunnelling matrix element. The methodology has been illustrated for simple protein systems for which the pathways are well understood. In particular, we have shown that tunnelling in the Azurin protein is dominated by either one, or at the most a few constructively interfering pathway tubes.
These results have been obtained by utilizing a formalism recently developed by us (Kobayashi et al. 2003). Electron tunnelling in protein systems is mediated by structural configurations that are dominated by single pathway tube(s) by way of constructive interference. In the ET process, the medium between donor and acceptor sites is referred as the bridge. The Green's function matrix of this isolated bridge system describes the ‘virtual’ propagation of the tunnelling electron between the donor and acceptor sites of the protein.
To better understand how protein mediation affects the tunnelling matrix element, we fully investigate the dependence of the Green's function matrix on the bridge nuclear coordinates and electronic states.
The tunnelling matrix (TDA) can be written by Lowdin partition as (Lowdin 1962; Priyadarshy et al. 1996)
where βDd and βAa are the electron interactions between the D(A) orbitals and the bridge orbitals and Hbridge is the Hamiltonian of isolated bridge system. The Green's function of the isolated system is defined as
In effectively chainlike bridges, ET coupling can be characterized by observing the decay per bond, which is represented by Balabin & Onuchic (1996, 1998)
where Gi,j is the isolated bridge Green's function between the ith and jth units. As such, we can use the decay of the Green's function to estimate how propagation of the tunnelling electron actually occurs though the bridge system.
In general, the entire protein system is much too large to consider a full ab initio calculation to determine quantitatively the information necessary to understand the ET process. As such, one of our motivations is to develop protocol that still provides useful and reliable understanding of the process, but which is more affordable in computational costs. We would also like to have reasonably quantitative results. We have shown that the calculations are reliably simplified when a carefully chosen semi-empirical methodology is coupled together with molecular dynamics. In our studies, the Austin Model 1 (AM1) semi-empirical methodology (Dewar et al. 1985), which generally assumes a zero-differential overlap (ZDO) approximation, is chosen. In the standard AM1 method, the ZDO approximation implies that the overlap matrix is set to a unitary matrix, which can be a rather severe approximation. As such, we have actually reformulated the AM1 implementation in the general atomic and molecular electronic structure system (Gamess) (Schmidt et al. 1993) program, so that it now includes differential overlap, in order to carry out more accurate Green's function calculations. This new implementation was tested and validated using the Azurin copper protein test system.
These calculations demonstrated that electron tunnelling in these systems is mediated by structural configurations that are dominated by a single pathway tube or a few tubes constructively interfering. Figures 1 and 2 show that, although the tunnelling matrix elements vary wildly due to quantum interference, only the conformations where constructive interference is maximized dominate tunnelling. For these conformations, tunnelling is very insensitive to the details of the electronic Hamiltonian (Kobayashi et al. 2003); calculations performed with full Hartree–Fock are in good agreement with semi-empirical results using AM1 non-ZDO.
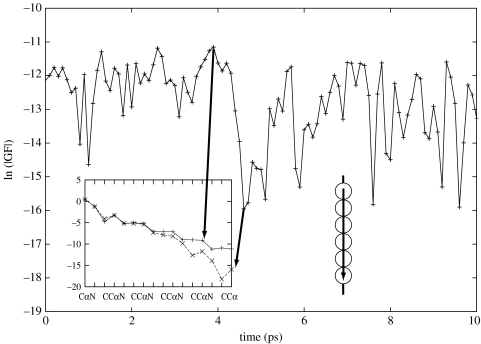
Figure 1.
Decays of Green's function matrix elements for a bridge system through a β strand—‘through covalent bonds’. The Green's function matrix elements have been calculated for conformations obtained from molecular dynamics (MD) trajectories. The insert shows the matrix element decays for the strongest and the weakest coupled conformations.
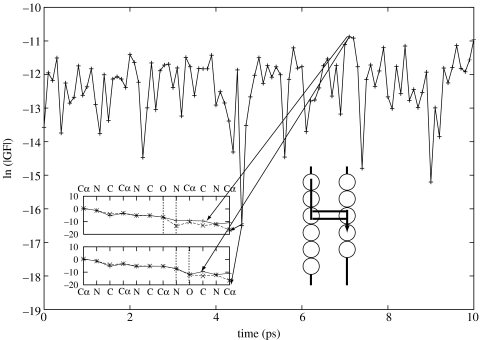
Figure 2.
Decays of Green's function matrix elements for the bridge system across two β strands—‘through hydrogen bonds’. The Green's function matrix elements have been calculated for conformations obtained from MD trajectories. The insert shows the matrix element decays for the strongest and the weakest coupled conformations. The vertical dashed lines are utilized to identify the hydrogen bond locations.
To explore how the conformational fluctuation modulates electron tunnelling, we have calculated the Green's function elements for the two pathways; the first one is a pathway through a β strand that includes covalent bonds primarily (figure 1) and the second pathway is across hydrogen bonds between two β strands (figure 2). We have determined that the Green's function elements fluctuate as a consequence of protein motion. The interesting observations are that even when the most likely structural conformation shows destructive interference, the system prefers to ‘fluctuate’ to less likely structures that offset this effect. These off-equilibrium configurations dominate the rate.
With this new procedure that combines AM1 non-ZDO semi-empirical calculations and molecular dynamics, we now have a tool to quantitatively explore electron tunnelling in larger proteins and protein complexes where most of the interesting biological ETs take place. Such a task would be impossible if full Hartree–Fock calculations and/or precise structural details of the protein were needed; the robustness of the tunnelling matrix element to these factors makes these calculations possible.
3. Functional transitions in proteins
Large-scale motions of biomolecules involve linear elastic deformations along low-frequency normal modes (Tama et al. 2000, 2003; Doruker et al. 2002; Kim et al. (2002); Cui et al. 2004; Wang et al. 2004), however for function, nonlinearity is essential. In addition, unlike macroscopic machines, biological machines can locally break and then reassemble during function. We have developed a model for global structural transformations, such as allostery and signalling that involves large-scale motions and possible partial unfolding events (Miyashita et al. 2003, 2005). This method has been illustrated with the conformational transition, which is linked to the catalytic turnover of adenylate kinase (Zhang et al. 1997; Wolf-Watz et al. 2004). Structural deformation between open and closed states occurs via low-frequency modes on separate reactant and product surfaces, switching from one state to the other when energetically favourable. The reactant and product states correspond to ligand-free and ligand-bound states of adenylate kinase, respectively, but different states may be chosen depending on the system that we apply our Marcus theory-like description. The switching model is the most straightforward anharmonic interpolation that enables the barrier for a conformational transition process to be estimated from a linear normal mode calculation, which alone cannot be used for activated events. Local unfolding or cracking may occur in regions where the elastic stress becomes too high during the transition. Cracking leads to the counterintuitive catalytic effect of added denaturant improving the allosteric enzyme function.
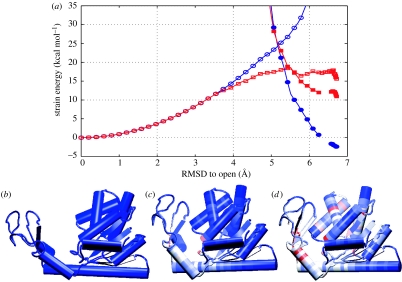
An important mechanistic consequence in these models is that regions that accumulate larger amounts of strain will more likely locally unfold (crack) during the conformational transition. This mechanism is shown in figure 3.
Figure 3.
Energy surface with cracking effects for adenylate kinase. (a) Calculations of energy profiles as functions of root mean square deviation (RMSD) from the open form without cracking (blue circles) and with cracking (red squares). Energies of the ligand-unbound state are shown by open markers, and the ligand-bound state is shown by filled markers. Cracking lowers the energy barrier. The energy surface of the ligand-bound states with low surface tension has higher energy than one without cracking, since some residues are partially unfolded. Actual conformational change would involve a refolding process, i.e. shift from the energy profile with cracking to the energy profile without cracking. (b–d) The structures along this conformational pathway are shown ((b) open form, (c) transition state and (d) closed form). The residues are coloured according to the strain energy calculated for the ligand-unbound state, i.e. the open form has no strain and the closed form has the largest strain; blue corresponding to no strain and red residues high strain. At the transition state, the strain energy is very localized, with the potential for cracking or partial unfolding.
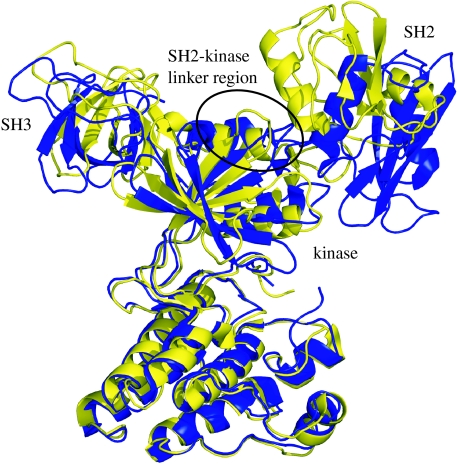
Inspired by this observation, we began a study of structural fluctuations associated with function of the Csk. Interestingly enough, possible strain regions determined from simple elastic calculations have shown substantial overlap with regions where single mutations disrupt functional communication on the kinase (figure 4; Wong et al. 2004). While Csk is not directly regulated through phosphorylation, recent studies suggest that internal structural dynamics may play an important role in activity control. For example, Csk has been crystallized in two unique forms readily distinguished by inter-domain contacts (Ogawa et al. 2002). Early experimental evidence suggests that the linker between the kinase and SH2 unfolds during the conformational transition (Ogawa et al. 2002; Wong et al. 2004). Effects elsewhere in Csk suggest that helix αC (kinase domain) and the SH2-kinase linker provide an important communication hub for movements in the SH2 domain. These data imply that the SH2 domain and the active site in Csk are dynamically coupled through specific structural elements in the small lobe of the kinase domain and the SH2-kinase linker, a finding consistent with our theoretical studies with elastic models, which indicate that molecular strain in these areas may facilitate catalysis (Wong 2004, 2005). These results are shown in figure 4.
Figure 4.
Overlay of the active (blue) and inactive (yellow) structures of Csk. The region predicted to undergo local unfolding upon activation is circled. Similarly to Φ-value experiments in protein folding, destabilizing mutations in the cracking regions will speed conformational transition rates allowing for a direct comparison between theory and experiments.
4. Conclusion
In this paper, we have shown two different situations that demonstrate how different biomolecular machines are from macroscopic machines. The fact that function in these machines is controlled by thermal fluctuations is what makes them very different from macroscopic machines. In the first case, we have shown how thermal fluctuations may maximize tunnelling. If that were not the case, in some situations tunnelling would be impossible due to destructive interference. In the second case, we have shown how, unlike macroscopic machines, biological machines can locally break and then reassemble during function. In this situation, global structural transformations such as allostery that involve large-scale motion and possible partial unfolding may become key factors in controlling biological function.
Acknowledgements
This work was supported by NSF grants PHY-0216576, 0225630 and MCB-0543906.
Footnotes
One contribution of 16 to a Discussion Meeting Issue ‘Quantum catalysis in enzymes—beyond the transition state theory paradigm’.
References
- Balabin I.A, Onuchic J.N. Connection between simple models and quantum chemical models for electron-transfer tunneling matrix element calculations: a Dyson's equations-based approach. J. Phys. Chem. 1996;100:11 573–11 580. doi:10.1021/jp953568g [Google Scholar]
- Balabin I.A, Onuchic J.N. A new framework for electron-transfer calculations—beyond the pathways-like models. J. Phys. Chem. B. 1998;102:7497–7505. doi:10.1021/jp9819442 [Google Scholar]
- Balabin I.A, Onuchic J.N. Dynamically controlled protein tunneling paths in photosynthetic reaction centers. Science. 2000;290:114–117. doi: 10.1126/science.290.5489.114. doi:10.1126/science.290.5489.114 [DOI] [PubMed] [Google Scholar]
- Beratan D.N, Betts J.N, Onuchic J.N. Protein electron transfer rates set by the bridging secondary and tertiary structure. Science. 1991;252:1285–1288. doi: 10.1126/science.1656523. [DOI] [PubMed] [Google Scholar]
- Cui Q, Li G.H, Ma J.P, Karplus M. A normal mode analysis of structural plasticity in the biomolecular motor F-1-ATPase. J. Mol. Biol. 2004;340:345–372. doi: 10.1016/j.jmb.2004.04.044. doi:10.1016/j.jmb.2004.04.044 [DOI] [PubMed] [Google Scholar]
- Dewar M.J.S, Zoebisch E.G, Healy E.F, Stewart J.J.P. Development and use of quantum mechanical molecular models. 76. AM1: a new general purpose quantum mechanical molecular model. J. Am. Chem. Soc. 1985;107:3902–3909. doi:10.1021/ja00299a024 [Google Scholar]
- Doruker P, Jernigan R.L, Bahar I. Dynamics of large proteins through hierarchical levels of coarse-grained structures. J. Comp. Chem. 2002;23:119–127. doi: 10.1002/jcc.1160. doi:10.1002/jcc.1160 [DOI] [PubMed] [Google Scholar]
- Kim M.K, Jernigan R.L, Chirikjian G.S. Efficient generation of feasible pathways for protein conformational transitions. Biophys. J. 2002;83:1620–1630. doi: 10.1016/S0006-3495(02)73931-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kobayashi C, Baldridge K, Onuchic J.N. Multiple versus single pathways in electron transfer in proteins: influence of protein dynamics and hydrogen bonds. J. Chem. Phys. 2003;119:3550–3558. doi:10.1063/1.1588293 [Google Scholar]
- Lowdin P.O. Studies in perturbation theory. IV. Solution of eigenvalue problem by projection operator formalism. J. Math. Phys. 1962;3:969–982. doi:10.1063/1.1724312 [Google Scholar]
- Miyashita O, Onuchic J.N, Wolynes P.G. Nonlinear elasticity, proteinquakes and the energy landscapes of functional transitions in proteins. Proc. Natl Acad. Sci. USA. 2003;100:12 570–12 575. doi: 10.1073/pnas.2135471100. doi:10.1073/pnas.2135471100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miyashita O, Onuchic N, Wolynes P.G. Simple energy landscape model for the kinetics of functional transitions in proteins. J. Phys. Chem. B. 2005;109:1959–1969. doi: 10.1021/jp046736q. doi:10.1021/jp046736q [DOI] [PubMed] [Google Scholar]
- Ogawa A, et al. Structure of the carboxyl-terminal Src kinase, Csk. J. Biol. Chem. 2002;277:14 351–14 354. doi: 10.1074/jbc.C200086200. doi:10.1074/jbc.C200086200 [DOI] [PubMed] [Google Scholar]
- Priyadarshy S, Skourtis S.S, Risser S.M, Beratan D.N. Bridge-mediated electronic interactions: differences between Hamiltonian and Green function partitioning in a non-orthogonal basis. J. Chem. Phys. 1996;104:9473. doi:10.1063/1.471690 [Google Scholar]
- Schmidt M.W, et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993;14:1347–1363. doi:10.1002/jcc.540141112 [Google Scholar]
- Tama F, Gadea F.X, Marques O, Sanejouand H. Building-block approach for determining low-frequency normal modes of macromolecules. Proteins. 2000;41:1–7. doi: 10.1002/1097-0134(20001001)41:1<1::aid-prot10>3.0.co;2-p. doi:10.1002/1097-0134(20001001)41:1<1::AID-PROT10>3.0.CO;2-P [DOI] [PubMed] [Google Scholar]
- Tama F, Valle M, Frank J, Brooks C.L., III Dynamic reorganization of the functionally active ribosome explored by normal mode analysis and cryo-electron microscopy. Proc. Natl Acad. Sci. USA. 2003;100:9319–9323. doi: 10.1073/pnas.1632476100. doi:10.1073/pnas.1632476100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y.M, Rader A.J, Bahar I, Jernigan L. Global ribosome motions revealed with elastic network model. J. Struct. Biol. 2004;147:302–314. doi: 10.1016/j.jsb.2004.01.005. doi:10.1016/j.jsb.2004.01.005 [DOI] [PubMed] [Google Scholar]
- Wolf-Watz M, Thai V, Henzler-Wildman K, Hadjipavlou G, Eisenmesser E.Z, Kern D. Linkage between dynamics and catalysis in a thermophilic–mesophilic enzyme pair. Nat. Struct. Biol. 2004;11:945–949. doi: 10.1038/nsmb821. doi:10.1038/nsmb821 [DOI] [PubMed] [Google Scholar]
- Wong L, et al. A single residue provides a dynamic link between the SH2 domain and active site of the COOH terminal Src kinase, Csk. J. Mol. Biol. 2004;341:93–106. doi: 10.1016/j.jmb.2004.05.060. doi:10.1016/j.jmb.2004.05.060 [DOI] [PubMed] [Google Scholar]
- Wong L, Lieser S.A, Miyashita O, Miller M, Tasken K, Onuchic J.N, Adams J.A, Woods V.L, Jr, Jennings P.A. Coupled motions in the SH2 and kinase domains of Csk control Src phosphorylation. J. Mol. Biol. 2005;351:131–143. doi: 10.1016/j.jmb.2005.05.042. doi:10.1016/j.jmb.2005.05.042 [DOI] [PubMed] [Google Scholar]
- Zhang H.J, Sheng X.R, Pan X.M, Zhou J.M. Activation of adenylate kinase by denaturants is due to the increasing conformational flexibility at its active sites. Biochem. Biophys. Res. Commun. 1997;238:382–386. doi: 10.1006/bbrc.1997.7301. doi:10.1006/bbrc.1997.7301 [DOI] [PubMed] [Google Scholar]