Linking protein structure and dynamics to catalysis: the role of hydrogen tunnelling

Abstract

Early studies of enzyme-catalysed hydride transfer reactions indicated kinetic anomalies that were initially interpreted in the context of a ‘tunnelling correction’. An alternate model for tunnelling emerged following studies of the hydrogen atom transfer catalysed by the enzyme soybean lipoxygenase. This invokes full tunnelling of all isotopes of hydrogen, with reaction barriers reflecting the heavy atom, environmental reorganization terms. Using the latter approach, we offer an integration of the aggregate data implicating hydrogen tunnelling in enzymes (i.e. deviations from Swain–Schaad relationships and the semi-classical temperature dependence of the hydrogen isotope effect). The impact of site-specific mutations of enzymes plays a critical role in our understanding of the factors that control tunnelling in enzyme reactions.

1. Introduction

The inherent complexity and multi-step nature of enzyme-catalysed reactions can greatly impede our ability to understand the chemical principles underlying nature's catalysts, cf. equation (1.1) for a single substrate (S) and single product (P) reaction:

$$\text{E}+\text{S}\rightleftharpoons \text{E}-\text{S}\rightleftharpoons {\text{E}}^{\prime }-\text{S}\rightleftharpoons {\text{E}}^{″}-\text{S}\to {\text{E}}^{″}-\text{P}\rightleftharpoons {\text{E}}^{\prime }-\text{P}\rightleftharpoons \text{E}-\text{P}\to \text{E}+\text{P},$$ (1.1)

where the chemical step, E″-S→E″-P, has been represented as an irreversible process and E′ and E″ are the modified protein forms (conformers or chemical intermediates). One of the most powerful tools to emerge in the deconstruction of such complexity is the kinetic isotope effect (KIE), which allows us to infer the contribution of the chemical step(s) to the measured kinetic constants. Under the conditions of steady state, isotope effects are generally measured on two fundamental kinetic parameters: k_cat, obtained at substrate saturation, and k_cat/K_m, obtained in the limit of zero substrate. These parameters can reflect the chemical step to varying (and often different) degrees.

The most commonly used isotopes in studying enzyme reactions are those of hydrogen, given the large inherent rate differences among H, D and T and the prevalence of H-transfer reactions.1 The process of C–H activation is especially amenable to study, as isotopes can be inserted into stable (non-exchangeable) positions within the substrate. From an historical perspective, the hydride transfer reaction, catalysed by the dehydrogenase class of enzymes that use the cofactor NADH or nicotinamide adenine dinucleotide, was the first to show anomalies in hydrogen isotope effects that had been predicted from quantum mechanical (QM) tunnelling (cf. Cha et al. 1989 and references therein). As more enzymatic data appeared, the phenomenon of biological hydrogen tunnelling became linked to electron transfer in initially unexpected ways, leading to theoretical models for hydrogen transfer that are conceptually much closer to Marcus theory than to the traditional transition state (TS) formalism (Knapp & Klinman 2002; Hatcher et al. 2004). An especially important distinction between hydrogen and electron tunnelling is the significantly smaller wavelength for the former, leading to a much greater dependence of rate on small changes in distance between the donor and acceptor atoms. A second important distinction is the availability of three isotopes of hydrogen. As will be described, the comparison of the behaviour of protium to that of deuterium and tritium provides a unique experimental window into the role of inter-atomic distance sampling in the course of the H-transfer process.

2. Use of the Swain–Schaad relationship as an indicator of tunnelling

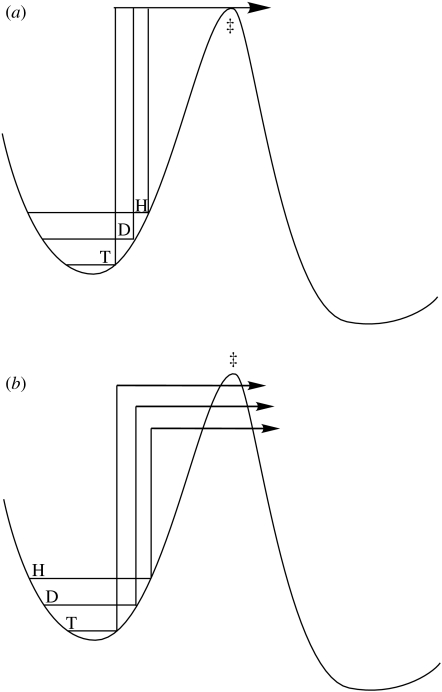
Within the semi-classical formalism of H-transfer, a barrier to the reaction is represented in a single dimension and represents the difference in energy between the ground state vibrational level of the reacting C–H bond and the TS (figure 1a). Differences in rate among H, D and T reflect the impact of isotopic mass on zero-point vibrational levels, and lead to an estimated maximal value of ca 7 for k_H/k_D (Melander & Saunders 1987). Observations of values of k_H/k_D that are reduced from 7 have been predicted and attributed to a cancellation of ground state by TS vibrational motions (Westheimer 1961).

Figure 1.

(a) The semi-classical view of H-transfer in which differences in rate among H, D and T arise from ground state vibrational levels. (b) A modification where tunnelling is allowed to occur below the top of the barrier. This is a tunnelling correction and is expected to be greater for H than D than T, given the trend in wavelengths as a function of the mass of the tunnelling particle.

Within the context of figure 1a, it is also possible to predict the relationships among H, D and T, since these are inter-related solely by their respective atomic masses. This has led to the well-known Swain–Schaad relationships summarized in equations (2.1) and (2.2) (Swain et al. 1958):

$${\left(\frac{k_{\text{H}}}{k_{\text{D}}}\right)}^{1.44}=\left(\frac{k_{\text{H}}}{k_{\text{T}}}\right),$$ (2.1)

$${\left(\frac{k_{\text{D}}}{k_{\text{T}}}\right)}^{3.26}=\left(\frac{k_{\text{H}}}{k_{\text{T}}}\right),$$ (2.2)

with the attendant exponent values of 1.44 and 3.26 representing the degree to which the smaller of the two isotope effects in each equation needs to be modified to match k_H/k_T. As introduced by Northrop (1975) and later discussed by Cha et al. (1989), the type of kinetic complexity illustrated in equation (1.1) is expected to lead to an inflation of the observed exponent in equation (2.1) and a reduction of the exponent in equation (2.2).

There are many documented examples where the measured k_H/k_D values exceed 7 and the explanation initially offered for this observation was the presence of tunnelling correction (Bell 1980). According to the ‘tunnel correction model’, the one-dimensional barrier becomes narrower near the top, allowing a certain degree of corner cutting. This increases the observed rate by allowing the reacting particle to pass through, rather than over, the barrier (figure 1b). This process is predicted to be heavily isotope-dependent, given the inverse relationship between wavelength and mass and leads to the expectation of corner cutting of the order of H≫D>T (Bell 1980; Truhlar et al. 1985; Garcia-Viloca et al. 2004).

The impact of corner cutting is also manifested in the Swain–Schaad relationships and is best illustrated in equation (2.2) that uses tritium transfer as a frame of reference for protium and deuterium transfer. With the greater probability of tunnelling for protium than deuterium, the exponent that relates k_D/k_T to k_H/k_T may be expected to become inflated, giving exponential values that are in considerable excess of 3.26. The upper bounds of this exponent within a semi-classical picture (i.e. in the absence of tunnelling) have been explored for values of k_H/k_T above 1.1, showing an exponent (EXP) that may, under certain circumstances, go as high as 4–5 (Kohen & Jensen 2002; Hirschi & Singleton 2005).

The reactions catalysed by the alcohol dehydrogenases from yeast, horse liver and Bacillus stearothermophilus have provided some of the most direct evidence for aberrant Swain–Schaad relationships that lie outside these semi-classical limits (Cha et al. 1989; Bahnson et al. 1997; Kohen et al. 1999; table 1). It is noteworthy that the summarized data have been observed for the secondary (non-transferred) hydrogen of alcohol substrates doubly labelled at the methylene position with either L=D, T or H, T; i.e. measurement of a secondary hydrogen/tritium (H/T) isotope effect reflects H-transfer, whereas the secondary deuterium/tritium (D/T) isotope reflects D-transfer:

Table 1.

Size of the exponent relating H/T and D/T secondary isotope effects in the alcohol dehydrogenase reaction.

enzyme	(kD/kT)EXP=kH/kT	references
YADHa	EXP=10	Cha et al. (1989)
HLADHb, L57F mutant	EXP=8.5	Bahnson et al. (1997)
B. stearothermophilus ADHc, 65 °C	EXP=15	Kohen et al. (1999)

^aYeast alcohol dehydrogenase.

^bHorse liver alcohol dehydrogenase.

^cAlcohol dehydrogenase from B. stearothermophilus.

Such non-classical behaviour in the secondary position had, in fact, been predicted in the instance of coupling between the motions of the primary and secondary hydrogen atoms and tunnelling of the primary hydrogen from donor to acceptor atoms (Husky & Schowen 1983; Knapp et al. in press). A very striking feature of the experimental data available from a large number of enzyme reactions is that the Swain–Schaad relationship for the primary isotope effect remains fairly close to the semi-classical limit when chemistry is rate determining (Knapp et al. in press). In fact, among the numerous primary isotope effects measured in enzyme-catalysed C–H abstraction reactions, there is no example of significant deviations from the semi-classical Swain–Schaad relationship in the direction expected for tunnelling. Although this has been attributed to the fact that the secondary KIE is much smaller than the primary effect and, hence more sensitive to deviations from semi-classical behaviour (Knapp et al. in press), other factors may also have a role to play (see below).

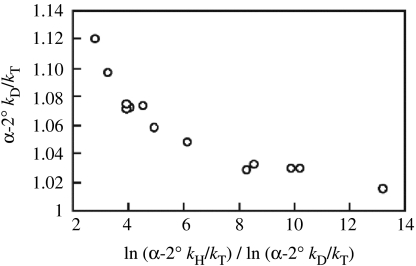
A second, highly unexpected property of the Swain–Schaad relationship that has emerged concerns the observed trends in the magnitude of the exponent relating measured D/T and H/T isotope effects as a function of the size of the D/T isotope effect. An extensive data set has been measured using (i) alcohol dehydrogenases (ADHs) from different sources, (ii) substrate analogues with altered driving forces and (iii) enzyme forms that have been mutated at their active sites (table 2; Cha et al. 1989; Rucker et al. 1992; Bahnson et al. 1993, 1997; Kohen et al. 1999). The latter involves either an increase in bulk at Leu57 or Phe93 (numbering refers to the horse liver alcohol dehydrogenase (LADH)), to alter the rate of substrate release from the active site pocket and make chemistry more rate determining, or a reduction in bulk at Val203 to alter its interactions with the C-4, reactive position of cofactor. As summarized, there is a regular trend in which the size of the exponent decreases as the magnitude of the secondary D/T isotope effects increases. The graphical representation (figure 2) of the α-2°k_D/k_T as a function of ln(α-2°k_H/k_T)/ln(α-2°k_D/k_T) clearly illustrates the regularity of the phenomenon (Knapp et al. in press).

Table 2.

Impact of change in protein or substrate structure on the exponent that relates the H/T and D/T secondary isotope effects in the alcohol dehydrogenase reaction.

enzymea	α-2° kH/kTb	α-2° kD/kTb	EXPc	references
YADH, WT (p-H)d	1.35 (0.015)	1.03 (0.006)	10.2 (2.4)	Cha et al. (1989)
YADH, WT (p-Cl)d	1.34 (0.01)	1.03 (0.010)	9.9 (4.2)	Rucker et al. (1992)
HLADH, L57F	1.318 (0.007)	1.033 (0.004)	8.5 (1)	Bahnson et al. (1993)
HLADH, F93W	1.333 (0.004)	1.048 (0.004)	6.3 (0.5)	Bahnson et al. (1993)
HLADH, V203A	1.316 (0.006)	1.058 (0.004)	4.9 (0.3)	Bahnson et al. (1997)
HLADH, L57V	1.332 (0.003)	1.065 (0.011)	4.55 (0.75)	Bahnson et al. (1993)
HLADH, V203L	1.38 (0.005)	1.074 (0.004)	4.5 (0.2)	Bahnson et al. (1997)
HLADH, WTe	1.335 (0.003)	1.073 (0.008)	4.1 (0.44)	Bahnson et al. (1993)
HLADH, ESEe	1.332 (0.004)	1.075 (0.003)	3.96 (0.16)	Bahnson et al. (1993)
HLADH, V203A:F93W	1.325 (0.004)	1.075 (0.004)	3.9 (0.2)	Bahnson et al. (1997)
HLADH, V203G	1.358 (0.007)	1.097 (0.007)	3.3 (0.2)	Bahnson et al. (1997)
YADH WT (p-MeO)d	1.34 (0.04)	1.12 (0.02)	2.78 (0.82)	Rucker et al. (1992)

^aHLADH is horse liver alcohol dehydrogenase and YADH is yeast alcohol dehydrogenase.

^bReported values±the standard errors.

^cThe error was calculated as follows: $\text{error}=\text{exp}{\left[{\{\delta \text{ln}(k_{\text{H}}/k_{\text{T}})/\text{ln}(k_{\text{H}}/k_{\text{T}})\}}^2+{\{\delta \text{ln}(k_{\text{D}}/k_{\text{T}})/\text{ln}(k_{\text{D}}/k_{\text{T}})\}}^2\right]}^{1/2}$.

^dThese experiments used benzyl alcohols with either H, Cl or MeO substituents in the para-position of the ring.

^eH-transfer may not be fully rate-determining for these two enzyme forms, leading to a somewhat reduced value for EXP.

Figure 2.

A plot of the exponent relating the secondary isotope effect for hydride transfer in the reactions of the alcohol dehydrogenases as a function of the magnitude of the D/T isotope effect. These data are from table 2. The value for EXP of 13 is from the ht-ADH at 65 °C (table 4).

Inspection of table 2 further indicates that the size of the α-2°k_H/k_T is almost invariant across the series, with an average value of 1.34 (0.01) for α-2°k_H/k_T. The constancy of the value for the secondary tritium isotope effects, which were collected over more than a decade by many different investigators, indicates that our understanding of the origin of the Swain–Schaad deviations requires re-evaluation. In the context of the ‘tunnel correction model’, protium is the particle that tunnels most significantly. Any perturbation in conditions that is expected to alter the tunnelling probability, such as a change in enzyme source, substrate structure or protein side chain, is expected to impact the reaction of protium to the greatest extent. In other words, the change in experimental conditions might be expected to give rise to the greatest variability among the H/T measurements, with much less variability among the D/T values—in marked contrast to the experimental observations. As will be discussed below, a ‘full tunnelling model’ offers a means of reconciling the apparent contradictory observations.

3. Temperature dependence of isotope effects as a measure of hydrogen tunnelling

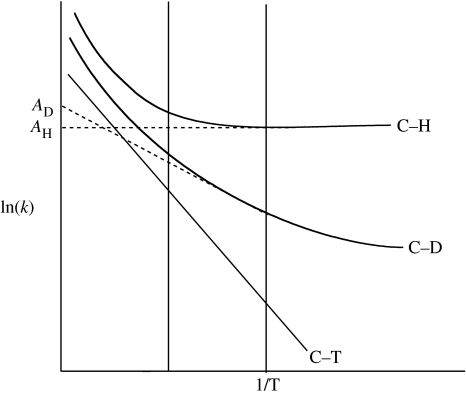
Deviations from the semi-classical predictions of Arrhenius behaviour provide a second powerful tool of hydrogen tunnelling. Analogous to deviations from the Swain–Schaad relationship, these were initially formulated in the context of tunnelling correction (Bell 1980). As illustrated in figure 3, the presence of tunnelling produces a faster rate than expected at a given temperature, a result of the capacity of a nucleus to move under a reaction barrier (cf. figure 1b). The isotope dependence of ‘under the barrier reaction’ produces differential curvature in the Arrhenius plots of H, D and T, such that the estimation of tangents within a given experimental temperature range leads to E_a(H)≪E_a(D)<E_a(T) in a direction that can far exceed the magnitude of the trend predicted from zero-point energy differences (figure 1a). Deviant behaviour is reflected as well in the Arrhenius pre-factor, with isotopic values, A₁/A₂ (where 1 and 2 represent the light and heavy isotope, respectively), predicted to fall far below close to unity values expected from a semi-classical treatment of H-transfer (Kohen & Klinman 1998).

Figure 3.

Predictions of the isotopic Arrhenius behaviour in the context of tunnelling correction, where greater movement through the barrier for H than D or T produces greater curvature in the Arrhenius plot.

Numerous temperature dependencies of isotope effects have been documented in the literature with A₁/A₂≪1, appearing to fit nicely into the ‘tunnelling correction model’ (e.g. Grant & Klinman 1989; Jonsson et al. 1994; Whittaker et al. 1998; Chowdhury & Banerjee 2000; Seymour & Klinman 2002). However, detailed studies of C–H activation in enzyme reactions have forced us to move beyond this simplistic view. As observed initially in the reaction catalysed by soybean lipoxygenase (SLO; Glickman et al. 1994; Hwang & Grissom 1994) and, subsequently, in a wide range of other enzyme-catalysed C–H abstraction reactions (e.g. Basran et al. 1999, 2001; Kohen et al. 1999; Abad et al. 2000; Harris et al. 2000; Francisco et al. 2002; Sikorski et al. 2004), the value of A₁/A₂ often lies considerably above unity. In one case (dihydrofolate reductase, (Sikorski et al. 2004)), a complex set of conditions have been postulated to explain A₁/A₂≫1 within the tenets of variational transition state theory (VTST; Pu et al. 2005). However, the appearance of A₁/A₂ in a wide range of enzymes that differ with regard to the nature and energetics of hydrogen transfer, the cofactors involved in C–H activation and the participation of enzyme active site residues necessitates a new physical paradigm.

SLO displays some of the most aberrant behaviour of any enzymatic C–H abstraction reaction studied, with an isotope effect close to 100 at 25 °C and an A_H/A_D value of 18 using wild-type enzyme (WT-SLO; Knapp et al. 2002). These experimental observations for H-transfer have been shown to be fitted by a model that takes its lead from Kuznetsov & Ulstrup (1999) and involves full tunnelling of all isotopes (Knapp & Klinman 2002; Knapp et al. 2002). The barrier for the reaction comes from the heavy atom reorganization needed to effect efficient wave function overlap, involving the capacity of the environment to tune the relative energy levels of the reactant and product together with the distance between the reactants, equation (3.1):

$$k_{\text{tun}}=(\text{constant})\left({\text{exp}}^{-{(\lambda +\mathrm{\Delta }{G}^{°})}^2/4\lambda RT}\right)(\text{F}.\text{C}.\text{term}).$$ (3.1)

As summarized in equation (3.1), the first exponential term controls the relative energy levels of the reactant and product and is analogous to the barrier commonly ascribed to electron tunnelling; this is described by two parameters, the reaction driving force ΔG° and the sum of the inner and outer sphere reorganization energy (λ). When hydrogen transfer occurs largely between the ground state vibrational levels of the reactant and product, this first exponential is expected to be largely isotope-independent, leading to the expectation of A₁/A₂>1.

The second important contributor to equation (3.1) is the probability of wave function overlap between the donor and acceptor atoms integrated over a range of possible distances between the hydrogen donor and acceptor, equation (3.2):

$$(\text{F}.\text{C}.\text{term})={\int }_{r_1}^{r_0}{\text{exp}}^{-m_{\text{H}}{\omega }_{\text{H}}{r}_{\text{H}}^2/2\hslash }{\text{exp}}^{-(E_{\text{x}}/k_{\text{B}}T)}\text{d}x,$$ (3.2)

where m_H and ω_H are the mass and frequency of the transferred hydrogen and r_H is the distance over which the hydrogen moves; ℏ is the Planck's constant divided by 2π. This static Franck–Condon term, reflected by the first exponential in equation (3.2), is multiplied by a second exponential that describes the energy, E_x, required to alter the reactants from their initial position (r₀) to a new position that facilitates greater wave function overlap. According to equation (2.1), E_x=(1/2)ℏω_xX² and X=r_x(m_xw_x/ℏ)^1/2, where m_x and ω_x are the mass and frequency, respectively, of the distance sampling mode and r_x is the displacement of this mode; k_B is the Boltzmann constant. Of considerable relevance for the interpretation of the experimentally available data, equation (3.2) predicts a larger barrier for deuterium or tritium in relation to protium, a consequence of the need for the donor atom bearing the heavier nucleus to approach the acceptor atom more closely. This property can lead to isotopic Arrhenius pre-factors in the direction A₁/A₂≪1.

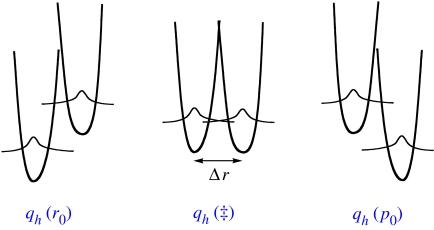
A pictorial representation of equation (3.1) is given in figure 4; as illustrated, the barrier to reaction represents, in part, the thermal energy needed to fluctuate from an initial endergonic relationship between reactant and product (figure 4a) to an isoenergetic state (figure 4b). Once an isoenergetic state has been achieved, further distance sampling may occur to generate more reactive configurations between the donor and acceptor than permitted by r₀. This is represented as Δr=r₀−r_x in figure 4. These properties of equation (3.1) offer an ‘umbrella’ view for tunnelling, predicting either temperature-independent isotope effects, when the barrier to reaction is dominated by ΔG° and λ (A₁/A₂>1), or highly temperature-dependent isotope effects, when distance sampling plays a dominant role in the differential reaction probability (A₁/A₂<1).

Figure 4.

A multidimensional picture of H-tunnelling in which the (a) reactant hydrogen coordinate samples different relative energy levels between reactant and product and different distances between the (b) donor and acceptor atoms (c) before proceeding to product.

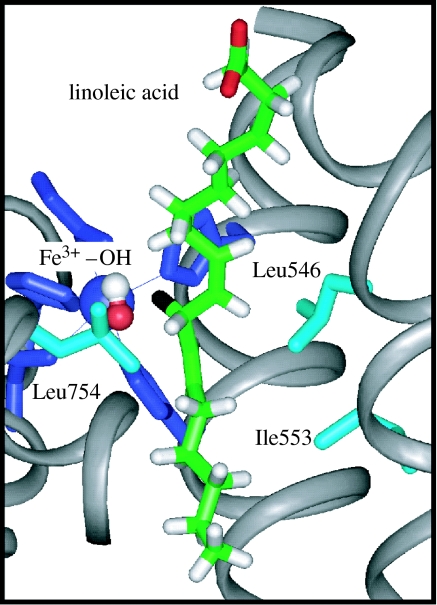
The generation and analysis of active site mutants of SLO have allowed us to investigate the robustness of equation (3.1). These mutants involve the introduction of packing defects into the interior of SLO via the reduction in the size of active site hydrophobic residues. The positions of mutations characterized so far are at Leu546, Leu754 and Ile553 (Knapp et al. 2002), with Leu546 and Leu754 lying on either side of the reactive C–H bond of bound substrate and Ile553 lying a helix turn away from Leu754 (figure 5). Focusing on the position 553, which has been changed to Leu, Val, Ala and Gly (Knapp et al. 2002; Meyer & Klinman 2005), a regular trend has been observed in which the temperature dependence of the isotope effect increases with decreasing bulk. In the case of I553G, the value of A_H/A_D is reduced from 18 for WT-enzyme to a very small number (table 3). Recent X-ray crystallographic characterization of the Ile553 mutants at close to atomic resolution shows very little structural perturbation in relation to WT-enzyme (Meyer et al. in preparation), pointing toward changes in protein dynamical properties as an explanation for the observed behaviour.

Figure 5.

Active site for soybean lipoxygenase illustrating the position of Leu754, Leu546 and Ile553 in relation to bound substrate. The reactive C–H of substrate is shown in black. The substrate has been modelled (Knapp et al. 2002) into the structure of the enzyme (Minor et al. 1996).

Table 3.

Comparison of parameters for the behaviour of WT-SLO and the I553G mutant^a.

enzyme	kH/kD, 30 °C	Ea(D)−Ea(H)	AH/AD
SLO-WT	81 (5)b	0.9 (0.2)	18 (5)
SLO-I553Gc	170 (16)b	5.3 (0.7)	0.027 (0.034)

^aSLO is the soybean lipoxygenase.

^bKnapp et al. (2002).

^cThe value of k_H/k_D at 10 °C is 388 (Liang et al. 2004a,b).

One very important feature of the data for mutant SLOs is that the changes in kinetic properties are seen to be most pronounced for the deuterated substrate. In the case of the protio-substrate, the rates are reduced to a relatively small extent (with a maximum of a fivefold reduction in rate in the case of I553G) and the enthalpies of activation are seen to be close to the values of WT-enzyme. In contrast, the kinetic behaviour of deuterated substrate indicates significantly increased values for the enthalpy of activation and in the case of I553G, an isotope effect increased to 170 at 30 °C (and to 388 at 10 °C) (table 3). This is reminiscent of the trends in the Swain–Schaad deviations (table 2 and figure 2), where site-specific mutagenesis was seen to have its greatest impact on the k_D/k_T measurements. Can the two types of tunnelling probes, non-classical Swain–Schaad relationships and non-classical Arrhenius behaviour, have a common physical origin?

4. Measured Swain–Schaad data and isotopic Arrhenius behaviour in the reaction of high-temperature alcohol dehydrogenase (ht-ADH)

The prokaryotic alcohol dehydrogenases form a homologous family of proteins that function across a wide temperature range, with the low temperature variant from the psychrophilic organism, Moraxella sp. TAE123 (ps-ADH) showing 55% identity with the ht-ADH from B. stearothermophilus (Liang et al. 2004a,b). Although an X-ray structure of the ps-ADH is not yet available, comparison of the available structures for ht-ADH (Ceccarelli et al. 2004) and the homologous Escherichia coli ADH (Karlsson et al. 2003) indicates a high degree of three-dimensional structure conservation, once again implying that functional differences among these enzymes arise from differences in dynamic properties of the proteins.

The best-studied enzyme of this class with regard to isotope effect behaviour is the ht-ADH. This remarkable enzyme shares a common transition (at ca 30 °C) in both its tunnelling behaviour (Kohen et al. 1999) and protein flexibility (as measured by hydrogen/deuterium exchange; Liang et al. 2004a,b). The data support a model in which the enzyme undergoes a temperature-dependent transition that leads to a local increase in the flexibility of the protein. This change in flexibility is accompanied by changes in both the temperature dependence of the observed primary isotope effects (k_H/k_D, k_H/k_T and k_D/k_T) and the Swain–Schaad relationship for the secondary k_D/k_T and k_H/k_T isotope effects (Kohen et al. 1999).

Focusing first on the primary isotope effects, these were seen to be fairly temperature-independent at elevated, physiologically relevant temperatures and to increase in magnitude as the temperature goes below 30 °C. Since detailed analysis of the kinetic mechanism of ht-ADH at high temperatures had indicated that the hydride transfer step was fully rate determining, the change in isotope effect behaviour at reduced temperatures could not be attributed to increasing kinetic complexity, which would reduce the size of the measured isotope effects. Rather, the data provide strong support for a change in protein structure (PS)/dynamics at the transition temperature of 30 °C, generating A₁/A₂>1 in the elevated temperature range and A₁/A₂<1 at the reduced temperatures (table 4). This shows how an alteration in PS/dynamics, introduced via temperature perturbation for a thermophilic enzyme, can produce a change in the pattern of A₁/A₂ analogous to that demonstrated in SLO upon site-specific mutagenesis (table 3). Turning to the secondary H/T and D/T isotope effects, these were also observed to increase as the temperature was reduced below 30 °C. Most significantly, the extent of increase in the D/T isotope effect greatly exceeded the H/T isotope effect, leading to a trend in the value of EXP, from a high value of ca 15 at 65 °C to a value near 4 at 5 °C (table 4).

Table 4.

Summary of isotopic Arrhenius parameters and the Swain–Schaad exponent for ht-ADH above and below the transition at 30 °C. (From Kohen et al. (1999).)

temperature range (°C)	AH/AD	AH/AT	AD/AT	EXP
5–30	1×10−5 (1×10−5)	0.26 (0.23)	0.23 (0.14)	6.12 (0.80)a
30–65	2.2 (1.1)	4.3 (0.6)	1.73 (0.26)	12.6 (1.52)

^aThe value of EXP at 30 °C has been used for the 30–65 °C and is excluded from the 5–30 °C calculation.

With the data summarized in table 4, ht-ADH offers a unique opportunity to compare trends in isotopic Arrhenius parameters with the Swain–Schaad exponent. If we start with the premise of tunnel correction (as was done in our original publication on ADH (Cha et al. 1989)), the increasing value of the EXP relating the secondary D/T and H/T isotope effects with increasing temperature is anticipated for a greater contribution of tunnelling by protium than deuterium. However, inspection of the Arrhenius behaviour indicates just the opposite: whereas greater tunnelling by H than D at the elevated temperature would predict a value for A₁/A₂<1, an A₁/A₂>1 is experimentally observed. In fact, the value of A₁/A₂ does not become inverse until the temperature is reduced into the range where the magnitude of EXP begins to appear more semi-classical. Thus, the two primary probes of tunnelling in the ht-ADH reaction lead to opposite conclusions, as long as the interpretation is restricted to the ‘tunnelling correction model’. Is it possible to reconcile the opposing trends in the context of a singular physical picture for catalysis? And can this model be extended both to the available data for SLO (table 3) and horse liver and yeast ADHs (table 2).

In the latter context, values of ht-ADH above and below 30 °C have been contrasted with the behaviour of yeast and horse LADH (table 5). It can be seen that the tetrameric yeast alcohol dehydrogenase is closest in behaviour to the tetrameric ht-ADH in its functionally relevant temperature range (above 30 °C), whereas below 30 °C ht-ADH looks much closer to the dimeric horse LADH when studied in MeOH/H₂O mixtures at sub-zero temperatures. Though there is no strict correlation between EXP and A₁/A₂ among the three enzymes, the trends are compatible with the behaviour in table 4.

Table 5.

Comparison of yeast and horse liver alcohol dehydrogenase to the ht-ADH^a.

enzyme	A1/A2	EXP	references
ht-ADH, >30 °C	4.3 (0.6) (H/T)	12.6 (1.52)b	Kohen et al. (1999)
2.1 (1.1 (H/D))
YADH	1.1 (0.1)d (H/D)	10.2 (2.4)c	Cha et al. (1989)
HLADH
>0 °C, H2O	0.49 (0.05) (H/T)	8.5 (1), L57Fc	Bahnson et al. (1993)
	6.3 (0.5), F93Wc
3 °C, MeOH/H2O	0.33 (0.16) (H/T)	5.7 (1.3)c	Tsai & Klinman (2001)
<0 °C, MeOH/H2O	1.5×10−3 (1.3×10−2) (H/D)	7.6 (0.4)b
ht-ADH, <30 °C	0.26 (0.33) (H/T)	6.1 (0.8)b	Kohen et al. (1999)
1×10−5 (1×10−5) (H/D)

^aYeast alcohol dehydrogenase is YADH and horse liver alcohol dehydrogenase is HLADH.

^bThe average value, over the temperature range.

^cMeasured at single temperatures.

^dPlapp (2005).

5. An integrated model for tunnelling in enzymes and implications for catalysis

The early introduction of the concept of a tunnel correction was extremely valuable in that it facilitated the interpretation of experimental data and aided in the eventual acceptance of non-classical behaviour in H-transfer reactions. However, it is important to keep in mind that this is only a ‘correction’ to semi-classical transition state theory and, as such, has limited value in representing the complexity of H-transfer in condensed phase. Historically, enzymes have offered many opportunities to illuminate the aspects of reaction dynamics, because of their characterized structures and well-defined reaction paths. The large body of data available for enzyme-catalysed C–H abstraction reactions provides a basis to postulate a physical model for H-transfer that is both encompassing and has predictive power.

We begin with the premise that there is no reason to formulate the behaviour of deuterium and tritium differently from protium and a QM model for the movement of all the hydrogen isotopes is an appropriate one. The data for SLO have necessitated such a treatment, cf. equations (3.1) and (3.2). Owing to the fact that the analytical equations derived for SLO were based on a non-adiabatic H-transfer process, we have been reluctant to extrapolate the treatment of SLO to the charge transfer that occurs in enzymatic proton or hydride transfer reactions (Knapp et al. in press). Despite this reservation, there is an important recurring theme that has been emerging from this laboratory as well as that of other investigators, independent of the nature of the H-transfer: (i) very often, enzyme-catalysed C–H cleavage reactions show close to temperature-independent isotope effects under optimal reaction conditions, a behaviour that is rarely observed for solution reactions and (ii) this observed isotopic Arrhenius behaviour is converted to a more temperature-dependent regime, when the reaction conditions are altered away from the optimal state.

In the context of full tunnelling model, the above behaviour implies that distance sampling between the donor and acceptor atoms will, where possible, be minimized at the enzyme active site. The degree of distance sampling (or gating) is kept to a minimum by appropriately placed residues, which are often found to be bulky and hydrophobic in nature. The interaction of these residues with bound substrate assures the optimal wave function overlap between the donor and acceptor without introducing a large energy barrier toward the achievement of this state, cf. equation (3.2). It is not to say that distance sampling is not taking place in the optimized enzymes. Rather, the force constant for this motion is fairly stiff and hence, the overall excursions from the initial binding configuration are fairly small.

In actuality, considerable dynamical behaviour within the protein may be necessary to achieve the initially optimized binding state. Consider the properties of the ht-ADH, in which it is found necessary to increase the flexibility of the enzyme (above 30 °C) to produce a situation where the isotope effect has become close to temperature-independent. The enhanced flexibility of the enzyme at the elevated temperatures permits the enzyme–substrate complex to achieve the family of states that promote close approach between the donor and acceptor. We refer to this motion as the ‘coarse tuning’ or preorganization, and anticipate that it can involve a large fraction of the protein and take place on a fairly wide time-scale from nanosecond to millisecond. The second type of motion is what accompanies the subsequent optimization of the active site environment including the distance between the donor and acceptor atoms. This is likely to be more local and occur on a much faster time-scale, picosecond to nanosecond; we refer to this motion as the ‘fine tuning’ or reorganization. Note that local motions within the reactive protein conformations (generated via the preorganization) are necessary to optimize the distance between reactants, and to achieve a transient energetic degeneracy between the H-donor and acceptor (figure 4). The latter may be expected to alter dipolar interactions and the dielectric properties of the active site. We had previously used the terms active and passive motion to describe the distance sampling between reactants versus other heavy atom motions that constitute the fine tuning of the active site. Though the use of the expression ‘active motion’ may imply direct coupling of vectorial motion to the H-transfer coordinate, these motions are more generally believed to be in thermal equilibrium with the solvent bath and to assume a probability (e.g. Boltzmann) distribution.

How do the observed Swain–Schaad exponents fit into this picture for H-transfer? It is important to keep in mind that the active site has been optimized for H, not D, transfer. This phenomenon becomes apparent from the much greater increase in E_a(D) than E_a(H) when site-specific mutants are introduced into the active site of SLO (table 3). In the case of deuterium transfer, it becomes necessary to bring the donor and acceptor atoms closer together than for protium transfer, in order to achieve functional wave function overlap. In native-optimized proteins, this is proposed to introduce a steric component to the D-transfer that is greater than for the H-transfer. The resulting steric crowding may impede the rehybridization of the bonds at the reacting carbon that normally accompanies the tunnelling of the primary nucleus. This is predicted to lower the magnitude of the secondary D/T isotope effect in relation to the secondary H/T isotope effect, both of which are measures of the inner sphere reorganization of the reacting molecules. Once again, the introduction of a site-specific mutant that widens the active site, by reducing the bulk of an active site residue, leads to transfer of both H and D at longer distances. A consequence is a reduction in steric constraints, allowing deuterated reactant to achieve fuller bond reorganization and bringing its behaviour more in line with that predicted from the protium-labelled reactant using the Swain–Schaad relationship. This is fully consistent with the observation that the greatest deviations in the Swain–Schaad relationship are seen for a pattern of substrate labelling in which deuterium has been placed into both the primary and secondary positions of substrate. This also explains why the Swain–Schaad deviations have been seen for secondary but not primary isotope effects.

The above arguments offer a reconciliation of the changes in Swain–Schaad exponents and isotopic Arrhenius behaviour as a function of changes in protein structure. The same phenomenon that optimizes the distance between the H-donor and acceptor is the one that can lead to anomalous secondary D/T isotope effects via steric crowding. Relaxation of the distance constraints via site-specific mutagenesis or a temperature-dependent change in protein structure alters the potential for the distance sampling, leading to a more temperature-dependent isotope effect and to more ‘normal’ secondary D/T isotope effects. This interpretation has been possible through the introduction of a full tunnelling model, and appears independent of the nature of the H-transfer process (hydrogen atom, proton or hydride ion).