Protein dynamics and catalysis: the problems of transition state theory and the subtlety of dynamic control

Abstract

This manuscript describes ongoing research on the nature of chemical reactions in enzymes. We will investigate how protein dynamics can couple to chemical reaction in an enzyme. We first investigate in some detail why transition state theory cannot fully describe the dynamics of chemical reactions catalysed by enzymes. We describe quantum theories of chemical reaction in condensed phase including studies of how the symmetry of coupled vibrational modes differentially affects reaction dynamics. We make reference to previous work in our group on a variety of condensed phase chemical reactions (liquid and crystalline) and a variety of enzymatically catalysed reactions including the reactions of lactate dehydrogenase and purine nucleoside phosphorylase. All the protein motions we have studied have been quite rapid. We will propose methods to find motions over a broad range of time-scales in enzymes that couple to chemical catalysis. We report recent findings which show that conformational fluctuations in lactate dehydrogenase can strongly affect its ability to catalyse reactions through protein motion, and that only a tiny minority of conformations appear to be catalytically competent.

1. Introduction

The physical and chemical details of the mechanisms by which enzymes catalyse chemical reactions are still a matter of some controversy. In this paper, we will first suggest that static models of enzymatic catalysis, dominant in the biochemistry field for many decades, are not sufficient to understand the nature of this phenomenon. In fact, we will explore in detail the main source of this view (in our opinion), the transition state theory (TST). We will discuss the assumptions of TST, and why these assumptions fail in biochemical reactions. Second, we will provide evidence that in a specific enzyme, nature has created the protein structure so that only a tiny subset of all possible conformations are perfectly designed to link dynamics to catalysis.

There are currently four generally accepted mechanisms for the manner in which this rate acceleration is accomplished. In the order of age of introduction, they are: transition state stabilization (Pauling 1948), substrate destabilization (Jencks 1975), reactive population or ‘near attack conformation (NAC)’ formation (Lau & Bruice 1998; Torres et al. 1999; Bruice & Benkovic 2000) and finally dynamic coupling of the protein motions to the reaction coordinate (Antoniou & Schwartz 2001; Caratzoulas & Schwartz 2001). We have previously reviewed this subject at length in a variety of publications (Antoniou et al. in press a,b; Schwartz 2004a,b, in press), and so will not repeat these detailed descriptions, but simply refer the reader to these publications. It is important to remember that no single mechanism is mutually exclusive of the others, and all may well be present to a greater or lesser degree in all enzyme reactions. We would now amend our previous reviews with a fifth mechanism that is closely related to both dynamic coupling and reactive population formation, and this may be termed configurational modification of reaction barriers. As in dynamic coupling mechanisms, motion of the protein couples to the reactive degree(s) of freedom in such a manner to affect the barrier to reaction; however, this modification happens on a sufficiently slow time-scale that the reaction may be viewed to occur in a statistical distribution of barrier heights. There is now significant evidence that such a mechanism is perhaps dominant in hydride transfer in dihydrofolate reductase (Agarwal et al. 2002a,b; Garcia-Viloca et al. 2003; Rod et al. 2003; Thorpe & Brooks 2003, 2004; Wong et al. 2005). We have in fact found clear evidence for direct dynamic coupling of the reaction coordinate to protein dynamics in the form of a promoting vibration in alcohol dehydrogenase (Antoniou et al. 2002; Caratzoulas et al. 2002; Kalyanaraman & Schwartz 2002); a similar coupling in lactate dehydrogenase (LDH) (Basner & Schwartz 2004) in fact helps to explain how almost identical isoforms can kinetically favour one side of a chemical reaction versus another depending on the physiological environment in which the enzyme is located. Recently, applying the transition path sampling methodology (Bolhuis et al. 1998, 2000; Csajka & Chandler 1998; Dellago et al. 1998), we have shown that a motion which extends from one end of the LDH protein to the other is required to allow the reaction to occur (Basner & Schwartz 2005). In fact, if any part of this vibrational motion extending through the body of the protein is blocked, then the reaction is in turn blocked. We have also shown that a vibrational motion in the enzyme purine nucleoside phosphorylase compresses a stack of oxygen atoms causing polarization of a bond being broken in the reaction, and thus creates a better leaving group (Nunez et al. 2004).

What is apparent in examining the evolving schools of thought regarding the physical mechanism for catalysis is a dichotomy between what might be termed a ‘static’ reaction coordinate view and a more dynamic view that naturally requires motion as part of the physical picture. We place static in quotes in the previous sentence because clearly all would view atomic motion as necessary for reaction—rather the static nature of the argument relates to the physical picture of passage over the reaction barrier. In both the transition state stabilization and reactant destabilization view, the reaction coordinate may be drawn as a fixed one-dimensional free-energy picture for all reactants as they make the transition to products. Generations of biochemistry students have seen such one-dimensional plots in their textbooks. On the other hand, the coupling of either slow or rapid motions to the reaction coordinate necessitates that a single unchanging reaction free energy diagram may not be drawn. Physical chemists have known for many decades that in gas-phase reactions, the passage over a barrier to reaction is a multi-dimensional event. In fact, even in the most trivial of all hypothetical chemistries, the collinear approach of H to H₂ to transfer a hydrogen and form H₂+H, a subtle combination of the symmetric and antisymmetric motions combine to form the reaction coordinate. It is well known that at low energies, the passage follows the minimum energy path on the potential energy surface, but as the energy gets higher, the motion can become far more complex with bobsledding-like motions far away from the saddle, which is the low-energy bottleneck to reaction. In fact, as the energy increases, the transition state moves off the saddle into the reactant and product channels (figure 1).

Figure 1.

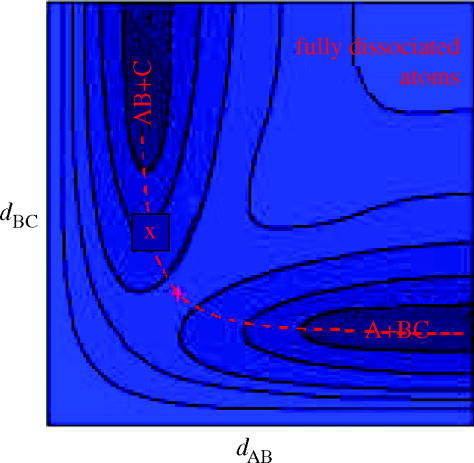
A contour plot of a generic potential energy surface for a triatomic reaction system. The red X occurs at the saddle on the surface. At very low energies, this saddle is also the bottleneck to the reaction or the transition state (TS). At higher energies, the TS moves symmetrically into the reactant and product channels.

If a single fixed reaction coordinate and one-dimensional energy diagram is not possible in this most trivial of reactions, then it seems impossible to understand how such a concept could have arisen in a system as complex as an enzymatic reaction with tens of thousands of degrees of freedom. We shall argue that in some sense, the fault lies with success. The success is the empirical success of TST. This methodology has been widely applied in areas from gas-phase reaction dynamics to condensed phase chemistry and biological chemical reactions. This paper presents two different areas of endeavour. First, we will explain why TST, though highly successful in some ways, has been deeply problematic for deeper understanding of biological reactions, and second, we will explore very recent results from our group suggesting that protein dynamics is employed in highly specialized ways to promote chemistry in enzymatic reactions. This work builds on the previous work of our group, which shows that in single conformations of a protein, promoting vibrations are crucial for the catalytic effect. We now show that only a tiny subset of protein conformations seems competent to employ such motions.

2. Transition state theory: assumptions that are not justified

Since TST has become so deeply entrenched as a tool for experimentalists to interpret their data, it is often forgotten that there are basic assumptions which are needed to justify the use of this approximate approach to reaction dynamics. The rigorous justification for TST was developed several years ago by Pechukas (Pechukas & Pollak 1979) and Miller (Chapman et al. 1975). For detailed derivations of the transition state formulae, we direct the reader to the basic literature. The basic assumptions of TST are as follows:

1. classical mechanics is an accurate description of the atomic motion on the potential energy hypersurface.

2. There is a dynamic bottleneck to reaction—not necessarily the saddle point on the surface. If there is more than one bottleneck, there is no interaction between the bottlenecks (transition states) or the degrees of freedom orthogonal to the reaction coordinate.

3. Any trajectory which reaches this bottleneck with infinitesimal kinetic energy in the directions of products will go on to react, and there is no recrossing back to the product side once the bottleneck has been passed.

4. The potential energy surface is strictly separable at the transition state, i.e. there is no dynamic coupling between the reaction coordinate motion and all other degrees of freedom when the reaction is in the vicinity of the transition state.

Pechukas & Pollak (1979) showed that if certain geometric constraints are met by the potential energy hypersurface, then in fact TST could be exact (if the above requirements are also met). In general, there are two reasons for TST failure. First, when the reaction involves the transfer of a light particle, such as a hydrogen atom, it is rarely the case that classical mechanics suffices to describe reaction dynamics. Second, as Miller (1974) has shown in a variety of ways, the separability condition inherent in TST is almost never met.

In fact, this failure can be quite spectacular, and one example of this failure is the case of the promoting vibration we have now described for a number of enzymatic systems (Antoniou & Schwartz 2001; Caratzoulas & Schwartz 2001). It is instructive to examine how the assumptions of TST can fail even in a simple model system. As we have described many times, the simplest mathematical model of a reaction coordinate in an environment coupled to a promoting vibration (a symmetrically coupled vibration) is given by the Zwanzig Hamiltonian with the addition of a symmetrically coupled mode:

$$H=\frac{P_s^2}{2m_s}+V_o+\sum _k\frac{P_k^2}{2m_k}+\frac{1}{2}{m}_k{\omega }_k^2{\left(q_k-\frac{c_{k}s}{m_k{\omega }_k^2}\right)}^2+\frac{P_Q^2}{2M}+\frac{1}{2}M{\Omega }^2{\left(Q-\frac{C{s}^2}{M{\Omega }^2}\right)}^2.$$ (2.1)

P_s is momentum of reaction coordinate particle, m_s is mass of same, V_o is reaction coordinate potential, P_k is momentum of coupled mode k, m_k is mass of coupled mode, ω_k is frequency of coupled mode, q_k is position of coupled mode, c_k is strength of coupling of mode and reaction coordinate, P_Q is momentum of promoting vibration, M is mass of promoting vibration, Q is position of promoting vibration, Ω is frequency of promoting vibration, C is coupling of promoting vibration.

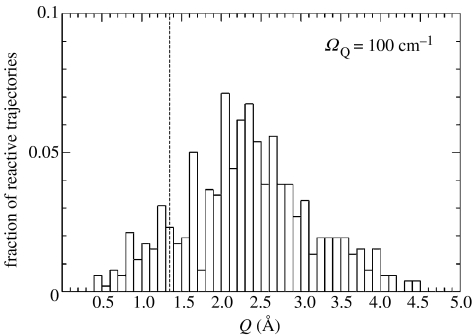
We studied this Hamiltonian purely classically with the help of transition path sampling (Antoniou & Schwartz 2004). The model we chose for the study was a symmetric double-well potential with a barrier height of 6 kcal mol⁻¹ and transfer distance of 1.0 Å. One thousand environmental, antisymmetrically coupled oscillators with frequency of 10–1000 wavenumbers were used. After generation of a large transition path ensemble, we plot a histogram of the location in the promoting vibration coordinate as reactive trajectories cross the reaction coordinate saddle. The results are shown in figure 2. What is apparent from this computation is that few trajectories pass through the saddle. One may make the argument that in this system the saddle point is not the bottleneck to the reaction, and so is not in fact the transition state, but it is also apparent from figure 2 that trajectories cross in a wide variety of locations and no single location is dominant. We would suppose that if a transition state were located by a variational procedure, it would probably be about 2.5 Å in Q. What is clear is that the detailed dynamics is far more complex in this simple model than that might be implied by TST. In fact, it is entirely conceivable that a rate computed using TST for this model would be fairly accurate when compared with classical flux over population type computations. It would, however, be giving an imprecise impression of the physics behind that rate. Herein lies both the success and difficulty of importance of TST. It does a fairly good job in predicting highly averaged properties such as rates, but it is not always the case that this model can help to produce an understanding of microscopic physics.

Figure 2.

A histogram of trajectories for a system of reaction coordinate, one promoting vibration and 1000 environmental degrees of freedom. The dotted line shows the location of the promoting vibration at the saddle. The reaction coordinate is a symmetric double well of height 6 kcal mol⁻¹ and transfer distance of 1 Å (adapted from Antoniou & Schwartz 2004).

3. Dynamics in multiple conformations

Having described the limitations of TST for understanding the dynamics of enzymatic reactions, we wish to understand how the protein matrix and the active site do in fact accomplish chemical catalysis. As stated earlier, we have found motions, termed promoting vibrations, that are directly coupled to passage along a reaction coordinate, and account for known experimental features such as suppression of primary kinetic isotope effects and anomalous signatures of tunnelling as a function of temperature in thermophilic enzymes. What remains a mystery is why a motion on a picosecond time-scale couples to a reaction in an enzyme that has a turnover rate of about 1 ms. We have long supposed that this is because the enzyme does a stochastic search through configuration space until all needed components of catalysis are in place. For example, the enzyme clearly does much more than bringing the donor and the acceptor close together. All the other features—charge stabilization, reactant pre-organization and expulsion of water from the active site to name a few—identified over the years as critical for the enzyme function must be present. As an indication of the importance of protein dynamics, we implemented a search on the potential energy surface of human LDH to identify the prevalence of conformations that are expected to be catalytically competent in a single component of catalysis, the donor–acceptor (DA) distance. The end result of our search reported later is that only a small fraction of conformations lower DA distance, and this supports the supposition that enzyme matrix is designed to search conformations and chemistry happens when those appropriate are found.

(a) Model preparation

Chain A of the muscle isoform of human l-LDH (PDB ID 1I10) was used in all molecular simulations reported in this work. The MMTSB toolset was used for structure file preparation. Using the CHARMm HBUILD utility, hydrogens were added in the PDB structure of the protein. Since LDH is complexed with oxamate, lactate was built by replacing the nitrogen of oxamate with a carbon in the original crystal structure. The parameters for lactate were assigned by analogy to existing parameters of some amino acid side chains. Hydrogens were added into the structures of lactate and nicotinamide adenine dinucleotide (NAD) by using the internal coordinate utilities of CHARMm. Crystallographic waters that have oxygen atoms that are within 10 Å of any of the lactate heavy atoms were retained in the final model. The total charge of the system is +1.

To energy minimize the position of hydrogen atoms, a harmonic restraining force of 50 kcal mol⁻¹ was applied on the heavy atoms, while the entire system was subjected to 10 000 steps of steepest descent (SD) minimization. The restraint was then removed and the system was allowed to further minimize in energy with 20 000 steps of SD and 5989 steps (after the gradient tolerance of 0.001 was satisfied) of adopted basis Newton–Raphson (ABNR) minimization. Protein structure (PSF) and CHARMm coordinate files were written for the entire system for further calculations.

(b) Search for unique conformations: Monte Carlo plus energy minimization

In order to search for unique minima that have shorter DA distance (short relative to the energy minimized X-ray structure), we utilized the Monte Carlo plus minimization strategy first proposed by Li & Scheraga (1987). We implemented this algorithm in the Monte Carlo module of CHARMm 29 (Dinner 1999). For this preliminary simulation, the only allowed move types were rotation of peptide side chain torsions, phi torsions, psi torsions and peptide bonds. The maximum allowed distortion for each move type was 70° for the side chain torsions and 15° for the rest of the move types. One thousand steps of SD minimization follow each move instance with gradient tolerance of 0.0001 and step tolerance of 0.0001. After minimizing the initially perturbed structure, the Metropolis acceptance criterion is implemented. One thousand Monte Carlo steps were implemented for this preliminary work and snapshots were saved for all 1000 steps.

Since the trajectory file contains only snapshots of configuration that were accepted in a Monte Carlo step in Metropolis Monte Carlo, we identified unique frames as those that have unique energies and unique r.m.s.d. when compared to the minimized X-ray structure. Seventy-nine out of the 1000 frames were identified as unique. Some representative numbers were obtained for these frames, namely: CHARMm potential energy; r.m.s.d. with respect to the minimized X-ray structure; distance between C_β atom (in CHARMm nomenclature) of valine 30 and NN1 of NAD; and distance between C2 of lactate and NC4 of NAD (DA distance).

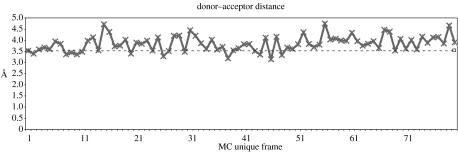
In order to compare the above measures of uniqueness with the information in the minimized crystal structure, we further allowed the energies of the unique configurations to minimize with 20 000 steps of SD and 15 000 steps of ABNR. Similar to what was imposed during the minimization of the crystal structure, a tolerance in gradient of 0.001 was also imposed during the ABNR steps. Potential energy, r.m.s.d. and atomic distances were again measured for this set of minimized frames. The DA distance in these 79 Monte Carlo frames is listed in figure 3.

Figure 3.

Unique Monte Carlo (MC) frames generated from 1000 MC moves. Seventy-nine are unique conformations. Of these, only 14 have DA distance at or lower than the crystal structure.

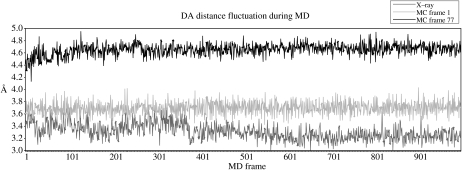
What is clear from this relatively crude search is that after thousands of Monte Carlo moves, only a small fraction of the minimized structures forms unique conformations and only a smaller fraction seems to have DA distances less than the minimized crystal structure. The clear suggestion from this is that there are quite a small number of catalytically competent conformations. To see how propagation in time with molecular dynamics would affect this result, we took the unique conformations identified in the Monte Carlo with minimization search and, after heating and equilibration as we have previously described, we propagated the structures using classical dynamics. In fact, a number of structures that seemed to have lower DA distance than the crystal structure under classical evolution had the DA distance open to yield a less favourable configuration. In addition, no tested structure during propagation formed a smaller DA distance than that of the crystal structure. Representative results are shown in figure 4.

Figure 4.

Molecular dynamics (MD) evolution of three structures generated in our Monte Carlo: the crystal structure (grey), a frame initially with lesser DA distance that opens to greater DA distance (light grey frame 1) and finally one which starts with greater DA and remains greater (black frame 77).

While there are certainly many more important factors in catalysis than DA distance, this factor is also critical for reactivity. It has long been wondered how motions such as promoting vibrations that are picosecond-type motions can fit into the millisecond time-scale of enzymatic turnover. This computation gives insight into why the enzyme takes so long to catalyse the reaction—it is simple that a large conformational space needs to be searched to find the rare conformation required to produce the needed dynamic effects.

4. Conclusions

This short paper has attempted to accomplish two connected goals. First, we have explored the basic assumptions behind TST, and shown why these assumptions cannot possibly be met in complex enzymatic reactions. We then presented a model system computation in which it was shown in a double well coupled to an environment and to a symmetrically coupled promoting vibration, reactive trajectories pass through a wide range of points, most of which are not the saddle, and which, incidentally correspond to large differences in potential energies as the reactants pass to products. In writing this manuscript, it has come to our attention that a recent paper by Vanden-Eijnden & Tal (2005) arrives at similar conclusions through very different analyses. We should point out that the limitations of the theory do not necessarily mean that it cannot reproduce average quantities such as rates in some cases (under the hands of true practitioners of the art). It does mean that it is not wise to interpret the accuracy of reproduction of an averaged quantity such as rate as a sign of physical understanding.

In the second part of this manuscript, we have continued our analysis on LDH. The principal conclusion from this work, at least as far as donor–acceptor distance is concerned, is that, of the many conformations available to the protein, it seems that only a tiny subset is actually catalytically competent. This fits well with our concept that the vast disparity between the promoting vibrations and barrier passage as compared to the rate of enzyme turnover must be related to a required stochastic search through protein conformation space needed to find the small region in phase space where the enzyme is able to catalyse the reaction.