Size exclusion chromatography does not require pores

Abstract

Separation of macromolecules on the basis of their molecular weight by size exclusion chromatography has long been considered to be caused by the geometry-dependent partition of macromolecules between a continuous phase and the porous interior of a gel or cross-linked bead. The volume of a pore accessible to a solute is limited by its relative dimensions, so larger molecules will have access to a smaller volume and will remain in a bead for a shorter time than smaller solutes. Our recent alternate picture proposes that the partition coefficient can be calculated from a thermodynamic model for the free energy of mixing of the solute with the gel phase. Size-dependent exclusion caused by the unfavorable entropy of mixing associated with the partition is predicted; the magnitude of the effect is modified by enthalpic interactions between the solute and the gel phase. This concept is extended here to describe the partition of macromolecules into a layer of terminally attached polymer chains grafted onto a solid bead. Both simple mean field and self-consistent field theory calculations predict size-dependent entropic exclusion. Experimental results obtained with neutral polymer chains grafted onto solid polystyrene latex beads confirm the predictions.

Descriptions of size exclusion chromatography are almost inextricably linked to the presence of a porous or gel-like solid phase. All theories except those discussed here assume that solute partition occurs because of geometric limitations on the volume available to the solute molecules within the pores of the chromatography material (1–7). We recently proposed an alternative way of picturing the partition process by considering the free energy of mixing of the solute with the polymeric gel phase (8). In this treatment the volume of the polymer phase was not explicitly considered. In principle exclusion should be present even if the solute interacts with a single layer of polymer molecules terminally grafted to a solid surface.

The properties of terminally attached polymer layers have been studied extensively because of their wide application as particle stabilizers (9) and as a means by which to modify macromolecular adsorption (10) and biological recognition reactions at interfaces (11). The behavior of the grafted chains, their configuration (mushroom or brush), and the forces generated when chains bound to separate surfaces are brought into overlap all have been considered theoretically and experimentally (12, 13). Because grafted polymers have been widely used to reduce protein adsorption, theoretical and experimental investigations of these effects also have been carried out (14, 15). That such grafted layers are capable of greatly reducing protein adsorption at some interfaces implies that an unfavorable free energy change occurs when protein interacts with a grafted layer. The magnitude of this free energy of mixing can be estimated for a polymer solution in equilibrium with a surface phase containing a second polymer plus solvent (16). Ignoring for the moment the terminal attachment of each chain, the first-order Flory–Huggins mean field expression for the partition coefficient of a dilute solution of polymer 3 is (8):

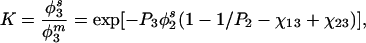1

where φ_i = volume fraction of component i defined below; i = 1, 2, 3 refers to solvent, surface phase polymer and solute polymer, respectively; superscripts refer to surface phase (s) or bulk medium (m);

where n_i = number of moles of component i; P_i = ratio of the volume of the molecule of polymer molecule i to the volume of the solvent molecule = number of segments per polymer molecule; χ_ij = Flory interaction parameter, defined by

where z = lattice coordination number; Δɛ_ij = interaction energy of an ij segment-segment or segment-solvent contact;

where kT = Boltzmann's constant x absolute temperature.

Eq. 1 predicts that at equilibrium the concentration of solute in the surface phase should be lower than in the bulk solution, the more so the higher the molecular weight of solute, the higher the surface phase polymer concentration and the higher the molecular weight of the surface phase polymer. A sequence of such equilibria between a mobile and stationary surface phase, therefore, would result in size exclusion chromatography.

Methods

Synthesis and Analysis of Grafted Core/Shell Latex.

Cationic surfactant-free poly(styrene) latex was prepared from a seed plus three growth stages by using 2,2′azobis(2-amidino propane)dihydrochloride as initiator (20). A copolymer shell of styrene and acrolein typically was synthesized at 5°C by preswelling 3.3% (wt/wt) latex in water with styrene (2 × 10⁻³ M/g latex), then adding acrolein, (2 × 10⁻³ M/g latex) followed by 9.2 × 10⁻⁴ M/liter initiator (all final concentrations), under Ar with stirring at 350 rpm in a 500-ml flask. Extensive dialysis and centrifugal washing in distilled then MilliQ-purified water then was carried out. Grafted layers of poly(methoxyethyl acrylamide) (PMEA) were synthesized in situ typically by stirring monomer (0.65–1.3 M), ≈20% latex, and 5.X 10⁻² M cerium (IV) ammonium nitrate in 10 mM nitric acid and stirring under Ar for 1 h at 4°C then at room temperature for ≈66 h before washing by centrifugation with 0.1 M sodium sulfite in 0.1 M acetic acid then 0.03 M EDTA followed by water. Aldehyde content was determined by reacting the latex with hydroxylamine hydrochloride followed by conductometric titration of the HCl released (21). 2-Methoxyethylacrylamide) (MEA) content was determined from the uptake of monomer as assessed by reverse-phase HPLC of the supernatants.

Chromatography.

Typically 20% latex in distilled water was packed under pressure in a steel HPLC 75 × 4.6-mm column and equilibrated with the mobile phase at room temperature at a flow rate of 0.1 ml/min. Solutions of proteins typically in 10 mM sodium phosphate, 300 mM sodium chloride, pH 7.2 were made up at 1 mg/ml (except myoglobin at 0.5 mg/ml). Low ionic strength solutions were identical except in 2.5 mM sodium phosphate, 2.5 mM sodium chloride. DNA (15.6 × 10⁻³ mg/ml) concentration was such that the elution time was independent of concentration. Aliquots of 20 μl of each protein solution were run on each column at a flow rate of 0.1 ml/min, monitoring at 260 nm for DNA and at 280 nm for protein. The void volume V₀ [determined with DNA or keyhole limpet hemocyanin (KLH)], total volume V_t (determined with sodium nitrate), number of theoretical units per m, N, permeability P, and partition coefficient K were calculated as described (22), with K given by K = (V_e − V_o)/(V_t − V_o), where V_e is the elution volume for each protein. The macromolecules used, followed by their molecular mass, radius of gyration (23) (R_g) and, except for KLH and DNA, isoelectric point are: insulin (5.8 kDa, 12.4, 5.3); Mb (17.2 kDa, 17.2, 7); trypsin inhibitor (21.5 kDa, 18.5, 4.5); ovalbumin (43 kDa, 23.4, 4.6); BSA (68 kDa, 27.2, 4.9); human serum albumin (66 kDa, 26.9, 4.9); KLH (3 × 10⁶ Da, 96.1); and Lambda DNA (3.2 × 10⁷ Da, 212).

Results

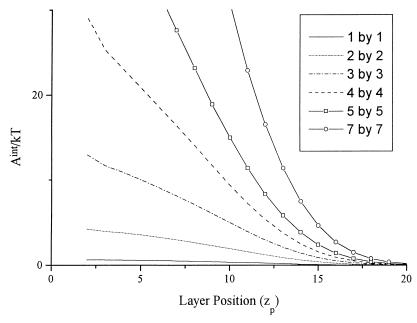
The simple mean-field result (Eq. 1) is expected to describe the general nature of the interaction correctly provided that the surface phase is deeper than the nominal diameter of the partitioning species. A more quantitative picture of a solute molecule's interaction with a brush layer requires a model for the surface phase that explicitly takes into account the terminal attachment of the polymer chains to the underlying solid. Self-consistent field (SCF) theory (17, 18) provides a general method for calculating polymer-segment density profiles of brushes in the direction normal to the grafting surface. We have converted SCF theory to cylindrical coordinates (19) to simulate the energetics of a particle positioned at the cylinder axis interacting with a brush of varying polymer density and chain length. Fig. 1 shows calculated interaction energies A^int (where A indicates a Helmholtz-type energy), including solvent redistribution effects, required to move cylindrical solute particles of varying size into a grafted-polymer brush under conditions where the brush-particle interaction is enthalpically neutral. At a given layer position (z_p) within the brush volume, A^int is positive, indicating a net repulsive brush-particle interaction, and increases sharply with increasing particle size. Penetration of a particle into the brush volume decreases the conformational entropy of the grafted chains, leading to a net repulsive A^int that strongly increases with particle size. This is the basis for polymer brush-mediated size-exclusion chromatography, which we call entropic interaction chromatography (EIC) to reflect the dominance of entropic effects in the separation.

Figure 1.

Brush-particle interaction energies, calculated from SCF theory for a 10% surface-density brush composed of chains of length n = 50, as a function of particle position and size. Flory interaction parameters for the brush-solvent (bo) and particle-solvent (po) are specified as χ_bo = χ_po = 0.4, for the particle-brush χ_bp = 0. Size of the cylindrical particle has been varied from R_p = L_p = 1 to R_p = L_p = 7, where R_p and L_p are the cylinder radius and length, respectively, and 1 by 1 indicated, for instance, a cylinder where R_p = L_p = 1.

To test the theoretical predictions we synthesized nonporous cationic core/shell surfactant-free polystyrene latex carrying terminally attached chains of PMEA of varying surface concentration and mean molecular weight. The PMEA grafts were initiated by CeIV reaction with surface aldehyde functions contained in a copolymer shell polymerized from a mixture of styrene and acrolein. A similar approach is used in the tentacle-type size exclusion gels available from Merck albeit in porous media. The surface concentration of reactive aldehyde functions was determined by a titration procedure and the mass of PMEA grafted was calculated from monomer depletion, allowing the mean molecular weight of the graft to be calculated, assuming all aldehydes reacted with CeIV and monomer. Various latex preparations were synthesized, as described in Table 1. Each latex preparation, plus one without the PMEA graft present, was packed into a 75 × 4.6-mm steel column and used as the stationary phase for chromatographic elution of each of a series of standard proteins.

Table 1.

Characterization of grafted beads and parameters of columns

Batch #	Particle diameter, μm	Polymerized MEA,* mole/g latex	Tether coverage,† MEA groups/Å2	Length of grafted chains,‡ DP	N,§ m−1	Permeability¶	Back pressure, bar
A1	2.30  ± 0.81	1.40  × 10−3	3.41	76	10,306	0.16	15
B1	2.66  ± 0.82	3.53  × 10−3	9.93	350	14,200	0.35	20
C1	2.76  ± 0.88	0.43  × 10−3	1.26	60	6,187	0.31	8
C2	2.76  ± 0.88	2.00  × 10−3	5.88	283	10,040	0.27	18

^*Calculated under the assumption that all polymerized MEA was distributed on the beads, using monomer conversion data (HPLC of the supernatant) and the amount of seed in each synthesis. 

^† Calculated from the formula: MEA/Ų = PN_A/10¹⁶ (SA/g), MEA groups/Ų, where P = polymerized MEA amount, moles/g latex; SA = surface area available on the latex, Ų/g latex; N_A = Avogadro's number, mole⁻¹. 

^‡ Assuming that all the aldehyde groups initially present on the latex started grafted chains; DP = degree of polymerization. 

^§ N = number of theoretical units per m. 

^¶ Units of volume per volume. 

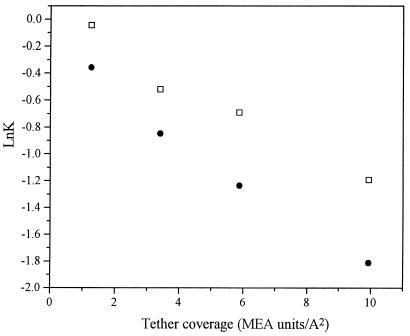
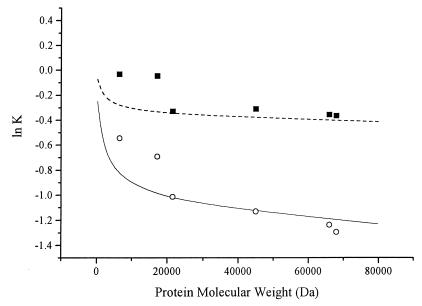
Fig. 2 shows that molecular weight-dependent separation was obtained in the presence but not in the absence of the surface layer of PMEA. The elution profiles of sodium nitrate were used to calculate column efficiency (i.e., number of theoretical units per unit length) and the equivalent permeability for each packing (Table 1). The void volume (data not shown) and back pressure for continuous operation also were measured (Table 1). The values of lnK for myoglobin and human serum albumin are plotted as a function of the number of monomers of MEA coupled per unit area in Fig. 3. Clearly, lnK decreases with increasing surface phase concentration, as predicted. Fig. 4 shows that the molecular weight dependence is also of the predicted form: lnK, where K is the solute partition coefficient, decreases with molecular weight of solute. Here, the calculated K is the average concentration of solute within the brush volume C_p^avg over the concentration in the bulk liquid phase C_p^bulk:

2

Moreover, assuming the calculated degrees of polymerization given in Table 1 are correct, the small increase in molecular weight sensitivity (i.e., greater slope of lnK vs. molecular weight) is in the direction predicted as the molecular weight of the graft is increased from C1 to C2.

Figure 2.

Elution volume as a function of analyte molecular weight (MW) for columns B0, packed with beads without PMEA graft (□) and B1, packed with beads carrying terminally attached chains (■). Solutes loaded are: sodium nitrate (log MW = 1.9), myoglobin (log MW = 4.2), human serum albumin (log MW = 4.8), and keyhole limpet hemocyanin (log MW = 6.5).

Figure 3.

Variation of the partition coefficient of myoglobin (□) and human serum albumin (■) versus grafted PMEA coverage for columns A1, B1, C1, and C2.

Figure 4.

Measured and calculated partition coefficients as a function of protein molecular weight for columns C1 (■) and C2 (□). Characteristics of both columns are provided in Table 1. Proteins are: insulin (5.8 kDa), myoglobin (17.2 kDa), trypsin inhibitor (21.5 kDa), ovalbumin (43 kDa), human serum albumin (66 kDa), and BSA (68 kDa). Calculations are based on SCF theory in a cylindrical geometry for surface-graft densities of 2% (C1 column) and 10% (C2 column). Model scaling was based on polymer and protein radius of gyration data, resulting in approximate tether coverages of 1.5 groups/Ų (upper curve) and 6 groups/Ų (lower curve); χ_ij as in Fig. 1.

Comparison of the experimental data with the predictions of the SCF calculation show that the curvature observed in the lnK-molecular weight plots are in fact predicted by the numerical model. Because it is assumed in the SCF calculations that the solute-brush interaction parameter is zero, the exclusion illustrated can be explained solely in terms of the unfavorable entropy of mixing occurring in the surface phase when the solute attempts to enter it. As such it is a perfectly general effect that does not depend on specific chemical properties of the solute. It is noteworthy that grafted layers of degree of polymerization <100 can produce such strong effects without the influence of the underlying solid surface being felt. Because most of the proteins applied to the column bore a net negative charge at the pH of the experiments and because the latex has a net positive surface charge from its cationic initiator, which must reside at the water/polystyrene interface, any significant exposure of the solid polymer would result in protein adsorption and peak broadening, which was not observed. Even at low ionic strength, the lnK vs. molecular weight plot for insulin, myoglobin, trypsin inhibitor, and ovalbumin was indistinguishable from the result obtained in 300 mM salt and no peak broadening was observed.

Discussion

The description of the grafted layers embodied in Table 1 provides their average properties, assuming a uniform distribution of polymerized monomer over the bead surface whose number density is given by the surface concentration of aldehyde groups. In fact, the real situation is likely to be more complicated because it is unlikely that all potential sites from which polymerization could be initiated (the aldehyde functions) carry chains of equal length, as is assumed in the calculations. Using CeIV initiation of MEA from cleavable hydroxyl functions on latex surfaces, we recently have shown that the molecular weight distribution of the grafted chains is trimodal, a highly unusual result (24). Nonetheless, such particles also exhibit SEC of proteins analogous to that illustrated here (data not shown). Hence, the molecular weight distribution of the surface polymer does not have to be narrow or monodisperse to provide size exclusion effects.

As chromatographic media, solid particles bearing surface polymer layers have some advantages compared with porous particles and gels. The calculations illustrated in Fig. 4 show that the strongest molecular weight dependence occurs for low molecular weight analytes, in contrast to normal SEC, which typically behaves poorly in this range. Also, the mass transfer kinetics for macromolecules interacting with polymer layers on impermeable beads are superior to permeable particles, albeit at the cost of reduced capacity. Finally, although we have not demonstrated this, it is likely that if solid latex was terminally derivatized with chains carrying ionizable groups or affinity ligands that interaction chromatography could be carried out, because the porous ion exchange beads manufactured by Merck carry similar “tentacle” chains and are very effective separation media.

In summary, the above results clearly show that SEC does not require a porous stationary phase and demonstrate a mode by which SEC may be performed. In addition, they suggest a rich theoretical and experimental approach to understanding interactions of macromolecules with surface polymer layers that, through the partition coefficient, provides a description of the interaction heretofore unavailable.

Abbreviations

PMEA

poly(methoxyethyl acrylamide)

MEA (2-methoxyethylacrylamide

SCF, self-consistent field