Determination of In Situ Bacterial Growth Rates in Aquifers and Aquifer Sediments

Abstract

Laboratory and field-scale studies with stained cells were performed to monitor cell growth in groundwater systems. During cell division, the fluorescence intensity of the protein stain 5-(and 6-)-carboxyfluorescein diacetate succinimidyl ester (CFDA/SE) for each cell is halved, and the intensity can be tracked with a flow cytometer. Two strains of bacteria, Comamonas sp. strain DA001 and Acidovorax sp. strain OY-107, both isolated from a shallow aquifer, were utilized in this study. The change in the average generation or the average fluorescence intensity of the CFDA/SE-stained cells could be used to obtain estimates of doubling times. In microcosm experiments, the CFDA/SE-based doubling times were similar to the values calculated by total cell counting and were independent of cell concentration. Intact and repacked sediment core experiments with the same bacteria indicated that changes in groundwater chemistry were just as important as growth rates in determining planktonic cell concentrations. The growth rates within the sediment cores were similar to those calculated in microcosm experiments, and preferential transport of the daughter cells was not observed. The experiments indicated that the growth rates could be determined in systems with cell losses due to other phenomena, such as attachment to sediment or predation. Application of this growth rate estimation method to data from a field-scale bacterial transport experiment indicated that the doubling time was approximately 15 days, which is the first known direct determination of an in situ growth rate for bacteria in an aquifer.

Field-scale studies have demonstrated that microbes can be transported significant distances in the subsurface over short periods of time. In contaminated aquifers, microbes with specialized properties that allow them to degrade contaminants usually become ubiquitous within a few years (4, 23). If these bacteria were not initially present, then transport of the microbes into the contaminated zone must have occurred. In areas of the subsurface that have been geologically sterilized by heat and subsequently cooled, a large and diverse population of microbes is now present (5, 42, 43). Laboratory and field experiments, however, have indicated that most microbes preferentially stick to geologic material and have a low propensity for transport (7, 15). These contradictory facts indicate that there must be mechanisms that enable microbes to rapidly populate new areas of the subsurface. Mechanisms that may facilitate microbial colonization of the subsurface include the existence of a range of microbial cell surface properties within each species (26, 39), slow continuous transport (44), and preferential transport of daughter cells (27, 30). The goals of this study were to develop a method that can track both the transport and the growth of viable cells in situ and then to utilize the method to determine how microbes propagate through and populate the subsurface.

During subsurface bacterial transport, bacteria can passively migrate with the ambient groundwater flow or swim along a chemical gradient, they can attach to or detach from the solid matrix, and they can grow, die, or be consumed by protists (29). During sampling of an aquifer, an increase in the growth or detachment rate or, conversely, a decrease in the death, predation, or attachment rate produces an increase in the number of observed planktonic cells. In previous studies workers have attempted to determine in situ growth rates from ex situ microcosm experiments (16), isotopic and geochemical analyses (31, 32, 34), and fitting growth rate parameters in coupled groundwater flow and transport models (29, 33). In pristine aquifers, the doubling times based on CO₂ production were estimated to be at least 100 days, which is longer than the doubling times for soils, lake sediments, and deep-sea sediments (32).

The use of 5-(and 6-)-carboxyfluorescein diacetate succinimidyl ester (CFDA/SE)-stained microbial cells coupled with flow cytometry has the potential to track both the transport and the growth of cells in situ (11, 24, 25). CFDA/SE is a nontoxic protein stain that divides evenly from the parent to the two daughter cells upon cell division (24). Stained cells can be easily distinguished from the indigenous microbial population and background fluorescent material with a flow cytometer, making determinations of concentration easy and precise (6, 11, 12). Additionally, a flow cytometer determines and stores the fluorescence intensity of every cell as it is counted so it can be analyzed further off-line. Under ideal conditions, each stained cell would have the same fluorescence intensity, and halving of the fluorescence intensity would be easily observed as each cell divides. Each generation would then have a single, unique fluorescence intensity equal to exactly one-half the fluorescence intensity of the previous generation. In reality, the fluorescence intensity of the CFDA/SE in any given batch of stained cells is better represented by a range of intensities distributed around a mean.

Tracking the temporal change in the CFDA/SE fluorescence intensity of stained cells as they divide can be utilized to determine growth rates. If the standard deviation in fluorescence intensity is small compared to the intensity shifts due to cell division, then the histogram representing each generation's CFDA/SE fluorescence distribution is resolvable. Determining the average generation time of the stained cells over time can then be utilized to determine a growth rate. The time required to increase the average generation number of the population is equivalent to the doubling time. Alternatively, the average fluorescence intensity of the bacterial population can be determined. The decrease in the average fluorescence intensity over time due to cell division can be utilized to derive the growth rate. Without determining cell concentrations and irrespective of cell losses, the growth rates can be determined for CFDA/SE-stained cells by recording the temporal decline in stain intensity.

The goal of this research was to develop a method in which CFDA/SE staining coupled with flow cytometry is used to determine microbial growth rates in situ without relying on groundwater flow models or ex situ techniques. A synthetic data set was utilized to develop the numerical methods. Microcosm studies conducted with both artificial groundwater (AGW) and real groundwater were employed to verify the method in a simple system, whereas flowthrough columns constructed with repacked and intact sediments were utilized to independently track cell division and cell transport. An estimate of the in situ growth rates for a shallow aquifer was derived by using results from a field-scale bacterial transport experiment. The results indicate that it is possible to determine growth rates in situ and to discriminate between changes in planktonic bacterial concentrations caused by changes in attachment or detachment rates and changes in planktonic bacterial concentrations caused by changes in growth rates. This method should be applicable to both contaminated and uncontaminated subsurface environments to better understand microbial growth and transport processes.

MATERIALS AND METHODS

Field site.

Field samples were collected at the DOE/NABIR South Oyster Bacterial Transport Field Site located on the southern Delmarva Peninsula near the town of Oyster, Va. This is an intensely cultivated sandy lowland where the surficial deposits are part of the late Pleistocene Columbia Aquifer and consist of medium-grained quartz sands with some gravelly layers and small amounts of clays and silts (35, 40). The groundwater has a subneutral pH and contains approximately 1.1 mM Cl, 1.0 mM Na, 0.5 mM SO₄²⁻, 0.5 mM NO₃⁻, 0.6 mM Ca, 0.4 mM Mg, 0.2 mM Si, and less than 0.5 mM total organic carbon. Water was collected from wells that were screened from approximately 3 to 9 m below the ground surface. Two focus areas were established at the site, the South Oyster focus area (SOFA), which was more heterogeneous with suboxic conditions, and the Narrow Channel focus area (NCFA), which was more homogeneous with oxic conditions (18, 26).

Bacterial strains.

An obligate aerobe and a facultative iron-reducing anaerobe were utilized for the experiments. Both bacteria were isolated from the shallow Columbia Aquifer at the Oyster site. The obligate aerobe was an adhesion-deficient variant of Comamonas sp. strain DA001 and is a nonmotile, hydrophilic, rod-shaped, gram-negative bacterium that is approximately 1 μm long and 0.5 μm wide. It has a near-neutral surface charge with a zeta potential of approximately −4.5 × 10⁻⁹ m²/Vs and a density of approximately 1.06 g/cm³ (9). OY-107 is a nonmotile, strongly hydrophilic, facultative, iron-reducing, gram-negative rod that is approximately 1.9 μm long and 1.0 μm wide with a near-neutral surface charge (H. Dong, personal communication). OY-107 has tentatively been identified as an Acidovorax sp. strain based on rRNA analysis (D. Balkwill, personal communication). OY-107 is able to grow on lactate with oxygen, nitrate, or Fe³⁺ as the terminal electron acceptor.

The CFDA/SE-stained bacteria were prepared by the method of Fuller et al. (11). The stain and staining method have been shown not to alter the adhesion characteristics or viability of the bacteria, and the CFDA/SE remains in the cells for weeks to months (11). Fresh batches of cells were grown, stained, and starved for each experiment, and they were used within 1 week of preparation.

Cell sorting.

After they are stained with CFDA/SE, the cells in a population have a range of fluorescence intensities spread around a mean. For initial experiments in which the potential of using CFDA/SE-stained cells to monitor cell growth was examined, cell sorting was performed to collect cells with CFDA/SE fluorescence intensities in a narrow distribution around the mean. Sorted cells have a smaller standard deviation in the range of observed CFDA/SE fluorescence intensities than nonsorted cells, and this allows even slight shifts in the mean fluorescence intensity of the cells to be determined. The CFDA/SE-stained Comamonas sp. strain DA001 and Acidovorax sp. strain OY-107 cells were sorted with a FACSVantage with the FACSDiVa option (Becton Dickinson Inc., San Jose, Calif.) into phosphate-buffered saline (PBS) (pH 7.4) by using a 50-μm tip. Approximately 2 × 10⁶ cells of each strain were collected in 3 ml of PBS. The PBS was amended for growth with the same amendments that were used in the microcosm experiments (see below), and the preparations were incubated at room temperature for 8 h. Samples were collected periodically, fixed, and analyzed as described below.

Microcosm experiments.

The microcosm experiments were conducted with AGW or real groundwater. AGW was used to develop the method. Groundwater was used to test the method in the presence of natural colloidal interference, indigenous bacteria competing for nutrients, and protozoans that may be predators of the bacteria. The AGW was prepared by using deionized distilled water and contained 0.41 mM MgSO₄ · 7H₂O, 1.4 mM NaHCO₃, 0.27 mM CaCl₂ · 2H₂O, 0.32 mM CaSO₄ · 2H₂O, 0.0017 mM NaH₂PO₄, and 0.11 mM KCl. The real groundwater was collected from either the NCFA (NCFA-GW) or the SOFA (SOFA-GW). All site groundwater was stored at 4°C and utilized within 1 month of collection. Except where noted below, groundwater and AGW microcosms were amended with 1.0 mM NaNO₃, 1.0 mM PO₄ (as K₂HPO₄ and KH₂PO₄, 12:88 [vol/vol]), and a trace element solution to obtain the following concentrations: 0.096 mM nitrilotriacetic acid, 0.160 mM MgSO₄ · 7H₂O, 0.009 mM FeSO₄ · 7H₂O, 0.004 mM MnSO₄ · H₂O, 0.002 mM, ZnSO₄ · 7H₂O, and 0.001 mM CoCl₂ · 6H₂O (14). This formulation (referred to as amendments below) was chosen to mimic nutrient-rich conditions that may be encountered in situ. The AGW and groundwater mixtures lacked nutrients that may be sorbed to sediment in real groundwater, such as trace metals. Therefore, in order to ensure that growth was not limited, these nutrients were added to the microcosms. Both groundwater and AGW were considered to be carbon limited. To stimulate cell growth, 10 mM sodium lactate was added.

Microcosms were prepared in polypropylene conical centrifuge tubes or glass bottles and were inoculated to obtain starting concentrations of approximately 10⁶ cells/ml. Although flow cytometry can detect concentrations as low as 10³ cells/ml, approximately 10⁶ cells/ml is required for statistically robust determination of CFDA/SE fluorescence intensity parameters. Microcosms were incubated at 15°C to simulate aquifer temperatures and were run in batch mode. Samples were collected periodically or continuously with a fraction collector and were fixed with formaldehyde at a final concentration of 1% (vol/vol).

Intact and repacked core experiments.

Flowthrough core experiments were utilized to test the method during transport when cells were attaching to and detaching from sediment. Repacked cores enabled development of the method with minimal potential for matrix-derived interference, such as indigenous bacteria and colloids. The intact core was utilized to test the method in the presence of the native microbial community which would be encountered in a field setting. The repacked cores were prepared with F-60 quartz sand (U.S. Silica, Berkeley Springs, W.Va.) that was sieved to pass through a 60-mesh sieve and was collected on a 120-mesh sieve, which yielded material that was 125 to 250 μm in diameter. The sand was washed by the procedure of Murphy et al. (30). The repacked cores were wet-packed into 25-cm-long aluminum tubes with an inside diameter of 7.2 cm. Intact core NC12-2 was collected from the bottom of a 2-m-deep trench dug at the NCFA. The aluminum tube was driven into the exposed sediment face parallel to the groundwater flow direction just above the water table. Additional details regarding the core apparatus and setup have been described by previously (10).

The repacked cores were run with AGW, and the intact core was run with SOFA-GW, both at a flow rate of 1 ml/min and a temperature of 15°C. The cores were initially inoculated with an approximately 0.5-pore volume (∼300-ml) pulse of CFDA/SE-stained cells (approximately 1 × 10⁸ cells/ml) in SOFA-GW or AGW, with Br (1.5 mM) added as a conservative tracer. This was followed by injection of cell- and Br-free SOFA-GW or AGW. Approximately 24 h after the inoculum was injected, biostimulation was performed by injecting a 6-pore volume, 24-h pulse of Br (1.5 mM) and sodium lactate (10 mM). The amendments utilized in the microcosm experiment were added to the biostimulation pulse for the repacked cores but not for the intact core, because it was assumed that the compounds were present on the NC12-2 sediments and available to the microorganisms for growth. After the biostimulation was complete, SOFA-GW or AGW was pumped though each core for an additional 24 h. The repacked cores were then extruded into six sections for examination of sediment-associated cells. Sediment-associated cell concentrations were determined by shaking 5 g of sediment with 5 ml of AGW containing 1% (vol/vol) formaldehyde for 2 h, allowing the sand to settle, and analyzing the supernatant by flow cytometry. Removing cells from sediment is difficult. In order to examine the stain intensity of cells after removal, the cells had to remain intact and unchanged. This precluded altering the water chemistry or utilizing aggressive measures to dislodge the cells. In the repacked cores cells should have been sorbed to the negatively charged sites on the clean quartz grains, and the cells should have been easily removed, with levels of cell recovery approaching 100%.

Field experiment data.

A field-scale bacterial transport experiment was conducted with CFDA/SE-stained Comamonas sp. strain DA001 cells at the NCFA in October 1999 (2, 12, 26). During this experiment aqueous samples were collected from 24 multilevel samplers for 10 days following the initial injection. The multilevel samplers were spaced over a 2-m vertical section of the aquifer and were located up to 7 m downgradient of the injection point. The CFDA/SE-stained cells were enumerated with multiple tracking methods, and the results were all in general agreement (12, 20). Following the successful development of the methodology described in this paper for determining growth rates, the field data were reanalyzed in order to determine an in situ growth rate of the DA001 cells injected during the field experiment. For this determination, the data from the injectate samples and groundwater samples from port 9 of each of the multilevel samplers were analyzed. Port 9 was located 7 m below the ground surface in a high-permeability zone that was the primary zone of transport. Flow cytometer data were available from 18 of the 24 multilevel samplers (12, 26). The elapsed time needed to calculate the growth rate was determined by using the average travel time of the bacterial cell plume to each sampling port.

Cell and chemical analyses.

Cell concentrations and fluorescence intensity values for the laboratory experiments were determined with a FACSort flow cytometer (Becton Dickinson Inc.). The field samples were analyzed with a FACScan flow cytometer. A 10-μl portion of 1.0-μm carboxylate-modified TransFluoSpheres (1.8 × 10⁵ spheres/μl; Molecular Probes, Inc., Eugene, Oreg.) was added to each sample prior to analysis to allow determination of cell concentrations and to provide a reference for fluorescence intensity (41). Identical instrument settings were utilized for all microcosm and core samples in order to facilitate comparison of results. High-concentration samples were diluted with filtered AGW before analysis. Total cell counting for the microcosm experiments was performed based on the side scatter versus forward scatter channel. Total cell counting for the effluents from the repacked and intact core experiments was performed by flow cytometry after cells were stained with the nucleic acid stain SYTO13 (Molecular Probes Inc.) at a concentration of 5 nM. Before substantial growth occurs, CFDA/SE alone provides a basis for accurate determinations of concentrations. However, after substantial growth begins, CFDA/SE begins to be diluted to the extent that cell concentrations based on this stain underpredict the true concentration (11). Therefore, SYTO13 was used to provide accurate estimates of cell concentrations.

Br concentrations were determined with an ion-selective Br probe (Cole-Parmer, Vernon Hills, Ill.) connected to a Corning pH/ion analyzer (Corning, Inc., Corning, N.Y.). Lactate and anion concentrations were determined with a Dionex DX-300 ion chromatograph under isocratic conditions with an AS-15 column (Dionex, Sunnyvale, Calif.).

Data analysis.

The flow cytometer data were collected on 1,024 channels. The 1,024 channels were divided into four log decades, with each log decade represented by 256 channels. The increase in fluorescence intensity of each bin was not uniform on a nonlog scale. Each log bin value was determined by n_i/256, where n_i is the channel value from 1 to 1,024. The fluorescence intensity then ranged from 0.004 to 4.000 in log space or from 1.009 to 10,000 in nonlog linear space. The actual value and units of the fluorescence intensity were arbitrary and based on the particular machine settings. However, fluorescent beads with a uniform size and fluorescence intensity could be utilized as an internal standard. The data were then graphed in log space on a scale from 0 to 4.

The flow cytometry data can be described by a normal distribution:

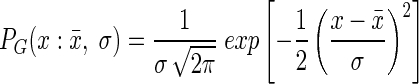(1)

where P_G is the probability, σ is the standard deviation, x is the bin value, and x̄ is the mean bin value. The flow cytometer data were normalized by dividing by the total number of events and the bin width to obtain the probability, P_G. Flow cytometer data were first processed by using WinMDI (Joseph Trotter, Scripps Institute, San Diego, Calif.) and LDATA (http://www.cyto.purdue.edu/flowcyt/software/Catalog.htm). The processed flow cytometer data from each sample were then fitted by utilizing PEST98 (Watermark Computing, Brisbane, Australia) (http://www.sspa.com/pest/), an automated parameter estimation program that minimized the sum of the difference between observed and predicted values. The fitting was performed in log space because the flow cytometer data were approximately log normally distributed.

Two methods were used to determine growth rates. The first method was based on the loss of fluorescence intensity per cell and was designated the average fluorescence intensity (AFI) method.

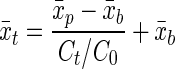(2)

For a cell concentration at time t (C_t) and the initial cell number (C₀), the average stain intensity (x̄_t) was lower after growth when the cell concentration had increased, given the initial stain intensity of the parents (x̄_p) and the background stain intensity (x̄_b). This calculation was done in nonlog space. Each time the concentration doubled, the fluorescence intensity was halved, accounting for the background fluorescence intensity. Conversely, each time the fluorescence intensity was halved, the number of cells was assumed to have doubled. With the AFI method the mean fluorescence intensity (x̄) and standard deviation (σ) of each sample were determined by fitting equation 1. The mean fluorescence intensity of the parent cells (x̄_p) was determined before growth occurred, and the mean fluorescence intensity of the background cells (x̄_b) was determined with unstained cells. Equation 2 could then be used to predict the mean fluorescence intensity (x̄_t) given the cell concentration or to predict the cell concentration at time t given the mean fluorescence intensity. The change in the mean fluorescence intensity obtained with the AFI method could then be used to determine a doubling time because the predicted cell concentration was known over time.

For the second method, the average generation (AG) method, we used the change in the average generation number to determine growth rates. The goal of this calculation was to determine the percentage of the population in each generation.

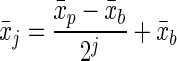(3)

The mean fluorescence intensity of a subsequent daughter generation (x̄_j) could be determined from the mean fluorescence intensity of the parent population (x̄_p) by accounting for the fluorescence intensity of the background (x̄_b). For the parent population, the generation number (j) was zero, and j was incremented for each successive generation. To assign generation numbers to each cell counted, the flow cytometer histogram was assumed to be the sum of the subhistograms from each generation. The standard deviations of the histograms for the generations were assumed to be identical. The subhistograms associated with each generation were summed to get the predicted histogram for the total population. The difference between the predicted and observed histograms was minimized by fitting the fraction of cells in each generation. The fractions of cells in the generations were the only adjustable parameters because the mean and standard deviation of the fluorescence intensity for each subhistogram were set by the values for the parent generation (x̄_p) and the background cells (x̄_b). The average generation of the population could then be determined and used to calculate a doubling time. The average generation was the sum of the fraction in each generation multiplied by the generation number. Each time the average generation increased by one, the number of cells doubled. In addition, loss from the parent generation could be used to calculate a doubling time for comparison.

RESULTS

Method development with synthetic data set.

A sensitivity analysis with synthetic data was performed to test the AFI and AG methods. The synthetic data set had a known standard deviation around a mean fluorescence intensity. An initial stain fluorescence intensity of 2.300 with standard deviations of 0.079, 0.146, and 0.204 and 10, 25, and 50% of the cells in the parent generation was utilized to create the synthetic data (Table 1). Both methods accurately reproduced the results, but for the AFI method the percent error increased as the standard deviation decreased (Table 1). Data acquired from a flow cytometer may have some noise associated with it, such as a slight shift in the mean fluorescence intensity or jaggedness in the observed histogram. To more closely simulate real data, two types of random noise were added to a synthetic data set with a 50:50 parent-daughter starting composition and a log standard deviation of 0.146, which is similar to that of nonsorted CFDA/SE-stained cells. First, a random shift between −10% and 10% was added to the mean fluorescence intensities of the parent and daughter population. Second, a random shift between −20% and 20% was added to the counts associated with each data point. Ten realizations were conducted in which the random noise was added; the resulting average percent errors for the AFI and AG methods were 5.1 and 11.5%, respectively (Table 1). From this numerical test, we concluded that both methods could be utilized to determine growth rates, but the AFI method may be better for noisy data sets.

TABLE 1.

Results of sensitivity analysis with synthetic data for which the parent cell mean fluorescence intensity was 2.3 and the standard deviation was variable

Standard deviation	% in the parent population/% in the daughter populationa	% Error
		AFI method	AG method
0.079	10/90	5.4	0.0
	25/75	11.0	0.0
	50/50	0.0	0.0
0.146	10/90	2.7	0.0
	25/75	3.9	0.0
	50/50	0.0	0.0
0.204	10/90	1.6	0.0
	25/75	2.2	0.0
	50/50	0.0	0.0
0.146b	50/50	5.1	11.5

^aPercentages in each generation that were utilized to construct the fluorescence intensity distribution with the mean and standard deviation. The data were then fit with either the AFI or the AG method, and the error was reported.

^bAverage data for 10 calculations when random noise was added to each data point and the mean fluorescence intensity of the parent and daughter generations.

Growth of sorted cells.

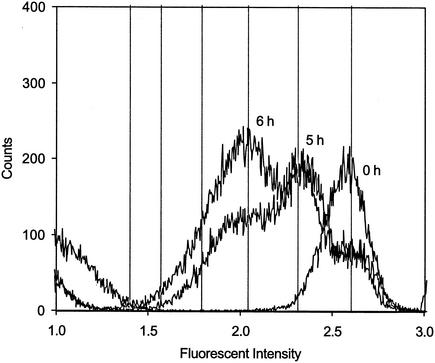
Sorting resulted in collection of approximately 10⁶ cells in 1 h, which decreased the width and standard deviation of the fluorescence intensity peak compared to the values for nonsorted cells. Growth of the sorted CFDA/SE-stained Comamonas sp. strain DA001 cells resulted in a decrease in fluorescence intensity (Fig. 1). The locations of the peaks coincided with the locations predicted by equation 3 for cell division, and the peak associated with each generation was easily observed (Fig. 1). Since the stain was apportioned equally into the daughter cells, no discernible change in the standard deviation around the mean fluorescence intensity occurred. The sorting procedure did not work as well with Acidovorax sp. strain OY-107 cells, and individual peaks were not as clearly visible (data not shown). Unfortunately, cell sorting is a viable method only for obtaining small numbers of cells, and all of the microcosm and core experiments that were performed required at least 10⁸ cells.

FIG. 1.

Fluorescence intensity of CFDA/SE-stained and sorted DA001 cells after 0, 5, and 6 h of growth with amendments and lactate. The fluorescence intensity is plotted in log space, and each unit of fluorescence intensity represents a decadal log increase. The vertical lines indicate predicted peak locations after cell division given an initial stain intensity of 2.6 and a background intensity of 1.2. For determinations of the daughter generations, the calculations must be performed in nonlog space by using equation 3.

Growth in aqueous microcosms.

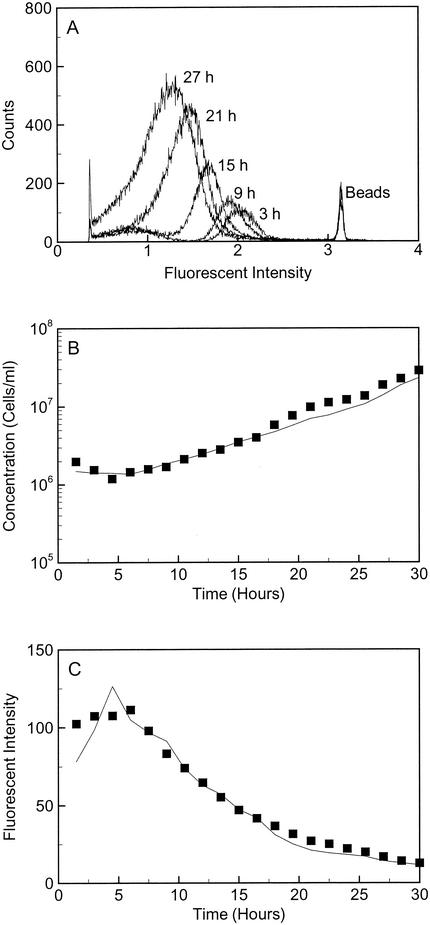
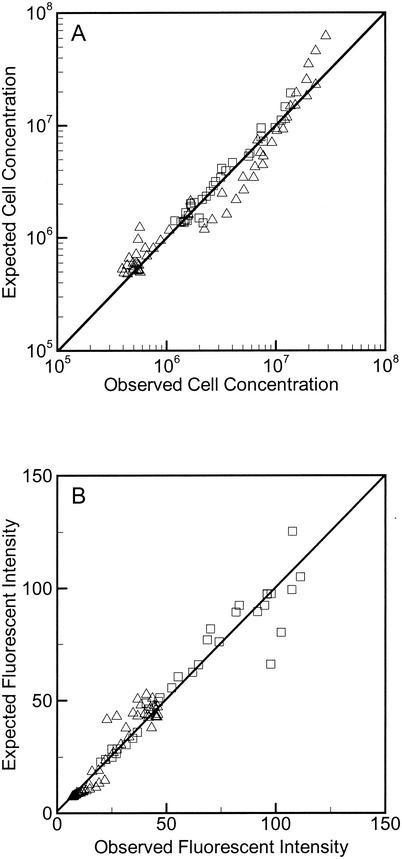
Comamonas sp. strain DA001 and Acidovorax sp. strain OY-107 in groundwater and AGW with amendments and lactate (biostimulation mixture) exhibited exponential growth (Fig. 2). Changes in CFDA/SE fluorescence intensity accurately predicted increases in cell numbers, and correspondingly, changes in cell numbers predicted decreases in CFDA/SE fluorescence intensity based on equation 2 (Fig. 2 and 3). Determinations of growth rates by the AFI method, the AG method, the loss of the parent population, and the total cell counts produced similar estimates of doubling times (Table 2). The percent error determined from the mean of the four methods was 10.6% ± 8.8% (average ± standard deviation) (Table 2). Limited growth of DA001 and OY-107 occurred in microcosms without lactate and with and without amendments (data not shown), and the changes in the CFDA/SE fluorescence intensity allowed even this limited amount of growth to be monitored.

FIG. 2.

(A) Raw flow cytometry data for OY-107 in SOFA-GW with amendments and lactate for every fourth sample over the course of the microcosm growth experiment. The fluorescence intensity is plotted in log space. An increase in cell counts and a decrease in fluorescence intensity were observed for the cell population as growth occurred. (B) Observed (▪) and predicted (solid line) OY-107 cell concentrations in SOFA-GW with amendments and lactate over time. The cell concentration was calculated from the observed average fluorescence intensity values by the AFI method (equation 2). (C) Observed (▪) and predicted (solid line) stain intensities of OY-107 cells in SOFA-GW with amendments and lactate. The average fluorescence intensity was calculated from the observed cell concentration by the AFI method (equation 2).

FIG. 3.

(A) Plot of observed versus predicted cell concentrations for DA001 with lactate (▵) and for OY-107 with lactate (□). (B) Plot of observed versus predicted CFDA/SE fluorescence intensities for DA001 with lactate (▵) and OY-107 with lactate (□). The 1:1 lines are shown for reference.

TABLE 2.

Calculated doubling times for microcosms with amendments and lactate

Growth rate calculation method	Doubling time (h)a
	Comamonas sp. strain DA001		Acidovorax sp. strain OY-107
	AGW	SOFA-GW	AGW	SOFA-GW
AFI method	5.17 (0.08)a	4.13 (0.25)	5.17 (0.34)	6.43 (0.22)
AG method	6.62 (1.99)	4.07 (0.18)	5.65 (0.12)	7.73 (1.24)
Decrease in parent generation	3.73 (0.99)	3.17 (0.60)	4.90 (0.56)	5.90 (0.67)
Increase in total cells	4.83 (0.24)	4.23 (0.26)	6.40 (1.00)	6.57 (0.09)
Avgb	5.08	3.90	5.53	6.67

^aThe values in parentheses are absolute errors.

^bAverage doubling times for the four methods.

Growth in sediment cores.

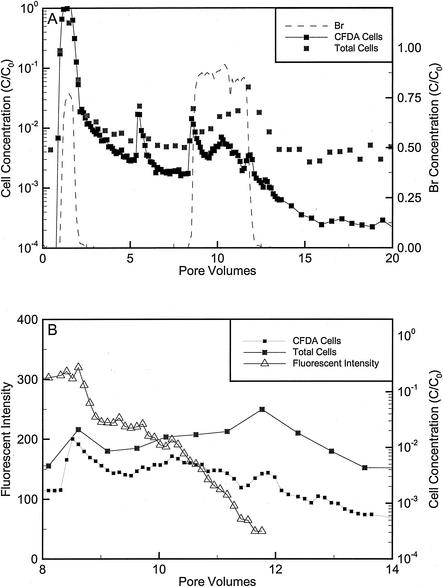
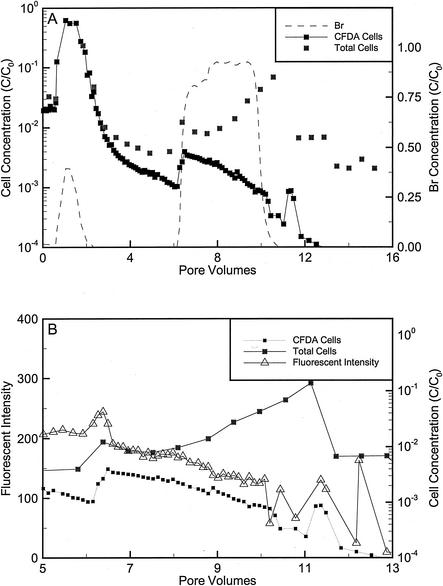
For the repacked cores approximately 95% of the Comamonas sp. strain DA001 and Acidovorax sp. strain OY-107 cells injected into the repacked cores were initially eluted, and the remainder of the injected cells became attached to the sand (Fig. 4 and 5; Table 3). The sorbed cells slowly eluted from the core during the extended tailing phase of transport. During tailing, the cell concentrations slowly decreased, except for an unexplained increase at 5.5 pore volumes in the core that received DA001 (Fig. 4). After approximately 8 pore volumes had eluted from the core with DA001 and 6 pore volumes had eluted from the core with OY-107, the amendments, lactate, and Br were added (Fig. 4 and 5). The amendments and lactate were provided in excess and eluted with the Br tracer (data not shown). The fluorescence intensity initially increased slightly and then decreased significantly. The decrease in fluorescence intensity occurred slightly after the breakthrough of Br (Fig. 4B and 5B). The cell concentration increased during elution of the biostimulation mixture before the fluorescence intensity decreased (Fig. 4 and 5). A more significant decrease in the fluorescence intensity of DA001 than in the fluorescence intensity of OY-107 was initially observed (Fig. 4B and 5B). The calculated doubling times for the cells eluting from the cores based on the AFI method were 3.97 to 7.07 h for DA001 and 33.08 h for OY-107. After approximately 8 pore volumes, the total counts for OY-107 started to increase, and the doubling time based on the AG method was 8.68 h. The doubling times for DA001 and OY-107 were shorter for late-time data than for early-time data. The total cell counts based on SYTO13 staining were similar to the CFDA/SE counts, except near the end of the biostimulation period, when the total cell concentrations increased (Fig. 4 and 5). The total counts of OY-107 started to increase significantly near the end of the biostimulation period, whereas only slight increases were observed for DA001. Adding the number of cells in generations 1 to 5 for DA001 produced cell counts similar to the total counts, but the same calculation for OY-107 underestimated the total counts (data not shown). The concentrations of cells that eluted with the AGW injected into the cores before and after biostimulation were similar. During the late-time tailing after biostimulation and growth had occurred, low concentrations of cells with the fluorescence intensity of the original parent population were still eluted (data not shown).

FIG. 4.

(A) Dimensionless Br and cell concentrations during the transport and biostimulation phases of the repacked core injected with DA001. Total counts were determined by counting cells stained with SYTO13 by flow cytometry. CFDA/SE concentrations were determined by counting stained cells with the flow cytometer. CFDA/SE concentrations may underestimate cell counts at late times because of stain loss. (B) Average fluorescence intensities, CFDA/SE cell counts, and total counts during the biostimulation phase of the core experiments. The initial concentrations (C₀) of bacteria and Br were 2.3 × 10⁸ cells/ml and 1.57 mM, respectively. One pore volume corresponded to 6.6 h with an average velocity of 0.9 m/day.

FIG. 5.

(A) Dimensionless Br and cell concentrations during the transport and biostimulation phases of the repacked core injected with OY-107. (B) Average stain intensities, CFDA/SE cell counts, and total counts during the biostimulation portion of the core experiments. The initial concentrations (C₀) of bacteria and Br were 3.4 × 10⁸ cells/ml and 1.52 mM, respectively. One pore volume corresponded to 6.9 h with an average velocity of 0.9 m/day.

TABLE 3.

Summary of data from intact and repacked core experiments performed with Comamonas sp. strain DA001 and Acidovorax sp. strain OY-107

Core	No. of cells sorbed after injectiona	Total no. of sorbed cells after exptb	No. of cells eluted during tailing by total counts	Doubling time by AFI method (h)	Length of lactate and amendment injection time (h)	Maximum no. of doublingsc
Repacked core with DA001	3.4 × 109d	1.3 × 1010	1.6 × 1010	6.12	24	3.9
Repacked core with OY-107	3.3 × 109-2.6 × 1010e	6.9 × 109	3.0 × 1010	33.33f	24	0.72 (2.7)g
Intact core with OY-107	8.5 × 109	NDh	1.36 × 1010 (4.8 × 109)i	6.07	24	4.0

^aThe number of cells was calculated by determining the difference between the number of injected cells and the number of eluted cells during the initial injection.

^bThe number of sorbed cells was calculated from the total counts on sediments.

^cThe maximum number of doublings was calculated by dividing the length of the injection time by the doubling time. This did not account for the lag time, which was at least 4 h in the microcosms.

^dUpper estimate because the amount of Br recovered was 86%, and this was used to scale down the recovery of cells.

^eThe core had a leak during injection, and the level of Br recovery was less than 100%. Thus, the level of cell recovery was estimated given the range of Br recovery.

^fThe doubling time determined by the AFI method was short, but using data from a later time with the AG method resulted in a longer doubling time (8.73 h).

^gThe number in parentheses is the number of doublings predicted by using the values from the AG method.

^hND, not determined. The total number of sorbed cells could not be determined because the background noise was too great with intact sediments to determine concentrations by flow cytometry.

ⁱThe value may be an overestimate because indigenous cells would also grow in the intact core. The value in parentheses is the number of CFDA/SE-stained cells eluted, which is a lower estimate for the number of OY-107 cells.

The total sand-associated DA001 and OY-107 cell counts after the transport experiment were approximately 1.3 × 10¹⁰ and 6.9 × 10⁹ cells, respectively (Table 3). CFDA/SE-stained cells extracted from the sand were not distinguishable from the background noise measured with the flow cytometer. A mass balance analysis of the number of cells injected and accounted for during the repacked core experiments was performed. The number of cells initially sorbed plus the number of newly grown cells should have balanced with the number of cells eluted during tailing and the number of sorbed cells at the end of the experiment. In the core that received DA001, the number of cells initially retained was approximately 10-fold less than the combined number of cells eluted and retained at the end of the injection. This indicates that the DA001 cells probably doubled two to four times in order to achieve a reasonable mass balance (Table 3). This is in agreement with the number of doublings predicted by the AFI method. In the core that received OY-107, the number of cells initially sorbed was slightly lower than the combined number of cells eluted and sorbed at the end of the experiment, which is in agreement with the longer doubling time of this organism as determined by the AFI method (Table 3).

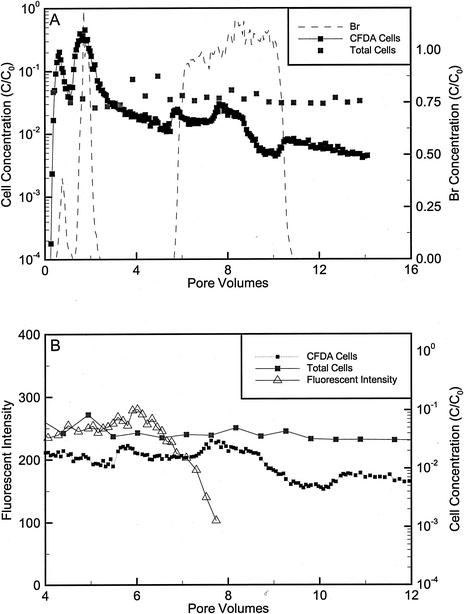
For intact core NC12-2, approximately 67% of the OY-107 cells were initially eluted. The inoculum was injected as two separate pulses due to a leak in the core that had to be sealed before proceeding (Fig. 6). Extended tailing of OY-107 was observed, and the concentrations in the core effluent slowly decreased. The SOFA-GW biostimulation mixture was added at approximately 5 pore volumes, and excess nutrients were observed to break through with the Br tracer (data not shown). A slight increase in the cell concentration was observed in the effluent when the biostimulation mixture initially eluted. As observed with the repacked cores, a slight increase in the fluorescence intensity of the eluted OY-107 cells occurred, followed by a decrease that occurred slightly after the arrival of Br. The doubling time calculated by the AFI method was 6.07 h. The total cell counts in the core effluent varied little throughout the injection, even during peak breakthrough, indicating that there may have been a problem with the procedure for enumerating total cells during this experiment. Late-time samples contained measurable amounts of cells with the original fluorescence intensity, indicating that a subpopulation of the injected cells did not divide in this core. Sediment-associated cell concentrations could not be determined after transport because desorption of humic and colloidal material along with the cells produced too much background interference with the flow cytometer.

FIG. 6.

(A) Dimensionless Br and cell concentrations during the transport and biostimulation phases of intact core NC12-2 injected with OY-107. (B) Average stain intensities, CFDA/SE cell counts, and total counts during the biostimulation portion of the core experiments. The initial concentrations (C₀) of bacteria and Br were 8.6 × 10⁷ cells/ml and 0.57 mM, respectively. Average stain intensities could not be calculated after approximately 8 pore volumes because of values near the background intensity. One pore volume corresponded to 5.2 h with an average velocity of 1.1 m/day.

Field data.

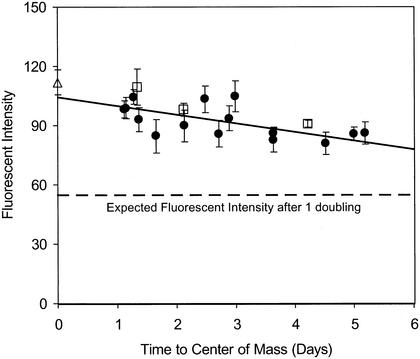
When the AFI method described above was applied to a data set from a field-scale experiment in which the transport of CFDA/SE-stained DA001 cells was examined, a slight and consistent decrease in the fluorescence intensity of the stained cells over time and distance was observed (Fig. 7). The average doubling time for the injected DA001 cells was 15 days when the AFI method was used. Three sampling locations were not used in the growth rate calculation because only a few data points were available along the corresponding breakthrough curves. The limited port 10 data revealed a slightly shorter doubling time (13 days), whereas utilizing all of the data, including the three breakthrough curves with limited data, resulted in a slightly longer doubling time (20 days).

FIG. 7.

Plot of CFDA/SE fluorescence intensity of injected DA001 cells versus time during a field-scale bacterial transport experiment conducted at the NCFA in 1999. Each data point represents the average for at least six samples selected from across the entire cell breakthrough curve. The error bars indicate the standard deviations of all the measurements obtained at each multilevel sampler. The samples were injectate (▵), port 9 (•), and port 10 (□) samples. The values for three sampling points are not shown because of insufficient data.

DISCUSSION

Growth rates were determined in microcosms, in flowthrough cores, and from reanalysis of a field-scale experiment data set. For the CFDA/SE-based methods we utilized the change in fluorescence intensity of the stained cells over time to determine the growth rate. These methods are independent of actual cell concentrations, and therefore they can be utilized with systems in which cell losses occur by death or lysis, predation, or attachment to sediment. In microcosms with lactate, the doubling times calculated by the two different CFDA/SE-based methods were similar and were comparable to growth rates based on total counts. In order to determine growth rates in flowthrough cores, we assumed that the growth rates of planktonic and sorbed cells were in equilibrium and that the eluted cells were representative of the total population. The occurrence of extended tailing indicated that bacterial cell-sediment interactions were continuously occurring.

The CFDA/SE-based methods for cell division are limited by the fluorescence intensity of the initial staining compared to the background intensity. For this reason, only five generations could be tracked. The AG method may be more appropriate for cell populations with small standard deviations in fluorescence intensity, whereas the AFI method may be more appropriate for noisier data with a larger standard deviation. In microcosms with amendments but without lactate, limited growth occurred, and changes in fluorescence intensity tracked the limited growth. This limited growth may have reflected (i) a starvation response of the cells (29), (ii) cryptic growth on endogenous carbon stores, or (iii) growth of cells on exogenous organic carbon still present in the aqueous phase after the cells were washed. The first of these explanations does not seem reasonable, given that the cells were incubated under starvation conditions for 48 to 72 h before they were used in the microcosm experiments and therefore limited amounts of carbon may have remained associated with the cells even after washing.

Laboratory and field transport experiments have been conducted to develop methods to track CFDA/SE-stained and unstained cells (6, 12, 17, 20). When different counting or tracking methods were compared, agreement within a factor of 2 was considered successful (6). Comparisons between the different methods did not enable sensitive determinations of growth rates to be made. In addition, the coupling of these methods could not discriminate between detachment from the sediment and cell growth as reasons for increases in the aqueous-phase cell concentration. These methods have proven to be powerful for tracking cells through the subsurface down to low concentrations, but they have not been shown to be able to track growth. This is the first study in which cell concentrations and growth rates were concurrently determined by the same methods under both strictly controlled laboratory conditions and less controlled field conditions.

In the flowthrough core experiments, the effluent CFDA/SE-stained cells were easily observed by flow cytometry during the transport phase. After injection of the stimulation mixture, cell concentrations were observed to change without a change in the fluorescence intensity. This indicated that growth was probably not occurring, but the changes in the chemistry of the groundwater (specifically, the increase in the concentration of bivalent cations) altered bacterial attachment (19, 22, 38). Bacteria are sensitive to changes in groundwater chemistry, and this could easily have been misconstrued as growth if only total cell counting was performed. After slightly more time, growth was observed, as shown by a decrease in the average fluorescence intensity of the eluted cells, even while the planktonic cell concentrations did not increase. During biostimulation, Comamonas sp. strain DA001 cells continued to divide, but planktonic cell concentrations did not change drastically. Near the end of the biostimulation phase, the total planktonic counts of Acidovorax sp. strain OY-107 did increase in the repacked core as the growth rate increased. This indicated that during cell division some cells detached from the sediment but a significant number stayed attached to the sediment. Preferential transport of the daughter cells did not appear to occur. It is possible that daughter cells attached to the sediment as they were produced until the sites for attachment were full. In general, observations of eluted planktonic cell concentrations were not a good predictor of if or when growth began. At the end of the experiment, total counts of sediment-associated bacteria verified that growth had indeed occurred without a concomitant increase in the effluent cell concentration.

The number of sorbed bacteria could not be determined for the NC12-2 core, but similar trends in the aqueous phase were observed, although with potentially smaller changes in the aqueous concentrations. The smaller variations in the planktonic cell concentrations may have been caused by greater attachment of Acidovorax sp. strain OY-107 cells to the larger number of positively charged sites in the heterogeneous natural sediment. The daughter cells may have attached to these sites during cell growth or after a small amount of transport, therefore not eluting from the core. This indicated that when workers attempt to determine bacterial growth rates in real aquifers with both aqueous and solid phases, it is important to distinguish between changes in bacterial transport due to changing groundwater chemistry and changes in bacterial transport due to growth (9, 28, 36).

Different species of bacteria exhibit a range of transport behaviors and are affected differently by changes in solution chemistry and the availability of nutrients (8, 13, 37, 39). The strains used in this study, Comamonas sp. strain DA001 and Acidovorax sp. strain OY-107, have similar cell properties and have been utilized for laboratory and field experiments because of their low adhesion to sediment. Most other species of bacteria have a higher affinity for solid surfaces. Despite these similarities between DA001 and OY-107, the two strains still had different growth responses after addition of a readily utilizable carbon source, lactate, in a simple system comprised of just clean quartz sand. Some previous work has indicated that the ratio of sorbed bacteria to planktonic bacteria is relatively constant (3), and therefore increases in cell numbers should be observed during growth. However, other work has shown that it is difficult to determine correlations between sorbed and planktonic cell concentrations (1, 21). Growth in the simple quartz sand cores appeared to be heterogeneous either physically, chemically, or biologically. Even after a significant amount of growth had clearly occurred, changes in effluent cell concentrations were not observed, and cells from the initial parent generation were still eluted. Excess nutrients were added, but oxygen may have limited the ability of the obligate aerobe DA001 to divide. In contrast, OY-107 is a facultative anaerobe, and nitrate was available as an alternative electron acceptor; growth of this strain should not have been limited when oxygen was depleted. However, parent OY-107 cells were also still observed in the effluent at the end of the experiments. It is likely that there is another reason that a portion of the initial parent generation was transported but did not divide.

Examination of the data from a field-scale bacterial transport experiment with no biostimulation indicated that the doubling time for injected Comamonas sp. strain DA001 was 15 days, which is similar to the lower estimates of doubling times for microbial communities in lake sediments, surface soils, and deep-sea sediments (32). This is the first known attempt to directly measure the growth rate of an introduced bacterial strain under in situ subsurface conditions. The cells were injected without nutrients, so the observed growth must have occurred on nutrients within the aquifer. Therefore, the calculated growth rate may be similar to that of the indigenous microbial population.

The results presented here suggest that continued transport and growth of injected cells occurred but preferential transport of the daughter cells did not occur. Microbial transport in aquifer systems may be enhanced by a range of cell properties within a monoclonal culture of bacteria (26), slow continuous transport caused by attachment and detachment of cells to grain surfaces (44), and slight perturbations to the groundwater chemistry (38). This consortium of factors may explain why microbes are observed to readily move through aquifer systems. However, more research is needed to better understand microbial transport in aquifer systems, particularly under growth conditions. The CFDA/SE-based methodology outlined in this paper has proven to be a sensitive technique that can track both cell growth and transport, and it should prove to be useful in future studies in which the microbial ecology of natural systems is examined.