Interference fine structure and sarcomere length dependence of the axial x-ray pattern from active single muscle fibers

Abstract

Axial x-ray diffraction patterns from single intact fibers of frog skeletal muscle were recorded by using a highly collimated x-ray beam at the European Synchrotron Radiation Facility. During isometric contraction at sarcomere lengths 2.2–3.2 μm, the M3 x-ray reflection, associated with the repeat of myosin heads along the filaments, was resolved into two peaks. The total M3 intensity decreased linearly with increasing sarcomere length and was directly proportional to the degree of overlap between myosin and actin filaments, showing that it comes from myosin heads in the overlap region. The separation between the M3 peaks was smaller at longer sarcomere length and was quantitatively explained by x-ray interference between myosin heads in the two overlap regions of each sarcomere. The relative intensity of the M3 peaks was independent of sarcomere length, showing that the axial periodicities of the nonoverlap and overlap regions of the myosin filament have the same value, 14.57 nm, during active contraction. In resting fibers the periodicity is 14.34 nm, so muscle activation produces a change in myosin filament structure in the nonoverlap as well as the overlap part of the filament. The results establish x-ray interferometry as a new tool for studying the motions of myosin heads during muscle contraction with unprecedented spatial resolution.

In resting skeletal muscles from vertebrates, the myosin head domains or cross-bridges have a roughly helical arrangement, with three layers of heads in each 43-nm helical repeat (1). During isometric contraction, this helical structure disappears, but the myosin heads retain a strong axial periodicity of 14.57 nm, 1.6% larger than the corresponding value at rest, 14.34 nm (1–7). Both structures produce an intense axial x-ray reflection called the M3. The M3 reflection during isometric contraction has been associated with force-generating myosin heads oriented roughly perpendicular to the filament axis (3, 4, 8–11), and the intensity of this reflection has been used to investigate the changes in myosin head conformation that drive force generation (8–11). The transition between myosin head conformations with 14.34 and 14.57 nm axial periodicities has roughly the same time course as isometric force development after electrical stimulation (3, 4, 7), but its functional significance is not understood.

We investigated this transition in isolated intact muscle fibers, by using the unprecedented spatial resolution of the small-angle x-ray scattering beamline ID2-SAXS at the European Synchrotron Radiation Facility (ESRF, Grenoble, France). At this resolution, the M3 reflection is split into closely spaced peaks by interference between the two arrays of myosin heads in each bipolar myosin filament (1, 2, 12). We recorded the interference fine structure of the M3 reflection during isometric contraction at different sarcomere lengths in the range 2.0 to 3.6 μm, to vary the degree of overlap between the myosin- and actin-containing filaments. The sarcomere length controls both the number of myosin heads that can interact with actin (13) and the distance between the two arrays of such heads in each sarcomere. The results show that the M3 reflection in active muscle comes from myosin heads in the overlap region of the sarcomere, whereas the 14.34 to 14.57 nm periodicity change on activation involves the entire myosin filament.

Methods

Fiber Preparation and Mounting.

Frogs (Rana temporaria) were killed by decapitation, followed by destruction of the brain and spinal cord. Single fibers (5–6 mm long) were dissected from the lateral head of the tibialis anterior muscle and mounted via aluminum foil clips between a strain-gauge force transducer (AE 801 SensoNor, Horten, Norway) and a loudspeaker motor (14). The temperature of the experimental trough was controlled at 4°C. Fiber dimensions and the relation between resting sarcomere length and fiber length were measured with the fiber horizontal. For x-ray measurements, the fiber was mounted vertically with the transducer at the top and the motor at the bottom, and fiber length was adjusted to give the desired sarcomere length in the resting fiber. Two mica windows, about 600 μm apart, minimized the x-ray path in the Ringer solution. Sarcomere length changes during activation were measured in a separate set of horizontally mounted fibers (15).

X-Ray Data Collection and Experimental Protocol.

X-ray measurements were made at the ID2-SAXS beamline at ESRF (16), by using a photon flux of up to 10¹³ s⁻¹ at 0.1 nm wavelength. The beam size at the fiber was 0.6 mm horizontally and 0.1 mm vertically (full width half-maximum); the beam divergence was 0.04 mrad horizontally and 0.025 mrad vertically. X-ray exposure was controlled by a fast shutter (switch time < 1 ms). High resolution x-ray diffraction patterns were recorded on storage PhosphorImage plates (Molecular Dynamics, A3 size) mounted in the evacuated camera tube 9.85 m from the fiber. Image plates were scanned off-line at nominal spatial resolution 100 μm by using a STORM 840 Molecular Dynamics scanner.

X-ray diffraction patterns were recorded at rest and at the plateau of an isometric tetanus from the same fiber, at the same resting sarcomere length. Fibers were electrically stimulated at 18–25 Hz for 2.3 s; the x-ray shutter opened from 0.3 to 2.3 s after the first stimulus. Three such frames were accumulated at 3-min intervals. Usually, the sarcomere length was then changed and the procedure repeated. Finally, resting x-ray patterns (3 × 2 s) were recorded at each length. To avoid the effects of radiation damage, fibers were moved vertically by 0.5 mm between each 2-s exposure. Fibers generally became inexcitable after ca. 30 s total exposure; up to this time the x-ray pattern and mechanical performance were unaffected. The sequence of sarcomere lengths used for the measurements was randomized, but, when the first x-ray exposure involved tetani at sarcomere lengths > 3.0 μm, signs of mechanical and structural damage appeared in subsequent tetani at short sarcomere length, so data from the latter were discarded. X-ray data in Results are from 11 fibers selected for large size (cross-sectional area, 25,600 ± 4,000 μm²; mean ± SD). For eight of these fibers, x-ray data are reported at two sarcomere lengths; for the other three, at only one sarcomere length.

X-Ray Data Analysis.

X-ray data were analyzed by using hv (Alex Stewart, Brandeis University, Waltham, MA) and peakfit (Jandel Scientific). X-ray patterns were aligned by using the centers of the equatorial 1,0 reflections and centered. The background under each x-ray reflection was fitted by a straight line and subtracted. The intensities of the axial reflections were determined by integrating radially from ±1/19 nm⁻¹ in the resting fiber and ±1/17 nm⁻¹ during active contraction, then axially as follows: M3 reflection, 1/14.0 to 1/14.8 nm⁻¹ (resting) and 1/14.2 to 1/15.0 nm⁻¹ (active); M6 reflection, 1/7.05 to 1/7.25 nm⁻¹ (resting) and 1/7.18 to 1/7.38 nm⁻¹ (active). The radial limits were chosen to include the full width of the axial reflections at long sarcomere length, but also include some of the off-axial layer lines. The choice of radial limits had a negligible effect on the results; for example, when the analysis was repeated with narrower radial limits (±1/80 nm⁻¹, resting; ±1/60 nm⁻¹, active), the intercept of I_M3n on the sarcomere axis (see Fig. 3A) changed from 3.63 to 3.58 μm. Measurements of spacing and fine structure of the axial reflections reported in Results were made with narrow radial integration limits (±1/80 nm⁻¹, resting; ±1/60 nm⁻¹, active) for maximum precision. Similar results were obtained with wider integration limits, however, indicating that effects of arcing of the reflections were negligible. Axial spacings and intensities of peaks were determined by fitting multiple Gaussian curves to the axial profiles by using peakfit. The overall spacing of each reflection was determined as the weighted mean of those of its component peaks. Spacings were calibrated assuming the resting spacing of the M3 reflection at sarcomere length 2.0–2.2 μm to be 14.340 nm (2).

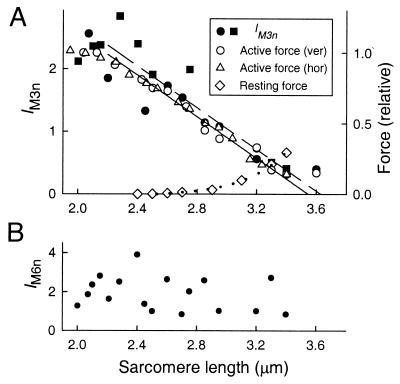
Figure 3.

Sarcomere length-dependence of I_M3n, active and resting force (A), and I_M6n (B). In A, all x-ray data and open circles (active force) are from vertically mounted fibers. Squares (filled circles) denote I_M3n in the first (second) set of active 3 × 2-s exposures in each fiber. Triangles denote active force in six segments of three horizontally mounted fibers, pooled according to sarcomere length 1 s after the start of stimulation in 0.1 μm bins; SE was typically 0.02 for force and 0.012 for sarcomere length. The continuous and dashed lines show linear regressions of active force against active sarcomere length and I_M3n against resting sarcomere length, respectively. Diamonds in A show resting force in one horizontal fiber; the dotted line is an exponential fit.

Results

The Axial X-Ray Pattern from Resting and Active Fibers at Full Filament Overlap.

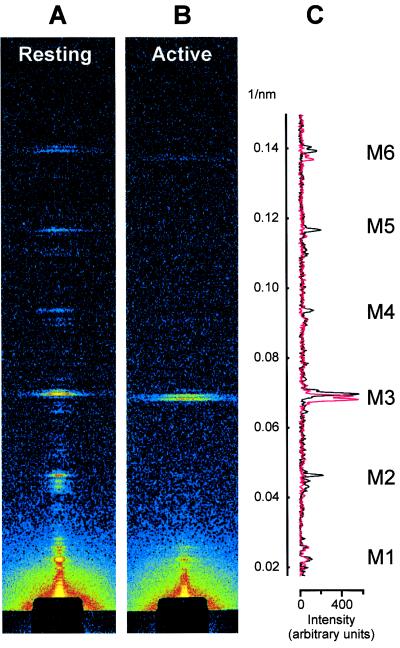
The axial x-ray pattern from resting whole muscles of vertebrates has been extensively characterized (1, 2, 4, 12), and a similar pattern can now be recorded from single muscle fibers [Fig. 1 A and C (black)]. The strong reflection labeled M3 is due to layers consisting of three myosin molecules at an average axial spacing of 14.34 nm. Successive layers are rotated by 40° so that the orientation is the same at every third layer and there is a quasi-helical repeat at 3 × 14.34 nm = 43 nm. The reflections that index on this period are labeled M1, M2, etc. The M2, M4, and M5 reflections are probably due to nonuniformities of the layer spacings (1, 17), and disappeared at the plateau of an isometric tetanus [Fig. 1 B and C (red)], indicating that the spacing had become uniform. The M3 and M6 remained strong, but their radial width increased by a factor of ca. 2.5, and their axial spacing by about 1.6% (Table 1).

Figure 1.

Axial x-ray diffraction patterns from a single muscle fiber at rest (A) and at the plateau of an isometric tetanus (B), and comparison of the respective axial intensity distributions (C; resting, black; active, red). Sarcomere length, 2.07 μm; exposure, 6 s in both conditions. Radial integration limits in C: ±1/80 nm⁻¹ (resting), ±1/60 nm⁻¹ (active).

Table 1.

Intensity, spacing, and radial width (full width at half-maximum) of the M3 and M6 reflections at sarcomere length 2.0–2.2 μm, at rest and during active contraction

	M3			M6
	Intensity	Spacing, nm	Width, nm−1	Intensity	Spacing, nm	Width, nm−1
Resting	1	14.341  ± 0.007	0.007  ± 0.002	0.25  ± 0.05	7.157  ± 0.005	0.005  ± 0.001
Active	2.64  ± 0.43	14.573  ± 0.007	0.016  ± 0.001	0.42  ± 0.06	7.286  ± 0.006	0.015  ± 0.003

Intensities were measured with narrow integration limits (see Methods), corrected for width changes as described in the text, and normalized to the resting M3 intensity. Means ± SD, 4 fibers. 

The interference fine structure of the M6 reflection was similar at rest and during contraction; the lower-angle peak had about twice the intensity of the higher angle peak in both states (Fig. 1C). In contrast, the interference fine structure of the M3 reflection changed dramatically between rest and active contraction. At rest [Fig. 1 A and C (black)], the M3 reflection was dominated by a peak at 14.35 nm, with smaller peaks at 14.15 and 14.55 nm (2, 12). During active isometric contraction, the M3 reflection was split into two peaks of roughly equal intensity, with spacings 14.46 and 14.67 nm [Fig. 1C (red)].

Dependence of the Intensity of the M3 Reflection on Filament Overlap.

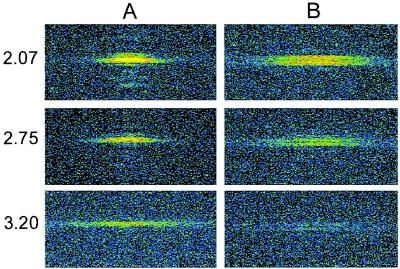
When the overlap between myosin and actin filaments was reduced by stretching the resting fiber, the integrated intensity of the M3 reflection decreased, but its radial width increased (Fig. 2A), probably as a result of reduced lateral coherence between filaments (3). During active contraction (Fig. 2B), the M3 intensity was more markedly reduced at longer sarcomere lengths, but its width was almost independent of sarcomere length. To determine the quantitative relation between M3 intensity and sarcomere length from these data, two methodological problems must be overcome. First, increased radial width reduces the observed intensity, because a smaller fraction of the 3D reciprocal lattice is sampled by the x-ray beam; a correction for this effect was applied by multiplying the integrated intensity by the width (3). Second, increasing the sarcomere length leads to an artifactual intensity decrease, because the fixed-size x-ray beam intersects fewer sarcomeres. This effect was eliminated by dividing each value of width-corrected M3 intensity during active contraction by the corresponding value in the same fiber at rest at the same sarcomere length. The resulting normalized intensity values, called I_M3n, can be compared directly in fibers of different size. Because the resting M3 intensity is independent of sarcomere length, at least in the range 2.0–3.2 μm (2), the sarcomere length-dependence of I_M3n should be determined by that of the active M3 intensity.

Figure 2.

Sarcomere length-dependence of the M3 reflection at rest (A) and at the plateau of an isometric tetanus (B). Top two rows (sarcomere lengths 2.07 and 2.75 μm) are from the same fiber; Bottom row is from another fiber, sarcomere length 3.20 μm. X-ray exposure, 6 s. Each panel is 1/65 nm⁻¹ vertically and ±1/57 nm⁻¹ horizontally.

I_M3n decreased linearly with increasing sarcomere length in the range 2.2–3.2 μm (Fig. 3A, filled circles and squares). Linear regression of I_M3n against sarcomere length in this range (dashed line) gave an intercept on the sarcomere length axis of 3.63 μm (95% confidence limits 3.38–4.06 μm). The myosin and actin filament lengths are 1.60 and 2.05 μm, respectively (18), so filament overlap should be abolished at sarcomere length 3.65 μm. The bare zone in the middle of the myosin filament, where myosin heads are absent, is about 0.16 μm long (19, 20), so maximum overlap between myosin heads and actin filaments should occur in the sarcomere length range 2.05–2.21 μm. Within experimental error, I_M3n was directly proportional to the degree of overlap between myosin heads and actin filaments, and therefore to the fraction of myosin heads that can interact with actin and generate force.

At sarcomere lengths greater than 2.2 μm, force during an isometric tetanus continues to increase slowly (“creep”) after its initial rapid rise (13), as sarcomeres near the ends of the fibers shorten at the expense of those in the central region, where the x-ray beam intersects the fiber. Active force (Fig. 3A, open circles) was determined by extrapolation of force creep to the start of the tetanus (13). Regression of active force against resting sarcomere length gave a sarcomere length intercept of 3.61 μm, similar to the value obtained for I_M3n. Sarcomere length changes on activation were small. For example, at resting sarcomere length 2.20 ± 0.03 μm (mean ± SE, n = 6 segments in 3 fibers), mean sarcomere lengths at 0.3, 1.1 and 2.3 s in the tetanus were 2.15 ± 0.04 μm, 2.15 ± 0.03 μm and 2.14 ± 0.04 μm respectively. Corresponding values for resting sarcomere length 2.81 ± 0.04 μm were 2.80 ± 0.04 μm, 2.80 ± 0.03 μm, and 2.82 ± 0.05 μm, respectively. The velocity of sarcomere length change was always less than 0.02 μm⋅s⁻¹, which should have a negligible effect on the relation between I_M3n and sarcomere length (21). Linear regression of active force against active sarcomere length measured 1 s after the start of the tetanus (triangles) gave a sarcomere length intercept of 3.55 μm (continuous line), close to that obtained for I_M3n.

The intensity of the M6 reflection during active contraction was normalized by the resting M6 intensity at the same sarcomere length and corrected for changes in radial width. The resulting parameter, I_M6n, was roughly independent of sarcomere length (Fig. 3B).

Dependence of the Fine Structure of the M3 Reflection on Filament Overlap.

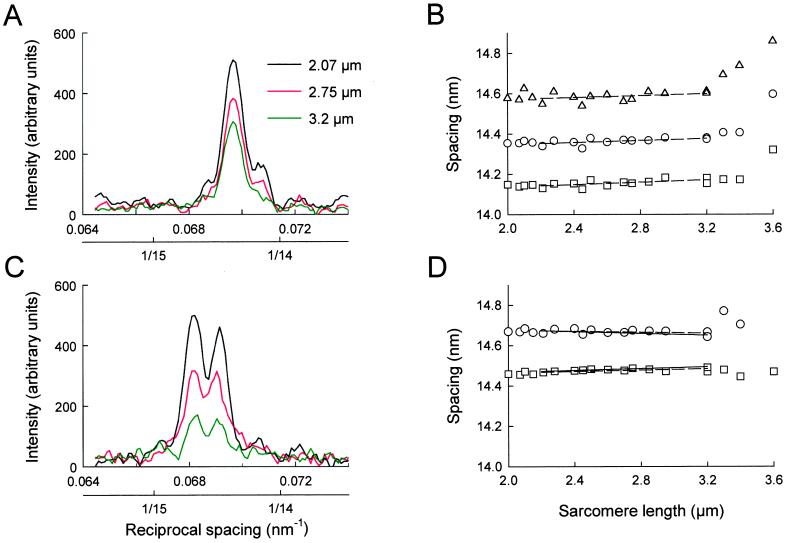
The relative intensities of the peaks of the M3 reflection were independent of sarcomere length in the range 2.0–3.2 μm, both at rest (Fig. 4A) and during active contraction (Fig. 4C). The relative intensities of the small peaks in the resting fiber with spacings of about 14.15 and 14.55 nm began to change at sarcomere lengths greater than 3.2 μm (not shown).

Figure 4.

Sarcomere length-dependence of the axial intensity distribution (A and C) and peak spacings (B and D) of the M3 reflection at rest (A and B) and at the isometric tetanus plateau (C and D). Dashed lines in B and D show regression of peak spacings in the sarcomere length range 2.2–3.2 μm; continuous lines in D show the spacings predicted by interference between the two arrays of myosin heads in the overlap zone of each sarcomere.

The spacings of the M3 peaks varied systematically with sarcomere length. At rest (Fig. 4B), the measured spacing of each peak increased slightly with increasing sarcomere length in the range 2.2–3.2 μm, then more steeply at longer sarcomere lengths. In the range 2.2–3.2 μm, the slopes of linear regression lines (dashed) for the spacings of the peaks at ca. 14.15, 14.35, and 14.55 nm were 0.022 ± 0.013, 0.025 ± 0.008, and 0.029 ± 0.008 nm⋅μm⁻¹ (±SE), respectively. There was no significant effect of sarcomere length on the separation between the peaks in the resting fiber, consistent with a fixed distance between the two arrays of myosin heads that are responsible for the interference fine structure of the reflection. The origin of the slight increase in all of the peak spacings with increasing sarcomere length is unknown, although the more pronounced increase at sarcomere lengths greater than 3.2 μm may be associated with high resting tension (Fig. 3A, diamonds).

In active contraction, the separation between the two major peaks of the M3 reflection decreased with increasing sarcomere length (Fig. 4D). The effect is more apparent at shorter lengths, where the spacing measurements are more reliable because the reflection is more intense (Fig. 4C). The slopes of regression lines (dashed) to the peak spacings were 0.017 ± 0.005 and −0.012 ± 0.007 nm⋅μm⁻¹ (±SE) for the ca. 14.46- and 14.67-nm peaks, respectively, in the sarcomere length range 2.2–3.2 μm. These slopes are significantly different (P < 0.01). This behavior is consistent with an increased interference distance between the two arrays of myosin heads that are attached to actin at longer sarcomere lengths, as shown below.

Discussion

Dependence of the M3 and M6 Intensities on Filament Overlap.

After taking into account changes in the width of the x-ray reflections and in the mass of the fiber in the x-ray beam, we found that the normalized intensity of the M3 reflection, I_M3n, and the active isometric force have the same dependence on sarcomere length in the range 2.0–3.2 μm (Fig. 3A). Both I_M3n and force are proportional to the degree of overlap between the actin filaments and the region of the myosin filaments containing myosin heads. Thus, the M3 reflection during active contraction arises predominantly from heads in the overlap region. The fraction of such heads that are bound to actin or bear force is unknown, but the large changes in I_M3 observed when rapid length steps are imposed during active contraction suggests that the M3 reflection is mainly due to actin-bound, force-generating heads (8–11).

The heads in the nonoverlap region of the sarcomere make little contribution to the active M3 reflection. These heads cannot attach to actin and may be tilted away from the perpendicular conformation characteristic of the force-generating heads (3, 4, 8–11). They may also be more disordered. In any case, the conformation of the detached heads in active muscle is clearly distinct from that of the detached heads in resting muscle, which produce an intense M3 reflection (Fig. 1A), and a set of myosin-based layer lines that are absent during active contraction (1, 3, 7).

In contrast with the behavior of the M3 reflection, the intensity of the M6 reflection during active contraction showed no clear dependence on sarcomere length (Fig. 3B). Better data will be required to determine what fraction of the M6 intensity is independent of filament overlap, but it seems likely that a large part of the M6 reflection comes from the filament backbone, detached heads, or other myosin filament proteins. This conclusion would explain why the M6 intensity shows little change after rapid length steps (8), and why the relative intensity of the M6 peaks is unaffected by activation (Fig. 1C).

The Fine Structure of the M3 Reflection.

In resting whole muscles, the splitting of the axial x-ray reflections into closely spaced peaks has been well characterized and has been explained quantitatively as an interference effect between myosin heads in the two halves of the filament (1, 2, 12). Our results from single muscle fibers at rest (Fig. 1 A and C; Fig. 4A) support this interpretation. Both the relative intensities of the interference peaks (Fig. 4A) and the separation between them (Fig. 4B) were independent of sarcomere length in the range 2.0–3.2 μm, as predicted.

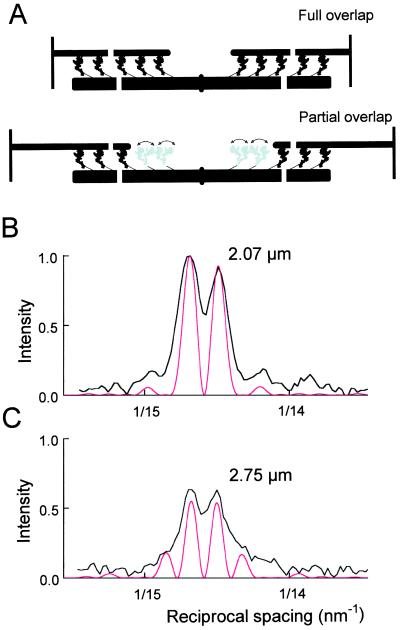
The fine structure of the M3 reflection during active contraction has not been characterized in detail previously. Splitting of the active M3 reflection has been observed in whole muscles but was interpreted in terms of two populations of myosin heads with different axial periodicities (22). The fine structure of the active M3 reflection can be quantitatively explained by interference between myosin heads in the two halves of the filament (Fig. 5A). Each half-filament consists of 49 layers of heads (19, 20) with axial periodicity 14.573 nm during active contraction. The two head arrays are separated by a bare zone of approximately 160 nm in the center of the filament (19, 20, 23). Thus the centers of the two arrays are separated by about 860 nm, or about 59 times the axial periodicity. According to the convolution theorem, the effect of x-ray interference between these two arrays is to multiply the relatively broad 14.573 nm reflection due to a single array of 49 heads by a cosine function with a much higher spatial frequency, corresponding to a periodicity of about 860 nm (see ref. 23, p. 359; ref. 24, p. 337). The result depends critically on the precise length of the bare zone, which determines the relative phase between the two head arrays. The observed fine structure (Fig. 5B, black) was best fit with a bare zone, defined as the separation of the centroids of the proximal heads, equal to 167.5 nm (Fig. 5B, red). At sarcomere length 2.0–2.2 μm, the centers of the two head arrays are then separated by 866.9 nm, which is close to 59.5 times the 14.573 nm repeat. This half-integral multiple makes the diffraction from the two head arrays interfere destructively at the center of the reflection so that the intensity there would be zero for ideal spatial resolution, and the reflection is split into two peaks of roughly equal intensity. If, on the other hand, the separation had been an integral number of 14.573 nm repeats, the fine structure would have shown a strong central peak with symmetrical side-peaks. The observed peak separation is quantitatively consistent with interference across the M-line of the sarcomere (the center of the myosin filament), but not with the larger interference distance across the Z-lines between adjacent sarcomeres. The total intensity of the M3 reflection (I_M3) depends on the conformation of the myosin heads (3, 4, 8–11), but the effect of interference on I_M3 is less than 2% at any interference distance above 800 nm.

Figure 5.

Structural modeling of the fine structure of the M3 reflection. (A) Schematic representation of myosin head conformations along the sarcomere at two sarcomere lengths. Myosin heads in the nonoverlap region (gray) are more disordered than those in the overlap region (black), shown in the conformation in ref. 11. (B and C) Observed (black, from Fig. 4B), and simulated (red) fine structure of the active M3 reflection at sarcomere lengths 2.07 and 2.75 μm, respectively, scaled to the observed intensity of the 14.67 nm peak at 2.07 μm.

The calculated intensity profile (Fig. 5B) accurately reproduced the spacings and relative intensities of the two main peaks, although the observed peaks were broader than the predicted ones, mainly because of the limited resolution of the image plate scanner. The calculated profile in Fig. 5B assumes that each myosin head acts as a point diffractor, i.e., the finite size and axial disorder of the heads were neglected. This assumption is a good approximation because the transform of a single head is roughly constant over the axial width of the M3 reflection, and essentially identical profiles (not shown) were calculated from an atomic model for the force-generating myosin head (11), shown at low resolution in Fig. 5A.

Force generation in muscle is thought to be driven by a change in conformation of the myosin heads in which the actin-binding sites are displaced axially toward the center of the sarcomere, and x-ray interferometry provides a very sensitive measure of these motions. For example, a change in shape of the heads that produced a centroid motion of only 0.5 nm in each half-sarcomere, corresponding to an axial tilt of the heads by only 5°, would change the relative intensity of the 14.46 and 14.67 nm peaks from 1:0.93 to 1:0.69, which would be easily resolved. This sensitivity, combined with the association of the M3 reflection with the force-generating population of myosin heads, makes the fine structure of the M3 reflection an extremely powerful tool for future studies of the mechanism of muscle contraction.

When the sarcomere length is increased, the distance between the centers of the two arrays of myosin heads that can bind to actin also increases (Fig. 5A). For example, at sarcomere length 3.2 μm, the distance between the centers of the two arrays would be 1362 nm. If, as argued above, the M3 reflection is due to the heads in the region of overlap with actin, the separation between the M3 peaks should be reduced, as observed. This effect was reproduced by the interference model (Fig. 4D, continuous lines; Fig. 5 B and C, red); the differences between data and model are not significant. However there seems to be an increasing discrepancy at longer sarcomere lengths, which might be due to an increasing number of detached heads with a shorter interference distance. The contribution of detached heads to the M3 reflection is small (Fig. 3A) but could become significant at long sarcomere lengths.

The relative intensity of the M3 peaks was independent of sarcomere length (Fig. 4C). This result is also explained by interference between the two arrays of heads in the overlap regions of the sarcomere (Fig. 5 B and C), provided that both the overlapped and nonoverlapped regions of the myosin filament have the same 14.57-nm periodicity during isometric contraction. In this case, the separation between the centroids of the two interfering arrays changes by exactly 14.57 nm as each layer of heads is withdrawn from the overlap region (Fig. 5A, black) and joins the population that cannot bind to actin (Fig. 5A, gray), so the phase relationship between them is constant.

The model calculations were repeated, allowing for a compliance of the myosin filament corresponding to an average strain of 0.12% under the isometric force at full overlap (5, 6, 11), with essentially identical results, except that the bare zone length under zero strain would be 0.8 nm shorter than the 167.5 nm obtained in the zero compliance model. Compliance has little effect on the relative intensity of the M3 peaks because the interference distance and average filament periodicity change roughly in proportion.

Structural Changes in the Myosin Filament on Activation.

The 1.6% increase in the periodicity of the myosin filament during active contraction (Table 1) is an order of magnitude larger than that expected from its compliance (5, 6, 11). The periodicity increase is seen in the M6 reflection (Table 1), which, unlike the M3, does not arise solely from myosin heads in the overlap region (Fig. 3B). The interference fine structure of the M3 reflection shows that the periodicity increase occurs in the region of the myosin filament that does not overlap with the actin filament, as discussed above. These results provide compelling evidence in support of the hypothesis that the structure of the entire myosin filament changes on activation, as originally suggested by measurements of the myosin-based layer lines and of the spacings of axial reflections from whole muscles activated at lengths where no overlap is expected (2, 25). The use of single muscle fibers in the present work avoids uncertainties related to incomplete activation and sarcomere length inhomogeneity in the whole muscle experiments. We also limited the quantitative analysis to the sarcomere length range 2.2–3.2 μm, in which filament overlap can be varied (although not abolished) while avoiding the ambiguities related to the irreversible or time-dependent effects seen at zero overlap (2, 25).

How can the part of the myosin filament that does not overlap with actin filaments respond to activation? One possibility is that myosin heads binding to actin in the overlap region trigger a cooperative transition that propagates along the filament. Another is that the structural change, although distinct from true compliance, is triggered by tension in the filament. A direct action of Ca²⁺ on the myosin filament is yet another possibility. Whatever the signaling mechanism, elongation of the myosin filament by 1.6% could have a significant effect on contractile function. The time course of the spacing change is similar to that of active force development (7). The tip of the myosin filament would be displaced toward the Z-line by about 13 nm. Because a shortening step of only 4 nm per half-sarcomere reduces the isometric force to zero and the working stroke is about 10 nm (26), this motion would have a substantial effect on force development.