True optical resolution beyond the Rayleigh limit achieved by standing wave illumination

Abstract

During the last decade, various efforts have been undertaken to enhance the resolution of optical microscopes, mostly because of their importance in biological sciences. Herein, we describe a method to increase the resolution of fluorescence microscopy by illuminating the specimen with a mesh-like interference pattern of a laser source and electronic postprocessing of the images. We achieve 100-nm optical resolution, an improvement by a factor of more than 2 compared with standard fluorescence microscopy and of 1.5 compared with confocal scanning.

Studies of biological samples require microscopes that combine high resolution with sufficient material contrast. Fluorescence microscopy is capable of selectively imaging individual components of the specimen, because dyes can be bound to specific molecules. The resolution of far field instruments is fundamentally limited by the wave nature of light. A practical definition of the resolving power is the well known Rayleigh criterion. It states that two points are just resolved if their lateral separation equals the radius of the first dark ring of the Airy pattern. For green light (wavelength 540 nm) and objectives with a numerical aperture (NA) of 1.4, this criterion imposes a limit of 240 nm (1). In the case of fluorescence microscopy, a resolution beyond the common Rayleigh limit can be achieved by means of a nonuniform excitation pattern that contains high spatial frequency components. In scanning confocal fluorescence microscopy (CFM), this pattern is a small light spot that is scanned over the specimen, theoretically yielding a 1.4-fold improved resolution compared with standard fluorescence microscopy (2–4).

In our harmonic excitation light microscopy (HELM), the nonuniform excitation pattern with high spatial frequency components consists of an extended two-dimensional interference field with closely spaced nodes and antinodes. This pattern covers the full field of view and can be shifted in two dimensions by piezo actuators. Five images for different positions of the pattern are recorded by a charge-coupled device (CCD) camera and postprocessed electronically. Frequency domain analysis shows that, as a result of harmonic excitation, additional high spatial frequency components of the specimen spectrum contribute to the image produced on the CCD chip. From the five acquired images, the sample spectrum is reconstructed within an extended passband by an algebraic approach. With our method, we even outperform the lateral resolving power of CFM by a factor of 1.5 and additionally avoid disadvantages of scanning methods.

Materials

Apparatus.

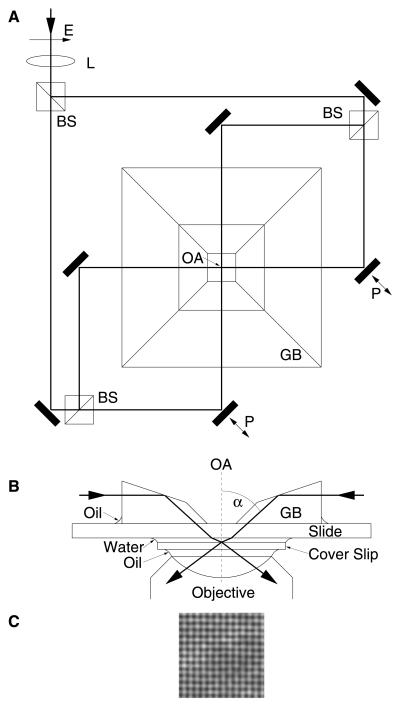
In our setup, an Ar-ion laser (Omnichrome, Chino, CA, 543-AP-A01; wavelength 488 nm) serves as a coherent light source. The laser is coupled to the interference-generating apparatus (Fig. 1) by a single-mode polarization maintaining fiber. Adjustment of laser power is possible by a rotatable half wave plate and a polarizer. In the interference-generating apparatus, four laser beams, which can be considered as plane waves, intersect in the object plane of the microscope under a common angle α = 55° to the optical axis. The electrical polarization is parallel to the image plane; therefore, only antiparallel beams (and not orthogonally directed ones) interfere. The path length for two laser beams can be varied by piezo-actuated mirrors to adjust the phase offset of the interference pattern.

Figure 1.

Interference-generating apparatus (A and B) and measured intensity distribution (C). (A) Top view. A collimated laser beam (λ = 488 nm) with a diameter of 1.5 mm is slightly focused by a weak lens (L; focal length 300 mm) before being split by beam splitters (BS) into four beams of equal intensity that cross at the optical axis (OA) of the microscope. The position of L is adjusted for a beam diameter of about 120 μm in the object plane. With this configuration, the curvature of the wavefronts is negligible in the small field of view (about 25 μm × 25 μm). Piezo actuated mirrors (P) are used to vary the path length for two beams. E, electrical polarization. (B) Cut view through the optical axis. The four laser beams (only two are shown) are coupled to the object by a glass block (GB) which is oil-immersed to the slide. A standard fluorescence filter cube (not shown; emission, bandpass 515–565 nm; beam splitter, dichroic long-pass 510 nm) turned out to be sufficiently selective to avoid problems linked to residual laser light on the CCD chip even though the intensity of the captured laser light was several orders of magnitude higher than that of the fluorescence light. (C) The interference pattern recorded with the fluorescence filter removed from the imaging path of the microscope. An additional neutral density filter with an attenuation rate of 10⁻³ is used to protect the eyes as well as the camera against the high intensities of the direct laser light. The nodal spacing is about 200 nm.

An inverted microscope (Zeiss Axiovert 100) with an uncooled industrial grade CCD camera attached (LV-8500, Leutron Vision, Glattbrugg, Switzerland) acquires images of the sample. A standard personal computer with a frame grabber (Pic-Port, Leutron Vision) reads out image data, controls the measurement sequence, and performs image calculations. The algorithm to calculate the final HELM image requires a few seconds only for a 1,024 × 1,024 pixel image.

Results

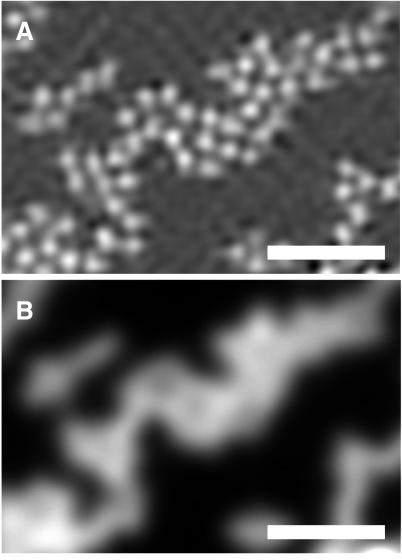
Fig. 2 shows fluorescent beads with a diameter of 100 nm, which is far below the Rayleigh limit for standard fluorescence microscopy and also below that of confocal devices. To compare the resolving power of different techniques, the same region of water-immersed beads was imaged by using HELM (Fig. 2A), standard illumination (Fig. 2B), and confocal scanning (Fig. 2C). As a reference for the actual locations of the individual beads, an atomic force microscope image is also given (Fig. 2D), which was acquired in air. The NA of the objective was 1.4 for the light microscopic images. For the confocal image, the pinhole diameter was set to 67% of the inner Airy disk diameter; the resolution deterioration caused by this finite pinhole size is about 15% (5). The resolution of the HELM image is clearly superior to that of the standard and also to that of the confocal image. Distinguishing individual beads is not possible in the latter ones but is possible in HELM, although for HELM resolving 100-mm beads is close to the limit.

Figure 2.

Identical area of a sample of 100-nm-diameter fluorescent polystyrene beads imaged with different techniques. (Bar = 1 μm.) (A) This panel was imaged by using HELM on a Zeiss Axiovert microscope with a Plan Apo ×63 1.4 NA objective. (B) This panel was imaged through identical lenses with standard illumination. The confocal image (C) was recorded on a Leica (Deerfield, IL) NTSP with a Leica Plan Apo ×100 1.4 NA objective. (D) This panel was recorded with an atomic force microscope (TopoMetrix Accurex II MS, Santa Clara, CA). The time-integrated laser power for the full field of view (25 μm × 25 μm) was about 30 mW for the confocal image and about 0.16 mW total for the five images required for HELM; the acquisition time was 6.5 s and 1.6 s, respectively. To stabilize the structures, we linked the carboxylate-modified surface of the beads (Fluoresbrite YG carboxylate microspheres, Polysciences) to the coverslip with polylysine (poly-l-lysine hydrobromide; molecular mass = 36 kDa; Sigma). The pixel distance of the CCD chip complied with the Shannon criterion; the quasicontinuous images presented herein were generated by band-limited interpolation. This interpolation procedure smoothes the pixel noise of the original images and is the reason for the granular structure of image (C).

Fig. 3 shows beads with a diameter of 200 nm, which approximately equals the Rayleigh limit for standard fluorescence microscopy. The HELM image in Fig. 3A demonstrates that such beads can be distinguished clearly by our method, even when they are closely packed. In the standard fluorescence microscopy image (Fig. 3B), in contrast, the individual beads remain blurred.

Figure 3.

Fluorescent beads with a diameter of 200 nm imaged with HELM (A) and standard fluorescence microscopy (B). (Bar = 1 μm.) The microscope system as well as the specimen preparation are identical to those described for Fig. 2. The center distance of the tightly packed beads approximates the Rayleigh limit of 240 nm. The almost invisible contrast dip between the individual beads in B is a consequence of the fact that the beads are not point sources. Furthermore, one has to take into account that, for water-immersed beads, the effective NA of the objective (nominal: 1.4) becomes smaller (28).

Theory

With z denoting the spatial coordinate along the optical axis and x and y being the coordinates parallel to the image plane, the propagation directions (x,y,z) of the four interfering laser beams are (s,0,c), (−s,0,c) (0,s,c), and (0,−s,c), respectively, where s = sin(α), c = cos(α), and α is the beam's angle to the optical axis. Neglecting scaling factors, the resulting intensity pattern I of the electric field can be written as

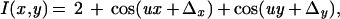1

where u = (4πn)sin(α)/λ is the spatial frequency of the harmonic excitation, n = 1.52 is the refractive index of glass, λ is the vacuum wavelength of excitation, and Δ_x and Δ_y describe the shift of the pattern relative to the sample in x and y direction, respectively.

For the illuminated sample, the fluorescence φ is proportional to the excitation intensity I times the density of dye molecules ψ; the latter is called the original image in the following text:

2

With ˜ denoting the two-dimensional Fourier transform of a variable, we obtain for the spectrum of the illuminated sample:

3

with A = ψ̃(k_x,k_y), B^± = ψ̃(k_x ± u,k_y), and C^± = ψ̃(k_x,k_y ± u).

φ̃ is a superposition of the original spectrum A plus four spectra B^±,C^± that have been shifted by the spatial frequency u in reciprocal space along the k_x and k_y axis in positive and negative directions. In frequency domain, the imaging property of the microscope can be described by a multiplication with an instrument-specific function T, called the optical transfer function (OTF; refs. 6–8):

4

where θ is the resulting image on the CCD chip.

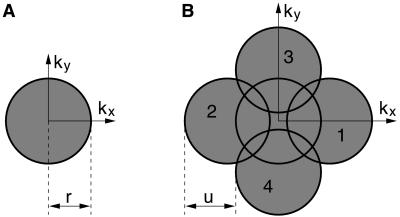
In regions where the OTF is nonzero, called the support of the OTF or the passband, the frequency components of the sample, in principle, can be reconstructed; however, outside this region, the information is irrecoverably lost. In case of fluorescence microscopy, the passband is a circular region centered at the origin with a cutoff radius r = 4πNA/λ, where λ is the vacuum wavelength of emission (about 540 nm for our fluorescein-like dyes) and NA is the NA of the objective. Inserting Eq. 3 into Eq. 4, we obtain an expression for the spectrum of the image in case of harmonic excitation:

5

The occurrence of the four shifted spectra B^± and C^± in Eq. 5 as a result of the standing wave excitation is the basis of our method. Through this shift, additional high frequency regions of the optical spectrum are brought into the passband of the microscope. Component B⁺, for instance, has been shifted by u to the left before the imaging process of the microscope cuts off a circular region centered at the origin of the reciprocal space. Consequently, component B⁺ transfers object information originating from a circular region centered at a point on the positive k_x axis at a distance u from the origin. Fig. 4 shows this enhanced support of the OTF achieved by our current setup.

Figure 4.

The enhancement of the support of the OTF by means of standing wave excitation. (A) The circular passband for standard fluorescence microscopy with cutoff frequency r. (B) The cloverleaf-shaped OTF of HELM. The four circular regions 1, 2, 3, and 4 are relocated copies of the circular passband from A and correspond to the components B⁺, B⁻, C⁺, and C⁻ from Eq. 5, respectively. The displacement u is equal to the spatial frequency of the harmonic excitation. The ratio of u to r displayed in this figure corresponds to the real situation, because the cutoff frequency of the overall system is ≈20% less than that one expected from the nominal NA of our objective.

The five images acquired for HELM, however, must be postprocessed electronically to extract the individual components A, B^±, and C^± and rearrange these to obtain the final high-resolution image. The extraction method used in this study is a two-dimensional extension of the algebraic approach described in ref. 9. For our two-dimensional case, one requires five images for which the nodes and antinodes of the excitation pattern are at different positions. In our setup, the x and y phase offsets (Δ_x and Δ_y) are adjusted sequentially to the values (0,0) (π/2,0), (π,0), (0,π/2), and (0,π) by piezo actuators. For the Fourier transforms of the five acquired images, Eq. 5 holds with the appropriate coefficients 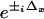and 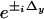. Thus, we obtain a 5 × 5 set of linear equations that can be solved for the five spectral components A, B^±, and C^±. Experimentally, we perform a fast Fourier transform on the measured images and solve the set of linear equations for every pixel. By doing so, we obtain the spectral components A, B^±, and C^±, which, additionally, have been attenuated by the OTF of the microscope. The remaining computational task is to shift the components back to their original position and, finally, superimpose them, taking into account the attenuation by the microscope's OTF.

Taking a more general theoretical perspective, the spatial resolution enhancement achieved is only possible at the expense of temporal resolution (the image rate in HELM is reduced, because five images are required to calculate one high-resolution image). The underlying invariance principle for the number of degrees of freedom of the optical message was established more than 30 years ago (10).†

Discussion

One important parameter in HELM is the beam's angle α to the optical axis, which determines the spatial frequency of excitation u. In Fig. 4, it can be seen that the choice of u requires trading off maximum cutoff frequency along the k_x and k_y axis vs. anisotropy of the resulting passband.

The chosen value (55°) is a good compromise and, additionally, allows direct observation of the interference pattern with immersion objectives.

Because of the nonisotropic passband, the images of the beads show some anisotropy and an overshooting near the edges of the beads; most noticeable are the dark zones in the diagonal directions in Fig. 2A. This effect could be avoided largely by using six or eight laser beams oriented in multiples of 60° or 45°, respectively.‡

Compared with CFM, the signal-to-noise ratio of the HELM image is superior, even though the time integrated laser power was more than 100 times higher for the CFM image in Fig. 2C. One fundamental reason for this improvement lies in the fact that the resolution enhancement of CFM compared with standard fluorescence microscopy can be achieved only by using a small pinhole in the emission light path (5, 13, 14). This arrangement necessitates trading off noise level vs. resolution. Conversely, in HELM, all photons entering the lenses can be collected by the camera.

For studies of dynamic objects, imaging speed is of major importance. The fundamental limitation of imaging speed in fluorescence microscopy is given by the maximum emission rate of the fluorophores caused by the finite lifetime of the excited state (“dye saturation”; ref. 15). In HELM, roughly one-half of the fluorophores are illuminated by the interference pattern at one time, whereas in the common single-point CFM, only a tiny fraction of the fluorophores is illuminated at one time (≈1 per million for a 1,024 × 1,024 pixel image). As a consequence, the total photon flux from the specimen is limited to values that are several orders of magnitude smaller for the sequential operation of CFM than for the parallel one of HELM. Because a minimum number of photons per image is required for a certain signal-to-noise level, HELM has the potential to acquire image data much faster than does CFM. In addition to this fundamental consideration, HELM reduces the speed problems linked to mechanical scanning mechanisms, because only five scans per image are performed in contrast to CFM, where one scan per line is required. Both the dye saturation problem and the mechanical scanning difficulties of CFM, however, can be reduced by the newer multipoint scanners.

The advantages in the field of imaging speed can also be seen in our experimental data. The total acquisition time for the five images required for HELM (Fig. 2A) was 1.6 s compared with 6.5 s for the confocal image (Fig. 2C). Taking into account the higher signal-to-noise ratio of the HELM image that is achieved with an uncooled industrial-grade CCD camera, the difference is clear.

A point of practical interest is the required stability of the interference pattern during the measurement. We found that phase offset errors of 1/10 of the nodal spacing (20 nm) are just tolerable, but larger errors lead to significant image deteriorations. The thermal drift of our setup (typically 20 nm/min in a non-temperature-controlled room) limits the acquisition time to several tens of seconds. This limitation, however, could be easily overcome by recalibrating the phase offsets during a long-term measurement. Refractive index heterogeneity of the specimen also leads to unwanted phase errors of the interference pattern, which are space-dependent in this case. As before, to limit these errors to tolerable values, the wavefront distortions introduced by refractive index heterogeneity should not exceed a few tens of nanometers. We expect that the requirements applying to HELM do not differ much from those guaranteeing high-resolution imaging with well corrected high NA objectives in standard microscopy. Further experimental data will be required to study the sensitivity of HELM against refractive index heterogeneity in practice.

For many applications, investigating the three-dimensional structure of the specimen is of major interest. Three-dimensional image data can be acquired by stepping the focus through the labeled (16) or unlabeled specimen (17, 18). Unfortunately, the axial resolution for standard fluorescence microscopy is strongly limited to about 0.9 μm for point-like objects and, even worse, can break down completely for arbitrary objects (19). This problem corresponds to the fact that the three-dimensional OTF has a missing cone around the k_z axis at the origin, and consequently, the resulting three-dimensional image shows potential artifacts. CFM, in contrast, has no missing cone and enables acquisition of three-dimensional images with an axial resolution of about 0.8 μm (20), which, however, is still inferior to the lateral one.

Different methods have been described to improve the axial resolution further. The so-called 4π microscope (21) is a derivative of the CFM with a second objective to collect the photons propagating toward the backside of the specimen chamber as well. The axial resolution theoretically can be as high as 100 nm, whereas the lateral resolving power equals that of CFM. The 4π microscope is also a scanning one.

A nonscanning approach is described in refs. 22 and 23. A strongly increased axial separation capability is achieved by means of an interference field that has its nodal and antinodal planes parallel to the image plane. This method is well suited to objects that are thinner than one period of the excitation pattern. Imaging of thicker specimens may result in artifacts, because the resulting passband still has a missing cone at the origin (9).

A further development that shares aspects of the latter method and 4π microscopy was demonstrated recently (I⁵M microscopy; ref. 24). I⁵M microscopy employs a more complicated interference field generated by a noncoherent light source to illuminate selectively the object plane and is a nonscanning method. The axial resolution equals that of 4π microscopy (100 nm), but the lateral resolution is not increased at all.

Enhanced axial resolution can also be achieved by illuminating the specimen with a fringe pattern produced, for example, by imaging a grating onto the object (25) or by interference of two laser beams (26). For these methods, the reconstruction algorithm applied differs significantly from ours, because the central transmission circle in Fig. 4 is omitted and because object information is transferred in two sidebands only (27). It can be shown, in this case, that the out-of-focus blur is reduced.

Desirable is a microscope with a uniformly high resolution of 100 nm in all space directions without the need for a scanning method. HELM, as established in our current setup, does not increase the axial resolution compared with standard fluorescence microscopy. However, the key idea is that harmonic excitation, together with a reconstruction algorithm similar to the one described herein, also works in spatial directions not parallel to the object plane. By using harmonic intensity patterns that have their nodal and antinodal planes in appropriate space directions, additional copies of the three-dimensional OTF are obtained in any desired direction. Such additional passband regions could be overlaid to one extended passband with a high cutoff frequency throughout reciprocal space.

Our idea for a future setup is to use continuous beam deflection units (like galvanometers or acousto-optical devices) to produce interference patterns easily in selected orientations in space and with various nodal spacings. Such a configuration would enable three-dimensional imaging and, simultaneously, resolve the anisotropy problems caused by the cloverleaf-shaped two-dimensional OTF.

Conclusions

A method has been described that allows two-dimensional imaging with a resolution of 100 nm, which is, to our knowledge, not achieved by any other far field method. Compared with the widely used confocal microscopes, fundamental considerations show advantages in the area of imaging speed and resolution, which are confirmed by the experimental data. The time consumption for electronic postprocessing amounts to a few seconds and will decrease further by advancements in computer technology. In our current setup, however, the axial resolution equals that of standard fluorescence microscopy. Future setups producing varying interference patterns not restricted to fixed orientations would enable us to increase the lateral resolving power as well as the axial one at the same time. Because the system requirements for microscopes based on the principle of harmonic excitation are similar to the ones for confocal devices, we expect that such systems could become a commercial alternative to confocal ones.

Abbreviations

CCD

charge-coupled device

CFM

confocal fluorescence microscopy

HELM

harmonic excitation light microscopy

NA

numerical aperture

OTF

optical transfer function