Native topology determines force-induced unfolding pathways in globular proteins

Abstract

Single-molecule manipulation techniques reveal that stretching unravels individually folded domains in the muscle protein titin and the extracellular matrix protein tenascin. These elastic proteins contain tandem repeats of folded domains with β-sandwich architecture. Herein, we propose by stretching two model sequences (S1 and S2) with four-stranded β-barrel topology that unfolding forces and pathways in folded domains can be predicted by using only the structure of the native state. Thermal refolding of S1 and S2 in the absence of force proceeds in an all-or-none fashion. In contrast, phase diagrams in the force-temperature (f,T) plane and steered Langevin dynamics studies of these sequences, which differ in the native registry of the strands, show that S1 unfolds in an allor-none fashion, whereas unfolding of S2 occurs via an obligatory intermediate. Force-induced unfolding is determined by the native topology. After proving that the simulation results for S1 and S2 can be calculated by using native topology alone, we predict the order of unfolding events in Ig domain (Ig27) and two fibronectin III type domains (⁹FnIII and ¹⁰FnIII). The calculated unfolding pathways for these proteins, the location of the transition states, and the pulling speed dependence of the unfolding forces reflect the differences in the way the strands are arranged in the native states. We also predict the mechanisms of force-induced unfolding of the coiled-coil spectrin (a three-helix bundle protein) for all 20 structures deposited in the Protein Data Bank. Our approach suggests a natural way to measure the phase diagram in the (f,C) plane, where C is the concentration of denaturants.

Nanomanipulation of biomolecules with atomic force microscopy (AFM) and optical tweezers is beginning to provide a molecular basis for understanding elastic behavior in titin (a muscle protein), tenascin (an extracellular matrix protein), and also T4 lysozyme (1–7). These proteins are made up of several individually folded protein domains with β-sandwich architecture. A series of single-molecule experiments on these elastic proteins and other recombinant constructs shows that, on application of force, there is a domain-by-domain unfolding. The clearest evidence for such unfolding comes from AFM experiments (1, 5, 6) that show a characteristic saw-tooth pattern in the force-extension profiles. The near constant spacing between the saw-tooth peaks gives an estimate for the extension length of the fully stretched domain. Because there is a considerable heterogeneity in the makeup of the wild-type titin and tenascin, recombinant methods have been used to synthesize multiple domains of Ig27 (the 27th module in titin; ref. 1) and fibronectin (TnFnIII; ref. 5). Force-induced unfolding of these constructs also leads to saw-tooth behavior similar to that observed for the wild-type proteins. These classes of experiments clearly show that unfolding can be induced by stretching. The force-extension profiles along with the pulling speed dependence of the threshold unfolding forces potentially can be used to map the underlying energy landscape of proteins. It has been suggested that characteristics of the energy landscape (barrier height distribution) in the absence of force can be measured by using AFM experiments in conjunction with fluorescence resonance energy transfer measurements (8).

The advances summarized above have also spurred theoretical activity designed to investigate global aspects and microscopic details of unfolding induced by force (8–11). Steered molecular dynamics (SMD; refs. 10 and 11) simulations, calculations, and simulations with lattice models (8, 9) have been instrumental in providing a framework for understanding AFM measurements. SMD simulations, which are typically carried out at forces that are orders of magnitude larger than those used in experiments, have given the microscopic picture of the unfolding pathways in Ig27 and ¹⁰FnIII (10, 11).

Although these computational studies have been successful in showing how the folding scaffolds of a protein respond to force, a simple framework for predicting the force-induced unfolding pathways has not yet emerged. In this paper, we take a step in this direction. We first studied in detail the equilibrium phase diagrams in the force-temperature plane (f,T) of two model off-lattice sequences with β-sandwich topology (just as in Ig27, ⁹FnIII, and ¹⁰FnIII). Then, we investigated the forced unfolding kinetics by using steered Langevin dynamics (SLD). From these results, we propose that force-induced unfolding characteristics (pathways and pulling speed dependence) can be predicted by using only the structure of the native state. This idea is applied to force-induced unfolding of Ig27, ⁹FnIII, and ¹⁰FnIII. The results are in near quantitative agreement with experiments and/or SMD simulations. We also predict unfolding mechanisms for spectrin, for which only limited experimental data are available.

Materials and Methods

Off-Lattice Models for β-Barrel Proteins.

We use coarse-grained continuum representations for proteins in which only the positions of C_α-carbons are retained (12). Sequences S1 and S2 are modeled as chains of 46 connected beads of three types, hydrophobic B, hydrophilic L, and neutral N. The potential energy includes the contributions from bond-length and bond-angle potentials, the dihedral angle potential V_DIH(φ), and nonbonded potentials (12). V_DIH(φ) is given by A(1 + cosφ) + B(1 + cos3φ). Along the β-strands trans-states are preferred, and accordingly, we chose A = B = 1.2ɛ_h, where ɛ_h = 1.25 kcal/mol is the strength of hydrophobic interactions. In the turn regions (i.e., in the vicinity of a cluster of N residues), A = 0 and B = 0.2ɛ_h. The interaction between a pair of hydrophobic residues is

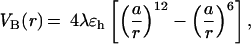where λ is a random factor unique for each pair of B residues (12) and a = 3.8 Å is the residue size. When the sequence is subject to external force f, the total energy is written as E_tot = E_p − (f⃗r⃗), where r⃗is the end-to-end vector.

Simulations.

The dynamics of stretching are obtained by integrating the Langevin equation in the overdamped limit (approximately at water viscosity). Two types of SLD simulations were carried out. (i) A constant force was applied to the termini. (ii) To mimic the AFM experiments, the carboxyl-terminal was pulled along the z axis with the force (10)

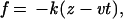1

where v is the pulling speed and k is the spring constant, which is equal to the constant used in the bond-length potential (12). The pulling speed was varied from 6 × 10³ μm/s to 6 × 10⁵ μm/s. These speeds are about four to five orders of magnitude faster than experimental values (1, 13) but are about 10⁴ times slower than the values used in SMD simulations (10, 11). Thermodynamic functions are computed by using a version of the multiple histogram method in which T and f are varied (8).

Predicting Unfolding Pathways by Using PDB Structures.

Using the results of the SLD study of S1 and S2, we developed a method for predicting the unfolding events on application of force to the termini of a protein. There are several steps in the application of our method. (i) From the PDB native structure of a given protein, a coarse-grained model is created. In this model, backbone is represented by C_α-carbons, and side chains are given by the positions of heavy atoms. (ii) The secondary structure blocks (i.e., strands and helices) are assigned in the coarse-grained model by using the secondary structure information in the headers of PDB entries. We assume that residues i and j form a tertiary contact, if the distance between any pair of heavy atoms in their side chains is less than 5.2 Å. By using this definition, the tertiary contact map is obtained, and the stabilization energy for each secondary structure block is computed as the energy of tertiary interactions of the respective block with other secondary structure blocks in the native structure. We use several contact potentials available in the literature (14–16) to ensure that qualitatively similar results are obtained. (iii) We compare the stabilization energies of both terminal blocks. The one with the lower stabilization energy unfolds first. We remove this block from the native conformation and recalculate the stabilization energies of all the remaining blocks. The stabilization energies of terminal blocks are once again compared to determine the next secondary structure block to unfold. If both terminal blocks have approximately equal stabilization energies, their simultaneous unfolding takes place. The procedure is repeated until the entire native structure is unfolded. Note that this method is valid when secondary structure blocks in the native state do not form subdomains, and forced unfolding may proceed only via unraveling of terminal blocks. With this method, the breakup of hydrogen bonds (11, 17) cannot be predicted. The method allows us to compute the order of unfolding events and energy profiles, the pathways and the structure of the transition state (TS), and the equilibrium forces f_eq for the force-induced unfolding.

Pulling Speed Dependence of Unfolding Forces.

The pulling speed dependence of forces is obtained with f_p ≈ f_eqln(v/v_min), where v_min = k_uΔz (k_u is the unfolding rate at f = 0, and Δz is the maximum extension). For Ig27, ¹⁰FnIII, and ⁹FnIII, k_u was taken from chemical denaturant experiments (6, 18, 19), and Δz was taken from AFM experiments. For spectrin, we use ΔG/RT ≃ M (where M is the number of residues) and the folding time τ_F ≈ τ₀M^4.2 (τ₀ ≈ 10⁻¹⁰ s; ref. 20) to obtain k_u (≈ 2.2 × 10⁻³ s⁻¹). For unfolding of strand A in titin and helix A in spectrin, we use f_eq ≈ ΔE/Δz, where ΔE is the loss in stability on removal of the particular block. By using the potentials in ref. 16, the values of ΔE and Δz are 3.9 kcal/mol and 3.8 nm for titin and 6.8 kcal/mol and 11 nm for spectrin, respectively.

Results

Phase Diagrams for S1 and S2.

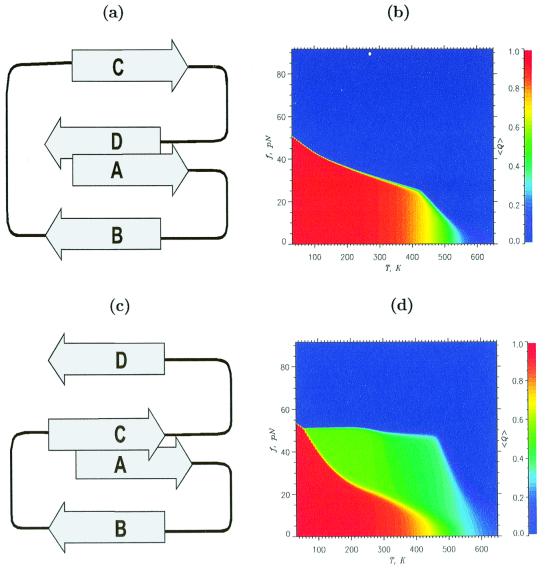
We first studied the unfolding of off-lattice models of proteins. The phase diagrams for S1 and S2, both with β-sandwich native topology (Fig. 1 a and c), are dramatically different (Fig. 1 b and d). There is a small green region in Fig. 1b (S1) that represents states with intermediate values of the fraction of native contacts, <Q>. This small region suggests that force-induced unfolding would be an all-or-none process. In contrast, the phase diagram for S2 (Fig. 1d) shows a broad region of intermediate states along the edge of stability of the native state (red region). This broad region indicates that unfolding must occur via an intermediate. The conclusion that S1 must unfold in an all-or-none manner and that S2 must unfold through an intermediate, which naturally emerges from the equilibrium phase diagram, is verified explicitly by SLD simulations (see below).

Figure 1.

Native structures and phase diagrams for S1 and S2. Schematic sketch of the native structures for S1 (a) and S2 (c). In S1, terminal strands are tightly packed and are stabilized by an almost equal number of tertiary contacts (59 and 58, respectively). Strand D in S2 is exposed and forms only 35 contacts as opposed to the 57 formed by strand A. Thermal refolding (f = 0) for S1 and S2 shows two-state behavior. The phase diagrams for S1 (b) and S2 (d) are quantified by the thermal average of the fraction of native contacts <Q(f,T)>. The values of <Q> are color coded according to the scales shown on the right. The green area in b, which corresponds to intermediate <Q>, is extremely narrow. There is a large green region in the diagram for S2 (d). This large area suggests that S2 unfolds through partially unfolded structure I, in which the strand D is stretched, whereas strands A–C maintain their native conformation.

The threshold force required to unfold the native state (determined from the edges of the red region) for S1 is larger than that required for S2 at all temperatures. At T = 300 K, the equilibrium unfolding force for S1 is about 28 pN, whereas for S2, it is only 14 pN. We deduce that the native state of S1 is more stable than that of S2. Equilibrium folding and unfolding simulations in the absence of force show that the free energy of stability of S1 is larger than that of S2 by a factor of 2.5 (4.3 kcal/mol vs. 1.7 kcal/mol). Thus, the phase diagrams can be used to obtain the free energies of stability in the absence of force.

Stretching Under Constant Force.

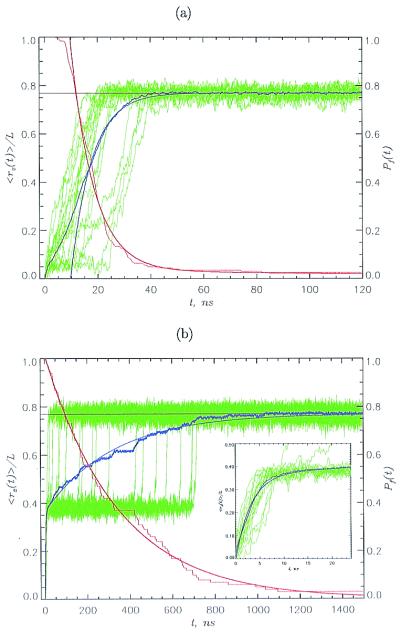
To probe the structural transitions on stretching, we performed SLD simulations by applying a constant force f_s along the z axis. For S1, the stretched state is reached in a single kinetic step, in which all strands unfold nearly simultaneously (Fig. 2a). There is, however, considerable heterogeneity in the time scales in which individual molecules (green curves in Fig. 2a) unfold. The strands unfold by an unzipping process in a cooperative manner without populating intermediates. A qualitatively different unfolding mechanism is found for S2 (Fig. 2b). The normalized extension, <r_z(t)>/L (L is the contour length), shows a biexponential behavior (blue line in Fig. 2b), indicating that S2 unravels by a two-step process. The unfolding kinetics is further revealed by examining the extension profiles for 20 individual trajectories (green curves in Fig. 2b). On a short time scale, the polypeptide chain unfolds from the native state N to a stable on-pathway intermediate I (the green region in Fig. 1d represents the area of stability of I). The transition N → I is reversible, i.e., on turning off the force, the chain spontaneously reaches the folded state without any evidence of hysteresis. Individual trajectories reach I (Fig. 2b Inset) by unzipping strand D. Fig. 2b shows that I is obligatory, i.e., all of the molecules reach S (stretched state) through I. The I → S transition also shows a broad distribution of unfolding times. Remarkably, individual transitions I → S occur over a narrower time interval compared with the events leading to I (compare with Fig. 2b Inset). The unfolding of I, in which three strands are pulled apart, occurs by a shearing-type motion, which is dynamically more cooperative (occurs extremely sharply) compared with the unzipping motion.

Figure 2.

Unfolding kinetics at constant force. We used f_s = 69 pN for S1 (a) and S2 (b). The normalized z component of the end-to-end distance <r_z(t)>/L, given in blue, is averaged over 50 trajectories. Smooth continuous blue curves are single (a) or double (b) exponential fits. Data in green show the extension for 20 individual trajectories. The fractions of folded molecules P_f(t) are given in red, and smooth red curves are double (a) and single (b) exponential fits. The unfolding times are given roughly by Poisson distribution. The large heterogeneity in unfolding times is surprising, because the initial state in unfolding simulations is a relatively well defined folded conformation. Horizontal black lines are the equilibrium extensions under simulation conditions. S1 unfolds by an unzipping motion in a single kinetic step in which all strands unfold simultaneously; S2 reaches S in two steps. An intermediate I [<r_z(t)>/L ≈ 0.4] is quickly formed, and the transition I → S occurs on a longer time scale. I is an on-pathway intermediate that exists in all unfolding trajectories. The dynamics of N → I are shown (Inset).

Pulling Speed Dependence.

On application of force, the barrier between N and S is lowered such that the unfolding rates increase (21). Thus, the threshold force and the unfolding rate must depend on the pulling speed v. We performed SLD simulations by fixing one of the termini and pulling the other at a constant v (Eq. 1). Force-extension profiles for S1 show a single peak at f ≈ 100 pN at an extension of about 0.07L (Fig. 3a). We conclude that the TS for force-induced unfolding occurs close to the folded native state, which is reminiscent of the unfolding seen in Ig27 (1, 6). For S2, there are two peaks in the force-extension profile (Fig. 3b). The one at f ≈ 58 pN with an extension of about 0.1L represents the breakup of strand D (Fig. 1c), thus creating the stable intermediate I. The dominant peak (f ≈ 130 pN and Δz ≈ 0.44L) represents the unraveling of I. From the dependence of the fraction of native contacts <Q> on Δz (red curve in Fig. 3b), we conclude that, after strand D unfolds, there are no major structural changes until Δz ≈ 0.44L, when the polypeptide chain dynamically reaches S. The simulations done at varying speeds result in the same mechanism as is suggested by constant force simulations. The unfolding mechanism is consistent with the expectations from the equilibrium phase diagrams (Fig. 1), a fact that underscores the importance of measuring the diagram of states. The fraction of nonnative contacts (blue curve in Fig. 3b) shows two peaks matching the positions of force peaks, suggesting the transient formation of nonnative structures during the unfolding process.

Figure 3.

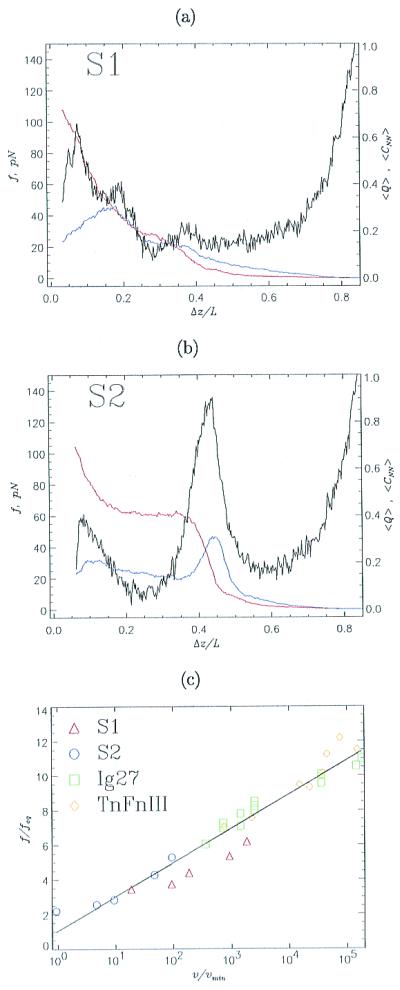
Unfolding kinetics at constant pulling speeds. Black curves (a for S1 and b for S2) show force-extension profiles at the pulling speed v = 6 × 10⁴ μm/s. The horizontal axis gives the normalized distance Δz/L between the fixed sequence terminal and the retaining point (10). The initial separation Δz/L is the equilibrium end-to-end distance at f = 0. Fractions of nonnative contacts <C_NN> and <Q> are given in blue and red, respectively. Data are obtained by averaging 100 trajectories. Because the force-induced unfolding of S1 is two-state, the force-extension profile has a single peak, whereas pulling S2, which has an intermediate I, produces two force peaks. (c) The threshold unfolding forces vs. pulling speeds are plotted for S1 (red triangles), S2 (transition I → S, blue circles), titin Ig27 domain (green squares), and tenascin module TnFnIII (yellow diamonds). Forces are normalized by f_eq either obtained from phase diagrams (Fig. 1) or calculated by using experimental data (1, 5). The pulling speed is expressed in units of the unfolding speed in the absence of force v_min, which is known from simulations or experimental data. The values of v_min are 1.4 × 10⁻⁵ μm/s and 1.3 × 10⁻⁵ μm/s for Ig27 and TnFnIII, respectively. The straight line is the linear fit to the data.

As predicted by Evans and Ritchie (21), the average threshold unfolding force depends logarithmically on the pulling speed (Fig. 3c). The unfolding forces, namely, f_p,S1 (for S1) and f_p,S2 (for unfolding I in S2), may be written as f_p,α ≈ f_eq,αln(v/v_min) (α = S1 or S2). Here, f_eq,α is the equilibrium unfolding force (obtained from the phase diagram) and the minimum pulling speed v_min = k_uΔz (k_u is the unfolding rate at f = 0, and Δz is the extension in going from N to S). We also show the scaled results for titin (1) and the recombinant tenascin segment TnFnIII (5). The parameterization proposed here (which is natural when the overall spring constant of the protein is comparable to the stiffness of cantilever) produces a scaling plot in which the results of simulations for model sequences and proteins lie essentially on one line. Thus, scaling the experimental data by v_min gives a direct measurement of f_eq. From the dependence of f_eq on denaturant concentration, which is easier to change than T in experiments, the phase diagram (Fig. 1) for the various proteins can be measured.

Native Topology Determines Force-Induced Unfolding Events.

The dramatic differences in the force-induced unfolding between S1 and S2, which are masked in thermal refolding (see legend to Fig. 1), can be predicted in terms of the topology of the native state. We have devised the following method (see Materials and Methods for technical details) by using the topology and the energetics of stabilization of the native structures to predict the order of unfolding events. (i) Starting with the native state, compute the energy of each strand by adding the various contact energies between the residues in a given strand with the rest of the structure. (ii) The strand with the highest energy is expected to be the first to unravel on stretching (“a chain is only as strong as its weakest link”). (iii) With the weakest strand removed, the stabilization energies for the remaining strands are recalculated. The one with the highest energy would unfold next and so on. (iv) If there are two strands of nearly equal energies, we predict that they may nearly simultaneously unfold or that there may be parallel unfolding pathways. With this method, we successfully reproduced the simulated force-induced unfolding characteristics of S1 and S2.

Predicting Force-Induced Unfolding Characteristics for β-Sandwich Proteins.

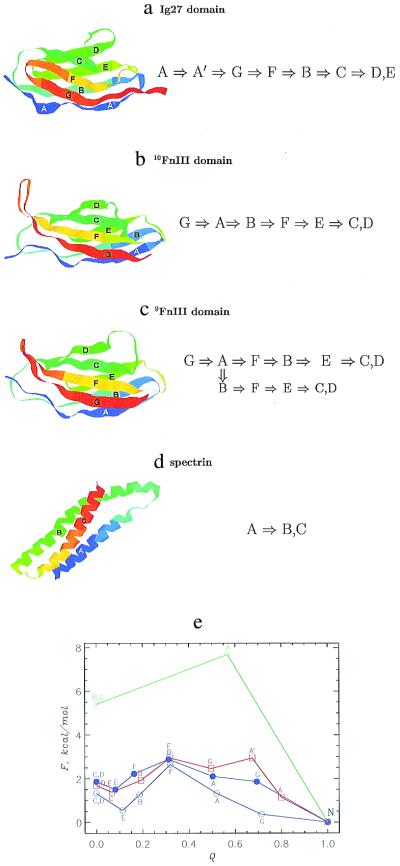
We applied this method to predict the unfolding pathways of three β-sandwich proteins, Ig27 (PDB code 1tit), ⁹FnIII (1fnf), and ¹⁰FnIII (1fnf), as well as the α-helical repeats of spectrin (1aj3). For all these modules, unfolding occurs by a shearing-type motion just as in I → S for S2. For Ig27 of the I band of titin, we find that the strand A unfolds first followed by A^′ and G (Fig. 4a). Strands C, D, and E retain their structural integrity until late in the unfolding process. These observations are in accord with SMD simulations (10). An estimate of the energy barrier, with Q as a reaction coordinate (ref. 23; Fig. 4e), shows that force-induced unfolding TS is highly structured and occurs close to the native state (1, 2, 6, 17).

Figure 4.

Unfolding pathways and barriers in wild-type proteins. The native structures of Ig27 domain (a), ¹⁰FnIII (b), ⁹FnIII (c), and spectrin (d) are shown with the labels for their secondary structure blocks. The unfolding pathways predicted by our method are given to the right as the order in which strands (helices) unfold on stretching. Some contact potentials (15) predict a parallel unfolding pathway in ⁹FnIII. These figures have been created with rasmol 2.6 (22). (e) Unfolding energy barriers for unraveling strands (helices) as a function of the fraction of native contacts Q. The data for Ig27 domain are given in red. The unfolding energies for ¹⁰FnIII and ⁹FnIII are given by solid and open blue circles, respectively. The data for spectrin are in green. This plot estimates the energy barrier that must be overcome to reach a given value of Q. Labels near data points indicate a strand (or helix) that unfolds on reaching a given Q.

From the pulling speed dependence of the forces required to unfold individual domains of titin (1) and the unfolding rate at f = 0 (ref. 6; see legend to Fig. 3c), we predict that the equilibrium unfolding force is about 18 pN. A recent AFM experiment has shown that there is a “hump” in the force-extension curves (at f ≈ 100 pN) on stretching tandem of repeats of individual Ig domains of human cardiac titin (17). The hump corresponds to an initial event in which strand A starts to shear away from the rest of the module (10, 17). Using various statistical potentials (see Materials and Methods), we find that the equilibrium unfolding force for A to unravel is f_eq ≈ 7 pN. With this value, we predict that the initial intermediate in Ig27 module should occur at f_p ≈ f_eqln(v/v_min) ≈ 80 pN at v = 0.5 μm/s.

Our method predicts that, in ¹⁰FnIII, strand G unravels first. This unraveling is followed by A, B, and F. On unfolding of B, the major barrier is overcome (Fig. 4e). The structure containing strands E, C, and D remains intact until late in the unfolding process. The calculations also predict a minor barrier between S and the conformation containing strands C and D. The order of unfolding sketched here is in excellent agreement with SMD simulations (11). Interestingly, the unfolding TS for ¹⁰FnIII is structurally more disordered than that for Ig27. More importantly, we predict that the unfolding TS is about halfway between N and S states (Fig. 4e). Refolding experiments with f = 0 on the isolated FnIII lead to the same conclusion (18, 19), implying that in this case, force-induced unfolding results are consistent with standard biochemical techniques (6).

The order of unfolding for ⁹FnIII is similar to ¹⁰FnIII. However, there are three notable differences. (i) In ⁹FnIII, after strands G and A unfold, either F or B may unravel depending on the contact potentials used, thus suggesting parallel unfolding pathways (24). The energy difference is sufficiently small that the potentials cannot discriminate between the two. (ii) The force required to unfold strand F is less than that needed to unfold strand B in ¹⁰FnIII. Because the threshold force is proportional to stability (for the conformations with similar topologies; Fig. 1), we conclude that ⁹FnIII is less stable than ¹⁰FnIII (19). (iii) Although the location and the structure of the unfolding TS for ⁹FnIII is rather similar to those for ¹⁰FnIII, the energy barrier is smaller; therefore, the unfolding rate for ⁹FnIII is greater than for ¹⁰FnIII.

Force-Induced Unfolding of Spectrin.

Finally, we predict the unfolding pathways for the triple-helix spectrin for which AFM measurements of only the unfolding forces are available (13). Here, helix A unfolds first and is followed by a simultaneous unraveling of B and C helices (Fig. 4d). There is only one energy barrier for the unfolding process. The calculation of the energy profile for unfolding (Fig. 4c) indicates that unfolding TS of spectrin occurs close to the native state. Remarkably, on unraveling of helix A, the stability of the remaining structure is greatly compromised, which suggests that there should be no intermediate for spectrin unfolding. These conclusions were unchanged when we applied our method to all 20 PDB structures for spectrin and used different statistical potentials (see Materials and Methods). Using the estimates f_eq ≃ 4.4 pN and v_min = 8.1 × 10⁻⁵ μm/s (see Materials and Methods), we predict that the force required to unfold spectrin domain at v = 0.8 μm/s is 40 pN (experimental value is ≈30 pN; ref. 13). Rief et al. (13) have reported the unfolding forces for spectrin at two pulling speeds (0.8 μm/s and 8 μm/s). From these measurements and using our parameterization of the dependence of f on v (Fig. 3c), we can calculate the unfolding rate when f = 0. We find that k_u(f = 0) ≈ 10⁻⁴ s⁻¹, which is only a factor of 20 smaller than the value obtained by using scaling arguments. Because f scales only logarithmically with v, this difference results in a relatively small error in predictions for f.

Conclusions

In this article, we have provided a general framework for predicting the force-induced unfolding characteristics (pathways, pulling speed dependence of the unfolding forces, and location of TSs). Our approach is based on the hypothesis that unfolding by stretching can be understood by using only the topology of the native state. This hypothesis was firmly established by studying in detail the unfolding of two off-lattice model sequences with β-sandwich architecture similar to that of Ig27 and fibronectin domains. The remarkable differences between the stretching behaviors of two model sequences, which are not evident in thermal refolding calculations, are predicted quantitatively with our method. The success of our method in nearly quantitatively predicting the pulling speed dependence and location of TSs in Ig27, ¹⁰FnIII, ⁹FnIII, and spectrin confirms the validity of our theoretical model. Thus, given the native state of a protein, one can predict the force profiles for tandem repeats of identical protein modules.

Our method for predicting the characteristics of force-induced unfolding also suggests a way to measure the phase diagram of the sort shown in Fig. 1. In AFM and optical tweezer experiments, it is easier to alter the concentration of denaturants, C, than temperature. We propose that, by measuring the unfolding forces as a function of C, the equilibrium phase diagram in the plane of (f,C) can be obtained. Such experiments (especially when combined with fluorescence resonance energy transfer measurements) can provide a detailed map of the energy landscape of proteins.

Although the model devised herein is in nearly quantitative agreement with the experiments conducted thus far, we should emphasize its certain limitations. In particular, the location of the unfolding TS and associated barriers can be affected by the entropy of the unfolded regions of the chain. However, under tension, the fluctuations in these regions are expected to be small compared with the case of thermally induced (or denaturant-induced) unfolding.

One of the major issues is the relationship between the sequence of events in thermally induced and force-induced unfolding of proteins. The unfolding pathways may be similar in the limit of very slow pulling speeds. However, it is less clear whether unfolding pathways remain unaltered at pulling speeds normally used in experiments. Recent study of forced unfolding of β-hairpin indeed suggests that unfolding events depend on the pulling speed (25). This difference is probably exaggerated in SMD simulations because of very large pulling speeds. It would be desirable to carry out experimental and computational studies to compare thermal and forced unfolding pathways. Our preliminary results on S1 and S2 sequences suggest that there are differences in the thermal and forced unfolding.

We have focused only on the stretching of proteins in this article. The theory and the computational protocol is general and can be used to describe the stretching of other biomolecules and complexes. In particular, applications to RNA stretching can be made as long as the crystal structure is known. Such applications would be particularly useful given that much less is known about the folding landscape of RNA (26).

Abbreviations

AFM

atomic force microscopy

SMD

steered molecular dynamics

SLD

steered Langevin dynamics

TS

transition state

Note Added in Proof

We have applied our computational protocol to obtain the unfolding force for T4 lysozyme. Using the statistical potentials derived in ref. 16, we found that f ≈ 73 pN at the pulling speed V = 1 μm/s. The experimental value is 64 ± 16 pN (7).