Abstract
Background
Simple sequence repeats (SSRs), microsatellites or polymeric sequences are common in DNA and are important biologically. From mononucleotide to trinucleotide repeats and beyond, they can be found in long (> 6 repeating units) tracts and may be characterized by quantifying the frequencies in which they are found and their tract lengths. However, most of the existing computer programs that find SSR tracts do not include these methods.
Results
A computer program named Poly has been written not only to find SSR tracts but to analyze the results quantitatively.
Conclusions
Poly is significant in its use of non-standard, quantitative methods of analysis. And, with its flexible object model and data structure, Poly and its generated data can be used for even more sophisticated analyses.
Background
Introduction to SSRs
Simple sequence repeats (SSRs) in DNA, also known as microsatellites and polymeric sequences, are composed of short (1 to 5 bp), tandemly repeating motifs or monomers that are exact in identity and repetition. Although the elongation of SSR tracts may be due to more than one mechanism [1], much is thought to be the result of slip-strand replication errors. In the process of nascent strand formation, reannealing can occur. And when the strands contain repetitive elements, such as with SSR tracts, the annealing can be imperfect, leading to the addition of the same elements. The errors become permanent when an additional round of replication occurs before they are discovered by repair enzymes [2,3].
The most abundant SSR tracts are the mononucleotide repeats or homopolymers: poly(dA).poly(dT) and poly(dG).poly(dC). Long (> 9 bp) homopolymer tracts of both types are found at higher than expected frequencies in the non-coding regions of eukaryote genomes. This is particularly true for poly(dA).poly(dT) tracts in the AT-rich genomes [4].
The biological importance of SSR tracts has been clearly deliniated. Homopolymer tracts, for example, can serve as protein binding signals, particularly as upstream promoter elements [5]. Also, long homopolymer tracts are spaced non-randomly in the genome of Dictyostelium discoideum, suggesting a preferential linker DNA location in the repeating nucleosome structure of this AT-rich organism [6]. While this restricted localization may be thermodynamically determined, the suggestion is that these tracts may serve some function determined by their accessibility in the linker DNA region between nucleosomes.
The heteropolymer tracts are at least as important biologically. Dinucleotide repeats are associated with human diseases such as Norrie's disease [7], and the expansion of trinucleotide repeats is often associated with neurodegenerative disease and chromosomal fragility, such as Huntington's disease and fragile X syndrome, respectively [8]. Many of the SSR tract monomer lengths can play a role in sequence-specific DNA binding by proteins [9]. In coding regions, homopolymer and dinucleotide tract elongation can lead to frame-shift errors, often resulting in cancers. And, trinucleotide tract elongation can lead to tandem amino acid repeats.
Existing methods and software for quantitative analyses
Numerous algorithms have been developed to locate repetitive elements in DNA. Nearly all of them aim to find approximate repeats, not the simpler problem of finding those that are tandem and exact. For example, the program Tandem Repeats Finder [10] locates repeats with motifs of any size and type, including repeats with insertions and deletions.
Some programs that have been developed are more suitable for tandem repeats with short motifs. The program Sputnik [11] (unpublished) uses recursion to search for both exact and approximate tandem repeats. Repeating unit lengths of 2 to 5 are sought, and a score is used to determine exactness.
Other programs use a dictionary of known repeats and motifs. Tandem Repeat Occurance Locator (TROLL) [12], for one, uses a keyword tree adapted from bibliographic searching techniques and attempts to match the keywords exactly.
In 1993, Marx et al. examined the enrichment of poly(dA).poly(dT) and poly(dG).poly(dC) tracts (and their complements) in the genome of slime mold Dictyostelium discoideum [4]. The data were plotted as log(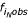
) vs. N, where the observed frequency 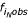equals the number of observed tracts 
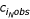normalized to the length of the entire source sequence lseq. Here, i is the monomer identity, and N is the number of monomers (Eqn. 1) (n.b., notation used throughout this article is modified and may not match that used in the references). The research showed higher than expected enrichment for A and T tracts of N > 10 in regions not coding for protein expression.
In 1998, Dechering et al. surveyed these frequencies across several diverse organisms [13]. Included in the survey is an expansion on the quantitative methods. The expected frequencies are also used, which are determined using the observed base compositions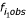 
of the organisms (Eqn. 2), where 1 in the subscript is the monomer length for homopolymers.
"Representation" (R), defined in Eqn. 3 and by Dechering et al., is the observed frequency of a tract, normalized to its expected frequency. From this, it can be determined whether frequencies are represented above (R > 1) or below (0 <R < 1) their expected values. These conditions describe the relative enrichment of an SSR tract and are referred to as "over-representation" and "under-representation," respectively.
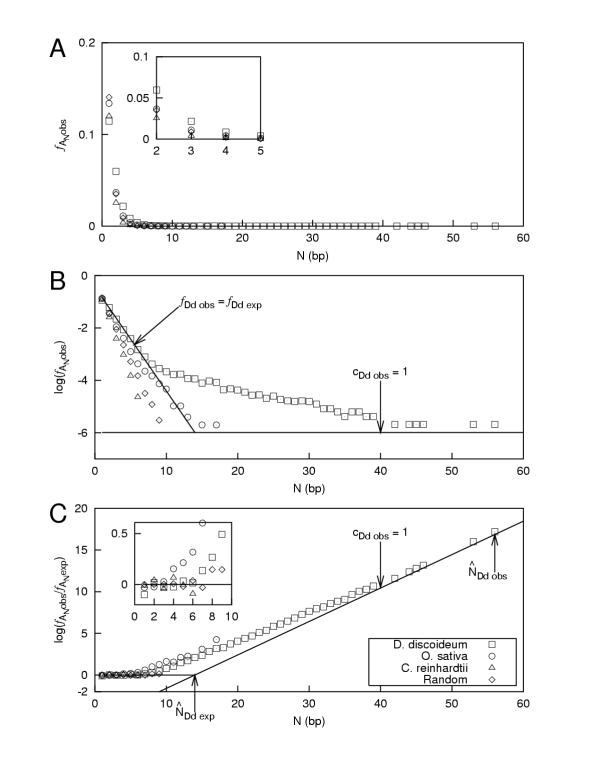
Fig. 1 shows the three types of frequency plots for the same data and how each plot differs. The analysis was performed on genomic DNA ranging the GC compositions: from the most AT-rich (low % GC) Dictyostelium discoideum, to the most GC-rich Chlamydomonas reinhardtii, plus Oryza sativa japonica and a randomly generated sequence, as described in the figure legend. Panel A plots the observed frequency of A tracts for all four sequences. The inset helps show the differences which appear at N ≤ 5, but beyond that the linear representation of the logarithmic decay makes it difficult to discern differences between organisms.
Figure 1.
Frequency plots (one per panel) for equivalent organism sequence data across a range of GC compositions: Dictyostelium discoideum (0.97 Mb at 26.% GC), Oryza sativa japonica (1.5 Mb at 45.% GC) and Chlamydomonas reinhardtii (0.35 Mb at 62.% GC), including a sequence produced by a random number generator with equal weights between bases (1.0 Mb at 50.% GC). The sequences are concatenated from GenBank document "source" sequences and analyzed by Poly as described in the text. These data are presented solely to illustrate the methods described here and not to describe new research.
Skipping to Panel C of Fig. 1, there is a representation plot (log (R) vs. N), described by Dechering et al., which is best at showing differences in the data after the transition to over-representation (for example, the D. discoideum plot at N > 7). Plus, it reduces the appearance of noise in the data at long tract lengths.
Panel B of Fig. 1 shows a plot of log(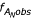
) vs. N, initially described by Marx et al. and then later by Dechering et al. It is better overall than the plot in Panel A. And, as can be seen by comparing it to the inset plot in Panel C, it is better than that plot at showing small differences before the point of transition to over-representation.
Both Panels B and C of Fig. 1 show lines where fDd obs = fDd exp (the observed frequency equals the expected frequency) and cDd obs = 1 (the number of observed tracts equals 1) for the genome of Dictyostelium discoideum (abbreviated "Dd"). These lines are useful for deriving additional quantitative methods as well as attempting to model the process of tract growth and reduction, and they will be discussed later in the text.
Described here, Poly is a computer program that finds SSR tracts and facilitates their quantitative analysis. The algorithm is simple, but the program output includes the results of quantitative methods that describe relative enrichment of the SSR tract in the sequence population being analyzed: those described by Marx et al. and Dechering et al. above, and some newer ones described below.
Importantly, Poly's data structure and object model allow for other methods to be added. Written in the object-oriented scripting language Python, Poly can be expanded with modules to implement other search algorithms and access the data objects. Additionally, data output is detailed enough for post-processing by other programs. Unlike the other programs described above, the emphasis of Poly is not on finding repeats but on generating useful quantitative results.
Results & Discussion
Operation of Poly
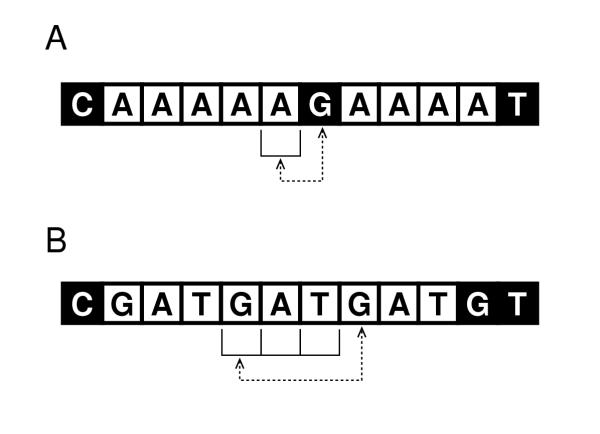
The program uses a sliding window of length n bp (the number of bases in the monomer), and the first (from the 5' end) base downstream of the window is compared with the first base in the window. This is illustrated in Fig. 2. When the next base matches the first base in the window, Poly considers the window to be on an SSR tract (a polymer is identified). For window sizes of even numbers, 4 or greater, Poly checks that the monomer isn't comprised of smaller monomers (is itself a polymer), which would lead to an incorrectly identified SSR tract. This is done once, upon encountering the second monomer of a repeat. When the next base does not match the first base in the window, and a polymer has already been identified in the window, the polymer's 3' end is found, and the polymer is saved in the data structure. In there, the tracts are identified by the sequence (or identity) of the monomer. In Poly, the short-hand identification for a poly(dC-dT).poly(dA-dG) tract, as an example, would be CT.
Figure 2.
Operation of the Poly algorithm on DNA sequences. Panel A illustrates the process for a window size of n = 1. Panel B illustrates the process for n = 3. The dotted lines show which bases are compared. White boxes represent bases which are part of an SSR tract, and black boxes represent those which are not.
Additional quantitative methods
In addition to the observed frequency, the expected frequency, and the representation (the formulas given in Eqns. 1–3), Poly computes the following values and includes them in the output.
The maximum expected length (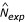
) of any given SSR tract is analogous to the expected frequency. It lies at the intersection of the lines 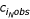= 1 and = 
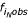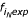(seen in Fig. 1C), and it is found by this derivation:
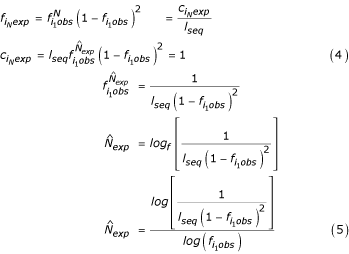
In Eqn. 4, the maximum expected count (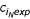
) of an SSR tract is set to 1. Eqn. 5 is solved for log10.
"Proportion" (P), defined in Eqn. 6, is the longest observed length (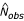
) normalized to the longest expected length (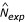). It is analogous to representation (R), although f and R are determined for each tract of length N, while 
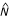and P are determined for each source sequence. This measure determines the amount by which the longest tract is either longer (P > 1) or shorter (0 <P < 1) than what can be generated randomly, using the number of monomers present in the entire source sequence. These conditions are referred to as "over-proportioned" and "under-proportioned," respectively. (P is not shown in Fig. 1.)
Proportion quantifies the tract length characteristics of a set of SSR tracts, and Fig. 1 Panel C shows where 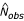and 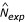are found in the sequence data for Dictyostelium discoideum. Thus, two major parameters (represented by the two axes of the plots given) of SSR tracts can be evaluated.
As with tract length, the maximum representation can be found, but a more interesting analysis would measure the characteristics of the transition from slope m = 0 to m > 0. The simplest way to do this is to ask what tract length N appears at a specific R value. This can be done for R values of 0.3 to 1.0, for example. The slope can also be found directly via linear regression of the points after the transition and where the plot becomes approximately linear again (for example, the D. discoideum plot at N > 7).
A survey of genomes was performed using Poly (submitted for publication). The representation plots for many sequences in the survey (D. discoideum, for example) reveal curves that appear to follow a mathematical function, possibly the sum of equations, including the lines 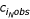= 1 and 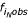= 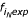(shown in Fig. 1 Panels B and C) and a transition function. Determining the formula would not only allow direct characterization of representation but could also lead to a model for the process of tract growth and reduction.
Limitations
Compute time varies negligibly with different monomer lengths. However, Poly finds all permutations for a given monomer length (n) present in the sequence, generating a quantity of data that varies by approximately 4n. (The user need only enter the monomer length of interest.) It is therefore recommended for use on SSR tracts ranging from homopolymers (mononucleotide repeats) to tetramers (tetranucleotide repeats).
As mentioned in the Results & Discussion, SSR tracts are identified by the sequence of the first repeating monomer found. Sequence 5'-AAGTAGTAGC-3', for example, contains a tract of type AGT and not TAG. This is an important consideration when evaluating the results, as the complementary sequence to the example given is 5'-GCTACTACTT-3' and read by Poly to contain the tract CTA, which is not the complement to AGT. Repeats of a specific biological type may therefore be identified as several, seemingly different tracts. If the goal of a study is to find such tracts, the user should consider all of the possible monomer types.
An unavoidable problem comes with the use of non-contiguous segments of DNA, such as with sequenced genes submitted to GenBank. Analyzing the nucleotide sequences of organisms as a collection of such segments, not only leaves out much of the organism's genome but also creates anomalies where the segments are artificially concatenated. As for SSR tracts, the concatenation of segments ending and beginning with these sequences can create a new, larger tract.
In Poly, if the sequences are separated by the XML tag pair <sequence> </sequence>, there will be no tract concatenation. However, the reverse problem cannot be resolved: If an SSR tract at the beginning or end of a DNA segment is cut short during sequencing, Poly can only categorize it by its apparent length.
Even when the concatenation problem is dealt with by Poly, some unusually long (N > 60) SSR tracts may appear in the data, causing noise in the measurement of proportion (P). As unusual occurrences, they appear only once for their specific identities and could be considered statistically insignificant and worth ignoring. Poly has the ability to count only those SSR tracts appearing more than a set number of times, as was done in the analysis that produced Fig. 1.
Flexibility of the model
Poly is developed using the scripting language Python, which will permit the program to be expanded with modules. Significantly, the algorithm of Poly has been abstracted from the rest of the program, so that other, more complex algorithms can be added.
The data structure is also designed for flexibility and post-processing. As mentioned earlier, polymers are stored in a hierarchical structure according to monomer identity and number. Additionally, Poly can output the data structure and all of the information in XML format.
Poly has the ability to automatically degenerate bases into IUPACna codes. This feature can be used to find repeats that are approximate in actual base identity but exact in base type.
The program is also capable of finding spacers: sequences separating SSR tracts. It uses the same data structure, placing individual bases in the monomer object and whole spacer sequences in the polymer object.
Features under development
There are several features under development. Poly will continue to acquire quantitative methods for the analysis of SSR tracts, particularly for the analysis of tract locations as they relate to other sequence elements. The algorithm may also be developed to allow for single nucleotide polymorphisms (SNPs) as well as small insertions and deletions so that more approximate tandem repeats can be analyzed.
Availability
Poly is open source software and available at http://bioinformatics.org/poly/.
Conclusions
Being written in an interpreted scripting language, Poly is not a particularly fast program. It does, however, have technical advantages over many of the programs developed for SSR identification. It includes methods for the quantitative analysis of tract frequencies and length, which are not standard statistical methods. It finds locations relative to other DNA sequence elements. And, it is flexible in both data structure and object model design, allowing it to be valuable in outputting additional data suitable for post-processing, a feature which may be very useful for ensuing research projects. Importantly, Poly takes a step beyond the identification of repetitive regions in DNA and enters the realms of more comprehensive quantitative analyses in biology and of comparative bioinformatics.
Methods
Nucleotide (DNA) sequences may be unannotated or raw, or they may be annotated with XML tags. The XML tags only serve to record where certain SSR tracts are located, and their actual names do not matter. Tag pairs <sequence> </sequence> identify where sequences are artificially concatenated and should be used to avoid creating anomalous tracts, as mentioned previously.
Other than the filename, Poly requires that the size of the moving window be specified, which is the length (n) of the monomer. Homopolymer tracts have a window size of 1. Heteropolymer tracts, such as dinucleotide and trinucleotide (triplet) repeats, have window sizes of 2 and 3, respectively. Poly can theoretically work with any window size with little increase in compute time.
Poly runs from the command line and is non-interactive. Data can be redirected (e.g., piped) via standard in, and are written to standard out.
Contributor Information
Jeff W Bizzaro, Email: jeff@bioinformatics.org.
Kenneth A Marx, Email: kenneth_marx@uml.edu.
References
- Toth G, Gaspari Z, Jurka J. Microsatellites in different eukaryotic genomes: survey and analysis. Genome Res. 2000;10:967–981. doi: 10.1101/gr.10.7.967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Streisinger G, Okada Y, Emrich J, Newton J, Tsugita A, Terzaghi E, Inouye M. Frameshift mutations and the genetic code. Cold Spring Harb Symp Quant Biol. 1966;31:77–84. doi: 10.1101/sqb.1966.031.01.014. [DOI] [PubMed] [Google Scholar]
- Kunkel TA, Soni A. Mutagenesis by transient misalignment. J Biol Chem. 1988;263:14784–14789. [PubMed] [Google Scholar]
- Marx KA, Hess ST, Blake RD. Characteristics of the large (dA).(dT) homopolymer tracts in D. discoideum gene flanking and intron sequences. J Biomol Struct Dyn. 1993;11:57–66. doi: 10.1080/07391102.1993.10508709. [DOI] [PubMed] [Google Scholar]
- Struhl K. Naturally occurring poly(dA-dT) sequences are upstream promoter elements for constitutive transcription in yeast. Proc Natl Acad Sci U S A. 1985;82:8419–8423. doi: 10.1073/pnas.82.24.8419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marx KA, Hess ST, Blake RD. Alignment of (dA).(dT) homopolymer tracts in gene flanking sequences suggests nucleosomal periodicity in D. discoideum DNA. J Biomol Struct Dyn. 1994;12:235–246. doi: 10.1080/07391102.1994.10508099. [DOI] [PubMed] [Google Scholar]
- Kenyon JR, Craig IW. Analysis of the 5' regulatory region of the human Norrie's disease gene: evidence that a non-translated CT dinucleotide repeat in exon one has a role in controlling expression. Gene. 1999;227:181–188. doi: 10.1016/S0378-1119(98)00611-8. [DOI] [PubMed] [Google Scholar]
- Ashley CT, Warren ST. Trinucleotide repeat expansion and human disease. Annu Rev Genet. 1995;29:703–728. doi: 10.1146/annurev.genet.29.1.703. [DOI] [PubMed] [Google Scholar]
- Richards RI, Holman K, Yu S, Sutherland GR. Fragile X syndrome unstable element, p(CCG)n, and other simple tandem repeat sequences are binding sites for specific nuclear proteins. Hum Mol Genet. 1993;2:1429–1435. doi: 10.1093/hmg/2.9.1429. [DOI] [PubMed] [Google Scholar]
- Benson G. Tandem repeats finder: a program to analyze DNA sequences. Nucleic Acids Res. 1999;27:573–580. doi: 10.1093/nar/27.2.573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sputnik http://abajian.net/sputnik/
- Castelo A, Martins W, Gao GR. TROLL-Tandem Repeat Occurrence Locator. Bioinformatics. 2002;18:634–636. doi: 10.1093/bioinformatics/18.4.634. [DOI] [PubMed] [Google Scholar]
- Dechering KJ, Cuelenaere K, Konings RN, Leunissen JA. Distinct frequency-distributions of homopolymeric DNA tracts in different genomes. Nucleic Acids Res. 1998;26:4056–4062. doi: 10.1093/nar/26.17.4056. [DOI] [PMC free article] [PubMed] [Google Scholar]