Correlated motion and the effect of distal mutations in dihydrofolate reductase

Abstract

Dihydrofolate reductase (DHFR) catalyzes the reduction of dihydrofolate to tetrahydrofolate. The catalytic rate in this system has been found to be significantly affected by mutations far from the site of chemical activity in the enzyme [Rajagopalan, P. T. R, Lutz, S., and Benkovic, S. J. (2002) Biochemistry 41, 12618–12628]. On the basis of extensive computer simulations for wild-type DHFR from Escherichia coli and four mutants (G121S, G121V, M42F, and M42F/G121S), we show that key parameters for catalysis are changed. The parameters we study are relative populations of different conformations sampled and hydrogen bonds. We find that the mutations result in long-range structural perturbations, rationalizing the effects that the mutations have on the kinetics of the enzyme. Such perturbations also provide a rationalization for the reported nonadditivity effect for double mutations. We finally examine the role a structural perturbation will have on the hydride transfer step. On the basis of our new findings, we discuss the role of coupled motions between distant regions in the enzyme, which previously was reported by Radkiewicz and Brooks.

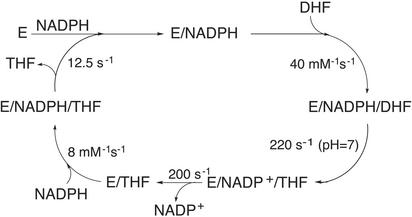
The enzyme dihydrofolate reductase (DHFR) catalyzes the cofactor-dependent reduction of 7,8-dihydrofolate (H₂F) to 5,6,7,8-tetrahydrofolate (H₄F), a key step in the biosynthesis of purines, thymidalate, and several amino acids. The importance of DHFR in the pathway to cellular production of these molecular building blocks has made it the focus of studies targeted toward the development of highly specific anti-cancer compounds and antibacterial agents (1). Fig. 1 depicts the sequence of biophysical and biochemical processes involved in the catalytic cycle of DHFR, which includes separate steps of binding of the cofactor, NADPH, ligand H₂F, protonation and hydride transfer from NADPH to H₂F, and subsequent release of H₄F and cofactor to complete the cycle.

Fig. 1.

The catalytic cycle for the reduction of H₂F to H₄F by DHFR as published in refs. 25 and 26.

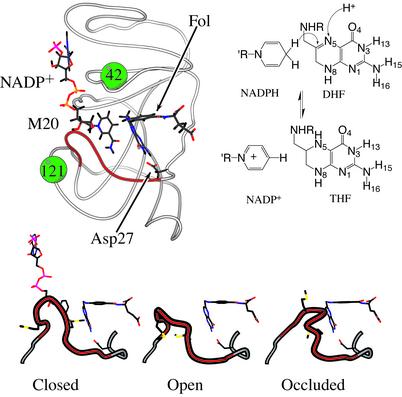
Structures of intermediates in the catalytic cycle have at this point not been solved, but structures of DHFR in both binary and ternary complexes exist, and these provide suggestions for structure–function relationships that complement the biochemical characterization of the catalytic cycle (2). The protein is comprised of two major domains that encompass the binding sites for the cofactor and ligands. Shown in Fig. 2 is the structure of DHFR complexed with NADP⁺and folate (F), a substrate mimic. From the extensive crystallographic studies, it is known that the protein adopts a number of different conformations depending on the nature of bound ligands. These studies have noted that the M20 loop, indicated in Fig. 2, exists in at least three well defined conformations. These have been named open, occluded, and closed (refs. 2 and 3; see Fig. 2). It has been suggested that these loop conformations play an important role in the catalytic mechanism (4, 5).

Fig. 2.

The structure for DHFR from E. coli in the closed conformation (PDB ID: IRX2) with NADP⁺ and folate bound to the enzyme. The locations of residues 42 and 121 from Table 1 are illustrated by solid balls. The structure was generated by using molscript (27). The panel below the structure illustrates the three primary loop conformations observed in crystal structures from PDB entries 1RX2, 1RD7 (B-chain), and 1RX7. (Right) The relevant chemical species and sites of reactivity are shown. The atoms where the proton and hydride are added to form H₄F are indicated by arrows.

Recently, Benkovic and coworkers (6–8) have shown that mutations far from the center of chemical activity in DHFR from Escherichia coli can affect several steps in the catalytic cycle significantly, though there is no direct contact between these residues and the center of chemical activity. A subset of their findings relevant for the chemical transformation step, i.e., a protonation of H₂F followed by hydride transfer from NADPH to H3F⁺, is listed in Table 1. In addition to the rate retardation, it is also noteworthy that mutation of Gly-121 and Met-42 is nonadditive (7, 8), even though these residues are ≈20 Å apart. The effect of mutating both residues is more severe than expected from the two single point mutations alone, assuming that the effect of a mutation on the barrier for hydride transfer is additive. This finding has been argued to support the notion that communication occurs between the two (sequentially and spatially distant) residues (7, 8). Other studies have also shown the existence of long-range and nonadditive effects (9, 10).

Table 1. Rates and pK_a values for the chemical transformation step in mutants of E. coli DHFR.

Mutant	kconf, s-1*	k2H, s-1†	pKa‡
Wild-type	-	228 ± 8	6.6 ± 0.3
M42F	-	159 ± 17
M42W	31	5.6 ± 0.4	6.8 ± 0.3
G121S	-	3.7 ± 0.4	6.3 ± 0.4
G121V	3.5	1.4 ± 0.2	6.3 ± 0.3
M42F/G121S	-	0.46 ± 0.08
M42W/G121S	0.64	0.07 ± 0.01	6.3 ± 0.4

The values are taken from ref. 8.

^*Rate for a conformational change preceding the chemical transformation step.

^†Rate for protonation followed by forward hydride transfer at pH 7. The rate constant k_hyd for the hydride transfer step only can be obtained from k_hyd = k_2H (1 + 10^pH-pK_a).

^‡The pK_a for the protonation preceding hydride transfer.

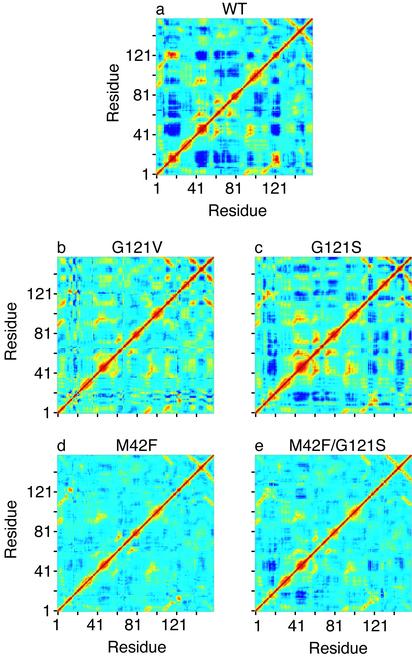
Earlier studies from our laboratory provide theoretical findings consistent with the experimental observations, and indicate that distant residues are coupled, exhibiting “correlated motions” (11). These results suggest that the same regions of the protein that significantly alter the catalytic hydride transfer step of the reaction when mutated are strongly coupled to each other in complexes representing the reactive Michaelis structure, but are uncoupled in the product complexes with NADP⁺or NADPH and H₄F. Moreover, a similar analysis of simulations for Michaelis complexes of mutant DHFRs (to be presented here) shows that the correlated motions are reduced in those complexes, correlating somewhat with the reduction in activity (see Fig. 3).

Fig. 3.

Covariance matrix for the fluctuations of the C_α atoms in wild-type DHFR (WT) and various mutants. Yellow and red regions indicate that the C_α atoms move in a concerted way (positively correlated movements), and dark blue means they move opposite to each other (anticorrelated movements). The scale goes from –0.6 (dark blue) to 1 (red). We note that we get the same qualitative picture for the correlated motions if all heavy atoms are included in the calculation of the covariance matrix.

The early theoretical results of Radkiewicz and Brooks have motivated further theoretical studies attempting to establish a coupling between protein dynamics and enzyme catalysis (7, 12, 13). A direct coupling might, for instance, be through the existence of promoting vibrational modes (14–17). A model that includes such a coupling is attractive because it can explain how a local structural change can have a global impact through perturbation of the normal modes. A single normal mode generally includes the motion of all of the atoms in the enzyme, and a perturbation of such a mode will therefore be of global character. To date, no direct evidence for such a coupling in DHFR exists (I. Thorpe and C.L.B., unpublished data), and although such an explanation is intriguing, we will here show that the observations by Benkovic and coworkers (6–8) can be rationalized on more traditional energy based grounds.

The present study is an attempt to understand why and how the distal mutations affect the chemical transformation step. Our primary focus is on thermodynamic (equilibrium as opposed to dynamic) factors that correlate observed mutational data with extensive computer simulations of complexes of mutant DHFR proteins with substrate and cofactor. To examine how changes in the environment surrounding the site of chemical reactivity might influence the apparent reaction rate, and how this might be coupled with mutations in the protein sequence, we carry out and analyze several long (10 ns) molecular dynamics simulations of some of the mutant proteins noted above. In addition to the wild-type enzyme, the M42F, G121S, G121V, and M42F/G121S mutants have been studied. We first explore how the correlated motions reported earlier by Radkiewicz and Brooks change on a mutation. Then we explore the influence of these mutations on the distribution of conformations sampled by the enzyme, particularly those of the M20 loop, and the effect on hydrogen bonds. Our findings show that mutants, even if distant from the active site, can perturb the active site structurally, thus rationalizing the observations by Benkovic and coworkers that distal mutations affect the rate. On the basis of these findings, we discuss how the mutations can affect correlated motions in the protein and the role these correlations will have on hydride transfer.

Methods

Simulations of the Michaelis complexes for wild-type DHFR from E. coli and the mutants G121S, G121V, M42F, and M42F/G121S mutants were performed by using explicit solvent. Each simulation was run for 10 ns and is similar to those described in ref. 11. The 1RX2 crystal structure was used as template for all of the Michaelis complexes studied. A detailed description of how the Michaelis complexes were constructed and how the simulations were set up is provided in the supporting information, which is published on the PNAS web site, www.pnas.org.

The M20 loop region provides a key marker for conformations which are poised for the hydride transfer step in DHFR catalysis (2). Thus, to explore conformations of this loop adopted by each protein variant during the molecular dynamics trajectories, we clustered the protein backbone conformations based on their dihedral angles, ψ and ι for residues 14–24. Clustering was carried out by using the K-means algorithm ART 2 (18), as implemented in CHARMM (19). To identify specific clusters with the key conformational states of the M20 loop observed in crystallographic studies, we “seeded” the combined trajectories from the simulations with the crystal structures representative of the three different M20 loop conformations, i.e., the crystal structures of 1RX2, 1RX7, and 1RD7 (chain B), representing the closed, occluded, and open conformations, respectively (see Fig. 2). A cutoff radius for the clustering was set to 60°, which is large enough to ensure well defined clusters with a significant life time, but small enough to separate the three crystal structures into different clusters. In this way a particular snap shot can be determined to belong to one of the three known M20 loop conformations, or possibly to some alternate conformation. If the cutoff radius is increased to >62° the IRX2 and IRX7 crystal structures end up in the same cluster.

The energy for a particular snap shot in the trajectory was calculated by removing the explicit water molecules and by using the generalized Born implicit solvent model developed by Lee et al. (20, 21) to get the solvation energy. The use of an implicit solvent model is a way of avoiding the large fluctuations associated with the water molecules (22). The average energy and the standard error for a particular conformation was obtained by summing over the energies for all snapshots belonging to a conformational cluster and particular mutant sequence.

The occupancies of hydrogen bonds were calculated as the percentage of time the distance between the hydrogen atom and the acceptor atom were within a cutoff distance of 2.4 Å.

We do not expect our calculated energies to quantitatively describe changes caused by mutations or conformational changes. We expect them, however, to be capable of capturing the trend generated by the mutations on a number of different parameters, which will assist us in deducing the mechanisms behind the changes imposed by the mutations.

Results and Discussion

Correlated Motions. First we analyze the mutants for the presence of residues which are dynamically coupled to each other. We quantitate the coupling between two residues by calculating the covariance between the fluctuations of the two residues in question. Fig. 3 shows the covariance matrix for the Cα atoms in wild-type (Fig. 3a) and mutant DHFRs (Fig. 3 b–e). Clearly, the extent of the coupled motions is decreased in the mutants. The G121S mutant shows less coupled motion than the wild-type (Fig. 3 a vs. c), but more so than the G121V (Fig. 3b), which correlates well with the observed rates for hydride transfer (see Table 1). Reduction of the coupled motions also suggests that a possible dynamic coupling is affected by the mutations, supporting the idea of such a coupling.

The M42F and M42F/G121S mutants (Fig. 3 d and e) also exhibit reduced correlated motions relative to the wild-type during the course of the simulations. The correlated motions taken as a whole for the M42F mutant are however not as significant as for the G121S mutant or the M42F/G121S mutant. This apparently contrasts a simple linear relationship of activity and correlated motions. On the other hand a subset of the correlated motions may be important for catalysis, and it is not possible to draw definitive conclusions on the basis of Fig. 3 alone. However, as we shall explore later, explanations other than the existence of long-range coupled motion are able to rationalize the observed experimental findings.

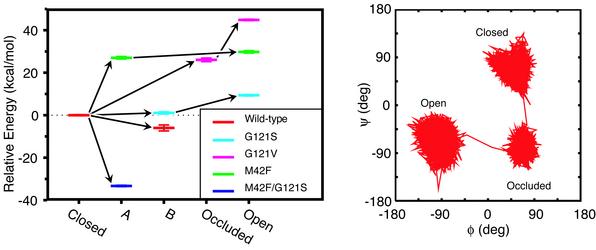
Conformational Changes. We now examine the range and extent to which different loop conformations are sampled in each of the simulations. The results from the cluster analysis are illustrated in Fig. 4. This figure indicates that the simulations sample five different and well defined clusters, which include the closed, open, and occluded conformations. Although the occluded conformation observed in our simulation studies is similar to the crystal structure, based on the conformation of the backbone of the M20 loop, it is important to note that the head of the cofactor is still in the enzyme pocket and not solvent exposed (2). Fig. 4 Right shows the extent of ψ–ι space sampled by Gly-17 (in the M20 loop) for the G121V mutant, demonstrating that the clusters are well separated in ψ–ι space.

Fig. 4.

(Left) Shown are the energy levels for different conformations of the M20 loop sampled in the simulations of native and mutant Michaelis complexes of DHFR, relative to the closed conformation. Each color represents a particular mutant, and the five different conformations found from our cluster analysis are shown along the horizontal axis. The energies are the average energies calculated by using a generalized Born implicit solvent model from snapshots from the portions of the trajectories belonging to particular loop conformations. The error bars represent the standard errors about these averages. The arrows indicate the progression in time. (Right) Shown is a representative trajectory in ψ–ι space for loop residue Gly-17 in the G121V mutant to illustrate the extent to which different conformations may be differentiated.

The general trend that can be elucidated from Fig. 4 is that there are several pathways between the closed and the open conformations. One path proceeds through a new conformation A, as observed in the M42F simulation. The G121V simulation proceeds through the occluded conformation, whereas the G121S simulation goes through another new and intermediate conformation, B, to reach an open-like conformation. The G121S mutant and the wild-type enzyme sample the occluded conformation as well, though only for short times (not shown in Fig. 4). The wild-type enzyme seems to follow the same path as the G121S mutant, and the M42F/G121S mutant seems to follow a similar path to the M42F mutant. However, in both cases they do not move all of the way from the closed to the open conformation during the course of the 10-ns simulations. Not surprisingly, all of the intermediate conformations are closer in ψ–ι space to the closed conformation than to the open conformation. The distance in the M20 loop ψ–ι space between the closed M20 loop conformation and the intermediate conformations is 240–280°, whereas it is 350° between the closed and open conformation.

It is clear from Fig. 4 that the mutations change the relative energy among the different M20 loop conformations. Therefore it is possible that different pathways from the closed to the open conformation are favored by different mutants, which would explain our observations. However, because of the limited sampling of conformational transitions, it cannot be excluded that the observations of different paths for different mutants is coincidental.

For some mutants a step before hydride transfer, a step believed to be a conformational change, has been observed experimentally (6, 8). This step is strongly affected by mutation (see Table 1). Our results indicate that if the conformational change is localized to the M20 loop, it will indeed be affected by mutations, because the mutations influence the conformational energies differently. The latter also means that the relative occupancies are changed. If factors linked to catalysis, such as protonation or hydride transfer, are favored differently for different conformations, this will have an impact on catalysis.

Hydrogen Bonds. The relative energy changes between different conformations shown in Fig. 4 Left are measures of equilibria, as opposed to dynamical, effects. These observations therefore point to an explanation other than that of a coupling between dynamics and catalysis. The shift in the energy levels indicates that structural perturbations occur in the micro environment encompassing the active site, even if the mutation is distant from the center of the chemical transformation step. However, the mutated residues are not far from the residues that encompass the active site and control its hydrophobic character. In the following we discuss the changes, which occur as a result of mutation, in hydrogen bonding. We restrict the discussion to the closed conformation and to hydrogen bonds to or from the M20 loop and to or from the ligands, but notice that other hydrogen bonds in the enzyme are modulated by the mutations as well. We focus on these particular interactions because they provide a connecting network between distal regions of the sequence and structure and may influence the behavior of correlated motion.

In the closed conformation, the M20 loop and the loop containing Gly-121 are hydrogen bonded to each other by an interaction between the neighboring Asp-122(O_δ1) residue and Gly-17(H_N), and another between Thr-123(O) and Ile-14(H_N). These two interactions are strongly influenced by mutations of Gly-121. In the G121V mutant, the hydrogen bond from Gly-17 is hardly affected (occupancy 80%), whereas the bond from Ile-14 is significantly reduced (occupancy 30%) because of the bulky Val side chain. For the G121S mutant, both hydrogen bonds are reduced (occupancies are 40% and 15% for the bonds from Ile-14 and Glu-17, respectively), and a new strong hydrogen bond is formed between the hydroxyl group of Ser-121(H_γ1) and Gly-15(O) (occupancy 95%). Interestingly, we observe the first structurally long-range as well as nonadditive effect here, because mutating the distant residue Met-42 to Phe on top of the G121S mutant to some extent restores the occupancy of the two reduced hydrogen bonds (occupancies 85% and 70%, respectively), whereas the new hydrogen bond involving the Ser side chain is unaffected. The two hydrogen bonds are unaffected in the M42F mutant relative to the wild-type enzyme.

In the region that contains residue 42, there are hydrogen bonds to or from the M20 loop as well, namely a bond from Asn-28(H_δ21) to His-45(O) and a bond to Asn-18(O) from Ser-49(H_γ1). These interactions are relatively weak, with occupancies that change as a result of the mutations. They are weakest in the wild-type and the M42F mutant (summed occupancy ≈60%) with twice the occupancy in the other mutants (summed occupancy ≈120%). The existence of these hydrogen bonds shows that the M20 loop links the regions around residue 42 and 121 together. Moreover, the M20 loop hydrogen bonds are clearly of importance for any conformational change involving the M20 loop, because such a change involves the breaking of one or more of these hydrogen bonds and the creation of others. Previously reported conformational changes on a longer time scale than studied here (millisecond) also involves breaking and formation of hydrogen bonds (2) and will therefore be affected by mutations. Indeed, Rajagopalan et al. (8) observe a conformational transition, presumably from the occluded to the closed conformation, which is affected by mutating residue 42 and/or 121 (see Table 1).

The hydrogen bonds linking H₂F to the enzyme are hardly affected by the mutations studied. NADPH, on the other hand, has a hydrogen bond from the amide in the nicotinamide moiety to the M20 loop (NADPH(H₇₁)-Ile-14(O)) that is significantly reduced in the G121V mutant (occupancy 25%, compared with ≈70% in the other mutants). Other hydrogen bonds between enzyme and NADPH are affected severely on mutation, most notably the bonds between the NADPH phosphate group and the Ser-63(H_γ1), Ser-64(H_γ1,H_N) residues. The occupancies of these bonds are only reduced in the M42F and M42F/G121S mutants (from ≈100% to ≈45%, though the bond from Ser-64(H_N) is reduced only to 75% in the M42F/G121S mutant) pointing to a single significant effect of mutating residue 42. Residue 42 itself forms a strong hydrogen bond to the neighboring Leu-62 independently of whether it is mutated. Finally, in all of the mutants except for the M42F/G121S mutant, the side chain of Ser-77(Oγ) forms a weak hydrogen bond with the Glu-80(H_N) residue. In the M42F/G121S mutant, this bond is absent and a relatively strong bond with the amine in the adenine moiety of NADPH (occupancy 85%) is formed instead. The side chain of Ser-77 also forms a very strong bond with Val-78(H_N) in the M42F/G121S mutant (occupancy 100%), which is either very weak or absent in the wild-type enzyme and the other mutants (occupancies 0–35%). These bonds illustrate another aspect of the long-range and nonadditive effects that mutations may have on conformational equilibria.

Nonadditive Effects. The above analysis suggests that mutations can have long-range structural effects, which will lead to conformational changes. Because of the nature of the perturbation, i.e., long range and structural, essentially everything related to catalysis will be affected. Later on we explore the role such long-range structural perturbations can have on the hydride transfer step, whereas here we examine how long-range structural perturbations can result in nonadditive energetic effects.

If the influence of a single point mutation is global, then the site for a second mutation will be perturbed as well. Hence, the structural effect of the second mutation on top of the first might be different from having only the second one. For instance, mutating Gly-121 to Ser in the M42F mutant causes a different structural perturbation than mutating Gly-121 to Ser in the wild-type enzyme. Such nonadditive effects are what we observed in our analysis of the hydrogen bond patterns. Furthermore, these observations rationalize the nonadditive effects on kinetic properties observed by Benkovic and coworkers (7, 8) as well as in other studies (refs. 9, 10, and 23; see also Table 1).

There is, in fact, experimental evidence for long-range structural and nonadditive perturbations in DHFR. This was noted by Brown et al. (10), who crystallized the binary complexes of the D27S, F137S, and the D27S/F137S mutants of E. coli DHFR complexed with the inhibitor methotrexate. It was shown that the effect on the catalytic turnover by the two single point mutations is nonadditive (23). The crystal structures show that, although the D27S and the F137S mutants only change the structures locally around the residue mutated, the double mutant undergoes an extended structural perturbation, explaining the non-additive effects on the kinetics. Gekko and coworkers (9) have, on the basis of circular dichroism spectra, also suggested that long-range structural effects can account for nonadditivity in mutations of Gly-67 and Gly-121, which are ≈30 Å apart from each other.

Unfortunately no crystal structures of the Gly-121 and Met-42 mutants are available, and we are therefore left to use other means. Although our calculated structures are not as reliable as those obtained from crystal structures, they do have some advantages such as accessibility to distribution of conformations and hydrogen bonding. Based on those parameters, we reach the same conclusion as Brown et al. (10), namely that mutations can lead to structural perturbations far beyond the region that is local to the mutation.

Correlated Motion. We now return to a discussion of the correlated motions depicted in Fig. 3. First, it should be mentioned that although the wild-type enzyme hardly samples conformations other than the closed conformation, the mutants sample multiple conformations. However, if the correlated motions are taken solely for the time interval where the mutants sample the closed conformation then they are still reduced compared with the wild-type enzyme. Plots of the covariance matrices taken for the closed conformations only are provided in the supporting information.

Our analysis of the hydrogen bonds indicates, at least to some extent, that hydrogen bonds mediate the correlated motions. This can especially account for the very strong coupling between the M20 loop (residues 14–24) and the region around residue 121. We have also shown that the M20 loop provides a link between the regions around residue 42 and 121, the dynamics of which are anticorrelated (see Fig. 3). The ligands provide other links between distal regions. The change in correlated motions, which is observed on a mutation (see Fig. 3), a conformational change, or change of ligand (11), may be rationalized rather simply as a reflection of changes in the underlying hydrogen bond pattern and subtle structural rearrangements.

The above discussion suggests that the correlated motions are messengers of the existence of long-range interactions in the underlying enzyme structure. They make it possible to deduce which regions are strongly coupled to each other, and where a mutation will be likely to have a long-range effect, consistent with the earlier observations by Radkiewicz and Brooks (11). It would be interesting to map the correlated motions for enzymes where it is known that long-range interactions exist. It has, for instance, been suggested that distal mutations in HIV-1 protease can cause drug resistence (24). Another class of proteins that make use of long-range interactions and draw increasing attention are membrane proteins, because they need to signal from one end of the protein to the other end. At present, membrane proteins still possess huge obstacles because of their size and complicated environment, but that might very well change in the near future, for instance, by using implicit solvent models.

Hydride Transfer. We conclude with a discussion of how long-range structural perturbations might affect the hydride transfer step. We consider the recent experimental results for forward and backward hydride transfer obtained by Benkovic and coworkers (7, 8), and theoretical and simulation results by Hammes-Schiffer and coworkers (7, 12, 13).

Experimentally it is found that the hydride transfer is severely affected by distal mutations, and for instance much more than the protonation is affected (see Table 1). Benkovic and coworkers (8) have measured the rates not only for the forward hydride transfer step but also for the reverse hydride transfer step, giving us a unique opportunity to study the effect the mutations have on the relative energies of the initial, final, and transition state for hydride transfer.

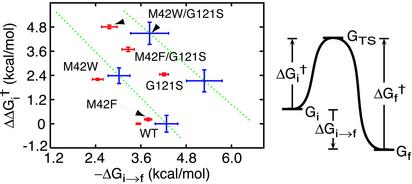
In Fig. 5, the forward activation free energy relative to that of the wild-type enzyme is plotted against the free energy change for hydride transfer for a number of different mutants. The two lines roughly describe the effect that mutating residue 42 has on the wild-type enzyme and the G121S mutant. The data demonstrate that the transition state free energy, ΔG^†, is increased in all of the mutants and that the reaction free energy, ΔG_i→f changes as well. On mutating Gly-121 to Ser, either in the wild-type enzyme or in the M42F, M42W mutants, the final state is stabilized relative to the intial state. On the other hand, when Met-42 is mutated to Phe or Trp, either in the wild-type enzyme or in the G121S mutant, the final state is destabilized relative to the initial state. This means that mutating Met-42 to Phe or Trp shifts the equilibrium toward the reactants, mutating Gly-121 to Ser has the opposite effect. The transition state free energy is more severely affected than the reaction energy and for all of the mutants it is increased. When mutating Gly-121 to Ser, the transition state free energy changes more than twice as much as the negative reaction free energy, and when mutating Met-42 the transition state free energy changes slightly less than twice as much as the positive reaction free energy. Thus, both forward and reverse hydride transfer are inhibited by a mutation. Note that a slope equal to one in Fig. 5 would imply that the barrier for reverse hydride transfer is unaltered.

Fig. 5.

(Right) Shift in activation free energy, 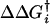, for forward hydride transfer is plotted against the reaction free energy ΔG_i→f. The free energy differences plotted are defined in Left. All calculated energies are based on the rates, reported in ref. 8, for forward and reverse hydride transfer, and the pK_a values for the protonation step. Data depicted by red points are based on the rates combining protonation and hydride transfer, i.e., they are pH dependent, whereas data depicted by blue points are based on rates solely for the hydride transfer step. These values are calculated from the pK_a values and pH-dependent rates determined by Rajagopalan et al. (8) and given in Table 1. No pK_a values have been determined for the two mutants where Met-42 is replaced with Phe. The green dotted lines follow the points for mutation of Met-42 to either Phe or Trp in the wild-type enzyme and in the G121S mutant.

Although protonation can only be affected indirectly through a structural perturbation, by altering the dielectric environment or the distance between the protonation site and the Asp-27 side chain, the effect on the hydride transfer can be expected to be more severe. This is because the two ligands are in contact with a large portion of the enzyme, see above discussion on hydrogen bonds and Fig. 2. The initial and final state, and in particular the transition state, will be sensitive to geometric restraints imposed by the enzyme (I. Thorpe and C.L.B., unpublished data), which in turn are sensitive to the structural perturbations. The experimental results imply that the transition state and the initial as well as final state are influenced differently by the mutations, i.e., that the structural perturbations act differently on the three states.

A more dynamic view can also be taken. The existence of a network in the enzyme that mediates the long-range interactions (as revealed by the correlated motions) suggests that the two large ligands cannot approach the transition state without the entire enzyme being involved: even distal residues contribute to the reaction path. Indeed, results by Hammes-Schiffer and coworkers (7, 12, 13) suggest that distal residues contribute to the reaction path. This contribution from distal residues indicates that distal mutations can affect the reaction path, and therefore also the barrier height. The difference between this argument and the more static one based on restraints is mainly semantic, though the change in reaction path automatically implies a shift in the barrier height, in agreement with experiment (see also discussion in ref. 17).

The long-range and nonadditive effects have been taken as support for the existence of a dynamic coupling; i.e., distal mutations can affect the hydride transfer rate by influencing the dynamical coupling. The above discussion suggests however that an explanation based on long-range structural perturbations is sufficient. Below we consider the implications that the experimental results, depicted in Fig. 5, have for this discussion.

The existence of correlated motions in the wild-type enzyme, which are reduced in mutants (see Fig. 3) and absent in product structures (11), has been interpreted as suggestive of a coupling between dynamics and catalysis. Because correlated motions are absent in product structures, a dynamic coupling should only exist for forward hydride transfer and not for reverse hydride transfer. Consequently, the possible effect of mutations on the dynamic coupling should only influence the forward hydride transfer and not the reverse hydride transfer. However, Fig. 5 illustrates that both forward and reverse hydride transfer are affected by the mutations, and therefore the alterations cannot be due solely to a change in a dynamic coupling. Either that is true, or the existence of correlated motions does not reflect the existence of a dynamic coupling.

We end this section by noting that the change in the backward hydride transfer rate seems to be correlated with the change in the forward hydride transfer, which implies that it is impossible to modulate the barrier for forward hydride transfer without modulating the barrier for reverse hydride transfer.

Conclusion and Summary

We have studied several equilibrium parameters of importance for catalysis and the transformations these parameters undergo as a result of different mutations. The parameters we examined are relative populations of different conformations and hydrogen bonds. Our analysis suggests that the mutations create subtle long-range structural perturbations that change the equilibrium distributions for the parameters studied. We suggest that the structural perturbations change the rate for forward as well as for backward hydride transfer, and that this will be the major effect of a mutation rather than altering some mode of dynamical coupling. In the case of DHFR, it appears that structural perturbations are sufficient to rationalize the effect of distal mutations on the rate for catalysis, and in particular for the development of an understanding of the nonadditive effects observed for several double mutants. We finally suggest that the existence of long-range interactions in an enzyme can be envisaged from the existence of correlated motions between structurally and sequentially distant regions in an enzyme.