Peripheral heme substituents control the hydrogen-atom abstraction chemistry in cytochromes P450

Abstract

We elucidate the hydroxylation of camphor by cytochrome P450 with the use of density functional and mixed quantum mechanics/molecular mechanics methods. Our results reveal that the enzyme catalyzes the hydrogen-atom abstraction step with a remarkably low free-energy barrier. This result provides a satisfactory explanation for the experimental failure to trap the proposed catalytically competent high-valent heme Fe(IV) oxo (oxyferryl) species responsible for this hydroxylation chemistry. The primary and previously unappreciated contribution to stabilization of the transition state is the interaction of positively charged residues in the active-site cavity with carboxylate groups on the heme periphery. A similar stabilization found in dioxygen binding to hemerythrin, albeit with reversed polarity, suggests that this mechanism for controlling the relative energetics of redox-active intermediates and transition states in metalloproteins may be widespread in nature.

The family of cytochrome P450 monooxygenases is ubiquitous in human biology, playing a key role in the metabolism of pharmaceutical agents and other ingested exogenous compounds (1). These enzymes insert an oxygen atom from O₂ into a wide variety of substrates, with substrate specificity determined by the nature of the protein active-site cavity. All members of the family are believed to share a common mechanism for such hydroxylation (2). In the catalytic cycle, dioxygen bound to an iron porphyrin undergoes a series of transformations to produce an intermediate capable of hydroxylating a C—H bond of the substrate. The currently accepted steps in this cycle are depicted in Fig. 1. We focus here on the bacterial isozyme cytochrome P450cam, for which camphor is the substrate, to exploit the wealth of experimental data measured for this system.

Fig. 1.

Common catalytic cycle in most cytochromes P450. 1, Resting state with water coordinated to iron; 2, substrate binding displaces coordinated water and first electron-reduction results in O₂ binding; 3, second electron reduction and distal oxygen protonation liberates a water molecule and the active compound I; 4, substrate (camphor in P450cam) hydroxylation and resting-state regeneration.

Because of its prominent role in biology and medicine, an exceptionally large amount of experimental and theoretical work has been invested in understanding the various steps of the cytochrome P450 reaction cycle (1–16). A complete atomic-level picture of the key steps, particularly the hydroxylation reaction, has yet to be produced, however. Such knowledge is essential in building quantitative models of P450-based contributions to drug metabolism and toxicity. This deficiency is due in part to the difficulties in carrying out incisive experimental and theoretical studies. Experimental investigation of the catalytically competent species in the hydroxylation reaction is hindered by the fact that the presence of substrate is necessary to initiate the reaction cycle. This situation can be contrasted with that in soluble methane monooxygenase (MMO). Formation of the key catalytic intermediate in the reaction cycle of the MMO hydroxylase can be initiated by dioxygen and then trapped in the absence of substrate. Such a result has yet to be duplicated in P450, as is discussed in more detail below. From a theoretical point of view, the P450 core chemistry is larger and more dispersed in the active site than that of MMO, rendering accurate computations to be a severe challenge.

The ferric superoxo species (3 in Fig. 1) is the last quasistable P450 intermediate characterized by a diverse set of spectroscopic and structural determinations (6, 13). The next steps in the P450 reaction cycle, leading to the formation of the proposed oxyferryl active intermediate and subsequent substrate hydroxylation, are the least understood features in the pathway. Experimental (15) and theoretical (8) studies have proved the need for reduction of 3 by a second electron before double protonation of the distal oxygen atom, in which crystallography revealed waters play a major role. After distal oxygen protonation, O—O bond cleavage and water formation, as observed in small theoretical models (9), results in a highly exothermic (by ≈80 kcal/mol) process leading to the oxyferryl species. This proposed oxidant is well known as compound I (4 in Fig. 1). Schlichting et al. (14), using low-temperature crystallography, observed a species with electron density near the iron, which they attributed to a doubly bonded oxygen atom. This identification was not definitive, however. More recently, Davydov et al. (5) used EPR and electron-nuclear double-resonance techniques at cryogenic temperatures in an attempt to observe a signal corresponding to an Fe(IV) ferryl species. They were unsuccessful and concluded that “there is no spectroscopic evidence for the buildup of a high valence oxyferryl/porphyrin π cation intermediate.” Thus, the existence of compound I at present is unresolved experimentally. The electron-nuclear double-resonance results, however, did provide substantial indirect evidence that the hydroxylation reaction proceeds via abstraction of a hydrogen atom from camphor by an oxyferryl species. The proposed hydroxylation mechanism is analogous to that operative in MMO. Here, a similar hydrogen-atom abstraction is performed by a nonheme diiron species, with the iron atoms in the Fe(IV) oxidation state as in the present case. Recent computational studies of the MMO reaction by our group (17) and others (18) are in excellent agreement with the experimental data. They reveal a classical hydrogen-atom abstraction transition state followed by formation of a bound radical. A competing concerted channel bypassing this species was also identified.

One possible explanation for the failure to observe the oxyferryl intermediate posited above is that the reactivity of this species is sufficiently high that it does not build up to levels that allow its detection with the experiments carried out to date. Previous theoretical studies (19), however, performed by using a minimal porphyrin model and methane as substrate, are inconsistent with this hypothesis. The model structure used in these studies (Fig. 2 Inset) uses hydrogen atoms as substituents on the porphyrin, an important limitation as explained below. In particular, the computed enthalpy for the hydrogen abstraction, defined as the energy of the products minus that of the reactants, was highly endothermic, 24 kcal/mol, and the corresponding activation barrier for the model was 27.5 kcal/mol. The reduced-model studies proposed the existence of a quartet-doublet two-state mechanism, the hydrogen abstraction activation barrier being the same for both states. These results, in conjunction with ultrafast radical-clock experiments, have motivated a search for alternative species as the oxidation agent (20, 21). A plausible alternative has not yet been established, however. Moreover, our recent studies of the MMO reaction (17) have reconciled the existence of a radical recoil/rebound process with the absence of purely radical derivatives.

Fig. 2.

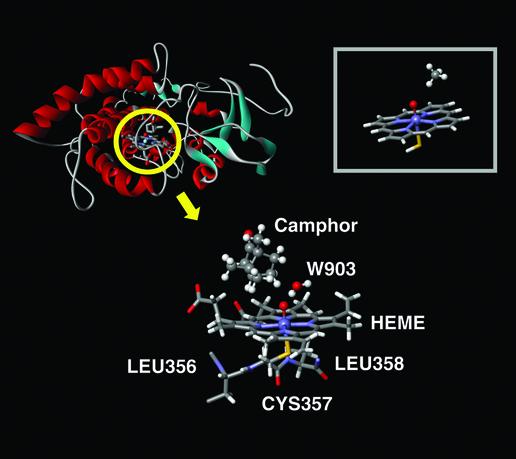
P450cam system with 7,467 atoms. The QM subsystem includes the heme group, the water 903, the camphor substrate, Cys-357, and a protein backbone cut in Leu-358 and -356, for a total of 126 QM atoms. (Inset) Reduced QM active-site model proposed in previous theoretical studies.

Here we exploit rapid advances in computational hardware and quantum chemical methods and software, coupled with a recently developed mixed quantum mechanics/molecular mechanics (QM/MM) technology, to provide what we believe to be a quantitatively accurate atomic-level description of the hydroxylation reaction in cytochrome P450cam. The results are fully consistent with available experimental data. Qualitatively, the hydroxylation of camphor by P450 is very similar to methane hydroxylation by MMO, and we exploit our extensive computational studies of the latter protein in our analysis of the reaction mechanism. Quantitatively, the challenge is to understand how the protein stabilizes the transition state for hydrogen-atom abstraction. In accomplishing this task, we have discovered a mechanism for shifting the relative energies of metalloenzyme intermediates and transition states with different redox states of the metal. We suggest that this mechanism is pervasive throughout metallobiochemistry, having found one additional example previously, and plays a key role in allowing metal-containing proteins to tune their energetics for biological function.

Methods

We model the hydroxylation reaction by cytochrome P450cam using mixed QM/MM techniques. Our methodology has been optimized specifically for protein modeling and, as extensively documented (22, 23), provides a parameterization of the interface that accurately reproduces fully quantum mechanical calculations for conformational energetics as well as for electrostatic and hydrogen-bonding interactions between the QM and MM regions.

For the QM part of the calculation, we use ab initio hybrid density functional theory (DFT/B3LYP) methods with polarized basis sets (LACVP*) to carry out geometry optimization and larger triple-zeta basis sets [cc-pVTZ(–f)] to compute single-point energies. The MM part utilizes the OPLS-AA MM force field. All crystallographic waters are incorporated in the QM/MM system. Surface polar amino acids, Lys, Arg, Glu, and Asp, are neutralized if they do not form a salt bridge, which yields a zero net charge of the overall system. Their position is then constrained throughout the minimization. Such a protocol introduces approximate solvation effects (i.e., screening of ionized groups on the protein surface by high dielectric water) and is justified by the buried nature of the active site. An optimized geometry for the reactant species (4), indicating which atoms are treated at the QM level, is shown in Fig. 2. The resulting calculation requires 126 QM atoms, which is a comparatively large QM region for a density functional theory-based QM/MM enzyme-modeling calculation.

All calculations are carried out with the SCHRÖDINGER suite of programs (24). Because the current implementation of QM/MM code does not support unrestricted calculations, we focused on the quartet spin state, for which the hydrogen abstraction barrier is degenerate with the doublet state (25, ¶).

Results

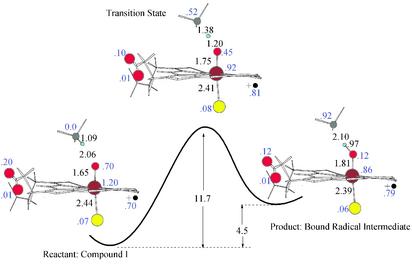
Fig. 3 depicts a series of stationary structures along the reaction path for hydrogen-atom abstraction, focusing only on the reactive core. The distance, charges, and spin densities of the main atoms involved in the reaction are quite similar to those obtained in the analogous MMO hydrogen abstraction. As shown in Fig. 3, the QM/MM results support a qualitative characterization of the porphyrin ring as a cation radical. The Cys sulfur, however, does not present a large radical component, as has already been observed in the stabilization of the sulfur p orbitals by hydrogen-bonding interactions (26). We also notice slight radical character in one of the porphyrin-ring peripheral carboxylate oxygen atoms, which play an important role as discussed below. The difference in reactant and product energies, on the order of 24 kcal/mol endothermic in the prior QM-model studies cited above, is reduced to 4.5 kcal/mol. The activation barrier is now only 11.7 kcal/mol (8.2 kcal/mol if we estimate the zero-point contribution to the value we obtained for an MMO-model system, on the order of 3.5 kcal/mol). This exceptionally small barrier would permit rapid formation of the hydroxylated product from the oxyferryl intermediate. It therefore provides a straightforward explanation of the experimental results of Davydov et al. (5); the catalytically competent intermediate in cytochrome P450 is extraordinarily difficult to observe because of the remarkably low barrier to hydrogen-atom abstraction exhibited by the system. Single-point calculations at optimized geometries of the reactants, products, and transition state using a large basis set [cc-pVTZ(–f) for the organic atoms, LACVP* for the iron atom] affect the results by <8%.

Fig. 3.

Energy profile and geometries for the stationary structures along the hydrogen-atom abstraction reaction. Distances in angstroms and energies in kcal/mol are shown in black, and main relevant spin densities are shown in blue. The spin density in the heme porphyrin ring is shown next to the radical cation sign.

How does the enzyme manage to achieve >10 orders of magnitude enhancement of the rate constant for hydrogen-atom abstraction as compared with the simple porphyrin-model system (19)? The wealth of detail available from accurate atomic-level computational studies provides us with the means to answer this question quite specifically. To accomplish the task, we complemented our QM/MM calculations with model-system studies. By combining model QM calculations with the QM/MM results, we are able to characterize systematically the features of the enzyme that are responsible for the dramatic rate acceleration.

Our first step is to separate the effects of the protein environment from those of the substrate and porphyrin chromophore. We do so by extracting the QM region of the QM/MM-optimized structures and recomputing the energy profile for the reaction with single-point density functional theory energy calculations. Thus, we use a snapshot of the QM region, as shown in Fig. 2, to model the reaction and constrain the coordinates to the optimized QM/MM geometry. The activation barrier and reactant/product relative energies in this protocol become 20 and 12.3 kcal/mol respectively, a result that clearly indicates the importance of the protein environment, stabilizing the transition state (by 8.3 kcal/mol) and products (by 7.8 kcal/mol). We then assess the degree of strain energy imposed by the protein by releasing the geometric constraints and optimizing the QM model at every step in the reaction path, constraining in this case only the reaction coordinates. This protocol yields values of 21 and 13.5 kcal/mol for the barrier and endothermicity, respectively; the strain-energy contribution to lowering the barrier is thus on the order of 1 kcal/mol.

The remainder of the differential barrier height (6.5 kcal/mol) and reactant/product energy separation (10.5 kcal/mol) between the reduced and larger models in Fig. 2 derives principally from the use of camphor instead of methane as substrate. Other differences, such as the inclusion of the actual substituents on the macrocycle and incorporation of Cys rather than a sulfhydryl group as the species ligating the iron atom, have only minor effects in the absence of the protein environment. The radical character in the substrate donor carbon, observed in the transition state and product, is better stabilized by camphor than methane. This stabilization, due to the inductive effects of the sp³ carbons directly bonded to the donor, has been observed already in several studies (27, 28) and partially explains why methane cannot be hydroxylated by P450 enzymes.

To proceed further, we must investigate in detail the effects of the protein environment on the core catalytic moiety. The first contribution of the protein has been manifested already through the QM-model optimization. By comparing the energy differences of the constrained QM model (QM/MM-constrained geometries) with that obtained from full geometry optimization, we can determine a stabilization of the transition state and/or products due to the protein restraints on the geometry of the reactive core. From the results we see that protein restraints on the geometry stabilize the products and transition state relative to the reactants by 1.2 and 1.0 kcal/mol, accounting for the first substantial component of reduction of the activation barrier by the protein. The main difference after geometry optimization is the enlargement of the Fe—S distance in the reactant species. The protein constrains the reactant Fe—S distance to 2.44 Å, which turns into 2.52 Å when extracting and optimizing the QM region. The QM/MM Fe—S distance of 2.44 Å, in better agreement with experimental result of 2.3 ± 0.2 Å (14), introduces restraint energy due to an antibonding interaction between the iron and sulfur orbitals. Constraining the Fe—S distance in the optimized reactant QM region to 2.44 Å resulted in a 0.75 kcal/mol increase in the energy, ≈75% of the total restraint energy observed. Thus, we can conclude that the protein restraint energy is mainly a reactant destabilization rather than stabilization of the transition state and product.

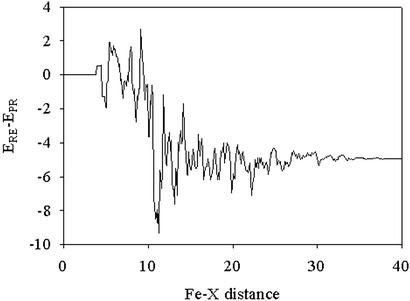
The largest contribution of the protein to the stabilization of the transition state and product comes from electrostatic interactions. This term can readily be evaluated in the QM/MM computations by examining the total energy of the MM point charges interacting with the QM region. We are interested in differential stability of the reactant and product species. Lowering of the transition state energy follows directly from reduction of the reaction endothermicity, to the extent that the transition state resembles the products. The effect of protein electrostatics on this quantity is obtained by subtracting the total electrostatic interaction energy for the product and reactant species; this value, 5 kcal/mol, is substantial, representing ≈64% of the total stabilization induced by the protein. A plot of this differential electrostatic energy as a function of distance from the central iron atom is given in Fig. 4, which reveals that the main stabilization is restricted to groups no more than 10–12 Å from the iron atom. Analysis on a residue by residue basis demonstrates that the largest effects are principally due to the presence of polar side chains next to the carboxylate substituents of the heme group.

Fig. 4.

Product/reactant difference (E_RE – E_PR) in electrostatic MM point charges' contribution to the QM electronic Hamiltonian. Individual MM atom contributions are added and presented versus the iron distance in angstroms.

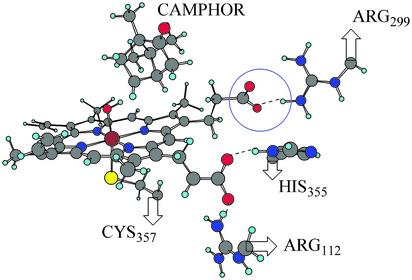
One simple physical picture that can be used to understand this result is to envision the hydrogen-atom abstraction reaction described above as a proton-coupled electron transfer. One electron of the C—H σ-bond is transferred to the ferryl-oxygen atom of the heme accompanied by C—H bond cleavage with concomitant proton transfer. Our calculations indicate that there are two main electronic effects operative in accommodating the excess charge injected into the heme. A significant fraction of the electron charge stays localized on the oxygen atom, and a minor portion of the charge is transferred to the iron atom through direct coupling, introducing partial Fe(III) character. In addition, there is an indirect electronic relaxation effect present that causes a significant reorganization of the occupied molecular orbitals that do not mix directly with the redox-active orbitals, giving rise to a notable charge redistribution in the porphyrin ring and its substituents. Formal charges derived from the electrostatic potentials on both the product and reactant indicate that one of the carboxylate groups, marked in Fig. 5 with a blue circle, has an excess charge of ≈0.06 electron units in the product as compared with the reactant. This additional negative charge interacts favorably with the positively charged hydrogen atoms on Arg-299 and translates into a differential electrostatic stabilization energy of 3.0 kcal/mol.

Fig. 5.

Positive residues surrounding the carboxylate substituents in the fully optimized QM/MM hydrogen-atom abstraction product. In a blue circle we underline the carboxylate group with oxygen spin densities.

A more detailed analysis of the molecular orbitals∥ reveals that the distinctively different charge distribution observed on the carboxylate group in compound I versus the radical intermediate is the consequence of a finely tuned mechanism of electron distribution designed to assist the redox reaction. In compound I, the most important electronic feature is a strongly oxidizing reaction center at the ferryl oxo moiety, which displays significant radical character of 0.70 electron units (Fig. 3). Generation of this unstable electronic structure is accomplished by a highly electron-deficient Fe(IV) center, which in turn is surrounded by a similarly electron-deficient porphyrin radical that formally displays an electron hole. In fact, compound I can be envisioned as the product of an intramolecular single electron-transfer reaction from the porphyrin ligand to a putative Fe(V) center to give the Fe(IV) moiety and a porphyrin radical ligand. In this environment, the electron-withdrawing ability of the carboxylate is not strong enough to maintain fully occupied lone-pair orbitals on its oxygen atoms, giving rise to the excess spin polarization of 0.2 on one of the two O atoms. After electron injection and formation of the radical intermediate, the carboxylate ligand removes an additional 0.08 electron units and becomes more negative by 0.06 units, resulting in the differential electrostatic stabilization described above.

The electron-withdrawing ability of the carboxylate group is affected largely by its immediate surroundings. For instance, the QM model directly extracted from the QM/MM system, with two carboxylate substituents, presents almost no porphyrin radical character because of the artificially increased orbital energy of the oxygen lone pairs in the gas phase. The carboxylate groups actually act as electron donors, transferring almost a full electron to the electron-deficient porphyrin system and diminishing the radical character completely. When the carboxylate is protonated, the lone-pair orbitals are stabilized and the radicaloid character on the porphyrin ring is maintained. The actual protein environment represents an intermediate situation, where the charged residues next to the carboxylate substituents stabilize the oxygen lone-pair orbitals although not as much as by the full addition of a proton. The result is an intermediate-strength electron-withdrawing carboxylate that partially decreases the radical character of the porphyrin ring. The electron-withdrawing ability of one of the carboxylate groups is substantially enhanced by the presence of Arg-112 and His-355, which create a highly positive environment, and therefore no radical character at the carboxylate group is observed. The other carboxylate, marked with a blue circle in Fig. 5, faces only Arg-299 and cannot withdraw enough electron density from the porphyrin radical to avoid displaying some radical character itself. This effect is larger in the reactant than in the product, because the porphyrin system is less electron-deficient on the product side. There is, consequently, a differential increment of electron charge in the product carboxylate oxygen. In a breakdown analysis of the individual amino acid electrostatic contributions, Arg-299, with almost 3 kcal/mol product stabilization, was the largest contributor. Enzymatic catalysis then is controlled by electrostatic interactions of the polar residues next to the active-site core, stabilizing the product after hydrogen abstraction from the substrate.

The third and final stabilization of the products by the protein is associated with the MM energy, arising from small shifts in atomic position in response to the different electronic species in the core, namely, the slight charge separation in the hydrogen abstraction product. The motions can be viewed primarily as a response to differential electrostatic forces discussed above. Some of the electrostatic stabilization energy is reorganized into the MM energy rather than appearing directly in the MM–QM electrostatic interactions. There is also a minor degree of van der Waals interactions. This purely MM contribution to the product stabilization results in 3 kcal/mol, with 2.6 kcal/mol due to electrostatic interaction. The breakdown of this last term does not point to any specific interaction but rather to the buildup of very small contributions along the entire protein.

A final issue that is worth discussing is the possible effect of electrostatic polarization in the MM region, which we do not treat explicitly, on our estimate of the electrostatic stabilization of the transition state. In principle, polarization response due to reorganization of the electrons in the MM region could damp the interaction between the MM-charged groups, such as Arg or His, and the QM region, the heme group. This feature could be modeled with the use of a dielectric constant other than unity, which is used in the actual calculations. In practice, the key charged groups are proximal to the heme, with no intervening MM atoms, thus the effective damping of interactions caused by the protein environment is expected to be minimal. We note that, in tests on analogous systems such as a model of the hemerythrin active site, in which a salt bridge is formed between a His residue ligated to one of the iron atoms and a Glu (29), virtually no difference was observed when the Glu residue was treated at the MM or fully QM level. In this case polarization effects are included explicitly. Note that if one were considering electrostatic interactions arising from net charges at a large distance, the effects of medium response as discussed above would have to be considered. Net charges on the protein surface are neutralized to reflect dielectric screening by the solvent, as discussed above.

Conclusion

In summary, we have produced an accurate calculation of the activation barrier in cytochrome P450cam hydrogen abstraction. The results provide an explanation for the otherwise surprising experimental data of Davydov et al. (5). The enzymatic mechanism introduces some questions about the two-state reactivity mechanism described by Shaik and coworkers (19). The models developed here can be used to obtain further detailed comparisons with experimental results and to suggest new experiments with this and other proteins that use protoporphyrin IX mutations of the enzyme. For instance, positive residues next to heme carboxylates might be altered by mutagenesis, or the protein might be reconstituted with a porphyrin in which the carboxylates have been replaced by ester or amide functionalities.

From a biological perspective, the results discussed above suggest that there are significant evolutionary advantages to acceleration of the hydrogen-atom abstraction reaction in cytochrome P450 enzymes. The most straightforward explanation is that the ferryl iron(IV) intermediate is highly reactive, and that rapid conversion of this species to an alcohol avoids alternative kinetic channels such as those leading to production of hydrogen peroxide. This hypothesis can be explored by further calculations. It can also be investigated experimentally. If one could raise the hydrogen abstraction barrier by targeted mutations or chemical alterations as suggested above, at some point one would expect to see enhanced production of peroxide when the barrier is sufficiently elevated.

Finally, the stabilization of the transition state by use of a carboxylate-Arg salt bridge may be representative of a more general principle in metalloprotein reaction chemistry. Oxidation state changes at the metal ion in the catalytic cycle of a metalloenzyme are well known to be delocalized out onto the ligands. Here we demonstrate stabilization of the substrate-donated electron by a positively charged Arg residue in the active-site cavity. In our recent study of reversible binding of dioxygen to hemerythrin (29), we observed a very similar phenomenon but with reversed polarity. In that case, the bound dioxygen species exists in a peroxo state, requiring withdrawal of electrons from the metal and its surrounding ligands. One of these ligands is a protonated His that is engaged in a strong hydrogen-bonding interaction with a neighboring carboxylate anion. When dioxygen binds, the proton on the His becomes more positive, and the strength of the hydrogen bond with the carboxylate increases by 3.2 kcal/mol. This value is similar to that observed here and constitutes a critical stabilization of the oxygenated form of the protein from the point of view of biological function. Inspection of the structures and functioning of metal-containing proteins should reveal how widespread the use of this mechanism is in nature.