Spatial parasite transmission, drug resistance, and the spread of rare genes

Abstract

The transmission of many parasitic worms involves aggregated movement between hosts of “packets” of infectious larvae. We use a generic metapopulation model to show that this aggregation naturally promotes the preferential spread of rare recessive genes, compared with the expectations of traditional nonspatial models. A more biologically realistic model also demonstrates that this effect could explain the rapid observed spread of recessive or weakly dominant drug-resistant genotypes in nematode parasites of sheep. This promotion of a recessive trait arises from a novel mechanism of inbreeding arising from the metapopulation dynamics of transmission.

The emergence of drug-resistant strains of a wide variety of pathogens is a major epidemiological challenge. One of the oldest and most economically important examples is that of gastrointestinal trichostrongylid nematode parasites of farmed ruminants (1–3). Drug resistance in trichostrongylids appears in many cases to be a single- or few-locus trait (4), though there has recently been evidence for polygenic resistance to Avermectin in Caenorhabditis elegans (5). Although resistance is commonly at least partially dominant, there is also a significant prevalence of autosomal, fully recessive traits such as resistance to Levamisole in Haemonchus contortus, as well as incompletely recessive two-locus traits such as resistance to Benzamidazole in H. contortus and Trichostrongylus colubriformis (4).

The existence of fully or predominantly recessive drug resistance is difficult to explain, even in the presence of a strong selection pressure during drug treatment. Assuming that the resistant allele preexists at a very low level, q, in the parasite population because of mutation (6), the resistant phenotype would only occur with vanishingly small frequency q², and so would never exist in sufficient numbers to invade a population. More generally, the “q² constraint” should inhibit the spread of any recessive trait from a rare beginning. By contrast, for dominant or sex-linked traits the resistant genotype occurs at a much higher frequency, proportional to q, and is easily spread.

Here, we show that the characteristically aggregated transmission of many parasites can overcome this constraint on rare recessives. Spatial aggregation of the infectious stage, within an intermediate vector host (7) or the definitive hosts' fecal deposits (8, 9), means that parasites tend to enter the host in “clumps” rather than singly. This process can make a significant contribution (10) to the characteristically aggregated (i.e., overdispersed) distributions of worm burdens among hosts (11, 12) [other processes that contribute to aggregated parasite distributions are heterogeneity of infection rates or immunity between hosts (8) and positive feedback in the reinfection dynamics (13)].

We focus here on the simplest epidemiological picture, the dynamics of trichostrongylid nematode parasite outbreaks in farmed ruminants, maintained at constant sticking density during a grazing season. Previous studies that combine clumped infection and genetics (14, 15) have focused on the initial dynamics soon after uninfected hosts are turned out onto pasture. Ingested larvae take a couple of weeks to become sexually mature worms, and any offspring will not become infectious for a further few weeks, so the early infection events involve preexisting larvae on pasture, the offspring of any adult worms in the hosts do not contribute. Using this simplification, we have shown that extrinsic infection by clumps containing genetically heterogeneous larvae may lead to deviations from Hardy–Weinberg mating rates, with significant repercussions on the population genetics of the system (14, 15). However, the dynamics of an epidemic are fueled by later generations of parasites, and the nonlinear rates of production of different genotypes complicate the system dramatically. Other nonlinearities such as acquired immunity and density dependence cloud the later picture still further.

Here we allow the size and genetic diversity of clumps to be determined by the subpopulation of worms that produced them, hence closing the “feedback loop” of infection that is an essential element of the dynamics of the epidemic. This study integrates clumped infection and population genetics into stochastic models of macroparasite epidemics. Because the larvae in a clump are the offspring of a finite number of worms, they will be somewhat related, especially at low worm burdens. When these larvae are ingested together, they will then be in a position to interbreed in their definitive host. This presents a potential route to inbreeding, which could promote the frequency of rare, resistant homozygotes.

Aggregation has previously been incorporated into models of the evolution of anthelmintic drug by imposing a negative-binomial distribution on the worm burdens (20, 21). This method modifies the parasites' mating probability and leads to a rich variety of nonlinear behavior. However, it is not clear whether this leads to significant deviations from Hardy–Weinberg mating rates unless some degree of mate choice is assumed, explicitly or implicitly (21, 22). By contast, the “spatial inbreeding” that is the topic of the present paper occurs under completely random mating within each host. It is produced by the specific ancestry of each infectious clump of larvae, so we need an underlying individual-based mechanistic model to investigate it.

We begin by studying a stochastic metapopulation model that encapsulates the essential biological processes of positive feedback through clumped (re-)infection. We are able to prove analytically that a rare, selectively neutral recessive trait has prevalence proportional to q rather than q² in this model. We then present simulation results for a more detailed model of parasitic gastrointestinal nematodes in farmed sheep, which demonstrate that the metapopulation dynamics of transmission leads to a much higher risk of invasion by a recessive drugresistant, relative to a model without spatial inbreeding.

Generic Metapopulation Model

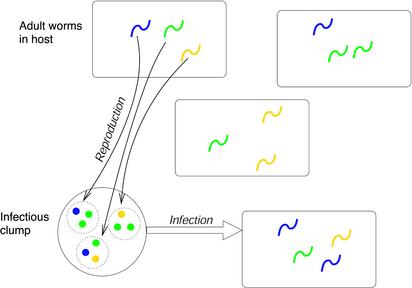
We begin with a generic model. This is a simple, stochastic branching process metapopulation, which examines the spread of alleles as a function of a clumping parameter, defined as the mean number of offspring per parent per clump, and is depicted schematically in Fig. 1. The model describes the invasion of a large (asymptotically infinite) number of patches (“hosts”) by a parasitic worm. The worms within a host mate and produce offspring; these pass out of the host in clumps whose size and genetic makeup will reflect the population of worms within that host. A clump can then infect another host at random. We focus on the initial growth of the parasite population, therefore ignoring effects that become important at higher densities such as density dependence and the hosts' immune response. We also assume that the initial growth of the population is very rapid compared with the mortality rate of the worms, and that the infectious stage is short-lived so that any infections take place instantaneously.

Fig. 1.

Schema of the generic branching metapopulation model. Adult worms mate in the host and produce offspring, which pass out of the host in “clumps.” A clump can then infect another host.

The clump size is a Poisson-distributed random number whose mean equals the clumping parameter multiplied by the number of worms in the host producing the clump. The clumped infection process leads to the worm burdens, and hence the clump sizes, becoming aggregated (overdispersed) over time. However, our clumping parameter is a property of the infection process, so it has no simple relationship to measures of the degree of aggregation of the worm population (such as Lloyd's mean crowding or the negative binomial k value), beyond the fact that these measures increase monotonically with the clumping parameter.

For simplicity, the parasite is assumed to be a diploid, nonselfing hermaphrodite, and is classified by a single-locus, two-allele trait. Worms are assumed to be promiscuous, so the genetic diversity within a clump reflects all possibly mating combinations within the host. All genotypes have equal fitness, so the mean allele frequency is constant over time. This gives a very conservative estimate of the impact of spatial clumping on the population genetics, because we allow no selective advantage to the resistant genotype. If there were no clumping in the infection process, the distribution of genotypes would automatically follow a Hardy–Weinberg scenario, and the distribution of worms between hosts would obey a Poisson distribution. The clumped infection process both allows the worms to have aggregated subpopulations, and also to have non-Hardy–Weinberg genetics.

Numerical results for the model can be obtained by simulating the number of worms of the three genotypes in each of a very large number (several million) of hosts. At each infection event, one host is chosen at random, and each worm in the host generates a Poisson-distributed clutch of offspring, with mean equal to the clumping parameter and genetics corresponding to random mating within the host. These offspring are all added to another randomly chosen host. Analytical results can also be obtained for this model, and these will be presented elsewhere. A formal definition of the model is given in Appendix.

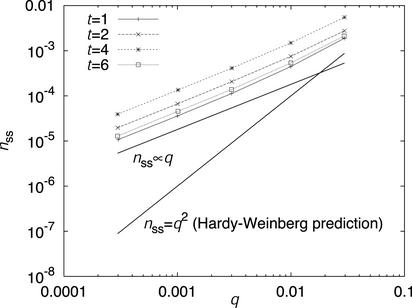
We start at a low level of infestation (two worms per host), with the rarer allele occurring with frequency q. Fig. 2 shows the frequency n_ss of the rare homozygote as a function of q, for one value of the clumping parameter at four different times t. At t = 0, n_ss begins at its Hardy–Weinberg value q², then increases rapidly to a maximum at t ≈ 3–5 (for these parameter values), then decreases slowly toward an asymptote. Under random mating, we would have n_ss = q² for all t, the rare homozygote clearly has a much higher prevalence than this Hardy–Weinberg prediction. This effect is strongest for small allele frequencies, and also when the clumping parameter is large (though this latter effect is not shown in the figure). In fact, we can establish analytically that, in the rare allele limit, n_ss is proportional to q rather than q². This can be seen in Fig. 2 from the fact that the data for a given time t lie parallel, on a log–log scale, to a line with n_ss ∞ q.

Fig. 2.

Simulations of the generic model, with clumping parameter 2: prevalence of the rare homozygote as a function of allele frequency at different times. Lines with n_ss ∞ q and n_ss = q² and are included for comparison purposes.

We have also run simulations of a similar model with dioecious worms. The same effect is present, though it is weaker than for an hermaphrodite model with the same parameters. This is because only half as many worms per clump can contribute eggs (assuming 1:1 sex ratio), which effectively reduces the clumping parameter. Comparing a dioecious model with a hermaphrodite model having half the fecundity and clumping parameter (and hence identical numbers of egg-producing individuals per clump and per host), we find similar values for n_ss, though it is nevertheless slightly smaller in the diecious model as the additional presence of males means that there is more mixing in the population.

The analysis of the generic metapopulation model shows that the promotion of rare homozygotes to a prevalence of order q rather than q² is a generic consequence of aggregated transmission in the invasion of a parasite–naive host population. This has very powerful implications: the aggregated spatio-temporal dynamics allow a wholly recessive trait to invade the population almost as quickly as a partially or wholly dominant trait. This is especially important for an allele that only has a selective advantage in the presence of drug treatment, and which, in the absence of the drug, will be maintained in the population at an extremely low level by mutation.

Sheep–Trichostrongylid Model

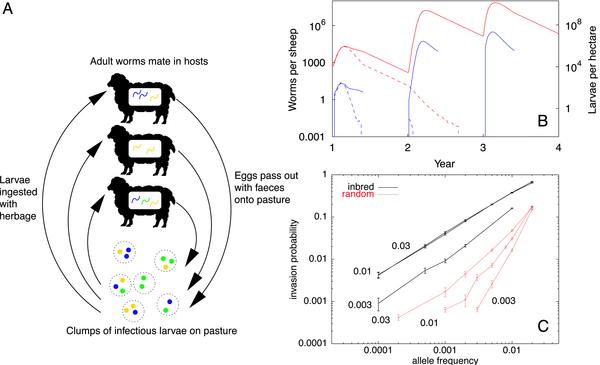
To explore applications to nematode drug resistance explicitly, we now consider a model for the immunoepidemiology of trichostrongylids in farmed ruminants, which takes into account the stochastic nature of the population dynamics and the spatial nature of the infection process (16). The life cycle of this dioecious parasite as we model it is depicted schematically in Fig. 3A. Hosts encounter “clumps” of herbage containing infectious larvae of mixed genotypes on pasture. When a host ingests a clump of larvae, a fraction of these may avoid immune exclusion and become established as mature parasites in the digestive tract of the host. The adult worms in a host mate randomly (within the host), and their offspring over some period are evacuated in the host's feces, and form a new infectious clump on pasture. The model is a stochastic version of a standard, deterministic model (17), and a formal definition may be found in Appendix.

Fig. 3.

Sheep–trichostrongylid model. (A) Schematic diagram. (B) Worms per host (in blue) and larvae per hectare (in red) for two typical realizations, one corresponding to extinction (dotted lines) and one to an epidemic (solid lines). (C) Invasion probability both with (inbred) and without (random) spatial inbreeding, for different values of the clumping parameter; the error bars are standard errors from the simulations (based on >10,000 realizations).

We performed simulations of our model with biologically realistic parameter values (taken from ref. 14), for a scenario where 50 initially uninfected hosts are left on pasture from spring to autumn. The pasture was originally infested with infectious larvae, a small number of which had the resistant allele; the hosts were treated prophylactically with a drug that reduced the lifetime of susceptible (homo- and heterozygote) adult worms in the host from 70 days to 2 days, while leaving the lifetime of the resistant homozygote unaltered. At the end of each season, the hosts are removed from pasture, the remaining larvae on pasture are thinned by overwinter mortality, and then a new cohort of uninfected, susceptible hosts is placed on pasture at the beginning of the next season.

The system rapidly progresses to one of two outcomes, either saturation with the resistant strain, or extinction of the parasite population, within three to four seasons, as illustrated in Fig. 3B. Note that this is roughly the time scale over which resistance is commonly seen to emerge in the field (18). The stochastic nature of the system means that either fate is possible with the same parameter values. We define the “invasion probability” as the fraction of realizations in which the parasite population has risen to saturation.

Fig. 3C shows the invasion probability as a function of the initial allele frequency, for differing degrees of clumping (for this model, we define the clumping parameter as the clump size, expressed as a fraction of the total number of offspring produced by one host's parasites in one day). The data from the model described above are labeled “inbred,” whereas “random” denotes data from an alternative model without the spatial inbreeding mechanism. The “random” model is equivalent to the “inbred” in all respects except one: the genetic makeup of infectious clumps is a mixture over the offspring of all parasite subpopulations, rather than the parasites in a single host. We do not simply compare with the case of smaller clumping parameter, because the need to find a mate in dioecious parasites introduces another nonlinearity at low densities, the “mating probability.” This interacts strongly with the degree of clumping even in the absence of genetic considerations.

Not only is the invasion probability for the “inbred” model orders of magnitude higher than the “random” model for the same parameter values, but also it is much less sensitive to the initial allele frequency, so that invasion is still possible even for much lower allele frequencies than we have shown in Fig. 3. We also performed simulations for other parameter values, and found that the effect persists under many conditions, being even stronger for lower values of the basic reproductive ratio.

The invasion probability varies nonlinearly with several parameters in the system, and there are other biological mechanisms, such as the mating probability (19), which interact with the clumping parameter, but nevertheless we observe an effect akin to the “q²” versus “q” of the simple branching process model. The effect persists if drug resistance is only partially recessive, and only disappears under conditions where the heterozygote is fit enough to invade the host population by itself, because then the invasion rate contains a component proportional to q even in the absence of spatial effects.

Discussion

These results illustrate a number of new, general points about the dynamics of rare recessive genes in sexual metapopulations. First, inbreeding is an emergent property of clumped transmission of dioecious parasites. This arises from adding the impact of spatial clumping to previous, important research on the impact of infrapopulation parasite mating frequency on the dynamics of resistance (20–22). Spatially generated inbreeding is important when resistance is a rare trait that only has a small probability of invading, but does so because of a large number of “replicates.” Similar results may be sought in any metapopulation where the size of migrating clusters increases with subpopulation size. The effect is initiated by the high variability in allele frequency between hosts when the worm burdens are low, and is dramatically weakened if the initial infection rate is increased.

Second, the spatial clumping mechanism may have implications for the management of resistance. It is commonly thought that allowing some exposure to parasites promotes acquired immunity in ruminants (24, 25), and is beneficial in combating the spread of drug resistance; our results suggests that the consequent reduction in variability of the allele frequency may be a further benefit of this practice. The induced inbreeding requires the simultaneous ingestion of related larvae, which in turn relies on the integrity of the fecal clumps. It is known that larvae on pasture disperse more readily in wet weather, and it is interesting to note that dry weather has been implicated in the promotion of anthelmintic drug resistance (25, 26). Experimental molecular ecology to explore these effects might be very fruitful.

More broadly, this is a generic model for the spread of rare genes in a metapopulation with clustered migration. Our model illustrates the often unexpected emergent properties arising from the interaction between population genetics and population dynamics (25, 26). This work also underlines the suitability of macroparasite systems for exploring the ecological and evolutionary dynamics of metapopulations.

Appendix

Definition of Branching Metapopulation Model. Finite number of hosts. The model is a Markov process in continuous time. The state of the system at time t is specified by ({W_i,j(t): i ∈ {1,... N}, j ∈ {1, 2, 3}}), where W_i,j is the number of parasites of genotype j in host i, N is the number of hosts, and j is an index corresponding to genotypes ss, sS, and SS, respectively (“s” denotes the rare allele and “S” the wild-type allele).

The system only changes through the infection of a host (i say) with a clump of parasites arising from another host (k say, where k = i is possible). Such infections take place at a rate λ/N, so that λ is the total rate at which the ith host encounters clumps. Given W_k,j, the clump is always of zero size if Σ_jW_k,j ≤ 1, because the worms do not self-fertilize. Otherwise, the clump has size (C₁, C₂, C₃), where the C_j have independent Poisson distributions with means γ_j, where

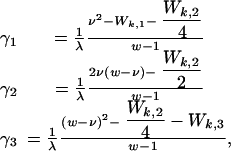and w ≡ W_k,1+W_k,2+W_k,3, ν ≡ W_k,1+W_k,2/2. Note that the mean number of offspring per clump per parent is 1/λ, so the mean number of worms per host is independent of λ.

Infinite number of hosts. The probability that a host is infected at any given instant with a clump of size C ≡ (C₁, C₂, C₃) is proportional to the average over all other hosts of the probability κ(C|W) that a host with W ≡ (W₁, W₂, W₃) worms will produce a clump of size C [since the C_j have Poisson distributions, we have 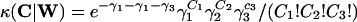, where the γ_i are defined in the previous section]. In the limit N → ∞, the average over all hosts becomes synonymous with the average over realizations of one particular host. It is now possible to consider only the dynamics of one subpopulation W, for which the transitions are: W → W + C at rate λ, where C is a random triple with P(C = c) = p_C(c, t).

This Markov process can be straightforwardly solved to yield the probability distribution p_W(w, t) ≡ P(W(t) = w) in terms of p_C(c, t). The clump size distribution, p_C, can then be expressed self-consistently in terms of p_W from the requirement that p_C(c, t) = Σ_W κ(c|w)p_W(w, t). Some headway may be made toward a full, explicit solution to the system by using generating function techniques.

Definition of the Sheep–Trichostrongylid Model. This model is a stochastic version of an original deterministic model described in G. Smith (17).

We define the model as a Markov process in continuous time t. The state of the model is specified by

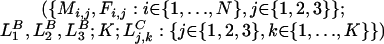where M_i,j(t) is the number of male adult parasites in host i of genotype j; F_i,j(t) is the number of female adult parasites in host i of genotype j; N is the number of hosts (fixed); 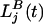is the number of “background” larvae of genotype j; 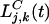is the number of larvae of genotype j in the kth clump; and K(t) is the total number of clumps.

Genotype index j = 1, 2, 3 correspond to ss (resistant homozygote), sS (susceptible heterozygote), and SS (susceptible homozygote), respectively. Transitions in the state of the system at time t occur at the following rates for all i ∈ {1,... N}, j ∈ {1, 2, 3}, k ∈ {1,..., K}, where the chance of multiple transitions occurring simultaneously can be ignored:

• Mortality

  
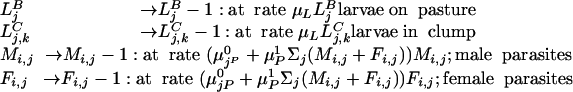
• Production of clumps of larvae

  

  Here, δ is the Kroneker delta and a is the clumping parameter.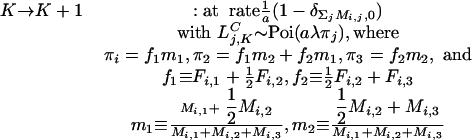
• Infection by background larvae

  

  where χ^M(t), χ^F(t) are independent, identically distributed Bernoulli variables with P(χ = 1) = φ(t), which allow for the possibility that ingested larvae may not become established as mature parasites within the host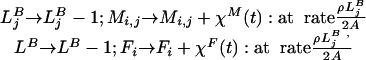
• Infection by clumps

  

  where ξ_j′(t), η_j′(t) are independent, identically distributed Poisson variables with mean .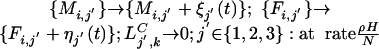

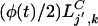The meanings of the parameters are given in Table 1, with the exception of the clumping parameter a. Note that we have assumed male and female parasites to be equally abundant.

Table 1. Sheep-trichostrongylid model parameters, with the values used.

Parameter	Meaning	Value
H	Host density per hectare (ha)	5 ha-1
ρ	Larval encounter rate per host	5 × 10-5 ha·day-1
λ	Egg production rate per female parasite	1,000 day-1
μL	Larval mortality rate	0.05 day-1
μjP0	Density-independent parasite mortality rate	μ1P0 = 0.014 day-1, μ2P0 = μ3P0 = 0.5 day-1
μP1	Density-dependent parasite mortality	1.44 × 10-6 day-1
ϕ(t) = (1/1 + Cebt)	Probability of establishment of ingested larvae as mature parasites	C = 0.0735, b = 0.073 day-1