Coupling between changes in human brain temperature and oxidative metabolism during prolonged visual stimulation

Abstract

A fundamental discovery of modern human brain imaging with positron-emission tomography that the blood flow to activated regions of the normal human brain increases substantially more than the oxygen consumption has led to a broad discussion in the literature concerning possible mechanisms responsible for this phenomenon. Presently no consensus exists. It is well known that oxygen delivery is not the only function of systemic circulation. Additional roles include delivery of nutrients and other required substances to the tissue, waste removal, and temperature regulation. Among these other functions, the role of regional cerebral blood flow in local brain temperature regulation has received scant attention. Here we present a theoretical analysis supported by empirical data obtained with functional magnetic resonance suggesting that increase in regional cerebral blood flow during functional stimulation can cause local changes in the brain temperature and subsequent local changes in the oxygen metabolism. On average, temperature decreases by 0.2°C, but individual variations up to ±1°C were also observed. Major factors contributing to temperature regulation during functional stimulation are changes in the oxygen consumption, changes in the temperature of incoming arterial blood, and extensive heat exchange between activated and surrounding brain tissue.

During the last century, substantial progress has been achieved in understanding of basic mechanisms and global relationships responsible for the temperature regulation in humans and animals (see, for example, refs. 1 and 2). However, detailed information on the temperature distribution and changes under different conditions in the intact living human brain is very limited. Such information would be of great importance for understanding of brain functioning. Indeed, temperature substantially effects the rate of chemical reactions (1, 3)—in the brain the average van't Hoff temperature coefficient, Q₁₀, is 2.3 (1). Temperature also substantially affects affinity of hemoglobin for oxygen, changing the blood oxygen saturation level, sO₂, by several percent with each degree Celsius (4). It has been known for decades that increases in the body temperature can worsen the neurological condition of patients with multiple sclerosis as well as other neurological diseases. Intriguing recent findings in animal models also indicate that the brain neurons are very sensitive to small, on the order of 2–3°C, variations in the temperature (5).

Heat in the brain is produced mostly by oxygen consumption. It is removed chiefly by blood flow. The balance between heat production and removal in resting state maintains brain temperature constant. Local changes in blood flow and metabolism during functional brain activation can be predicted to upset the balance of factors maintaining a constant brain temperature. It is now widely appreciated that under such circumstances blood flow increases more than oxygen consumption (6). This uncoupling of blood flow and oxygen consumption might predict a lowering of local brain temperature because heat removal increases more than does heat generation. However, changes in the temperature of incoming blood and heat exchange between activated regions and tissue at rest might also affect temperature balance in a new “activated” state. In addition, hemodynamic delay on the order of 2–4 sec in the vasculature response to activation may lead to a very small transient increase in the brain temperature because of increase in activated tissue metabolism. Some in vivo information on temperature regulation during functional brain activation is available from animal studies. Localized temperature variations under visual, auditory, and somatic stimulation that were variable in duration, sign, magnitude, and form and ranged from 0.01°C to 0.2°C were observed in cat brain (7–9). Local decreases in brain temperature on the order of 0.2°C were observed in awake monkeys after short amygdala stimulation (10). An infrared mapping technique (11) was used to detect thermal changes on the surface of rat brain. Time- and animal-dependent differences in temperature of up to 0.5°C were registered in different cortical areas (12) during the resting state. Short visual stimulation invoked temperature rise on the order of 0.1°C on the surface of the skull covering the visual cortex (11, 12).

The above-mentioned observations, while limited in number and scope, do suggest that brain temperature changes during functional activation. However, they do not provide systematic information on the mechanisms responsible for brain temperature regulation and the range of temperature changes accompanying brain functioning. Nor do they give any information on the role that changing temperature plays in brain metabolism and function. Such information would be very important for developing models of temperature regulation in the human brain during functional activity. It will also be important for our understanding of the role that increased blood flow plays during functional activation. Note also that details of temperature regulation in animals and humans may be substantially different (1).

Theory

Heat Balance in the Brain.

Most of the energy required for brain activity is generated from the net chemical reaction of oxygen and glucose (glucose + 6O₂ → 6CO₂ + 6H₂O). This reaction at 37°C is associated with a release of ΔH° = 470 kJ of enthalpy per mol of O₂ (3). While some of this energy (33%) immediately dissipates into heat, the rest (67%) is used to produce 38 ATP molecules that will further maintain a complex chain of chemical reactions that ensure proper brain functioning. However, because no mechanical work is performed in the brain, the final ATP hydrolysis releases the energy back to the system and as a result almost all of this energy ends up as heat (3). Some of this energy, ΔH_b (13), however, is used to release oxygen from hemoglobin. Hence the amount of heat, Q_r⁺ locally generated per gram of brain tissue per minute is proportional to the product of the regional cerebral metabolic rate of oxygen (rCMRO₂) and the difference between ΔH° and ΔH_b:

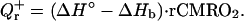1

The anaerobic pathway of glucose consumption (1, 3) (glucose → 2 lactate) can also contribute to energy release, especially during functional stimulation (14, 15); however, only about 15–20% of glucose is metabolized anaerobically (3), and the energy resource of this reaction is much smaller (about 7%) (1) compared with the oxidative metabolism. Hence, only about 1% of heat is generated by the anaerobic pathway. We will omit this contribution in the current consideration.

Given that an average rCMRO₂ in the human brain is 1.5 μmol⋅g⁻¹⋅min⁻¹ (3), and an average ΔH_b is 28 kJ (13), on average 0.66 J is released every minute per gram of brain tissue. This internal local heat is removed mainly by blood flow. Because local heat diffusivity in the brain tissue is expected to be very high (the corresponding coefficient in pure water is 140 μm²/msec), the heat generated at any part of the brain reaches the nearest capillary in a matter of milliseconds. Heat transfer is also enhanced by extensive fluid exchange at capillary level. The temperature of outflowing blood can be considered in equilibrium with the tissue temperature, T (16). Hence, the rate of heat removal from the brain tissue, Q_r⁻, can be estimated as a product of regional cerebral blood flow, rCBF, blood heat capacity, C_B, blood density, ρ_B, and the temperature difference between the tissue and inflowing arterial blood:

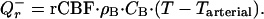2

For brain regions at rest the steady-state condition, Q_r⁺ = Q_r⁻ holds. Therefore, the equilibrium (resting tissue) regional brain temperature, T₀, should satisfy the following condition:

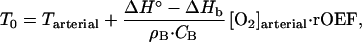3

where we introduce in a standard manner the regional oxygen extraction fraction, rOEF:

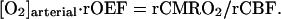4

Given that an average rCBF is about 0.55 ml⋅g⁻¹⋅min⁻¹ (3), and assuming ρ_B and C_B are the same as for pure water, we estimate that in the resting state the temperature difference between incoming blood and tissue is about 0.3°C.

It would be natural to assume that in a resting state (baseline condition) the temperature of inflowing blood remains constant across the brain. Hence, to maintain a homogeneous brain temperature rOEF should be regionally independent. It is well known from positron-emission tomography (PET) data (17, 18) that rCMRO₂ maps in the normal human brain are largely flat despite considerable regional differences in rCBF and rCMRO₂ maps. This striking correlation leads one to the conclusion that the architecture of blood vessels in the [human] brain contributes to brain temperature regulation in the resting state.

While contribution from the second term in Eq. 3 is quite small (we estimate 0.3°C) in the normal resting brain, it could be substantially larger in abnormal cases. For example, in patients with the carotid artery occlusion without distal infarction one would predict temperature elevation in the active brain areas where blood flow is reduced but normal metabolism is maintained.

The dynamic bio-heat equation describes the rate of temperature change in the brain, Ṫ, when the resting state is disturbed by global changes in blood flow, incoming blood temperature, or oxygen consumption:

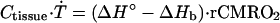5

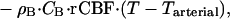where C_tisssue is the heat capacity of the tissue. The general solution of this equation, which describes the time course of temperature approaching equilibrium, has a simple exponential form with the temperature relaxation time constant

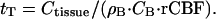6

It follows from Eq. 3 that by manipulating the incoming blood temperature, the brain temperature may be changed temporarily. According to Eq. 6, the rate of temperature return to the equilibrium is proportional to the rCBF. In the case of functional brain activation, focal changes in blood flow and metabolism in the activated regions will drive the temperature of these regions to a new equilibrium. Because of heat diffusivity, substantial heat exchange may take place between activated tissue and surrounding tissue at rest. This effect is not accounted for in Eq. 5 and will be discussed only qualitatively herein.

Influence of the Brain Temperature Changes on Magnetic Resonance (MR) Signal Intensity.

MR has already proved useful in the investigation of the functional response to the brain activation. The technique typically relies on the changes in the MR imaging (MRI) signal intensity due to blood oxygenation level-dependent (BOLD) contrast (19, 20)—i.e., the functional MRI (fMRI) signal. On the other hand, the frequency of the MR signal is temperature dependent (21). It has been demonstrated by means of MRI (22) and spectroscopy (23) that this phenomenon can be used for in vivo noninvasive evaluation of tissue temperature changes.

To quantify MR signal intensity changes we rely on the model of functional MR (fMR) signal behavior developed previously (24, 25). The presence of a blood vessel network modifies the intensity of free induction decay (FID) signal by a factor exp(−R2′⋅τ). The R2′ relaxation rate constant depends on the characteristics of the blood vessel network in the imaging voxel (24):

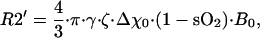7

where ζ is a tissue volumetric fraction of blood vessels with reduced oxygenation level compared with arterial—i.e., the apparent venous volume fraction (includes veins and adjacent to them part of capillaries), Δχ₀ is the susceptibility difference between fully oxygenated and fully deoxygenated blood, sO₂ is the oxygen saturation of outflowing (venous) blood, B₀ is the strength of the external magnetic field, and γ is the nuclear gyromagnetic ratio. Changes in the tissue temperature cause changes in the tissue metabolic rate, consequent changes in the sO₂, hence changes in the R2′ relaxation time constant. For a constant blood flow, ΔsO₂ = −(1 − sO₂)⋅ΔrCMRO₂/rCMRO₂ (26) where sO₂ and rCMRO₂ reflect initial temperature state. By simplifying the Van't Hoff formulation rCMRO₂(T + ΔT) = rCMRO₂(T)⋅Q₁₀^ΔT/10 (1), for small changes in the tissue temperature, we can derive the following equation: ΔrCMRO₂/rCMRO₂ = 0.1⋅ln Q₁₀⋅ΔT. By making use of the above equations, we finally arrive at the equation that describes the relationship between changes in the R2′ relaxation rate constant and tissue temperature:

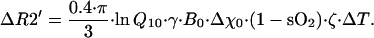8

Hence Eq. 8 predicts that changes in the tissue temperature will cause changes in the MR signal intensity even without changes in blood flow.

Methods

Functional Paradigm.

We conducted fMR studies during prolonged passive stimulation of the visual cortex. The visual stimulation was administered by means of an array of light-emitting diodes mounted in specially designed goggles (Grass Instrument Company). It follows from Eq. 6 that the time characterizing temperature changes in the human brain is on the order of minutes. Accordingly, for our functional studies we chose a long activation paradigm that included 4 min of resting, followed by 4 min of stimulation at 8 Hz, followed by 4 min of rest.

Subjects.

Volunteers were instructed to look straight ahead, and keep their eyes open during the entire session (although they could blink). If volunteers felt sleepy upon arrival, they were asked to drink a cup of coffee. Immediately before a 12-min functional block, volunteers were given an awakness test—they had to repeat four numbers after the examiner. To control volunteers' alertness during the scan, they were furnished with a push-button and every 30 sec they had to respond to the question, “Can you hear me?”. At the end of each experiment, volunteers were asked if they felt sleepy at any time. About 20% of collected data were discarded on the basis of these tests. Here we report results obtained in 17 scans acquired from nine volunteers (males, ages 21–50, females, ages 18–51).

MR Technique.

To acquire the fMR signal we chose a localized volume signal excitation technique (27) based on a double spin echo PRESS sequence (28) with high-performance rf pulses (29). We implemented on our 1.5-T Siemens Magnetom Vision scanner (Siemens, Erlangen, Germany) a version of the PRESS sequence, which allows for oblique voxels that could be fit to the area of the visual cortex. To avoid distortions of the MR signal from eddy currents, we used small (4 mT/m) but long (10 msec) crushing gradients around 180° refocusing pulses. To minimize low-pass filter ringing artifacts, the crushing gradients were ramped down slowly over a 4-msec time interval followed by a 20-msec waiting period before the start of the signal acquisition. The first 180° refocusing pulse was placed 20 msec after the 90° excitation pulse and the second one followed 70 msec later. This protocol resulted in a spin echo time of 140 msec. To minimize MR signal loss caused by the effects of radiation damping (30) between the two refocusing rf pulses, the signal was dephased immediately after the first one by using the gradient that was a part of a crushing gradient structure. Each individual signal acquisition occurred over 512 msec with a repetition period of 2 sec. A typical voxel size was 10 ml, and no signal averaging was used. Before volume localized data acquisition an imaging protocol was performed that included global shimming followed by acquisition of anatomical images and positioning of the spectroscopic voxel in the area of visual cortex. If volume-localized MR signal linewidth was more than 6 Hz, additional local shimming was performed.

MR Signal Intensity Evaluation.

We found that the maximal free induction decay signal intensity changes between the stimulated and resting state take place at a time τ elapsed after the spin echo (τ is an analog of gradient echo time in an imaging experiment) of about 70–100 msec and used the intensity difference at τ = 100 msec to characterize the BOLD effect.

We used the following approach to evaluate changes in R2′ relaxation time constant. For the PRESS technique that we use, in a long post-spin-echo time limit (τ = 100 msec), changes in the fMR signal intensity may be evaluated as:

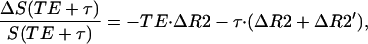9

where TE is a spin echo time (140 msec in our experiment) and R2 is the MR signal relaxation rate constant responsible for the irreversible part of the signal decay. Changes in the MR signal intensity at the spin echo (τ = 0) may be evaluated as

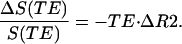10

It is important to note that Eqs. 9 and 10 are valid in the presence of macroscopic field inhomogeneities (25) that may affect MR signal because of imperfections in local shimming but that do not change with functional activation. Because information on MR signal at the spin echo time is also available from our data, Eqs. 9 and 10 allow evaluation of changes in R2 and R2′ relaxation rate constants individually.

MR Signal Frequency Evaluation.

The frequency of the MR signal of water depends on temperature and changes with a coefficient of about −0.01 ppm/°C (21). In vitro studies have demonstrated that this coefficient remains practically independent of tissue type (31) and pH (32). Although a precise relationship between the water proton NMR frequency and temperature for in vivo brain tissue is yet to be established, preliminary data in cell cultures (32) and different biological tissues (31) indicate that this dependence is close to that cited above for pure water. In our experiments, the frequency of the water signal was determined by fitting of the phase of the complex MR signal to a quadratic polynomial: ϕ(τ) = ϕ₀ + 2⋅π⋅ν⋅τ + A⋅τ², with ϕ₀ and ν being signal initial phase and frequency. The parameter A was introduced to account for frequency drift during measurement caused by magnet instability, brain movement caused by patient breathing, and cardiac output. The average R² value of the fit was 0.9999 and an error in the frequency estimate was less than 0.005 Hz. The average linewidth of the water MR signal was on the order of 6 Hz. However, it is well known that this is not the only parameter that defines the accuracy in the estimation of the MR signal frequency. In the case of a single line as we have, according to ref. 33, this accuracy is Δν = (R2*/SNR)⋅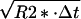, where R2* is the MR signal decay rate constant and Δt is a sampling rate. For our data, this estimate gives accuracy on the order of 0.002 Hz, which is in accord with the above estimate.

To test for possible instrumental errors, in three human experiments we used a double-voxel sequence that allows simultaneous (interleaved) acquisition of data from two voxels. One voxel was positioned in the area of visual cortex and another, control voxel, well outside of this area. In each case, BOLD signal and changes in frequency were observed in the area of visual cortex, whereas no systematic changes in signal intensity and frequency were found in the control voxel. In addition, we conducted studies with the goggles positioned on a water phantom under exactly the same protocol as in humans. No systematic changes in the signal frequency or intensity were found.

Results and Discussion

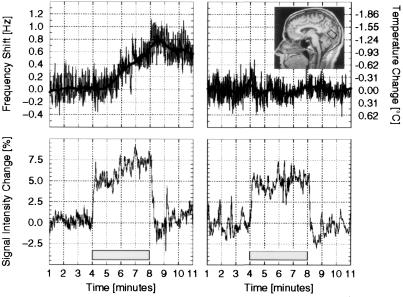
Two examples of time courses of the fMR signal intensity (i.e., BOLD) changes (percent of signal change relative to the average signal before activation onset) each obtained within a single 12-min protocol (original data, no averaging of repeated protocols) are shown in the lower panels of Fig. 1. Corresponding time courses of the signal resonance frequency changes are shown in Fig. 1 Upper. We have found that in all cases the fMR signal intensity (i.e., BOLD contrast) demonstrates a transition phase of about 30 sec after the onset of stimulation (Fig. 1 Lower). During this period the signal sharply increases in the time interval of about 15–20 sec and often goes through a local maximum. After the transition phase the signal enters a “slow phase” characterized by a slow, monotonic, near-linear change during the remainder of the stimulation period (3.5 min). The poststimulus fMR signal intensity shows a complicated behavior with a sharp poststimulus decrease, often with undershoot and a subsequent slow return to an equilibrium intensity, which is sometimes different from the prestimulus baseline. The frequency of the signal does not show any significant sharp changes (Fig. 1 Upper). Rather it exhibits slow monotonic changes.

Figure 1.

Two examples of the data representing the change in resonance frequency of the MR signal (Upper) and the change in the BOLD MR signal (Lower) as observed in human primary visual cortex of a single volunteer during visual stimulation. The equivalent change in local brain temperature is plotted as a bold line and noted on the right-hand axis of Upper. (Inset) Midsagittal MRI image of one subject participating in these studies. The rectangle represents voxel positioned over primary visual cortex with the calcarine sulcus running through the middle, parallel to its long axis. The visual stimulation used in this study predictably produces large increases in blood flow in this region. Shaded area indicates the time when functional stimulation was used.

At 1.5 T, the magnetic field strength used for these experiments, the temperature vs. frequency coefficient is −0.64 Hz/°C. Estimated temperature changes are plotted in Fig. 1 Upper (bold line). Hence, our experimental data suggest that in some instances during functional stimulation the temperature of the region of activated brain tissue changes. For example, in the data set shown in Fig. 1 Left, the temperature decreases during 4 min of stimulation by about 1°C. At the same time, the data set shown in Fig. 1 Right demonstrates relatively little fluctuation in the temperature during the entire functional experiment.

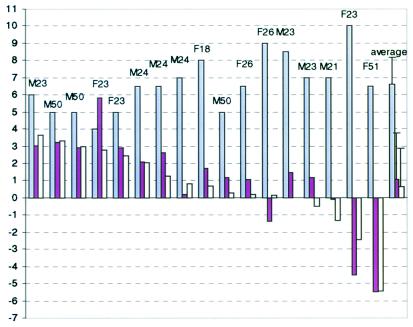
Major characteristics of all 17 data sets are presented in Fig. 2. The most dramatic feature of all data sets is a very strong correlation between the fMR signal intensity changes and the frequency changes during the slow phase of the activation period. These observed correlated changes also support our hypothesis of brain temperature changes during functional activation. Consider for example Fig. 1 Left. Because the rate of chemical reactions depends on tissue temperature, a continuous decrease in the tissue temperature observed in Fig. 1 Upper Left should result in a continuous decrease of the oxygen consumption, hence continuous increase in the venous blood oxygenation level, hence continuous increase in the fMR signal (Eq. 8). This interpretation is remarkably consistent with the result of Fig. 1 Lower Left. At the same time, no systematic changes in the fMR signal frequency (tissue temperature) are seen during the slow phase in Fig. 1 Upper Right. Consistent with our hypothesis, no systematic changes in fMR signal intensity during the slow phase can be observed in Fig. 1 Lower Right.

Figure 2.

Summary of the results obtained from 17 studies. The first 17 blocks of columns represent results of individual studies. The last block is an average over all 17 studies (error bars represent standard deviation). Letters indicate volunteer's gender and age. First (white) column in each block is an initial BOLD signal—percent of signal intensity change between baseline and initial fast phase of the activation period. Second (yellow) column in each block represents a change in the percent of signal intensity change over the slow phase of the activation period. Third (green) column in each block represents signal frequency change (scaled by a factor of 5) over the slow phase of the activation period. Note that initial BOLD signal is always positive. Also note very high correlation [Δ(ΔS/S)(%) = 5.44⋅Δν(Hz), R = 0.9] between changes in the signal intensity and frequency during the slow phase of activation period.

Because blood flow to activated areas increases more than oxygen consumption (6, 14), it follows from the second term in Eq. 3 that the new equilibrium temperature of the activated state will be less than that of the resting state (increased heat removal exceeds increased heat production) if the temperature of inflowing blood remains constant. Given that rOEF during brain stimulation of this type decreases by about 30% (14), this should lead—according to Eq. 3—to a temperature decrease on the order of −0.1°C. An average decrease in the tissue temperature during activation can be estimated from the last column in Fig. 2 and is about −0.2°C. This is a reasonable agreement. However, some individual data sets in Fig. 2 demonstrate substantially larger, up to 1°C, changes in the temperature that can be both negative and positive. According to Eq. 3, such large changes may result only from similar changes in the temperature of incoming blood during functional stimulation. Changes in the temperature of incoming blood are not paradoxical. Indeed, the blood temperature varies significantly throughout the body, especially between superficial and deep-lying tissues (see discussion below). Blood has only several seconds (blood transit time) to equilibrate its temperature with the surrounding tissue, hence even local changes in blood flow accompanying functional activation might substantially affect the local temperature of incoming blood. Increases in the arterial blood temperature on the order of 0.1°C during short amygdala stimulation in the monkey were reported previously (10).

Our finding that brain temperature during functional activation may exhibit either a decrease or an increase is also consistent with previous study in the monkey brain (10). The authors reported that turning off the lights during the day might cause a rise, a fall, or no change in blood and brain temperature. Characteristic transition time scale for these changes was several minutes, which is similar to our results. Different directions in brain temperature changes during visual stimulation were also observed in cat brain (7); however, the functional paradigm was substantially different and the magnitude of the effect was much smaller.

The magnitude and intersubject variability of the temperature effect that we found is also not unexpected. First, considerable temporal temperature variations up to 2°C in the body and brain have been observed by direct temperature measurements in neurosurgical patients (34). Second, substantial brain–body temperature gradients were observed in these patients: on average ventricular temperature was 0.33°C higher than average rectal temperature; however, individual variations as large as 2.3°C were found. Third, a large intracerebral temperature gradient between the epidural and ventricular temperature was also reported in these studies. The largest observed difference was 1°C, whereas the average was 0.47°C. These data are also consistent with the results of the previously noted monkey study (10), where an average intracerebral gradient of 0.5°C was found. Also, studies of the cat brain (9) reported that the blood was on the average 0.34°C cooler than the thalamus, with a maximum difference of 2.3°C.

Since blood flow during visual stimulation is about 0.8 ml⋅g⁻¹⋅min⁻¹ (14), Eq. 6 predicts that the new equilibrium temperature should be approached exponentially with the time constant t_T ≈ 1.2 min. However, because of the strong heat exchange between activated and resting tissue—an effect not included in Eq. 6—the effective time constant may be substantially higher. In fact, almost none of the data sets show evidence of an approach to temperature equilibrium during the 4 min of stimulation. Hence, our data suggest that a substantial role in maintaining tissue temperature belongs to heat transfer within the tissue between the area(s) of high activity and surrounding areas of low activity. For long periods of stimulation, local perturbations in the temperature can trigger temperature changes in remote areas of the brain because of high heat diffusivity and heat transfer with blood flow. Such “heat waves” were previously observed on the brain surface during functional activation in a rat model by infrared mapping (11). It should be noted that fluctuations in the recorded signal frequency seen in Fig. 1 because of the subject breathing, cardiac output, and magnet instabilities do not allow a statistically significant choice between linear and exponential behavior.

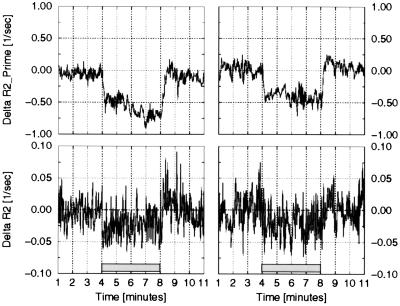
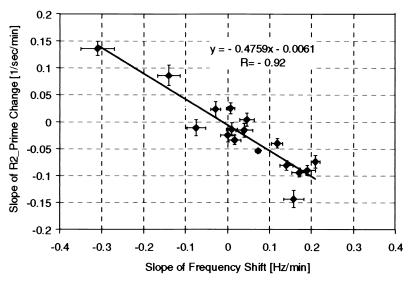
To further quantify the correlation between fMR signal intensity changes and signal frequency (tissue temperature) changes during the slow phase of activation period we evaluate changes in R2 and R2′ relaxation rate constants as described in Methods, Eqs. 9 and 10. Results are shown in Fig. 3 for the same data sets as in Fig. 1. Note that changes in R2 during functional activation may be due to BOLD susceptibility effects and temperature-induced changes in the nuclear diffusivity. While statistically significant, they are order of magnitude smaller than changes in R2′. Fig. 4 is the plot of the slope that characterizes the time changes in R2′ relaxation rate constant vs. the slope that characterizes the time changes of the signal frequency during the slow phase for all 17 data sets. A very high correlation with the R value of 0.92 is seen in these data. The regression analysis gives the following relationship between changes in the R2′ relaxation rate constant and changes in the MR signal frequency during the slow phase of activation period:

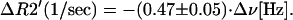11

This equation can be compared with Eq. 8 that we derived theoretically. First, we should note that Eq. 8 was derived under the assumption that blood volume and blood flow remain constant. Because we do not directly control blood volume and blood flow in our experiment, we will use assumptions that are consistent with the results obtained by others. Because changes in the blood volume are naturally attributed to the changes in the blood flow (35), and because increased blood flow remains constant during prolonged activation (6, 36), it is logical to assume that increased blood volume also remains constant during the slow phase of the activation period. By comparing Eq. 11 with Eq. 8, and substituting Q₁₀ = 4.4 from human studies (37), Δχ₀ = 1.08⋅10⁻⁷ for blood with a hematocrit of 40% (26), sO₂ = 0.7 during functional activation (6), and MR frequency temperature coefficient of −0.01⋅10⁻⁶ ppm/°C for pure water (21), we find that apparent venous blood volume, ζ, should be equal to 0.037. If we use Q₁₀ = 3.5 from monkey measurements (38), we estimate ζ as 0.044. Finally, if we use an average value Q₁₀ = 2.3 from animal studies (1), we estimate ζ as 0.066. However, if we adopt an MR frequency vs. temperature coefficient of −0.007⋅10⁻⁶ ppm/°C from the in vivo measurement in a canine brain (39), then all above estimates for ζ should be scaled by a factor of 0.7, which gives 0.026, 0.031, and 0.047, correspondingly. Although we do not have exact measurement of ζ, these estimates can be considered as reasonable, especially given the number of simplifying assumptions made (brain venous volume fraction is typically cited as ≈3–4%).

Figure 3.

Two examples of the changes in the R2 and R2′ relaxation rate constants. Results are shown for the same data sets as in Fig. 1. Note that changes in R2 during functional activation, while statistically significant, are order of magnitude smaller than changes in R2′.

Figure 4.

Plot of the slope that characterizes the time changes in the R2′ relaxation rate constant vs. the slope that characterizes the time changes of the signal frequency during the slow phase of activation period for all 17 data sets. Error bars represent the accuracy of the linear regression. A very high correlation with the R value of 0.92 is seen in these data. Because changes in the R2′ relaxation rate constant are proportional to the changes in the amount of deoxyhemoglobin and changes in the fMR signal frequency are proportional to the changes in the tissue temperature, the correlation suggests that changes in the brain temperature during functional activation are accompanied by correlated changes in the activated tissue metabolic rate.

Possible Ramifications.

Our findings might also shed a new light on such well known but previously unexplained effects in fMRI as a signal intensity baseline drift and variations in poststimulus undershoot and poststimulus baseline. All these effects are seen in our data and could be explained by variations in the brain temperature and consequent variations in oxygen consumption during local changes in brain functional activity and resting state. Even such intriguing observation as the often discussed fMRI signal intensity decreases at the onset of stimulation (40) could be, at least partially, attributed to these changes. Indeed, while changes in the brain temperature are very slow, the change in the temperature of incoming arterial blood occurs synchronously with the change in blood flow. Because of the blood frequency shift of −0.01 ppm/°C, the arterial blood signal will be slightly out of phase with the tissue signal. If feeding arteries occupy a substantial part of an imaging voxel, this relative dephasing will result in an fMRI signal intensity decrease. However, this effect will be substantially masked by a much bigger positive BOLD effect as soon as the oxygenation level of draining veins in this voxel increases.

Other Possible Sources of MR Signal Frequency Change.

In addition to temperature changes, two other sources may contribute to the signal frequency changes during functional brain activation. (i) Blood susceptibility changes may, in principle, also affect signal frequency. If this would be the case, the time course of the BOLD signal would be the same as the time course of the signal frequency changes. It follows from our experimental data that this is not the case. (Note: the crushing gradients present in our double spin echo PRESS sequence around 180° rf pulses effectively suppress (dephase) most of the signal directly arising from moving blood except the capillary blood.) (ii) Oxygen molecules are paramagnetic and may change tissue susceptibility, Δχ, which in turn affects signal frequency: Δν/ν ≈ π⋅Δχ. A typical maximum tissue partial oxygen pressure on the order of 40 mmHg results in 1 g of water containing 0.0013 ml of O₂. We can estimate, using the Curie law, that at 37°C the contribution of this oxygen to the water susceptibility is Δχ = 1.8⋅10⁻¹⁰. At 1.5 T this would create a frequency shift of 0.04 Hz. This number is substantially smaller than frequency changes observed in our experiments.

Conclusion.

We have offered evidence with MR that synchronous changes in tissue temperature and tissue oxygen metabolism take place during local changes in the functional activity of the normal human brain. A better understanding of these phenomena should enrich our understanding of brain function and the techniques to study it, such as fMR. Further studies are also required to answer important questions regarding the influence of these phenomena on brain cognitive performance and possible effects on numerous neurological disorders.

Finally, we note that although the experimental results presented above are supportive of our theoretical development concerning the interplay of metabolic rate, blood flow, temperature, and rOEF—the latter two quantities reflected in the water resonance frequency and BOLD signal—we have not provided confirmation by independent temperature measurement nor have we developed an activation protocol that modulates brain temperature in a predictable manner. Future human and animal studies can be envisaged that would provide a definitive assessment of the concepts explored herein.

Abbreviations

rCMRO₂

regional cerebral metabolic rate of oxygen

rCBF

regional cerebral blood flow

rOEF

regional oxygen extraction fraction

MR

magnetic resonance

fMR

functional MR

MRI

MR imaging

fMRI

functional MRI

BOLD

blood oxygenation level-dependent