Antibody-Directed Effector Cell Therapy of Tumors: Analysis and Optimization Using a Physiologically Based Pharmacokinetic Model

Abstract

The failure of the cellular immune response to stop solid tumor growth has been the subject of much research. Although the mechanisms for tumor evasion of immune response are poorly understood, one viable explanation is that tumor-killing lymphocytes cannot reach the tumor cells in sufficient quantity to keep the tumor in check. Recently, the use of bifunctional antibodies (BFAs) has been proposed as a way to direct immune cells to the tumor: one arm of the antibody is specific for a known tumor-associated antigen and the other for a lymphocyte marker such as CD3. Injecting this BFA should presumably result in cross-linking of lymphocytes (either endogenous or adoptively transferred) with tumor cells, thereby enhancing therapy. Results from such an approach, however, are often disappointing — frequently there is no benefit gained by using the BFA. We have analyzed the retargeting of endogenous effector cells by BFA using a physiologically based whole-body pharmacokinetic model that accounts for interactions between all relevant species in the various organs and tumor. Our results suggest that the design of the BFA is critical and the binding constants of the antigen and lymphocyte binding epitopes need to be optimized for successful therapy.

Introduction

Adoptive effector cell therapy relies on the delivery of lymphokine-activated and expanded effector cells or specific tumor-infiltrating lymphocytes and activated natural killer cells. Administration of interleukin-2-activated effector cells has been shown to create significant clinical toxicity [1,2], and the isolation of specific lymphocytes that target tumor tissues is difficult and only possible when antigens have been isolated from the specific tumor cell line. For clinical application, an ideal immunotherapy would direct the body's endogenous effector cells to a tumor and only activates the effector cells in the presence of tumor antigens. Such therapies are being explored using bifunctional antibodies (BFAs) that have specificity for both a tumor antigen and the T-cell receptor-CD3 complex on T cells [3–14]. These BFAs have been engineered with the expectation that they will induce the T-cell repertoire to generate lytic and inflammatory responses at the tumor site. F(ab′)₂ BFAs, which lack functional Fc portions, have been shown to induce lymphocyte proliferation only in the presence of tumor cells and produce no in vivo systemic activation [8,15]. The availability of many antitumor antibodies, including several that demonstrate broad antitumor reactivity against a variety of human adenocarcinoma cell lines, and the ability of F(ab′)₂ antibodies to penetrate tumors more efficiently than full-size antibodies has generated considerable interest in this form of therapy [3–5,10].

The application of retargeting endogenous effector cells using BFAs will require the optimization of several BFA properties and treatment conditions. The systematic evaluation of the effects of changing these variables is perfectly suited to analysis using a physiologically based pharmacokinetic model. Such a model can be used to study BFA and lymphocyte biodistribution by examining the significance of transport mechanisms and BFA properties with respect to the localization of effector cells at a tumor site. The results from these modeling studies can be used to more effectively guide preclinical experiments and bridge the gap between the optimal preclinical conditions and therapy in humans.

The objective of the research presented in this paper is to develop a pharmacokinetic model that can be used in the design of BFA-directed effector cell therapies. Two previously developed models that were used to individually study the distribution of antibodies [16] and effector cells [17,18] form the basis for this work. Both models are physiologically based, using measurable physiological parameters such as organ volumes and blood flow rates and incorporating the mechanism-based transport processes that determine how antibodies and effector cells distribute in the body.

Data collected by Bakacs et al. [19] was used to estimate unknown parameters for use in the model in the absence of experimental values for these parameters. Bakacs et al. followed the biodistribution of a BFA after IV administration in a syngeneic mammary adenocarcinoma BALB/c mouse model. A lung metastasis model and a subcutaneous solid tumor model were considered. In the former, 64PT cells were IV injected into the tail vein of BALB/c mice. BFA treatment was found to prolong the survival of these mice. In contrast, the BFA was unable to prolong the survival of mice with subcutaneous 64PT tumor grafts. A biodistribution study showed that the BFA was accumulating preferentially in the spleen and lymph nodes, as it was designed to bind to the T cells abundant in these tissues, rather than in the subcutaneous tumor. The authors suggested that poor vascularity or physiological barriers presented by the solid tumors may have prevented the BFA and T cells from infiltrating the tumor. Smaller tumors, such as those in the lung metastases model, may not present such barriers. Our research focuses on the poor homing of BFA to solid tumors. Our model supports the observations of Bakacs et al. and further examines how the interplay between BFA, lymphocytes, and tumor antigen may be exploited to optimize antibody-mediated adoptive immunotherapy.

Methods

Model Development

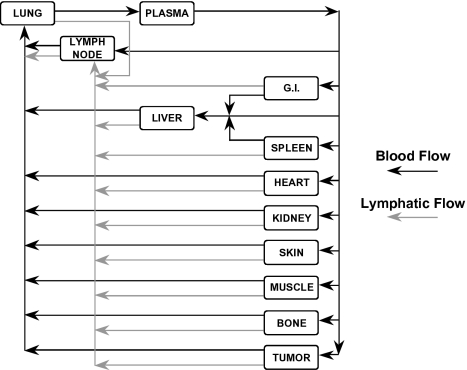
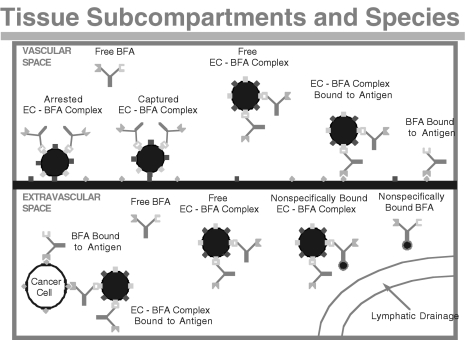
The model we developed to study BFA distribution and retargeting of lymphocytes is based on two previously developed models. A whole-body physiologically based model is used in which the major organs of the body are represented as compartments that are connected in an anatomical manner by the systemic and lymphatic circulation (Figure 1). The organ compartments are then further subdivided into vascular and extravascular subcompartments. The detailed description of the antibody and effector cell transport processes is adapted from previous models [18,20,21]. Briefly, the main transport processes in the antibody model include: convective and diffusive transport across capillary walls; reversible, nonsaturable, nonspecific binding in the extravascular compartments; reversible, saturable, specific binding to tumor antigens; and elimination through the kidneys. The main transport processes in the effector cell model include: capture and arrest at the endothelial wall through cell adhesion molecules; extravasation of arrested lymphocytes into the extravascular compartment; and depletion of cells through either a catabolic process or apoptosis. In addition to these processes, the model developed in the present study accounts for saturable binding between BFAs and lymphocytes and the normal production of endogenous lymphocytes. Functional, immunohistochemical, and morphologic studies indicate that the vascular endothelium of tumor vessels may be partially composed of tumor cells exposed to the blood flow [22–24]. Therefore, the model also accounts for binding of BFA and BFA-lymphocyte complexes to antigens in the vascular space of the tumor compartment. Figure 2 shows a schematic of the two subcompartments of the tumor compartment and the associated BFA, lymphocyte, and BFA-lymphocyte complex species. The model nomenclature is given in Appendix A and the mass balance and other model equations can be found in Appendices B and C, respectively.

Figure 1.

Whole-body pharmacokinetic model. All the major organs are included in the model, and the various compartments are interconnected by the blood (black arrows) and lymphatic (gray arrows) systems.

Figure 2.

The various species considered in the model. Effector cells (large circles) can be bound to BFA (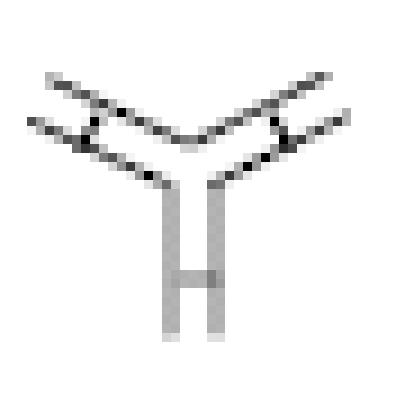), which can bind to tumor antigen (green diamonds) or CD3 (blue squares). Antibody can also bind nonspecifically in the interstitial space (small circles).

Model Parameters

To facilitate comparison between model predictions and the experimental data collected by Bakacs et al. [19], the physiological parameters for mice were used in the simulations (see Appendix A). The plasma flow rates for the tumor, muscle, and skin were determined experimentally; other plasma flow rates were obtained from the literature [25]. Lymphatic flow rates and interstitial fluid recirculation rates (J_R,i) were determined by fitting model predictions to experimental data [21]. Total organ volumes were determined experimentally by weighing each organ and assuming a density of 1 g ml^-1 except for the bone where a density of 1.5 g ml^-1 was assumed. Vascular and interstitial volumes of organs were calculated as percentages of total organ volume as given in the literature [21,26,27]. These physiological parameters are summarized in Appendix A.1.

The BFA osmotic reflection coefficients (σ_S, σ_L) for small and large pores have been determined previously to be 0.96 and 0.11, respectively [21] and the BFA permeability-surface area products (PS_S, PS_L) have been determined to have values of 2.3x10^-5 and 7.9x10^-6 ml min^-1 g^-1, respectively [21]. The binding affinity of the BFA to antigen has been determined by Bakacs et al. [19] to be 3.0x10⁶ M^-1. The reverse binding rate constant of BFA to antigen has been determined to be approximately 1.0x10^-2 min^-1 [21], which results in a forward binding constant of 3.0x10⁷ ml mol^-1 min^-1. The binding affinity of BFA to CD3 molecules on lymphocytes was determined by Bakacs et al. [19] to have a value of 1.0x10⁷ M^-1. The reverse binding rate constant of BFA to CD3 is not known; therefore, as an initial estimate, the value for the reverse binding rate constant between BFA and antigen was used (1.0x10^-2 min^-1), which resulted in a forward binding constant of 1.0X10⁸ ml mol^-1 min^-1. The density of CD3 molecules on lymphocytes was estimated to be 7.5X10⁴ molecules per cell, and a tumor antigen density of 1.2x10^-11 mol ml^-1 was used as reported in the literature [28]. Nonspecific binding of the BFA in the extravascular space was assumed to be negligible due to the absence of an Fc domain that normally accounts for the majority of nonspecific binding. The final parameter related to BFA distribution is the rate of elimination in the kidneys; this parameter was determined by fitting the model to the experimental data.

The extravasation of lymphocytes from the vascular to the extravascular space of organs requires (i) contact and adhesion of the lymphocytes with the endothelial walls (cell capture), (ii) stable adhesion (cell spreading), and (iii) extravasation into the interstitium. The relevant model parameters are the density of endothelial adhesion sites in each organ, the binding affinity between the lymphocytes and adhesion sites, and the migration rate of a bound lymphocyte across the endothelium.

The transcapillary migration rate used in the simulations was 2.9x10^-4 min^-1 as estimated previously [17]. The rate of capture, release, and arrest is expected to vary between organs. Zhu et al. [17] achieved varying rates by fixing the adhesion site density in each organ and calculating a varying capture and arrest rate constant for each organ by fitting model predictions to experimental data. In the simulations for this study the capture, release, and arrest rate constants were assumed to be equal in all organs with values of 9.0x10¹⁷ ml mol^-1 min^-1, 200 min^-1, and 1x10^-3 min^-1, respectively, which are the average values determined by Zhu et al. for nonactivated T cells [17]. This assumption was made as a first approximation due to a lack of experimental organ specific values. However, this is a reasonable assumption because capture and arrest rates are expected to vary between organs primarily because of differences in adhesion site densities, not differences in the rate constants. Adhesion site densities were allowed to vary between organs and were estimated by fitting model predictions to experimental data.

The rate of lymphocyte recirculation in the extravascular space through the lymphatic circulation was previously determined by Zhu et al. [17] to have values of 0.018, 0.01, and 1.0 for the lymph node, tumor, and all other tissues, respectively.

The lymphocyte depletion rate constant was set at 4.2x10^-3 min^-1 in the lungs and zero in other tissues as determined by Zhu et al. [17]. The rate of lymphocyte generation in the body was determined by fitting the modelcalculated steady-state concentration of lymphocytes in the plasma to the known concentration in mice, 9.0x10^-18 mol ml^-1 [29]. Appendix A.2 summarizes the kinetic parameters used in the model simulations.

Model Simulations

A FORTRAN program that incorporated the ordinary differential equation solver LSODE was written to perform the simulations. The differential equations that describe the mass balance of each species in each tissue and subcompartment are given in Appendix B.

As mentioned previously, the unknown parameters that were estimated by fitting experimental data were the elimination rate of BFA in the kidneys, the normal rate of generation of lymphocytes needed to maintain a constant level in the body, and the density of adhesion sites on the vascular endothelium in different organs. Data collected by Bakacs et al. [19] was used in the parameter-estimation process. Bakacs et al. studied the distribution of BFA in BALB/c mice bearing subcutaneous tumors. Mice were given subcutaneous injections of 64PT cells, which express high levels of MMTV gp52 envelope glycoprotein, 6 days before BFA treatments. Radiolabeled BFA, with specificity for gp52 and CD3, was given through tail vein injection, and organ radioactivity was measured at various times after injection to determine the BFA biodistribution. This data was used in the estimation of the vascular adhesion site densities and the elimination rate of BFA in the kidneys.

The first step in the model simulations was to determine the generation rate of lymphocytes required to maintain the known normal steady-state concentration of lymphocytes in the blood in the absence of BFA. This was accomplished by setting the adhesion site density in each tissue to an estimated initial value and then determining the generation rate of lymphocytes required to maintain the correct concentration of lymphocytes in the blood. The second step in the simulations was to fit the organ concentrations of BFA (as determined by Bakacs et al.). Because BFAs are able to bind to lymphocytes, the concentration of BFA in the tissues is in part regulated by the concentration of lymphocytes in each tissue, which is in turn controlled by the adhesion site density in the vascular space of the tissue. Therefore, the BFA concentrations calculated by the model were fit to the experimental data of Bakacs et al. by varying the adhesion site density in each tissue in addition to the elimination rate of BFA in the kidneys. The fitted values of adhesion site density were then substituted for the initial values used in the first step to calculate steady-state levels of lymphocytes, and a new lymphocyte-generation rate was calculated. This two-step fitting process was repeated until the model produced good fits using the same parameter values in both fitting steps.

Nonlinear regression fitting routines were used to fit the experimental data. Two different routines were used, and the resulting parameters were compared as a check of consistency. The two routines produced parameter values with the same order of magnitude. In addition, the estimated parameters resulting from the two different routines varied by less than 15%, and the majority of the parameters varied by less than 5%. These slight differences can be attributed to differences in the convergence algorithm.

After determining the model parameters that gave the best fit to the experimental data, we performed a sensitivity analysis. Each parameter of the model was varied and the percent change in exposure (area under the curve [AUC]) to lymphocytes in the plasma, tumor, and lung was determined.

Results

Lymphocyte Distribution

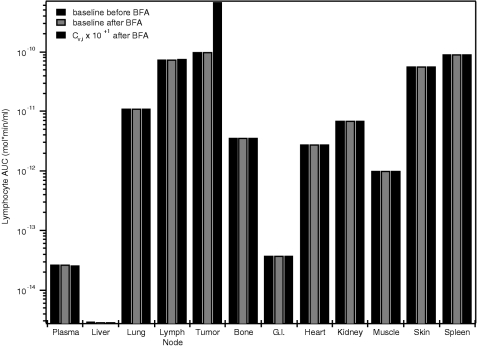
We first analyzed the lymphocyte distributions before and after administration of the BFA using the baseline parameters given in Appendices A.1–3. The lymphocyte profiles at 48 hours after injection of BFA were also analyzed for the cases where the model parameters were varied from the baseline values. AUC values for the lymphocyte profiles were calculated for each organ as a measure of the cumulative exposure of the tissue to lymphocytes after 48 hours. Figure 3 shows the predicted lymphocyte AUC values for the baseline case before and after administration of the BFA (black and dark gray bars, respectively) and for the case where C_V,i in the tumor was increased by one order of magnitude (light gray bars). The AUC values are based on organ concentrations that include the lymphocytes in the vascular and interstitial space of the organ as well as those captured or arrested at the vascular endothelium. In general, the highest level of exposure to lymphocytes is observed in the tumor, followed by the spleen, lymph node, and skin. The lowest concentrations are in the liver.

Figure 3.

BFA does not alter the effector cell distribution. Black bars represent the steady-state effector cell AUC in the various organs before BFA injection. The dark gray bars are the predicted AUC values after BFA administration. The parameters associated with these runs are shown in Appendices A.1–3. In each organ, lymphocyte concentrations varied by less than 1% after injection, indicating that the BFA is not effective in directing the effector cells to the tumor under these conditions. The light gray bars show the effect of increasing the capture site density in the tumor (CV,_tumor) by one order of magnitude on the AUC. Adjusting this parameter has a significant effect on the level of lymphocyte exposure in the tumor.

BFA Kinetics

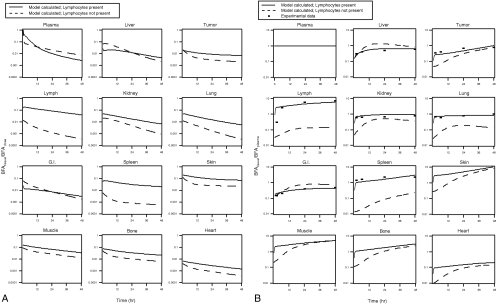
The model predicts a lack of effector cell homing to the tumor in the baseline case. The model-calculated levels of BFA in mice are shown in Figure 4, A and B. In each panel the solid line represents the best-fit level of BFA in each tissue when lymphocytes are present, and the dotted line represents the BFA levels in each organ using the same model parameters but without BFA binding to lymphocytes (lymphocytes are not present). The plots in Figure 4A show the amount of BFA in each tissue normalized with respect to the total dose of BFA. Figure 4B shows the same data except with the amount of BFA in each tissue normalized to plasma BFA levels. As a result, the trends in Figure 4B indicate the rate of elimination from each organ relative to plasma; increasing values (positive slope) indicate that BFA is accumulating in the tissue relative to plasma, and decreasing values indicate that the BFA is being eliminated from the tissue at a higher rate than from the plasma. Also shown in Figure 4B is the experimental data of Bakacs et al., which compares reasonably well with the modelcalculated data. The model parameters estimated by fitting the model predictions to experimental data are shown in Appendix A.3.

Figure 4.

BFA kinetics are determined by the lymphocyte distribution. (A) BFA clearance curves normalized to injected dose for the various organs. Solid lines represent the case where lymphocytes are present, and the dotted lines are runs without lymphocytes. Note that the presence of lymphocytes affects the pharmacokinetics of the BFA, especially in lymphocyte-rich tissue. (B) BFA clearance curves normalized to the plasma levels. Although there appears to be some relative accumulation in the tumor, the endogenous trafficking of the lymphocytes still dominates the system.

Sensitivity Analysis

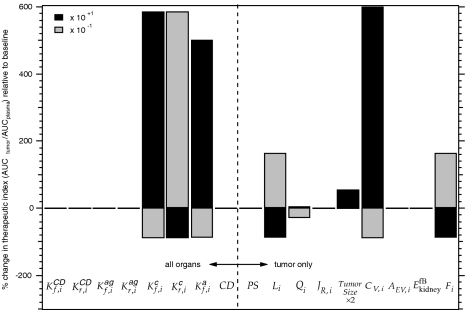
A sensitivity analysis was performed to assess the effect of each parameter on the model solution. The information obtained from this analysis is important in determining the effect of unknown or estimated parameter values on the results and in predicting how the system responds to variations from the baseline case, which can be useful in optimizing the treatment design. Figure 5 shows the sensitivity of the therapeutic index (TI) to the model parameters. The TI is defined as AUC_tumor/AUC_plasma where the AUC represents the cumulative exposure to lymphocytes after 48 hours. The sensitivity of TI to changes in the model parameters was calculated as a percent change from the baseline case. The effects of increasing and decreasing each parameter by an order of magnitude are shown in Figure 5 as dark and light bars, respectively. Positive values signify an increase in TI as a result of the parameter change, and negative values indicate a decrease. The TI is the most sensitive to the adhesion site density in the tumor vasculature (C_V,i) followed by the association and dissociation rate constants for the capture of the effector cell-BFA complex ($K_{\text{f},i}^c$ and $K_{\text{r},i}^c$) and the association rate constant for the arrest of the complex ($K_{\text{f},i}^c$).

Figure 5.

Sensitivity of the therapeutic index (TI) to selected model parameters. Values represent the percent change compared to the baseline values for $K_{f,i}^{CD}$ (association constant for binding between BFA and CD3); $K_{r,i}^{CD}$ (dissociation constant for binding between BFA and CD3); $K_{f,i}^{ag}$ (association constant for binding between BFA and antigen); $K_{r,i}^{ag}$ (dissociation constant for binding between BFA and antigen); $K_{f,i}^c$ (association constant for capture of EC-BFA complex); $K_{r,i}^c$ (dissociation constant for capture of EC-BFA complex); $K_{f,i}^a$ (rate constant for arrest of EC-BFA complex); CD (number of CD binding sites per cell); PS (permeability-surface area product); L_i (lymph flow out of tumor); Q_i (blood flow into tumor); J_R,i (fluid recirculation flow rate of tumor). Tumor size; C_V,i (density of capture sites in the vascular space of tumor); A_EV,i (density of antigen binding sites in the extravascular space of tumor); $E_{kidney}^{fB}$ (elimination rate constant for free BFA in kidney); F_i (fraction of EC-BFA complex in extravascular space of tumor that recirculates). Dark and light bars correspond to an order of magnitude increase or decrease in the parameter, respectively. The left-hand panel shows parameters that affect all organs; those on the right are specific to the tumor, except for $E_{kidney}^{fB}$.

Discussion

The predictions of the model clearly show that physiological conditions must be carefully considered for successful BFA-directed effector cell therapy. Figure 3 indicates that rather than guiding the T cells to the target tissue, the BFA is being dragged around the system by the cells. Lymphocyte concentrations in each organ varied by less than 1% after injection of BFA, indicating that the BFA is not effective in redirecting the effector cells under these conditions. Figure 4A shows the specificity of the localization of the BFA, as all data are relative to plasma levels. Note that compartments with higher baseline concentrations of lymphocytes (e.g., lymph and spleen) show the largest differences between runs with and without effector cell-BFA binding. The normalized BFA levels in these compartments are significantly higher with effector cell- BFA binding, suggesting that the effector cells are changing the distribution of the BFA, not vice versa, as was originally hoped.

It is also important to consider the nonnormalized data in Figure 4B because, in the absence of toxic side effects, it is the absolute area under these curves that determine therapeutic benefit. Even larger differences are apparent here between the runs with and without BFA-effector cell binding, and the differences are again largest in compartments rich in lymphocytes.

Figure 5 shows the sensitivity of the TI (TI=AUC_tumor/AUC_plasma) to changes in various model parameters. The sensitivity analysis indicates that the greatest positive impact on the effectiveness of therapy is achieved by increasing the number of adhesion sites available for lymphocyte capture in the tumor. Varying the rate constants for lymphocyte capture and arrest also have a significant effect on the TI. This implies that selectively modifying the tumor vasculature by increasing (C_V,i) or by changing the rate constants in favor of capture and arrest will have a favorable effect on the therapy. Figure 3 shows that increasing C_V,i by one order of magnitude in the tumor is capable of increasing the effector cells AUC in the tumor by more than six times the baseline case. Though these parameters have the greatest impact on the TI, they may be difficult to manipulate. Some consideration, therefore, should be given to other parameters that may be easier to control. For example, Figure 5 shows that the TI is also sensitive to the tumor lymph flow rate. Decreasing this flow rate encourages the accumulation of effector cells in the tumor; therefore, this parameter should also be considered in the optimization of this therapy approach.

Figure 5 also shows that the TI is relatively insensitive to changes in the BFA. Varying BFA binding to CD3 and to tumor antigens appear to have little effect on the TI. This implies that under the model conditions, BFA is not able to home effector cells to the tumor. Changing the BFA binding parameters by one order of magnitude is not sufficient to significantly alter lymphocyte accumulation in the tumor, and more drastic changes are necessary for successful BFAdirected effector cell therapy.

1. Concentrations
$C_{\text{V},i}^{\text{fB}}$	free BFA in vascular space of compartment i (mol cm-3)
$C_{\text{EV},i}^{\text{fB}}$	free BFA in extravascular space of compartment i (mol cm-3)
$C_{\text{V},i}^{\text{bB}}$	BFA bound to effector cell (EC) in vascular space of compartment i (mol cm-3)
$C_{\text{EV},i}^{\text{bB}}$	BFA bound to EC extravascular space of compartment i (mol cm-3)
$C_{\text{V},i}^{\text{EB}}$	EC-BFA complex in vascular space of compartment i (mol cm-3)
$C_{\text{EV},i}^{\text{EB}}$	EC-BFA complex in extravascular space of compartment i (mol cm-3)
$C_{\text{V},i}^{\text{agB}}$	BFA bound to antigen in vascular space of compartment i (mol cm-3)
$C_{\text{EV},i}^{\text{agB}}$	BFA bound to antigen in extravascular space of compartment i (mol cm-3)
$C_{\text{V},i}^{\text{cEB}}$	captured EC-BFA complex in vascular space of compartment i (mol cm-3)
$C_{\text{V},i}^{\text{aEB}}$	arrested EC-BFA complex in vascular space of compartment i (mol cm-3)
$C_{\text{V},i}^{\text{agEB}}$	EC-BFA complex bound to antigen in vascular space of compartment i (mol cm-3)
$C_{\text{EV},i}^{\text{agEB}}$	lymphocyte-BFA complex bound to antigen in extravascular space of compartment i (mol cm-3)
$C_{\text{EV},i}^{\text{nB}}$	nonspecifically bound BFA in vascular space of compartment i (mol cm-3)
$C_{\text{EV},i}^{\text{nEB}}$	nonspecifically bound EC-BFA complex in extravascular space of compartment i (mol cm-3)
$C_{\text{V},i}^{\text{total}}$	total concentration of cells in vascular space of compartment i (mol cm-3)
$C_{\text{EV},i}^{\text{total}}$	total concentration of cells in extravascular space of compartment i (mol cm-3)
2. Kinetic Parameters
$K_{f,i}^{\text{CD}}$	association constant for binding between BFA and CD3 on EC in compartment i (cm3 mol-1 min-1)
$K_{r,i}^{\text{CD}}$	dissociation constant for binding between BFA and CD3 on EC in compartment i (min-1)
$K_{f,i}^{\text{ag}}$	association constant for binding between BFA and antigen in compartment i (cm3 mol-1 min-1)
$K_{r,i}^{\text{ag}}$	dissociation constant for binding between BFA and antigen in compartment i (min-1)
$K_{f,i}^{\text{c}}$	association constant for capture of EC-BFA complex in compartment i (cm3 mol-1 min-1)
$K_{r,i}^{\text{c}}$	dissociation constant for capture of EC-BFA complex in compartment i (min-1)
$K_{f,i}^{\text{a}}$	rate constant for arrest of EC-BFA complex in compartment i (min-1)
$K_{f,i}^{\text{n}}$	association constant for nonspecific binding of BFA in compartment i (min-1)
$K_{r,i}^{\text{n}}$	dissociation constant for nonspecific binding of BFA in compartment i (min-1)
$E_{kidney}^{\text{}\text{fB}}$	elimination rate constant for free BFA in kidney (cm3 min-1)
$E_i^{\text{cE}\text{}\text{B}}$	elimination rate constant for captured EC-BFA complex in compartment i (min-1)
$E_i^{\text{}\text{aEB}}$	elimination rate constant for arrested EC-BFA complex in compartment i (min-1)
$J_i^{\text{}\text{aEB}}$	transmigration rate constant for arrested EC-BFA complex in compartment i (min-1)
$J_i^{\text{}\text{fB}}$	transcapillary exchange rate of free BFA in compartment i (mol min-1)
JS,i	transcapillary fluid flow rate through small pores in compartment i (cm3 min-1)
JL,i	transcapillary fluid flow rate through large pores in compartment i (cm3 min-1)
JR,i	fluid recirculation flow rate of compartment i (cm3 min-1)
P	baseline production rate of EC in plasma (mol min-1)
3. Flow Rates
Qi	blood flow into compartment i (cm3 min-1)
Li	lymph flow out of compartment i (cm3 min-1)
Qhepatic	blood flow into liver before the addition of blood flow from GI and spleen (cm3 min-1)
4. Volumes
VV,i	vascular volume of compartment i (cm3)
VEV,i	extravascular volume of compartment i (cm3)
5. Other Parameters
Fi	fraction of EC-BFA complex in extravascular space of compartment i that recirculates
CD	number of CD binding sites per cell (mol mol-1)
AV,i	density of antigen binding sites in the vascular space of compartment i (mol cm-3)
AEV,i	density of antigen binding sites in the extravascular space of compartment i (mol cm-3)
CV,i	density of capture sites in the vascular space of compartment i (mol cm-3)
fCDV,i	density of free CD3 sites in the vascular space of compartment i (mol cm-3)
fCDEV,i	density of free CD3 sites in the extravascular space of compartment i (mol cm-3)
oCDV,i	density of occupied CD3 sites in the vascular space of compartment i (mol cm-3)
oCDEV,i	density of occupied CD3 sites in the extravascular space of compartment i (mol cm-3)
fCV,i	density of free capture sites in the vascular space of compartment i (mol cm-3)
fAV,i	density of free antigen sites in the vascular space of compartment i (mol cm-3)
fAEV,i	density of free antigen sites in the extravascular space of compartment i (mol cm-3)
PeS,i	Peclèt number for flow through small pores in compartment i
PeL,i	Peclèt number for flow through large pores in compartment i
ki	partition coefficient for free BFA between vascular and extra vascular space in compartment i
PS	permeability-surface area product (cm3 min-1 g-1)

Appendix B

Mass Balance Equations

• Plasma

  • Free BFA

    $$\begin{array}{l}{V}_{\text{v},\text{plasma}}\frac{d{C}_{\text{V,plasma}}^{\text{fB}}}{dt}=\left(Q_{\text{lung}}-L_{\text{lung}}\right)C_{\text{V,lung}}^{\text{fB}}\\ -\left(\begin{array}{l}{Q}_{\text{hepatic}}+Q_{\text{lnode}}+Q_{\text{tumor}}+Q_{\text{bone}}+Q_{\text{GI}}\\ +Q_{\text{heart}}+Q_{\text{kidney}}+Q_{\text{muscle}}+Q_{\text{skin}}+Q_{\text{spleen}}\end{array}\right)C_{\text{V,plasma}}^{\text{fB}}\\ -K_{f,\text{plasma}}^{\text{CD}}{C}_{\text{V},\text{plasma}}^{\text{fB}}fC{D}_{\text{V,plasma}}{V}_{\text{V,plasma}}\\ +K_{r,\text{plasma}}^{\text{CD}}{C}_{\text{V,plasma}}^{\text{bB}}{V}_{\text{V,plasma}}\end{array}$$

  • Free BFA-effector cell complex

    $$\begin{array}{l}{V}_{\text{v},\text{plasma}}\frac{d{C}_{\text{V,plasma}}^{\text{EB}}}{dt}=\left(Q_{\text{lung}}-L_{\text{lung}}\right)C_{\text{V,lung}}^{\text{EB}}\\ -\left(\begin{array}{l}{Q}_{\text{hepatic}}+Q_{\text{lnode}}+Q_{\text{tumor}}+Q_{\text{bone}}+Q_{\text{GI}}\\ +Q_{\text{heart}}+Q_{\text{kidney}}+Q_{\text{muscle}}+Q_{\text{skin}}+Q_{\text{spleen}}\end{array}\right)C_{\text{V,plasma}}^{\text{EB}}\\ +P\end{array}$$

  • BFA bound to effector cells

    $$\begin{array}{l}{V}_{\text{v},\text{plasma}}\frac{d{C}_{\text{V,plasma}}^{\text{bB}}}{dt}=\left(Q_{\text{lung}}-L_{\text{lung}}\right)C_{\text{V,lung}}^{\text{EB}}{C}_{\text{V,lung}}^{\text{bB}}/C_{\text{V,lung}}^{\text{total}}\\ -\left(\begin{array}{l}{Q}_{\text{hepatic}}+Q_{\text{lnode}}+Q_{\text{tumor}}+Q_{\text{bone}}+Q_{\text{GI}}\\ +Q_{\text{heart}}+Q_{\text{kidney}}+Q_{\text{muscle}}+Q_{\text{skin}}+Q_{\text{spleen}}\end{array}\right)C_{\text{V,plasma}}^{\text{bB}}\\ +K_{f,\text{plasma}}^{\text{CD}}{C}_{\text{V,plasma}}^{\text{fB}}fC{D}_{\text{V,plasma}}{V}_{\text{V,plasma}}\\ -K_{r,\text{plasma}}^{\text{CD}}{C}_{\text{V,plasma}}^{\text{bB}}{V}_{\text{V,plasma}}\end{array}$$

• Liver

  • Free BFA in vascular space

    $$\begin{array}{cc}\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}{V}_{\text{V,liver}}\frac{d{C}_{\text{V,liver}}^{\text{fB}}}{dt}=\\ \end{array}\\ \end{array}\\ \end{array}\\ \begin{array}{c}\begin{array}{c}\\ \end{array}\\ \end{array}\end{array}& \begin{array}{l}{Q}_{\text{hepatic}}{C}_{\text{V,plasma}}^{\text{fB}}\\ +(Q_{\text{spleen}}-L_{\text{spleen}})C_{\text{V,spleen}}^{\text{fB}}\\ +(Q_{\text{GI}}-L_{\text{GI}})C_{\text{V,GI}}^{\text{fB}}\\ -(Q_{\text{liver}}-L_{\text{liver}})C_{\text{V,liver}}^{\text{fB}}\\ -J_{\text{liver}}^{\text{fB}}\\ -K_{f\text{,liver}}^{\text{CB}}{C}_{\text{V,liver}}^{\text{fB}}fC{D}_{\text{V,liver}}{V}_{\text{V,liver}}\\ +K_{r,\text{liver}}^{\text{CD}}{C}_{\text{V},\text{liver}}^{\text{bB}}{V}_{\text{V},\text{liver}}\end{array}\end{array}$$

  • Free EC-BFA complex in vascular space

    $$\begin{array}{cc}\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}{V}_{\text{V,liver}}\frac{d{C}_{\text{V,liver}}^{\text{EB}}}{dt}=\\ \end{array}\\ \end{array}\\ \end{array}\\ \begin{array}{c}\begin{array}{c}\\ \end{array}\\ \end{array}\end{array}& \begin{array}{l}{Q}_{\text{hepatic}}{C}_{\text{V,plasma}}^{\text{EB}}\\ +(Q_{\text{spleen}}-L_{\text{spleen}})C_{\text{V,spleen}}^{\text{EB}}\\ +(Q_{\text{GI}}-L_{\text{GI}})C_{\text{V,GI}}^{\text{EB}}\\ -(Q_{\text{liver}}-L_{\text{liver}})C_{\text{V,liver}}^{\text{EB}}\\ -K_{f\text{,liver}}^{\text{c}}{C}_{\text{V,liver}}^{\text{EB}}f{C}_{\text{V,liver}}^{\text{fB}}{V}_{\text{V,liver}}\\ +K_{r,\text{liver}}^{\text{c}}{C}_{\text{V},\text{liver}}^{\text{cEB}}{V}_{\text{V},\text{liver}}\end{array}\end{array}$$

  • Captured EC-BFA complex in vascular space

    $$\begin{array}{cc}\begin{array}{c}{V}_{\text{V,liver}}\frac{d{C}_{\text{V,liver}}^{\text{cEB}}}{dt}=\\ \begin{array}{c}\begin{array}{c}\\ \end{array}\\ \end{array}\end{array}& \begin{array}{l}{K}_{f,\text{liver}}^{\text{c}}{C}_{\text{V,liver}}^{\text{EB}}f{C}_{\text{V,liver}}{V}_{\text{V,liver}}\\ -K_{r,\text{liver}}^{\text{c}}{C}_{\text{V,liver}}^{\text{cEB}}{V}_{\text{V,liver}}\\ -K_{f,\text{liver}}^{\text{a}}{C}_{\text{V,liver}}^{\text{cEB}}{V}_{\text{V,liver}}\\ -E_{\text{liver}}^{\text{cEB}}{C}_{\text{V,liver}}^{\text{cEB}}{V}_{\text{V,liver}}\end{array}\end{array}$$

  • Arrested EC-BFA complex in vascular space

    $$\begin{array}{cc}\begin{array}{c}\begin{array}{c}{V}_{\text{V,liver}}\frac{d{C}_{\text{V,liver}}^{\text{aEB}}}{dt}=\\ \end{array}\\ \end{array}& \begin{array}{l}{K}_{f,\text{liver}}^{\text{a}}{C}_{\text{V,liver}}^{\text{cEB}}{V}_{\text{V,liver}}\\ -E_{\text{liver}}^{\text{aEB}}{C}_{\text{V,liver}}^{\text{aEB}}{V}_{\text{V,liver}}\\ -J_{\text{liver}}^{\text{aEB}}{C}_{\text{V,liver}}^{\text{aEB}}{V}_{\text{V,liver}}\end{array}\end{array}$$

  • BFA bound to effector cells in vascular space

    $$\begin{array}{cc}\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}{V}_{\text{V,liver}}\frac{d{C}_{\text{V,liver}}^{\text{bB}}}{dt}=\\ \end{array}\\ \end{array}\\ \end{array}\\ \begin{array}{c}\begin{array}{c}\\ \end{array}\\ \begin{array}{c}\begin{array}{c}\begin{array}{c}\\ \end{array}\\ \end{array}\\ \end{array}\end{array}\end{array}& \begin{array}{l}{Q}_{\text{hepatic}}{C}_{\text{V,plasma}}^{\text{bB}}\\ +(Q_{\text{spleen}}-L_{\text{spleen}})C_{\text{V,spleen}}^{\text{bB}}{C}_{\text{V,spleen}}^{\text{EB}}/C_{\text{V,spleen}}^{\text{total}}\\ +(Q_{\text{GI}}-L_{\text{GI}})C_{\text{V,liver}}^{\text{bB}}{C}_{\text{V,GI}}^{\text{EB}}/C_{\text{V,GI}}^{\text{total}}\\ -(Q_{\text{liver}}-L_{\text{liver}})C_{\text{V,liver}}^{\text{bB}}{C}_{\text{V,liver}}^{\text{EB}}/C_{\text{V,liver}}^{\text{total}}\\ +K_{f\text{,liver}}^{\text{CD}}{C}_{\text{V,liver}}^{\text{fB}}fC{D}_{\text{V,liver}}{V}_{\text{V,liver}}\\ -K_{r,\text{liver}}^{\text{CD}}{C}_{\text{V},\text{liver}}^{\text{bB}}{V}_{\text{V},\text{liver}}\\ -J_{\text{liver}}^{\text{aEB}}{C}_{\text{V},\text{liver}}^{\text{aEB}}{C}_{\text{V},\text{liver}}^{\text{bB}}{V}_{\text{V},\text{liver}}/C_{\text{V},\text{liver}}^{\text{total}}\\ -E_{\text{liver}}^{\text{cEB}}{C}_{\text{V},\text{liver}}^{\text{cEB}}{C}_{\text{V},\text{liver}}^{\text{bB}}{V}_{\text{V},\text{liver}}/C_{\text{V},\text{liver}}^{\text{total}}\\ -E_{\text{liver}}^{\text{aEB}}{C}_{\text{V},\text{liver}}^{\text{aEB}}{C}_{\text{V},\text{liver}}^{\text{bB}}{V}_{\text{V},\text{liver}}/C_{\text{V},\text{liver}}^{\text{total}}\end{array}\end{array}$$

  • Free BFA in the extravascular space

    $$\begin{array}{cc}\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}{V}_{\text{EV,liver}}\frac{d{C}_{\text{EV,liver}}^{\text{fB}}}{dt}=\\ \end{array}\\ \end{array}\\ \end{array}\\ \begin{array}{c}\begin{array}{c}\\ \end{array}\\ \end{array}\end{array}& \begin{array}{l}{J}_{\text{liver}}^{\text{fB}}\\ -L_{\text{liver}}{C}_{\text{EV,liver}}^{\text{fB}}\\ -K_{f\text{,liver}}^{\text{CD}}{C}_{\text{EV,liver}}^{\text{fB}}fC{D}_{\text{EV,liver}}{V}_{\text{EV,liver}}\\ +K_{r\text{,liver}}^{\text{CD}}(C_{\text{EV,liver}}^{\text{bB}}-C_{\text{EV,liver}}^{\text{nEB}})V_{\text{EV,liver}}\\ -K_{f\text{,liver}}^{\text{n}}{C}_{\text{EV,liver}}^{\text{fB}}{V}_{\text{EV,liver}}\\ +K_{r,\text{liver}}^{\text{n}}{C}_{\text{EV},\text{liver}}^{\text{nB}}{V}_{\text{EV},\text{liver}}\end{array}\end{array}$$

  • Nonspecifically bound BFA in the extravascular space

    $$\begin{array}{cc}\begin{array}{c}\begin{array}{c}\begin{array}{c}{V}_{\text{EV,liver}}\frac{d{C}_{\text{EV,liver}}^{\text{nB}}}{dt}\\ \end{array}\\ \end{array}\\ \end{array}& \begin{array}{l}=K_{f\text{,liver}}^{\text{n}}{C}_{\text{EV,liver}}^{\text{fB}}{V}_{\text{EV,liver}}\\ -K_{r\text{,liver}}^{\text{n}}{C}_{\text{EV,liver}}^{\text{nB}}{V}_{\text{EV,liver}}\\ -K_{f,\text{liver}}^{\text{CD}}{C}_{\text{EV,liver}}^{\text{nB}}{C}_{\text{EV,liver}}^{\text{EB}}fC{D}_{\text{EV,liver}}{V}_{\text{EV,liver}}/C_{\text{EV,liver}}^{\text{total}}\\ +K_{r,\text{liver}}^{\text{CD}}{C}_{\text{EV,liver}}^{\text{nEB}}{V}_{\text{EV,liver}}\end{array}\end{array}$$

  • Free EC-BFA complex in the extravascular space

    $$\begin{array}{cc}\begin{array}{c}\begin{array}{c}\begin{array}{c}{V}_{\text{EV,liver}}\frac{d{C}_{\text{EV,liver}}^{\text{EB}}}{dt}\\ \begin{array}{c}\begin{array}{c}\\ \end{array}\\ \end{array}\end{array}\\ \end{array}\\ \end{array}& \begin{array}{l}=J_{\text{liver}}^{\text{aEB}}{C}_{\text{V,liver}}^{\text{aEB}}{V}_{\text{V,liver}}\\ +K_{r\text{,liver}}^{\text{n}}{C}_{\text{EV,liver}}^{\text{nEB}}{V}_{\text{EV,liver}}\\ -K_{f,\text{liver}}^{\text{n}}{C}_{\text{EV,liver}}^{\text{EB}}oC{D}_{\text{EV,liver}}{V}_{\text{EV,liver}}/C_{\text{EV,liver}}^{\text{total}}\\ -L_{\text{liver}}{C}_{\text{EV,liver}}^{\text{EB}}{F}_{\text{liver}}\\ -K_{f,\text{liver}}^{\text{CD}}{C}_{\text{EV,liver}}^{\text{nB}}{C}_{\text{EV,liver}}^{\text{EB}}fC{D}_{\text{EV,liver}}{V}_{\text{EV,liver}}/C_{\text{EV,liver}}^{\text{total}}\\ +K_{r,\text{liver}}^{\text{CD}}{C}_{\text{EV,liver}}^{\text{nEB}}{V}_{\text{EV,liver}}\end{array}\end{array}$$

  • Nonspecifically bound EC-BFA complex in the extravascular space

    $$\begin{array}{cc}\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}{V}_{\text{EV,liver}}\frac{d{C}_{\text{EV,liver}}^{\text{nEB}}}{dt}=\\ \end{array}\\ \end{array}\\ \end{array}\\ \end{array}& \begin{array}{l}{K}_{f\text{,liver}}^{\text{n}}{C}_{\text{EV,liver}}^{\text{EB}}oC{D}_{\text{EV,liver}}{V}_{\text{EV,liver}}/C_{\text{EV,liver}}^{\text{total}}\\ -K_{r\text{,liver}}^{\text{n}}{C}_{\text{EV,liver}}^{\text{nEB}}{V}_{\text{EV,liver}}\\ +K_{f\text{,liver}}^{\text{CD}}{C}_{\text{EV,liver}}^{\text{nB}}{C}_{\text{EV,liver}}^{\text{EB}}fC{D}_{\text{EV,liver}}{V}_{\text{EV,liver}}/C_{\text{EV,liver}}^{\text{total}}\\ -K_{r\text{,liver}}^{\text{CD}}{C}_{\text{EV,liver}}^{\text{nEB}}{V}_{\text{EV,liver}}\end{array}\end{array}$$

  • BFA bound to effector cells in the extravascular space

    $$\begin{array}{l}{V}_{\text{EV,liver}}\frac{d{C}_{\text{EV,liver}}^{\text{bB}}}{dt}=K_{f,\text{liver}}^{\text{CD}}{C}_{\text{EV,liver}}^{\text{fB}}fC{D}_{\text{EV,liver}}{V}_{\text{EV,liver}}\\ \begin{array}{ccc}\begin{array}{ccc}& & \end{array}& & \begin{array}{l}-K_{r,\text{liver}}^{\text{CD}}\left(C_{\text{EV},\text{liver}}^{\text{bB}}-C_{\text{EV,liver}}^{\text{nEB}}\right)V_{\text{EV,liver}}\\ +K_{f,\text{liver}}^{\text{CD}}{C}_{\text{EV,liver}}^{\text{nB}}{C}_{\text{EV},\text{liver}}^{\text{EB}}fC{D}_{\text{EV,liver}}{V}_{\text{EV,liver}}/C_{\text{EV,liver}}^{\text{total}}\\ -K_{r,\text{liver}}^{\text{CD}}{C}_{\text{EV,liver}}^{\text{nEB}}{V}_{\text{EV,liver}}\\ +J_{\text{liver}}^{\text{aEB}}{C}_{\text{V,liver}}^{\text{aEB}}{C}_{\text{V,liver}}^{\text{bB}}{V}_{\text{V,liver}}/C_{\text{V,liver}}^{\text{total}}\\ -L_{\text{liver}}{C}_{\text{EV,liver}}^{\text{EB}}{F}_{\text{V,liver}}{C}_{\text{EV,liver}}^{\text{bB}}/C_{\text{EV,liver}}^{\text{total}}\end{array}\end{array}\end{array}$$

• Lung

  • Free BFA in vascular space

    $$\begin{array}{cc}\begin{array}{l}{V}_{\text{V,lung}}\frac{d{C}_{\text{V,lung}}^{\text{fB}}}{dt}=\\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \end{array}& \begin{array}{l}(Q_{\text{liver}}-L_{\text{liver}})C_{\text{V,liver}}^{\text{fB}}\\ +(Q_{\text{kidney}}-L_{\text{kidney}})C_{\text{V,kidney}}^{\text{fB}}\\ +(Q_{\text{tumor}}-L_{\text{tumor}})C_{\text{V,tumor}}^{\text{fB}}\\ +(Q_{\text{skin}}-L_{\text{skin}})C_{\text{V,skin}}^{\text{fB}}\\ +(Q_{\text{muscle}}-L_{\text{muscle}})C_{\text{V,muscle}}^{\text{fB}}\\ +(Q_{\text{bone}}-L_{\text{bone}})C_{\text{V,bone}}^{\text{fB}}\\ +(Q_{\text{heart}}-L_{\text{heart}})C_{\text{V,heart}}^{\text{fB}}\\ +Q_{\text{lnode}}{C}_{\text{V,lnode}}^{\text{fB}}\\ +L_{\text{lnode}}{C}_{\text{EV,lnode}}^{\text{fB}}\\ -(Q_{\text{lung}}-L_{\text{lung}})C_{\text{V,lung}}^{\text{fB}}\\ -J_{\text{lnode}}^{\text{fB}}\\ -K_{f\text{,lung}}^{\text{CD}}{C}_{\text{V, lung}}^{\text{fB}}f{C}_{\text{V, lung}}{V}_{\text{V, lung}}\\ +K_{r\text{,lung}}^{\text{CD}}{C}_{\text{V,lung}}^{\text{bB}}{V}_{\text{V,lung}}\end{array}\end{array}$$

  • Free EC-BFA complex in vascular space

    $$\begin{array}{cc}\begin{array}{l}{V}_{\text{V,lung}}\frac{d{C}_{\text{V,liver}}^{\text{EB}}}{dt}=\\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \end{array}& \begin{array}{l}(Q_{\text{liver}}-L_{\text{liver}})C_{\text{V,liver}}^{\text{EB}}\\ +(Q_{\text{kidney}}-L_{\text{kidney}})C_{\text{V,kidney}}^{\text{EB}}\\ +(Q_{\text{tumor}}-L_{\text{tumor}})C_{\text{V,tumor}}^{\text{EB}}\\ +(Q_{\text{skin}}-L_{\text{skin}})C_{\text{V,skin}}^{\text{EB}}\\ +(Q_{\text{muscle}}-L_{\text{muscle}})C_{\text{V,muscle}}^{\text{EB}}\\ +(Q_{\text{bone}}-L_{\text{bone}})C_{\text{V,bone}}^{\text{EB}}\\ +(Q_{\text{heart}}-L_{\text{heart}})C_{\text{V,heart}}^{\text{EB}}\\ +Q_{\text{lnode}}{C}_{\text{V,lnode}}^{\text{EB}}\\ +L_{\text{lnode}}{C}_{\text{EV,lnode}}^{\text{EB}}{F}_{\text{lnode}}\\ -(Q_{\text{lung}}-L_{\text{lung}})C_{\text{V,lung}}^{\text{EB}}\\ -K_{f\text{,liver}}^{\text{c}}{C}_{\text{V, liver}}^{\text{EB}}f{C}_{\text{V, liver}}{V}_{\text{V, lung}}\\ +K_{r\text{,liver}}^{\text{c}}{C}_{\text{V,liver}}^{\text{cEB}}{V}_{\text{V,lung}}\end{array}\end{array}$$

  • Captured EC-BFA complex in vascular space

    $$\begin{array}{cc}\begin{array}{c}\begin{array}{c}{V}_{\text{V,lung}}\frac{d{C}_{\text{V,liver}}^{\text{cEB}}}{dt}=\\ \end{array}\\ \end{array}& \begin{array}{l}{K}_{f,\text{lung}}^c{C}_{\text{V,lung}}^{\text{EB}}f{C}_{\text{V,lung}}{V}_{\text{V,lung}}\\ -K_{r,\text{lung}}^{\text{c}}{C}_{\text{V,lung}}^{\text{cEB}}{V}_{\text{V,lung}}\\ -K_{f,\text{lung}}^{\text{a}}{C}_{\text{V,lung}}^{\text{cEB}}{V}_{\text{V,lung}}\end{array}\end{array}$$

  • Arrested EC-BFA complex in vascular space

    $$\begin{array}{cc}\begin{array}{c}\begin{array}{c}{V}_{\text{V,lung}}\frac{d{C}_{\text{V,liver}}^{\text{aEB}}}{dt}=\\ \end{array}\\ \end{array}& \begin{array}{l}{K}_{f,\text{lung}}^{\text{a}}{C}_{\text{V,lung}}^{\text{cEB}}{V}_{\text{V,lung}}\\ -E_{\text{lung}}^{\text{aEB}}{C}_{\text{V,lung}}^{\text{aEB}}{V}_{\text{V,lung}}\\ -J_{\text{lung}}^{\text{aEB}}{C}_{\text{V,lung}}^{\text{aEB}}{V}_{\text{V,lung}}\end{array}\end{array}$$

  • BFA bound to effector cells in vascular space

    $$\begin{array}{cc}\begin{array}{l}{V}_{\text{V,lung}}\frac{d{C}_{\text{V,liver}}^{\text{bB}}}{dt}=\\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \end{array}& \begin{array}{l}(Q_{\text{liver}}-L_{\text{liver}})C_{\text{V,liver}}^{\text{bB}}{C}_{\text{V,liver}}^{\text{EB}}/C_{\text{V,liver}}^{\text{total}}\\ +(Q_{\text{kidney}}-L_{\text{kidney}})C_{\text{V,kidney}}^{\text{bB}}{C}_{\text{V,kidney}}^{\text{EB}}/C_{\text{V,kidney}}^{\text{total}}\\ +(Q_{\text{tumor}}-L_{\text{tumor}})C_{\text{V,tumor}}^{\text{bB}}{C}_{\text{V,tumor}}^{\text{EB}}/C_{\text{V,tumor}}^{\text{total}}\\ +(Q_{\text{skin}}-L_{\text{skin}})C_{\text{V,skin}}^{\text{bB}}{C}_{\text{V,skin}}^{\text{EB}}/C_{\text{V,skin}}^{\text{total}}\\ +(Q_{\text{muscle}}-L_{\text{muscle}})C_{\text{V,muscle}}^{\text{bB}}{C}_{\text{V,muscle}}^{\text{EB}}/C_{\text{V,muscle}}^{\text{total}}\\ +(Q_{\text{bone}}-L_{\text{bone}})C_{\text{V,bone}}^{\text{bB}}{C}_{\text{V,bone}}^{\text{EB}}/C_{\text{V,bone}}^{\text{total}}\\ +(Q_{\text{heart}}-L_{\text{heart}})C_{\text{V,heart}}^{\text{bB}}{C}_{\text{V,heart}}^{\text{EB}}/C_{\text{V,heart}}^{\text{total}}\\ +Q_{\text{lnode}}{C}_{\text{V,lnode}}^{\text{bB}}{C}_{\text{V,lnode}}^{\text{EB}}/C_{\text{V,lnode}}^{\text{total}}\\ +L_{\text{lnode}}{C}_{\text{EV,lnode}}^{\text{bB}}{C}_{\text{EV,lnode}}^{\text{EB}}{F}_{\text{lnode}}/C_{\text{EV,lnode}}^{\text{total}}\\ -(Q_{\text{lung}}-L_{\text{lung}})C_{\text{V,lung}}^{\text{bB}}{C}_{\text{V,lung}}^{\text{EB}}/C_{\text{V,lung}}^{\text{total}}\\ +K_{f\text{,lung}}^{\text{CD}}{C}_{\text{V,lung}}^{\text{bB}}fC{D}_{\text{V,lung}}{V}_{\text{V,lung}}\\ -K_{r\text{,lung}}^{\text{CD}}{C}_{\text{V, lung}}^{\text{bB}}{V}_{\text{V, lung}}\\ -J_{\text{lung}}^{\text{aEB}}{C}_{\text{V,lung}}^{\text{aEB}}{C}_{\text{V,lung}}^{\text{bB}}{V}_{\text{V,lung}}/C_{\text{V,lung}}^{\text{total}}\\ -E_{\text{lung}}^{\text{cEB}}{C}_{\text{V,lung}}^{\text{cEB}}{C}_{\text{V,lung}}^{\text{bB}}{V}_{\text{V,lung}}/C_{\text{V,lung}}^{\text{total}}\\ -E_{\text{lung}}^{\text{aEB}}{C}_{\text{V,lung}}^{\text{aEB}}{C}_{\text{V,lung}}^{\text{bB}}{V}_{\text{V,lung}}/C_{\text{V,lung}}^{\text{total}}\end{array}\end{array}$$

  • Free BFA in the extravascular space

    $$\begin{array}{cc}\begin{array}{l}{V}_{\text{EV,lung}}\frac{d{C}_{\text{EV,lung}}^{\text{fB}}}{dt}=\\ \\ \\ \\ \\ \end{array}& \begin{array}{l}{J}_{\text{lung}}^{\text{fB}}\\ -L_{\text{lung}}{C}_{\text{EV,lung}}^{\text{fB}}\\ -K_{f\text{,lung}}^{\text{CD}}{C}_{\text{EV,lung}}^{\text{fB}}fC{D}_{\text{EV,lung}}{V}_{\text{EV,lung}}\\ +K_{r\text{,lung}}^{\text{CD}}(C_{\text{EV,lung}}^{\text{bB}}-C_{\text{EV,lung}}^{\text{nEB}})V_{\text{EV,lung}}\\ -K_{f\text{,lung}}^{\text{n}}{C}_{\text{EV,lung}}^{\text{fB}}{V}_{\text{EV,lung}}\\ +K_{r\text{,lung}}^{\text{n}}{C}_{\text{EV,lung}}^{\text{nB}}{V}_{\text{EV,lung}}\end{array}\end{array}$$

  • Nonspecifically bound BFA in the extravascular space

    $$\begin{array}{cc}\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}{V}_{\text{EV,lung}}\frac{d{C}_{\text{EV,lung}}^{\text{nB}}}{dt}=\\ \end{array}\\ \end{array}\\ \end{array}\\ \end{array}& \begin{array}{l}{K}_{f\text{,lung}}^{\text{n}}{C}_{\text{EV,lung}}^{\text{fB}}{V}_{\text{EV,lung}}\\ -K_{r\text{,lung}}^{\text{n}}{C}_{\text{EV,lung}}^{\text{nB}}{V}_{\text{EV,lung}}\\ -K_{f,\text{lung}}^{\text{CD}}{C}_{\text{EV,lung}}^{\text{nB}}{C}_{\text{EV,lung}}^{\text{EB}}fC{D}_{\text{EV,lung}}{V}_{\text{EV,lung}}/C_{\text{EV,lung}}^{\text{total}}\\ +K_{r\text{,lung}}^{\text{CD}}{C}_{\text{EV,lung}}^{\text{nEB}}{V}_{\text{EV,lung}}\end{array}\end{array}$$

  • Free EC-BFA complex in the extravascular space

    $$\begin{array}{l}{V}_{\text{EV,lung}}\frac{d{C}_{\text{EV,lung}}^{\text{fB}}}{dt}=J_{\text{lung}}^{\text{aEB}}{C}_{\text{V,lung}}^{\text{aEB}}{V}_{\text{V,lung}}\\ \begin{array}{cc}& \begin{array}{cc}\begin{array}{cc}& \end{array}& \begin{array}{cc}& \begin{array}{l}+K_{r\text{,lung}}^{\text{n}}{C}_{\text{EV,lung}}^{\text{nEB}}{V}_{\text{EV,lung}}\\ -K_{f\text{,lung}}^{\text{n}}{C}_{\text{EV,lung}}^{\text{EB}}oC{D}_{\text{EV,lung}}{V}_{\text{EV,lung}}/C_{\text{EV,lung}}^{\text{total}}\\ -L_{\text{lung}}{C}_{\text{EV,lung}}^{\text{EB}}{F}_{\text{lung}}\\ -K_{f\text{,lung}}^{\text{CD}}{C}_{\text{EV,lung}}^{\text{nB}}{C}_{\text{EV,lung}}^{\text{EB}}fC{D}_{\text{EV,lung}}{V}_{\text{EV,lung}}/C_{\text{EV,lung}}^{\text{total}}\\ +K_{r\text{,lung}}^{\text{CD}}{C}_{\text{EV,lung}}^{\text{nEB}}{V}_{\text{EV,lung}}\end{array}\end{array}\end{array}\end{array}\end{array}$$

  • Nonspecifically bound EC-BFA complex in the extravascular space

    $$\begin{array}{l}{V}_{\text{EV,lung}}\frac{d{C}_{\text{EV,lung}}^{\text{nEB}}}{dt}=K_{f\text{,lung}}^{\text{n}}{C}_{\text{EV,lung}}^{\text{EB}}oC{D}_{\text{EV,lung}}{V}_{\text{EV,lung}}/C_{\text{EV,lung}}^{\text{total}}\\ \begin{array}{cc}\begin{array}{cc}\begin{array}{cc}& \end{array}& \begin{array}{cc}& \end{array}\end{array}& \begin{array}{l}-K_{r\text{,lung}}^{\text{n}}{C}_{\text{EV,lung}}^{\text{nEB}}{V}_{\text{EV,lung}}\\ +K_{f\text{,lung}}^{\text{CD}}{C}_{\text{EV,lung}}^{\text{nB}}{C}_{\text{EV,lung}}^{\text{EB}}fC{D}_{\text{EV,lung}}{V}_{\text{EV,lung}}/C_{\text{EV,lung}}^{\text{total}}\\ -K_{r\text{,lung}}^{\text{CD}}{C}_{\text{EV,lung}}^{\text{nEB}}{V}_{\text{EV,lung}}\end{array}\end{array}\end{array}$$

  • BFA bound to effector cells in the extravascular space

    $$\begin{array}{l}{V}_{\text{EV,lung}}\frac{d{C}_{\text{EV,lung}}^{\text{bB}}}{dt}=K_{f\text{,lung}}^{\text{CD}}{C}_{\text{EV,lung}}^{\text{fB}}fC{D}_{\text{EV,lung}}{V}_{\text{EV,lung}}\\ \begin{array}{cc}\begin{array}{cc}\begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}& \end{array}& \begin{array}{l}-K_{r\text{,lung}}^{\text{CD}}\left(C_{\text{EV,lung}}^{\text{bB}}-C_{\text{EV,lung}}^{\text{nEB}}\right)V_{\text{EV,lung}}\\ +K_{f\text{,lung}}^{\text{CD}}{C}_{\text{EV,lung}}^{\text{nB}}{C}_{\text{EV,lung}}^{\text{EB}}fC{D}_{\text{EV,lung}}{V}_{\text{EV,lung}}/C_{\text{EV,lung}}^{\text{total}}\\ -K_{r\text{,lung}}^{\text{CD}}{C}_{\text{EV,lung}}^{\text{nEB}}{V}_{\text{EV,lung}}\\ +J_{\text{lung}}^{\text{aEB}}{C}_{\text{V,lung}}^{\text{aEB}}{C}_{\text{V,lung}}^{\text{bB}}{V}_{\text{V,lung}}/C_{\text{V,lung}}^{\text{total}}\\ -L_{\text{lung}}{C}_{\text{EV,lung}}^{\text{EB}}{F}_{\text{lung}}{C}_{\text{EV,lung}}^{\text{bB}}/C_{\text{EV,lung}}^{\text{total}}\end{array}\end{array}\end{array}$$

• Lymph Node

  • Free BFA in vascular space

    $$\begin{array}{cc}\begin{array}{l}{V}_{\text{V,lnode}}\frac{d{C}_{\text{V,lnode}}^{\text{fB}}}{dt}=\\ \\ \\ \\ \\ \end{array}& \begin{array}{l}{Q}_{\text{lnode}}{C}_{\text{V,plasma}}^{\text{fB}}\\ -Q_{\text{lnode}}{C}_{\text{V,lnode}}^{\text{fB}}\\ -J_{\text{lnode}}^{\text{fB}}\\ -K_{f\text{,lnode}}^{\text{CD}}{C}_{\text{V,lnode}}^{\text{fB}}fC{D}_{\text{V,lnode}}{V}_{\text{V,lnode}}\\ +K_{r\text{,lnode}}^{\text{CD}}{C}_{\text{V,lnode}}^{\text{bB}}{V}_{\text{V,lnode}}\end{array}\end{array}$$

  • Free EC-BFA complex in vascular space

    $$\begin{array}{cc}\begin{array}{c}\begin{array}{c}\begin{array}{c}{V}_{\text{V,lnode}}\frac{d{C}_{\text{V,lnode}}^{\text{EB}}}{dt}=\\ \end{array}\\ \end{array}\\ \end{array}& \begin{array}{l}{Q}_{\text{lnode}}{C}_{\text{V,plasma}}^{\text{EB}}\\ -Q_{\text{lnode}}{C}_{\text{V,lnode}}^{\text{EB}}\\ -K_{f,\text{node}}^{\text{c}}{C}_{\text{V,lnode}}^{\text{EB}}f{C}_{\text{V,lnode}}{V}_{\text{V,lnode}}\\ +K_{r,\text{node}}^{\text{c}}{C}_{\text{V,lnode}}^{\text{cEB}}{V}_{\text{V,lnode}}\end{array}\end{array}$$

  • Captured EC-BFA complex in vascular space

    $$\begin{array}{l}{V}_{\text{V,lnode}}\frac{d{C}_{\text{V,lnode}}^{\text{cEB}}}{dt}=K_{f,\text{node}}^{\text{c}}{C}_{\text{V,lnode}}^{\text{EB}}f{C}_{\text{V,lnode}}{V}_{\text{V,lnode}}\\ \begin{array}{cccc}\begin{array}{ccc}& & \end{array}& & & \begin{array}{l}-K_{r,\text{node}}^{\text{c}}{C}_{\text{V,lnode}}^{\text{cEB}}{V}_{\text{V,lnode}}\\ -K_{f,\text{node}}^{\text{a}}{C}_{\text{V,lnode}}^{\text{cEB}}{V}_{\text{V,lnode}}\\ -E_{\text{node}}^{\text{cEB}}{C}_{\text{V,lnode}}^{\text{cEB}}{V}_{\text{V,lnode}}\end{array}\end{array}\end{array}$$

  • Arrested EC-BFA comples in vascular space

    $$\begin{array}{l}{V}_{\text{V,lnode}}\frac{d{C}_{\text{V,lnode}}^{\text{aEB}}}{dt}=K_{f,\text{node}}^{\text{a}}{C}_{\text{V,lnode}}^{\text{cEB}}{V}_{\text{V,lnode}}\\ \begin{array}{cccc}\begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}& & & \begin{array}{l}-E_{\text{node}}^{\text{aEB}}{C}_{\text{V,lnode}}^{\text{aEB}}{V}_{\text{V,lnode}}\\ -J_{\text{node}}^{\text{aEB}}{C}_{\text{V,lnode}}^{\text{aEB}}{V}_{\text{V,lnode}}\end{array}\end{array}\end{array}$$

  • BFA bound to effector cells in vascular space

    $$\begin{array}{l}{V}_{\text{V,lnode}}\frac{d{C}_{\text{V,lnode}}^{\text{bB}}}{dt}=Q_{\text{lnode}}{C}_{\text{V,plasma}}^{\text{bB}}\\ \begin{array}{cccc}\begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}& & & \begin{array}{l}-Q_{\text{lnode}}{C}_{\text{V,lnode}}^{\text{bB}}{C}_{\text{V,lnode}}^{\text{EB}}/C_{\text{V,lnode}}^{\text{total}}\\ +K_{f,\text{lnode}}^{\text{CD}}{C}_{\text{V,lnode}}^{\text{fB}}fC{D}_{\text{V,lnode}}{V}_{\text{V,lnode}}\\ -K_{r,\text{lnode}}^{\text{CD}}{C}_{\text{V,lnode}}^{\text{bB}}{V}_{\text{V,lnode}}\\ -J_{\text{lnode}}^{\text{aEB}}{C}_{\text{V,lnode}}^{\text{aEB}}{C}_{\text{V,lnode}}^{\text{bB}}{V}_{\text{V,lnode}}/C_{\text{V,lnode}}^{\text{total}}\\ -E_{\text{lnode}}^{\text{cEB}}{C}_{\text{V,lnode}}^{\text{cEB}}{C}_{\text{V,lnode}}^{\text{bB}}{V}_{\text{V,lnode}}/C_{\text{V,lnode}}^{\text{total}}\\ -E_{\text{lnode}}^{\text{aEB}}{C}_{\text{V,lnode}}^{\text{aEB}}{C}_{\text{V,lnode}}^{\text{bB}}{V}_{\text{V,lnode}}/C_{\text{V,lnode}}^{\text{total}}\end{array}\end{array}\end{array}$$

  • Free BFA in the extravascular space

    $$\begin{array}{cc}\begin{array}{l}{V}_{\text{V,lnode}}\frac{d{C}_{\text{V,lnode}}^{\text{fB}}}{dt}=\\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \end{array}& \begin{array}{l}{J}_{\text{lnode}}^{\text{fB}}\\ +L_{\text{lung}}{C}_{\text{EV,lung}}^{\text{fB}}\\ +L_{\text{GI}}{C}_{\text{EV,GI}}^{\text{fB}}\\ +L_{\text{liver}}{C}_{\text{EV,liver}}^{\text{fB}}\\ +L_{\text{spleen}}{C}_{\text{EV,spleen}}^{\text{fB}}\\ +L_{\text{heart}}{C}_{\text{EV,heart}}^{\text{fB}}\\ +L_{\text{kidney}}{C}_{\text{EV,kidney}}^{\text{fB}}\\ +L_{\text{skin}}{C}_{\text{EV,skin}}^{\text{fB}}\\ +L_{\text{muscle}}{C}_{\text{EV,muscle}}^{\text{fB}}\\ +L_{\text{bone}}{C}_{\text{EV,bone}}^{\text{fB}}\\ +L_{\text{tumor}}{C}_{\text{EV,tumor}}^{\text{fB}}\\ -L_{\text{lnode}}{C}_{\text{EV,lnode}}^{\text{fB}}\\ -K_{f\text{,lnode}}^{\text{CD}}{C}_{\text{EV,lnode}}^{\text{fB}}fC{D}_{\text{EV,lnode}}{V}_{\text{EV,lnode}}\\ +K_{r\text{,lnode}}^{\text{CD}}(C_{\text{EV,lnode}}^{\text{bB}}-C_{\text{EV,lnode}}^{\text{nEB}})V_{\text{EV,lnode}}\\ -K_{f,\text{lnode}}^{\text{n}}{C}_{\text{EV,lnode}}^{\text{fB}}{V}_{\text{EV,lnode}}\\ +K_{r,\text{lnode}}^{\text{n}}{C}_{\text{EV,lnode}}^{\text{nB}}{V}_{\text{EV,lnode}}\end{array}\end{array}$$

  • Nonspecifically bound BFA in the extravascular space

    $$\begin{array}{l}{V}_{\text{EV,lnode}}\frac{d{C}_{\text{EV,lnode}}^{\text{nB}}}{dt}=K_{f,\text{node}}^{\text{n}}{C}_{\text{EV,lnode}}^{\text{fB}}{V}_{\text{EV,lnode}}\\ \begin{array}{cc}\begin{array}{cc}& \end{array}& \begin{array}{l}-K_{r,\text{lnode}}^{\text{n}}{C}_{\text{EV,lnode}}^{\text{nB}}{V}_{\text{EV,lnode}}\\ -K_{f,\text{lnode}}^{\text{CD}}{C}_{\text{EV,lnode}}^{\text{nB}}{C}_{\text{EV,lnode}}^{\text{EB}}fC{D}_{\text{EV,lnode}}{V}_{\text{EV,lnode}}/C_{\text{EV,lnode}}^{\text{total}}\\ +K_{r,\text{lnode}}^{\text{CD}}{C}_{\text{EV,lnode}}^{\text{nEB}}{V}_{\text{EV,lnode}}\end{array}\end{array}\end{array}$$

  • Free EC-BFA complex in the extravascular space

    $$\begin{array}{l}{V}_{\text{EV,lnode}}\frac{d{C}_{\text{EV,lnode}}^{\text{fB}}}{dt}=L_{\text{lung}}{C}_{\text{EV,lung}}^{\text{EB}}{F}_{\text{lung}}\\ \begin{array}{cc}\begin{array}{cc}& \end{array}& \begin{array}{l}+L_{\text{GI}}{C}_{\text{EV,GI}}^{\text{EB}}{F}_{\text{GI}}\\ +L_{\text{liver}}{C}_{\text{EV,liver}}^{\text{EB}}{F}_{\text{liver}}\\ +L_{\text{spleen}}{C}_{\text{EV,spleen}}^{\text{EB}}{F}_{\text{spleen}}\\ +L_{\text{heart}}{C}_{\text{EV,heart}}^{\text{EB}}{F}_{\text{heart}}\\ +L_{\text{kidney}}{C}_{\text{EV,kidney}}^{\text{EB}}{F}_{\text{kidney}}\\ +L_{\text{skin}}{C}_{\text{EV,skin}}^{\text{EB}}{F}_{\text{skin}}\\ +L_{\text{muscle}}{C}_{\text{EV,muscle}}^{\text{EB}}{F}_{\text{muscle}}\\ +L_{\text{bone}}{C}_{\text{EV,bone}}^{\text{EB}}{F}_{\text{bone}}\\ +L_{\text{tumor}}{C}_{\text{EV,tumor}}^{\text{EB}}{F}_{\text{tumor}}\\ -L_{\text{lnode}}{C}_{\text{EV,lnode}}^{\text{EB}}{F}_{\text{lnode}}\\ +J_{\text{lnode}}^{\text{aEB}}{C}_{\text{V,lnode}}^{\text{aEB}}{V}_{\text{V,lnode}}\\ +K_{r,\text{lnode}}^{\text{n}}{C}_{\text{EV,lnode}}^{\text{nEB}}{V}_{\text{EV,lnode}}\\ -K_{f,\text{lnode}}^{\text{n}}{C}_{\text{EV,lnode}}^{\text{EB}}oC{D}_{\text{EV,lnode}}{V}_{\text{EV,lnode}}/C_{\text{EV,lnode}}^{\text{total}}\\ -K_{f,\text{lnode}}^{\text{CD}}{C}_{\text{EV,lnode}}^{\text{nB}}{C}_{\text{EV,lnode}}^{\text{EB}}fC{D}_{\text{EV,lnode}}{V}_{\text{EV,lnode}}/C_{\text{EV,lnode}}^{\text{total}}\\ +K_{r,\text{lnode}}^{\text{CD}}{C}_{\text{EV,lnode}}^{\text{nEB}}{V}_{\text{EV,lnode}}\end{array}\end{array}\end{array}$$

  • Nonspecifically bound EC-BFA complex in the extravascular space

    $$\begin{array}{l}{V}_{\text{EV,lnode}}\frac{d{C}_{\text{EV,lnode}}^{\text{nEB}}}{dt}=K_{f,\text{lnode}}^{\text{n}}{C}_{\text{EV,lnode}}^{\text{EB}}oC{D}_{\text{EV,lnode}}{V}_{\text{EV,lnode}}/C_{\text{EV,lnode}}^{\text{total}}\\ \begin{array}{ccc}& & \begin{array}{l}-K_{r,\text{lnode}}^{\text{n}}{C}_{\text{EV,lnode}}^{\text{nEB}}{V}_{\text{EV,lnode}}\\ +K_{f,\text{lnode}}^{\text{CD}}{C}_{\text{EV,lnode}}^{\text{nB}}{C}_{\text{EV,lnode}}^{\text{EB}}fC{D}_{\text{EV,lnode}}{V}_{\text{EV,lnode}}/C_{\text{EV,lnode}}^{\text{total}}\\ -K_{r,\text{lnode}}^{\text{CD}}{C}_{\text{EV,lnode}}^{\text{nEB}}{V}_{\text{EV,lnode}}\end{array}\end{array}\end{array}$$

  • BFA bound to effector cells in the extravascular space

    $$\begin{array}{l}{V}_{\text{EV,lnode}}\frac{d{C}_{\text{EV,lnode}}^{\text{bB}}}{dt}=L_{\text{lung}}{C}_{\text{EV,lung}}^{\text{EB}}{F}_{\text{lung}}{C}_{\text{EV,lung}}^{\text{bB}}/C_{\text{EV,lung}}^{\text{total}}\\ \begin{array}{ccc}& & \begin{array}{l}+L_{\text{GI}}{C}_{\text{EV,GI}}^{\text{EB}}{F}_{\text{GI}}{C}_{\text{EV,GI}}^{\text{bB}}/C_{\text{EV,GI}}^{\text{total}}\\ +L_{\text{liver}}{C}_{\text{EV,liver}}^{\text{EB}}{F}_{\text{liver}}{C}_{\text{EV,liver}}^{\text{bB}}/C_{\text{EV,liver}}^{\text{total}}\\ +L_{\text{spleen}}{C}_{\text{EV,spleen}}^{\text{EB}}{F}_{\text{spleen}}{C}_{\text{EV,spleen}}^{\text{bB}}/C_{\text{EV,spleen}}^{\text{total}}\\ +L_{\text{heart}}{C}_{\text{EV,heart}}^{\text{EB}}{F}_{\text{heart}}{C}_{\text{EV,heart}}^{\text{bB}}/C_{\text{EV,heart}}^{\text{total}}\\ +L_{\text{kidney}}{C}_{\text{EV,kidney}}^{\text{EB}}{F}_{\text{kidney}}{C}_{\text{EV,kidney}}^{\text{bB}}/C_{\text{EV,kidney}}^{\text{total}}\\ +L_{\text{skin}}{C}_{\text{EV,skin}}^{\text{EB}}{F}_{\text{skin}}{C}_{\text{EV,skin}}^{\text{bB}}/C_{\text{EV,skin}}^{\text{total}}\\ +L_{\text{muscle}}{C}_{\text{EV,muscle}}^{\text{EB}}{F}_{\text{muscle}}{C}_{\text{EV,muscle}}^{\text{bB}}/C_{\text{EV,muscle}}^{\text{total}}\\ +L_{\text{bone}}{C}_{\text{EV,bone}}^{\text{EB}}{F}_{\text{bone}}{C}_{\text{EV,bone}}^{\text{bB}}/C_{\text{EV,bone}}^{\text{total}}\\ +L_{\text{tumor}}{C}_{\text{EV,tumor}}^{\text{EB}}{F}_{\text{tumor}}{C}_{\text{EV,tumor}}^{\text{bB}}/C_{\text{EV,tumor}}^{\text{total}}\\ +K_{f,\text{lnode}}^{\text{CD}}{C}_{\text{EV,lnode}}^{\text{fB}}fC{D}_{\text{EV,lnode}}{V}_{\text{EV,lnode}}\\ -K_{r,\text{lnode}}^{\text{CD}}\left(C_{\text{EV,lnode}}^{\text{bB}}-C_{\text{EV,lnode}}^{\text{nEB}}\right)V_{\text{EV,lnode}}\\ +K_{f,\text{lnode}}^{\text{CD}}{C}_{\text{EV,lnode}}^{\text{nB}}{C}_{\text{EV,lnode}}^{\text{EB}}fC{D}_{\text{EV,lnode}}{V}_{\text{EV,lnode}}/C_{\text{EV,lnode}}^{\text{total}}\\ -K_{r,\text{lnode}}^{\text{CD}}{C}_{\text{EV,lnode}}^{\text{nEB}}{V}_{\text{EV,lnode}}\\ +J_{\text{lnode}}^{\text{aEB}}{C}_{\text{V,lnode}}^{\text{aEB}}{C}_{\text{V,lnode}}^{\text{bB}}{V}_{\text{V,lnode}}/C_{\text{V,lnode}}^{\text{total}}\\ -L_{\text{lnode}}{C}_{\text{EV,lnode}}^{\text{EB}}{F}_{\text{lnode}}{C}_{\text{EV,lnode}}^{\text{bB}}/C_{\text{V,lnode}}^{\text{total}}\end{array}\end{array}\end{array}$$

• Tumor

  • Free BFA in vascular space

    $$\begin{array}{cc}\begin{array}{l}{V}_{\text{V,tumor}}\frac{d{C}_{\text{V,tumor}}^{\text{fB}}}{dt}=\\ \\ \\ \\ \\ \\ \\ \end{array}& \begin{array}{l}{Q}_{\text{tumor}}{C}_{\text{V,plasma}}^{\text{fB}}\\ -(Q_{\text{tumor}}-L_{\text{tumor}})C_{\text{V,tumor}}^{\text{fB}}\\ -J_{\text{tumor}}^{\text{fB}}\\ -K_{f\text{,tumor}}^{\text{fB}}{C}_{\text{V,tumor}}^{\text{fB}}fC{D}_{\text{V,tumor}}{V}_{\text{V,tumor}}\\ +K_{r\text{,tumor}}^{\text{CD}}(C_{\text{V,tumor}}^{\text{bB}}-C_{\text{V,tumor}}^{\text{agEB}})V_{\text{V,tumor}}\\ -K_{f\text{,tumor}}^{\text{ag}}{C}_{\text{V,tumor}}^{\text{fB}}f{A}_{\text{V,tumor}}{V}_{\text{V,tumor}}\\ +K_{r\text{,tumor}}^{\text{ag}}{C}_{\text{V,tumor}}^{\text{agB}}{V}_{\text{V,tumor}}\end{array}\end{array}$$

  • BFA bound to vascular antigens in vascular space

    $$\begin{array}{l}{V}_{\text{V,tumor}}\frac{d{C}_{\text{V,tumor}}^{\text{agB}}}{dt}=K_{f\text{,tumor}}^{\text{ag}}{C}_{\text{V,tumor}}^{\text{fB}}f{A}_{\text{V,tumor}}{V}_{\text{V,tumor}}\\ \begin{array}{cc}& \begin{array}{cc}\begin{array}{cc}& \end{array}& -K_{r,\text{tumor}}^{\text{ag}}\end{array}\end{array}{C}_{\text{V,tumor}}^{\text{agB}}{V}_{\text{V,tumor}}\\ \begin{array}{cc}\begin{array}{cc}& \end{array}& \begin{array}{cc}& -\end{array}\end{array}{K}_{f,\text{tumor}}^{\text{CD}}{C}_{\text{V,tumor}}^{\text{agB}}{C}_{\text{V,tumor}}^{\text{EB}}fC{D}_{\text{V,tumor}}/C_{\text{V,tumor}}^{\text{total}}\\ \begin{array}{cc}\begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}& +\end{array}{K}_{r,\text{tumor}}^{\text{CD}}{C}_{\text{V,tumor}}^{\text{agEB}}{V}_{\text{V,tumor}}\end{array}$$

  • Free EC-BFA complex in vascular space

    $$\begin{array}{l}{V}_{\text{V,tumor}}\frac{d{C}_{\text{V,tumor}}^{\text{EB}}}{dt}=Q_{\text{tumor}}{C}_{\text{V,plasma}}^{\text{EB}}\\ \begin{array}{cc}\begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}& -(Q_{\text{tumor}}-L_{\text{tumor}})C_{\text{V,tumor}}^{\text{EB}}\end{array}\\ \begin{array}{cc}\begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}& \begin{array}{l}-K_{f,\text{tumor}}^{\text{c}}{C}_{\text{V,tumor}}^{\text{EB}}f{C}_{\text{V,tumor}}{V}_{\text{V,tumor}}\\ +K_{r,\text{tumor}}^{\text{c}}{C}_{\text{V,tumor}}^{\text{cEB}}{V}_{\text{V,tumor}}\\ -K_{f,\text{tumor}}^{\text{ag}}{C}_{\text{V,tumor}}^{\text{EB}}f{A}_{\text{V,tumor}}oC{D}_{\text{V,tumor}}{V}_{\text{V,tumor}}/C_{\text{V,tumor}}^{\text{total}}\\ +K_{r,\text{tumor}}^{\text{ag}}{C}_{\text{V,tumor}}^{\text{agEB}}{V}_{\text{V,tumor}}\\ -K_{f,\text{tumor}}^{\text{CD}}{C}_{\text{V,tumor}}^{\text{agB}}{C}_{\text{V,tumor}}^{\text{EB}}fC{D}_{\text{V,tumor}}{V}_{\text{V,tumor}}/C_{\text{V,tumor}}^{\text{total}}\\ +K_{r,\text{tumor}}^{\text{CD}}{C}_{\text{V,tumor}}^{\text{agEB}}{V}_{\text{V,tumor}}\end{array}\end{array}\end{array}$$

  • Normal captured EC-BFA complex in vascular space

    $$\begin{array}{cc}\begin{array}{c}\begin{array}{c}{V}_{\text{V,tumor}}\frac{d{C}_{\text{V,tumor}}^{\text{EB}}}{dt}=\\ \\ \end{array}\\ \end{array}& \begin{array}{l}{K}_{f,\text{tumor}}^{\text{c}}{C}_{\text{V,tumor}}^{\text{EB}}f{C}_{\text{V,tumor}}{V}_{\text{V,tumor}}\\ -K_{r,\text{tumor}}^{\text{c}}{C}_{\text{V,tumor}}^{\text{cEB}}{V}_{\text{V,tumor}}\\ -K_{f,\text{tumor}}^{\text{a}}{C}_{\text{V,tumor}}^{\text{cEB}}{V}_{\text{V,tumor}}\\ -E_{\text{tumor}}^{\text{cEB}}{C}_{\text{V,tumor}}^{\text{cEB}}{V}_{\text{V,tumor}}\end{array}\end{array}$$

  • Enhanced captured EC-BFA complex in vascular space

    $$\begin{array}{cc}\begin{array}{l}{V}_{\text{V,tumor}}\frac{d{C}_{\text{V,tumor}}^{\text{agEB}}}{dt}=\\ \\ \\ \\ \\ \end{array}& \begin{array}{l}{K}_{f\text{,plasma}}^{\text{ag}}{C}_{\text{V,tumor}}^{\text{EB}}f{A}_{\text{V,tumor}}oC{D}_{\text{V,tumor}}{V}_{\text{V,tumor}}/C_{\text{V,tumor}}^{\text{total}}\\ -K_{r\text{,tumor}}^{\text{ag}}{C}_{\text{V,tumor}}^{\text{agEB}}{V}_{\text{V,tumor}}\\ -K_{f\text{,tumor}}^{\text{a}}{C}_{\text{V,tumor}}^{\text{agEB}}{V}_{\text{V,tumor}}\\ -E_{\text{tumor}}^{\text{cEB}}{C}_{\text{V,tumor}}^{\text{agEB}}{V}_{\text{V,tumor}}\\ +K_{f\text{,tumor}}^{\text{CD}}{C}_{\text{V,tumor}}^{\text{agB}}{C}_{\text{V,tumor}}^{\text{EB}}fC{D}_{\text{V,tumor}}{V}_{\text{V,tumor}}/C_{\text{V,tumor}}^{\text{total}}\\ -K_{r\text{,tumor}}^{\text{CD}}{C}_{\text{V,tumor}}^{\text{agEB}}{V}_{\text{V,tumor}}\end{array}\end{array}$$

  • Arrested EC-BFA complex in vascular space

    $$\begin{array}{cc}\begin{array}{c}\begin{array}{c}\begin{array}{c}{V}_{\text{V,tumor}}\frac{d{C}_{\text{V,tumor}}^{\text{aEB}}}{dt}=\\ \end{array}\\ \end{array}\\ \end{array}& \begin{array}{l}{K}_{f,\text{tumor}}^{\text{a}}{C}_{\text{V,tumor}}^{\text{cEB}}{V}_{\text{V,tumor}}\\ +K_{f,\text{tumor}}^{\text{a}}{C}_{\text{V,tumor}}^{\text{agEB}}{V}_{\text{V,tumor}}\\ -E_{\text{tumor}}^{\text{aEB}}{C}_{\text{V,tumor}}^{\text{aEB}}{V}_{\text{V,tumor}}\\ -J_{\text{tumor}}^{\text{aEB}}{C}_{\text{V,tumor}}^{\text{aEB}}{V}_{\text{V,tumor}}\end{array}\end{array}$$

  • BFA bound to effector cells in vascular space

    $$\begin{array}{l}{V}_{\text{V,tumor}}\frac{d{C}_{\text{V,tumor}}^{\text{bB}}}{dt}=Q_{\text{tumor}}{C}_{\text{V,tumor}}^{\text{bB}}\\ \begin{array}{cc}\begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}& -(\end{array}{Q}_{\text{tumor}}-L_{\text{tumor}})C_{\text{V,tumor}}^{\text{bB}}{C}_{\text{V,tumor}}^{\text{EB}}/C_{\text{V,tumor}}^{\text{total}}\\ \begin{array}{cc}& \begin{array}{cc}& \begin{array}{cc}& \begin{array}{l}\text{+}{K}_{f,\text{tumor}}^{\text{CD}}{C}_{\text{V,tumor}}^{\text{fB}}fC{D}_{\text{V,tumor}}{V}_{\text{V,tumor}}\\ -K_{r,\text{tumor}}^{\text{CD}}(C_{\text{V,tumor}}^{\text{bB}}-C_{\text{V,tumor}}^{\text{agEB}})V_{\text{V,tumor}}\\ +K_{f,\text{tumor}}^{\text{CD}}{C}_{\text{V,tumor}}^{\text{agB}}{C}_{\text{V,tumor}}^{\text{EB}}fC{D}_{\text{V,tumor}}{V}_{\text{V,tumor}}/C_{\text{V,tumor}}^{\text{total}}\\ -K_{r,\text{tumor}}^{\text{CD}}{C}_{\text{V,tumor}}^{\text{agEB}}{V}_{\text{V,tumor}}\\ -J_{\text{tumor}}^{\text{aEB}}{C}_{\text{V,tumor}}^{\text{aEB}}{C}_{\text{V,tumor}}^{\text{bB}}{V}_{\text{V,tumor}}/C_{\text{V,tumor}}^{\text{total}}\\ -E_{\text{tumor}}^{\text{cEB}}{C}_{\text{V,tumor}}^{\text{cEB}}{C}_{\text{V,tumor}}^{\text{bB}}{V}_{\text{V,tumor}}/C_{\text{V,tumor}}^{\text{total}}\\ -E_{\text{tumor}}^{\text{cEB}}{C}_{\text{V,tumor}}^{\text{agEB}}{C}_{\text{V,tumor}}^{\text{bB}}{V}_{\text{V,tumor}}/C_{\text{V,tumor}}^{\text{total}}\\ -E_{\text{tumor}}^{\text{aEB}}{C}_{\text{V,tumor}}^{\text{aEB}}{C}_{\text{V,tumor}}^{\text{bB}}{V}_{\text{V,tumor}}/C_{\text{V,tumor}}^{\text{total}}\end{array}\end{array}\end{array}\end{array}\end{array}$$

  • Free BFA in the extravascular space

    $$\begin{array}{l}{V}_{\text{EV,tumor}}\frac{d{C}_{\text{EV,tumor}}^{\text{fB}}}{dt}=J_{\text{tumor}}^{\text{fB}}\\ \begin{array}{cc}\begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}& \begin{array}{l}-L_{\text{tumor}}{C}_{\text{EV,tumor}}^{\text{fB}}\\ -K_{f,\text{tumor}}^{\text{CD}}{C}_{\text{EV,tumor}}^{\text{fB}}fC{D}_{\text{EV,tumor}}{V}_{\text{EV,tumor}}\\ +K_{r,\text{tumor}}^{\text{CD}}(C_{\text{EV,tumor}}^{\text{bB}}-C_{\text{EV,tumor}}^{\text{nEB}}-C_{\text{EV,tumor}}^{\text{agEB}})V_{\text{EV,tumor}}\\ -K_{f,\text{tumor}}^{\text{ag}}{C}_{\text{EV,tumor}}^{\text{fB}}f{A}_{\text{EV,tumor}}{V}_{\text{EV,tumor}}\\ +K_{r,\text{tumor}}^{\text{ag}}{C}_{\text{EV,tumor}}^{\text{agB}}{V}_{\text{EV,tumor}}\\ -K_{r,\text{tumor}}^{\text{n}}{C}_{\text{EV,tumor}}^{\text{fB}}{V}_{\text{EV,tumor}}\\ \text{+}{K}_{r,\text{tumor}}^{\text{n}}{C}_{\text{EV,tumor}}^{\text{nB}}{V}_{\text{EV,tumor}}\end{array}\end{array}\end{array}$$

  • BFA bound to tumor antigens in the extravascular space

    $$\begin{array}{l}{V}_{\text{EV,tumor}}\frac{d{C}_{\text{EV,tumor}}^{\text{agB}}}{dt}=K_{f,\text{tumor}}^{\text{ag}}{C}_{\text{EV,tumor}}^{\text{fB}}f{A}_{\text{EV,tumor}}{V}_{\text{EV,tumor}}\\ \begin{array}{cc}& \begin{array}{l}-K_{r,\text{tumor}}^{\text{ag}}{C}_{\text{EV,tumor}}^{\text{agB}}{V}_{\text{EV,tumor}}\\ -K_{f,\text{tumor}}^{\text{CD}}{C}_{\text{EV,tumor}}^{\text{agB}}{C}_{\text{EV,tumor}}^{\text{EB}}fC{D}_{\text{EV,tumor}}{V}_{\text{EV,tumor}}/C_{\text{EV,tumor}}^{\text{total}}\\ +K_{r,\text{tumor}}^{\text{CD}}{C}_{\text{EV,tumor}}^{\text{agEB}}{V}_{\text{EV,tumor}}\end{array}\end{array}\end{array}$$

  • Nonspecifically bound BFA in the extravascular space

    $$\begin{array}{l}{V}_{\text{EV,tumor}}\frac{d{C}_{\text{EV,tumor}}^{\text{nB}}}{dt}=K_{f,\text{tumor}}^{\text{n}}{C}_{\text{EV,tumor}}^{\text{fB}}{V}_{\text{EV,tumor}}\\ \begin{array}{cc}& \begin{array}{l}-K_{r,\text{tumor}}^{\text{n}}{C}_{\text{EV,tumor}}^{\text{nB}}{V}_{\text{EV,tumor}}\\ -K_{f,\text{tumor}}^{\text{CD}}{C}_{\text{EV,tumor}}^{\text{nB}}{C}_{\text{EV,tumor}}^{\text{EB}}fC{D}_{\text{EV,tumor}}{V}_{\text{EV,tumor}}/C_{\text{EV,tumor}}^{\text{total}}\\ +K_{r,\text{tumor}}^{\text{CD}}{C}_{\text{EV,tumor}}^{\text{nEB}}{V}_{\text{EV,tumor}}\end{array}\end{array}\end{array}$$

  • Free EC-BFA complex in the extravascular space

    $$\begin{array}{l}{V}_{\text{EV,tumor}}\frac{d{C}_{\text{EV,tumor}}^{\text{EB}}}{dt}=J_{\text{tumor}}^{\text{aEB}}{C}_{\text{V,tumor}}^{\text{aEB}}{V}_{\text{V,tumor}}\\ \begin{array}{cc}& \begin{array}{l}-K_{f,\text{tumor}}^{\text{ag}}{C}_{\text{EV,tumor}}^{\text{EB}}f{A}_{\text{EV,tumor}}oC{D}_{\text{EV,tumor}}{V}_{\text{EV,tumor}}/C_{\text{EV,tumor}}^{\text{total}}\\ +K_{r,\text{tumor}}^{\text{ag}}{C}_{\text{EV,tumor}}^{\text{agEB}}{V}_{\text{EV,tumor}}\\ -K_{f,\text{tumor}}^{\text{n}}{C}_{\text{EV,tumor}}^{\text{EB}}oC{D}_{\text{EV,tumor}}{V}_{\text{EV,tumor}}/C_{\text{EV,tumor}}^{\text{total}}\\ +K_{r,\text{tumor}}^{\text{n}}{C}_{\text{EV,tumor}}^{\text{nEB}}{V}_{\text{EV,tumor}}\\ -L_{\text{tumor}}{C}_{\text{EV,tumor}}^{\text{EB}}{F}_{\text{tumor}}\\ -K_{f,\text{tumor}}^{\text{CD}}{C}_{\text{EV,tumor}}^{\text{agB}}{C}_{\text{EV,tumor}}^{\text{EB}}fC{D}_{\text{EV,tumor}}{V}_{\text{EV,tumor}}/C_{\text{EV,tumor}}^{\text{total}}\\ -K_{f,\text{tumor}}^{\text{CD}}{C}_{\text{EV,tumor}}^{\text{nB}}{C}_{\text{EV,tumor}}^{\text{EB}}fC{D}_{\text{EV,tumor}}{V}_{\text{EV,tumor}}/C_{\text{EV,tumor}}^{\text{total}}\\ +K_{r,\text{tumor}}^{\text{CD}}{C}_{\text{EV,tumor}}^{\text{agEB}}{V}_{\text{EV,tumor}}\\ +K_{r,\text{tumor}}^{\text{CD}}{C}_{\text{EV,tumor}}^{\text{nEB}}{V}_{\text{EV,tumor}}\end{array}\end{array}\end{array}$$

  • Nonspecifically bound EC-BFA complex in the extravascular space

    $$\begin{array}{l}{V}_{\text{EV,tumor}}\frac{d{C}_{\text{EV,tumor}}^{\text{nEB}}}{dt}=K_{f,\text{tumor}}^{\text{n}}{C}_{\text{EV,tumor}}^{\text{EB}}oC{D}_{\text{EV,tumor}}{V}_{\text{EV,tumor}}/C_{\text{EV,tumor}}^{\text{total}}\\ \begin{array}{cc}\begin{array}{cc}& \end{array}& \begin{array}{l}-K_{r,\text{tumor}}^{\text{n}}{C}_{\text{EV,tumor}}^{\text{nEB}}{V}_{\text{EV,tumor}}\\ +K_{f,\text{tumor}}^{\text{CD}}{C}_{\text{EV,tumor}}^{\text{nB}}{C}_{\text{EV,tumor}}^{\text{EB}}fC{D}_{\text{EV,tumor}}{V}_{\text{EV,tumor}}/C_{\text{EV,tumor}}^{\text{total}}\\ -K_{r,\text{tumor}}^{\text{CD}}{C}_{\text{EV,tumor}}^{\text{nEB}}{V}_{\text{EV,tumor}}\end{array}\end{array}\end{array}$$

  • EC-BFA bound to tumor antigens in the extravascular space

    $$\begin{array}{cc}\begin{array}{c}\begin{array}{c}\begin{array}{c}{V}_{\text{EV,tumor}}\frac{d{C}_{\text{EV,tumor}}^{\text{agEB}}}{dt}=\\ \end{array}\\ \end{array}\\ \end{array}& \begin{array}{l}{K}_{f,\text{tumor}}^{\text{ag}}{C}_{\text{EV,tumor}}^{\text{EB}}f{A}_{\text{EV,tumor}}oC{D}_{\text{EV,tumor}}{V}_{\text{EV,tumor}}/C_{\text{EV,tumor}}^{\text{total}}\\ -K_{r,\text{tumor}}^{\text{ag}}{C}_{\text{EV,tumor}}^{\text{agEB}}{V}_{\text{EV,tumor}}\\ +K_{f,\text{tumor}}^{\text{CD}}{C}_{\text{EV,tumor}}^{\text{agB}}{C}_{\text{EV,tumor}}^{\text{EB}}fC{D}_{\text{EV,tumor}}{V}_{\text{EV,tumor}}/C_{\text{EV,tumor}}^{\text{total}}\\ -K_{r,\text{tumor}}^{\text{CD}}{C}_{\text{EV,tumor}}^{\text{agEB}}{V}_{\text{EV,tumor}}\end{array}\end{array}$$

  • BFA bound to effector cells in the extravascular space

    $$\begin{array}{l}{V}_{\text{EV,tumor}}\frac{d{C}_{\text{EV,tumor}}^{\text{bB}}}{dt}=K_{f,\text{tumor}}^{\text{CD}}{C}_{\text{EV,tumor}}^{\text{fB}}fC{D}_{\text{EV,tumor}}{V}_{\text{EV,tumor}}\\ \begin{array}{cc}& \begin{array}{l}-K_{r,\text{tumor}}^{\text{CD}}(C_{\text{EV,tumor}}^{\text{bB}}-C_{\text{EV,tumor}}^{\text{agEB}}-C_{\text{EV,tumor}}^{\text{nEB}})V_{\text{EV,tumor}}\\ +K_{f,\text{tumor}}^{\text{CD}}{C}_{\text{EV,tumor}}^{\text{agB}}{C}_{\text{EV,tumor}}^{\text{EB}}fC{D}_{\text{EV,tumor}}{V}_{\text{EV,tumor}}/C_{\text{EV,tumor}}^{\text{total}}\\ -K_{r,\text{tumor}}^{\text{CD}}{C}_{\text{EV,tumor}}^{\text{agEB}}{V}_{\text{EV,tumor}}\\ +K_{f,\text{tumor}}^{\text{CD}}{C}_{\text{EV,tumor}}^{\text{nB}}{C}_{\text{EV,tumor}}^{\text{EB}}fC{D}_{\text{EV,tumor}}{V}_{\text{EV,tumor}}/C_{\text{EV,tumor}}^{\text{total}}\\ -K_{r,\text{tumor}}^{\text{CD}}{C}_{\text{EV,tumor}}^{\text{nEB}}{V}_{\text{EV,tumor}}\\ +J_{\text{tumor}}^{\text{aEB}}{C}_{\text{V,tumor}}^{\text{aEB}}{C}_{\text{V,tumor}}^{\text{bB}}{V}_{\text{V,tumor}}/C_{\text{EV,tumor}}^{\text{total}}\\ -L_{\text{tumor}}{C}_{\text{EV,tumor}}^{\text{EB}}{F}_{\text{tumor}}{C}_{\text{EV,tumor}}^{\text{bB}}/C_{\text{EV,tumor}}^{\text{total}}\end{array}\end{array}\end{array}$$

• Other Organs (Bone, Gl, Heart, Kidney, Muscle, Skin, and Spleen)

  • Free BFA in vascular space (bone, Gl, heart, muscle, skin and spleen)

    $$\begin{array}{cc}\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}{V}_{\text{V,}i}\frac{d{C}_{\text{V},i}^{\text{fB}}}{dt}=\\ \end{array}\\ \end{array}\\ \end{array}\\ \end{array}& \begin{array}{l}{Q}_i{C}_{\text{V,plasma}}^{\text{fB}}\\ -(Q_i-L_i)C_{\text{V},i}^{\text{fB}}\\ -J_i^{\text{fB}}\\ -K_{f,i}^{\text{CD}}{C}_{\text{V},i}^{\text{fB}}fC{D}_{\text{V,}i}{V}_{\text{V,}i}\\ +K_{r,i}^{\text{CD}}{C}_{\text{V},i}^{\text{bB}}{V}_{\text{V,}i}\end{array}\end{array}$$

  • Free BFA in vascular space (kidney)

    $$\begin{array}{cc}\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}{V}_{\text{V,kidney}}\frac{d{C}_{\text{V,kidney}}^{\text{fB}}}{dt}=\\ \end{array}\\ \end{array}\\ \end{array}\\ \begin{array}{c}\begin{array}{c}\\ \end{array}\\ \end{array}\end{array}& \begin{array}{l}{Q}_{\text{kidney}}{C}_{\text{V,plasma}}^{\text{fB}}\\ -(Q_{\text{kidney}}-L_{\text{kidney}})C_{\text{V},\text{kidney}}^{\text{fB}}\\ -J_{\text{kidney}}^{\text{fB}}\\ -K_{f\text{,kidney}}^{\text{CD}}{C}_{\text{V,kidney}}^{\text{fB}}fC{D}_{\text{V,kidney}}{V}_{\text{V,kidney}}\\ +K_{r\text{,kidney}}^{\text{CD}}{C}_{\text{V},\text{kidney}}^{\text{bB}}{V}_{\text{V},\text{kidney}}\\ -E_{\text{kidney}}^{\text{fB}}{C}_{\text{V,kidney}}^{\text{bB}}\end{array}\end{array}$$

  • Free EC-BFA complex in vascular space

    $$\begin{array}{cc}\begin{array}{c}\begin{array}{c}\begin{array}{c}{V}_{\text{V},i}\frac{d{C}_{\text{V,}i}^{\text{EB}}}{dt}=\\ \end{array}\\ \end{array}\\ \end{array}& \begin{array}{l}{Q}_i{C}_{\text{V,plasma}}^{\text{EB}}\\ -(Q_i-L_i)C_{\text{V,}i}^{\text{EB}}\\ -K_{f,i}^{\text{c}}{C}_{\text{V,}i}^{\text{EB}}f{C}_{\text{V,}i}{V}_{\text{V,}i}\\ +K_{r,i}^{\text{c}}{C}_{\text{V,}i}^{\text{cEB}}{V}_{\text{V,}i}\end{array}\end{array}$$

  • Captured EC-BFA complex in vascular space

    $$\begin{array}{cc}\begin{array}{c}\begin{array}{c}\begin{array}{c}{V}_{\text{V},i}\frac{d{C}_{\text{V,}i}^{\text{cEB}}}{dt}=\\ \end{array}\\ \end{array}\\ \end{array}& \begin{array}{l}{K}_{f,i}^{\text{c}}{C}_{\text{V,}i}^{\text{EB}}f{C}_{\text{V,}i}{V}_{\text{V,}i}\\ -K_{r,i}^{\text{c}}{C}_{\text{V,}i}^{\text{cEB}}{V}_{\text{V,}i}\\ -K_{f,i}^{\text{a}}{C}_{\text{V,}i}^{\text{cEB}}{V}_{\text{V,}i}\\ -E_i^{\text{cEB}}{C}_{\text{V,}i}^{\text{cEB}}{V}_{\text{V,}i}\end{array}\end{array}$$

  • Arrested EC-BFA complex in vascular space

    $$\begin{array}{cc}\begin{array}{c}\begin{array}{c}{V}_{\text{V},i}\frac{d{C}_{\text{V,}i}^{\text{aEB}}}{dt}=\\ \end{array}\\ \end{array}& \begin{array}{l}{K}_{f,i}^{\text{a}}{C}_{\text{V,}i}^{\text{cEB}}{V}_{\text{V,}i}\\ -E_i^{\text{aEB}}{C}_{\text{V,}i}^{\text{aEB}}{V}_{\text{V,}i}\\ -J_i^{\text{aEB}}{C}_{\text{V,}i}^{\text{aEB}}{V}_{\text{V,}i}\end{array}\end{array}$$

  • BFA bound to effector cells in vascular space

    $$\begin{array}{cc}\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}{V}_{\text{V,}i}\frac{d{C}_{\text{V,}i}^{\text{bB}}}{dt}=\\ \end{array}\\ \end{array}\\ \end{array}\\ \begin{array}{c}\begin{array}{c}\\ \end{array}\\ \begin{array}{c}\\ \end{array}\end{array}\end{array}& \begin{array}{l}{Q}_i{C}_{\text{V,plasma}}^{\text{bB}}\\ -(Q_i-L_i)C_{\text{V},i}^{\text{bB}}{C}_{\text{V,}i}^{\text{EB}}/C_{\text{V,}i}^{\text{total}}\\ +K_{f,i}^{\text{CD}}{C}_{\text{V},i}^{\text{fB}}fC{D}_{\text{V},i}{V}_{\text{V},i}\\ -K_{r,i}^{\text{CD}}{C}_{\text{V},i}^{\text{bB}}{V}_{\text{V},i}\\ -J_i^{\text{aEB}}{C}_{\text{V},i}^{\text{aEB}}{C}_{\text{V},i}^{\text{bB}}{V}_{\text{V},i}/C_{\text{V},i}^{\text{total}}\\ -E_i^{\text{cEB}}{C}_{\text{V},i}^{\text{cEB}}{C}_{\text{V},i}^{\text{bB}}{V}_{\text{V},i}/C_{\text{V},i}^{\text{total}}\\ -E_i^{\text{aEB}}{C}_{\text{V},i}^{\text{aEB}}{C}_{\text{V},i}^{\text{bB}}{V}_{\text{V},i}/C_{\text{V},i}^{\text{total}}\end{array}\end{array}$$

  • Free BFA in the extravascular space

    $$\begin{array}{cc}\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}{V}_{\text{EV,}i}\frac{d{C}_{\text{EV,}i}^{\text{fB}}}{dt}=\\ \end{array}\\ \end{array}\\ \end{array}\\ \begin{array}{c}\begin{array}{c}\\ \end{array}\\ \end{array}\end{array}& \begin{array}{l}{J}_i^{\text{fB}}\\ -L_i{C}_{\text{EV},i}^{\text{fB}}\\ -K_{f,i}^{\text{CD}}{C}_{\text{EV},i}^{\text{fB}}fC{D}_{\text{EV},i}{V}_{\text{EV},i}\\ +K_{r,i}^{\text{CD}}(C_{\text{EV},i}^{\text{bB}}-C_{\text{EV},i}^{\text{nEB}})V_{\text{EV},i}\\ -K_{f,i}^{\text{n}}{C}_{\text{EV},i}^{\text{fB}}{V}_{\text{EV},i}\\ +K_{r,i}^{\text{n}}{C}_{\text{EV},i}^{\text{nB}}{V}_{\text{EV},i}\end{array}\end{array}$$

  • Nonspecifically bound BFA in the extravascular space

    $$\begin{array}{cc}\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}{V}_{\text{EV},i}\frac{d{C}_{\text{EV,}i}^{\text{nB}}}{dt}=\\ \end{array}\\ \end{array}\\ \end{array}\\ \end{array}& \begin{array}{l}{K}_{f,i}^{\text{n}}{C}_{\text{EV},i}^{\text{fB}}{V}_{\text{EV,}i}\\ -K_{r,i}^{\text{n}}{C}_{\text{EV},i}^{\text{nB}}{V}_{\text{EV,}i}\\ -K_{f,i}^{\text{CD}}{C}_{\text{EV},i}^{\text{nB}}{C}_{\text{EV},i}^{\text{EB}}fC{D}_{\text{EV,}i}{V}_{\text{EV,}i}/C_{\text{EV},i}^{\text{total}}\\ +K_{r,i}^{\text{CD}}{C}_{\text{EV},i}^{\text{nEB}}{V}_{\text{EV,}i}\end{array}\end{array}$$

  • Free EC-BFA complex in the extravascular space

    $$\begin{array}{cc}\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}{V}_{\text{EV,}i}\frac{d{C}_{\text{EV,}i}^{\text{EB}}}{dt}=\\ \end{array}\\ \end{array}\\ \end{array}\\ \begin{array}{c}\begin{array}{c}\\ \end{array}\\ \end{array}\end{array}& \begin{array}{l}{J}_i^{\text{aEB}}{C}_{\text{V},i}^{\text{aEB}}{V}_{\text{V},i}\\ +K_{r,i}^{\text{n}}{C}_{\text{EV},i}^{\text{nEB}}{V}_{\text{EV},i}\\ -K_{f,i}^{\text{n}}{C}_{\text{EV},i}^{\text{EB}}oC{D}_{\text{EV},i}{V}_{\text{EV},i}/C_{\text{EV},i}^{\text{total}}\\ -L_i{C}_{\text{EV},i}^{\text{EB}}{F}_i\\ -K_{f,i}^{\text{CD}}{C}_{\text{EV},i}^{\text{nB}}{C}_{\text{EV},i}^{\text{EB}}fC{D}_{\text{EV},i}{V}_{\text{EV},i}/C_{\text{EV},i}^{\text{total}}\\ +K_{r,i}^{\text{CD}}{C}_{\text{EV},i}^{\text{nEB}}{V}_{\text{EV},i}\end{array}\end{array}$$

  • Nonspecifically bound EC-BFA complex in the extravascular space

    $$\begin{array}{cc}\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}{V}_{\text{EV},i}\frac{d{C}_{\text{EV,}i}^{\text{nEB}}}{dt}=\\ \end{array}\\ \end{array}\\ \end{array}\\ \end{array}& \begin{array}{l}{K}_{f,i}^{\text{n}}{C}_{\text{EV},i}^{\text{EB}}oC{D}_{\text{EV,}i}{V}_{\text{EV,}i}/C_{\text{EV},i}^{\text{total}}\\ -K_{r,i}^{\text{n}}{C}_{\text{EV},i}^{\text{nEB}}{V}_{\text{EV,}i}\\ +K_{f,i}^{\text{CD}}{C}_{\text{EV},i}^{\text{nB}}{C}_{\text{EV},i}^{\text{EB}}fC{D}_{\text{EV,}i}{V}_{\text{EV,}i}/C_{\text{EV},i}^{\text{total}}\\ -K_{r,i}^{\text{CD}}{C}_{\text{EV},i}^{\text{nEB}}{V}_{\text{EV,}i}\end{array}\end{array}$$

  • BFA bound to effector cells in the extravascular space

    $$\begin{array}{cc}\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}{V}_{\text{EV,}i}\frac{d{C}_{\text{EV,}i}^{\text{bB}}}{dt}=\\ \end{array}\\ \end{array}\\ \end{array}\\ \begin{array}{c}\begin{array}{c}\\ \end{array}\\ \end{array}\end{array}& \begin{array}{l}{K}_{f,i}^{\text{CD}}{C}_{\text{EV},i}^{\text{fB}}fC{D}_{\text{EV},i}{V}_{\text{EV},i}\\ -K_{r,i}^{\text{CD}}(C_{\text{EV},i}^{\text{bB}}-C_{\text{EV},i}^{\text{nEB}})V_{\text{EV},i}\\ +K_{f,i}^{\text{CD}}{C}_{\text{EV},i}^{\text{nB}}{C}_{\text{EV},i}^{\text{EB}}fC{D}_{\text{EV},i}{V}_{\text{EV},i}/C_{\text{EV},i}^{\text{total}}\\ -K_{r,i}^{\text{CD}}{C}_{\text{EV},i}^{\text{nEB}}{V}_{\text{EV},i}\\ +J_i^{\text{aEB}}{C}_{\text{V},i}^{\text{aEB}}{C}_{\text{V},i}^{\text{bB}}{V}_{\text{V},i}/C_{\text{V},i}^{\text{total}}\\ -L_i{C}_{\text{EV},i}^{\text{EB}}{F}_i{C}_{\text{EV},i}^{\text{bB}}/C_{\text{EV},i}^{\text{total}}\end{array}\end{array}$$

Appendix C

Other Model Equations

• Plasma

  • Adhesion site density

    $$fC{D}_{\text{V,plasma}}=C_{\text{V,plasma}}^{\text{EB}}CD-C_{\text{V,plasma}}^{\text{bB}}$$

• Tumor

  • Transcapillary exchange rate of free BFA

    $$\begin{array}{l}{J}_{\text{tumor}}^{\text{fB}}=J_{L,\text{tumor}}(1-{\sigma }_{L,\text{tumor}})C_{\text{V,tumor}}^{\text{fB}}\\ \begin{array}{cc}& +{\text{PS}}_{L\text{,tumor}}[\end{array}{C}_{\text{V,tumor}}^{\text{fB}}-(C_{\text{EV,tumor}}^{\text{fB}}/k_{\text{tumor}})]{\text{Pe}}_{L\text{,tumor}}/(e^{{\text{Pe}}_{L\text{,tumor}}}-1)\\ \begin{array}{cc}& \begin{array}{l}+{\text{J}}_{\text{S,tumor}}(1-{\sigma }_{S,\text{tumor}})C_{\text{V,tumor}}^{\text{fB}}\\ +{\text{PS}}_{S\text{,tumor}}[C_{\text{V,tumor}}^{\text{fB}}-(C_{\text{EV,tumor}}^{\text{fB}}/k_{\text{tumor}})]{\text{Pe}}_{S\text{,tumor}}/(e^{{\text{Pe}}_{S\text{,tumor}}}-1)\end{array}\end{array}\end{array}$$

  • Total concentration of cells

    $$\begin{array}{l}{C}_{\text{V,tumor}}^{\text{total}}=C_{\text{V,tumor}}^{\text{EB}}+C_{\text{V,tumor}}^{\text{agEB}}+C_{\text{V,tumor}}^{\text{cEB}}+C_{\text{V,tumor}}^{\text{aEB}}\\ \\ C_{\text{EV,tumor}}^{\text{total}}=C_{\text{EV,tumor}}^{\text{EB}}+C_{\text{EV,tumor}}^{\text{agEB}}+C_{\text{EV,tumor}}^{\text{nEB}}\end{array}$$

  • Adhesion site densities

    $$\begin{array}{l}fC{D}_{\text{V,tumor}}=C_{\text{V,tumor}}^{\text{total}}CD-C_{\text{V,tumor}}^{\text{bB}}\\ \\ fC{D}_{\text{EV,tumor}}=C_{\text{EV,tumor}}^{\text{total}}CD-C_{\text{EV,tumor}}^{\text{bB}}\\ \\ oC{D}_{\text{V,tumor}}=C_{\text{V,tumor}}^{\text{bB}}\\ \\ oC{D}_{\text{EV,tumor}}=C_{\text{EV,tumor}}^{\text{bB}}\\ \\ f{A}_{\text{V,tumor}}=A_{\text{V,tumor}}-C_{\text{V,tumor}}^{\text{agEB}}-C_{\text{V,tumor}}^{\text{agB}}\\ \\ f{A}_{EV,tumor}=A_{EV,tumor}-C_{EV,tumor}^{\text{agEB}}-C_{EV,tumor}^{\text{agB}}\\ \\ f{C}_{V,tumor}=C_{tumor}-C_{V,tumor}^{\text{cEB}}-C_{V,tumor}^{\text{aEB}}\end{array}$$

• Other Organs (Lung, Liver, Lymph Node, Bone, GI, Heart, Kidney, Muscle, Skin, and Spleen)

  • Transcapillary exchange rate of free BFA

    $$\begin{array}{cc}\begin{array}{c}\begin{array}{c}\begin{array}{c}{J}_i^{\text{fB}}=\\ \begin{array}{c}\\ \end{array}\end{array}\\ \end{array}\\ \end{array}& \begin{array}{l}{J}_{L,i}(1-{\sigma }_{L,i})C_{\text{V},i}^{\text{fB}}\\ +{\text{PS}}_{L,i}\left[C_{\text{V},i}^{\text{fB}}-\left(C_{\text{EV},i}^{\text{fB}}/k_i\right)\right]{\text{Pe}}_{L,i}/\left(e^{{\text{Pe}}_{L,i}}-1\right)\\ +J_{S,i}\left(1-{\sigma }_{S,i}\right)C_{\text{V},i}^{\text{fB}}\\ +{\text{PS}}_{S,i}\left[C_{\text{V},i}^{\text{fB}}-\left(C_{\text{EV},i}^{\text{fB}}/k_i\right)\right]{\text{Pe}}_{S,i}/\left(e^{{\text{Pe}}_{S,i}}-1\right)\end{array}\end{array}$$

  • Total concentration of cells

    $$\begin{array}{l}{C}_{\text{V},i}^{\text{total}}=C_{\text{V},i}^{\text{EB}}+C_{\text{V},i}^{\text{cEB}}+C_{\text{V},i}^{\text{aEB}}\\ \\ C_{\text{EV},i}^{\text{total}}=C_{\text{EV},i}^{\text{EB}}+C_{\text{EV},i}^{\text{nEB}}\end{array}$$

  • Adhesion site densities

    $$\begin{array}{l}fC{D}_{\text{V},i}=C_{\text{V},i}^{\text{total}}CD-C_{\text{V},i}^{\text{bB}}\\ \\ fC{D}_{\text{EV},i}=C_{\text{EV},i}^{\text{total}}CD-C_{\text{EV},i}^{\text{bB}}\\ \\ oC{D}_{\text{V},i}=C_{\text{V},i}^{\text{bB}}\\ \\ oC{D}_{\text{EV},i}=C_{\text{EV},i}^{\text{bB}}\\ \\ f{C}_{\text{V},i}=C_i-C_{\text{V},i}^{\text{cEB}}-C_{\text{V},i}^{\text{aEB}}\end{array}$$