A Bayesian framework for combining heterogeneous data sources for gene function prediction (in Saccharomyces cerevisiae)

Abstract

Genomic sequencing is no longer a novelty, but gene function annotation remains a key challenge in modern biology. A variety of functional genomics experimental techniques are available, from classic methods such as affinity precipitation to advanced high-throughput techniques such as gene expression microarrays. In the future, more disparate methods will be developed, further increasing the need for integrated computational analysis of data generated by these studies. We address this problem with magic (Multisource Association of Genes by Integration of Clusters), a general framework that uses formal Bayesian reasoning to integrate heterogeneous types of high-throughput biological data (such as large-scale two-hybrid screens and multiple microarray analyses) for accurate gene function prediction. The system formally incorporates expert knowledge about relative accuracies of data sources to combine them within a normative framework. magic provides a belief level with its output that allows the user to vary the stringency of predictions. We applied magic to Saccharomyces cerevisiae genetic and physical interactions, microarray, and transcription factor binding sites data and assessed the biological relevance of gene groupings using Gene Ontology annotations produced by the Saccaromyces Genome Database. We found that by creating functional groupings based on heterogeneous data types, magic improved accuracy of the groupings compared with microarray analysis alone. We describe several of the biological gene groupings identified.

In recent years, increasing quantities of high-throughput biological data have become available. Many of these, such as protein–protein interaction studies [affinity precipitation (1), two-hybrid techniques (2), synthetic rescue (3) and lethality (3, 4) experiments, and microarray analysis (5)], assess functional relationships between gene products on a large scale. Because the functions of significant numbers of proteins remain unknown, even in model organisms, these high-throughput data may be key to assigning accurate functional annotation on a large scale. Such predictions can advance experimental studies by providing specific hypotheses for targeted experimental testing.

However, many high-throughput methods sacrifice specificity for scale. Microarray analysis can provide gene function predictions by assessing coexpression relationships in a high-throughput fashion. Whereas gene coexpression data are an excellent tool for hypothesis generation, microarray data alone often lack the degree of specificity needed for accurate gene function prediction. For such purposes, an increase in accuracy is needed, even if it comes at the cost of some sensitivity. This improvement in specificity can be achieved through incorporation of heterogeneous functional data in an integrated analysis.

The value of combining groupings of genes obtained from different methods has been illustrated by several studies where functional predictions were made based on several types of data (6–9). For example, Marcotte et al. predicted a number of potential protein functions for Saccharomyces cerevisiae based on a heuristic combination of different types of data (6, 7). However, these studies combine the information from different sources in a semimanual and heuristic fashion, where confidence levels for protein–protein links are defined subjectively on a case-by-case basis and no general scheme or probabilistic representation is applied. Other groups have developed methods to combine gene expression data with one or two specific nonmicroarray data sources (10–15), and such combinations lead to improved functional annotation (16, 17). There is a need for a general method of integrating disparate high-throughput biological data for gene function prediction.

Here we introduce magic (Multisource Association of Genes by Integration of Clusters), a flexible probabilistic framework for integrated analysis of high-throughput biological data. The current version of the system is implemented for S. cerevisiae, for which multiple useful data sources exist. The system is based on a Bayesian network (18) that combines evidence from diverse data sources (including microarray analysis methods) to predict whether two proteins are functionally related (involved in a common biological process). The network essentially performs a probabilistic “weighting” of data sources, thus avoiding double counting evidence and allowing for formal representation of expert knowledge about the methods. Each predicted functional relationship is assigned a posterior belief, allowing the user to vary the level of stringency of the predictions.

In this study, we describe magic and illustrate its utility on physical and genetic interactions data, information about experimentally determined transcription factor binding sites, and a published S. cerevisiae stress-response expression dataset. We show that magic can systematically incorporate nonexpression biological data in microarray analysis, a task that cannot be accomplished by simply adding this complex pairwise data to microarray clustering methods. We demonstrate an increase in accuracy of predicted functional relationships by magic, as compared with its input methods. We describe top gene groupings created by magic and functional predictions based on them.

Methods

System Design. The magic system has a distributed design that promotes flexibility for adding new input methods and datasets. magic provides a general framework that can incorporate a number of data types and microarray analysis methods. The network includes yeast protein–protein interactions from General Repository of Interaction Datasets (GRID) (19) and pairs of genes that have experimentally determined binding sites for the same transcription factor, derived from The Promoter Database of Saccharomyces cerevisiae (20). In addition, magic incorporates gene expression data analyses by the three most widely used microarray analysis methods: K-means clustering, self-organizing maps, and hierarchical clustering.

The inputs of the system are groupings (or clusters) of genes based on coexpression or other experimental data (e.g., transcription factor binding sites). magic's main component, its Bayesian network, combines evidence from input groupings and generates a posterior belief for whether each gene i–gene j pair has a functional relationship. For each pair of genes, magic essentially asks the following question: What is the probability, based on the evidence presented, that products of genes i and j have a functional relationship (i.e., are involved in the same biological process)? We define biological process broadly as a systematic combination of molecular functions for the purpose of a specific biological goal, e.g., metabolism. This definition is based on the definition of biological process given by the Gene Ontology (GO) Consortium (21).

The Bayesian network receives as input gene–gene relationship matrices, each representing one data source, where element s_i,j ≠ 0 if genes i and j are believed to have a functional relationship and s_i,j = 0 if they do not. As each different method (or a different set of parameters of the same method) creates each matrix, the definition of criteria for functional relationship for each input matrix relies on the method used to create the particular matrix (e.g., genes that are in the same cluster for clustering algorithms). The score s_i,j corresponds to the strength of each method's belief in the existence of relationship between genes i and j. This score can be a binary (e.g., results of coimmunoprecipitation experiments), continuous, or discrete variable (e.g., -1 ≤ s ≤ 1 for Pearson correlation; see supporting information, which is published on the PNAS web site, www.pnas.org, and at genome-www.stanford.edu/magic).

The flexible input format allows genes to be members of more than one group or cluster and thus does not exclude biclustering or fuzzy clustering methods. The output format is the same as the input format. The flexibility of input and output formats ensures that magic can incorporate any type of gene–gene grouping, including protein–protein interaction data, outputs of clustering methods, and sequence-based data (e.g., similar transcription factor binding sites).

magic is implemented in C++ under Linux, and a web-based user interface is under development. The implementation uses smile library and the genie modeling environment developed by the Decision Systems Laboratory of the University of Pittsburgh (www.sis.pitt.edu/~dsl).

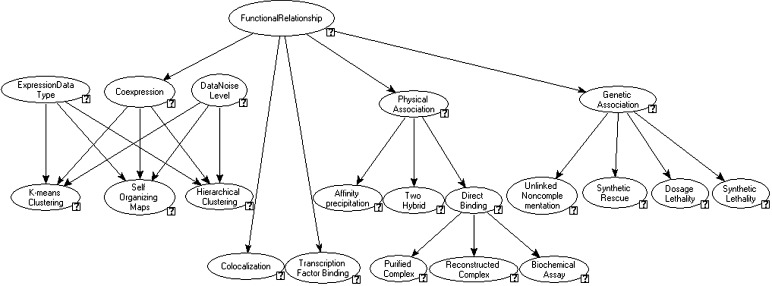
Structure of the magic Bayesian Network. To design a Bayesian network structure that adequately reflects relationships between evidence from different data types for the purpose of ensemble analysis and avoids double counting of evidence, we consulted experts in microarray analysis and yeast molecular biology. The resulting structure∥ (Fig. 1, and see Fig. 5, which is published as supporting information on the PNAS web site and at genome-www.stanford.edu/magic) combines inputs based on the type of relationship they detect (e.g., coexpression for microarray clustering methods). It makes some independence assumptions that allow for a more accurate population of the conditional probability tables based on information elicited from yeast experts. Given the relatively sparse nature of nonmicroarray experimental data, these independence assumptions are unlikely to affect the results. In addition, the different underlying principles of the methods represented in the network make their combination robust for functional inference (7, 11, 16).

Fig. 1.

General architecture of the magic Bayesian Network. A separate network is instantiated for each pair of genes by initializing bottom-level nodes with evidence. Conditional probability tables for each connection were assessed formally from yeast genetics experts. The network contains discrete nodes and uses the clustering algorithm for belief updating, as initially proposed in ref. 31. The combination of outputs of expression clustering methods is performed through a single “Coexpression” node, which allows all of the expression analysis method's outputs for one dataset to be combined based on each method's characteristics, such as robustness to noise level in data or optimality for a specific data type (e.g., temporal data). The input nodes for expression-based clustering methods (K-means Clustering, Self Organizing Maps, and Hierarchical Clustering) incorporate pairwise data binned into three categories: high, medium, and low confidence, based on Pearson correlation to the cluster centroid (see supporting information). Nonexpression-based data are incorporated through binary input nodes for colocalization data, experimentally identified transcription factor binding sites, and various experimental evidence for physical or genetic associations of two proteins. The genetic and physical relationship data are divided into experimental evidence types according to the GRID database (http://biodata.mshri.on.ca/grid/servlet/HelpHtmlPages?pageID=3; see supporting information for details).

The prior probabilities were formally assessed from seven experts in the field of yeast molecular biology.** The experts were questioned independently and displayed substantial agreement in their prior beliefs. The method of constructing Bayesian networks based on probabilities provided by experts in the field has been successfully used, for example, in the PATHFINDER Network for pathology diagnosis (the network structure and prior probabilities for PATHFINDER were based on consultations with one pathology expert; ref. 22). In the future, when a sufficient amount of functional data are available, the network priors and structure could be automatically learned (23).

Evaluation Method. To evaluate the quality of a gene grouping, we need to measure the biological relevance or accuracy of gene–gene functional pairs belonging to that gene grouping. Biological relevance is the key criterion in evaluating pairs of genes with predicted functional relationships, yet it is a difficult metric to assess. If genes i and j are predicted to have a functional relationship, but no prior biological knowledge links their functionality, is that a relevant clustering, an experimental error, or a biological discovery? Although no perfect gold standard for gene groupings exists, the curator-controlled annotation of the S. cerevisiae genome with GO terms (21, 24) provides a reflection of the current biological knowledge and thus a reasonable biological standard for the evaluation of functional pairs of S. cerevisiae genes.

GO contains three types of terms: (i) molecular function, (ii) biological process, and (iii) cellular component. GO has a hierarchical structure with multiple inheritance, and each gene (or protein) can be annotated with one or more GO terms from disparate parts of the GO tree. For the purpose of this evaluation, we focus on the biological process part of GO, which is the most relevant part of the ontology for evaluation of gene groupings based on the presence of functional relationships, because genes annotated to the same GO term from the biological process ontology are believed (in current biological literature) to be involved in the same biological process.

The hierarchical nature of GO and multiple inheritance in the GO structure can lead to evaluation problems if we consider only the particular GO term with which a gene is annotated. For example, gene i may be annotated with term g, and gene j with g's immediate ancestor, g′ (e.g., gene i is annotated with “GO:0007216: metabotropic glutamate receptor signaling pathway” and gene j is annotated with “GO:0007215: glutamate signaling pathway,” a parent node of GO:0007216). Although genes i and j are functionally similar based on their GO annotation, they are technically annotated with different GO terms. To alleviate this problem, we consider any gene annotated with GO term g to be also implicitly annotated with every ancestor of g, up to level 3 of the GO tree (with “Gene Ontology” considered level 1). On tests we found that this rule is robust to changes of the exact level of cutoff.

Because of the cost of follow-up experimental investigation, the key problem in creating biologically relevant gene groupings tends to be specificity, not sensitivity. Unfortunately, calculating specificity and sensitivity requires knowledge of the total number of true positives (TP) and true negative pairs of related genes in S. cerevisiae, numbers that are currently impossible to assess accurately. Therefore, we assess the accuracy of each method through the proportion of TP pairs in its predictions, where TP pairs are defined as pairs of genes i and j, such that genes i and j have an overlapping (explicit or implicit) GO term annotation:

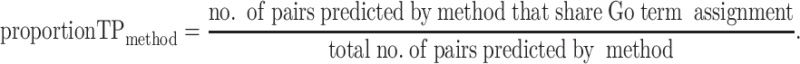The predicted pairs for each input method are available from gene–gene relationship matrices representing gene groupings, as described above.

magic integrates various gene groupings in a systematic fashion, yielding posterior probabilities for functional relationship between every pair of genes in the yeast genome. Because the stringency of magic's predictions can be controlled by varying a cutoff for the posterior beliefs sufficient to consider two genes functionally related, we can compare magic's performance at different levels of stringency to that of its input methods. We can vary the stringency of the input clustering methods by varying cutoff of score (s_{A, B}), the average correlation of two genes (A, B) to the centroid of the cluster (c) they are both members of

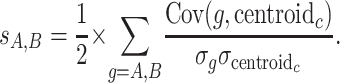Such optimization is not performed when these clustering methods are used routinely for microarray analysis. By comparing the performance of the input clustering methods and magic at each stringency level, we avoid the problem of favoring methods that predict a smaller number of pairs in this evaluation.

Results and Discussion

To illustrate the utility of magic for integrated analysis of heterogeneous biological data, we use magic to combine S. cerevisiae protein–protein interactions (from GRID; see Methods) and transcription factor binding sites (from The Promoter Database of Saccharomyces cerevisiae; see Methods) data with clustering analyses (hierarchical, self-organizing maps, and k-means) of a stress-response microarray dataset (25). We evaluate the accuracy of predicted functional pairs for magic as compared with the input clustering methods and demonstrate the utility of magic in combining heterogeneous information.

Our evaluation reflects the biological relevance of gene groupings by using GO as a gold standard. This evaluation approach is not flawless: GO may have annotation errors, and the functions of many genes in the yeast genome are unknown. The evaluation is conservative: a false positive (FP) pair of genes could represent a true error or a novel discovery. There may be some biases in the subsets of genes that are or are not currently annotated by GO terms, but there is no reason to believe these biases would affect clustering methods differently. This method therefore provides a reasonable and biologically grounded comparative evaluation framework for gene groupings.

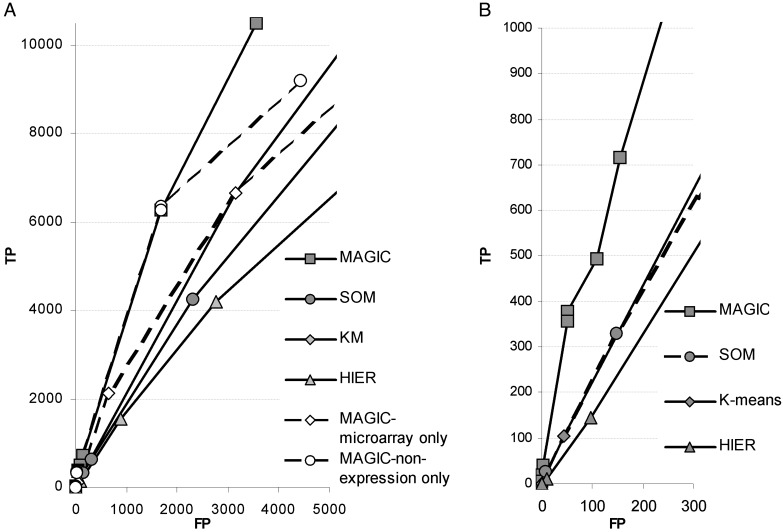
magic incorporates gene groupings based on microarray analysis with the often more accurate nonexpression-based data sources, and magic consistently increases the proportion of TP pairs when compared with its input methods (Fig. 2A). In gene function prediction, high specificity is key for creating biologically relevant gene groupings. We thus focus on the highest specificity region, where 1,000 and fewer TP pairs are predicted by each method (Fig. 2B). When we consider predictions with the highest proportion of TP pairs made by each method (when at least 100 TP pairs are predicted), magic, which uses the nonoptimized inputs, performs better than the optimized clustering methods, with a 17% increase in proportion of TP pairs over the best of the input methods and the largest number of TP pairs predicted (see Fig. 6, which is published as supporting information on the PNAS web site and at genome-www.stanford.edu/magic). This difference in performance declines at very large numbers of predicted pairs (40,000 and higher), where proportion of TP rates for all methods is around or below 50% and thus at levels not suitable for accurate gene function prediction. Thus, magic creates more biologically relevant gene groupings, with the highest improvement seen in the high-specificity region.

Fig. 2.

Tradeoff between the number of TP and FP pairs for each method. (A) magic increases the proportion of TP pairs in a broad high-specificity region compared with expression-based clustering methods, magic based on purely microarray data (magic-microarray only) or purely on nonexpression data (magic-nonexpression only). (B) Comparison in the region of highest accuracy (<1,000 TP pairs). magic predicts more TP pairs than its input methods for each number of FPs.

magic relies on microarray data (which is very sensitive but often not specific enough) and nonexpression data (which is often more specific but significantly more sparse). It is thus interesting to consider magic's performance based only on microarray data or only on nonexpression data. magic partly draws its accuracy from incorporating nonexpression experimental data in the analysis. It is thus not surprising that magic's performance without the microarray data is similar to that of the complete system for the range with <6,200 TP pairs predicted (Fig. 2 A). As the number of predictions increases further, magic application based on purely nonexpression data does not perform as well as the full version, probably because it gets close to the limit of information available from nonexpression data sources. On the other hand, when only microarray data are considered, magic improves performance over that of clustering methods for the region with small number of pairs but displays clearly lower TP rates than the full version of magic. For larger numbers of pairs (more than ≈4,000), the microarray-only method performs approximately on the same level as the clustering methods. Thus, magic builds on both types of inputs. It creates highly accurate gene groupings based largely on reliable sources of nonmicroarray experimental data (e.g., affinity precipitation). These grouping are enriched based on microarray data and other high-sensitivity methods (e.g., two-hybrid data), often with genes whose function is unknown and for which functional predictions can thus be made.

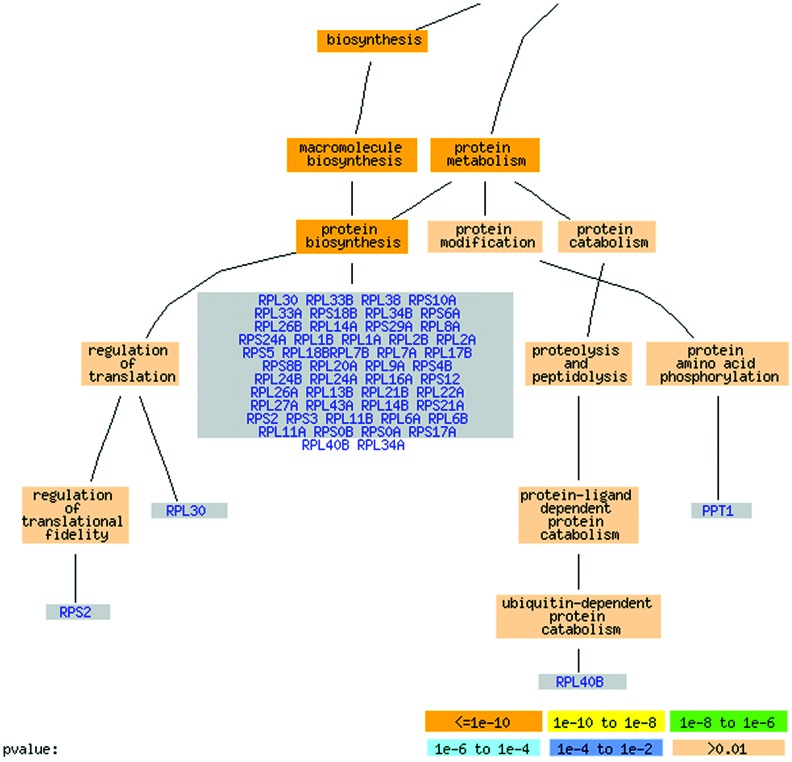
We construct groupings of genes (clusters) based on magic's pairwise output by considering all genes with functional relationship to the same gene a group (see Conversions Between Pairs and Gene Groupings in Supporting Text, which is published as supporting information on the PNAS web site). magic identifies clusters that represent the general environmental stress response described by Gasch et al. (ref. 25; repressed ribosomal genes, genes involved in RNA metabolism and protein biosynthesis, and induced genes involved in carbohydrate metabolism, protein degradation, vacuolar functions, etc.). These clusters are more specific for a particular biological process than manually chosen clusters based on hierarchical clustering. For example, magic detects a cluster of Rgt1, Snf3, and five hexose transporters induced in response to glucose (compared with a heterogeneous carbohydrate metabolism cluster based on hierarchical clustering, as described in ref. 25). The transporters are induced in response to glucose by regulator Rgt1, which in turn receives signals from Snf3, a glucose sensor in the membrane (see Table 1, which is published as supporting information on the PNAS web site and at genome-www.stanford.edu/magic). magic also identifies larger gene groupings for coherent processes involving a large number of genes, such as protein biosynthesis (Fig. 3). In the protein biosynthesis cluster, 49 of 58 known genes are annotated to protein biosynthesis. The cluster also includes 10 genes with unknown annotations that our analysis predicts may be involved in protein biosynthesis.

Fig. 3.

Protein biosynthesis group identified by magic, represented using GO Term Finder (http://genome-www4.stanford.edu/cgi-bin/SGD/GO/goTermFinder). The color of each GO term is associated with its P value, representing the level of significance of that GO term's assignment to the cluster (see http://genome-www.stanford.edu/Saccharomyces/help/goTermFinder.html). Only known genes associated with protein biosynthesis are shown. The cluster contains 49 genes annotated to protein biosynthesis and 10 unknown genes. It also includes nine genes not directly annotated to protein biosynthesis but involved in potentially related processes: three genes involved in ribosome biogenesis and assembly (RRB1, SIK1, and CBF5), two transcription-related genes (RPA49 and RPC40), two involved in budding and sporulation (BUD28 and LSG1), and PRS1, a ribose-phosphate pyrophosphokinase involved in histidine biosynthesis.

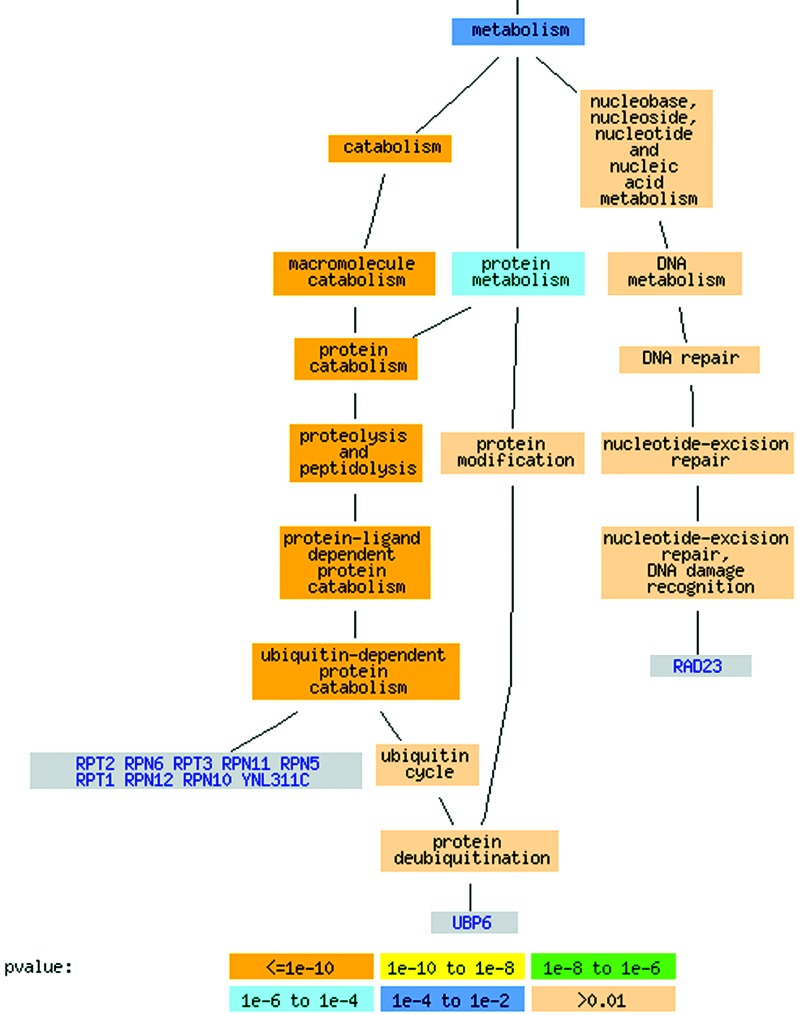
Genes involved in protein degradation are induced during the response to environmental stress. magic identifies a cluster of genes involved in ubiquitin-dependent protein catabolism, provides potential functional annotation for an ORF present in that cluster (YGL004C), and confirms the recently added annotation for YNL311C (Fig. 4). This group also includes Rad23, although its current GO annotation is to “nucleotide-excision repair, DNA damage recognition.” On examination of the literature for Rad23, we find that its involvement in DNA repair is likely due to its inhibition of the degradation of repair proteins in response to DNA damage (26). It has been shown that Rad23 physically interacts with the 26S proteasome and may also be involved in other protein degradation pathways (26). The grouping generated by magic identifies the outdated and potentially misleading annotation of Rad23.

Fig. 4.

Ubiquitin-dependent protein catabolism cluster represented using GO Term Finder (http://genome-www4.stanford.edu/cgi-bin/SGD/GO/goTermFinder). The cluster contains 12 genes. In the version of SGD annotations used for evaluation in this study, nine of the proteins are annotated to ubiquitin-dependent protein catabolism, one (RAD23) is annotated to “nucleotide excision repair,” and YNL311C and YGL004C do not have a known biological process assignment. magic predicted that YNL311C and YGL004C are likely involved in ubiquitin-dependent protein catabolism. In the most recent release of the annotation (February 2003), YNL311C has been annotated to this process. The other unknown ORF, YGL004C, is annotated as biological process unknown (not shown), but has been assigned the Saccharomyces Genome Database reserved name RPN14. This example illustrates the utility of magic as a tool to aid gene function annotation.

Thus, in addition to predicting the function of unknown genes that are found in groups with well characterized genes, magic also provides a means of quality control for the existing functional annotations of partially characterized genes. Another such example is a group that consists of three genes: BUD31, CEF1, and PRP8. Both CEF1 and PRP8 are well characterized splicing factors (27, 28). BUD31 is currently annotated to bud site selection based on a genome-wide screen for mutants defective in the bipolar budding pattern (29). However, Ni and Snyder found that several nuclear proteins, including genes involved in RNA processing, also exhibit defects in bud site selection, most likely as an indirect effect of the processing of RNA for genes directly involved in budding (29). In addition, BUD31 has a putative nuclear localization signal (ref. 30; http://us.expasy.org/cgi-bin/sprot-ft-details.pl?P25337@DOMAIN@2@11). Thus, BUD31 might be involved in RNA processing rather than directly playing a role in bud site selection. By searching for genes with annotations that do not fit with the other annotations of genes in a group, one can target particular genes that may be associated with spurious or incomplete functional information.

Conclusions and Future Work. We have shown that magic is an accurate and efficient gene function annotation tool. The system integrates heterogeneous biological information in a rigorous probabilistic fashion, leading to more biologically accurate gene groupings, which can be used for gene function prediction. magic circumvents the problem of identifying an “ideal” clustering algorithm for microarray data by incorporating outputs of several methods and incorporates the knowledge of yeast biology experts in the prior probabilities of the Bayesian framework. The flexibility of the system allows for easy inclusion of new methods and data sources, as well as data from different organisms.